3D график построить: Построить трехмерный график онлайн

Содержание

Matplotlib. Урок 5. Построение 3D графиков. Работа с mplot3d Toolkit

До этого момента все графики, которые мы строили были двумерные, Matplotlib позволяет строить 3D графики. Этой теме посвящен данный урок.

Линейный 3D-график
Точечный 3D-график
Каркасная поверхность
Поверхность

Импортируем необходимые модули для работы с 3D:

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

В библиотеке доступны инструменты для построения различных типов графиков. Рассмотрим некоторые из них более подробно.

Линейный график

Для построения линейного графика используется функция plot().

Axes3D.plot(self, xs, ys, *args, zdir=’z’, **kwargs)

xs: 1D массив
- x координаты.
ys: 1D массив
- y координаты.
zs: скалярное значение или 1D массив
- z координаты. Если передан скаляр, то он будет присвоен всем точкам графика.
zdir: {‘x’, ‘y’, ‘z’}
- Определяет ось, которая будет принята за z направление, значение по умолчанию: ‘z’.
**kwargs
- Дополнительные аргументы, аналогичные тем, что используются в функции plot() для построения двумерных графиков.

x = np.linspace(-np.pi, np.pi, 50)
y = x
z = np.cos(x)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(x, y, z, label='parametric curve')

Точечный график

Для построения точечного графика используется функция scatter().

Axes3D.scatter(self, xs, ys, zs=0, zdir=’z’, s=20, c=None, depthshade=True, *args, **kwargs)

xs, ys: массив
- Координаты точек по осям x и y.
zs: float или массив, optional
- Координаты точек по оси
  z. Если передан скаляр, то он будет присвоен всем точкам графика. Значение по умолчанию: 0.
zdir: {‘x’, ‘y’, ‘z’, ‘-x’, ‘-y’, ‘-z’}, optional
- Определяет ось, которая будет принята за z направление, значение по умолчанию: ‘z’
s: скаляр или массив, optional
- Размер маркера. Значение по умолчанию: 20.
c: color, массив, массив значений цвета, optional
- Цвет маркера. Возможные значения:
  - Строковое значение цвета для всех маркеров.
  - Массив строковых значений цвета.
  - Массив чисел, которые могут быть отображены в цвета через функции cmap и norm.
  - 2D массив, элементами которого являются RGB или RGBA.
depthshade: bool, optional
- Затенение маркеров для придания эффекта глубины.
**kwargs
- Дополнительные аргументы, аналогичные тем, что используются в функции scatter() для построения двумерных графиков.

np.random.seed(123)
x = np.random.randint(-5, 5, 40)
y = np.random.randint(0, 10, 40)
z = np.random.randint(-5, 5, 40)
s = np.random.randint(10, 100, 20)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z, s=s)

Каркасная поверхность

Для построения каркасной поверхности используется функция plot_wireframe().

plot_wireframe(self, X, Y, Z, *args, **kwargs)

X, Y, Z: 2D массивы
- Данные для построения поверхности.
rcount, ccount: int
- Максимальное количество элементов каркаса, которое будет использовано в каждом из направлений. Значение по умолчанию: 50.
rstride, cstride: int
- Параметры определяют величину шага, с которым будут браться элементы строки / столбца из переданных массивов. Параметры rstride, cstride и rcount, ccount являются взаимоисключающими.
**kwargs
- Дополнительные аргументы, определяемые Line3DCollection.

u, v = np.mgrid[0:2*np.pi:20j, 0:np.pi:10j]
x = np.cos(u)*np.sin(v)
y = np.sin(u)*np.sin(v)
z = np.cos(v)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_wireframe(x, y, z)
ax.legend()

Поверхность

Для построения поверхности используйте функцию plot_surface().

plot_surface(self, X, Y, Z, *args, norm=None, vmin=None, vmax=None, lightsource=None, **kwargs)

X, Y, Z : 2D массивы
- Данные для построения поверхности.
rcount, ccount : int
- см. rcount, ccount в “Каркасная поверхность“.
rstride, cstride : int
- см.rstride, cstride в “Каркасная поверхность“.
color: color
- Цвет для элементов поверхности.
cmap: Colormap
- Colormap для элементов поверхности.
facecolors: массив элементов color
- Индивидуальный цвет для каждого элемента поверхности.
norm: Normalize
- Нормализация для colormap.
vmin, vmax: float
- Границы нормализации.
shade: bool
- Использование тени для facecolors. Значение по умолчанию: True.
lightsource: LightSource
- Объект класса LightSource – определяет источник света, используется, только если shade = True.
**kwargs
- Дополнительные аргументы, определяемые Poly3DCollection.

u, v = np.mgrid[0:2*np.pi:20j, 0:np.pi:10j]
x = np.cos(u)*np.sin(v)
y = np.sin(u)*np.sin(v)
z = np.cos(v)
fig = plt.figure()
ax = fig. add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, cmap='inferno')
ax.legend()

P.S.

Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.

Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.

3D график по x,y,z

← →
shkeeper (2004-04-22 22:33) [0]

Очень нужно! Есть ли какой нибудь спрособ «малой кровью» построить 3Д график (по x,y,z)?
Вариант строить в Excel слишком банален и неудобен. Может кто подскажет где что мона взять?

← →
shkeeper (2004-04-22 22:33) [0]

← →
shkeeper (2004-04-22 23:15) [1]

ну и… что никто не сталкивался… это ужасно..

← →
shkeeper (2004-04-22 23:15) [1]

ну и… что никто не сталкивался… это ужасно..

← →
Yegorchic © (2004-04-22 23:19) [2]

Посмотри программу в кладовке…
как называется не помню… вроде «Математика 0.5″…
там есть построение 3D графика…

← →
Yegorchic © (2004-04-22 23:19) [2]

Посмотри программу в кладовке. ..
как называется не помню… вроде «Математика 0.5″…
там есть построение 3D графика…

← →
SergLight © (2004-04-23 10:26) [3]

TChart

←

→
SergLight © (2004-04-23 10:26) [3]

TChart

← →
Курдль © (2004-04-23 11:30) [4]

> Очень нужно! Есть ли какой нибудь спрособ «малой кровью»
> построить 3Д график (по x,y,z)?

А что Вы называете «малой кровью»? Такие проги писать — одно сплошное эстетическое удовольствие (жаль, что их редко заказывают). Все проще пареной репы — берете TImage и на его Canvas-е строите все, что заблагорассудится!

← →
Курдль © (2004-04-23 11:30) [4]

Все проще пареной репы — берете TImage и на его Canvas-е строите все, что заблагорассудится!

← →
Algol (2004-04-23 12:09) [5]

> одно сплошное эстетическое удовольствие

Я б так не сказал. Создание интерактивных графиков произвольного типа, с шаблонами, с поддержкой внедрения, да еще и 3D — задача не тривиальная, и довольно сложная.

← →
Algol (2004-04-23 12:09) [5]

> одно сплошное эстетическое удовольствие

← →
Курдль © (2004-04-23 12:12) [6]

> Я б так не сказал. Создание интерактивных графиков произвольного
> типа, с шаблонами, с поддержкой внедрения, да еще и 3D
> — задача не тривиальная, и довольно сложная.

Но для меня приятнее, чем создание каких-нить бухгалтерских интерактивных отчетов произвольного типа, с шаблонами, с поддержкой внедрения 🙂

← →
Курдль © (2004-04-23 12:12) [6]

← →
shkeeper (2004-04-23 15:20) [7]

После того как я обрал весь Инет в поисках удобного и НОРМАЛЬНОГО компонента я зациклился на TChart Pro 6.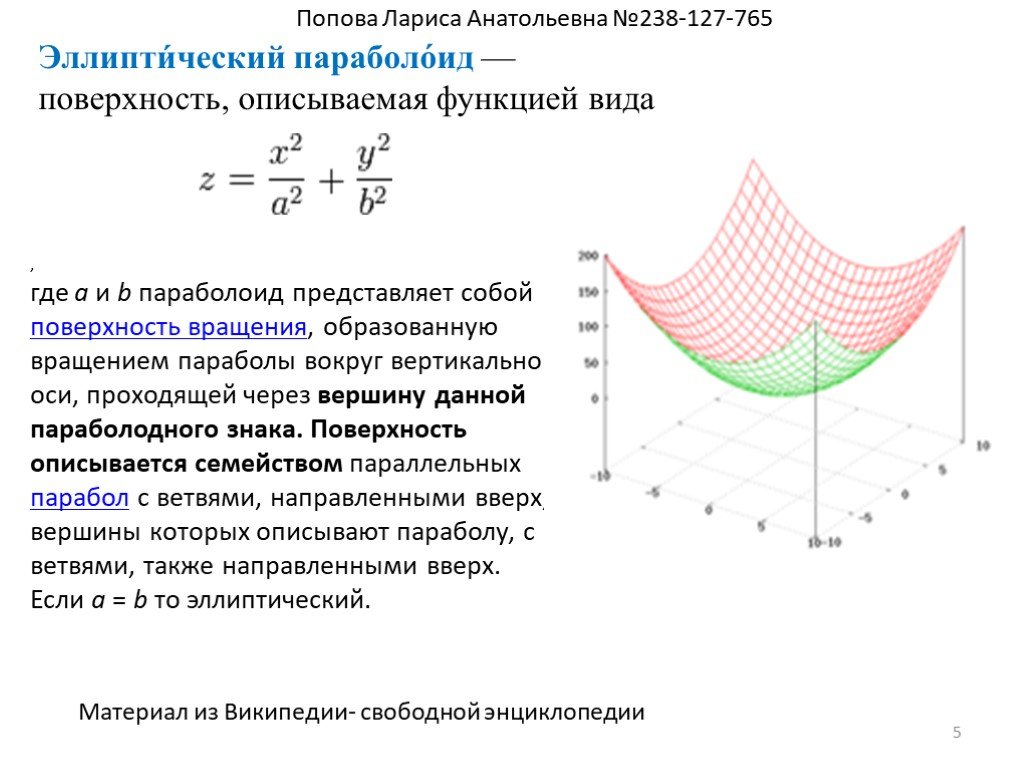 0. Но он выдает все время ошибки, избавится от них никак не могу. А посему пришел к выводу, что еще никто такого компонента не придумал, а те что есть не могут построить диаграмму по 3-м осям, если записей например больше 5000.
Так что нечего тут говорить, что это просто… было бы просто уже б кто нибудь подсказал что-то конкретоное, а все грамотные, пока по делу не начнем говорить… 🙁

← →
shkeeper (2004-04-23 15:20) [7]

После того как я обрал весь Инет в поисках удобного и НОРМАЛЬНОГО компонента я зациклился на TChart Pro 6.0. Но он выдает все время ошибки, избавится от них никак не могу. А посему пришел к выводу, что еще никто такого компонента не придумал, а те что есть не могут построить диаграмму по 3-м осям, если записей например больше 5000.
Так что нечего тут говорить, что это просто… было бы просто уже б кто нибудь подсказал что-то конкретоное, а все грамотные, пока по делу не начнем говорить. .. 🙁

← →
Курдль © (2004-04-23 15:26) [8]

> а все грамотные, пока по делу не начнем говорить… 🙁

Я Вам абсолютно грамотно подсказал, как грамотно пстроить диаграмму по 3-м осям! Надо брать и строить, а не компоненты искать!
Если медленно работает — переходите на ассемблер!
Как сделаете лучший и менее глючный, чем есть — напишите мне — я куплю за большие деньги!

← →
Курдль © (2004-04-23 15:26) [8]

← →
WebErr © (2004-04-23 16:41) [9]

Всё оч. просто:
Дано: исходный вектор P = (x, y, z), найти простейший вариант отображения на плоскость экрана.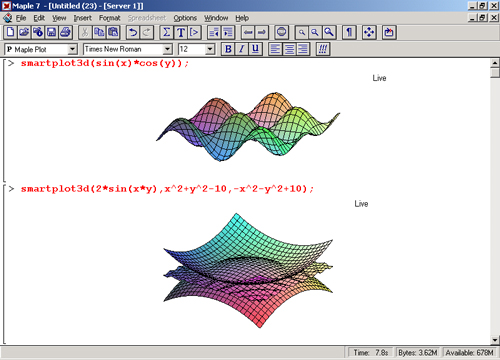
Решение:
Пусть некий объект расположен неподалёку от точки O = (0, 0, 0).
(Иначе делаем перенос координат!)
Пусть «камера» направлена в эту точку и имеет сферические координаты с углами (a, b).
Поворачиваем P, используя матрицу поворота T(a, b) =
|| cos(a) -sin(a) 0 || || sin(a)*cos(b) cos(a)*cos(b) -sin(b) || || sin(a)*sin(b) cos(a)*sin(b) cos(b) ||
Q = T*P.
Q = (X, Y, Z).
Итак мы отобразили (непроективно — это посложнее!) P на плоскость экрана.
Теперь можно сделать косметическое преобразование:
xs = X*k + x0 ys = Y*k + y0
И всё! :))))

← →
WebErr © (2004-04-23 16:41) [9]

← →
WebErr © (2004-04-23 17:03) [10]

Z координату мы используем для Z-буффера, если надо.
А при проективном преобразовании нужно знать ещё и 3-ю сферическую координату «камеры» r, т. е. C = (r, a, b) в сферических координатах.
Также надо знать длину до фокуса камеры = d.
Получаем преобразование R = R(Q), при некоем p = r/(r-Z).
xr = X*p yr = Y*p zr = r-d-Z
R = (xr, yr, zr).
Т.е. проекция применяется после поворота и перед «косметическим» масштабированием. :))))
Литература: «Программирование компьютерной графики» Виктора Порева.

← →
WebErr © (2004-04-23 17:03) [10]

Z координату мы используем для Z-буффера, если надо.
А при проективном преобразовании нужно знать ещё и 3-ю сферическую координату «камеры» r, т.е. C = (r, a, b) в сферических координатах.
Также надо знать длину до фокуса камеры = d.
Получаем преобразование R = R(Q), при некоем p = r/(r-Z).
xr = X*p yr = Y*p zr = r-d-Z
R = (xr, yr, zr).
Т.е. проекция применяется после поворота и перед «косметическим» масштабированием. :))))
Литература: «Программирование компьютерной графики» Виктора Порева.

← →
WebErr © (2004-04-23 17:06) [11]

Разумеется точки, которые после поворота получили координату Z >= r-d не отображаются на экран, т.к. находятся за камерой! :))))
Прошу послать данный материал автору сабжа! :))))

← →
WebErr © (2004-04-23 17:06) [11]

← →
WebErr © (2004-04-23 17:17) [12]

Могу ещё про вертексное построение с закраской Гуро или Фонга рассказать, но лучше сами почитайте книжку — она того стоит!!! :))))

← →
WebErr © (2004-04-23 17:17) [12]

← →
Дмитрий (2004-04-23 17:27) [13]

Компоненты есть. .. И очень даже хорошие… Просто искать надо уметь… Я бы тебе выслал одну, да она на домашнем компе висит… А его я увижу, ой, как нескоро… К сожалению не помню как зовётся…
Ещё вариант — OpenGl… Малой крови не обещаю, зато надёжно и со вкусом…

← →
Дмитрий (2004-04-23 17:27) [13]

Компоненты есть… И очень даже хорошие… Просто искать надо уметь… Я бы тебе выслал одну, да она на домашнем компе висит… А его я увижу, ой, как нескоро… К сожалению не помню как зовётся…
Ещё вариант — OpenGl… Малой крови не обещаю, зато надёжно и со вкусом…

← →
WebErr © (2004-04-23 17:27) [14]

Если что-то непонятно спрашивайте!

← →
WebErr © (2004-04-23 17:27) [14]

Если что-то непонятно спрашивайте!

← →
WebErr © (2004-04-23 17:29) [15]

> Дмитрий (23. 04.04 17:27) [13]

Это всё здорово, но всегда нужно знать как это всё работает! Это касается не только OpenGL & DirectX, но и всеми любимой VCL — WinAPI знать надо не хуже родных библиотек! :))))

← →
WebErr © (2004-04-23 17:29) [15]

> Дмитрий (23.04.04 17:27) [13]

Это всё здорово, но всегда нужно знать как это всё работает! Это касается не только OpenGL & DirectX, но и всеми любимой VCL — WinAPI знать надо не хуже родных библиотек! :))))

← →
WebErr © (2004-04-23 18:14) [16]

Кстати, если неизвесны сферические координаты камеры, а только декартовы (xc, yc, zc), то это даже лучше, тогда оператор T(a, b) считается быстрее, т. к.
< пусть rxy = sqrt(sqr(xc)+sqr(yc)),
тогда r = sqrt(sqr(r0)+sqr(zc)) >
cos(a) = yc/rxy, sin(a) = xc/rxy cos(b) = zc/r, sin(b) = rxy/r
С уважением, Керимов Владимир. (с) :)))) (спец по 3D графике)

← →
WebErr © (2004-04-23 18:14) [16]

Кстати, если неизвесны сферические координаты камеры, а только декартовы (xc, yc, zc), то это даже лучше, тогда оператор T(a, b) считается быстрее, т.к.
< пусть rxy = sqrt(sqr(xc)+sqr(yc)),
тогда r = sqrt(sqr(r0)+sqr(zc)) >
cos(a) = yc/rxy, sin(a) = xc/rxy cos(b) = zc/r, sin(b) = rxy/r
С уважением, Керимов Владимир. (с) :)))) (спец по 3D графике)

← →
WebErr © (2004-04-23 18:16) [17]

Где r = sqrt(sqr(rxy)+sqr(zc)) — расстояние от начала координат, до камеры! :))))

← →
WebErr © (2004-04-23 18:16) [17]

Где r = sqrt(sqr(rxy)+sqr(zc)) — расстояние от начала координат, до камеры! :))))

← →
WebErr © (2004-04-23 18:50) [18]

Если rxy < eps (rxy близко к нулю), то можно взять любые (a, b), в том числе и (0, 0). :))))

← →
WebErr © (2004-04-23 18:50) [18]

Если rxy < eps (rxy близко к нулю), то можно взять любые (a, b), в том числе и (0, 0). :))))

← →
csr © (2004-04-24 12:32) [19]

Давай, я те такую прогу напишу гы 😉 Это ж проще пареной репы! Математику надо было учить :). Естессно за вознаграждение! 😉

← →
csr © (2004-04-24 12:32) [19]

← →
Piter © (2004-04-24 14:01) [20]

22. 04.04 22:33
Очень нужно! …

22.04.04 23:15
ну и… что никто не сталкивался

нда..

← →
Piter © (2004-04-24 14:01) [20]

22.04.04 22:33
Очень нужно! …

22.04.04 23:15
ну и… что никто не сталкивался

нда..

Help Online — Учебные пособия — Основы 3D-графики

Все книгиКниги, не связанные с программированием　Руководство пользователя　Учебники　Быстрая справка　Справка OriginКниги по программированию　X-Function　Origin C　LabTalk Programming　Python　Python (внешний)　Automation Server　LabVIEW VI　Приложения　Разработка приложений　Code Builder　Лицензия Orlab 9　gMOCA0012

Содержание

1 Краткое описание
2 Чему вы научитесь
3 Создайте 3D-поверхность и точечную диаграмму
4 Сглаживание 3D-графика поверхности

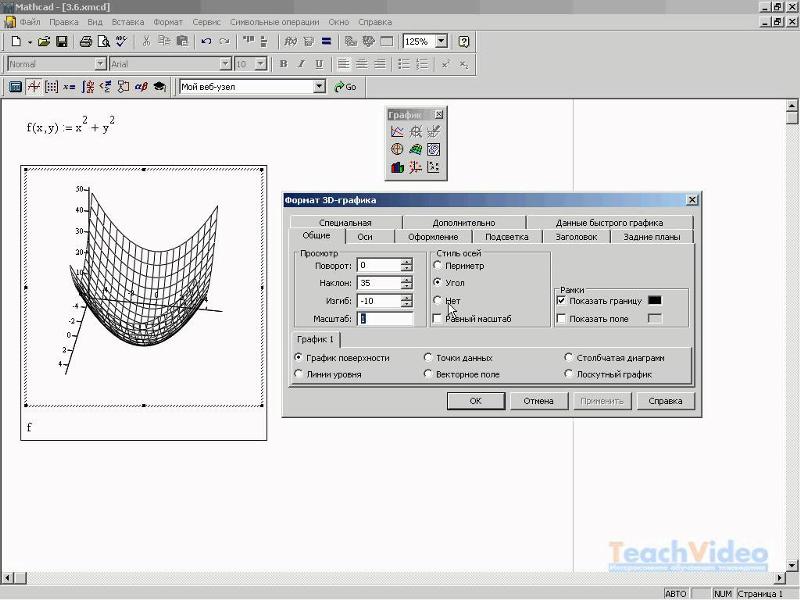
Резюме

В исходной точке контурные графики и 3D-графики, такие как графики Color Map Surface, могут быть созданы непосредственно из данных XYZ.

Но, если вы хотите построить более гладкую 3D-поверхность, настоятельно рекомендуется использовать одну из встроенных процедур построения сетки Origin для преобразования данных XYZ в матрицу.

Требуемая минимальная версия Origin: Origin 9.0 SR1

Чему вы научитесь

Из этого туториала вы узнаете, как:

Создание трехмерного графика из данных XYZ
Используйте диалоговое окно Layer Contents для добавления/удаления графика данных
Преобразование данных XYZ в матрицу
Использование диалогового окна Сведения о графике для настройки графика

Создание 3D-поверхности и точечной диаграммы

Выберите Данные: Подключиться к файлу: Текст/CSV , чтобы импортировать файл \Samples\Matrix Conversion and Gridding\XYZ Random Gaussian.dat с настройками по умолчанию.
Выделите столбец C и нажмите кнопку Z на появившейся мини-панели инструментов.
Выберите Plot > 3D : 3D ColorMap Surface , чтобы создать график 3D Colormap Surface (по умолчанию Graph2).
Щелкните правой кнопкой мыши значок слоя в левом верхнем углу графика, чтобы открыть диалоговое окно Layer Contents . В этом диалоговом окне нажмите на и выберите 3D Scatter/Trajectory/Vector из всплывающего меню.
Выберите столбец C на левой панели и нажмите кнопку Add Plot , чтобы добавить на график трехмерную точечную диаграмму. Щелкните OK , чтобы закрыть диалоговое окно.
Дважды щелкните точечную диаграмму Graph2, чтобы открыть диалоговое окно Подробности графика . На вкладке Symbol установите Shape на Ball , Size на 12 и Цвет от до Карта: Col(C) (разверните Выбор цвета, чтобы выполнить настройки на подвкладке По точкам , как показано ниже).
На вкладке Линии сброса снимите флажок Параллельно оси Z .
На вкладке Colormap щелкните заголовок столбца Fill… , чтобы открыть диалоговое окно. В диалоговом окне Fill выберите Load Palette , нажмите Select Palette и выберите из списка Rainbow .
Выберите Layer1 на левой панели диалогового окна Plot Details . На вкладке Lighting выберите Directional как Mode и выполните настройки в разделе Light Color , как показано на изображении ниже. Щелкните OK , чтобы закрыть диалоговое окно.
График должен выглядеть следующим образом:

Нажмите клавишу «S» при наведении курсора на трехмерный график openGL. Курсор будет менять режимы. Перетащите мышью или используйте клавиши со стрелками, чтобы изменить направление источника освещения.

Сглаживание трехмерной поверхности

Если вы хотите создать 3D-поверхность, которая будет более гладкой, чем приведенный выше график поверхности (созданный из данных XYZ), вы можете сначала преобразовать данные XYZ в матрицу с помощью инструмента Сетка XYZ . Затем используйте полученные данные Matrix для создания 3D-поверхности.

Повторно активируйте рабочую книгу XYZ Random Gaussian .
Выберите Worksheet: Convert to Matrix: XYZ Gridding , чтобы открыть диалоговое окно. Разверните ветвь Gridding Settings , выберите Random (Thin Plate Spline) из раскрывающегося списка Gridding Method and Parameters и задайте для Columns и Rows значение 30 . Щелкните OK , чтобы преобразовать данные XYZ в матрицу.
Активируйте матрицу и выберите Plot > 3D: 3D Colormap Surface , чтобы создать еще один трехмерный график, говорит Graph3 .
Вернитесь к Graph2 , щелкните правой кнопкой мыши любое пустое место в кадре слоя, чтобы выбрать Формат копирования: все форматы стиля в контекстном меню.
Снова переключитесь на Graph3 , щелкните правой кнопкой мыши фрейм Layer, выберите Paste Format в контекстном меню.
Выбрать Формат: График… из главного меню, чтобы открыть диалоговое окно Подробности графика . Перейдите на вкладку Colormap/Contours , снимите флажок Enable Contours :

Graph3 должен выглядеть следующим образом:

Английский | немецкий |日本語

Построение трехмерных поверхностей в Python с использованием Matplotlib

Улучшить статью

Сохранить статью

Уровень сложности: Средний
Последнее обновление: 22 авг, 2022

Читать

Обсудить

Улучшить статью

Сохранить статью

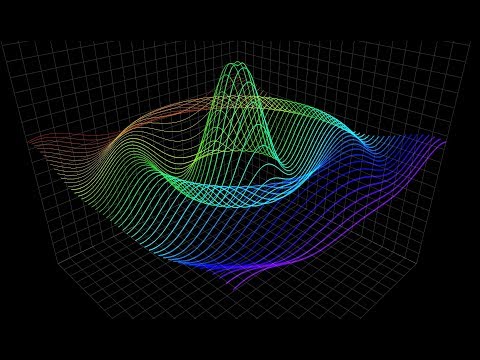
A Поверхностный график представляет собой трехмерный набор данных. Он описывает функциональную связь между двумя независимыми переменными X и Z и назначенной зависимой переменной Y, а не показывает отдельные точки данных. Это сопутствующий сюжет контурного сюжета.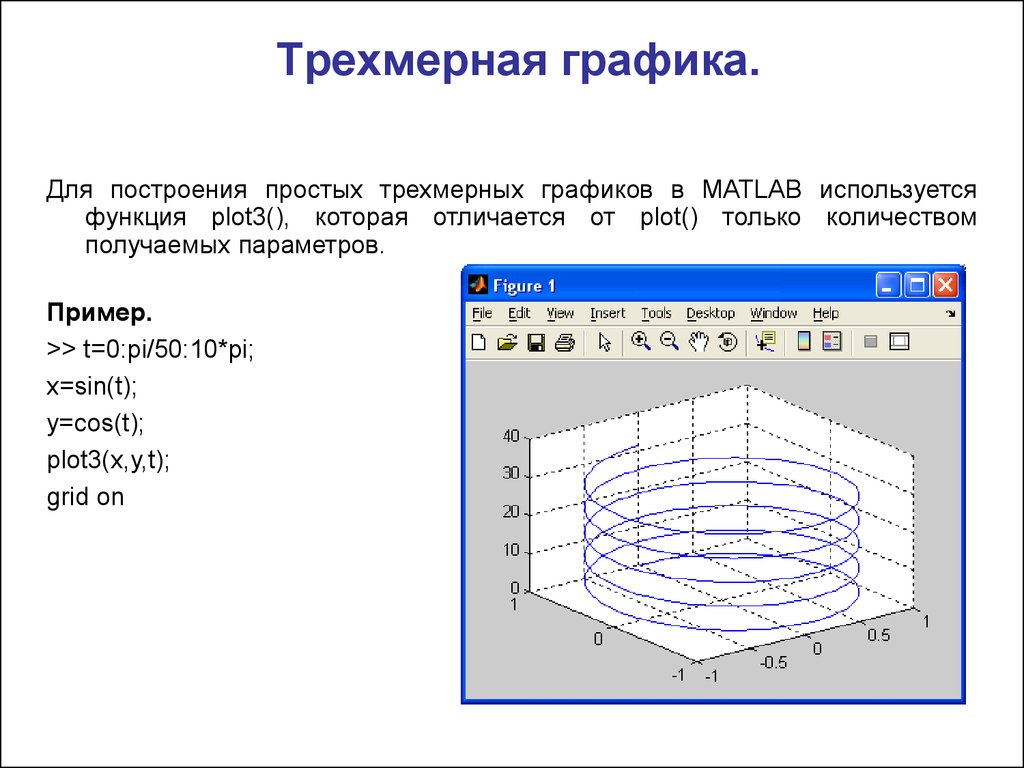 Он похож на каркасный график, но каждая грань каркаса представляет собой заполненный многоугольник. Это помогает создать топологию поверхности, которая визуализируется.

Создание 3D-графика поверхности

axes3d, присутствующий в наборе инструментов mpl_toolkits.mplot3d от Matplotlib, предоставляет необходимые функции, используемые для создания 3D-графиков поверхности. Графики поверхности создаются с помощью функции ax.plot_surface().
Синтаксис:

 ax.plot_surface(X, Y, Z)

где X и Y — двумерный массив точек x и y, а Z — двумерный массив высот. Еще несколько атрибутов функции ax.plot_surface() перечислены ниже:

Attribute	Description
X, Y, Z	2D arrays of data values
cstride	array of column stride(step size)
rstride	array of row шаг (размер шага)
счет	количество используемых столбцов, по умолчанию 50
rcount	количество используемых строк, по умолчанию 50
Color	Цвет поверхности
CMAP	Colmap для поверхности
Норма	Экспожа	максимальное значение карты
цвета лица	цвет лица индивидуальной поверхности
оттенок	оттенок цвета лица

Example: Let’s create a 3D surface by using the above function

Python3

from mpl_toolkits import mplot3d

import numpy as np

import matplotlib. pyplot as plt

x = np.outer1 - 0370 3 , 3 , 32 ), np.ones( 32 ))

y = x.copy().T

z = (np.sin(x * * 2 ) + np.cos(y * * 2 ) )

рис. = табл.рис.(рис.размер = ( 14 , 9 ))

ax = plt. axes(projection = '3d' )

AX.Plot_Surface (X, Y, Z)

PLT.Show ()

. трехмерного поверхностного графика с двухмерным контурным графиком. На этом графике 3D-поверхность окрашена так же, как 2D-контур. Части, которые находятся высоко на поверхности, имеют другой цвет, чем части, которые находятся ниже поверхности.
Синтаксис:

Surf = ax.plot_surface(X, Y, Z, cmap=, linewidth=0, antialiased=False)

Атрибут cmap= устанавливает цвет поверхности. Цветную полосу также можно добавить, вызвав fig.colorbar. The code below create a gradient surface plot:
Example:

Python3

from mpl_toolkits import mplot3d

import numpy as np

import matplotlib. pyplot as plt

x = np.outer(np.linspace( - 3 , 3 , 32 ), np.ones( 32 ))

y = x.copy().T

z = (np.sin (х * * 2 ) + np.cos(y * * 2 ) )

fig = plt.figure(figsize = ( 14 , 9 ))

ax = plt. axes(projection = '3d' )

my_cmap = plt.get_cmap( 'hot' )

surf = ax.plot_surface(x, y, z,

cmap = my_cmap,

Edgecolor = 'NONE' )

Fig.col0012

shrink = 0.5 , aspect = 5 )

ax. set_title( 'Surface plot' )

Plt.Show ()

Выход:

3D Surface Plotion, имеющий 2D -контурные запланированные участки

3D Surface Plots, участки с помощью Matplotlib, могут быть продемонстрированы на 2D. Приведенный ниже код создает трехмерные графики и визуализирует их проекцию на двухмерный контурный график:
Example:

Python3

from mpl_toolkits import mplot3d

import numpy as np

import matplotlib.pyplot as plt

x = np. outer(np.linspace( - 3 , 3 , 32 ), np.ones( 32 ))

y = x.copy().T

z = (np.sin(x * * 2 ) + np.cos(y * * 2 ) )

fig = plt.figure(figsize = ( 14 , 9 ))

ax = plt.axes(projection = '3d' )

my_cmap = plt. get_cmap( 'hot ' )

surf = ax.plot_surface(x, y, z,

rstride = 8 ,

cstride = 8 ,

alpha = 0.8 ,

cmap = my_cmap)

cset = ax.contour(x, y, z,

zdir = 'z' ,

смещение = np. min (z),

cmap = my_cmap)

cset = ax.contourf(x, y, z,

zdir = 'x' ,

offset = - 5 ,

cmap = my_cmap)

cset = ax.contourf(x, y, z,

ZDIR = 'Y' ,

Офсет = Офсет = . cmap = my_cmap)

fig.colorbar(surf, ax = ax,

shrink = 0.5 ,

aspect = 5 )

ax.set_xlabel( 'X-axis' )

ax.set_xlim( - 5 , 5 )

ax.set_ylabel( 'Y-axis' )

ax.set_ylim( - 5 , 5 )

ax.

Matplotlib. Урок 5. Построение 3D графиков. Работа с mplot3d Toolkit

3D график по x,y,z

Help Online — Учебные пособия — Основы 3D-графики

Содержание

Резюме

Чему вы научитесь

Создание 3D-поверхности и точечной диаграммы

Сглаживание трехмерной поверхности

Построение трехмерных поверхностей в Python с использованием Matplotlib

Создание 3D-графика поверхности

Python3

Python3

3D Surface Plotion, имеющий 2D -контурные запланированные участки

Python3

Добавить комментарий Отменить ответ

`Добавить комментарий Отменить ответ`