Размер матрицы все, что нужно знать | Статьи | Фото, видео, оптика
Раньше было вполне логичным, что покупая компактную камеру, вы получали небольшую матрицу, а если выбирали крупногабаритную зеркалку со сменными объективами, матрица на ней была значительно больше. Это сказывалось на качестве фотографий, поскольку чем больше матрица, тем более детализированы были изображения.
Сейчас это в принципе, тоже в какой-то мере актуально, матрица — это самая дорогая часть камеры в плане производства, и чем больше матрица, тем и камера, соответственно, дороже. Потому на дорогие камеры обычно не устанавливаются матрицы 1/2.3 дюймовые, а на дешевых, соответственно, не найти полнокадровую.
Но надо сказать, что сейчас многие производители стали предлагать компактные камеры с относительно большими матрицами, точно так же как и камеры под сменные объективы с меньшими матрицами. Так что разобраться в ситуации, пожалуй, стало сложнее. Небольшие матрицы способны отлично срабатывать в различных условиях, и даже имеют некоторые преимущества перед большими.
За последние годы и сама технология создания матриц значительно продвинулась вперед, так что сегодня большое количество предлагаемых вариантов может смутить даже опытного пользователя, что уж говорить о тех, кто приобретает первую фотокамеру. А ведь размер матрицы еще и на фокусном расстоянии сказывается, так что учитывать при выборе камеры действительно нужно очень многое.
Итак, мы решили разобраться в различных типах матриц, чтобы расставить все по местам. Но для начала нужно уточнить, как именно размер матрицы влияет на эффективное фокусное расстояние.
Фокусное расстояние
Итак, мы уже выяснили, что размер матрицы связан с фокусным расстоянием, то есть с тем, какой именно объектив подойдет вашей камере. Если вы приобретаете компактный девайс с не съемным объективом, проблема сама собой отпадает, то есть с позиции покупателя это гораздо проще. Но не просто так профессионалы выбирают именно те камеры, где объективы можно менять. Любой объектив должен иметь поле (круг) изображения или диаметр света, который существует в объективе и который покрывает размер матрицы.
Есть одно исключение, к которому мы вернемся позже.
Итак, встроенные или нет, объективы всегда помечены реальным фокусным расстоянием, а не эффективным фокусным расстоянием, которое вы получите при использовании на той или иной камере. Но проблема в том, что различные объективы с различной маркировкой могут в итоге обеспечить одно и то же фокусное расстояние для работы. Почему? Потому что они предназначены для разных матриц. Именно поэтому производители помимо маркировки указывают эквивалент, где основным расстоянием считается 35мм или полнокадровая матрица.
Вот — один из примеров: камера с матрицей меньше чем полнокадровая вполне может использоваться с 18-55мм объективом, но на деле фокусное расстояние, которое вы получите будет ближе к 27-82мм. Это все происходит потому, что матрица не достаточно велика, чтобы использовать объектив точно так же как смог бы полнокадровый. Из-за того, что периферическое пространство внутри объектива не принимается в расчет, получается тот же эффект как от использования объектива с большим фокусным расстоянием.
В компактных камерах может был установлен 19мм объектив, но из-за размера матрицы, который меньше фуллфрейма, вы получите в итоге большее фокусное расстояние, около 28мм. Точная длина определяется кроп-фактором, то есть числом, на которое нужно увеличить данное под фуллфрейм фокусное расстояние, чтобы выяснить какое расстояние получится на той или иной камере.
Размеры матриц
1/2.3 дюйма
Размер такой матрицы примерно 6.3 x 4.7 мм. Это — самая маленькая матрица, которую можно найти в современных камерах, и чаще всего — в бюджетных компактных моделях. Разрешение такой матрицы составляет, как правило, 16-20 Мп.
По крайней мере такой расклад был самым популярным какое-то время назад. Сегодня многие производители стали делать больший упор на любительские фотоаппараты с большими матрицами, так что и размер такой не так распространен как ранее.
Однако, преимущество в том, что такой размер позволяет получить компактную камеру и использовать ее с длиннофокусными объективами, например компактными суперзумами.
А большая матрица значит, что и объектив понадобится больший.
При хорошем освещении такие камеры могут предоставить неплохой результат, но для более придирчивых фотографов они точно не подойдут, поскольку при низкой освещенности будут зернить.
1/1.7 дюймов
Размер этих матриц 7.6 x 5.7мм. С такой матрицей гораздо проще выделить объект съемки из фона, и соответственно, производительность в плане деталей как в тени, так и на свету. Так что использовать их можно уже в более разнообразных условиях. Раньше такие камеры были самыми распространенными среди любителей, но сейчас их место стремительно занимают дюймовые матрицы, о которых речь и пойдет дальше.
А вот 1/1.7 дюймовые матрицы используются в некоторых относительно устаревших камерах Q-серии Pentax.
Дюймовые матрицы
Размер дюймовой матрицы 13.2мм x 8.8мм. Сегодня такие матрицы очень популярны на различных типах камер, размер позволяет им оставаться легкими и компактными. Логично, что самый популярный способ применения для дюймовой матрицы — это карманные любительские камеры, на которых объектив будет лимитирован 24-70мм или 24-100мм (если брать эквивалент 35мм).
Однако, на некоторых суперзум камерах он тоже используется?, примеры — это Sony RX10 III и Panasonic FZ2000.
Гораздо лучше дюймовая матрица нам знакома по камерам Nikon серии 1, например Nikon 1 J5 — отличной и легкой камере, которая способна делать отличные фото и снимать 4К видео. Такую матрицу можно встретить даже среди смартфонов — Panasonic CM1.
Камеры с дюймовой матрицей способны показать результаты, значительно отличные от предыдущих вариантов. Качество их будет высоким, а даже компактные камеры, как правило, имеют широкую максимальную апертуру, так что на матрицу попадает достаточно света, потому и фотографии выходят четкими и резкими.
Частично, это результат технологии, а не только размера матрицы. Матрицы современного производства могут более эффективно захватывать свет.
Микро 4/3
Матрица микро 4/3 имеет физический размер 17.3 x 13мм. Этот формат используется в компактных зеркалках и беззеркалках Olympus и Panasonic. Они ненамного больше по размеру, чем дюймовые матрицы, но меньше чем APS-C, речь о которых пойдет ниже.
По сути, микро 4/3 — это четверть размера полнокадровой матрицы, так что считать для нее активное фокусное расстояние предельно просто: достаточно умножить фокусное расстояние на 2.
Иными словами, 17мм объектив на камере с матрицей микро 4/3 обеспечит фокусное расстояние такое же, как 34мм объектив на полнокадровой матрице. По аналогии, 12-35мм даст 24-70мм и так далее.
На камере Lumix DMC-LX100 используется матрица микро 4/3 разрешением 12.8 Мп. Это — одна из компактных цифровых камер, которые обладают большим количеством функций и небольшим размером. Камера оснащена объективом Leica с фокусным расстоянием 24-75мм.
APS-C
Средний физический размер такой матрицы 23.5 x 15.6мм. Такая матрица используется на зеркальных камерах для начинающих и любительских камерах, а сейчас и на многих беззеркалках. Матрица APS-C обеспечивает отличный баланс между качеством изображения, размером и вариативностью в плане совместимости с различными объективами.
Не все APS-C матрицы одинаковы по размеру, ведь это зависит от производителя тоже.
Например, матрицы APS-C на камерах Canon физически немного меньше чем те, что установлены в Nikon и Sony, таким образом ее кроп-фактор равен 1.6x, а не 1.5x. В любом случае, APS-C — это всегда отличный вариант и профессиональные фотографы нередко предпочитают его для съемок природы и спортивных мероприятий, потому что благодаря кроп-фактору появляется возможность “приблизиться” к объекту съемки имеющимся объективом.
APS-C доступны на некоторых компактных камерах, например Fujifilm X100F, это обеспечивает высокое качество для фотографий на портативных камерах, особенно в комплекте с объективами с постоянным фокусным расстоянием. 23мм объектив на Fujifilm X100F, имеет широкую максимальную апертуру, потому с помощью этой камеры можно без труда добиться узкой глубины резкости.
APS-H
Размер матриц APS-H как правило равен 26.6 x 17.9мм. Сегодня этот формат практически не встречается, и ассоциируется только с устаревшими моделями Canon EOS-1D (EOS-1D Mark III и Mark IV).
Сейчас, правда, в этой серии используются фуллфреймы.
Поскольку APS-H больше чем APS-C, но меньше полнокадровой матрицы, кроп-фактор, соответственно равен 1.3х, потому 24мм объектив обеспечит на такой камере фокусное расстояние приблизительно 31мм.
Одна из последних фотокамер, где можно встретить такую матрицу — это Sigma sd Quattro H. Однако и Canon решили не отказываться от APS-H совсем, и предпочли применить эту матрицу для камер наблюдения, а не для зеркальных фотоаппаратов.
Фуллфрейм
36 x 24мм она же фуллфрейм, она же полнокадровая матрица и она же примерно такая же по размеру как негатив пленочной фотографии. Используются полнокадровые матрицы на любительских и профессиональных камерах и считаются самым удобным вариантом для съемок. Размер такой матрицы позволяет ей принимать на себя больше света, вследствие чего и фото получаются выше по качеству чем с меньшими матрицами. Соответственно, и когда речь идет о количестве пикселей, выбор больше. А разрешение полнокадровых матриц варьируется от 12 до 50Мп.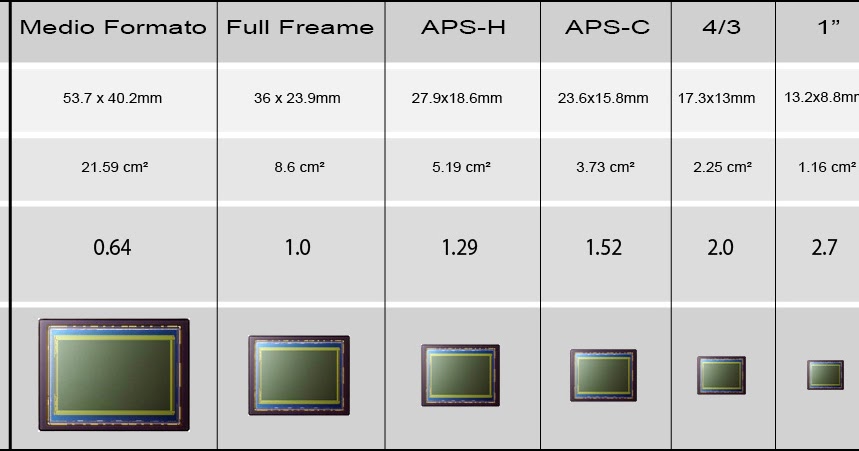
Кроп-фактор, конечно, в случае с полнокадровой матрицей значения не имеет, так как маркировка объектива будет соответствовать активному фокусному расстоянию. Однако же, некоторые объективы, созданные под APS-C матрицы все равно можно использовать с фуллфреймами, но разрешение будет ограничено (камера обрежет углы, чтобы избежать виньетирования). Но проверять совместимость, разумеется, нужно всегда, иначе есть риск повредить зеркало.
Средняя (медиум) матрица
44мм x 33мм — размер такой матрицы. Это, очевидно, больше фуллфрейма и с момента появления такие матрицы вызвали оживленный интерес и дискуссии. Они использованы в камерах Fujifilm GFX 50S, Hasselblad X1D и Pentax 645Z, последняя немного старше остальных. Применяются они в основном, исключительно профессиональными фотографами в силу цены таких камер и их специфики.
Не факт, что на этом развитие матриц как таковых остановится, но пока что это — все доступные на рынке типы матриц, а какая подойдет для ваших фото интересов, решать только вам.
Микра 4/3 или полный кадр? мифы сектантов — Сайт профессионального фотографа в Киеве
По поводу микры 4/3 у меня полностью сформированное мнение, которое я подробно изложил в этой статье. Тем не менее, забавно смотреть видео, где кто-то ещё пытается доказывать, что в ней есть какой-то смысл. Olympus продал фото-подразделение, а Panasonic на микру забил и штампует полнокадровые камеры одну за другой. О чём можно ещё говорить? Но говорят же ещё…и что же говорят?
Какой смысл в покупке фотоаппарата на системе микро 4/3 в 2020 году?
В общем-то никакого. Сделаю небольшое отступление.
Я обнаружил, все ролики про микру имеют нечто общее: в них постоянно оправдываются и доказывают, что эти камеры не такие плохие, как кажется. Прям наблюдается некоторый комплекс неполноценности — у нас маленький…сенсор, но мы ещё огого и всем покажем. В каждом ролике различные адепты микры стараются как-то оправдать маленький размер сенсора их камер и объяснить, что они в чём-то не уступают полному кадру и даже как-то его превосходят.
Этот перечень я взял из вышеуказанного видео. Эти тезисы так или иначе воспроизводятся и во всех продающе-пропагандистких роликах про микру 4/3.
Преимущества микры 4/3 над полным кадром
- Стоимость
Фотоаппараты на системе микра 4/3 стоят так же, как и кроп-камеры, и как полнокадровые (модели начального и среднего уровня). Olympus OM-D E-M1 Mark II стоит аналогично Canon 6D mark II. Olympus OM-D E-M10 Mark III стоит аналогично Canon m50 или 800D. Если с тушками всё ясно, то с оптикой сектанты прибегают к уловкам. Самая прямолинейная и наглая из них — сравнивать объективы с f2.8 на микре и на полном кадре. Это чушь полнейшая. Подробней об этом напишу ниже в разделе про вес и габариты.
- Глубина резкости
Странно приводить меньшую глубину резкость как преимущество. Обычно в таких случаях адепты данной секты вещают, что ваши объекты всегда будут резкими и не будут выпадать из грипа, как это бывает на полном кадре. Часто упоминают предметную съёмку, где микра на той же диафрагме обеспечит вам более резкие контуры небольших предметов — и это правда. Но забывают упомянуть о другом. На полном кадре или кропе вы можете больше поджать диафрагму до наступления эффектов диафракции и получить тоже самое и даже больше. Больше в том плане, что микра 4/3 очень слабая система по части передачи текстур и полутонов. Также эта система сильно ограничена в разрешении матриц. Если современные APS-C камеры могут уверенно выдавать 24-26МП и такая картинка смотрится хорошо даже с приближением, то 16-20МП на микре 4/3 приближать не стоит, ведь изображение шумит даже на базовых ISO, а детализация оставляет желать лучшего (если вам есть, с чем сравнивать).
Ещё касательно глубины резкости…на полном кадре вы ей управляете и у вас выбор. Хотите, чтоб человек в кадре был полностью резким при f1.4 на полном кадре? Ну так сделайте несколько шагов назад и будет он резким, даже на f1.4. Меня возмущает откровенная ложь и подмена понятий при разговорах об этих уже неактуальных фотоаппаратах на микре 4/3. На грип влияет не только размер матрицы. Существует 5 факторов, определяющих глубину резкости. Но амбассадоры микры то ли об этом не знают, то ли сознательно вешают людям лапшу на уши.
- Достаточность
Это вообще самый забавный и, на самом деле, сильный аргумент. Его нельзя никак оценить и сопоставить в отличии от всех других пунктов. Он целиком и полностью субъективный. Что означает « достаточность«? Я несколько раз перефразирую этот тезис: мне и так нравится; никто не увидит разницы; разница есть, но не существенна; моим клиентам и так нравится. С такими вещами можно спорить бесконечно, так как против утверждения — я купил и мне достаточно — не попрёшь.
Тут можно сказать, что большинству фотографов, всё таки этого недостаточно, раз микра 4/3 так стремительно потеряла рыночную долю. Ещё по поводу «я купил и мне достаточно» могу добавить, что зачастую у таких людей просто нет опыта съёмки на полный кадр или обычный кроп. Не надо опираться на тесты в интернете, где вам показывают бок о бок две фотографии и говорят, что вот — разницы почти нет.Такие тесты не отображают реального состояния вещей. Постарайтесь поснимать сами — только так вы сможете адекватно сравнить различные камеры. Процитирую знакомого, снимающего на Panasonic S1:
- Размеры и вес
Вес камеры Olympus OM-D E-M1 Mark II (микра 4/3) составляет 574гр, вес Canon RP (полный кадр) 485гр, вес Sony A7C (полный кадр) 509гр. Продолжать?
Ок, продолжим по объективам. На этом этапе свидетели микры обожают брать в пример полнокадровые 24-70mm f2.
8 (~900гр) или 70-200mm f2.8 (1.3кг). Удобно тыкать пальцем в топовые и самые тяжёлые и громоздкие объективы. Потом они сравниваются с такими объективами, как Olympus M.Zuiko Digital ED 12-40mm F2.8 PRO (382гр) или Olympus 40-150mm f/2.8 PRO (800гр). Мнимый выигрыш по весу в полтора-два раза. И тут я хочу сказать стоп и разобраться в ситуации. Во-первых, это не эквивалентные объективы и их нельзя сравнивать ( но это очень любят делать адепты описываемой секты). Диафрагма f2.8 на полном кадре и на микре даст вам одинаковую экспозицию — это так. Но глубина резкости будет абсолютно разная. Картинка на 12-40mm F2.8 на микре и на 70-200mm f2.8 просто несопоставима. Если выбирать сопоставимые объективы, то нужно сравнивать объектив с f5.6 на полном кадре и объектив с f2.8 на микре. Если взять полнокадровый зум 70-200mm f4, то у него вес уже около 700грамм и он уже весит МЕНЬШЕ, чем даже не аналогичный Olympus 40-150mm f/2.8 PRO (800гр). Только полнокадровый объектив 70-200 f4 не только весит меньше, но ещё и стоит ощутимо меньше, чем не аналогичный 40-150mm f/2.
8. Картинка на 70-200мм будет лучше по всем параметрам.
Что ещё не важно?
Выше я прошёлся по аргументам из видео Робина Вонга. Но они не исчерпывающие. Также Свидетели Превосходства Микры 4/3 любят порассказывать о различных технологических преимуществах их фотоаппаратов. Выглядит со стороны это нелепо — когда в ролике вам 20 минут сравнивают размер буфера при скоростной съёмке, тип SD карт (I или II), степень пыле-влагозащиты и прочие параметры, которые реально ни на что не влияют. Но задача таких видео создать у зрителя впечатление, что микра по большому количеству каких-то параметров превосходит другие камеры. И нужно отдельно, конечно же, помолиться Великому Матричному Стабу, который решает ВСЕ проблемы криворуких фотолюбителей. Мне досадно только, что адепты данной секты не хотят и слышать даже о существовании такой вещи, без которой серьёзные фотосъёмки не обходятся, а именно — о штативе.
Да и в целом создаётся ощущение, что подавляющее количество людей с такими фотоаппаратами не снимает вовсе, а только занимается доказательствами состоятельности их системы в комментариях.
Итого
Причину истинной популярности бренда Olympus я вижу больше в плоскости истории, нежели технологий. Кстати, надо также помнить, что на просторах СНГ эти камеры не столь популярны, как на их родине — Японии.
Olympus — компания, которой в 2019 году исполнилось 100 лет. Она — часть культуры страны восходящего солнца. В 1963 году была выпущена легендарная компактная камера Olympus Pen. Это была предтеча современной урезанной матрицы. Цифровая версия этой камеры увидела свет в 2016 году. Но наводнить рынок своими фотоаппаратами Olympus успели несколько раньше — на расцвете эры цифровых фотоаппаратов.
Есть категория людей, покупающих камеры исходя из лояльности к бренду, а не из рациональных соображений. Именно на этом, я считаю, и держится эта система микра 4/3. Ведь объективных преимуществ перед кроп-фотоаппаратами или полнокадровыми у неё нет. Людям, желающим просто купить хороший фотоаппарат, к рассмотрению не рекомендуется.
Декабрь 2020
Статья Микра 4/3 против кропа APS-C: подробный разбор
линейная алгебра.
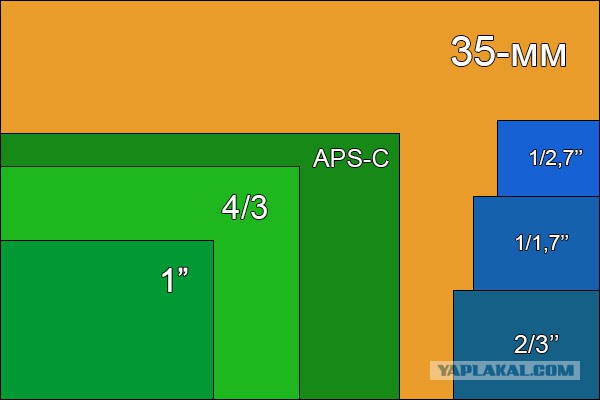Найдите матрицу 4×3 B такую, что AB = IЗадать вопрос
спросил
Изменено 5 лет, 11 месяцев назад
Просмотрено 4к раз
$\begingroup$ 93$, так как столбцов больше, чем строк. Но я не могу понять, как найти матрицу $\bf B$, потому что я не могу реализовать «суперрасширенную» матрицу и выполнить исключение Гаусса-Жордана. Похоже, мне нужно что-то сделать с 4-м столбцом $\bf A$ и 4-й строкой $\bf B$. Что вы думаете?
Спасибо!
- линейная алгебра
- матрицы
$\endgroup$
2
$\begingroup$
Вы можете использовать метод расширенной матрицы!
\начать{выравнивать}
\left[\begin{массив}{cccc|ccc}
1 и 1 и 1 и 1 и 1 и 0 и 0 \\
0 и 1 и 1 и 0 и 0 и 1 и 0 \\
0 и 0 и 1 и 1 и 0 и 0 и 1
\конец{массив}\справа]
&\к
\left[\begin{массив}{cccc|ccc}
1 и 1 и 0 и 0 и 1 и 0 и -1 \\
0 и 1 и 0 и -1 и 0 и 1 и -1 \\
0 и 0 и 1 и 1 и 0 и 0 и 1
\конец{массив}\справа]
\\&\к
\left[\begin{массив}{cccc|ccc}
1 и 0 и 0 и 1 и 1 и -1 и 0 \\
0 и 1 и 0 и -1 и 0 и 1 и -1 \\
0 и 0 и 1 и 1 и 0 и 0 и 1
\конец{массив}\справа]
\end{выравнивание}
Теперь левая часть представляет собой уравнения, а каждый столбец в правой части представляет собой постоянные члены в линейной системе.
Например, первая система $$ \begin{случаи} х_1+х_4=1\\ х_2-х_4=0\\ х_3+х_4=0 \end{случаи} $$ поэтому первый столбец правой инверсии равен (выбор $x_4=0$) $$ \begin{bmatrix}1\\0\\0\\0\end{bmatrix} $$ Таким образом, правый обратный $$ \begin{bматрица} 1 и -1 и 0 \\ 0 и 1 и -1 \\ 0 и 0 и 1 \\ 0 и 0 и 0 \end{bmatrix} $$
$\endgroup$
$\begingroup$
- Одним из способов сделать это является продукты Кронекера 93$.
Заметим, что $e_2 = a_2 — a_1$ и $e_3 = a_3 — a_2$, где $e_i$ — $i$-й стандартный единичный вектор. Затем, полагая $B = \begin{bmatrix} 1 и -1 и 0 \\ 0 и 1 и -1 \\ 0 и 0 и 1 \\ 0 и 0 и 0 \end{bmatrix}$, имеем \начать{выравнивать} АБ =& \begin{bматрица} а_1 и а_2 и а_3 и а_4 \end{bmatrix} \begin{bматрица} 1 и -1 и 0 \\ 0 и 1 и -1 \\ 0 и 0 и 1 \\ 0 и 0 и 0 \end{bmatrix} \\ =& \begin{bmatrix} а_1 & -а_1 + а_2 & — а_2 + а_3 \end{bматрица} \\ =& \begin{bmatrix} е_1 и е_2 и е_3 \end{bматрица} \\ =& I_3.
\end{выравнивание}
\end{выравнивание}$\endgroup$
2
$\begingroup$
B — матрица 4*3. мы найдем столбцы B, используя тот факт, что столбцы AB являются линейными комбинациями столбцов A с элементами столбцов B.
$\\1\begin{bmatrix}
1\\
0\\
0
\end{bmatrix}+0\begin{bmatrix}
1\\
1\\
0
\end{bmatrix}+0\begin{bmatrix}
1\\
1\\
1
\end{bmatrix}+0\begin{bmatrix}
1\\
0\\
1
\end{bmatrix}=\begin{bmatrix}
1\\
0\\
0
\end{bmatrix}$ Таким образом, первый столбец B задается как $ \begin{bmatrix}
1\\
0\\
0\\
0
\end{bmatrix}$
аналогично $ \\-1\begin{bmatrix}
1\\
0\\
0
\конец{bmatrix}+1\begin{bmatrix}
1\\
1\\
0
\end{bmatrix}+0\begin{bmatrix}
1\\
1\\
1
\end{bmatrix}+0\begin{bmatrix}
1\\
0\\
1
\end{bmatrix}=\begin{bmatrix}
0\\
1\\
0
\end{bmatrix}$, так что второй столбец B задается $\begin{bmatrix}
-1\\
1\\
0\\
0
\end{bmatrix}$
$\\0\begin{bmatrix}
1\\
0\\
0
\end{bmatrix}-1\begin{bmatrix}
1\\
1\\
0
\конец{bmatrix}+1\begin{bmatrix}
1\\
1\\
1
\end{bmatrix}+0\begin{bmatrix}
1\\
0\\
1
\end{bmatrix}=\begin{bmatrix}
0\\
0\\
1
\end{bmatrix}$ Таким образом, третий столбец B задается $\begin{bmatrix}
0\\
-1\\
1\\
0
\end{bmatrix}$
$B=\begin{bmatrix}
1 &-1 &0 \\
0& 1 &-1 \\
0& 0 & 1 \\
0 и 0 и 0
\end{bmatrix}$.
Обратите внимание, что матрица B не уникальна.
$\endgroup$
R Матрица — Учим на примере
Что такое матрица?
Матрица — это набор элементов одного типа, расположенных в двумерном макете.
В двух словах, матрица — это просто двумерный вектор.
При использовании R вы часто будете сталкиваться с четырьмя основными типами матриц, а именно. логический, символьный, целочисленный и двойной (часто называемый числовым).
Создать матрицу
Вы можете создать матрицу, используя функцию matrix() и указав данные и количество строк и столбцов для создания матрицы.
# Создать числовую матрицу
m <- матрица (1:6, nrow=2, ncol=3)
м
[1] [2] [3]
[1,] 1 3 5
[2,] 2 4 6
Матрица также может содержать символьные значения.
# Создать матрицу символов
буквы <- c("a","b","c","d","e","f")
m <- матрица (буквы, nrow=2, ncol=3)
м
[1] [2] [3]
[1,] "а" "в" "е"
[2,] "б" "д" "ф"
Необязательно указывать и ncol, и nrow.
Если вы укажете один, R автоматически узнает, каким должен быть другой.
m <- матрица(1:6, nrow=2)
м
[1] [2] [3]
[1,] 1 3 5
[2,] 2 4 6
По умолчанию матрица заполняется столбец за столбцом. Установив byrow=TRUE , вы можете заполнить матрицу построчно .
m <- матрица(1:6, nrow=2, ncol=3, byrow=TRUE)
м
[1] [2] [3]
[1,] 1 2 3
[2,] 4 5 6
Объединение векторов в матрицу
Вы также можете создать матрицу, используя функции cbind() и rbind() . Однако имейте в виду, что связываемые векторы должны быть одинаковой длины и одного типа.
v1 <- с(1, 2, 3) v2 <- с(4, 5, 6) v3 <- с(7, 8, 9) rbind(v1, v2, v3) [1] [2] [3] v1 1 2 3 v2 4 5 6 v3 7 8 9
Функция cbind() делает что-то подобное. Он связывает векторы как столбцы матрицы.
v1 <- с(1, 2, 3)
v2 <- с(4, 5, 6)
v3 <- с(7, 8, 9)
cbind(v1, v2, v3)
v1 v2 v3
[1,] 1 4 7
[2,] 2 5 8
[3,] 3 6 9
Изменить размер матрицы
С помощью функции dim() можно получить размер матрицы, не глядя на структуру.
# Печать размерности матрицы m <- матрица (1:6, nrow=2, ncol=3) тусклый (м) [1] 2 3
Функцию dim() также можно использовать для установки размерности матрицы.
# Изменить размерность матрицы
# определить матрицу 2x3
m <- матрица (1:6, nrow=2, ncol=3)
м
[1] [2] [3]
[1,] 1 3 5
[2,] 2 4 6
# сделать это 3x2
тусклый (м) <- с (3,2)
м
[1] [2]
[1,] 1 4
[2,] 2 5
[3,] 3 6
# делаем 1x6
тусклый (м) <- с (1,6)
м
[1] [2] [3] [4] [5] [6]
[1,] 1 2 3 4 5 6
Именование строк и столбцов матрицы
R позволяет назначать описательные имена строкам и столбцам матрицы. Это полезно для подмножества и печати матрицы.
Это можно сделать, назначив атрибуту dimnames список из двух элементов, содержащих имена строк и столбцов.
# Назначить имена строкам и столбцам
m <- матрица (1:6, nrow=2, ncol=3)
dimnames(m) <- list(c("r1","r2"), c("c1","c2","c3"))
м
с1 с2 с3
р1 1 3 5
г2 2 4 6
Вы даже можете назвать строки и столбцы при создании матрицы, передав аргумент dimnames.
# Именование строк и столбцов при создании матрицы
m <- matrix(1:6, nrow=2, ncol=3, dimnames=list(c("r1","r2"), c("c1","c2","c3")))
м
с1 с2 с3
р1 1 3 5
г2 2 4 6
Используя функции rownames() и colnames() , вы можете отдельно назначать имена строк и имена столбцов.
# Назначить имена строкам и столбцам отдельно
m <- матрица (1:6, nrow=2, ncol=3)
имена строк (m) <- c ("r1", "r2")
colnames(m) <- c("c1","c2","c3")
м
с1 с2 с3
р1 1 3 5
г2 2 4 6
Вы можете использовать одни и те же функции dimnames() , colnames() и rownames() для печати имен столбцов и имен строк.
# вывести имена столбцов имена столбцов (м) [1] "с1" "с2" "с3" # вывести имена строк имена строк (м) [1] "р1" "р2" # напечатать оба имена (м) [[1]] [1] "р1" "р2" [[2]] [1] "с1" "с2" "с3"
Подмножество матриц
В R подмножество элементов из матриц очень похоже на подмножество элементов из векторов.
Единственное отличие состоит в том, что теперь вам нужно указать позицию строки и столбца в порядке [строка, столбец] .
Подмножество положительным целым числом
Подмножество с положительными целыми числами возвращает элементы в указанных позициях.
m <- матрица(1:9, nrow=3, ncol=3)
м
[1] [2] [3]
[1,] 1 4 7
[2,] 2 5 8
[3,] 3 6 9
# подмножество для 2-й строки
м[2,]
[1] 2 5 8
# подмножество для 3-го столбца
м[3]
[1] 7 8 9
# выбрать один элемент
м[2,3]
[1] 8
# подмножество для строк 1 и 2, но сохранить все столбцы
м[1:2,]
[1] [2] [3]
[1,] 1 4 7
[2,] 2 5 8
# подмножество для строк и столбцов
м[1:2,2:3]
[1] [2]
[1,] 4 7
[2,] 5 8
# использовать вектор для подмножества
м[1:2,с(1, 3)]
[1] [2]
[1,] 1 7
[2,] 2 8
При поднаборе одной строки или столбца результатом всегда будет вектор. Чтобы избежать этого, вы можете установить аргумент drop равным FALSE.
m <- матрица(1:9, nrow=3, ncol=3)
м
[1] [2] [3]
[1,] 1 4 7
[2,] 2 5 8
[3,] 3 6 9
# упрощает вывод в вектор
м[ 2]
[1] 4 5 6
класс (м [ 2])
[1] "целое число"
# сохраняет вывод в виде матрицы
м[ 2, падение = ЛОЖЬ]
[1]
[1,] 4
[2,] 5
[3,] 6
класс (м [ 2, падение = ЛОЖЬ])
[1] «матрица»
Подмножество с отрицательным целым числом
Подмножество с отрицательными целыми числами будет опускать элементы в указанных позициях.
m <- матрица(1:9, nrow=3, ncol=3)
м
[1] [2] [3]
[1,] 1 4 7
[2,] 2 5 8
[3,] 3 6 9
# опустить 2-ю строку
м[-2,]
[1] [2] [3]
[1,] 1 4 7
[2,] 3 6 9
# опустить 3-ю колонку
м[-3]
[1] [2]
[1,] 1 4
[2,] 2 5
[3,] 3 6
# опустить 2-ю строку и 3-й столбец
м[-2,-3]
[1] [2]
[1,] 1 4
[2,] 3 6
Подмножество логических значений
Подмножество логических значений вернет элементы, для которых соответствующее логическое значение равно ИСТИНА.
m <- матрица(1:9, nrow=3, ncol=3)
м
[1] [2] [3]
[1,] 1 4 7
[2,] 2 5 8
[3,] 3 6 9
# выбрать элементы, у которых соответствующее логическое значение равно TRUE
m[c(ИСТИНА,ЛОЖЬ,ИСТИНА),c(ИСТИНА,ИСТИНА,ЛОЖЬ)]
[1] [2]
[1,] 1 4
[2,] 3 6
# выбрать элементы больше 5
м [м > 5]
[1] 6 7 8 9
# выделяем четные элементы
м[м %% 2 == 0]
[1] 2 4 6 8
Подмножество по именам
Подмножество с именами вернет элементы с совпадающими именами.
m <- матрица(1:9, nrow=3, ncol=3)
dimnames(m) <- list(c("r1","r2","r3"), c("c1","c2","c3"))
# подмножество для 2-й строки
м["r2",]
с1 с2 с3
2 5 8
# подмножество для 3-го столбца
м["с3"]
р1 р2 р3
7 8 9
# подмножество для 1-й и 3-й строки, но сохранить все столбцы
м[с("r1","r3"),]
с1 с2 с3
р1 1 4 7
р3 3 6 9
# выбрать один элемент
м["r2","c3"]
[1] 8
Добавление новых строк и столбцов в матрицу
Вы также можете использовать функции cbind() и rbind() для добавления новых строк и столбцов в матрицу.
Однако имейте в виду, что добавляемые векторы должны быть одинаковой длины и одного типа.
m <- матрица(1:6, nrow=2, ncol=3)
м
[1] [2] [3]
[1,] 1 3 5
[2,] 2 4 6
# добавить новый столбец
cbind(м, с(7,8))
[1] [2] [3] [4]
[1,] 1 3 5 7
[2,] 2 4 6 8
# добавить новую строку
rсвязать(м, с(10,20,30))
[1] [2] [3]
[1,] 1 3 5
[2,] 2 4 6
[3,] 10 20 30
Изменение элементов матрицы
Изменение элемента матрицы довольно просто. Получите доступ к элементу с помощью оператора [] и просто присвойте новое значение.
m <- матрица(1:6, nrow=2, ncol=3)
# изменить один элемент
м[1,2] <- 99
м
[1] [2] [3]
[1,] 1 99 5
[2,] 2 4 6
# изменить вторую строку
м[2,] <- с(10,20,30)
м
[1] [2] [3]
[1,] 1 99 5
[2,] 10 20 30
# изменить элементы менее 5
м[м > 5] <- 0
м
[1] [2] [3]
[1,] 1 0 5
[2,] 0 0 0
Операции с матрицами
Наиболее мощной функцией R является простота выполнения операций с матрицами. Поскольку большая часть статистики зависит от матричных операций, R выполняет их простым и оптимизированным способом:
- Транспонирование матрицы
- Создание единичной матрицы
- Скалярное кратное матрицы
- Сложение и вычитание матриц
- Умножение матриц
- Матрица инверсия
Транспонирование матрицы
Транспонирование матрицы — это просто перевернутая версия исходной матрицы, полученная путем замены строк столбцами.
Чтобы транспонировать матрицу, используйте t() функция.
m <- матрица(1:6, nrow=2, ncol=3)
м
[1] [2] [3]
[1,] 1 3 5
[2,] 2 4 6
т (м)
[1] [2]
[1,] 1 2
[2,] 3 4
[3,] 5 6
Создание матрицы идентичности
Матрицу идентичности можно создать с помощью функции diag() . Его поведение зависит от того, какой аргумент вы передаете.
Если вы передадите одно положительное целое число, то diag() создаст единичную матрицу этого измерения.
# Создать матрицу идентичности 3x3
диаг.(3)
[1] [2] [3]
[1,] 1 0 0
[2,] 0 1 0
[3,] 0 0 1
Если вы передаете матрицу, diag() вернет диагональные элементы матрицы.
# Возврат диагональных элементов матрицы
m <- матрица (1:9, nrow=3, ncol=3)
м
[1] [2] [3]
[1,] 1 4 7
[2,] 2 5 8
[3,] 3 6 9
диаг.(м)
[1] 1 5 9
Скалярное кратное матрицы
При умножении матрицы на скалярное значение (одно число) каждый отдельный элемент умножается на это значение.