Похожие вопросы
Нужное полное решение с графиком…
Запиши несколько смешанных чисел, удовлетворяющих неравенству: 5<=у<6…
Обсчитать:
2sin 22,5° cos 22,5°=?…
Катя выехала из колледжа на велике со скоростью 150м/мин. Даша осталась на факультативные занятия и выехала только через 20 минут со скоростью 210м/мин.Через какое время Даша дагонит Катю?сделайте решение так чтобы был ответ:а)50мин;б)150мин;в)80МИН;Г)40МИН
…
570 дм+1 м 193 см+47 дм 560 мм=см.
Сумма трех положительных чисел равна 20.Тогда произведение двух больших из них не может быть…?
…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский языкХимия
Физика
Биология
Другие предметы
История
Обществознание
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
9 точек 4 линии
 Если у вас не получилось разгадать эту головоломку, не отчаивайтесь. На этой странице вы сможете найти несколько решений этой знаменитой непростой задачи о девяти точках, которые напрягли умы уже многих тысяч, если не миллионов людей.
Если у вас не получилось разгадать эту головоломку, не отчаивайтесь. На этой странице вы сможете найти несколько решений этой знаменитой непростой задачи о девяти точках, которые напрягли умы уже многих тысяч, если не миллионов людей.Оглавление:
- Условие задачи
- Верное решение
- Творческий подход к головоломке
- Другие решения
- Отзывы и комментарии
Условие задачи
Условие: нужно соединить нарисованные девять точек четырьмя прямыми линиями не отрывая ручки от листа бумаги.
ОБНОВИТЬ РИСУНОК
Условие: нужно соединить нарисованные девять точек четырьмя прямыми линиями не отрывая ручки от листа бумаги.
Эта задача является не такой уж простой, как может показаться. Чтобы ее решить нужно думать нестандартно и применить свое творческое мышление, иначе ничего не получится. Если пытаться действовать в лоб начать соединять все точки стандартными линиями, то вы можете потратить уйму времени и так и не решить задачу девяти точек. Наше стандартное мышление, которому нас учат в школе, направляет нас искать решение, опираясь лишь на шесть типичных линий: 4 стороны квадрата и 2 его диагонали. Большинству людей кажется, что решение головоломки о 9 точках должно лежать именно в этих рамках. Но его там нет. Его даже не найти если подключить еще 2 линии между центрами сторон квадрата:
Наше стандартное мышление, которому нас учат в школе, направляет нас искать решение, опираясь лишь на шесть типичных линий: 4 стороны квадрата и 2 его диагонали. Большинству людей кажется, что решение головоломки о 9 точках должно лежать именно в этих рамках. Но его там нет. Его даже не найти если подключить еще 2 линии между центрами сторон квадрата:
Вообще между всеми девятью точками можно провести всего 20 прямых линий: 4 стороны квадрата; 2 диагонали; 6 линий, соединяющих центры сторон большого квадрата; 8 линий соединяющих центры сторон большого квадрата с его углами. Как нарисовать все отрезки, соединяющие наши 9 точек, показано на рисунке ниже:
Но, даже используя эту схему, невозможно найти 4 линии, которыми можно было бы соединить все девять точек, не отрывая руки.
Верное решение «теста 9 точек»
Решение этой головоломки лежит несколько шире нашего стандартного восприятия задачи. Для того, чтобы самостоятельно найти верный подход вспомните, что:
- Через любые 2 точки можно провести только одну прямую линию.

- Прямая линия – это не отрезок и, следовательно, нам не обязательно ограничиваться при рисовании линий нашими девятью синими кружками.
Таким образом, давайте попробуем продолжить линии за пределы, ограничивающего нас до недавнего времени квадрата. Тут видно, что область нашего поиска значительно увеличилась. Потрудившись немного можно прийти к одному из правильных решений.
Последовательность соединений девяти точек четырьмя линиями:
- Для начала проведите линию, соединяющую точку №1 и точку №7, через точку №4. Не останавливайте движение и рисуйте дальше примерно столько, сколько от точки №4 до точки №7.
- Далее двигайтесь по диагонали направо-вверх, соединяя точки №8 и №6. Не останавливайтесь на точке №6 и продолжайте линию до мысленной прямой, проходящей через верхнюю сторону нашего квадрата.
- Нарисуйте линию справа налево последовательно через точки №3, №2 и №1. Остановитесь на точке №1.
- Теперь проведите финальный отрезок через точки №1, №5 и №9.
 Все 9 точек, и правда, соединены четырьмя линиями, как и требовалось в условии задачи.
Все 9 точек, и правда, соединены четырьмя линиями, как и требовалось в условии задачи.
Другие варианты. Этот способ не единственный, начинать можно от любого угла и двигаться одном из двух направлений. На сайте 4brain таких вариантов решения задачи «9 точек 4 линии» представлено минимум 12:
Только подумайте, задача, которую многие никак не могут решить, имеет 12 способов решения. Также смотрите упрощенный вариант этой задачи: как соединить 4 точки тремя линиями, чтобы линии замыкались в целую фигуру.
Творческий подход в этой головоломке
Большинство людей, которые решали эту задачу, так и не смогли выбраться за рамки стандартного мышления, которое в данном тесте выражено квадратом, образованным девятью точками. Нам комфортно смотреть на любую жизненную задачу прямо, наиболее просто. С другой стороны, человек может потратить много времени и сил для того, чтобы, используя стандартный подход, найти верное решение, когда это решение лучше искать, изначально подойдя к процессу творчески.
В нашей жизни мы часто сталкиваемся с такими задачами о «девяти точках и четырех линиях», и для того, чтобы их решать развивайте свое креативное мышление, в том числе и при помощи нашего тренинга. Ведь задача о 9 точках имеет и другие решения (об этом читайте дальше).
Другие способы решения
Изменив наш фрейм или применив латеральный разрыв можно найти и другие варианты решения этой задачи. Например, метод гиперболизации при создании латерального разрыва может нас привести к мысли, что никто не уточняет, что в задаче должны применяться стандартные условия геометрии (о бесконечной малости точек и бесконечной тонкости линий). Пусть наша линия будет настолько широкой, что сможет сразу пересекать несколько точек по своей ширине. Тогда мы не то что 4-мя линиями сможем соединить все 9 точек, а даже одной.
Кроме того, даже в нашем изображении 4-х точек, которое дано в нашем условии головоломки о 9 точках, сами точки-кружки достаточно большие, чтобы можно было их соединить 3-мя линиями вот так:
А может вообще не стоит ограничиваться двухмерным пространством или использовать концепцию искривления пространства. Также мы можем акцентировать внимание на фразу «не отрывая ручки от листа бумаги», и просто положив ручку на бок передвинуть ее и таким образом нарисовать просто 3 параллельных линии.
Также мы можем акцентировать внимание на фразу «не отрывая ручки от листа бумаги», и просто положив ручку на бок передвинуть ее и таким образом нарисовать просто 3 параллельных линии.
Евгений Буянов
← Творческие игры Друдлы →
3-8Совершенные квадраты и квадратные корни (видео и практика)
mp4″ src=»https://player.vimeo.com/video/586551852?h=5f7f472e3f&app_id=122963″ frameborder=»0″ allow=»autoplay; fullscreen; picture-in-picture» allowfullscreen=»»>Часто задаваемые вопросы и практика
Здравствуйте, в этом видео мы рассмотрим, как упростить квадратных корней и найти идеальных квадратов .
Символ в математике, который мы используем для представления квадратных корней, называется радикалом и выглядит следующим образом: \(\sqrt{}\). Число, стоящее под корнем, называется 9.{1}\), но 1 не пишем, потому что это данность, в квадратных корнях есть что-то подобное. В изогнутом плече радикала есть заданная 2, которую мы обычно не пишем, когда ищем квадратный корень, \(\sqrt[2]{}\). Это число называется индексом и определяет, какой корень подкоренного числа мы пытаемся найти. Например, это: \(\sqrt{20}\) запрашивает квадратный корень или второй корень из 20, а это: \(\sqrt[3]{125}\), которое мы читаем как « кубический корень из ста двадцати пяти», просит нас найти третий корень из 125.
Я хочу, чтобы вы попрактиковались в этом сами. Приостановите видео и пометьте разные части этого выражения: \(\sqrt[4]{200}\).
Думаешь, у тебя получилось? Корневой символ — радикал. Индекс равен 4, потому что это число на согнутой руке радикала. Подкоренное число — это число под подкоренным символом, поэтому в данном случае 200.
\(\sqrt{}\) — подкоренное число
4 — индекс
200 — подкоренное число
Великолепная работа!
Теперь давайте поговорим о том, как мы находим квадратный корень из числа. Для этого мы спрашиваем себя: «Какое число, умноженное само на себя, даст нам подкоренное число?» Например, чему равен квадратный корень из 25: \(\sqrt{25}\)? Множители 25 равны \(5\умножить на 5\), что означает, что квадратный корень из 25 равен 5. Это также то, что мы называем идеальным квадратом. Совершенный квадрат — это когда мы упрощаем квадратный корень и под радикалом ничего не остается.
Чему равны квадратные корни из 36, 81 и 144? Поставьте видео на паузу и попробуйте сами. Когда вы закончите, мы просмотрим их вместе.
\(\sqrt{36}=6, \text{ потому что}\text{ }6\times 6=36\)
\(\sqrt{81}=9, \text{ потому что}\text{ }9\times 9=81\)
\(\sqrt{144}=12, \text{ потому что}\text{ }12\times 12=144\)
Мы получили эти милые, красивые числа потому что мы извлекаем квадратные корни из полных квадратов. Но что, если нам не дан идеальный квадрат? Что ж, тогда нам придется упрощать квадратный корень.
Упрощение квадратных корней
При упрощении квадратного корня мы вытащим все правильные квадраты из-под корня, а все, что останется от множителей подкоренного, останется под корнем. Давайте посмотрим на пример.
Упростите квадратный корень из 40: \(\sqrt{40}\).
Мы начнем с нахождения множителей 40, которые равны \({2}\times {2}\times {2}\times{5}\).
Так как \(2\times{2}\) образует идеальный квадрат, мы можем поставить 2 на передний план, и под радикалом останется \(2\times{5}\).
Больше нет полных квадратов, поэтому мы просто перемножаем эти числа, чтобы получить новое подкоренное число.
Следовательно, квадратный корень из 40 равен 2 квадратным корням из 10: \(\sqrt{40}\) = \(2\sqrt{10}\).
Теперь я хочу, чтобы вы попробовали один. Упростите квадратный корень из 96: 96. Приостановите видео здесь и упростите. Когда вы закончите, мы посмотрим на это вместе.
Думаешь, у тебя получилось? Во-первых, нам нужно найти множители числа 96.
\(96 = 2 \times {2}\times {2}\times {2} \times {2}\times{3}\)
Легко увидеть идеальные квадраты, когда множители записаны в такой форме. Мы можем вытащить два набора из 2 из нашего подкоренного числа, что оставит нам \(2\times{2}=4\) перед нашим новым радикалом. У нас все еще есть 2 и 3 из нашего списка множителей, поэтому мы перемножаем эти числа вместе, чтобы получить 6, и это наш новый подкоренной член. Поэтому самая упрощенная форма:
\(\sqrt{96}= 4\sqrt{6}\)
Надеюсь, это видео о квадратных корнях и правильных квадратах было полезным. Спасибо за просмотр и удачной учебы!
Спасибо за просмотр и удачной учебы!
Часто задаваемые вопросы
Q
Как найти квадратный корень?
A
Квадратный корень является обратным квадрату числа. Когда мы возводим число в квадрат, мы умножаем число само на себя. 4 в квадрате — это \(4\times4\), что равняется 16. 16 — это полный квадрат, а 4 — это квадратный корень из 16. Не все числа имеют хороший квадратный корень из целых чисел. Например, такое число, как 50, не является полным квадратом, потому что оно не имеет целого квадратного корня. Невозможно умножить целое число само на себя, чтобы получить произведение 50. 50 не имеет целого квадратного корня, но 49делает. Квадратный корень из 49 равен 7, потому что \(7\times7\) равно 49. 49 считается полным квадратом , а 7 считается квадратным корнем . Подкоренной символ используется для обозначения квадратных корней. Например, квадратный корень из 49 выражается как \(\sqrt{49}\):\(\sqrt{49}=7\). Это читается как «квадратный корень из 49 равен 7».
Это читается как «квадратный корень из 49 равен 7».
Q
Чему равно целое число квадратных корней от 1 до 20?
A
Квадратные корни целых чисел от 1 до 20 равны \(\sqrt1=1\),\(\sqrt4=2\),\(\sqrt9=3\) и \(\sqrt{16}=4\).
Не все числа имеют квадратные корни из целых чисел. Например, 1 имеет квадратный корень, потому что 1 можно представить как произведение двух равных целых чисел 1x1. 4 имеет квадратный корень из целого числа, потому что его можно выразить как произведение 2x2. Однако обратите внимание, что числа 2 и 3 не имеют квадратных корней из целых чисел. 2 не может быть выражено как целое число, умноженное само на себя. Точно так же 3 не может быть выражено как целое число, умноженное само на себя.
В
Какие числа имеют целые квадратные корни?
A
Числа с целыми квадратными корнями называются совершенными квадратами . Например, 64 — это число с целым квадратным корнем. 64 — это произведение \(8\times8\). Когда число может быть получено путем умножения целого числа само на себя, оно называется полным квадратом. Примерами чисел с целыми квадратными корнями являются 1, 4, 9, 16 и 25. Все эти числа имеют целые квадратные корни. 25 — это совершенный квадрат, который является произведением \(5\х5\). Это означает, что 5 — это квадратный корень из 25.
64 — это произведение \(8\times8\). Когда число может быть получено путем умножения целого числа само на себя, оно называется полным квадратом. Примерами чисел с целыми квадратными корнями являются 1, 4, 9, 16 и 25. Все эти числа имеют целые квадратные корни. 25 — это совершенный квадрат, который является произведением \(5\х5\). Это означает, что 5 — это квадратный корень из 25.
Не все числа имеют целые квадратные корни. Например, 5 не имеет целого квадратного корня. Никакое целое число не может быть произведением 5. Мы можем приблизиться: \(1\times=1\), \(2\times2=4\) и \(3\times3=9\), но 5 не равно полный квадрат, поэтому он не имеет целого квадратного корня.
Q
Каковы первые 20 идеальных квадратов?
A
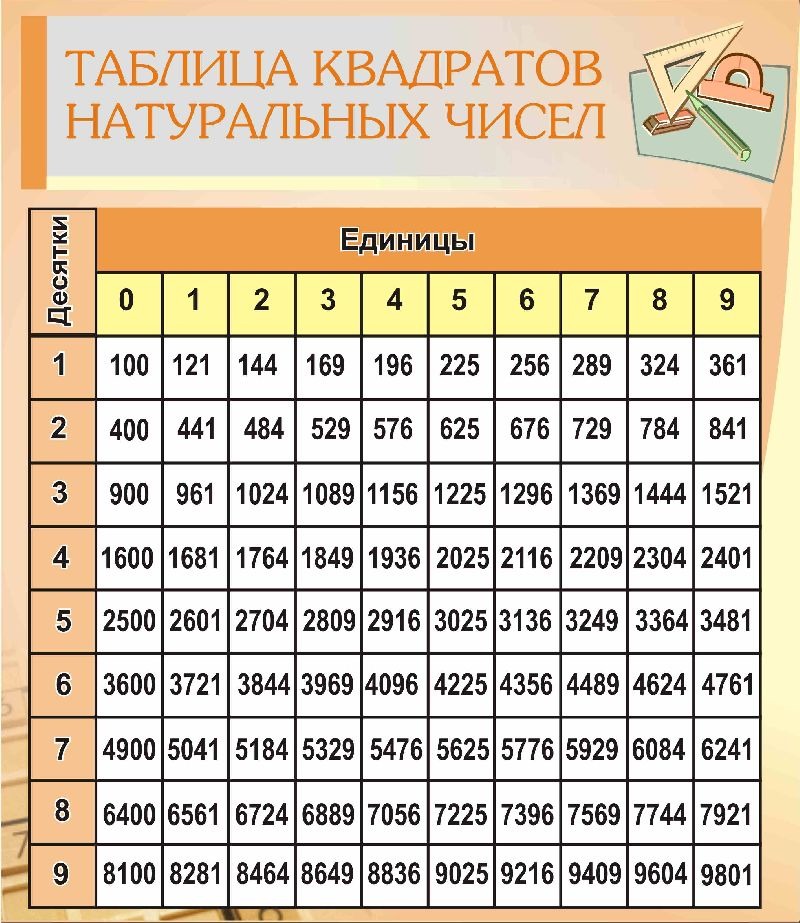
Первые 20 полных квадратов: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361 и 400. Совершенные квадраты находятся путем возведения в квадрат целого числа. \(1\times1=1\),\(2\times2=4\),\(3\times3=9\),\(4\times4=16\)… и так далее.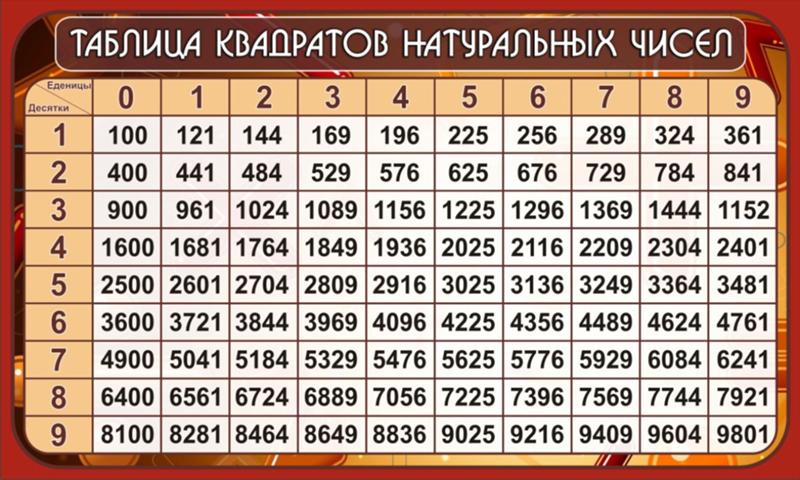 Не каждое число будет идеальным квадратом. Совершенные квадраты можно рассматривать как буквальные квадраты. Квадрат создается с использованием двух равных целых чисел в качестве длин сторон. Это означает, что результатом или продуктом будет идеальный квадрат.
Не каждое число будет идеальным квадратом. Совершенные квадраты можно рассматривать как буквальные квадраты. Квадрат создается с использованием двух равных целых чисел в качестве длин сторон. Это означает, что результатом или продуктом будет идеальный квадрат.
Q
Каковы идеальные квадраты от 1 до 100?
A
Есть только десять полных квадратов от 1 до 100. 1, 4, 9, 16, 25, 36, 49, 64, 81 и 100. Эти совершенные квадраты являются результатом умножения числа на себя. Например, 1 — идеальный квадрат, потому что \(1\times1=1\). 4 — идеальный квадрат, потому что \(2\times2=4\). 9 — идеальный квадрат, потому что \(3\times3=9\). Не все числа являются идеальными квадратами. Может быть полезно думать о идеальных квадратах как о реальных квадратах с длиной и шириной. Например, 100 — это совершенный квадрат, построенный из сторон с длинами 10 и 10. \(10\times10=100\), поэтому 100 — это совершенный квадрат.
Q
Как определить правильные квадраты?
A
Числа, которые считаются полными квадратами являются результатом умножения целого числа на себя. 2=36\), поэтому 36 считается идеальным квадратом.
2=36\), поэтому 36 считается идеальным квадратом.
Q
Почему нет идеальных квадратов между 144 и 169?
A
Полные квадраты — это результат возведения числа в квадрат. Например, 81 — это полный квадрат, потому что это результат возведения в квадрат 9: \(9\times9=81\). 144 — идеальный квадрат, потому что это результат возведения в квадрат 12: \(12\times12=144\). 169 — идеальный квадрат, потому что это результат возведения в квадрат 13: \(13\times13=169\). Обратите внимание, что между 144 и 169 нет идеальных квадратов. Если число находится между 144 и 169, его квадратный корень должен быть между \(\sqrt{144}=12\) и \(\sqrt{169}=13\). Поскольку между 12 и 13 нет целых чисел, между 144 и 169 нет идеальных квадратов.
Мы не можем создать идеальный квадрат, умножив что-то вроде \(11,5\times11,5\), потому что это не произведение двух равных целые числа. Квадратные корни идеальных квадратов должны быть целыми числами.
Практические вопросы
Вопрос №1:
Какой набор чисел содержит все полные квадраты?
33, 99, 55, 66
33, 99, 55, 66
36, 9, 25, 100
81, 36, 25, 41
Показать Ответ
:
. ответ: 36, 9, 25, 100. Тридцать шесть — это совершенный квадрат, составленный из \(6×6\), девять — это совершенный квадрат, составленный из \(3×3\), двадцать пять — это совершенный квадрат, составленный из из \(5×5\), а сотня — это полный квадрат, составленный из \(10×10\).
ответ: 36, 9, 25, 100. Тридцать шесть — это совершенный квадрат, составленный из \(6×6\), девять — это совершенный квадрат, составленный из \(3×3\), двадцать пять — это совершенный квадрат, составленный из из \(5×5\), а сотня — это полный квадрат, составленный из \(10×10\).
Скрыть ответ
Вопрос №2:
Какая пара показывает правильное соответствие между полным квадратом и квадратным корнем из его целого числа?
\(\sqrt{144}=12\)
\(\sqrt{36}=2\)
\(\sqrt{25}=4\)
\(\sqrt{100}=11 \)
Показать ответ
Ответ:
Правильный ответ: \(\sqrt{144}=12\). Сто сорок четыре — это полный квадрат, составленный из \(12×12\). Тридцать шесть — это полный квадрат, но он не состоит из \(2×2\). Вместо этого он состоит из \(6×6\). Двадцать пять — это полный квадрат, но он не состоит из \(4×4\).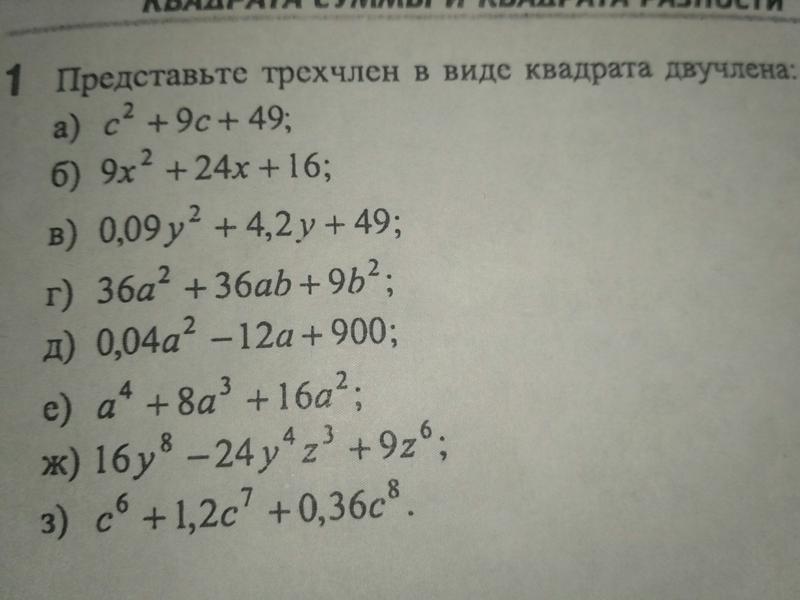 Вместо этого он состоит из \(5×5\). Сто — это полный квадрат, но он не состоит из \(11×11\). Вместо этого он состоит из \(10×10\).
Вместо этого он состоит из \(5×5\). Сто — это полный квадрат, но он не состоит из \(11×11\). Вместо этого он состоит из \(10×10\).
Скрыть ответ
Вопрос №3:
Чему равен квадратный корень из 49?
Показать ответ
Ответ:
Правильный ответ: 7. Квадратный корень из 49 равен 7, потому что \(7×7=49\). Это также означает, что 49 — совершенный квадрат.
Скрыть ответ
Вопрос № 4:
Какое значение НЕ является полным квадратом?
81
100
64
99
Показать Ответ
Ответ:
Правильный ответ: 99. Поскольку не существует целого числа, которое можно умножить само на себя и получить 99, это не полный квадрат. Восемьдесят один — это совершенный квадрат, составленный из \(9×9\), сто — это совершенный квадрат, составленный из \(10×10\), а шестьдесят четыре — это совершенный квадрат, составленный из \(8×8\). .
Восемьдесят один — это совершенный квадрат, составленный из \(9×9\), сто — это совершенный квадрат, составленный из \(10×10\), а шестьдесят четыре — это совершенный квадрат, составленный из \(8×8\). .
Скрыть ответ
Вопрос № 5:
Какая пара показывает неправильное совпадение между полным квадратом и его целым числом квадратным корнем?
\(\sqrt{49}\) и \(7\)
\(\sqrt{4}\) и \(2\)
\(\sqrt{64}\) и \(8\) )
\(\sqrt{9}\) и \(6\)
Показать ответ
Ответ:
Правильный ответ: \(\sqrt{9}\) и \(6\). Квадратный корень из 9 — это полный квадрат, но он состоит из \(3×3\), а не из \(6×6\).
Скрыть ответ
Вернуться к предварительным алгебраическим видео
648063
Упрощение радикалов — Полный курс алгебры
Навыки
в
A L G E B R A
Содержание | Главная
27
Простейшая форма
Подобные радикалы
2-й уровень
Упрощение квадратного корня из степеней
Дробное подкоренное число
МЫ ГОВОРИМ, ЧТО РАДИКАЛ КВАДРАТНОГО КОРНЯ упрощен, или в его простейшей форме, когда подкоренное число не имеет квадратных множителей.
Радикал также находится в простейшей форме, когда подкоренное число не является дробью.
Пример 1. 33, например, не имеет квадратных множителей. Его делители равны 3 · 11, ни один из которых не является квадратным числом. Таким образом, в его простейшей форме.
Пример 2. Извлечение квадратного корня. 18 имеет квадратный множитель 9.
18 = 9 · 2.
Следовательно, это не самая простая форма. У нас есть,
=
Теперь мы можем извлечь или вычесть квадратный корень из 9:
= = 3.
теперь упрощен. Подкоренное число больше не имеет квадратных множителей.
Основанием для извлечения квадратного корня из 9 является следующая теорема:
Квадратный корень из произведения
равен произведению квадратных корней
каждого множителя.
Мы докажем это, когда дойдем до рациональных показателей, Урок 29. Вот простая иллюстрация:
Вот простая иллюстрация:
Что касается , то оно равно квадратному корню из 9, умноженному на квадратный корень из 2, что иррационально. 3.
Пример 3 Упрощение .
Раствор . = = 5.
75 имеет квадратный коэффициент 25. И квадратный корень из (25 умножить на 3)
равен квадратному корню из 25, умноженному на квадратный корень из 3.
теперь упрощен.
Пример 4. Упрощение .
Раствор . Мы должны разложить 42 на множители и посмотреть, есть ли у него квадратные множители. Мы можем начать факторинг любым способом. Например,
42 = 6 · 7
Мы можем продолжать разлагать 6 как 2 · 3, но мы не можем продолжать разлагать 7, потому что 7 — простое число. Поэтому
42 = 2 · 3 · 7
Теперь мы видим, что, поскольку множители не повторяются, число 42 не имеет квадратных множителей. поэтому находится в простейшей форме.
Сравните пример 1 и задачу 2 предыдущего урока.
2 · 3 · 7 — простая факторизация числа 42.
2, 3 и 7 — простые числа.
Пример 5. Упрощение .
Раствор. Мы должны искать квадратные множители, которые будут повторяющимися множителями.
180 = 2 · 90 = 2 · 2 · 45 = 2 · 2 · 9 · 5 = 2 · 2 · 3 · 3 · 5
Следовательно,
= 2 · 3 = 6.
Проблема 1. Чтобы упростить радикал, почему мы ищем квадратные множители?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!
Для того, чтобы извлечь его квадратный корень из корня.
| Задача 2. Как правильно? |
Проблема 3. Упростите следующее. Сделайте это, проверив каждое подкоренное число на квадратный множитель: 4, 9., 16, 25 и так далее.
Упростите следующее. Сделайте это, проверив каждое подкоренное число на квадратный множитель: 4, 9., 16, 25 и так далее.
а) =
б) = = = 5
в) = = = 3
г) = = 7
д) = = 4
е) = = 10
г) = = 5
ч) = = 4
Задача 4. Сведение к наименьшим терминам.
| а) | 2 | = | 2 | = | 2 | = |
| б) | 3 | = | 3 | = | 3 | = | 2 |
| в) | 2 | = | Радикал в своей простейшей форме. Дробь нельзя уменьшить. Дробь нельзя уменьшить. |
Подобные радикалы
Подобные радикалы имеют одинаковые радикалы. Мы добавляем их как похожие термины.
| 7 + 2 + 5 + 6 − | = | 7 + 2 + 6 + 5 − | |
| = | 7 + 8 + 4. | ||
2 и 6 похожи, как 5 и -. Мы объединяем их, складывая их коэффициенты.
На практике нет необходимости менять порядок терминов. Студент должен просто увидеть , у которых радикалы имеют одинаковые подкоренные числа.
Что касается 7, то она не «принадлежит» какому-либо радикалу.
Задача 5. Упростите каждый радикал, затем добавьте аналогичные радикалы.
а) + = 3 + 2 = 5
| б) 4 − 2 + | = | 4 − 2 + |
| = | 4 · 5 − 2 · 7 + | |
| = | 20 − 14 + | |
| = | 7 | |
| в) 3 + − 2 | = | 3 + − 2 |
| = | 3 · 2 + 2 − 2 · 4 | |
| = | 6 + 2 − 8 | |
| = | 2 − 2 | |
| г) 3 + + | = | 3 + + |
| = | 3 + 2 + 3 | |
| = | 3 + 5 | |
| e) 1 − + | = | 1 − + |
| = | 1 − 8 + 3 | |
| = | 1 − 5 | |
Проблема 6. Упростите следующее.
Упростите следующее.
| а) | 2 | = | 2 | = | 2 — , | при делении каждого члена числителя на 2. |
Сравните пример 4 здесь.
Чтобы увидеть, что 2 является множителем радикала, вам сначала нужно упростить радикальный. Сравните задачу 4.
| б) | 5 | = | 5 | = | 2 + |
| в) | 6 | = | 6 | = | 3 | при делении каждого члена на 2. |
2-й уровень
Первый урок о радикалах
Следующий урок: Умножение и деление радикалов
Содержание | Главная
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.

 Все 9 точек, и правда, соединены четырьмя линиями, как и требовалось в условии задачи.
Все 9 точек, и правда, соединены четырьмя линиями, как и требовалось в условии задачи.