4 из 20 сколько вариантов комбинаций: правила игры, условия выигрыша и что можно выиграть в лотерею «Спортлото «4 из 20»

Содержание

Стратегия-«Повторение»-«Гослото «4 из 20» — lottery-statistics.ru

последний известный тираж № 5657 от 2023-01-04 22:00:00. Номера : [

]. Сумма чисел = 65.

На нашем ресурсе отсутствует реклама. Если вам нравится пользоваться данным ресурсом, то мы принмаем в дар стейблкоины (USD Tether ERC20) для поддержания проекта. Адрес нашего кошелька: 0x0efedd8Ad1cD0059BCfA8c97dD7440D0230b879a

На графике-«Визуализация побед на истории» по вертикальной шкале отражены категории выигрышей по возрастанию, где 12 — это Суперприз.

Вероятность выигрыша в «Гослото 4 из 20»

Стратегия-«Повторение», основана на применении тех же шаров, что выпали в прошлом тираже.

Напомним, что для «Гослото 4 из 20», математическая общая вероятность выигрыша составляет 1 к 3.4 .

На графике-«Изменение показателя WR» каждое движение вниз говорит о том, что в этом тираже был выигрыш, а каждое движение вверх говорит о неудаче.

В левой части таблицы представлены результаты тиражей. В правой части таблицы представлены «Прогнозные шары», которые мы использовали для каждого из тиражей. По середине располагается столбец-«победа», являющийся результатом соотнесения прогнозных и выпавших шаров. Показателем эффективности стратегии является столбец-«WR».
Для примера в таблице представлены лишь последние 200 тиражей стратегии, а также прогноз на будущий тираж.

ВЫВОД

Стратегия показывает результаты соответствующие математической вероятности выигрыша в лотерею. Бывают иногда отклонения текущего показателя WR от средних значений вероятности выигрыша, но потом они все равно стабилизируются.
Использование «Повторения» приносит математическую вероятность выигрыша при большом количестве испытаний. У неё нет преимуществ, но есть один недостаток. Этот недостаток заключается в том , что вероятность выпадания Всех тех же самых чисел, необходимых для выигрыша суперприза, второй раз подряд, ничтожно мала. То есть, если вероятность угадать все числа составляет 1 к 24 млн., то тут это значение надо ещё возвести в квадрат. Поэтому, если вы хотите использовать качественную случайность, то лучше брать значение предыдущих тиражей, например, из истории других лотерей.

Результаты, полученные в прошлом, не являются гарантией их повторения в будущем. Использование или не использование этой стратегии на практике, является сугубо вашим личным делом. Мы только предоставляем статистику и анализ, и не несём никакой ответственности за ваши действия.

Сколько комбинаций лотереи вам нужно, чтобы гарантировать джекпот?

Можете ли вы представить, как выигрыш в лотерею может сделать вашу жизнь лучше? Вы можете инвестировать в бизнес или бросить работу и путешествовать по миру.

Стать обладателем главного приза остается мечтой для большинства людей.. Чтобы стать игроком, выигравшим джекпот, нужно много удачи. Вы когда-нибудь задумывались, есть ли способ гарантировать победу? Сколько лотерейных комбинаций вам нужно приобрести, чтобы получить главный приз?

В этом руководстве обсуждается подход к покупке всех потенциальных комбинаций при розыгрыше лотереи и выясняется, насколько это выгодно. Вот что вам следует знать о том, как выиграть главный приз этим методом!

Сколько комбинаций гарантирует джекпот для каждой лотереи?

Единственный способ гарантировать, что вы выиграете главный приз, — это купить все возможные комбинации для розыгрыша. Наш калькулятор шансов лотереи может помочь вам определить количество комбинаций для конкретной игры в лото. Вы также можете найти расчеты для самых популярных лотерей ниже!

Powerball

US Powerball имеет гарантированный фонд джекпота в размере 40 миллионов долларов. Он использует концепцию двух барабанов, которая устанавливает максимальное количество комбинаций в 292,201,338 XNUMX XNUMX. Вот сколько билетов нужно купить, чтобы быть победителем.

Play Powerball от Yhao сейчас!

MegaMillions

Математика показывает, что MegaMillions имеет даже больше возможных комбинаций, чем Powerball. Ваши шансы на выигрыш джекпота составляют 1: 302,575,350 XNUMX XNUMX. Вам понадобится столько билетов, чтобы охватить все возможные варианты рисования. Однако есть способ уменьшить это, исключив некоторые маловероятные комбинации, такие как «1, 2, 3, 4, 5».

Play MegaMillions от Yhao сейчас!

EuroJackpot

EuroJackpot самая популярная европейская континентальная лотерея. Используемая концепция — 5/50 + 2/10, что указывает на то, что это игра с двумя барабанами. Количество комбинаций, гарантирующих выигрыш — 95,344,200 XNUMX XNUMX. Чтобы сделать игру более увлекательной, в лото проводятся два розыгрыша в неделю.

Play EuroJackpot от Yhao сейчас!

EuroMillions

EuroMillions это еще одна континентальная лотерея, доступная игрокам из Европы, но также и из остального мира. У него худшие шансы, чем у его основного конкурента, но несколько лучшие призы. Для выигрыша джекпота необходимо приобрести 139,838,160 XNUMX XNUMX комбинаций.

Play EuroMillions от Yhao сейчас!

SuperEnalotto

Эта игра возникла в Италии, но популярна во всем мире. Это потому что SuperEnalotto джекпоты могут увеличиваться до огромных сумм. Однако эта концепция предусматривает крайне невыгодные шансы. Вам нужно будет купить 622,614,630 XNUMX XNUMX комбинаций, чтобы охватить все возможности. SuperEnalotto имеет концепцию одного барабана 6/90, что является самым большим количеством шаров в одном барабане в мире.

Play SuperEnalotto от Yhao сейчас!

Мега Сена

Бразилия Мега Сена проводится два розыгрыша еженедельно по концепции 6/60. Это лотерея с одним барабаном, насчитывающая 50,063,860 XNUMX XNUMX комбинаций.. Джекпот может значительно увеличиться, если выпадет несколько ролловеров.. Обратной стороной является то, что Mega Sena предлагает только три призовых уровня.

Играйте в Brazil Mega Sena прямо сейчас!

Лото Франции

Еще одна популярная европейская лотерея с концепцией двух барабанов.. Лото Франции имеет формулу 5/49 + 1/10, согласно которой выигрыш составляет 19,068,840 XNUMX XNUMX комбинаций.. Гарантированный главный призовой фонд составляет 2 миллиона евро, и каждую неделю вы можете участвовать в трех розыгрышах.

Играйте в Лото Франции прямо сейчас!

Германия Лото

Германия — самая большая страна в Европе, и Немецкое Лото входит в число крупнейших национальных лотерей. Лимит пролонгации джекпота составляет 12 раз, что ограничивает главный приз. Поскольку это концепция с двумя барабанами, общее количество комбинаций составляет 139,838,160 XNUMX XNUMX.

Играйте в German Lotto прямо сейчас!

Национальная лотерея Великобритании

Камелот стоит за Национальная лотерея Великобритании. Игра предлагает щедрые призы и простой формат 6/59 с бонусным шаром. The lottery ограничивает перенос джекпота до пяти раз, поэтому победитель будет определяться каждые шесть розыгрышей или меньше. Общее количество комбинаций, необходимых для гарантированного выигрыша джекпота, составляет 45,057,474 XNUMX XNUMX.

Тандербол

Громовой шар Великобритании имеет много преимуществ, например, не делить главный приз с другими. В лотерее проводится четыре розыгрыша в неделю по принципу двух барабанов.. Фактическая формула — 6/39 + 1/14, что означает, что общее количество комбинаций составляет 8,060,598 XNUMX XNUMX.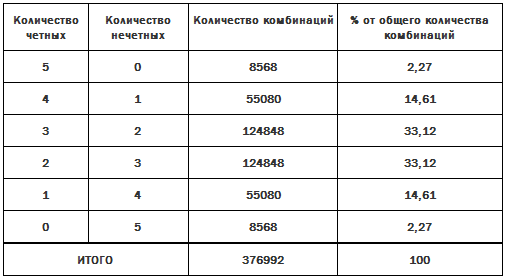 Это не так уж много, если сравнивать с некоторыми другими национальными лотереями.

Играйте в UK Thunderball прямо сейчас!

Можете ли вы получить прибыль, если купите все комбинации лотереи?

Звучит здорово, что вы можете выиграть джекпот, купив все комбинации для розыгрыша. Главный вопрос — выгодно ли это. Стоит ли это вашего времени и усилий, и имеет ли это вообще смысл?

Вот простой способ понять математику. Вы должны учитывать цену отдельного билета и умножать ее на количество комбинаций, которые вам нужны для игры.. Это даст вам необходимые вложения. Теперь сравните это с джекпотом и посмотрите, стоит ли оно вашего времени.

Расчет за этим

Лучший способ объяснить, почему покупка всех комбинаций вряд ли выгодна, — это на примере.. Давайте PowerballСтоимость билета составляет 2 доллара США. Количество возможных комбинаций составляет 292,201,338 XNUMX XNUMX, поэтому мы делаем это:

«292,201,338 2 584,402,676 * XNUMX = XNUMX XNUMX XNUMX»

Вам понадобится $ 584,402,676 XNUMX XNUMX, чтобы купить все возможные комбинации. . Компания Powerball Джекпот начинается с 40 миллионов долларов, но не имеет ограничений. Компания самая большая победа когда-либо составляет 1.58 миллиарда долларов, что указывает на то, что этот метод может быть прибыльным. Но если вы так думаете, вы ошибаетесь!

Это потому, что вы никогда не получите заявленную сумму джекпота. Вот причины, почему:

Применимые налоги. Некоторые страны не применяют налоги. Однако применимые налоги на лотереи в США могут превышать 30%, что снижает ваш потенциальный приз на треть. Ознакомьтесь с нашими калькулятор лотерейного налога чтобы узнать больше о правилах в разных странах.

Аннуитетные выплаты или единовременные выплаты. Вы можете сразу получить джекпот, что значительно уменьшит размер приза. А если вы выберете единовременные выплаты, вы получите вознаграждение по годовой ставке. Это означает, что пройдут годы, прежде чем вы даже вернете первоначальные вложения.
Опасность разделения приза. Вы купили все возможные комбинации. Однако это не мешало другим играть. Что, если кто-то разыграет выигрышные комбинации? В большинстве игр вам придется делить приз!

Как видите, именно эти факторы являются причиной того, что этой стратегии невероятно сложно быть прибыльной.

Сможете ли вы даже приобрести все доступные комбинации лотереи?

Чтобы купить все комбинации для одного розыгрыша, потребуется много времени и усилий.. Вам нужно будет купить миллионы билетов, и между двумя розыгрышами часто бывает всего 2-3 дня.. Это означает, что вам нужно будет только купить билеты и несколько дней ничего не делать. И, скорее всего, вам понадобятся руки помощи даже в этом случае. Чтобы осуществить этот трюк, нужна отличная организация!

Кто-то пытался купить все билеты в прошлом?

Да, и он оказался в числе самых известные победители лотереи . Имя игрока Стефан Мандель, и он родился в Румынии. Как математик, он разбирался в расчетах и шансах в национальной лотерее. . Он стремился не к джекпоту, а ко второму призу. Он предполагал правильное угадывание пяти из шести чисел.

Мандель сделал это несколько десятилетий назад, когда покупка всех билетов не всегда превышала сумму призового фонда.. Его история свидетельствует о том, что ему удавалось разыграть различные лотереи и выиграть 14 раз. Из-за защитных механизмов, применяемых лотереями, сегодня его тактику сложно применить.

Законно ли покупать все лотерейные билеты?

С технической точки зрения покупка всех лотерейных комбинаций является законной. Однако это может привлечь внимание властей. Сегодня у вас офлайн и продавцы онлайн-лотерей. Это означает, что вы не можете купить все билеты. Даже если только онлайн, другие игроки могут играть, хотя их комбинации будут пересекаться с вашими.

Последние мысли — стоит ли покупать все the Lottery Билеты?

The lotterСо временем они извлекли уроки из своих ошибок. Сегодня большинство провайдеров лото применяют защитные механизмы, чтобы никто не мог использовать этот метод для получения прибыли. Хотя теоретически вы можете купить все лотерейные билеты, в реальности это требует больших усилий. И даже если вы это сделаете, велика вероятность, что вы в конечном итоге потеряете деньги. Даже если стоимость билетов не превышает фонд джекпота, главный приз будет уменьшен за счет налогов, вариантов оплаты или возможного распределения призов.

Решение — расслабиться и получить удовольствие от игры the lotterу. Вы можете использовать разные стратегии лото чтобы повысить ваши шансы на победу. В конечном счете, the lottery невероятно весело, и вам понравится азарт, наблюдая за розыгрышем и проверяя результаты. И если вам посчастливится выиграть джекпот, это будет огромным бонусом!

сколько комбинаций с 9 цифрами без повторов

AlleBilderVideosShoppingMapsNewsBücher

suchoptionen

Следовательно, общее количество возможностей равно 9×9! =3265920. Следовательно, 3265920 способов можно составить 9-значные числа из разных цифр.

_{28. Дез. 2022}

Сколько 9-значных чисел можно составить из разных цифр? — Vedantu

www.vedantu.com › вопрос-ответ › 9-значное-количество-разных-цифр…

Hervorgehobene Snippets

Ähnliche Fragen

Сколько существует комбинаций 9-значных чисел?

Как найти количество комбинаций без повторений?

Сколько возможных комбинаций из 3 цифр от 0 до 9 с повторением?

Сколько комбинаций можно составить из чисел 0 9?

Если мне дано 9 цифр для работы, сколько возможных комбинаций… -возможно…

Существует 72 возможных комбинации 2 цифр из заданных 9 или 72 способа выбрать 2 цифры из 9.

Сколько существует 9-значных чисел от 1 до 9? — Quora

Учитывая 9 цифр для работы, сколько возможных комбинаций из 3 …

Между 0-9 сколько возможных комбинаций из 4 цифр может быть … — Quora

Сколько комбинаций вы можете составить из 1, 2 , 3 и 4 … — Quora

Weitere Ergebnisse von www. quora.com

Сколько комбинаций возможно с 9 числами? — Study.com

homework.study.com › … › Алгебра › Комбинации

Количество возможных комбинаций с 9 числами равно 511. Чтобы определить, сколько комбинаций возможно с 9 числами, потребуется ужасно …

Номера социального страхования — Math Central

mathcentral.uregina.ca › database › chris1

Система счисления должна включать как можно больше девятизначных комбинаций с использованием чисел 0–9в нескольких разных местах.

[ЗАПРОС] Сколько комбинаций из 9 цифр? : r/theydidthemath

www.reddit.com › комментарии › psvekd › request_ho…

21.09.2021 · Сказали не повторяться, поэтому им нужны перестановки, а не комбинации.

Если повторы не допускаются, сколько 9-значных чисел может быть …

math.stackexchange.com › вопросы › если-нет-повторения…

Число n делится на 4, если и только если nmod100 делится на 4 (последние две цифры). Другие правила делимости можно найти здесь: …

Комбинации с повторением и без него: Сколько $6$-цифровых слов…

Используя числа 1, 2, 3, 4 и 5, сколько трехзначных комбинаций…

Комбинации из 10 цифр — Mathematics Stack Exchange

Сколько различных 4-значных комбинаций будет включать хотя бы одну 7 …

Дополнительная информация по math.stackexchange.com

Сколько 9-значных комбинаций можно составить из чисел …

math. answer.com › Науки › Математика и арифметика

120 комбинаций, используя каждую цифру один раз для каждой комбинации. Есть 625 комбинаций, если вы можете повторить цифры. Сколько различных комбинаций …

Калькулятор комбинаций без повторений: n=11, k=3

www.hackmath.net › комбинации-и-перестановки

Подсчитывает количество комбинаций без повторений или количество комбинаций. … Узнайте, сколькими способами можно выбрать k предметов из n предметов.

Комбинация без калькулятора повторений

www. omnicalculator.com › статистика › комбинации…

10.10.2022 · Пример: Сколько возможных комбинаций из 4-х чисел без повторения … вне десятичной системы (числа от 0 до 9) .

Найдите общее количество 9-значных чисел, все цифры которых разные.

www.toppr.com › … › Перестановки

Найдите общее количество 9-значных чисел, все цифры которых разные. … 537621), без повторения цифр. … Перестановки и комбинации.

Bilder

Allo Anzeigen

Alle Anzeigen

Ahnliche Sulanfragen

9 Digit

Комбинированный калькулятор

Combemance Combement Combement

2 Digit

. 2

Перестановки и комбинации

Факториалы
Перестановки
Комбинации
Обобщенные комбинации

Удобно определить факториал n, обозначаемый как n! как произведение первых n натуральных чисел. Например, 4! = 4 × 3 × 2 × 1 = 24. Очевидно, что 1! = 1, и мы определяем 0! = 1.

Перестановка — это порядок или расположение объектов. P(n,r) обозначает количество различных расположений r объектов из n объектов. Например, P(5,2) = 20, потому что имеется 20 упорядоченных пар букв abcde, а именно. ab, ac, ad, ae, ba, bc, bd, be, ca, cb, cd, ce, da, db, dc, de, ea, eb, ec, ed. Это число может быть получено как 5 × 4 = 20, потому что есть пять вариантов для первой буквы, и после того, как он удален, остается четыре варианта для второй буквы. Вы выбираете первую букву и вторую букву, следовательно, это пример правила умножения (и).

Обратите внимание, что количество размещений n различных объектов равно P(n,n) = n!.

Количество способов, которыми вы можете выбрать президента, вице-президента и секретаря из класса из семи учеников, равно P(7,3) = 7 × 6 × 5 = 210. Это также можно записать как 7!/(7- 3)!. В общем случае P(n,r) = n!/(n-r)!; Это можно интерпретировать как размещение всех n объектов, а затем удаление порядка (n-r) объектов, которые не выбраны, путем деления на количество способов их размещения.

Упражнение: Если у вас есть 7 различных объектов, сколько существует перестановок всех 7?, 6 из них?, пять из них? четыре из них? трое из них? двое из них? один из них? ноль из них? Что означает перестановка одного объекта или нуля объектов?

C(n,r) (читается как n выбирает r) — это количество различных неупорядоченных выборок размера r, которые можно выбрать из n различных объектов. Например, C(5,2) = 10, потому что ab, ac, ad, ae, bc, bd, be, cd, ce, de — единственные пары букв, которые можно выбрать из abcde (P(5,2) = 20, потому что каждую из этих пар можно упорядочить двумя способами, как указано выше). C(5,2) = 5!/((5-2)!×2!), что можно интерпретировать как упорядочивание всех 5 объектов, а затем удаление порядка среди 3 невыбранных, а также среди 2 выбранных . В общем случае C(n,r) равно n!/((n-r)!×r!)

Классическая запись для C(n,r) имеет n выше r в скобках, но это трудно сделать в ascii, и это не запись текста.

Часто бывает интересно различить некоторых, но не всех выбранных индивидуумов.