01Математика — 9 класс. Алгебра — Построение графика корня \(\small y=k\sqrt{x}, k
Заполним таблицу значений функции \(\displaystyle y=-2\sqrt{x}{\small :}\)
| \(\displaystyle x\) | \(\displaystyle 0\) | \(\displaystyle 1\) | \(\displaystyle 2\) | \(\displaystyle 3\) | \(\displaystyle 4\) | \(\displaystyle 5\) | \(\displaystyle 6\) |
| \(\displaystyle y=-2\sqrt{x}\) | \(\displaystyle -2\sqrt{0}\) | \(\displaystyle -2\sqrt{1}\) | \(\displaystyle -2\sqrt{2}\) | \(\displaystyle -2\sqrt{3}\) | \(\displaystyle -2\sqrt{4}\) | \(\displaystyle -2\sqrt{5}\) | \(\displaystyle -2\sqrt{6}\) |
Вычислим значения \(\displaystyle y{\small .} \)
Поскольку \(\displaystyle -2\sqrt{0}=0{ \small ,}\,-2\sqrt{1}=-2\) и \(\displaystyle -2\sqrt{4}=-4{ \small ,} \) то нужно лишь приближенно вычислить значения
\(\displaystyle -2\sqrt{2}{ \small ,}\, -2\sqrt{3}{ \small ,}\,-2\sqrt{5} \) и \(\displaystyle -2\sqrt{6}{\small .
2+\color{blue}{ 1}} \approx \color{green}{ 1}+\frac{\color{blue}{ 1}}{2\cdot \color{green}{ 1}}=1{,}5{\small .}\)
Значит,
\(\displaystyle 2\sqrt{ 2}\approx 2\cdot 1{,}5=3{\small .}\)
Таким образом, \(\displaystyle -2\sqrt{2}\approx -3{\small .} \)
\(\displaystyle -2\sqrt{3} \) равно примерно \(\displaystyle -3{,}5\)
\(\displaystyle -2\sqrt{5} \) равно примерно \(\displaystyle -4{,}5\)
\(\displaystyle -2\sqrt{6} \) равно примерно \(\displaystyle -5\)
Заполним таблицу значений функции:
| \(\displaystyle x\) | \(\displaystyle 0\) | \(\displaystyle 1\) | \(\displaystyle 2\) | \(\displaystyle 3\) | \(\displaystyle 4\) | \(\displaystyle 5\) | \(\displaystyle 6\) |
| \(\displaystyle y=-2\sqrt{x}\) | \(\displaystyle 0\) | \(\displaystyle -2\) | \(\displaystyle -3\) | \(\displaystyle -3{,}5\) | \(\displaystyle -4\) | \(\displaystyle -4{,}5\) | \(\displaystyle -5\) |
Построим точки на плоскости:
Построим примерный график функции \(\displaystyle y=-2\sqrt{x}\) по полученным точкам, добавляя еще точки, если это необходимо:
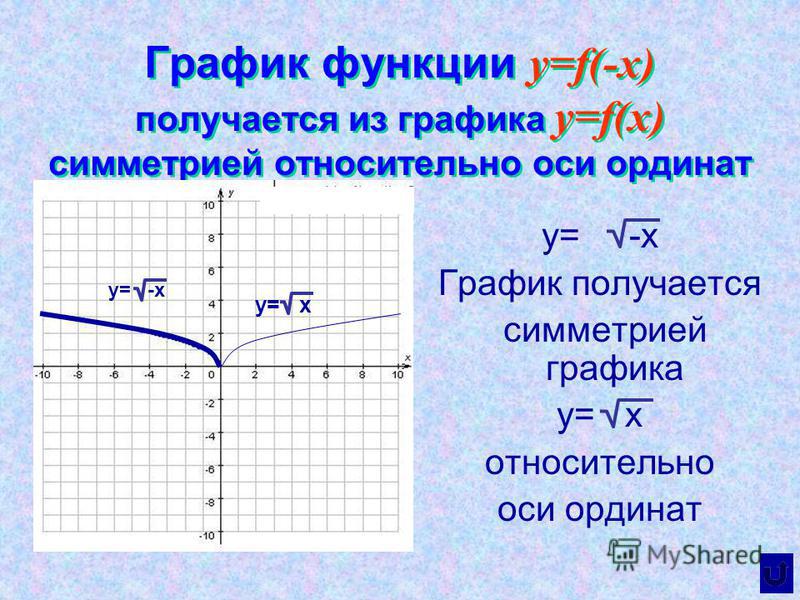
Функция квадратного корня
| Функция извлечения квадратного корня |
ФУНКЦИЯ КВАДРАТНОГО КОРНЯ:
(полупарабола.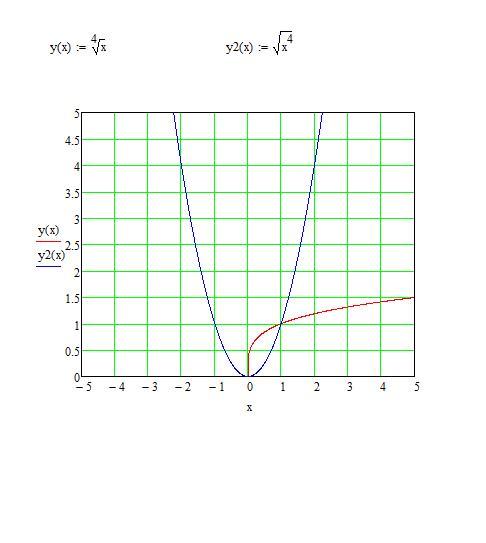
)
b = ± 1 , поэтому любое другое значение выносится за скобки.
пример:
, если бы 4 в квадратном корне было 4, мы все равно извлекли бы корень из 4, но b было бы = 1.
| Таблица свойств квадратного корня | правило: | |||
| Домен: x > ч If B = +1, 76> H IF B = +1, 7676> ч. = 1, | Диапазон: Y < K, A <0, Y > K, A> 00006 | |||
зависит от модификации
зависит от модификации
РЕШЕНИЕ УРАВНЕНИЯ КВАДРАТНОГО КОРНЯ:
NB: Решения должны быть проверены и только главный (положительный) квадратный корень разрешено.
Чтобы решить уравнение с квадратными корнями:
Извлечь квадратный корень и возвести в квадрат обе стороны .
Если какая-либо из сторон является двучленом ВОЗВРАЩАЙТЕ ЭТО ДОЛЖНЫМ ОБРАЗОМ КАК ДВУНОМ!!
Пример
замена x = 4: ü
замените x = ¾, поэтому x = ¾ не является решением.
Уроки, примеры и практика решения радикальных уравнений см. Урок 6.4 . в The Algebra MathRoom .
Решение неравенств с квадратным корнем
Мы решаем эти неравенства, как всегда, соблюдая основное правило:
обратное направление неравенство
когда мы умножаем или делим на минус .
Есть еще 2 проблемы с квадратными корнями, так как
1) мы должны возвести в квадрат штук , чтобы освободить переменные от знака корня.
Возведение в квадрат — опасная операция , поскольку она может превратить ложь в правду — как политики .
7 = 7 неверно
но, когда возводим обе стороны в квадрат….
49 = 49 верно!!
вот почему мы должны проверять наши решения при работе с четными корнями.
2) Даже корень накладывает ограничения на домен функции.
Если рассматриваемый корень определен только для
пример: Решите это неравенство с квадратным корнем (коренное)
областью определения является x > 1
Возведение обеих сторон в квадрат дает: 9( x + 1) < (2 x 3) 2
Это дает нам, что: 9 x + 9 < 4 x 3 3 x + 9 ((двучлен) 2 = трехчлен!!!)
После транспонирования: 4 x 2 21 x > 0
Коэффициент We: x ( 4 x 21) > 0
Теперь либо создайте числовую строку и проверьте, чтобы значения продукта были положительными (> 0), либо
Анализ x (4 x 21) графически вот так:
y = 4 x 2 21 x определяет открывающуюся вверх параболу (квадратичную)с нулями в x = 0 и x = 5,25
Положительные значения y слева от 0 и справа от 5,25
Решение: поскольку нам нужно просто > 0, а не = 0, мы не можем включать конечные точки:
мы также не можем включить x вне домена ( x < 1) поэтому,
решение 1 < x < 0 объединение с x > 5,25
Когда мы проверяем, мы обнаруживаем, что только x > 5,25 является допустимым решением.
.
Поиск правила
См. Функции MathRoom: поиск правила, пример 3
Словесная задача
При любой функциональной проблеме, как только у нас есть правило соответствия, мы можем спросить только о двух вещах. Либо мы знаем y -значение(я), и нам нужно найти x -значение(я) или наоборот.
Итак, здесь, как только мы найдем правило, нам нужно найти промежуток времени между 2 x -значениями ( c и d ) в паре с 6 метрами и 4 метрами в высоту.
Решение:
вершина равна (0, 10) — кривая движется вправо, поэтому b = 1 — точка P равна (25, 0) .
Итак, наша первая версия правила:
Подключение в x = 25 и F ( x ) = 0 :, SO 5 A = 9 и A = 6 и A = 6 и A = 9 6 и A = 9 6 и 5 A = 9 6 и 5 A = 2
Это означает, что .
Теперь положим f ( x ) = 6 и f ( x 6 ) = 9, чтобы найти0072 c и d .
Если, , то c = 4 .
Если, , то d = 9 .
Водяной ползунок находится под брезентом на 5 секунд .
.
Практика
1/ Приведите эти правила функции квадратного корня в стандартную форму (напоминание: b = ± 1)
| а) | б) |
| в) | d) |
2/ Перечислите значения параметров a, b, и вершины ( h, k ) для 4 функций в вопросе № 1.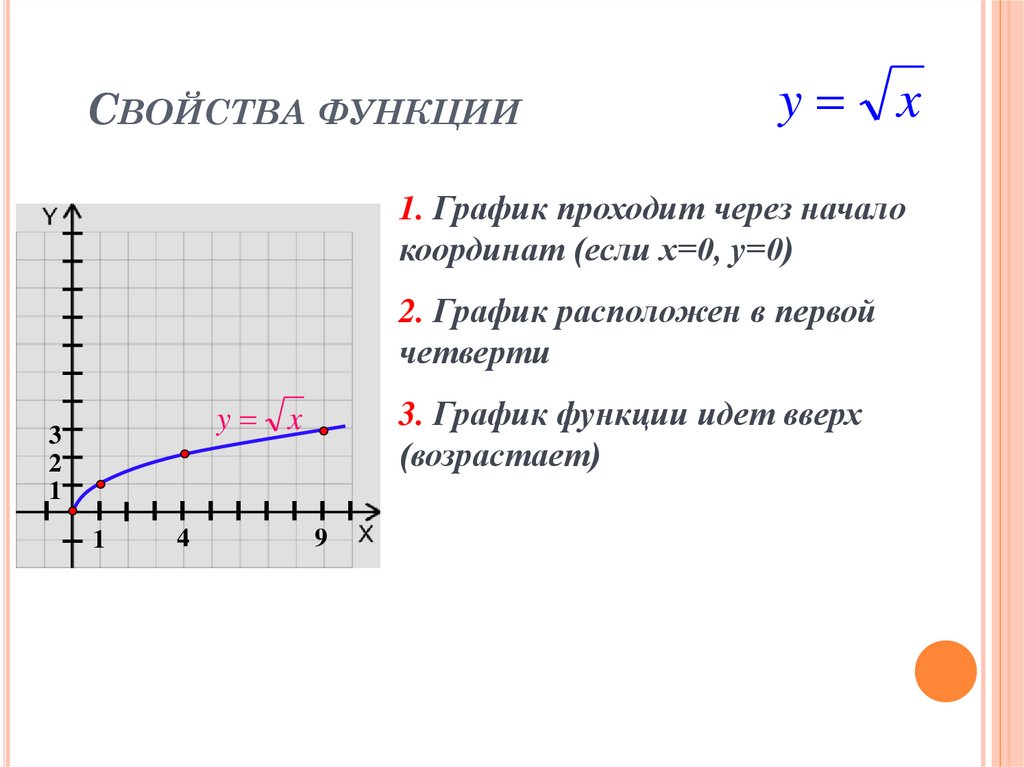
3/ Перечислите свойства функции: (область, диапазон, пересечения, вершина, вариация, знаки)
для 4 функций в вопросе № 1.
4/ Постройте график правил функции в пунктах № 1 (а) и (с).
5/ Укажите правило и любые ограничения для обратной функции квадратного корня:
| а) | б) |
| в) | г) |
6/
На схеме изображена столовая гостиницы.
Красная кривая, которая определяет крышу, представляет собой функцию квадратного корня с
.
правило соответствия, как показано.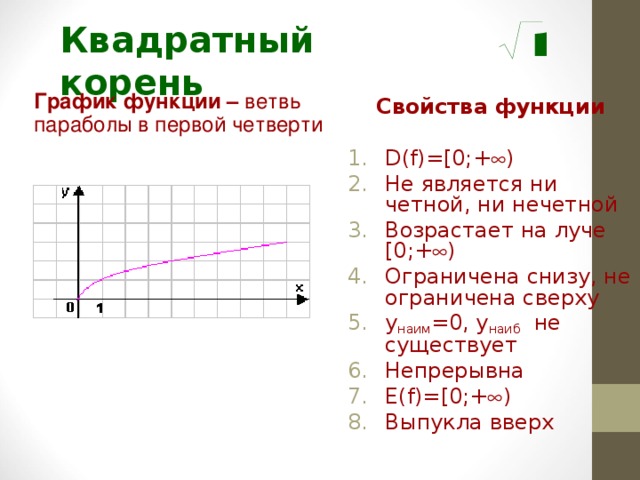
а) Найдите расстояние между гостиницей и столовой.
б) Найдите высоту прямоугольной стены столовой, обращенной в сторону гостиницы.
c) На какой высоте над землей находится ОСНОВАНИЕ флагштока?
.
.
Решения:
1/ Приведите эти правила функции квадратного корня в стандартную форму (напоминание: b = ± 1)
| а) | |
| в) | |
| г) | |
2/
| а) а = 6 | б = 1 | (ч, к) = ( 2, 3 ) | б) а = 2 | б = 1 | (ч, к) = ( 1, 2 ) |
| в) | б = 1 | (ч, к) = ( ¾ , 0 ) | г) а = ¼ | б = 1 | (h, k) = (32, 1) |
3/ а)
| домен : a) x > 2 или B) x < 1 или C) x > C) x > 6666666. | 9666666. 6666. x > . г) x < 32 или | диапазон: a) y > 3 , или b) y > 2, or c) y < 0 or d) у < 1 или | вершина: а ) (h, k) = ( 2, 3 ) b) (h, k) = ( 1, 2 ) c) (h, k) = ( 3/4, 0 ) d) (h, k) = ( 32, 1 ) |
| нули: a > 0 и k = 2 c) ( ¾, 0 ) d) (16 , 0) | у-внутр: а) б) ( 0, 4 ) в) г) | по возрастанию: а) б) никогда. в) никогда. г) . | |
| по убыванию: а) никогда. б) . в) . г) никогда. | отрицательный (< 0) : а) [ 2, 7/4 [ б) никогда; g(x) > 0 = x в) ; г) | положительный ( > 0) : а) б) в) никогда, ч ( x ) < 0 для всех x d) ] 16, 32 [ |
4/ a) Вершина (2, 3) перемещается вверх и вправо.
c) Вершина ( ¾, 0) перемещается вниз и вправо.
5/ Укажите правило и любые ограничения для обратной функции квадратного корня:
| а) возведи в квадрат и найди y . так, сейчас, ограничения: x > 3; и у < 1. | б) выделяем корень так, квадрат, решаем: ограничения: х < 2; и y > 3. |
| c) возводим в квадрат и решаем, чтобы получить: ограничения: x < 7; и у > 4. | г) Сейчас, ограничения: x < 5; и у < 2. |
6)
В стандартной форме правило соответствия:
а) Расстояние между гостиницей и столовой = ч = 5 метров.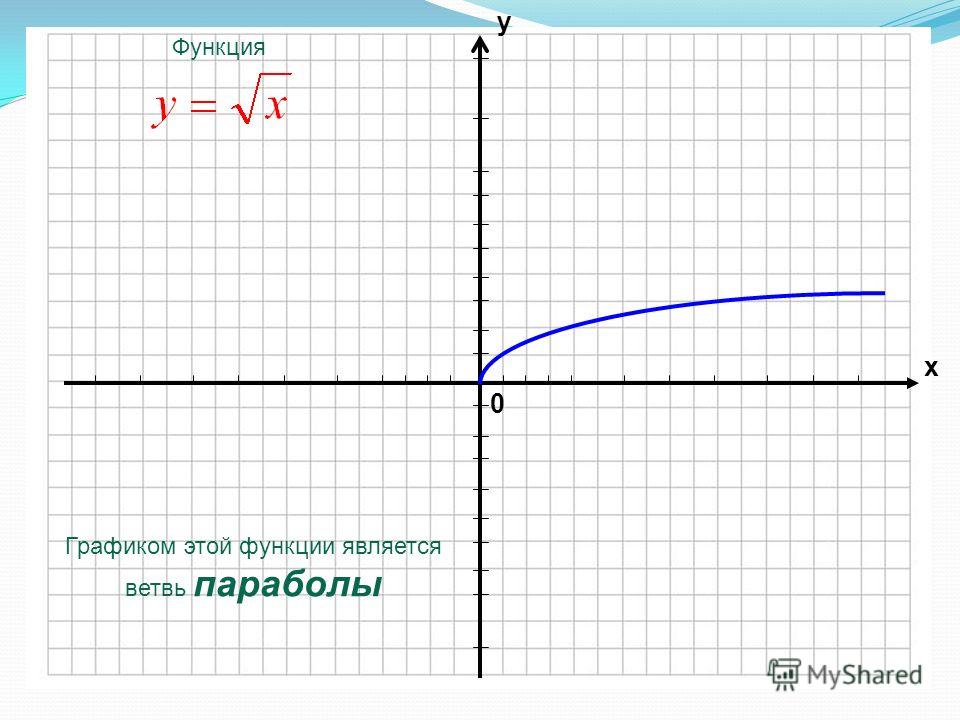
б) Высота стены = k = 6 метров.
c) Высота основания флагштока равна y-значению при x = 14 метров (5 метров + 9 метров).
установив х = 14, получим высоту основания флагштока 12 метров.
(индекс Mathroom функций)
( весь контент © MathRoom Learning Service; 2004 — ).
Список корней четвертой степени
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
12.2001 
Пожалуйста, помогите мне, потому что это немного срочно, и крайний срок уже близок, и я еще не понял, как это решить.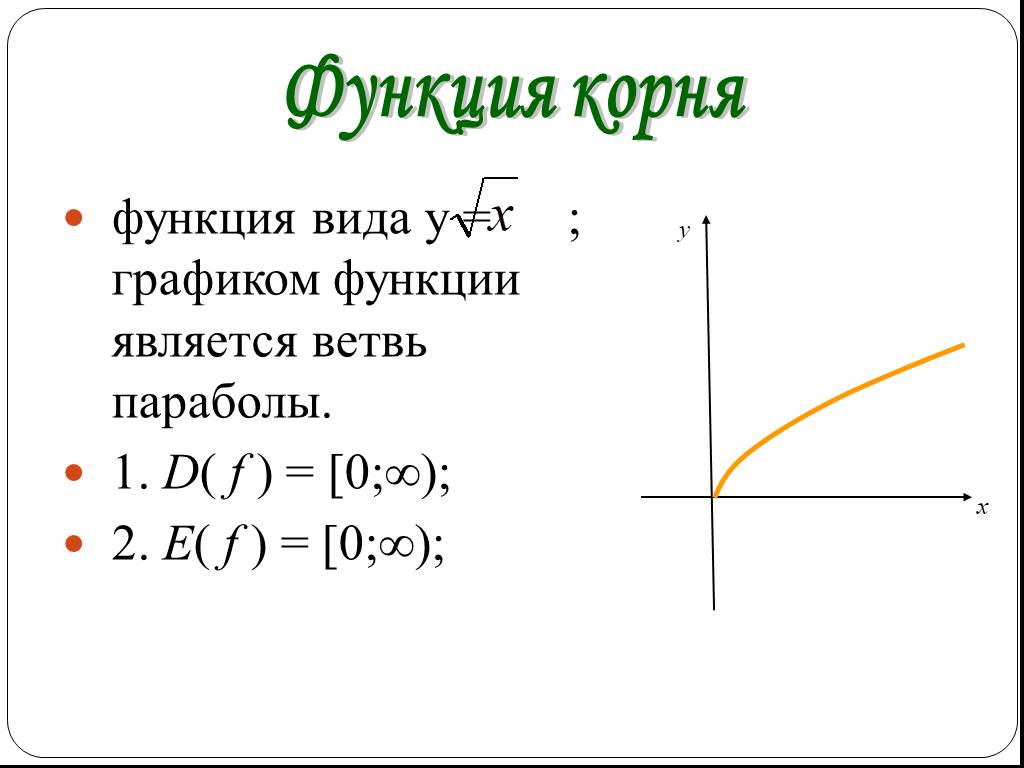
Вам просто нужна хорошая программа для прояснения сложных проблем. Вам не нужен репетитор, потому что, во-первых, это очень дорого, а во-вторых, его не будет рядом с вами, когда вам понадобится помощь. Программное обеспечение лучше, потому что вам нужно купить его только один раз, и оно будет вашим навсегда. Я советую вам попробовать Алгебратор, потому что он лучший. Поскольку он может решить практически любые математические задачи, вы наверняка будете использовать его очень долго, как и я. Я получил его давным-давно, когда учился на Basic Math, но до сих пор иногда им пользуюсь.
Но этот замечательный алгебра помог мне пройти всю мою коррекционную алгебру, предварительную алгебру и базовую математику. Я только набрал задачу, и пошаговое решение моего домашнего задания по алгебре появлялось на экране, просто нажимая «Решить». Я действительно рекомендую Алгебратор.
Он не только поможет вам решить математические задачи, но и подробно покажет все необходимые шаги, чтобы вы могли лучше понять предмет.