4 степень числа: Таблица 4 степени. Степени 4. Степени числа 4. Таблица степеней 4. 4 в степени

Четвертая и пятая степень числа (Таблица)

Справочная таблица дает значения четвертой и пятой степени чисел от 1 до 100. Будет полезна школьникам и студентам при решении математических и физических задач, подготовке к зачетам, экзаменам и егэ.

Чис­ло, n	Четве­ртая сте­пень, n4	Пя­тая сте­пень, n5
1	1	1
2	16	32
3	81	243
4	256	1024
5	625	3125
6	1296	7776
7	2401	16807
8	4096	32768
9	6561	59049
10	10000	100000
11	14641	161051
12	20736	248832
13	28561	371293
14	38416	537824
15	50625	759375
16	65536	1048576
17	83521	1419857
18	104976	1889558
19	130321	2476099
20	160000	3200000
21	194481	4034101
22	234256	5153632
23	279841	6436343
24	331776	7962624
25	390625	9765625
26	456976	11881376
27	531441	14348907
28	614656	17210368
29	707281	20511149
30	810000	24300000
31	923521	28629151
32	1048576	33554432
33	1185921	39135393
34	1336336	45435424
35	1500625	52521875
36	1679616	60466176
37	1874161	69343957
38	2085136	79235168
39	2313441	90224199
40	2560000	102400000
41	2825761	115856201
42	3111696	130691232
43	3418801	147008443
44	3748096	164916224
45	4100625	184528125
46	4477456	205962976
47	4879681	229345007
48	5308416	254803968
49	5764801	282475249
50	6250000	312500000
51	6765201	345025251
52	7311616	380204032
53	7890481	418195493
54	8503056	459165024
55	9150625	503284375
56	9834496	550731776
57	10556001	601,692 057
58	11316496	656356763
59	12117361	714924299
60	12960000	777600000
61	13845841	844596301
62	14776336	916132832
63	15752961	992436543
64	16777216	1073741824
65	17850625	1160290625
66	18974736	1252332576
67	20151121	1350125107
68	21381376	1453933563
69	22667121	1564031349
70	24010000	1680700000
71	25411681	1804229351
72	26873856	1934917632
73	28398241	2073071593
74	29986576	2219006624
75	31640625	2373046875
76	33362176	2535525376
77	35153041	2706784157
78	37015056	2887174363
79	38950031	3077056399
80	40960000	3276800000
81	43046721	3486784401
82	45212176	3707398432
83	47453321	3939040643
84	49737136	4182119424
85	52200625	4437053125
86	54700816	4704270176
87	57289761	4984209207
88	59969536	5277319163
89	62742241	5584059449
90	65610000	5904900000
91	68574961	6240321451
92	71639296	6590815232
93	74805201	6956883693
94	78074896	7339040224
95	81450625	7737809375
96	84934656	8153726976
97	88529281	8587340257
98	92236816	9039207968
99	96059601	9509900499
100	100000000	10000000000

 

Степень числа и как её найти.

Как возвести число в степень #

ГДЗ 1 класс

ГДЗ 10 класс

  

Категория: Математика

 Уже во втором классе на уроках математики дети сталкиваются с такими величинами, как площадь и объем. Учителя рассказывают, что площадь измеряется в квадратных сантиметрах или метрах и  так далее, а объем — в кубических. Дети просто запоминают и пишут см² или м² или мм³. Очень немногие в тот момент задумывались, что же означает приписанная в верхнем уголке единицы длины цифра. По-настоящему со степенью мы познакомимся в пятом классе, а если хотите это сделать самостоятельно, можете и раньше :))

Что такое степень числа?

Как вы знаете, с помощью произведения удобно записывать сумму нескольких одинаковых слагаемых. Например 5 + 5 + 5 + 5 + 5 + 5 = 5 * 7

А если это будет не сумма, а произведение одинаковых чисел? Например, множитель 5 взять 7 раз: 5 * 5 * 5 * 5 * 5 * 5 * 5? Для более краткого обозначения такого произведения математики и придумали степень.

5 * 5 * 5 * 5 * 5 * 5 * 5 = 5⁷ 

Выражение  5⁷ называют «степень», читается как пять в седьмой степени или седьмая степень числа 5. При этом 5 — основание степени, а 7 — показатель степени.

Число 7 показывает, сколько одинаковых множителей содержит произведение.

Как возвести число в степень?

Чтобы найти степень, нужно основание перемножить на себя столько раз, сколько написано в показателе.

          25  125  625 3125 15625
5⁷ = 5  *  5  *  5  *  5  *   5    *    5  *  5 = 78125
                       7 раз

Тут иногда возникает путаница оттого, что дети считают не количество цифр основания, а количество знаков умножения. Считать нужно цифры, а не знаки умножения. 5 * 5 — это уже вторая степень, потому что пятерки две.  5 * 5 * 5 = 5³,    5 * 5 * 5 * 5 = 5⁴ и так далее.

Рассмотрим еще примеры:

3² = 3 * 3 = 9
2³ = 2 * 2 * 2 = 8
а⁴ = а * а * а * а
(5b)² = 5b * 5b

Вторую степень числа называют «квадрат числа». Например, 3² читается как «три в квадрате» или квадрат числа три.

Третью степень числа называют «куб числа». Например 2³ читается как «два в кубе» или куб числа два.

Может ли показатель степени быть равным 1? Да, может. Но если любое число взять 1 раз, то получится то же самое число, то есть а¹ = а. А поскольку не принято рассматривать произведения, состоящие из одного множителя, то единичку в показателе степени обычно не пишут.

Например 8¹ = 8, 456¹ = 456

Возведение числа в степень — это арифметическое действие

Если в выражение входит степень, то сначала выполняют возведение в степень, а потом — остальные действия в приоритетном порядке.

Например: 5 * 2² = 5 * 4 = 20
                   5 + 2² = 5 + 4 = 9

 

А теперь вы поняли, что такое см²?  Правильно, это   см * см. Именно так мы находим площадь прямоугольника, умножая длину одной стороны в см на длину другой.  
А мм³?   Это мм * мм * мм. Так мы находим объем.

Чтобы закрепить знания о степени числа, посмотрите видео:

• Назад
• Вперед

 
умножить наподелить на

 

• Уроки
• Математика

Степень многочлена — определение

Многочлены являются одним из важных понятий математики, как и степень многочленов, которая определяет максимальное количество решений, которые может иметь функция, и количество раз, когда функция пересекает ось x. когда графически. Это самая высокая экспоненциальная степень в полиномиальном уравнении. Давайте узнаем подробно об этом понятии и о том, как найти степень многочлена.

1.	Что такое степень многочлена?
2.	Как найти степень многочлена?
3.	Классификация на основе степени многочлена
4.	Степень многочлена Приложения
5.	Часто задаваемые вопросы о степени многочлена

Что такое степень многочлена?

Степень полинома является наивысшей экспоненциальной степенью в полиномиальном уравнении. Для проверки степени любого полинома учитываются только переменные, коэффициенты игнорируются. Для полиномиальной функции n ^{-й степени} с вещественными коэффициентами и x как переменной, имеющей наибольшую степень n, где n принимает целые числовые значения, степень полинома p (x) = a _n x ⁿ + a _n-1 x ^n-1 + _n-2 x ^n-2 + .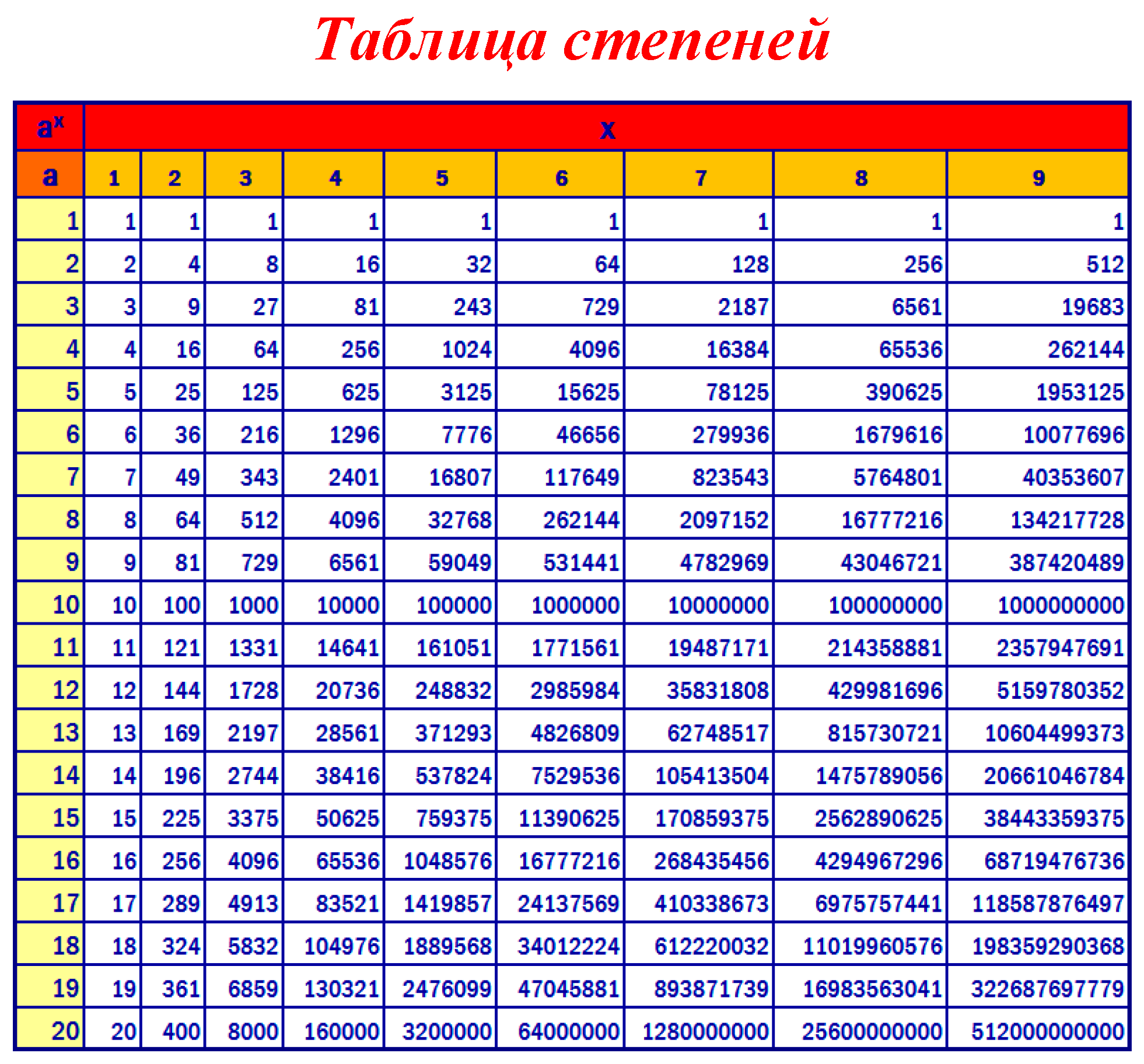 .. + a ₁ x ¹ + a ₀  в стандартной форме обозначается как «n».

Степень полинома Определение

Степень полинома — это наибольшая степень переменной в полиномиальном уравнении. Для определения степени полиномиальной функции рассматриваются только члены с переменными, чтобы узнать степень полинома. Наивысшая экспоненциальная степень переменного члена в полиноме указывает на степень этого полинома.

Посмотрите на полиномиальную функцию, приведенную ниже, где наибольшая степень x равна n. Следовательно, n — степень полинома этой функции.

Как найти степень многочлена?

Рассмотрим многочлен: p(x): 2x ⁵ −12x ³ +3x−π. Член с наибольшей степенью x равен 2x ⁵ , а соответствующий (наивысший) показатель степени равен 5. Следовательно, мы будем говорить, что степень этого многочлена равна 5. Таким образом, степень многочлена есть наибольшая степень переменная в полиноме. Мы можем представить степень многочлена как Deg(p(x)). Ниже приведены некоторые примеры:

• Градус(х ³ +1) = 3
• Градус(1+x+x ² +x ³ +…+x ⁵⁰ ) = 50
• град(х+π ³ ) = 1

Обратите внимание, что степень является наивысшим показателем переменного члена, поэтому, даже если показатель степени π равен 3 (см. последний пример, приведенный выше), это не имеет значения для определения степени многочлена.

Степень нулевого полинома

Когда все коэффициенты равны нулю, полином считается нулевым полиномом. Оно имеет вид f(x) = 0. Мы можем записать его как:

• f(x) = 0x ⁰
• f(x) = 0x ¹
• f(x) = 0x ²
• и так далее.

К этому времени вы, возможно, поняли, что степень нулевого многочлена не может быть определена. Таким образом, степень нулевого многочлена либо не определена, либо иногда она определяется отрицательным образом (-1 или -∞).

Степень постоянного многочлена

Постоянный многочлен (P(x) = c) не имеет переменных. Поскольку переменной нет, она не имеет силы. Таким образом, это можно записать как P(x) = Cx ⁰  as x ⁰  = 1. Таким образом, степень постоянного многочлена равна нулю. Например: Для 6 или 6x ⁰ степень = 0.

Степень полинома с более чем одной переменной

Степень полинома с более чем одной переменной можно вычислить путем сложения показателей степени каждой переменной в нем . Например: 5x ³ + 6x ² y ² + 2xy.

• 5x ³ имеет степень 3 (x имеет показатель степени 3).
• 6x ² y ² имеет степень 4 (x имеет показатель степени 2, y имеет 2, поэтому 2+2=4).
• 2xy имеет степень 2 (x имеет показатель степени 1, y имеет 1, поэтому 1+1=2).

Наибольшая степень из них равна 4, поэтому полином имеет степень 4 .

Классификация на основе степени многочлена

Каждый из многочленов имеет определенную степень и на основании этого им присвоено определенное имя. Давайте классифицировать многочлены на основе степени многочлена с примерами.

Многочлены	Степень	Примеры
Постоянный многочлен	Многочлены со степенью 0	3
Линейный многочлен	Многочлены со степенью 1	х + 8
Квадратичный многочлен	Полиномы степени 2	3x 2 — 4x + 7
Кубический многочлен	Полиномы степени 3	2x 3 + 3x 2 + 4x + 6
Многочлен четвертой степени	Многочлены степени 4	x 4 -16
Полином пятой степени	Многочлены степени 5	4x 5 + 2x 3 — 20

Степень полинома Приложения

Ниже приведены несколько применений степени многочлена:

• Чтобы определить максимальное количество решений, которые может иметь функция.
• Чтобы определить максимальное количество раз, когда функция пересекает ось X при построении графика.
• Чтобы проверить, является ли полиномиальное выражение однородным, определите степень каждого члена. Когда степени членов равны, то полиномиальное выражение является однородным, а когда степени не равны, то выражение называется неоднородным. Например, в 4х ³ + 3xy ² +8y ³ степень всех слагаемых равна 3. Следовательно, данный пример является однородным полиномом степени 3.

Степень многочлена Советы и хитрости:

Чтобы найти степень многочлена, выполните следующие действия:

1. Определите каждый член данного многочлена.
2. Объедините все подобные термины, переменные термины; игнорировать постоянные термины.
3. Расположите эти термины в порядке убывания их силы.
4. Найдите член с наибольшим показателем степени, определяющий степень многочлена.

Важные примечания о степени полинома:

• Степень полинома только с одной переменной: наибольший показатель степени переменной в полиноме (используя правило знаков Декарта)
• Степень многочлена с более чем одной переменной: сложите показатели степени каждой переменной, заданной в члене, и найдите, какой член имеет наибольшую степень. Это и будет считаться степенью многочлена.
• Степень рационального выражения: Берем степень верха (числитель) и вычитаем степень низа (знаменатель).

☛ Статьи по теме:

Проверьте эти интересные статьи, связанные с понятием степени многочленов в математике.

• Калькулятор степени полинома
• Полиномы одной переменной
• Калькулятор степени полинома

 

Степень многочлена Примеры

1. Пример 1: Определите старший коэффициент и степень многочлена следующего многочлена 5x ² — 20x — 20.

   Решение:

   Дано полиномиальное выражение, 5x ² — 20х — 20 , Старший показатель переменной x равен 2, поэтому степень многочлена равна 2. Коэффициент с наибольшим показателем степени будет старшим коэффициентом полинома, поэтому старший коэффициент равен 5.

   Ответ: Следовательно, степень = 2 и старший коэффициент = 5.

2. Пример 2: Найти степень многочлена 5x ⁴ + 3x ² — 7x ⁵ + x ⁷ .

   Решение:

   Чтобы найти степень, проверьте каждый член данного полинома. Все они непохожи на термины с x в качестве переменной. Расположите эти члены в порядке убывания их степеней, что дает x ⁷ — 7x ⁵ + 5x ⁴ + 3x ² . Термин с наибольшим или наивысшим показателем степени равен x ⁷ .

   Ответ:  Следовательно, степень многочлена равна 7.

3. Пример 3: Найдите многочлен четвертой степени, удовлетворяющий следующим условиям: имеет корни (x-2), (x+5) и должен делиться на 4x ² .

   Решение:

   Мы уже знакомы с тем фактом, что многочлен четвертой степени является многочленом степени 4. Также мы знаем, что мы можем найти многочленное выражение по его корням.
   Первое условие: (x-2) (x+5) = x(x+5) — 2(x+5) = x ² +5x-2x-10 = x ² +3x-10.
   Второе условие: (x ² +3x-10)(4x ² ) = x ² ,4x ² + 3x,4x ² — 10,4x ² = 4x ⁴ +12x ³ -40x ²

   Ответ: Следовательно, искомый многочлен равен 4x ⁴ + 12x ³ — 40x ² .

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по степени многочлена

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о степени многочлена

Что такое степень многочлена?

степень многочлена — высшая степень переменного члена с ненулевым коэффициентом в многочлене.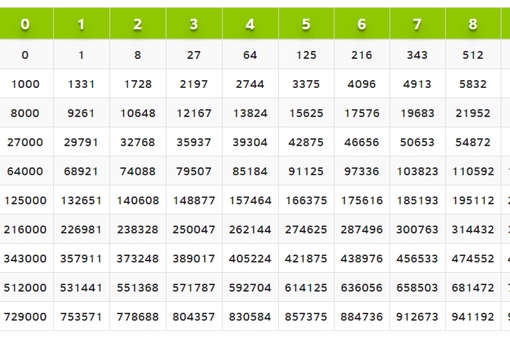

Что такое степень квадратного многочлена?

Квадратичные многочлены характеризуются как многочлены степени 2. Таким образом, степень квадратного многочлена равна 2.

Что такое многочлен степени 3?

Полиномы степени 3 известны как кубические полиномы. Они имеют 3 как самый высокий показатель степени переменной. Одним из примеров степени многочлена 3 является x ³ + 5x — 20.

Как найти степень многочлена с более чем одной переменной?

Иногда многочлен может иметь несколько переменных. В этом случае добавьте показатели всех переменных, чтобы вычислить степень каждого термина. Тогда высшая степень — это степень многочлена. Рассмотрим пример ниже.

Пример:  Найдите степень многочлена 5xy — 7x ² y + 10x ²  y ³ .

Решение:

Вычислим степень каждого члена, складывая показатели степени.

• Степень 5xy (= 5x ¹ y ¹ ) равна 1 + 1 = 2.
• Степень 7x ² y (= 7x ² y ¹ ) равна 2 + 1 = 3.
• Степень 10x ²  y ³  равно 2 + 3 = 5.

Среди всех этих степеней 5 является наибольшим числом, и, следовательно, степень данного многочлена равна 5.

Какова степень нулевого многочлена?

У нулевого многочлена все переменные коэффициенты равны нулю. Это постоянный многочлен со значением 0. Таким образом, степень нулевого многочлена не определена.

Какова степень многочлена 5x

⁴ ?

Для многочлена 5x ⁴ показатель степени с переменной x равен 4. Таким образом, степень многочлена 5x ⁴ равна 4.

Какова степень многочлена 5√3?

Степень многочлена 5√3 равна нулю, поскольку нет переменной, а степень любого многочлена определяется наибольшей экспоненциальной степенью его переменного члена. Кроме того, степень любой константы равна 0,9.0003

Почему важна степень многочлена?

Степень полиномиальной функции имеет большое значение, поскольку она определяет максимальное количество точек пересечения по оси x, которые может иметь функция, и максимальное количество пересечений функции с осью x при построении графика.

Почему степень постоянного многочлена?

Постоянный многочлен — это многочлен, в состав которого входит только константа. Постоянная функция имеет вид f(x) = c и может быть записана как f(x) = cx ⁰ . Здесь сам старший показатель равен 0 и, следовательно, степень постоянного многочлена равна 0.

Количество различных действительных корней многочлена степени 4

$\begingroup$

Предположим, у меня есть уравнение степени 4, и я не знаю правильного метода решения этого типа уравнения (например, завершение квадрата является правильным методом решения квадратного уравнения), так как или какие необходимые шаги я должен следуйте, чтобы я мог точнее угадать корни такого уравнения. 92+x-1=0 $ равно $\_\_\_\_\_$

Все мы знаем, что многочлен степени n может иметь максимум n корней. Таким образом, приведенное выше уравнение может иметь максимум 4 корня. Поэтому я написал 4 в качестве ответа, так как не было отрицательной отметки, но я проверил, построив график этого уравнения в графическом калькуляторе, который показал, что это уравнение имеет 2 корня. Так что, если бы я знал, как узнать корни, это могло бы наградить меня большим количеством баллов.

Так что же делать?

• полиномы 92+1), $$ что везде положительно.

  Редактировать (спасибо, almagest): Этот аргумент дает верхнюю границу количества корней. Завершение аргумента требует проверки функции, чтобы продемонстрировать, что она имеет по крайней мере два корня, например. при оценке функции при -1, 0 и 1.

  $\endgroup$

  4

  $\begingroup$

  Это, наверное, не лучший ответ, но я бы сделал это именно так, так как я думаю, что в этом виде экзамена время матерится? 92 + 24x + 1 > 0$$. Таким образом, $+1$ — это всего лишь движение справа налево на графике.

  Таким образом, вывод состоит в том, что $f'(x) > 0 \ \для всех x > -\lambda, \ f'(x) < 0 \ \для всех x < -\lambda$. Следовательно, согласно логике и теоремам, у $f(x) = 0$ есть только два различных решения $f(x) = 0$. Остальные сложные, но различные ли они?

  Я знаю, что это неправильно, но, как я уже говорил, вы хотели ответить на вопрос как можно быстрее.

  $\endgroup$ 9{\простое}(17) &= 17 &>0. \end{случаи} таким образом, $P(x)$ выпукла, причем два действительных корня лежат в одном $(-1,0)$, а другом в $(0,1)$.

  $\endgroup$

  $\begingroup$

  Хорошо, это может быть спорным вопросом в настоящее время, но вот двухэтапный метод, который я бы использовал, чтобы «найти количество различных корней». Это НЕ попытка найти то, что они есть.

  1. Правило изменения знака Декарта

      y(x): {1, -4, 12, 1, -1} --> 3 смены знака
     y(-x): {1, 4, 12, -1, -1} --> 1 изменение знака
      

  Возможные сценарии

   Поз. отр. Комм. Cnj. Всего пара
       3 1 0 4
       2 1 1 4
   

  2. Найдите знак дискриминанта многочлена четвертой степени.

     No related posts.