Факультативное занятие в 5 классе по теме «Факториал»
Факультативное занятие в 5 классе
Понятие факториала
Задача №1:
Семье, состоящей из бабушки, папы, мамы, дочери и
сына, подарили 5 разных чашек. Сколькими способами можно разделить чашки между членами семьи?
Решение:
Бабушка
5
Папа
4
Мама
3
2
Дочь
Учебник «Математика – 5» Н.Я.Виленкин, задача №694 стр.106
Сын
1
5*4*3*2*1=120 способов
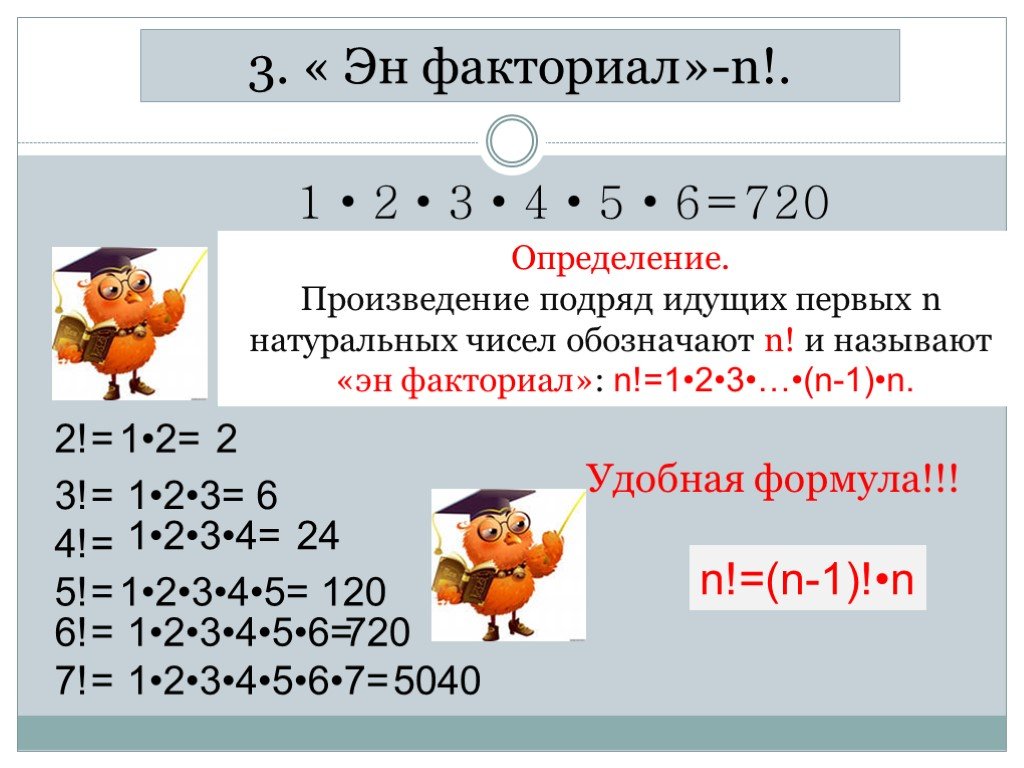
Определение:
Произведение подряд идущих первых n натуральных чисел обозначают n! и называют «эн факториал»:
n! = 1 × 2 × 3 × … ×(n – 1)×n.
Таблица факториалов
n
1
2
3
4
5
6
7
2
24
720
n!
1
6
120
5040
Пользуясь таблицей факториалов, вычислите:
6! : 60 =
40 – 4! =
3! ∙ 5 =
7! – 5000 =
5! : 3! =
6! + 2! =
5! +125 =
4! : 2! +56 =
4!-2 =
6! – 120 =
Задача №2:
Сколькими способами четыре вора могут по одному разбежаться на все четыре стороны?
Решение:
Пусть воры разбегаются поочередно.
У первого – 4 варианта выбора
У второго – 3 варианта выбора
У третьего – 2 варианта выбора
У четвертого – 1 вариант выбора
По правилу умножения:
4 ∙ 3 ∙ 2 ∙ 1 = 4! = 24
Ответ: 24 способа.
Задача №3:
В среду пятом классе пять уроков: математика, история, русский язык, природоведение и физкультура. Сколько различных вариантов расписания на среду можно составить?
Решение:
Для математики – 5 вариантов расположения в расписании, для истории – 4 варианта, для русского языка – 3 варианта, для природоведение – 2 варианта, для физкультуры – 1 вариант. По правилу умножения получаем:
Задача № 733 «Математика 5» Н.Я.Виленкин
5 ∙ 4 ∙ 3 ∙ 2 ∙ 1 = 5! = 120
Задача №4:
В семье – шесть человек, а за столом в кухне – шесть стульев. В семье решили каждый вечер, ужиная, рассаживаться на эти шесть стульев по-новому.
Сколько дней члены семьи смогут делать это без повторений?
Решение:
Для удобства будем считать , что семья будет рассаживаться поочередно.
У бабушки – 6 вариантов выбора стульев.
У дедушки – 5 вариантов выбора стульев.
У мамы – 4 варианта выбора стульев.
У папы – 3 варианта выбора стульев.
У дочери – 2 варианта выбора стульев.
У сына – 1 вариант выбора стульев.
По правилу умножения:
6×5×4×3×2×1 = 720 (дней).
Задача № 5:
Ребята Андрей, Боря, Витя, Гриша, Дима и Женя решили покататься на карусели. На ней было 6 сидений. Одно изображало льва, другое – тигра, третье – слона, четвёртое – оленя, пятое – медведя, шестое – жирафа. Ребята заспорили, кому на какого зверя садиться. Поэтому они решили перепробовать все способы. Сколько раз пришлось им покататься на карусели?
Решение:
Пусть первым выбирает место Андрей.
Он мог сесть на любого из шести зверей, поэтому у него было 6 возможностей выбора. Но когда он занял своё место, Боре оставались лишь 5 возможностей. Точно так же Вите остались 4 варианта выбора, Грише – 3, Диме – 2, а когда садился на карусель Женя, ему оставалось
только одно свободное место. Значит, ребята
могли сесть на карусель 6! способами.
Ответ: 6!= 720.
Задача № 6:
Ольга помнит, что телефон подруги оканчивается цифрами 5,7,8, но забыла, в каком порядке эти цифры следуют. Укажите наибольшее число вариантов, которые ей придётся перебрать, чтобы дозвониться подруге.
Решение:
Три последние цифры телефонного номера могут быть расположены в одном из 3!=6 возможных порядков, из которых только один верный. Оля может сразу набрать верный вариант, может набрать его третьим, и т.д. Наибольшее число вариантов ей придётся набрать, если правильный вариант окажется последним, т.
шестым.
Задача № 7:
В гостинице семь одноместных номеров, и семеро гостей желают в них разместиться. Найдите число возможных комбинаций:
а) если гости заранее не бронировали места;
б) если трое гостей зарезервировали конкретные номера.
Решение:
а) Номеров – 7 и гостей – 7, значит, число возможных комбинаций равно 7!= 5040.
б) Три гостя, зарезервировавших номера, займут свои номера. Четвёртый гость может выбрать любой из 4 свободных мест, пятый – из 3, шестой – из 2, седьмой займёт 1 оставшийся номер. Общее
число способов расселения равно
4∙3∙2∙1=4!=24
Задача № 8:
Семь мальчиков, в число которых входят Олег и Игорь, становятся в ряд. Найдите число возможных комбинаций, если:
а) Олег должен находиться в конце ряда;
б) Олег должен находиться в начале ряда, а Игорь – к конце ряда.
Решение:
а) Всего 7 мальчиков на 7 местах, но Олег должен находиться в конце ряда. Значит, число возможных комбинаций при этом равно числу перестановок 6 мальчиков, стоящих перед Олегом, т.е. 6!=720.
б) Олег должен находиться в начале ряда, а Игорь – в конце, значит, число комбинаций равно числу перестановок 5 мальчиков, т.е.
5!=120 .
Задача № 9:
Одиннадцать футболистов строятся перед началом матча. Первым становится капитан, вторым – вратарь, а остальные – случайным образом. Сколько существует способов построения?
Решение:
После капитана и вратаря третий игрок может выбрать любое из оставшихся 9 мест, следующий – из 8, и т.д. Общее число способов построения равно 9!=362880
Задача № 10:
Современные пятиборцы в течение двух дней участвуют в соревновании по следующим видам спорта: фехтование, плавание, стрельба и бег.
а)Сколько существует вариантов порядка прохождения видов соревнования?
б) Сколько существует вариантов прохождения видов соревнования, если известно, что последним видом должен быть бег?
в) Сколько существует вариантов прохождения видов соревнования, если известно, что первым видом должен быть бег, а последним — стрельба?
Решение:
а) 4!=24
б) 3!=6в) 2!=2
Задача №11:
«Вороне Бог послал кусочек сыра», брынзы, колбасы, сухарика и шоколада. «На ель Ворона взгромоздясь, позавтракать совсем уж было собралась, да призадумалась»:
а) если есть кусочки по очереди, то из скольких вариантов выбирать;
б) сколько получится вариантов, если какой-то кусочек всё-таки бросить Лисе, а потом ответить на первый вопрос?
Решение:
а) Если есть кусочки по очереди это значит выбирать только порядок их следования, т.
е. 5!=120
б) Если бросить Лисе кусочек, то останутся 4 кусочка, которые можно съесть одним из 4!=24 способами. Но Лисе можно бросить любой из 5 кусочков, поэтому общее число вариантов рано
5*4!=120.
До новых встреч
с занимательными задачами
Как сделать Факториал?
Как сделать Факториал?
Факториалом числа называют произведение всех натуральных чисел до него включительно. Например, факториал числа 5 равен произведению 1 * 2 * 3 * 4 * 5 = 120. Формула нахождения факториала: n!
Как расписать N Факториал?
Факториал натурального числа – это число, умноженное на «себя минус один» , затем на «себя минус два» , и так далее до 1 . Факториал n обозначается как n! Задача – написать функцию factorial(n) , которая возвращает n! , используя рекурсию.
В каком классе изучается комбинаторика?
Изучение элементов комбинаторики, статистики и теории вероятностей целесообразно начать в 5–6 классах.
Можно ли складывать Факториалы?
Чтобы вычесть факториал из факториала, никакого общего правила нет: всё, что можно сделать, это вынести за скобки общий множитель, ну например: Тут ничего хитрого нет. Ну и получается, что нужно считать факториал только меньшего числа. С суммой всё получится аналогично.
Что такое Факториал в программировании?
Это функция, вычисляющая произведение последовательных натуральных чисел от 1 до N включительно: N! … Факториал — быстрорастущая функция, уже для небольших значений N значение N! имеет много значащих цифр. Попробуем реализовать эту функцию на языке программирования.
Что такое Факториал в теории вероятности?
N-факториал или N! – это количество перестановок из N объектов, вычисляемое по формуле PN=N! =1∗2∗3∗… ∗(N−1)∗N.
Что такое размещение в комбинаторике?
В комбинаторике размеще́нием (из n по k) называется упорядоченный набор из k различных элементов из некоторого множества различных n элементов.
…
Что такое сочетание в комбинаторике?
Сочетаниями из n элементов по k называются соединения, которые можно образовать из n элементов, собирая в каждое соединение k элементов; при этом соединения отличаются друг от друга только самими элементами (различие порядка их расположения во внимание не принимается).
Как понять Комбинаторику?
В узком смысле комбинаторика – это подсчёт различных комбинаций, которые можно составить из некоторого множества дискретных объектов. … Принципиально важно, что эти объекты поддаются перечислению – их три (дискретность) и существенно то, что среди них нет одинаковых.
Как понять размещение или сочетание?
Объясните понятным языком. Представляйте себе, что сочетание — это беспорядочная кучка, а размещение — когда предметы из кучки РАЗМЕСТИЛИ, за каждым закрепили МЕСТО. … В комбинаторике сочетанием называют неупорядоченный набор, а размещением — упорядоченный набор.
Что такое размещение?
Более формально, размеще́нием (из n по k) называется упорядоченный набор из k различных элементов из некоторого множества различных же n элементов.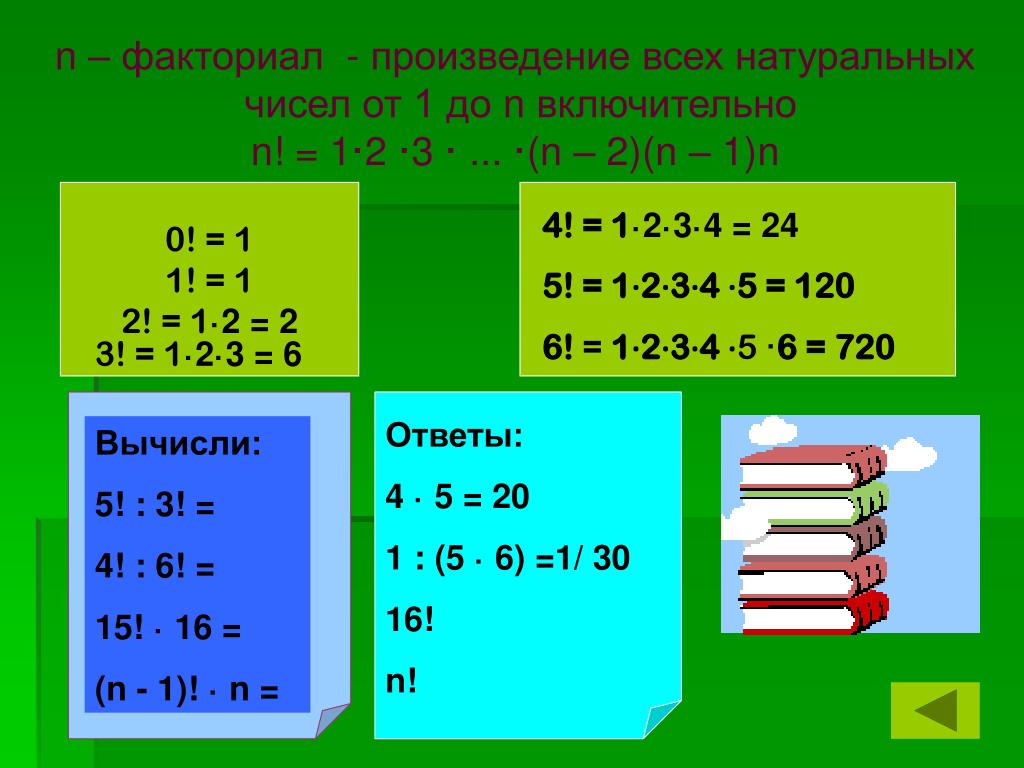
…
Что такое размещение формула?
Размещения, формула Общее число размещений из m элементов в группах по n обозначается A m n. Это число равно произведению n последовательных целых чисел, из которых наибольшее равно m. 1.
Чем размещение отличается от перестановки?
Перестановки из n элементов — частный случай размещения элементов из Е по k, при k=n. Иными словами, перестановками называют размещения без повторений из n элементов, в которые входят все элементы.
Как найти число размещений?
Формула для числа размещений. Размещениями из n элементов по m (мест) называются такие выборки, которые имея по m элементов, выбранных из числа данных n элементов, отличаются одна от другой либо составом элементов, либо порядком их расположения. Anm = n·(n − 1)·(n − 2)·… ·(n − m + 1) = n!/(n − m)!
Как посчитать количество перестановок?
Общая формула, которая позволяет найти число перестановок из n элементов, имеет вид (она же — формула для факториала числа n): Pn=n!
Что такое число перестановок?
Определение 3.
Группы элементов, состоящие из одних и тех же элементов и отличающиеся друг от друга только их порядком, называются перестановками этих элементов. Число всевозможных перестановок n элементов обозначается Pn. Как это будет ниже показано, оно равно произведению всех натуральных чисел от 1 до n.
Как называется любое множество состоящее из k элементов взятых из данных n элементов?
Перестановки. Размещения. Сочетания. Размещением из n элементов по k (k n) называется любое множество, состоящее из любых k элементов, взятых в определённом порядке из данных n элементов.
Что изучает комбинаторика?
Комбинаторика — это раздел математики, в котором изучают, сколько комбинаций, подчинённых тем или иным условиям, можно составить из данных объектов. Прежде чем переходить к общим принципам, рассмотрим несколько примеров.
Где используется комбинаторика?
Комбинаторика используется в музыке, в мебельном производстве, в различных играх (нарды, шашки, шахматы), где приходится рассматривать различные сочетания фигур, и выигрывать, изучив и зная выигрышные комбинации и умея избегать проигрышных.
Для чего нужна комбинаторика?
Комбинаторика – раздел математики , в котором изучается, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Задача комбинаторики – это задача размещения объектов по специальным правилам и нахождение числа способов таких размещений.
Что такое комбинаторика и для чего она нужна?
Комбинато́рика — это область математики, прежде всего связанная с подсчетом, как средство и цель получения результатов, так и с определением свойств конечных структур. …
В чем заключается правило произведения?
Правило произведения. Пусть объект a можно выбрать m способами, после чего объект b можно выбрать n способами. Тогда упорядоченную пару (a, b) можно выбрать mn способами; иными словами, существует mn различных упорядоченных пар (a, b).
Чем занимается комбинаторный анализ?
Комбинаторика, комбинаторный анализ — один из разделов дискретной математики, который играет важную роль, как в связи с его использованием в теории вероятностей, математической логике, теории чисел, кибернетике, так и имеющий важное самостоятельное значение при решении задач, связанных с подсчетом числа способов .
..
Какой способ используется для решения комбинаторных задач?
Методы решения комбинаторных задач
- Простые задачи решают обыкновенным полным перебором возможных вариантов без составления различных таблиц и схем.
- Самые разные комбинаторные задачи решаются с помощью составления специальных схем. …
- Решить комбинаторные задачи можно с помощью таблиц.
чему равен факториал 5?
Калькулятор факториала До 10 000
Здесь вы можете найти ответы на такие вопросы, как: каков факториал числа 5? Чему равен факториал числа 5? Каковы последние цифры факториала числа 5? Сколько нулей в конце факториала 5? Сколько цифр в факториале 5? Воспользуйтесь приведенным выше калькулятором факториала, чтобы найти факториал любого натурального числа в диапазоне от 0 до 10 000.
Что такое факториал?
Определение факториала
Факториал — это количество, определенное для любого целого числа n, большего или равного 0.
Факториал — это произведение всех целых чисел, меньших или равных n, но больших или равных 1. Значение факториала 0 по определению равно 1. Для отрицательных целых чисел факториалы не определены. Факториал можно рассматривать как результат умножения последовательности убывающих натуральных чисел (например, 3 × 2 × 1).
Символ факториала — восклицательный знак!.
Формула факториала
Если n — натуральное число, большее или равное 1, то
n! = n x (n — 1) x (n — 2) x (n — 3) … 3 x 2 x 1
Если n = 0, то n! = 1, по соглашению.
Пример: 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720
Ярлык для поиска конечных нулей в факториале
Конечные нули представляют собой последовательность нулей в десятичном представлении числа, после которой не следуют никакие другие цифры. В этом видео показано, как легко найти конечные нули факториала.
Таблица факториалов до 30
| нет | нет! |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
| 8 | 40320 |
| 9 | 362880 |
| 10 | 3628800 |
| 11 | 39916800 |
| 12 | 47 00 |
| 13 | 6227020800 |
| 14 | 87178291200 |
| 15 | 1307674368000 |
| 16 | 20922789888000 |
| 17 | 355687428096000 |
| 18 | 6402373705728000 |
| 19 | 121645100408832000 |
| 20 | 2432 |
| 21 | 51090942171709440000 |
| 22 | 1124000727777607680000 |
| 23 | 25852016738884976640000 |
| 24 | 620448401733239439360000 |
| 25 | 15511210043330985984000000 |
| 26 | 403291461126605635584000000 |
| 27 | 10888869450418352160768000000 |
| 28 | 304888344611713860501504000000 |
| 29 | 8841761993739701954543616000000 |
| 30 | 265252859812191058636308480000000 |
Factorial Calculator
Please ссылка на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.
Пример расчета факториала.
- Factorial of 690
- Factorial of 300
- Factorial of 80
- Factorial of 77
- Factorial of 64
- Factorial of 57
- Factorial of 59
- Factorial of 107
- Factorial of 36
Отказ от ответственности
Несмотря на то, что мы прилагаем все усилия для обеспечения точности информации, представленной на этом веб-сайте, ни этот веб-сайт, ни его авторы не несут ответственности за какие-либо ошибки или упущения. Поэтому содержимое этого сайта не подходит для любого использования, связанного с риском для здоровья, финансов или имущества.
Чему равен факториал числа 5?
Ответить
Проверено
167,4 тыс.+ просмотров
Подсказка : Здесь, в этом вопросе, мы покажем, как вычислить факториал 5 и дать точный ответ. Факториал 5 означает, что мы умножаем 5 на каждое число под ним.
Полный пошаговый ответ :
Факториал — это величина, определяемая как любое целое число \[x\], большее или равное 0.
Факториал — это произведение всех целых чисел, меньших или равных \[ x\], но больше или равно 1. Значение факториала 0 по определению равно 1. Для отрицательных целых чисел факториалы не определены. Факториал можно рассматривать как результат умножения последовательности убывающих натуральных чисел.
Символом факториала является восклицательный знак ‘ \[!\] ’.
В общем случае формула факториала представлена в виде
Если n — натуральное число, большее или равное 1, то
\[n! = n \times \left( {n — 1} \right) \times \left( {n — 2} \right) \times \left( {n — 3} \right) \times \,\,… \,3 \раз 2 \раз 1\] .
Если \[p = 0\], то \[p! = 1\] по соглашению.
Рассмотрим заданный вопрос
Нам нужно найти значение факториала 5.