Конспект урока математики в 5 классе «Комбинаторные задачи» | Математика
Тема «Комбинаторные задачи» входит в содержание учебного материала за курс 5 класса по предмету Математика, учебник под редакцией А.Г. Мерзляк. Данная тема находится в составе раздела «Умножение и деление натуральных чисел» и впервые встречается детям, как первоначальные сведения из раздела «Теория вероятности». Для данного возраста тема сложна для восприятия, поэтому необходимо подобрать содержание таким образом, чтобы дети, используя имеющийся опыт математического образования смогли применить в новой ситуации. Образовательная деятельность, организованная в рамках учебного занятия, предполагает включенность каждого школьника в деятельность, направленную на повышение познавательной активности, повышение уровня овладения предметными умениями и обеспечения формирования математической грамотности. На каждом этапе урока используются приемы системно- деятельностного подхода:
-Организационный момент: вызов к побуждению действий, в индивидуальном продвижении и повышении мотивации к обучению;

-Выход на тему и целеполагание: использование игровой технологии (расшифровать ребус) и проблемного обучения позволяют развивать логическое мышление, аналитические навыки и умение обобщать, формулировать четкие, измеримые цели и планировать деятельность по их достижению, что обеспечивает новые образовательные результаты (регулятивные, познавательные, логические)
В течение всего урока дети включены в контрольно-оценочную деятельность через использование рабочего листа, напоминающий лист обратной связи (накопительная оценка на этапе освоения новых знаний и первичного закрепления), что позволяет определить уровень овладения предметным содержанием, организовать индивидуальную коррекционную работу в дальнейшем. При открытии новых знаний используются задания, направленные на формирование математической грамотности. Дети работают в группу по самостоятельному выбору.
Приёмы «Схематизация», «Яркое пятно», «» обеспечивают полное включение обучающихся в познавательную деятельность, развитие внимание, верное построение математического высказывания и контроля качества полученных знаний.
Данная форма проведения учебного занятия и методические приемы могут быть использована на любом занятии по предмету математика, физика, химия. Используемые в уроке приемы обеспечивают включенность всех школьников в активную деятельность.
Содержательная часть
Класс: 5 Предмет: Математика
Тема «Комбинаторные задачи» Тип урока: открытие новых знаний
Цель: организовать деятельность, направленную на успешное овладение планируемыми образовательными результатами.
Планируемые образовательные результаты:
|
Предметные умения Математическая грамотность |
Метапредметные |
Личностные |
|
Распознавать комбинаторные задачи среди других математических задач; Перечислять способы решения комбинаторных задач; Применять различные способы решения комбинаторных задач; Строить графы и применять правило умножения
Математическая грамотность: Применять предметные умения и жизненный опыт при решении задач; Описывать реальные ситуации на языке математики; Интерпретировать содержание задачи в виде графов; Структурирует данные согласно заданному условию Читательская грамотность: извлекать необходимую информацию в явном виде в сплошном и не сплошном видах текста, преобразовывать информацию, заданную в разной форме, интерпретировать информацию в виде схемы, графа
|
Познавательные: сравнивать, анализировать, обобщать и делать вывод, читать графическую и текстовую информацию; Регулятивные: Определять образовательную цель и планировать действия по её достижению, контролировать правильность выполнения задания, оценивать собственные действия; формулировать трудности, определять границы знания и незнания Коммуникативные: работать в группе, высказывать своё мнение, приводить аргументы для доказательства своего высказывания, договариваться, сотрудничать |
Давать оценку собственным умениям в соответствии с критериями; Определять индивидуальный рост овладения предметными умениями и планировать собственную деятельность по преодолению трудностей. |
Ход учебного занятия
|
Этап урока |
Содержание деятельности |
|
|
Организационный момент |
-Доброе утро, мои богатыри и боярыни! Вы не ослышались! Вы богатыри, потому что берете на себя тяжелую ношу новых знаний, а вы- боярыни, которые тихо, но с достоинством принимаете знания и применяете их. Каждый день вы стоите на пороге выбора: работать, не покладая рук, или просто провести время. Вот и сейчас настал момент выбора: мы постучимся в дверь в страну новых открытий или останемся на одном месте |
|
|
Актуализация знаний |
Прежде, чем открыть новые знания, нужно сосредоточиться, размяться и получить первые баллы. измерения 1 группа 2 группа 3 группа Sогорода Vдома Vбани Sсада Sучастка Sогорода Vдома Vбани Sсада Sучастка Sучастка Vдома Vбани длина 5 8 3 3 9 5 7 2 3 10 9 8 4 ширина 6 7 2 2 10 3 5 2 3 10 11 6 4 высота 1 3 2 2 1 1 2 2 2 3 1 3 2 Составьте код в рабочих листах в колонке ОТВЕТ О А Б Н О К Е Р Н Т Ы М И
|
99 8 144 12 90
-Какие умения вам понадобились, чтобы составить правильный код? (знать формулы площади прямоугольника, объема пар-да) -Составьте математический термин, который получился из трех ваших кодов? (комбинаторные) Как связан этот термин с содержанием слайда 2. |
|
Определение темы и целей урока (Прием «Ребус»), планирование их достижения |
Ну что ж, первое слово получено, найдены ассоциации этого понятия с реальной ситуацией, а значит ли это, что они нам могут пригодиться в жизни? (конечно) Тогда давайте попробуем определить, с чем разобраться, чем нам нужно овладеть, чтобы применять это в жизни? (дети формулируют цели, на сладе они записаны в хаотичном порядке). Ребята, я успела их зафиксировать, предложите, как изменить их места, чтобы наши знания по этой теме были последовательными. (дети предлагают начать с определения понятия Комбинаторика. —
|
|
|
Открытие нового (используется приём сравнения, исследовательский метод)
первичное закрепление и контроль |
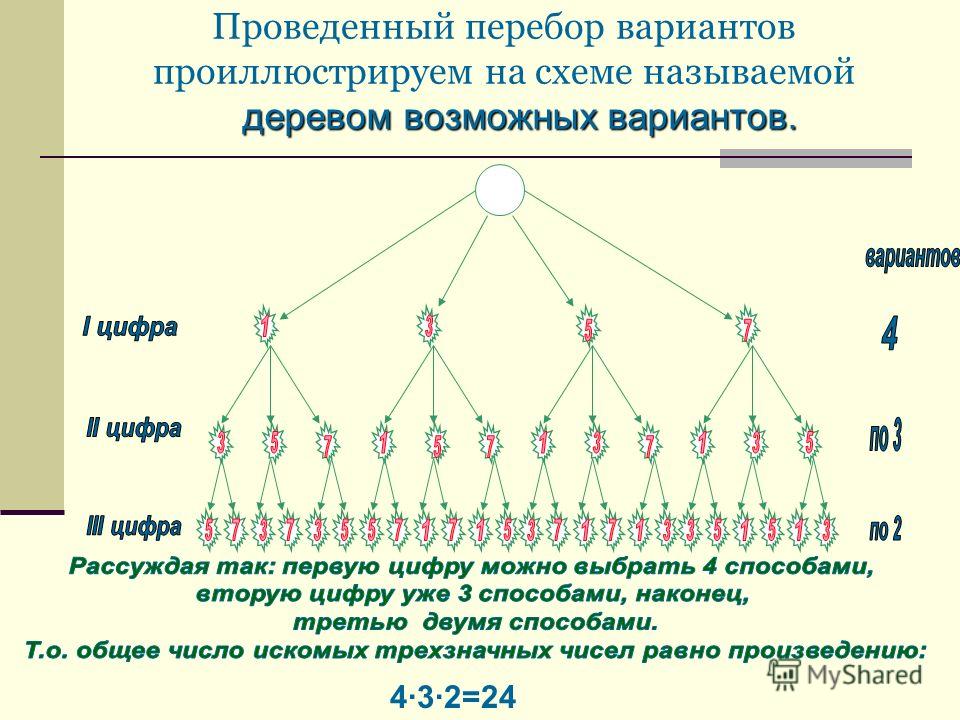
Молодцы! Я предлагаю вам ознакомиться с определением данного понятия по группам (каждой группе по 1 определению) (слайд5). -Прочтите полученные определения. Давайте выберем то, которое вам наиболее понятно (дети выбирают и делают запись в тетрадь по памяти). За эту работу поставьте себе баллы в рабочий лист в соответствии с критериями. -Ну что ж, продолжаем наш путь по дороге открытия новых знаний. Чтобы решить задачу нужно овладеть… (дети продолжают предложение СПОСОБАМИ решения комбинаторных задач-слайд 6). Итак, переходим к достижению данной цели. (включается отрывок аудиобасни И.А.Крылова «Квартет»). В какой последовательности сидели герои-животные? (Вместе обозначаем символами каждого из зверей) В группе составьте все возможные варианты и записывают в рабочие листы, как они могут присесть по-другому. Назовите свои варианты. Сколько Вариантов у вас получилось? (Всего 24 варианта, но они могут получить или нет, тогда возможны 2 исхода ситуации) Почему у вас не получилось такого ответа? Почему вы затратили много времени? Как можно назвать этот способ (СП-Б ПЕРЕБОРА (слайд7)).
ФИЗМИНУТКА (слайд 8)
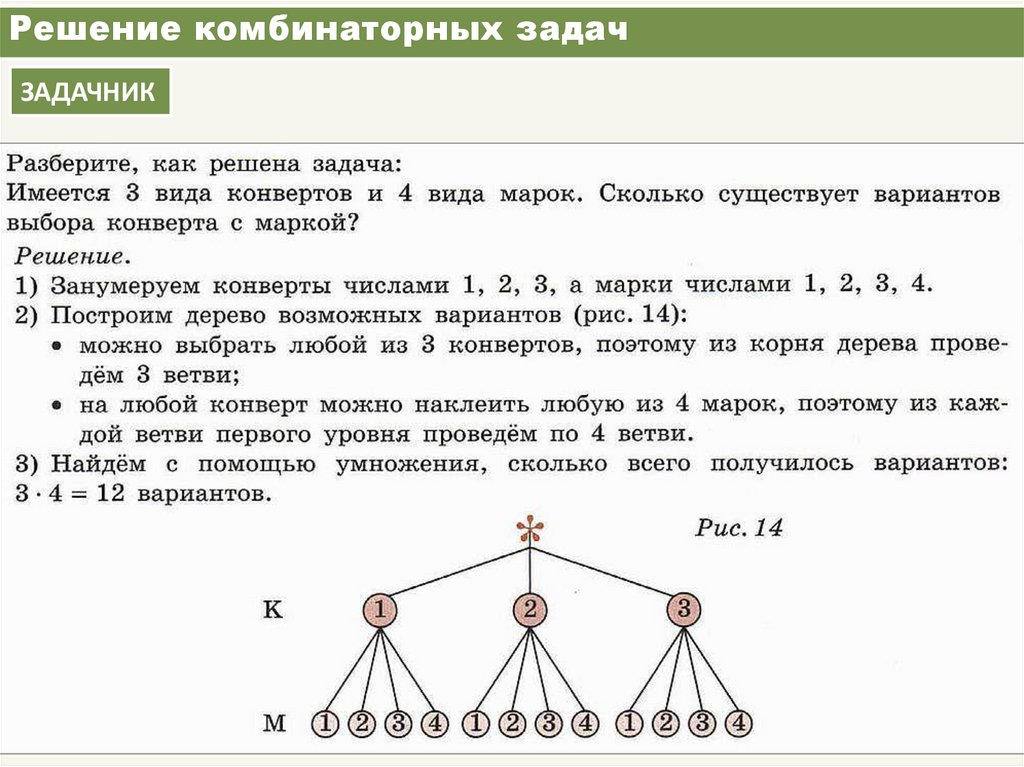
Была ли комбинаторная задача в физминутке. Какой способ решения этой задачи изображен на слайде (слайд 10)? Как записать с помощью третьего способа – правила умножения? (дети предлагают вариант) Сейчас я предлагаю себя проверить. Придя в школу, повесив одежду, вы всегда отправляетесь посмотреть расписание уроков, точнее их последовательность. Представьте, что расписания нет, вы можете пойти на любой из пяти сегодняшних уроков. Что же будет? ХАОС!!! Нужна ваша помощь завучу!
1 группа использует способ перебора, 2 группа –Дерево вариантов, 3 группа с помощью правила умножения. На работу 5 минут! Затем дети сравнивают с эталонами, которые им раздаются в группы. Оценивают свою работу в рабочих листах в соответствии с критериями.
|
|
|
Домашнее задание |
В рабочих листах у вас задача 2 к этому же условию задачи (на слайде 11 задача 2). |
|
|
Подведение итогов |
Посчитайте итоги в рабочем листе и переведите баллы в отметку в соответствии с нашими критериями Улыбнитесь те, кто получил5! И 4! Проанализируйте, смогли бы вы получить отметку выше той, которую получили? Что помешало этому? Как мы справились с целями? Запланируйте ваши действия на следующий урок, чтобы повысить свой результат
|
|
|
Рефлексия |
Составь хотя бы 2 варианта из предложенных участников последовательности, кому бы ты с удовольствием рассказал о том, какие умения приобрел сегодня на уроке (на 1 место поставь того, кому в первую очередь рассказал бы, на второе кому потом и так далее).
|
|
Приложение 1
Рабочий лист по теме «Решение комбинаторных задач» ФИ_________________________________
|
Этап урока |
Содержание деятельности |
Ответ |
Критерии |
Набранное количество баллов |
|
Разминка |
Родители решили купить земельный участок под строительство своего собственного дома, сделали сами план расположения построек, записав их размеры в таблицу (указав даже лишние измерения). Вам стало интересно и вы решили узнать, участок какой площади они покупают, какую площадь нам предстоит обрабатывать (где будет огород), каков будет объем надворных построек, и, возможно, вы дадите совет родителям об изменении измерений будущих построек: измерения 1 группа 2 группа 3 группа Sогорода Vдома Vбани Sсада Sучастка Sогорода Vдома Vбани Sсада Sучастка Sучастка Vдома Vбани длина 5 8 3 3 9 5 7 2 3 10 19 18 4 ширина 6 7 2 2 10 3 5 2 3 10 11 4 4 высота 1 3 2 2 1 1 2 2 2 3 1 7 6 Составьте код в рабочих листах в колонке ОТВЕТ О А Б Н О К Е Р Н Т Ы М И 168 70 6 15 9 30 96 100 209 8 392 12 90
|
1группа
|
Верно составлен код -2балла |
|
|
2группа
|
Верно составлен код -2балла |
|
||
|
3группа
|
Верно составлен код -2балла |
|
||
|
Определение темы и целей урока |
Запиши тему и собственные цели Тема урока: Мои цели: |
Активно участвовал -1балл |
|
|
|
Работа с информацией |
Выписать определение понятия КОМБИНАТОРИКА КОМБИНАТОРИКА- это |
Определение записал своими словами, используя главные слова из предложенного текста -2балла Определение переписал без изменения -1балл |
|
|
|
Решение задачи |
Проказница Мартышка (М), Козёл (К), Осёл(О) и Косолапый Мишка(П-Потапыч) затеяли сыграть квартет…Рассади героев в другом порядке. Решение задачи:
|
Верно решена задача заданным способом -4балла Задача имеет несколько вариантов или начата решать, но не хватило время -2балла Задача решена неверно -0баллов |
|
|
|
Решение задачи |
В физминутке распознать комбинаторную задачу (КЗ) и решить её: |
Распознал КЗ верно – 1балл Не нашел КЗ-0б Участвовал в решении -1б Решение просто записал – 0б |
|
|
|
Контроль умений -решаем в тетрадях!!! |
Придя в школу, повесив одежду, вы всегда отправляетесь посмотреть расписание уроков, точнее их последовательность. 1. В вашем 5А классе сегодня 5 уроков: физкультура, русский язык, литература, история, и математика. Сколько можно составить вариантов расписания на день, зная точно, что математика – первый урок |
Решил сам верно-5баллов Решил, но воспользовался помощью группы – 3балла Решал сам, но допустил ошибки -1б Решил неверно -0 баллов |
|
|
|
ДЗ |
2.Что изменилось в решении задачи, если бы не было условия про первый урок? Выбрать удобный способ и решить дома. Составить свою комбинаторную задачу. |
Решил сам верно-5баллов Решил, но воспользовался помощью одноклассников– 3балла Решал сам, но допустил ошибки -1б Решил неверно -0 баллов |
|
|
|
ИТОГ |
Посчитайте итоги в рабочем листе до раздела ДЗ и переведите баллы в отметку в соответствии с нашими критериями |
«5»- 15-16 баллов «4»-12-14баллов «3»-7-11 баллов |
|
|
Полный текст статьи см. приложение https://cloud.mail.ru/public/5YaY/LAZGfpUTL
приложение https://cloud.mail.ru/public/5YaY/LAZGfpUTL
Тест: Комбинаторные задачи — Математика 5 класс
Тест: Комбинаторные задачи — Математика 5 классАнглийский язык
Астрономия
Белорусский язык
Биология
География
ИЗО
Информатика
История
Итальянский язык
Краеведение
Литература
Математика
Музыка
Немецкий язык
ОБЖ
Обществознание
Окружающий мир
ОРКСЭ
Русский язык
Технология
Физика
Физкультура
Химия
Черчение
Для учителей
Дошкольникам
VIP — доступ
- Предметы »
- Математика »
- 5 класс »
- Комбинаторные задачи
Комбинаторные задачи
задачи на нахождение количества вариантов, можно использовать методы перебора, построение дерева вариантов, комбинаторные формулы, свойства.
Математика 5 класс | Автор: Евзрезова Елена Владимировна | ID: 8256 | Дата: 17.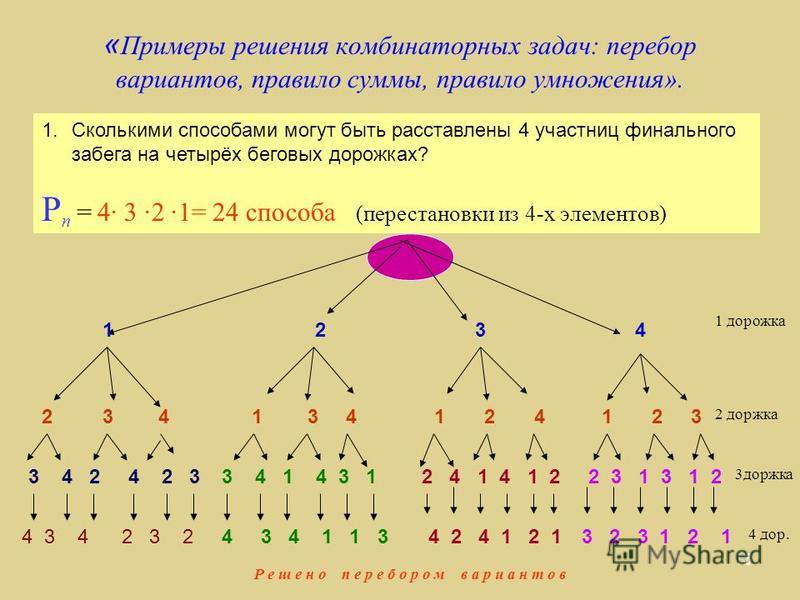 4.2016
4.2016
Помещать страницу в закладки могут только зарегистрированные пользователи
Зарегистрироваться
Вопрос №
1
В магазине «Все для чая» есть 5 разных чашек и 3 разных блюдца. Сколькими способами можно купить чашку с блюдцем?
Введите ответ:
Вопрос №
2
В магазине «Все для чая» есть еще 4 чайные ложки. Сколькими способами можно купить комплект из чашки, блюдца и ложки?
Введите ответ:
Вопрос №
3
В магазине «Все для чая» по-прежнему продается 5 чашек, 3 блюдца и 4 чайне ложки. Сколькими способами можно купить два предмета с разными названиями?
Введите ответ:
Вопрос №
4
В Стране Чудес есть три города: А, Б и В. Из города А в город Б ведет 6 дорог, а из города Б в город В — 4 дороги. Сколькими способами можно проехать от А до В?
Из города А в город Б ведет 6 дорог, а из города Б в город В — 4 дороги. Сколькими способами можно проехать от А до В?
Введите ответ:
Вопрос №
5
С Стране Чудес есть четыре города: А, Б и В и Г. Из города А в город Б ведет 6 дорог, а из города Б в город В — 4 дороги. Из города А в город Г — две дороги, и из города Г в город В — тоже две дороги. Сколькими способами можно проехать от А до В?
Введите ответ:
Вопрос №
6
Назовем натуральное число «симпатичным», если в его записи встречаются только нечетные цифры. Сколько существует 4-значных «симпатичных» чисел?
Введите ответ:
Вопрос №
7
Монету бросают трижды. Сколько разных последовательностей орлов и решек можно при этом получить?
Сколько разных последовательностей орлов и решек можно при этом получить?
Введите ответ:
Вопрос №
8
Каждую клетку квадратной таблицы 2 х 2 можно покрасить в черный или белый цвет. Сколько существует различных раскрасок этой таблицы?
Введите ответ:
Вопрос №
9
Сколькими способами можно заполнить одну карточку в лотерее «Спорт-прогноз»? (В этой лотерее нужно предсказать итог тринадцати спортивных матчей. Итог кажого матча — победа одной из команд либо ничья; счет роли не играет).
Введите ответ:
Вопрос №
10
Алфавит племени Мумбо-Юмбо состоит из трех букв А, Б и В. Словом является любая последовательность, состоящая не более, чем из 4 букв.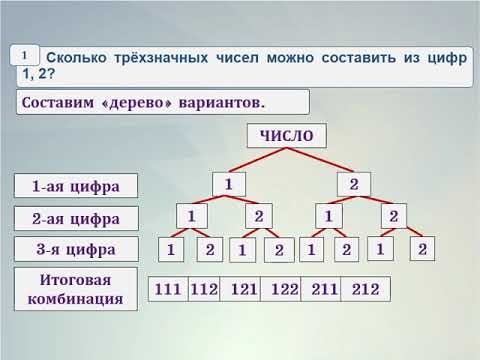 Сколько слов в языке племени Мумбо-Юмбо?
Сколько слов в языке племени Мумбо-Юмбо?
Указание: сосчитаейте отдельно количество одно-, двух-, трех- и четырехбуквенных слов.
Введите ответ:
Показать ответы
Получение сертификата
о прохождении теста
Доступно только зарегистрированным пользователям
© TestEdu.ru 2013-2022
E-mail администратора: [email protected]
Комбинации задач с решениями
Задача 1 :
Найдите количество способов, которыми можно выбрать 4 буквы из слова БУХГАЛТЕР.
Решение :
Задача 2 :
В коробке два белых, три черных и четыре красных шара. Сколькими способами можно достать из коробки три шара, если в розыгрыше должен быть хотя бы один черный шар?
Решение:
Количество белых шаров = 2
Количество черных шаров = 3
Количество красных шаров = 4
Количество нечерных шаров = 2 + 4 = 6
Количество вынимаемых черных шаров | Количество выпавших красных шаров | Всего выпавших шаров |
3 С 1 | 6 С 2 | 3 |
3 С 2 | 6 С 1 | 3 |
3 С 3 | 6 С 0 | 3 |
Количество путей
= ( 3 C 1 ⋅ 6 C 2 ) + ( 9 5 2 3 0047 ⋅ 6 C 1 ) +( 3 C 3 ⋅ 6 C 0 )
= (3 ⋅ 15) +(3 кор. = 45 + 18 + 1
= 45 + 18 + 1
= 64
Задача 3 :
Найдите количество строк из 4 букв, которые можно составить из букв слова ЭКЗАМЕН?
Решение:
Есть 11 букв, не все разные.
Это AA, II, NN, E, X, M, T, O.
Возможны следующие комбинации:
Случай 1:
Количество способов выбора 2 одинаковых, 2 одинаковых
= 3 C 2 = 3 способа
Случай 2:
Количество. C 1 ⋅ 7 C 2 ==> 3 x 21 ==> 63 способа.
Случай 3 :
Количество способов выбора всех 4 разных = 8 C 4
= 70 способов.
Общее количество комбинаций = 3 + 63 + 70 = 136 способов.
Общее количество перестановок с (1) по (3)
= 3 ⋅ (4!/2!2!) + 63 ⋅ (4!/2!) + 70 ⋅ 4!
= 18 + 756 + 1680
= 2454
Задача 4 :
Сколько треугольников можно получить, соединив 15 точек на плоскости, в которых нет прямой, соединяющей любые три точки?
Решение:
Из заданного вопроса мы узнали, что любые три точки не лежат на одной прямой.
Выбрав любые три точки из 15 точек, мы рисуем треугольник.
Количество способов нарисовать треугольник = 15 C 3
= (15 ⋅ 14 серва 7 членов должны быть выбраны из 6 артистов, 4 певцов и 5 писателей. Сколькими способами это можно сделать, если в комиссии должно быть не менее одного члена от каждой группы и не менее 3 художников?
Решение:
Для данного условия возможные способы выбора членов комитета из 7 человек.
(3A, 3S, 1W) —-> 6C3 ⋅ 4C3 ⋅ 5C1 = 20 ⋅ 4 ⋅ 5 = 400 ⋅ 10 = 800
(3A, 2S, 2W) —-> 6C3 ⋅ 4C2 ⋅ 5C2 = 20 ⋅ 6 ⋅ 10 = 1200
(4A, 2S, 1W) —-> 6C4 ⋅ 4C2 ⋅ 5C1 = 15 ⋅ 6 ⋅ 5 = 450
(4A, 1S, 2W) —-> 6C4 ⋅ 4C1 ⋅ 5C2 = 15 ⋅ 4 ⋅ 10 = 600
(5A, 1S, 1W) —-> 6C5 ⋅ 4C1 ⋅ 5C1 = 6 ⋅ 4 ⋅ 5 = 120
Таким образом, общее количество путей
= 400 + 800 + 1200 + 450 + 600 + 120
= 3570
Задача 6 :
Верховный суд вынес от 6 до 3 решений в пользу суда низшей инстанции. Найдите количество способов, которыми он может дать решение большинства, отменяющее решение суда низшей инстанции.
Найдите количество способов, которыми он может дать решение большинства, отменяющее решение суда низшей инстанции.
Решение :
Поддержать нижестоящий суд означает поддержать его решение.
Отмена решения суда низшей инстанции означает возражение против его решения.
Всего по 9 делам (6 + 3 = 9) он может вынести 5, 6, 7, 8 или 9 решений, отменяющих решение суда низшей инстанции. И не может быть 4 или меньше 4. Потому что большинство из 9составляет 5 и более.
Возможные комбинации, в которых он может дать решение большинства, отменяющее решение суда низшей инстанции, следующие: из 9 —-> 9C7 = 36
8 из 9 —-> 9C8 = 9
9 из 9 —-> 9C9 = 1
Таким образом, общее количество путей равно
= 126 + 84 + 36 + 9 + 1
= 256
Задача 7:
Пять лампочек, три из которых неисправны, нужно проверить в двух точках в темной комнате. Найдите количество попыток, при которых можно осветить комнату.
Решение:
Дано: 3 лампочки неисправны из 5. В темной комнате есть две точки с лампочками.
Одной лампочки (или двух) в хорошем состоянии достаточно для освещения комнаты.
Так как есть две точки с лампочками, мы должны выбрать 2 из 5 лампочек.
Количество способов выбора 2 лампочек из 5:
= 5P2
= 10
(Включает в себя выбор двух хороших ламп, двух дефектных ламп, одной хорошей и одной неисправной лампы. Таким образом, этими 10 способами , комната может быть освещена или не освещена)
Количество способов выбрать 2 неисправные лампочки из 3:
= 3C2
= 3
(Включает в себя выбор только двух неисправных ламп. Таким образом, этими 3 способами комната не может быть освещена)
Число способов освещения комнаты:
= 10 — 3
= 7
Пожалуйста, присылайте свои отзывы на [email protected]
Мы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all. com
com
Комбинаторика | Практика | Альберт
Основные принципы счета
«Как я люблю тебя? Дай мне посчитать пути!» По мере того, как количество вариантов увеличивается, методы подсчета имеют основополагающее значение для определения количества возможных результатов и порядков. Изучите принципы, лежащие в основе комбинаторики.
Принципы умножения и сложения
16 вопросов
Не начато
Принципы умножения
16 вопросов
Not started
Permutations and Combinations
23 questions
Not started
Permutations
12 questions
Not started
Combinations
11 questions
Not started
Cards, Игра в кости и лотереи
23 вопроса
Не начато
13 вопросов
Не начато
10 вопросов
Не начато
Биномиальные коэффициенты
В ситуациях, когда порядок не важен, биномиальные коэффициенты используются для расчета количества возможных комбинаций при заданном количестве вариантов. Начните практиковать базовые комбинации и приемы счета. 11 вопросов0002 Комбинаторные идентичности
Начните практиковать базовые комбинации и приемы счета. 11 вопросов0002 Комбинаторные идентичности
5 Вопрос
Не запускается
Многономическая теорема
10 Вопрос
Не начался
Элементы m$ помещаются в категории $n$, и $m > n$, некоторые категории должны содержать более одного элемента. Примените следствия этого простого, но мощного принципа.
Основная форма принципа голубей
10 Вопрос
Не начался
Сильная форма принципа голубей
9.
Не запускается
Распределительные проблемы
. одинаковые предметы в коробки. Продолжите изучение разделов и композиций целых чисел.
Распределение предметов по ящикам
11 Вопрос
Не запустили
Разделы и композиции
.
Числа Стирлинга
10 вопросов
Не начато
Включение-исключение
Поднимите диаграммы Венна на новый уровень, исследуя мощность объединений и пересечений множеств.

 В группе вы можете распределить обязанности для того, чтобы быстрее выполнить задание. Но рабочие листы (Приложение 1) каждому, возьмите, подпишите их. Свои ответы вы будете вписывать в колонку «Ответ», а в колонку «Мой результат» будете выставлять набранные баллы в соответствии с критериями, указанными в колонке «Критерии оценивания». На экране (слайд3) и на карточке 1 имеется задание и некоторые данные. Вам необходимо вычислить результат, а ответ записать в виде буквенного кода
В группе вы можете распределить обязанности для того, чтобы быстрее выполнить задание. Но рабочие листы (Приложение 1) каждому, возьмите, подпишите их. Свои ответы вы будете вписывать в колонку «Ответ», а в колонку «Мой результат» будете выставлять набранные баллы в соответствии с критериями, указанными в колонке «Критерии оценивания». На экране (слайд3) и на карточке 1 имеется задание и некоторые данные. Вам необходимо вычислить результат, а ответ записать в виде буквенного кода (Выбор, комбинация)
(Выбор, комбинация)

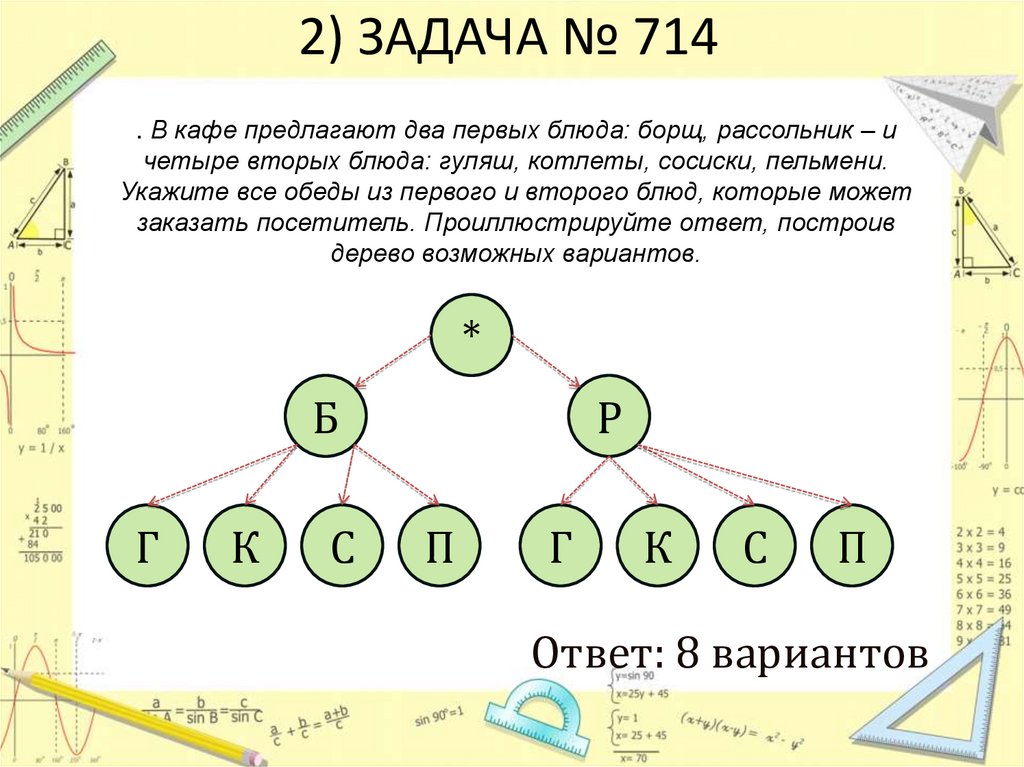 Посмотрите на слайде задачу (слайд 11)
Посмотрите на слайде задачу (слайд 11) Её вы можете решить любым из способов решения комбинаторных задач. На дополнительную отметку вы можете придумать для ребят свою комбинаторную задачу, которую мы поместим в наш сборник «САМЫЕ ИНТЕРЕСНЫЕ ЗАДАЧИ 5А»
Её вы можете решить любым из способов решения комбинаторных задач. На дополнительную отметку вы можете придумать для ребят свою комбинаторную задачу, которую мы поместим в наш сборник «САМЫЕ ИНТЕРЕСНЫЕ ЗАДАЧИ 5А»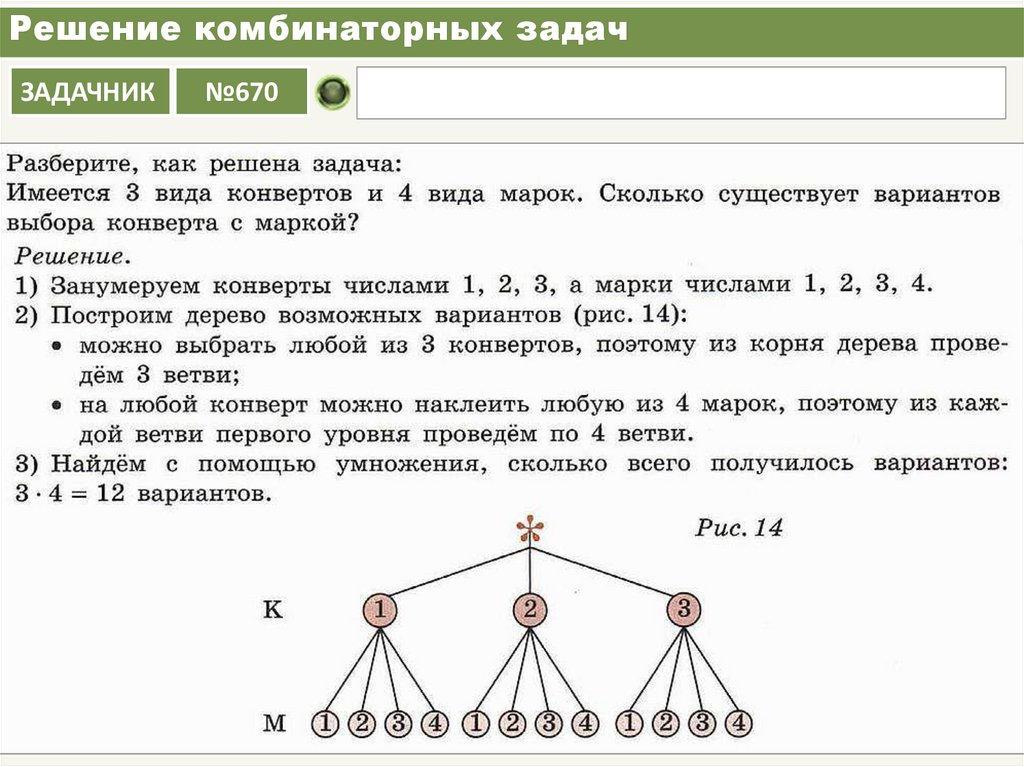 Вычисли дома все возможные варианты (по желанию)
Вычисли дома все возможные варианты (по желанию) Найди все возможные варианты способом, заданным учителем
Найди все возможные варианты способом, заданным учителем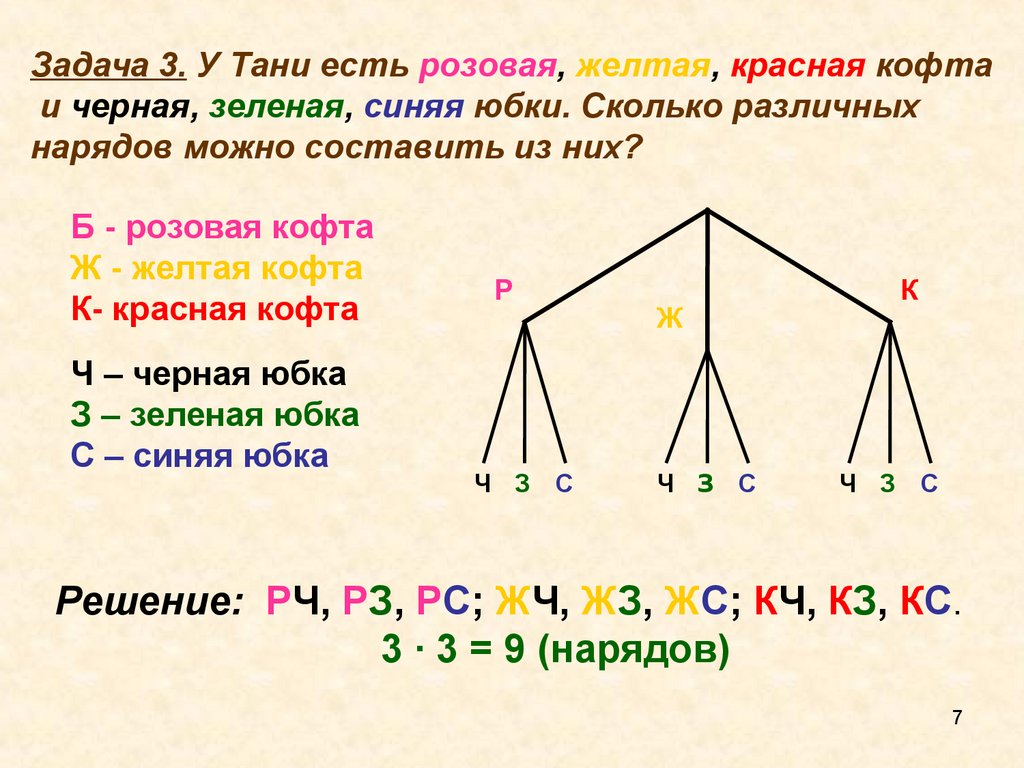 Представьте, что расписания нет, вы можете пойти на любой из пяти сегодняшних уроков. Что же будет? ХАОС!!! Нужна ваша помощь завучу!
Представьте, что расписания нет, вы можете пойти на любой из пяти сегодняшних уроков. Что же будет? ХАОС!!! Нужна ваша помощь завучу!