6 класс примеры на все действия с дробями: Памятка по математике на тему «Действия с дробями» (6 класс)

Действия с дробями. 6-й класс

• Шайбакова Ида Гаденановна

Разделы: Математика, Конкурс «Презентация к уроку»

Класс: 6

---

Презентация к уроку

Загрузить презентацию (1 МБ)

---

Цель урока: повторение правил сравнения, сложения, вычитания, умножения и сокращения дробей; развитие логического мышления, вычислительных навыков и укрепление интереса к предмету.

Задачи урока:

Образовательные:

• закрепить полученные знания: правила сложения, вычитания, умножения, сокращения обыкновенных дробей и смешанных чисел;
• сформировать умения применять полученные знания для решения задач;
• осуществить контроль знаний с помощью теста и интерактивной доски.

Развивающие: развивать познавательный интерес к предмету и логическое мышление, интеллектуальные и творческие способности учащихся.

Воспитательные:

• обучать самостоятельной деятельности по овладению знаниями;
• формировать осознанные мотивы учения, самосовершенствования, самовоспитания;
• воспитывать взаимопомощь.

Ход урока

1. Устный счет, индивидуальная работа.
2. Тест.
3. Закрепление.
4. Итог урока.
5. Домашнее задание.

I. Сегодня мы будем повторять все действия с обыкновенными дробями и смешанными числами. К доске пойдут 3 ученика (Слайд 4–6), а остальные будут работать устно (блиц-опрос).

Блиц-опрос.

1. Что называется общим знаменателем двух дробей?
2. Если знаменатели дробей – взаимно простые числа, то общий знаменатель этих дробей равен…

3. Как сравнить (сложить) дроби с разными знаменателями?
4. Чтобы из целого числа вычесть дробь, надо…
5. Как сложить смешанные числа?
6. Как умножить дробь на натуральное число, на дробь?
7. Что значит “сократить дробь”?
8. Какая дробь называется несократимой?
9. Чтобы умножить два смешанных числа, надо…

А теперь проверим работу ребят у доски (Слайд 4–6, ответы на интерактивной доске):

Слайд 4:

Слайд 5:

2 = 200%; 0,39 = 39%; 0,7 = 70%;

Слайд 6:

3)

Объявить оценки обучающимся, работающим у доски и с места.

II. А сейчас приготовьте листочки для теста по вариантам. За 5–7 минут нужно выполнить следующие задания с выбором верного ответа

(Слайд 7).

После завершения работы обменяйтесь листочками для взаимопроверки (Слайд 8, ответы на интерактивной доске). Отметьте верные ответы знаком “+”, а неверные знаком “ – ” и поставьте оценку (критерии оценки вы знаете) и верните тест соседу.

Ответы (на Слайде 8):

1-й Вариант № задания 1 2 3 4 ответ 3 4 2 1

2-й Вариант № задания 1 2 3 4 ответ 4 3 3 2

III. Мы повторили действия над дробями и смешанными числами. А теперь применим наши знания. Решим задание 478 (е) из учебника [Н.Я.Виленкин “Математика 6 класс].

Задание:

К доске идет один ученик.

Проверим, верно ли он решил (Слайд 9 на интерактивной доске).

Решение: (на Слайде 9)

А сейчас вспомним сказку П. П.Ершова “Конек-Горбунок” (Слайд 10–11). Интересно, какой урожай собрали браться с трех полей? (Слайд 12).

Задача: Какой урожай собрали братья с трех полей, если размеры полей были такими: I поле длиной 5 км, а шириной 2 км; II поле длиной 4 км, а шириной 2км; III поле длиной 2км, а шириной 2км. А урожайность везде была одинаковая – 2т с 1 кв.км.

Желающего решить задачу вызвать к доске.

Проверим верно ли вы решили? (Слайд 13).

Решение задачи:

Ответ: 73,5 т

Дополнительное задание для тех, кто первым решит задачу (Слайд 14):

Вычислите:

IV. Итог урока.

Что нового вы сегодня узнали на уроке? Как вы считаете, вы готовы к контрольной работе? Молодцы. Сегодня все хорошо поработали (объявить оценки за урок).

V. Домашнее задание.

513 (3 строка), 527, 528, 534 (б).

1. 05.2012

Сайт vpr-klass.com — впр-класс.ком : гдз, решебник, гиа, егэ, решение задач, задания, варианты, подготовка к экзамену, тесты, презентации.

Error in links file

 Сайт vpr-klass.com — впр-класс.ком : гдз, решебник, гиа, егэ, решение задач, задания, варианты, подготовка к экзамену, тесты, презентации. Образовательный сайт vpr-klass.com (впр-класс.ком) — готовые решения задач!

У нас вы найдете много учебных материалов: решебники, ГДЗ, тестовые задания, видео уроки, генераторы задач, решения упражнений гиа и егэ.

 Расскажи друзьям Ищи САЙТ в Яндексе и Google по слову: vpr-klass или впр-класс Сохрани сайт в закладки — нажми Ctrl+D Презентации Детские презентации Презентации по математике Презентации по астрономии Демо-варианты: ЕГЭ Математика Русский язык Физика Обществознание Английский язык Информатика История Биология Химия Литература География ГИА (ОГЭ) Математика Русский язык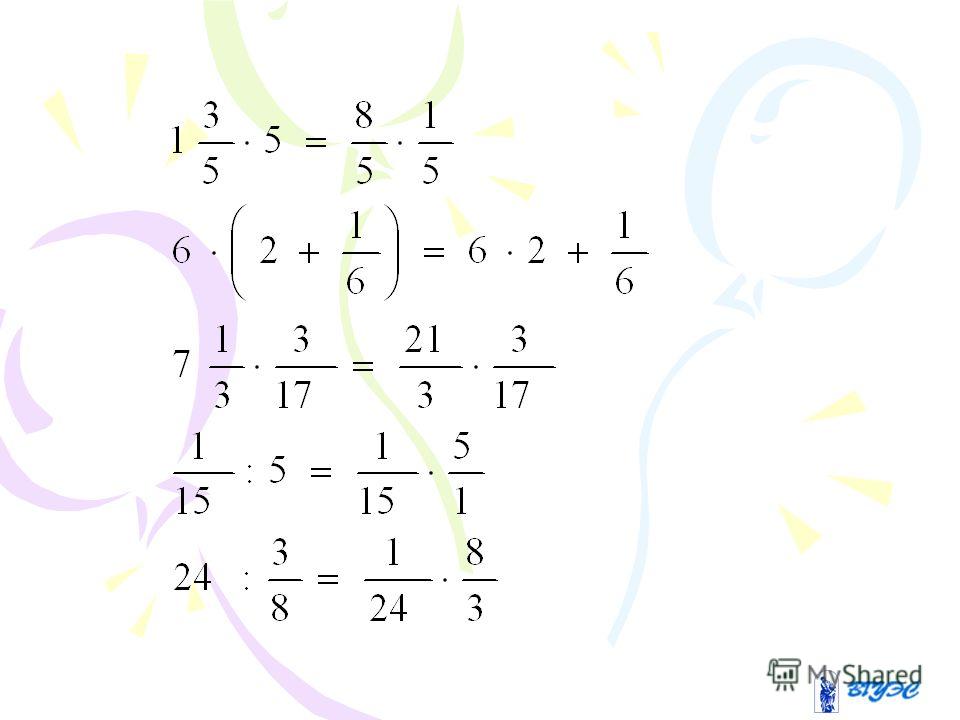

Разделы сайта vpr-klass. com (впр-класс) Последние новости ГИА и ЕГЭ 2017. ГИА по математике. ЕГЭ по математике. КДР по математике. Математика 1-4 класс. Математика 5-6 класс. Алгебра и геометрия 7-9 класс. Алгебра и геометрия 10-11 класс. ГДЗ, решебники по математике, алгебре, геометрии. Онлайн калькуляторы по математике. Генераторы случайных примеров и задач по математике. Презентации. Другие школьные предметы. Новое на сайте: Сайт Vpr-klass.com — это учебный-образовательно-познавательный сайт для школьников! Приветствуем на уникальном сайте помощи всем ученикам 1-11 классов. На образовательном ресурсе полно полезной, учебной информации от способов решения заданий по математике до разных генераторов задач по алгебре и онлайн калькуляторов по геометрии, которые облегчат жизнь школьника. В частности, сделан больший уклон на решебники и ГДЗ, ведь правильная домашняя работа — это хорошие оценки и учеба в школе. Также имеется достаточно материалов, которые пригодятся к экзаменам в 9-ых и 11-ых классах. Есть много готовых решенных задач ЕГЭ (ГИА, ОГЭ) и упражнений для отличной самоподготовки к экзаменам. Имеются демонстрационные варианты разных лет и онлайн тесты на основе КИМов для качественной самопроверки знаний. Также есть уникальные генераторы заданий, которые помогут учителям создать карточки для учеников. Есть разделы посвещенные контрольным и самостоятельным и проверочным работам для 3-4-ых и 5-6 классов. Помимо прочего имеются полезные презентации для учителей по разным школьным предметам — биология, обж, информатика, кубановедение, химия и другие. Кроме того есть обучающие видео уроки по математике (ЕГЭ, ГИА, КДР) и информатике (ОГЭ), которые принесут огромную пользу старшеклассникам в подготовке к экзаменам 2018 учебного года.

 Интересно ГИА (ОГЭ) по математике Много разных решений Тесты ГИА онлайн. Видео — ГИА 2013: геометрия Видео — ГИА 2012 Видео — Демо-вариант 2012. Решение Демо-варианта 2013 года (2014 года). Задача №1, Вычислить. Задача №2, Числа и прямая. Задача №3, Сравнение чисел. Задача №4, Уравнения. Задача №5, Графики и формулы. Задача №6, Прогрессии. Задача №7, Упростить выражение. Задача №8, Неравенства, системы неравенств. Задача №9, Задания по геометрии. Генератор вариантов ГИА 2014 ЕГЭ по математике Много разных решений. Онлайн тесты. Видео уроки ЕГЭ по математике. Генератор вариантов ЕГЭ 2014 Книги, справочники Решение демо варианта ЕГЭ по математике 2014 Задания B1, задача. Задания B2, диаграммы. Задания B5, уравнения. Задания B8, производная. Задания B10, вероятность. ОГЭ по информатике Видео уроки

Copyright © 2017 vpr-klass.com | Если какой-либо из материалов нарушает ваши авторские права, просим немедленно связаться с Администрацией!!! Наш e-mail: [email protected] | Правообладателям | sitemap. xml

Конспект урока по математике «Все действия с обыкновенными дробями» 6 класс

Урок в 6 классе по новому ФГОС

с применением Технологии развития критического мышления

Учитель: Цыжипова Цыцыгма Нимаевна – учитель математики МКОУ ООШ №12 с. Согда Верхнебуреинского района Хабаровского края.

Тема: «Все действия с обыкновенными дробями»

Цель: Учащиеся будут выполнять все действия с обыкновенными дробями и получат возможность выбирать наиболее удобный способ решения дробных выражений и оценивать правильность выполнения действий, согласно критериям.

предметные результаты: формулировать и применять правила действий с обыкновенными дробями;

метапредметные результаты: применять знания в различных ситуациях; предлагать разные варианты в зависимости от предложенной ситуации; находить ошибки;

личностные результаты: организовывать свою деятельность, т. е. ставить личные цели, их достигать и оценивать результаты.

Педагогические задачи:

• Создать условия для повышения мотивации у учащихся в потребности усвоения новых умений;

• Организовать ситуацию постановки учебной проблемы;

• Помочь учащимся в постановке цели урока и поиске путей решения данной проблемы;

• Создать ситуацию самостоятельного поиска новых способов решения в группе, в паре;

• Создать условия для самоконтроля и самооценивания.

Технологическая карта + структура урока

Фазы урока

Приложение 1. Составьте схему-кластер по данной теме, где в центре-основное изучаемое понятие, а гроздья-все действия , которые умеете выполнять с этим понятием.

Приложение 2. «Как мы справились с домашним заданием?»

№

заданий

Приложение 3-1.

Вопросы экзамена:

1. Каким действием можно заменить дробную черту?

2. Для того чтобы сравнить дроби с разными знаменателями нужно…

3. Для нахождения общего знаменателя нужно найти НОК или НОД?

4. Расскажите правило сложения и вычитания дробей.

5. Расскажите правило умножения дробей?.

6. Какая дробь называется правильной?

7. Расскажите правило деления дробей.

Приложение 3-2.

Приложение 3-3. (слайд 8) Давайте узнаем на деле, насколько дружим с дробями:

А) ; Б) ; В) ; Г) ; Д) ; Е) Ответы: А) 1; Б) 7

Приложение 4.(Может отвлечемся на минуту?) Делаем так: если вы согласны – головой вращаем направо и налево, а если не согласны – руки на плечи и вращаем вперед и назад. Итак: 3/4 — правильная, 4/12 – несократимая, 13/14 – несократимая, 5/7 – правильная, 3/10 – сократимая, 6/5 – правильная, 10/15 – неправильная, 3/5 – правильная, 5/7 – несократимая.

Приложение 5-1. Задания на выбор «Действия с дробями».

Приложение 5-2. Самопроверка: 2) ; 3) ; ; 4) ; 16; .

Приложение 6. Тест и образец для взаимопроверки.

Список используемой литературы:

1. Виленкин Н.Я., Жохов В.И. и др. Математика 6.- М: «Мнемозина» 2008г

2. Дидактические материалы по математике для 6 класса (Авторы: Чесноков А.С., Нешков К.И. издательство «Просвещение», Москва 2003)

3. Вычисляем без ошибок. Работы с самопроверкой для учащихся 5-6 классов. С.С. Минаева. М: Издательство «Экзамен», 2014г.

Текущее время урока	Действия учителя	Действия учащихся
Вызов	1 мин	I. Организационно- мотивационный момент. Предлагается загадка: Она бывает охотничья, барабанная и математическая. (дробь) (Слайд 1)	Ответ: дробь
	2 мин	II. Определение темы и целей урока. (Слайд 2,3,4) На протяжении всей своей жизни мы постоянно сталкиваемся с дробями. А сейчас на уроках учимся выполнять различные действия с дробями. Предлагается каждому составить кластер: в центре-название дроби, а по сторонам-умения.	Составляют кластеры-передают друг другу по цепочке-дополняют-обсуждают.(приложение 1) Вместе с учителем делают вывод, определяют тему урока и цели урока.
	3 мин	III. Проверка домашнего задания. (Слайд 5) Предлагается заполнить таблицу. (приложение 2)	Д.з. проверяют по образцу и заполняют таблицу. Делают вывод.
	7 мин 1 мин	IV. Актуализация опорных знаний. Устные упражнения. 1) Игровой момент «Экзамен» (на знание правил действий с обыкновенными дробями). (приложение 3-1), (Слайд 6) 2) Устные упражнения: а) «Найдите лишнее»; (приложение 3-2) (Слайд 7) б) «Дружим ли с дробями?»; (приложение 3-3), (Слайд 8) Физкультминутка (приложение 4), (Слайд 9)	Желающий выбирает билет с вопросом и отвечает, остальные оценивают. 1. Вытягивают билеты и сразу отвечают на их вопросы; 2. а) Находят лишнее число и поясняют ответ; б) Путем умножения дробей, выясняют правильность заданного ответа;
Осмысление	17 мин	V. Система заданий на выбор: «Действия с дробями». Каждое задание оценивается по 3 балла. (приложение 5-1), (Слайд 10)	Решают задания (по желанию работают в группе, в паре или индивидуально).
	1 мин	VI. Самопроверка выполнения работ. Корректировка (если необходимо) (приложение 5-2), (Слайд 11)	По модельному ответу проводят самопроверку работ.
	7 мин	VII. Тест. (приложение 6) и по окончании предлагается образец для взаимопроверки. (Слайд 12)	Индивидуальная работа и взаимопроверка по образцу.
Рефлексия	3 мин	VIII. Выводы. Составление синквейна по теме данного урока. (Слайд 13)	Формулируют выводы по изученному материалу и составляют синквейны.
	2 мин	IX. Оценка результатов урока. Подведение итогов урока.	Заполняют лист самоконтроля и таблицу саморефлексии.
	1 мин	X. Поясняет и дает рекомендации к Д/З.	Записывают д/з.
ответы	+	—	?
№106 с. 93	; 2) 63 Ответ: 63 м²
№107 с.93	26;
№159 а
№159 б
№159 в	22

Электронный справочник по математике для школьников арифметика сложение вычитание умножение деление дробей действия со смешанными числами



Справочник по математике

Арифметика

Обыкновенные и десятичные дроби

Содержание

Сложение и вычитание дробей

Умножение и деление дробей

Действия со смешанными числами

Сложение и вычитание дробей

При сложении (вычитании) дробей с одинаковыми знаменателями получается дробь с тем же знаменателем, а её числитель равен сумме (разности) числителей рассматриваемых дробей.

Например,

При сложении (вычитании) дробей с разными знаменателями предварительно нужно привести их к общему знаменателю. Для упрощения вычислений желательно приводить дроби к наименьшему общему знаменателю, хотя это не является обязательным.

Например,

(в уголках сверху здесь обозначены дополнительные множители).

Умножение и деление дробей

При умножении дробей получается дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.

Например,

Деление дробей осуществляется в соответствии со следующим правилом:

Иногда это правило формулируют так: для того, чтобы разделить первую дробь на вторую, нужно первую дробь умножить на перевернутую вторую.

В частности,

Действия со смешанными числами

Для того, чтобы избежать ошибок при выполнении арифметических действий со смешанными числами, рекомендуется сначала обратить смешанные числа в неправильные дроби, затем выполнить нужные арифметические действия, а потом, если это требуется, обратить результат в смешанное число.

ПРИМЕР. Найти сумму, разность, произведение и частное смешанных чисел

  и  

РЕШЕНИЕ. Преобразуем эти числа в неправильные дроби:

Далее получаем:

Наверх

Демонстрационные варианты ЕГЭ и ОГЭ

С демонстрационными вариантами ЕГЭ и ОГЭ по всем предметам, опубликованными на официальном информационном портале Единого Государственного Экзамена, можно ознакомиться на специальной страничке нашего сайта.

Наши учебные пособия для школьников

При подготовке к ЕГЭ и к ОГЭ по математике Вам могут также пригодиться наши учебные пособия.

• Решение рациональных неравенств

• Задачи на проценты

• Решение показательных неравенств

• Квадратный трехчлен

• Метод координат на плоскости

• Решение иррациональных неравенств

• Фигуры на координатной плоскости

• Решение алгебраических уравнений

• Уравнения и неравенства с модулями

• Решение показательных уравнений

• Арифметическая и геометрическая прогрессии

• Решение логарифмических уравнений

• Решение логарифмических неравенств

• Системы уравнений

• Решение тригонометрических уравнений

• Тригонометрия в ЕГЭ по математике

• Степень с рациональным показателем

методика и ее реализация, примеры решения задач

Математика

12. 11.21

13 мин.

Расчеты выполняются не только с натуральными целыми числами, но и с дробными. На уроках математики в 6 классе примеры умножения обыкновенных дробей изучаются более подробно. Для правильного вычисления необходимо применить определенную методику, которую разработали специалисты для этой цели. Они рекомендуют сначала приобрести базовые знания, а затем перейти к их практической реализации.

Оглавление:

• Общие сведения
• Виды обыкновенных дробей
• Работа со смешанными числами
• Правила сокращения
• Алгоритм умножения

Общие сведения

Процесс нахождения произведения двух обыкновенных дробных тождеств очень прост. Однако существуют «подводные камни», которые могут вызвать много ошибок. Чтобы этого не случилось, необходимо руководствоваться специальным алгоритмом, который предлагают ведущие преподаватели-специалисты.

Обыкновенная дробь имеет два компонента — числитель и знаменатель. Первый находится вверху и называется делимым, а второй — внизу. Последний называется делителем. Следует отметить, что дробный вид — представление частного, т. е. результата операции деления. Эта форма записи применяется для читабельной формы, поскольку иногда одно число не делится на другое.

Например, при делении 2 на 3 образуется десятичная бесконечная периодическая дробь. Ее можно записать в таком виде: 0,(6). Скобки означают, что число 6 повторяется бесконечное количество раз, так обозначается периодичность.

Однако бывают случаи, когда образуется десятичная непериодическая величина, а ее каким-то образом нужно записать с точностью до десятитысячной доли. Эта операция невозможна, поскольку после целой части будут следовать 10000 разрядов. Вот для ее записи и необходимо применять обыкновенную дробь.

Следует отметить, что умножать бесконечные непериодические дроби также проблематично. Их нужно преобразовать в обыкновенные величины, а далее применить соответствующий алгоритм. Чтобы воспользоваться методикой, требуется получить базовые знания. К ним относятся следующие:

1. Классификация обыкновенных дробных чисел.
2. Работа со смешанными дробями обыкновенного типа.
3. Сокращение.

Следует отметить, что каждый компонент необходимо подробно разобрать, поскольку от качественного изучения материала зависит скорость обучения. Если ученик не понял различия между правильной и неправильной дробями, то не имеет смысла переходить ко второму пункту. Это вызовет путаницу, а драгоценное время будет потрачено впустую.

Виды обыкновенных дробей

Классификация дробных выражений позволяет понять основные их свойства, методы конвертации и основные различия между собой. Они бывают трех типов: правильными, неправильными и смешанными. Для удобства необходимо записать дробь в математическом представлении «p/t», где р — числитель, а t — знаменатель.

Правильной дробью называется выражение, в котором числитель меньше знаменателя, т. е. выполняется условие p<t. Если величина «t» превышает «р», то дробное тождество является неправильным.

Однако при расчетах можно в учебниках (например, Виленкина Н. Я.) увидеть смешанное представление. Например, 6[2/3]. Последнее состоит из целой и дробной частей, причем последняя представлена в виде обыкновенного дробного значения. Эта форма записи применяется для конечного отображения результата, полученного при расчетах.

Математики рекомендуют всегда преобразовывать ответ в читабельный вид, чтобы им в дальнейшем могли воспользоваться другие люди. Далее требуется подробно разобрать работу со смешанными числовыми представлениями, поскольку в этом случае умножать обыкновенные дроби проблематично. Отсутствие конвертации может привести к возникновению множества ошибок при вычислениях.

Работа со смешанными числами

Для работы со смешанными числами также существует определенный алгоритм. Он имеет два направления: прямое и обратное преобразование. В первом случае выполняется конвертация смешанного дробного тождества в неправильную дробь обыкновенного типа. Он имеет следующий вид:

1. Написать величину: M[p/t].
2. Рассчитать значение числителя «Р» по такой формуле: Р=Мt+p.
3. Записать неправильную дробь: Р/t.

Следует отметить, что алгоритм преобразования неправильной обыкновенной величины выполняется строго в обратном порядке. Методика выглядит следующим образом:

1. Записать неправильное тождество обыкновенного дробного вида: Р/t.
2. Выделить целочисленную константу, разделив числитель на знаменатель: Р/t=M.
3. Вычислить новый числитель, который должен быть меньше знаменателя: р=Р-М*t.
4. Записать искомое значение: М[p/t].

Следует отметить, что при последнем действии дробную часть рекомендуется сократить. Эту операцию требуется делать постоянно, чтобы оптимизировать дальнейшие расчеты. Далее необходимо разобраться с методикой сокращения числителя и знаменателя.

Правила сокращения

Сокращение числителя и знаменателя необходимы для уменьшения объема вычислений. Например, требуется выполнить операцию умножения для двух дробных значений 44/55 и 90/100. Если оставить выражения в таком виде, то для вычисления произведения нужно оперировать с большими числами, а это очень неудобно. Следовательно, дроби нужно сократить. Для этой цели используется специальная методика. Она имеет такой вид:

1. Записать дробную величину.
2. Найти общий множитель для числителя и знаменателя.
3. Вынести величину, полученную в первом пункте.
4. Сократить дробь, записав результат.

Однако алгоритм нужно отработать на практике. Его реализация имеет такой вид:

1. 44/55 и 90/100.
2. 11 и 10 — общие множители для двух значений дробного вида.
3. (11*4)/(11*5) и (10*9)/(10*10).
4. 4/5 и 9/10.

Следует отметить, что выполнять любые арифметические операции с дробями обыкновенного вида, полученными на четвертом шаге алгоритма, удобнее, чем с их первоначальными значениями. На основании этого можно сделать вывод о том, что сокращение — вынужденная мера, используемая во всем мире для оптимизации вычислений. Далее можно переходить к самой методике умножения дробей в 6 классе.

Алгоритм умножения

Методика умножения дробных обыкновенных значений довольно проста. Однако в математике бывает всего три случая, которые на уроках не всегда поддаются объяснению (очень часто преподаватели не обращают на них внимания учеников):

1. Одинаковые знаменатели.
2. Равные между собой числители, но разные знаменатели.
3. Каждый элемент равен однотипному компоненту, т. е. числитель первой дроби эквивалентен числителю второй, а знаменатели также равны между собой.

На самом деле умножение простых дробей с разными знаменателями является одной и той же операцией, т. е. поиск решения осуществляется по одному принципу. Чтобы его объяснить, нужно разобрать методику выполнения. Она имеет следующий вид:

1. Записать две дроби.
2. Конвертировать смешанные числа в неправильные дробные числа.
3. Привести их к нормальному виду при помощи операции сокращения.
4. Сократить числитель и знаменатель одной величины на элементы неправильной дроби другого значения.
5. Перемножить числители и знаменатели.
6. Записать искомый результат, сокращая его при необходимости и переводя в правильную дробь.

Для понимания алгоритма нужно научиться решать задачи на умножение дробей с разными знаменателями для 6 класса. Например, необходимо перемножить 6[4/8] и 3[20/35]. Их произведение находится по следующей методике:

1. 6[4/8] и 3[20/35].
2. Конвертацию нужно выполнять только после приведения дробных величин к оптимальному виду: 6[4/8]=6[½] и 3[20/35]=3[4/7].
3. Перевод в неправильные дробные тождества: 13/2 и 25/7.
4. Сокращение между величинами невозможно, поскольку 25 не делится нацело на 2, а 13 на 7.
5. Перемножение: (13*25)/(2*7)=325/14.
6. Для сокращения нужно найти общий множитель для чисел 325 и 14 (минус — не делится, а плюс — делится): 2 (-), 3 (-), 4 (-), 5 (-), 6 (-), 7 (-), 8 (-), 9 (-). Невозможно сократить дробное выражение.
7. Запись в смешанной форме, руководствуясь методикой конвертации неправильного дробного значения в смешанное число: 23[(325−23*14)/14]=23[3/14].

Следует отметить, что каждый шаг методики необходимо оптимизировать. Для этого необходимо избавляться от лишних вычислений, постоянно сокращая дробные величины. Однако некоторые могут не понять, как влияет методика умножения на результат. Для этого нужно решить пример другим методом:

1. Для удобства сократить величины дробного вида: 6[½] и 3[4/7].
2. Перемножить целые и дробные части: 18[4/14].
3. Сократить: 18[2/7].

Следует отметить, что результаты не совпадают, поскольку последний способ является неверным. На основании этого можно сделать вывод о том, что требуется решать задачи по методике. Если не следовать правилам, то могут появиться ошибки при расчетах.

Таким образом, для выполнения операции произведения двух обыкновенных дробей необходимо использовать определенный алгоритм, а также уметь сокращать дробные величины и преобразовывать смешанные числа.

Задания: Действия с десятичными дробями

Математический тренажер по теме

«Совместные действия с десятичными дробями»

Составила учитель математики

Толмачева Надежда Алексеевна

МБОУ СОШ №69 г. Нижний Тагил

Пояснительная записка

Тренажер по математике предназначен для учащихся 5кл-6кл, его можно использовать в работе с любым УМК по математике, а также при подготовке учащихся 9 класса к сдаче ОГЭ.

Тренажер предназначен как для работы в классе, так и для самостоятельной работы дома.

Тренажер обеспечивает возможность выработки осознанного применения всех правил действий с десятичными дробями.

Тренажер можно использовать в виде первичного контроля знаний, а также и в коррекционной работе. Задания тренажера позволяют предложить ученику выполнить больший объем вычислений за небольшое время. Таким образом оттачиваются не только вычислительные навыки, но и тренируется внимание, развивается оперативная память ученика.

Задания тренажера можно предлагать как для индивидуальной , так и для коллективной работы в классе.

Математический тренажер

Действия с десятичными дробями

Вариант 1
1	15,3 * 5,4 — 4,2* (5,12 – 4,912) + 16,0036
2	9,84 — 16,32 * ( 8 – 7,45) + 2,186
3	(2,12 + 1,07) * (2,12 – 1,07)
4	86,4 * (17,01 : 4,2) : 6,4
5	42,26 – 34,68 : (33,32 : 9,8)
6	40 – ( 7,12 + 11,043 : 2,7)
7	12,6 : (2,04 + 4,26) – 0,564
8	7,371 : (5 – 3,18) + 2,05 *(17,82 – 7)
9	(5,2 : 26 + 26 : 5,2) *6,1 + 5,25 : 5
10	27,5967 : (8 – 1,186) + 3,02
11	(20 – 13,7 ) * 7,4 + 18 : 0,6
12	( 4,694 — 3,998) : 4,35 + ( 4,5 * 5,4 – 0,06)
13	(4,6 * 3,5 + 15,32) : 31,42 + ( 7,26 – 5,78) : 0,148
14	(101,96 – 6,8 * 7,2) : 4,24 – 3,4 * ( 10 – 6,35)
15	7,72 * 2,25 – 4,06 : ( 0,824 + 1,176) – 12,423
16	51,328 : 6, 4 + 3,2 * (10 – 4,7) * 2,05
17	(42,12 * 0,12 + 112,016* 0,1) : 1,6 – 9,424
18	( (4,2 *0,81 – 6,8*0,05) : 0,5) ) : 200
19	2,6* (4,4312 + 15,5688) – 6,66 : (8,2 – 6,72)
20	( 0,624 : 4,16 + 6,867 : 2,18) *2,08 – 4,664
21	4260 + 42,6 : (62,06 + 37,94) – 42,6 : (52,44 — 52,43)
22	5 : 0,25 + 0,6 *(9,275 – 4,275) : 0,1
23	3,1 : 100 + ( 6 – 0,3 : 100) *10
24	0,415 +(2,85 : 0,6*3,2 – 2,72 : 8) + 5,134 : 0,17
25	0,1: 0,002 – 0,5*( 7,91 : 0,565 – 11,1 :1,48)
26	0,2 : 0,004 + (7,91 : 0,565 – 44,4 : 5,92) *0,5
27	4,735 : 0,5 + 14,95 : 1,3 + 2,121 : 0,7
28	( 0,1955 + 0,187) : 0,085
29	(86,9 + 667,6) : (37,1 + 13,2)
30	(0,008 + 0,992) * (5 *0,6 – 1,4)

Математический тренажер

Действия с десятичными дробями

Вариант 2
1	(130,2 – 30,8) : 2,8 — 21,84
2	3,712 : ( 7 – 3,8) + 1,3* (2,74 + 0,66)
3	( 3,4 : 1,7 + 0,57 : 1,9)* 4,9 + 0,0825 : 2,75
4	10,79 : 8,3*0,7 — 0,46 * 3,15 : 6,9
5	( 21,2544 : 0,9 + 1,02 * 3,2 ) : 5,6
6	4,36 : ( 3,15 + 2,3) + ( 0,792 – 0,78) * 350
7	( 3,91 : 2,3 * 5,4 – 4,03 ) * 2,4
8	6,93 : ( 0,028 + 0,36 * 4,2 ) — 3,5
9	42,165 – 22,165 : ( 0,61 + 3,42)
10	( (4 : 0,128 + 14628,25) : 1,011* 0,00008 + 6,84) : 12,5
11	687,8 + ( 88,0802 – 85,3712) : 0,045
12	(3,1 * 5,3 – 14,39) : 1,7 + 0,8
13	( 3,8 * 1,75 : 0,95 – 1,02) : 2,3 + 0,4
14	( ( 23,79 : 7,8 – 6,8 : 17) * 3,04 – 2,04 ) * 0,85
15	0,15 : 0,01 + ( 6 + 9,728 : 3,2) * 2,5 – 1,4
16	1,44 : 3,6 + 0,8 + 3,6 : 1,44* ( 0,1 — 0,02)
17	3,45 * ( 11,2 + 75,6) – 0,93 * 1,26
18	4,25 : 0,25 – 0,06 * 82 + 0,4
19	( 0,237 + 45,6) * 12,01 — 11,1* ( 237,1 – 229,9)
20	5,8 – 0,27 * 3,6 + 5,172
21	12 – 5,3 : ( 19,6 : 0,35 — 0,06 * 50)
22	( 0,6 + 0,25 – 0,125) * 3,2 + 4,5 : 100
23	( 15,5 : 0,25 – 0,08 * 200) : 2,3 – 1,3
24	( 87,05 * 2,7 – 55,68 :32) * 0,8 : 0,02
25	522,348 : 87 + 2,7 * ( 0,84 – 0,128 : 0,16)
26	6400 * 0,0145 – ( 1272,6 : 0,42 – 3000)
27	( 0,7 : 1,4 – 0,02) : 0,012 + 1,6 * (0,548 – 0,023)
28	( 1,184 : 3,2 + 0,832 : 0,4) : 0,5 + 1,5
29	4,96 ; 10 + 35,8 : 100 — 0,0042
30	( 0,04 + 3,59) * ( 7,35 + 2,65 ) : 300

Математический тренажер

Действия с десятичными дробями

Вариант 3
1	2,5 + 0,56* 28 + 0,125*15 – 0,12*7
2	12,8 : 4 + 76,8 : 12 – 42,6 : 6 – 2,4
3	4,01 + 43,6 : 10 – 73,2 : 30 + 15,4 : 100
4	176,4 : 100 – 0,041*40 + 13,5 :50 +0,3
5	(16,4 + 13,2)*3 – ( 10,6 + 4,8) *2 – 23,2
6	(40,65 — 32,6) : 5 + ( 4,72 _ 2,24)*3
7	4,735 : 0,5 + 14,95 : 1,3 + 2,121 : 0,7 – 21,6
8	0,01105 + 0,05 — 0,3417 : 34 -_ 0,875 : 125
9	(5,72 – 3,21 )*5 + ( 86,9 + 667,6) : (37,1 + 13,2)
10	( 0,1955 + 0,187) : 0,085 – (4,72 – 4,72 )*0,157
11	4,9 – (0,008 + 0,992) * (5 *0,6 – 1,4)
12	(50000 – 1397,3) : (20,4 + 33,603) – 856
13	3,7 *0,18 + 35,9 *0,26 – 0,109 *91
14	34,98 : 6,6 + 5,141 : 0,53 – 0,8379 : 0,057
15	0,131 *470 + 26,97 : 2,9 — 50,4 *1,4
16	0,439 *97 – 182,75 : 4,3 + 31,9 *0,43
17	(20,4 – 18,23)* 4,3 + (0,40713 + 0,44176) : 0,67
18	(0,357 + 7,043)*0,85 + (52 – 1,928) : 5,69
19	(1,5 — 0,4732)* 35 – (0,6092 + 0,0718) : 0,75
20	(139,4 + 16,6)* 0,039 — ( 20 – 17,54) : 2,5
21	4,1819 + 0,73 *( 5,375 + 2,595)
22	5,0143 – 65,9*( 0,0612 + 0,0058)
23	(0,83 *3,7 + 9,741 :51 – 0,012) : 0,325
24	(67,21 : 0,143 – 0,546*850 + 2,1) : 1,25
25	( 79* 0,63 – 9,558 : 5,4 – 26,94) : 0,324
26	(11,328 : 16 + 7,752 : 7,6) : 0,16
27	13,7 – (0,53 *6,7 + 1,77*3,1 + 0,004) : 0,66
28	5,3 : (2,87* 0,53 – 0,043 *7,7 – 0,19)
29	(3,06 – 2,97) * (5,6*0,93 – 0,84*6,2)
30	(5,4*0,77 – 0,008) : (2,747 : 0,67+ 0,05)

Математический тренажер

Действия с десятичными дробями

Вариант 4
1	589,72 :16 – 18,305 :7 + 5,67 : 4
2	(86,9 + 667,6 ) : (37,1 +13,2)
3	( 0,93 + 0,07 ) : (0,93 – 0,805)
4	1,35 : 2,7 + 6,02 – 5,9 + 0,4 : 2,5 *(4,2 – 1,075)
5	( (14,068 + 15,78) : (1,875 + 0,175)) : (0,325+ 0,195)
6	(0,578 + 0,172)* ( 0,823 + 0,117) – 1,711 : (4,418 + 1,382)
7	(39,3 + 116,7) *0,39 – (19,01 -16,56) : 2,5
8	(2,747 : 0,67 + 0,05) : (0,54* 7,7 – 0,008)
9	5,76*4,76 : 6,12 + 81,9 : 58,5*2,05
10	25,6 : (38,07 + 1,93) + 0,037 *10
11	(3,7011: 0,73 – 9,27: 4,5 – 1,41) :1,6
12	40,86 : 4,5 – 0,6039 : 5,49 + 0. 338: 0,13
13	(85,9 +667,1) : ((37 +13,2) + (11,44 – 6,42)*10
14	1,224 : (7 – 2,92) + 1,06*(13,5 – 3)
15	(7,5* 48 – 8,2* 9,5 + 141,4) : (254,1 :4,2)
16	0,63*69 – 10,048 : 6,4 – 19,44 : 32,4 *0,8
17	(3,8 : 19 + 1,9 : 3,8) *5,2 + 7,28 : 7
18	(4,9 + 1,06 – 0,98) : ( 0,83*0,6) : 2,4
19	(28,7 *0,15) : (0,25 *0,21) + 22,5 :1,25
20	0,1 : 0,002 + (7,91 : 0,565 — 11,1 : 1,48)
21	(0,2028 :0,24 – 0,32 *1,5) *(4,05 – 13,1625 : 4,05)
22	(97,44 : 0,48 + 128,64 : 3,2) *0,25 – 17,89
23	5,4 + ( (4,7 – 2,85)*1,8 + 0,0156 : 0,13)
24	(1,2 *0,15 + 12 :100 – 1,4 : 10) : 0,1
25	0,545 : 0,5 +2,75 *0,4 – 0,45 *3,8
26	0,6 * (7,24 : 0,8 – 0,968 : 0,16) + 2,25 *0,04
27	(6,4 *0,025 + 7,07 : 3,5 – 3,68 : 4) : 0,9
28	2,5 *( 3 : 6 – 0,2 : 5 + 1,2 *0,15)
29	( 5,508 : 0,27 – 10,2 *1,3) : 0,7 + 1,3 : 0,1
30	1,5 + 0,5*( 4,214 : 0,14 – 5,436 : 1,8) * 0,1

Ответы

Математический тренажер

Действия с десятичными дробями

	Вариант 1	Вариант 2	Вариант 3	Вариант 4
1	99,4972	13,66	19,215	35,66
2	2,8868	5,58	0,1	15
3	3,3495	11,3	6,084	8
4	54,675	0,7	0,694	1,12
5	32,06	4,8	34,8	28
6	28,79	5	9,05	0,41
7	1,436	12,36	2,4	59,86
8	26,231	1	0,044	1
9	32,77	36,665	27,55	7,35
10	7,07	0,64	4,5	1,01
11	76,62	100	3,3	1
12	24,4	2	44	11,57
13	11	3	0,081	7,5
14	0,09	5,1136	0,3	11,43
15	2,917	21,2	0,31	7
16	42,788	1,4	13,8	41,42
17	0,736	298,2882	10,598	4,68
18	0,03062	12,48	15,09	2,4
19	47,5	470,58237	35,03	100
20	2,2	10	5,1	56,5
21	0,426	11,9	10	0,292
22	50	2,365	0,599	42,91
23	60,001	18,7	10	8,85
24	45,475	9331,8	6,4	16
25	46,75	6,112	65	10,38
26	53,25	62,8	10,8	1,89
27	24	40,84	0	1,4
28	4,5	6,4	5,3	1,6
29	15	0,8498	0	23,2
30	1,6	0,121	1	2,854

6 Упражнения для отработки дробей на числовой прямой

3-й класс

Купить сейчас

4 класс

Купить сейчас

5-й класс

Купить сейчас

2 класс

Купить сейчас

10 апреля 2018 г. 69 Комментарии

В этой записи блога я рассмотрю общие базовые математические стандарты третьего класса 3.NF.2 и 3.NF.3 и предоставлю вам задания, которые вы можете использовать со своими учениками. Эти мероприятия также хорошо подходят для учащихся 4-х и 5-х классов, нуждающихся в исправлении ошибок.

Числа и операции – дроби

// 3.NF.2

• Я могу разделить числовую прямую на половины, трети, четверти или шестые.
• Я умею представлять дроби в числовой строке.

// 3.NF.3

• Я могу использовать модели, числовые ряды и слова, чтобы объяснить эквивалентность дробей.
• Я могу сравнивать дроби, рассуждая об их размере.
• Я могу представить целые числа в виде дробей.

1. Используйте столбцы дробей

Учащиеся, как правило, хорошо понимают площадные модели. Они могут взять прямоугольник и разбить его на трети, четверти и так далее. Они могут использовать дроби для сравнения и объяснения, почему половина больше, чем одна четвертая.

Итак, давайте воспользуемся тем, что учащимся удобно, чтобы представить дроби в числовом ряду.

В приведенном выше упражнении учащиеся будут заштриховывать столбчатую диаграмму , чтобы представить дробь. Затем они используют гистограмму, чтобы помочь себе разбить числовую строку . Наконец, они строят дробь .

Вы можете использовать эту распечатку во время небольших групп. Существует  три версии  этой печатной формы, поэтому при необходимости вы можете легко различать их.

• Первая версия имеет дроби, перечисленные на странице.
• Во второй версии есть место, где учащиеся могут написать дробь.
• Третья версия является самой сложной, потому что учащиеся должны разделите числовую прямую и постройте дробь.

(Эту бесплатную печатную форму можно загрузить в конце этой записи в блоге.)

2. Используйте математическую сортировку

Ученикам нравится работать с математической сортировкой. Всегда приятно, когда можно преподать сложную тему в увлекательной игровой форме. Это занятие не только побуждает учащихся вырезать/вставлять, но также побуждает учащихся объяснять свои мысли.

• Шаг 1: Разрежьте карты
• Шаг 2: Найдите 4 дроби
• Шаг 3: Найдите модель стержня, соответствующую дроби
• Шаг 4: Найдите модель числовой линии, которая соответствует модели дроби и столбца
• Шаг 5: Объясните, как связаны между собой три карты
• Шаг 6: Клей

(Эту бесплатную печатную форму можно загрузить в конце этой записи в блоге.)

3. Заставьте студентов двигаться!

Объедините учащихся в группы и пусть они будут создать модель линии большого числа . Они могут использовать диаграммную бумагу, ленту, веревку или что-нибудь еще, что может быть у вас в классе.

Цель состоит в том, чтобы побудить учащихся двигаться и творить! Я напечатал 5 различных страниц с заданиями, которые вы можете использовать со своими учениками. Они включают в себя место для записи, поэтому учащиеся могут записать, как выглядит их числовая линия.

В эту бесплатную загрузку включены 5 страниц с дифференцированными заданиями

• Группа студентов
• Каждая группа получает страницу активности
• Учащиеся работают вместе, чтобы нарисовать и разделить числовую прямую
• Студенты сюжет дроби
• Студенты записывают свою числовую строку на бумаге
• Учащиеся представляют свои числовые строки классу

 

 

4. Вырезать и вставить – Смешанные числа, практическая страница

Дроби больше единицы могут сбивать с толку при моделировании на числовой прямой. Я выполняю следующие шаги:

1. Считайте равные части, пока не дойдете до первого целого (единицы).
2. Укажите, какая дробь равна единице. Например: 2/2 = 1
3. Продолжайте считать равные части. Например: 3/2

Теперь запишем дробь больше единицы в виде смешанного числа .

1. Выделите последнее целое число, которое вы передали. Например: 1
2. Подсчитайте, сколько равных частей вам нужно перепрыгнуть из целого числа, чтобы получить дробь больше единицы. Например: 1/2
3. Запишите смешанное число: 1 1/2

Приведенная выше печатная форма включена в бесплатную загрузку (в конце этого поста). Я также включил версию, которая идеально подходит для занятий по математике под руководством . В видео ниже показан пример того, как вы можете повторить этот навык с учащимися, испытывающими затруднения.

5. Проект додекаэдра

Я начинаю с того, что показываю своим ученикам, как выглядит окончательный проект. Они сразу же очень заинтересованы и готовы приступить к работе. Всегда приятно, когда удается заинтересовать учащихся сложной темой.

1. Предложите учащимся сначала заполнить страницы карандашом
2. Проверьте проблемы
3. Дайте учащимся время на раскрашивание
4. Вырезать круги
5. Скрепите круги вместе, чтобы сформировать додекаэдр

Ниже приведен пример того, как один учитель представил финальные проекты.

6. Интерактивные цифровые математические центры

Привлекайте учащихся с помощью этих увлекательных интерактивных математических центров. В каждом стандарте есть 2 практических файла. Вы могли бы..

• Назначить через Google Classroom
• Учащиеся могут выполнять задания в математических центрах (рабочие столы или iPad)
• Заполните всю группу с помощью интерактивной доски

instagram.com/p/BexwdyLh2nX/» data-instgrm-version=»8″>

Сообщение, опубликованное Math Tech Connections (@mathtechconnections) 4 февраля 2018 г. в 6:05 утра по тихоокеанскому времени

Просмотреть цифровые ресурсы

 

---

 

Подпишитесь на рассылку новостей

Подпишитесь и получите 4 бесплатные печатные формы на ваш почтовый ящик!

Мы не будем рассылать вам спам. Отписаться в любое время. Работает на ConvertKit

Рубрики: Дроби и десятичные дроби, Math Workshop

Скачать бесплатно!

Занятия по математике для 3-го класса: распечатка и цифровая математика

Получите доступ к ТРЕМ печатным и цифровым математическим играм для повторения дробей!

Я хочу эту халяву!

Вам также могут понравиться эти публикации

Взаимодействие с читателями

Math Tech All Access

Получите мгновенный доступ ко всем ресурсам Math Tech Connections!

Вступай в клуб!

Интерактивные цифровые математические слайды

Все ресурсы

Привет, друзья!

Я Мариэла! Мне нравится создавать печатные и цифровые математические ресурсы, основанные на стандартах и ​​привлекательные. Я считаю, что использование модели математического семинара — лучший способ достучаться до каждого ученика. Я надеюсь, что мои ресурсы сэкономят вам время и сделают математику увлекательной!

Познакомьтесь с Мариэлой

Управление согласием

5 способов сделать сравнение дробей более увлекательным!

Сравнение дробей — это БОЛЬШОЙ шаг вперед по сравнению с простым определением дробей и форм разбиения. Теперь мы просим студентов посмотреть на две разные письменные дроби и использовать язык сравнения, например больше, меньше или равно. Это не шутка!

Если вы когда-либо преподавали сравнение дробей, вы знаете, что сложный характер содержания иногда может мешать учащимся полностью погрузиться в процесс обучения. В этом посте я описал пять моих любимых способов сделать сравнение дробей более увлекательным для ваших учеников!

Сравнение дробей в искусстве и фотографии 

Если вы не знали, «Разговоры о числах» — одно из моих самых любимых занятий! Они создают такое сильное сообщество математиков и создают удивительные возможности для студентов, чтобы развивать навыки общения вокруг их математического мышления!

Дроби могут стать интересной темой для «Разговоров о числах».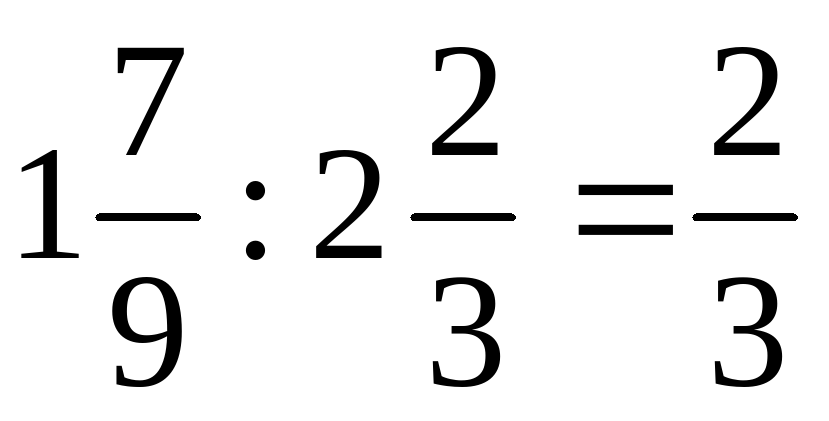 В то время как мы можем абсолютно точно написать несколько дробей на доске и попросить учащихся сравнить их (это СОВЕРШЕННО действительные и полезные разговоры о числах), также может быть интересно поменять местами! Один из моих любимых способов — спроецировать фотографию и предложить учащимся найти в ней дроби.

Некоторые примеры могут включать работы таких художников, как Пит Мондриан (см. изображение его работы ниже). Они отлично подходят для начала разговора и предлагают так много возможностей для обсуждения цветов и представления различных фракций. Мне также нравится, что в подобных беседах с цифрами есть несколько точек доступа, поэтому учащиеся могут изменять или расширять беседу, чтобы легче бросить вызов себе на своем «нужном уровне».

Изображение предоставлено Creative Commons, художник Робсон.

Другие забавные изображения включают здания, окна, фотографии организационных решений (вы знаете… с десятками ящиков!) С ними есть неограниченные возможности!

Создайте прогулку по галерее фракций

После демонстрации того, как обсуждать дроби на фотографиях/картинах во время «Разговоров о числах», вы можете превратить это в независимый центр в своих классах! Разместите фотографии/картины в своей комнате или сделайте их ксерокопии, чтобы ученики могли поместить их в свои математические журналы и позволить им начать писать о том, что они видят. Позвольте им рисовать, писать и/или использовать числа, чтобы поделиться своими мыслями о различных дробях, которые они видят.

Вы можете добавить к этому упражнению «банк слов», если хотите, чтобы они начали сравнивать дроби определенным образом (например, больше, меньше, целое, равно и т. д.).

Scaffolding Student Work

Прежде чем предложить учащимся начать самостоятельное сравнение дробей, я обязательно включу несколько бесед о числах и мини-уроков по следующим темам:

• Сравнение дробей с одинаковым числителем
• Сравнение дробей с одинаковым знаменателем
• Использование эталонных дробей для сравнений

Однако, как только мы выработали базовое понимание и разработали несколько полезных стратегий, пришло время дать им возможность попробовать их самостоятельно… конечно, с некоторой подготовкой!

У меня есть несколько любимых занятий, когда нужно помочь учащимся сравнивать дроби. Они начинаются ОЧЕНЬ просто, и их можно использовать снова и снова, чтобы получить повторяющуюся, но содержательную практику (лично я держусь как можно дальше от одноразовых рабочих листов).

В этих упражнениях с дробями домино (также доступны с кубиками, если у вас нет домино) учащиеся сравнивают дроби с помощью встроенных визуальных средств.

Во-первых, мне нравится, когда они разделяют и затеняют свои формы (мы уже вместе поработали над этим). Имея на месте эти конкретные изображения, учащиеся могут легче расшифровать, какая дробь больше другой, а затем написать предложение для сравнения. По мере того, как они знакомятся, я предлагаю им сначала попытаться обосновать сравнение, а затем использовать визуальные эффекты, чтобы подтвердить (или нет) свои первоначальные мысли.

Вторая версия меняет изображение на числовую строку. Мои ученики часто сталкиваются с трудностями при работе с дробями на числовой прямой, поэтому предоставление им возможности поработать с ними было очень полезно! Я всегда стараюсь делать это в одну секунду, потому что тогда они уже знакомы с идеей и самим действием, так что теперь все, что им нужно сделать, это сосредоточиться на числовой прямой.

Предложение выбора вместо сравнения дробей

Всякий раз, когда я предлагаю своим ученикам ВЫБОР, вовлеченность возрастает! Это означает, что я ввожу несколько разных занятий (их не должно быть много, но 2-3) и позволяю им выбирать, как они хотят учиться.

Два из моих любимых заданий, которые я могу предложить ученикам на выбор, — это «Переверни дробь и сравни » (возможно, ты знаешь его как старую карточную игру «Война») и одно, которое я создал вместе со своими учениками под названием « Заказ готов! ”

Fraction Flip & Compare очень легко реализовать, потому что учащиеся часто имеют предыдущий опыт игры. Мне лично нравится иметь доску или какое-нибудь наглядное пособие, которое помогает учащимся отделить числитель от знаменателя.

Я заставляю учеников вести записи, когда они играют, по 3 причинам:

1. Это позволяет мне видеть их понимание, даже если меня нет, потому что я работаю с небольшой группой.
2. Студенты несут ответственность за свою работу. Внедрение листов для записей стало отличным лайфхаком для управления классом!
3. Дает мне чистое и аккуратное место для включения модели линейки дробей, чтобы помочь учащимся стать более независимыми.

Заказ готов! Это еще один фаворит класса (я имею в виду, это пицца!). Это задание сложнее, чем «Перевернуть и сравнить дроби», потому что оно переходит от сравнения двух дробей к упорядочению четырех разных дробей от наименьшей к наибольшей. Опять же, я обязательно включаю модель дроби для поддержки и часто прошу студентов вести страницу с записью по всем тем же причинам, упомянутым выше.

Моим ученикам НРАВИТСЯ возможность выбирать, как они будут сравнивать дроби. Когда они мотивированы выбором, их уровень вовлеченности повышается. Когда их уровень вовлеченности повышается, их внимание увеличивается, и они с большей вероятностью улучшат свое понимание. ПОБЕДИТЬ!!!

Бесплатное упражнение «Сравнение дробей»

Ваши ученики испытывают затруднения при сравнении дробей, используя эталонные дроби? Загрузите эту бесплатную загрузку со встроенной визуальной поддержкой, чтобы помочь им практиковаться!

Дай это мне!

Групповые игры, которыми они не могут насытиться!

Если вы раньше посещали мой блог, то знаете, что моя любимая игра для небольших групп — Kaboom! Я клянусь, вы можете использовать эту игру практически для каждого навыка в каждом предмете, который вы преподаете…. так что, конечно, я использую его, когда учу сравнивать дроби!

Если вы не знакомы с Kaboom, вам определенно захочется просмотреть этот пост в блоге, где я разбиваю его и даю несколько полезных советов о том, как его настроить и организовать в вашем классе.

Несколько лет назад я проходил собеседование на новую преподавательскую должность, и пришло время администрации прийти и посмотреть демонстрационный урок. На самом деле я поставил эту ТОЧНУЮ игру в один из моих математических центров, когда я преподавал в небольшой группе по математике. (Да, я достаточно доверяю этой игре, чтобы сделать это во время формального наблюдения во время интервью.)  

Я получил много положительных отзывов, касающихся как уровня вовлеченности, так и ответственности учащихся на странице записи. И… если вам интересно, я получил работу!

Надеюсь, эти советы были вам полезны. ВСЕ студенческие игры и задания можно найти в моем Fraction Mega Pack , и он не зря называется мегапаком! Это почти 400 страниц ВСЕХ моих любимых игр для обучения дробям в третьем классе. Нажмите ЗДЕСЬ, чтобы проверить!

Пять забавных упражнений для обучения дробям с едой

25 Акции

• Более

Обучение дробям с помощью еды

Обучение дробям с помощью еды — это естественный способ начать изучение дробей. Дети любят (и часто требуют!) мультисенсорный подход к обучению, и что может быть лучше, чем еда.

Некоторые обычные продукты не только способствуют преподаванию и обучению, но и являются предметом разговора. Дети мгновенно расскажут вам историю, которая была вызвана тем, что они увидели конкретный шоколадный батончик или почувствовали запах апельсина.

Содержание

Это пять моих любимых продуктов для обучения дробям.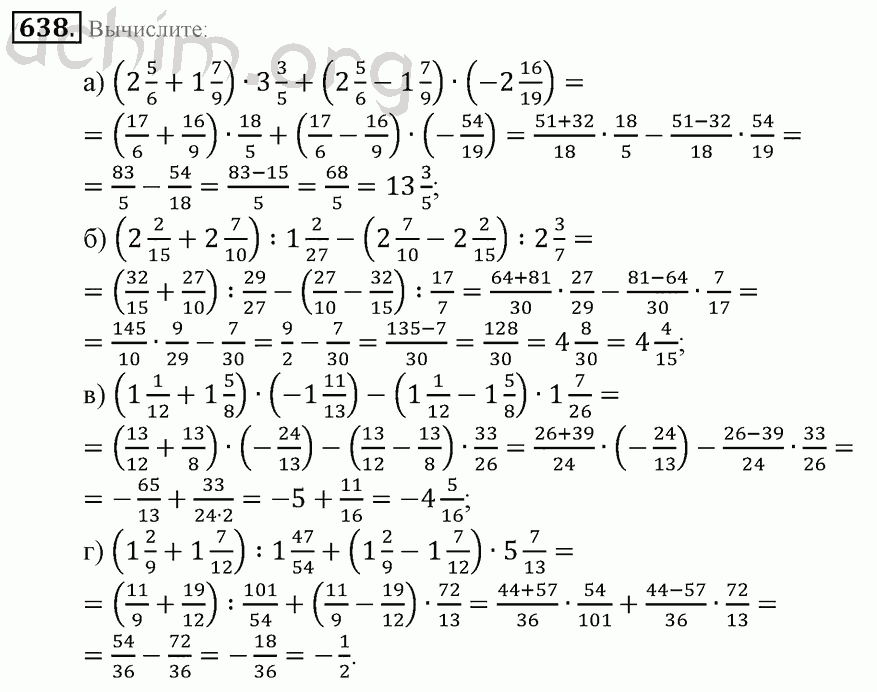 В конце у меня есть бесплатные рабочие листы для печати, которые также помогут вам представить эквивалентные дроби с едой.

После того, как вы прочитаете это или поделитесь им со своими учениками, я уверен, что они придумают что-то еще. Спрашивать у них больше идей о Fraction Foods — это здорово, чтобы стимулировать творческое мышление.

На прошлой неделе мы начали наш отряд с еды. Есть одна вещь, в которой мои мальчики преуспевают (на самом деле их больше, чем одна), но они невероятные едоки. Они очень активны и имеют аппетит, соответствующий их уровню движения.

Итак…..если мы перекусим, пока учимся, я супермама…по крайней мере, на несколько минут.

Упражнения с дробными продуктами

Есть много продуктов, которые уже разделены на равные части, и использование этих продуктов для введения дробей позволяет детям начать устанавливать связи, используя свои базовые знания.

Я создал простую карточку с заданием, которую можно распечатать в качестве руководства для нас, когда мы «играли» с нашей едой, и нам понравилось работать с ней и изучать концепцию дробей. К концу нашей недели введения фракций с едой я их не использовала. Удивительно, но у меня было много жалоб. Я думаю, мы должны следовать рутине!!!!

Эквивалентные фракции с пищей

Подготовка к каждому уроку была очень простой. Очевидно, вам нужна еда… мы доберемся до этого, но у меня также была готова распечатка для моих детей.

1. Сначала я распечатал карточки с заданиями на картонной бумаге.
2. Затем я вырезал их и заламинировал.
3. Вы можете проделать в них отверстие и надеть на них маленькое кольцо, чтобы скрепить их.
4. Подготовьте немного сухостираемого маркера, и вы готовы к работе!

Фракции еды

Каждый день я раздавал еду, и мы определяли ее целиком.

Далее мы просто работали с карточками задач . Первая карточка спрашивает ученика, можно ли разделить еду поровну между двумя людьми. Дети знают все о том, как делиться, и понимают, насколько важно, чтобы каждый человек получил изрядную сумму!

Когда мы «делились» своей едой, я постоянно укреплял идею о том, что знаменатель говорит нам, сколько равных групп должно составлять целое. И важно, чтобы их группы были равны.

С этой едой, как видите, легко разделить Кит-Кат на две равные части. Мы нарисовали, как выглядит каждая часть, и написали, что из двух частей каждый получит одну… 1/2.

Далее мы придумали эквивалентные дроби. Например, легко увидеть, что в каждой группе по две штуки Kit Kat. Мы обсудили (и я показал им), что эквивалентная дробь будет равна двум четвертым.

Мы просмотрели каждую карточку с заданием, и если бы это был простой способ поделиться едой, мы бы сделали эту карточку с заданием.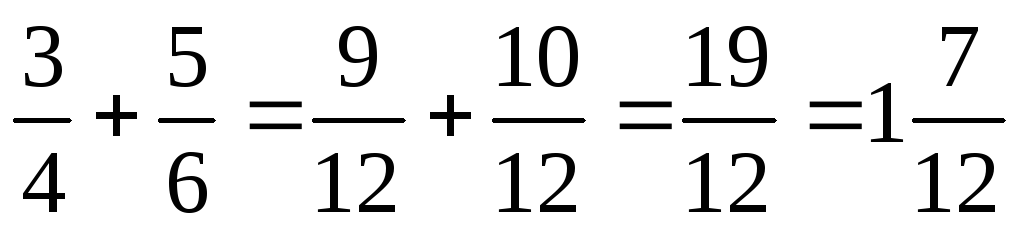 Kit Kat идеально подходил для совместного использования вчетвером, и нам удалось сделать это даже с восемью людьми.

Поскольку мои дети были маленькими, мы не делали фракций, которые нельзя было бы легко разделить. Трудно разделить крекер Грэма на трети, но возможно.

Если бы я работал с пятиклассниками, я мог бы попробовать это с ними. Мыслительный процесс будет полезен, поскольку они делят и умножают дроби позже.

Какие продукты идеально подходят для дроби?

Крекеры

Эта закуска идеально подходит для большого класса и является быстрым способом ввести 1/2 и его эквивалентную форму 2/4. Очевидно, 1/4 тоже легко увидеть.

Если бы меня спросили, я думаю, что большинство детей предпочли бы крекеры из муки грубого помола. Но подойдет Saltines или любой другой крекер с перфорированными швами.

Батончики Hershey

Это мой любимый батончик. Мало того, что они имеют прекрасный вкус, потому что они шоколадные. Но есть потрясающая книга, которая будет вести деятельность за вас. В этот день я не использовал карточки с заданиями. Мы только что прочитали книгу, и концепция дробей и эквивалентных дробей ясно объяснена.

[amazon box=»04392″ template=»horizontal»]

Это был один из любимых уроков моего ученика, когда я преподавал в четвертом классе, и он не подвел меня, когда я делал его со своими мальчиками. Однако, пожалуйста, знайте, что он больше не издается (грустное лицо). Вот почему это немного дорого для книги в мягкой обложке.

Учителя очень находчивые люди. Проверьте продажи подержанных книг и тому подобное. Вы никогда не знаете, у кого может быть копия. (кто-нибудь из коллег уходит на пенсию?? у них может быть старая копия)

Нам удалось покрыть 1/2 и эквивалент 3/6. Мы также работали с масштабами 1/3, 1/4 и 1/6 и их эквивалентами.

Апельсины

Апельсины не являются идеальным дробным продуктом, но они отлично работают и полезны для здоровья. Если вы решите использовать апельсины, вам нужно будет обсудить, что все дольки не идеально равны . Они довольно близки, и когда мы нашли очень маленький кусочек, мы просто оставили его с большим куском. Это может быть проблемой для некоторых негибких мыслителей.

Кроме того, с апельсином вам не гарантируется четное число или любое количество долек. У обоих из нас оказалось по 9 ломтиков, что дало нам возможность использовать дроби 1/3 и 3/9.

Kit Kats

Они очень похожи на крекеры Грэма, но показывают учащимся другой способ приготовления 1/2 и 1/4. Вы даже можете попробовать 1/8 с дополнительным перерывом или если вы получите несколько гигантских.

Наборы крекеров для закусок

Я люблю их, потому что они показывают, что иногда целое — это не просто один кусок еды. Целое может быть суммой любой равной вещи.

Это также отличное введение в такие задачи, как вычисление 1/2 от 12. Часто эти задачи сбивают с толку детей, потому что они думают о дробях только в отношении к кругу или квадрату, разрезанному на части.

Когда мы учим дроби, нам нужно предоставить много разных образцов, и пакеты с едой — отличное место для начала. Небольшой пакетик кеглей, M&M или пачка крекеров — вот лишь несколько замечательных примеров.

Мне нравятся крекеры, потому что в них одинаковое количество и они не сладкие. Я знал, что мы можем найти дроби 1/2, 1/3 и 1/6.

Они дали нам возможность исследовать эквивалентные фракции, которые были исключены из Kit Kats и крекеров Graham.

Обучение дробям с едой

После того, как мы «поиграли» с едой, мы выбирали одну дробь и распечатывали дробь дня. Это был еще один способ просмотреть то, что мы рассмотрели, но также дать им возможность увидеть дробь на числовой прямой.

Действия с фракциями еды

Это будет играть важную роль, когда мы начнем играть в игры, чтобы закрепить эквивалентные дроби и различные способы их иллюстрации. Не пропустите все самое интересное, что есть у меня на сайте и на TeachersPayTeachers страница для обучения эквивалентным дробям.

пищевые фракции

Вот это да!

пищевые фракции

25 Акции

• Более

Как складывать дроби за 3 шага и 5 увлекательных занятий Сложение дробей

Возможно, ваши ученики знают, как обращаться с числителем и знаменателем, но готовы ли они к тому, что будет дальше? Внезапно пришло время учить складывать дроби — и ваш класс запутался.

Чувствуете страх?

Вы не одиноки. Добавление дробей может показаться сложным, но это не обязательно.

Почему учащиеся испытывают трудности с дробями?

Дроби — особенно операции с дробями — сложный предмет для большинства учащихся. Проблемы с дробями могут снизить уверенность в математике и привести к математическому беспокойству, если учащиеся не получают достаточной поддержки по предмету.

Фракции — это борьба по нескольким причинам. Исследования показали, что самыми большими проблемами являются:

1. Понимание того, что означают числа

До дробей учащиеся привыкли работать с целые числа : основные числа, представляющие целые суммы. Дроби знакомят учащихся с рациональными числами , которые имеют совершенно новый набор правил и шаблонов.

Значение дробей сбивает с толку, если сравнивать их с целыми числами. Целые числа выражаются только одним способом, в то время как дроби могут быть выражены разными способами и по-прежнему представляют одну и ту же сумму.

Например, число три можно представить только одним способом, но ²⁄₄ представляет то же количество, что и ½, 0,5 и 50%. Будучи студентом, это трудно уложить в голове.

2. Различные операции с целыми числами и дробями

Методы сложения, вычитания, умножения и деления целых чисел отличаются от тех же операций с дробями. Правила становятся гораздо более непредсказуемыми и запутанными. Многие студенты и учителя имеют ограниченное представление о том, как и почему используются эти методы.

Дроби сложнее представить с помощью визуальных или манипулятивных средств, а правила их добавления труднее понять. Изучение того, как умножать и делить дроби, может еще больше запутать, так как учащиеся должны помнить различия между этими операциями. Это большая корректировка для студентов, которые уже знакомы с арифметикой целых чисел.

Типы дробей

Учащиеся должны сначала понять разницу между каждым типом дроби , чтобы успешно складывать их.

Начнем с основных компонентов дроби.

Дробь представляет части целого. Числитель (верхнее число) показывает количество деталей, которые у вас есть. Знаменатель (нижнее число) показывает общее количество частей, на которые делится целое.

На приведенном выше рисунке наш круг разделен на четыре части. Это означает, что четыре — наш знаменатель. Из этих четырех частей одна выделена. Это означает, что один — наш числитель. Итак, наша дробь равна ¼ или одной четверти.

Существуют три основные категории дробей: Правильные, неправильные и смешанные.

В дополнение к этому уравнения дробей будут разделены на две отдельные категории: те, в которых похожи на дроби , и те, в которых не похожи на дроби .

Базовые знания об этих типах помогут учащимся понять, что делать, когда они сталкиваются с вопросом о сложении дробей.

Теперь, когда вы знакомы с каждым типом дроби, вы можете приступить к сложению! Научите своих учеников приведенной ниже трехэтапной формуле, чтобы уверенно решать уравнения сложения дробей.

3 простых шага для сложения дробей

Сначала это может показаться пугающим, но сложение дробей может быть простым. Все, что вам нужно сделать, это выполнить три простых шага:

• Шаг 1: Найдите общий знаменатель
• Шаг 2: Сложите числители (и сохраните знаменатель)
• Шаг 3: Упростите дробь

Давайте рассмотрим каждый шаг в немного более подробно.

Шаг 1: Найдите общий знаменатель

Если ваши два знаменателя уже совпадают, вы складываете дроби с как знаменатель . Фантастика! Это означает, что вы можете перейти ко второму шагу.

Если у вас разные знаменатели, вы складываете дроби с в отличие от знаменателей. При сложении разных дробей необходимо найти общий знаменатель , чтобы можно было сложить две дроби вместе.

Посмотрите видео ниже, чтобы понять , почему нам нужен общий знаменатель для сложения дробей.

Вы можете найти общий знаменатель, используя эквивалентных дробей : дроби, имеющие одинаковое значение. Например, ²⁄₄, ³⁄₆ и ⁴⁄₈ являются эквивалентными дробями, потому что все они могут быть уменьшены до ½.

Существует два основных метода нахождения общего знаменателя.

1) Метод общего знаменателя

В этом методе вы умножаете верхнюю и нижнюю часть каждой дроби на знаменатель другой. Например, рассмотрим следующее уравнение:

⅓ + ⅙

Наши дроби имеют два разных знаменателя: три и шесть. Нам нужно умножить числитель и знаменатель в ⅓ на шесть, а затем умножить числитель и знаменатель в ⅙ на три.
Когда мы это сделаем, наши новые дроби станут ⁶⁄₁₈ и ³⁄₁₈.

Две новые дроби имеют одинаковый знаменатель, так что теперь мы можем их сложить!

2) Метод наименьшего общего знаменателя

Этот метод включает в себя нахождение наименьшего из всех общих знаменателей, а затем умножение ваших исходных дробей, чтобы получить этот знаменатель.

Чтобы найти наименьший общий знаменатель, перечислите все числа, кратные этому числу, и найдите среди них наименьшее из одинаковых чисел.

Например, используя то же уравнение, что и раньше — ⅓ + ⅙ — вы можете составить таблицу для определения наименьшего общего кратного.

Как видно из нашей таблицы, наименьшее число, кратное одному и тому же, равно шести.

Итак, для ⅓ числитель и знаменатель нужно умножить на два, чтобы получить ²⁄₆. Для ⅙ числа нужно умножить на единицу, чтобы дробь осталась прежней. И снова наши фракции готовы к добавлению!

Шаг 2: Сложите числители (сохраните знаменатель)

Этот шаг довольно прост. Сложите числители, чтобы сумма стала новым числителем, а знаменатель остался прежним.

Давайте воспользуемся нашим предыдущим примером:

⅓ + ⅙

Используя наше новое уравнение из метода общего знаменателя — ⁶⁄₁₈ + ³⁄₁₈ — нам нужно сложить шесть и три вместе. В знаменателе по-прежнему будет восемнадцать.

Шесть плюс три равно девять, поэтому наш ответ ⁹⁄₁₈.

Шаг 3: Упростите дробь

Если ваша дробь содержит большие числа, вам может потребоваться упростить ее.

Упрощение включает в себя нахождение наименьшей возможной эквивалентной дроби. В нашем предыдущем уравнении наш ответ был ⁹⁄₁₈. Это число кажется немного большим, поэтому посмотрим, сможем ли мы упростить его до более простого числа.

Чтобы упростить дробь, вам нужен общий делитель : число, которое делится на оба числа поровну. Например, два — это общий делитель четырех и шести, потому что оба числа можно разделить на два.

Два самых простых метода упрощения дроби:

1) Метод проб и ошибок

Для этого метода просто продолжайте делить числитель и знаменатель на маленькие числа. Начните с двух, затем трех, четырех и так далее, пока не получите наименьший возможный ответ.

С нашим ответом ⁹⁄₁₈ мы можем продолжать делить на маленькие числа, пока не найдем то, которое работает.

Можно ли разделить девять и восемнадцать на два? Нет. Мы не можем разделить девять на два поровну.

Хорошо, попробуем другой номер.

Можно ли разделить девять и восемнадцать на три? Да! Когда мы делим оба числа на три, наша дробь становится ³⁄₆.

Теперь, когда у нас есть более простой ответ, пришло время посмотреть, сможем ли мы упростить его еще больше. И три, и шесть можно снова разделить на три, поэтому наш окончательный ответ — ½.

2) Найдите наибольший общий делитель (НОД)

НОД — это наибольшее число, которое делится на два или более чисел без остатка.

Этот метод похож на нахождение наименьшего общего знаменателя — вы найдете ответ, перечислив все возможные факторы.

Используя наш предыдущий пример с ⁹⁄₁₈, мы найдем и перечислим все делители каждого числа, начиная с единицы. После того, как вы перечислили все множители этого числа, все, что вам нужно сделать, это найти наибольшее число, повторяющееся в обоих списках.

В этом также поможет удобный стол.

Воспользуемся нашей таблицей, чтобы найти наибольшее число, общее для обоих чисел. В этом случае наибольший общий делитель для девяти и восемнадцати равен девяти. Теперь мы можем разделить оба числа на девять, чтобы получить уменьшенную дробь: ½.

Если объединить все три шага сложения дробей, получится следующее:

Сложение смешанных дробей

Описанные выше шаги прекрасно подходят для правильных и неправильных дробей, но как насчет сложения дробей с целыми числами?

Складывать смешанные дроби на самом деле очень просто: просто преобразуйте их в неправильные дроби, и вы готовы начать сложение!

Любую смешанную дробь можно превратить в неправильную. Например, 1 ¾ — это то же самое, что ⁷⁄₄.

Источник изображения: Central Bucks School District

Преобразование смешанных дробей в неправильные осуществляется в три этапа:

1. Умножьте целое число на знаменатель

Возьмем 1 ¾. Если мы умножим наше целое число (один) на наш знаменатель (четыре), мы получим четыре.

2. Добавьте это число к числителю

Наше новое число (четыре) плюс наш числитель (три) равно семи.

3. Напишите новый числитель над исходным знаменателем

Наш новый числитель (семь) по отношению к исходному знаменателю (четыре) равен ⁷⁄₄. Теперь вы можете сложить дробь!

Важность сложения дробей

Как учитель, вы, вероятно, хорошо знакомы с извечным вопросом, который задают ученики: «Зачем я вообще это делаю?»

В этом контексте это, безусловно, правильный вопрос. Почему сложение дробей так важно для изучения?

Во-первых, у этой арифметики есть множество реальных применений. Во многих случаях вам нужно будет найти общее количество частей целого, когда они объединены.

Вот несколько возможных примеров сложения дробей в реальной жизни:

1. Упражнения : Если вы пробежали ¼ мили в понедельник и ¾ мили во вторник, какое расстояние вы пробежали за оба дня?
2. Тайм-менеджмент : Если вы работаете 8 ½ часов в понедельник и 6 ¾ часов во вторник, сколько часов вы проработали в оба дня?
3. Приготовление/выпечка : Если вы добавите ½ стакана стружки молочного шоколада и ⅓ стакана стружки белого шоколада в тесто для печенья, каково общее количество шоколадной стружки в вашем рецепте?

Если этого недостаточно, знание операций с дробями на самом деле очень важно для изучения более сложных математических и естественных наук, что в конечном итоге приводит к успеху во многих академических или карьерных сферах.

Ограниченные знания в операциях с дробями могут привести к более слабым навыкам в более поздних математических и естественных науках. Одно исследование показало, что в Соединенных Штатах и ​​​​Великобритании знание дробей учащимися начальных классов может предсказать общие математические способности в старшей школе.

Опрос навыков, технологий и методов управления на рабочем месте (STAMP) показал, что 68% работающих людей в возрасте 18 лет и старше используют дроби в своей повседневной работе. Это означает, что значительному количеству взрослых в Соединенных Штатах требуется твердое базовое знание дробей и их операций. Изучение этих навыков как можно раньше является ключом к успеху на многих рабочих местах.

5 Увлекательные занятия по сложению дробей

Теперь, когда вы знаете, чему научить своих учеников складывать дроби, давайте сосредоточимся на том, как. Вдохновитесь этими пятью увлекательными идеями занятий, которые дополнят ваши уроки сложения дробей.

1) Prodigy

Prodigy – это учебная платформа, ориентированная на учебную программу, с более чем 1 500 навыками, позволяющими детям практиковать математику. Используйте его, чтобы освоить все виды дробей, от базового понимания до более сложных операций, таких как сложение.

Prodigy отправляет игроков в захватывающее приключение, где они отвечают на математические вопросы, чтобы «сразиться» с другими персонажами. Платформа предназначена для вовлечения учащихся в игру, поэтому они действительно захотят, чтобы продолжала играть и, как результат, больше занималась математикой!

Платформа — отличный инструмент для дополнения уроков, домашних заданий и многого другого. Это также может помочь вам дифференцировать обучение и определить конкретные проблемные места, помогая каждому учащемуся добиться успеха в своем собственном темпе.

«Наш последний тест был на Fractions, и это был первый раз, когда я действительно убедился, что каждый день в Prodigy они отрабатывают эти конкретные навыки, и результаты теста очень хорошо отражали дополнительную практику, которую они получили! »  — Жюстин Хилл  учитель 3-го класса, центральные школы Восточных Сиракуз-Миноа

2) Игра с ударами

Стимулируйте здоровую конкуренцию в классе с помощью увлекательной настольной игры, в которой игроки «ударяют» друг друга дроби, чтобы претендовать на место на доске.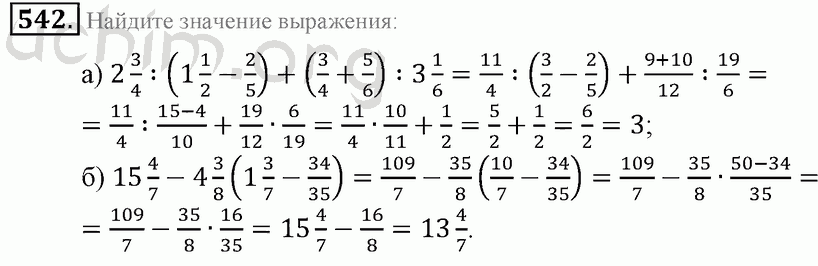

Вы можете найти множество игр на разные темы. В этом выпуске с добавлением дробей игроки должны бросать кости, чтобы найти соответствующее уравнение, а затем размещать свои игровые фишки на дроби, которая соответствует ответу.

Игрок, который первым соберет все свои фишки на доске, становится победителем!

4) Словесные задачи

Словесные задачи для уравнений дробей представляют собой реальные примеры вопросов, на которые учащиеся отвечают, помогая им понять цель таких вопросов.

Источник изображения: Teachers Pay Teachers

Карточки с задачами Word и рабочие листы — отличный способ задать эти вопросы. Если вы хотите, чтобы ваш класс был более вовлечен, вы можете использовать манипуляторы или даже самих учеников.

Например, «если три человека одеты в зеленое, а двое — в синее, какова доля в классе людей, одетых в зеленое или синее?»

4) Составители уравнений

В этом упражнении учащиеся рисуют или строят уравнения, чтобы визуализировать, как выглядит сложение дробей.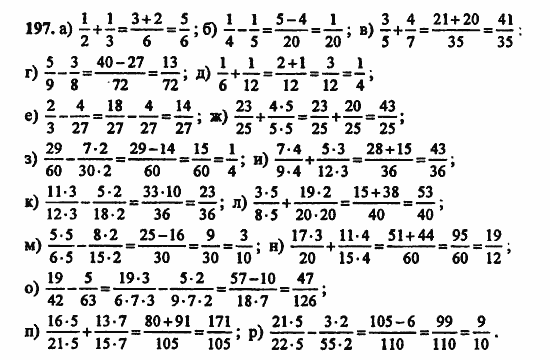

Источник изображения: Desert Designed

Попросите учащихся составить уравнения или использовать манипуляции, чтобы лучше понять, что на самом деле означает сложение дробей. Дробные полосы или шкала дробей — отличные варианты, чтобы сделать эту абстрактную концепцию более удобоваримой и конкретной.

Проверьте три типа дробей Примечания

5) Math mates

Эта активная игра поднимает учеников со своих мест, сотрудничая с одноклассниками и практикуя математику… все сразу!

У каждого ученика своя фракция. Игроки ходят по комнате, находят партнеров и работают вместе, чтобы сложить свои фракции.

Эта игра отлично подходит для отработки навыков, полученных в классе, и поощрения командной работы.

Заключительные мысли о добавлении дробей

Переход от базовых навыков дробей к сложению, безусловно, пугает, но добавление дробей можно упростить, выполнив три простых шага, описанных выше.

Используйте информацию из этого руководства, чтобы победить на следующем уроке математики и упростить сложение дробей для ваших учеников. Далее: вычитание, умножение и деление. О боже!

Создайте или войдите в свою учетную запись учителя на Prodigy – игровой платформе для обучения математике, ориентированной на учебную программу, с полезными инструментами как для преподавателей, так и для учащихся.

Преподавание дробей: пять любимых стратегий для осмысления дробей Веб-семинар, часть I — Профессиональное обучение учителей | Грамотность, математика

Стенограмма видео

Некоторые вещи, которые я хочу выделить в этом разделе, которые я хочу, чтобы мы рассмотрели, как эти понятия связаны с целыми числами с дробями, являются понятиями единиц, а также как дроби — это числа, а эквивалентные дроби, сложение и вычитание — дроби, а умножение и деление — дроби.

Вот список из общих основных государственных стандартов, стандартов, связанных с этим. И здесь в сокращенной форме показаны стандарты дробей для каждого уровня обучения. И тогда [неразборчиво] состояние не является общим СЕРДЦЕМ. Эти ссылки и порядок контента, который будет разрабатываться с дробями по годам, довольно согласован во всех государственных стандартах. И эти стандарты здесь дают хорошее направление относительно некоторых мест, где имеет смысл строить понятия дробей на основе понятий целых чисел.

На этой диаграмме мы можем видеть несколько мест, выделенных красным или оранжевым, я думаю, которые являются основными местами для соединения дробей с целыми числами, в том числе места, где общие стандарты CORE фактически прямо указывают, что работа с дробями должна быть связана с и построен на предварительном понимании с целыми числами.

Еще я заметил, что они выделены фиолетовым цветом… В стандартах есть ежегодное указание на использование визуальных моделей. Я просто хотел подчеркнуть это, поскольку именно это мы только что подчеркнули здесь, на вебинаре. Хорошо. Итак, первое, единицы. А единицы? Что ж, с разрядным значением у нас есть все целые числовые единицы, основанные на единицах.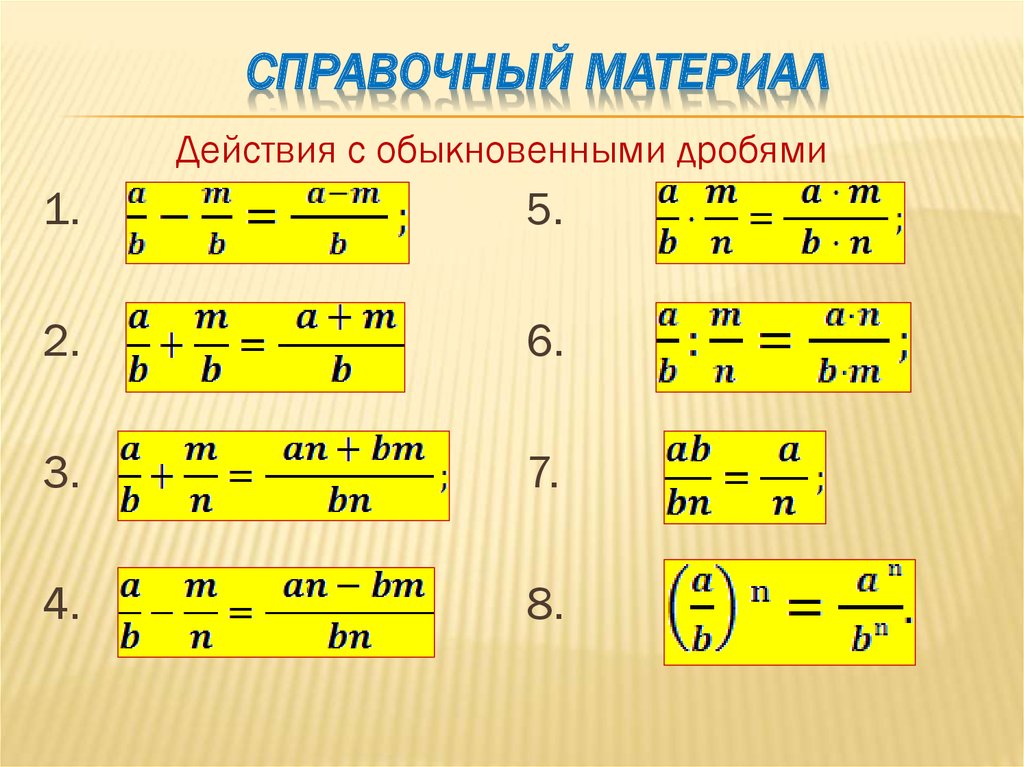 Это значение центрального блока. Десятки или 10 штук в комплекте. Сотни — это 10 десятков или 100 единиц, связанных вместе и т. д.

Десятые, сотые, тысячные и т. д. также следует рассматривать по отношению к единицам как часть единиц единицы. Дроби также являются единицами. Половинки, трети, четверти — все это части единого целого. Знаменатель… извините. Знаменатель говорит нам единицу измерения. Если знаменатель, например, равен 10, или 100, или 1000, то дроби легко преобразуются в десятичное представление. Но в любом случае знаменатель является единицей и последовательно частью единицы единицы.

Идея заключается в том, что единица делится на более мелкие единицы. И кстати, любая дробь с единицей в числителе на самом деле называется единичной дробью. И по этой причине, потому что дробь является ровно одной единицей любого знаменателя. Как я уже упоминал ранее, я просто еще раз повторю, насколько важны числовые линии, потому что вы должны понимать, что дроби — это числа, что вы можете считать их так же, как и целые числа.

Работа, которую мы выполняем над числовыми рядами, помещая их в числовые ряды, действительно поддерживает идею о том, что дроби — это числа. Это количества, как и целые числа. Теперь эквивалентные дроби. Я хочу поговорить об этом здесь несколькими способами. Сначала я просто хочу указать на идею о том, как мы делаем эквивалентные дроби. И это построено на целых числах. И я просто сначала напомню вам свойство мультипликативной идентичности.

Вы, возможно, не помните его названия, но идея, думаю, всем ясна, что любое число, умноженное на единицу, равно одному и тому же числу. Таким образом, 18 умножить на один равно 18. Это очень простое свойство, но на самом деле очень важное свойство не только целых чисел и дробей, но и всей алгебры. И это в средней и старшей школе, а также на уровне колледжа по математике. Это очень простое свойство играет огромную роль на всем протяжении.

Теперь, с дробями, это свойство работает точно так же. Итак, две пятых умножить на один. Это по-прежнему равняется двум пятым. Однако конечный результат не всегда выглядит одинаково с дробями. Это своего рода ответ с целыми числами, конечно. Умножаем целое число на единицу, в итоге получается то же целое число. Но с дробями это действительно обычно выглядит иначе.

Предположим, мы умножаем две пятых на три трети. Результат выглядит как другое значение. Я имею в виду, что это другая дробь, но это не другое значение. Тогда в этом разница. И здесь нам нужно помочь школьникам. Мы должны помочь им действительно сосредоточиться на концепции умножения на единицу, чтобы значение количества оставалось неизменным. Значение остается прежним. Используя визуальные эффекты, такие как складывание бумаги, взгляд на числовую прямую и использование того, что мой знакомый учитель четвертого класса называет умножением на большую плохую единицу. В результате получается еще одна дробь, равная по значению первой.

Так же, как и с нашим складыванием бумаги, когда две четверти и четыре восьмых равны половине листа бумаги, две пятых умножить на единицу в версии с тремя третями равно шести пятнадцатым . Это одно и то же значение. Таким образом, этот тип иллюстраций и фраз с большой ошибкой и связи с другими конкретными и визуальными представлениями помогают учащимся действительно удерживать, запоминать и понимать эту математику.

Хорошо. Еще одна вещь, связанная с эквивалентными представлениями, о которой я хочу поговорить, — это связь идеи эквивалентных дробей с очень важной идеей математики о том, что существует множество эквивалентных представлений чисел. Неважно, какие это числа, но всегда есть несколько разных способов их записи.

Учащиеся могут построить, вспоминая даже целые числа, например 451, которые могут быть выражены многими способами, поскольку вы видите здесь только четыре из них. И, глядя на четвертый, D, мы могли видеть, что он выражается как три сотни, 14 десятков и 11 единиц, что на самом деле является необходимым способом представления 451, потому что, если мы хотим вычесть из него 273, то вот как мы собираемся представить его, потому что нам нужно будет перегруппировать сотни, десятки и единицы, чтобы выполнить вычитание.

Как и дроби, их можно представить несколькими способами, как мы видим здесь. Но если бы нам нужно было сделать что-то вроде вычитания двух пятых из двух пятых, то было бы полезно представлять две пятых по-другому, как на самом деле шесть пятнадцатых. Таким образом, повторный запуск значений, которые представляют собой различные эквивалентные формы, является важной идеей в математике. И от операций, целых чисел до дробей, и далеко за его пределами, как я упоминал ранее. Поэтому очень важно придать большое значение этой большой идее в математике и помочь учащимся увидеть, как идея о том, что любое количество может быть представлено несколькими способами, преобразуется из целых чисел в дроби, и это общая идея, а не конкретная процедура. или умение, которое просто происходит с дробями.

55 математических заданий для средней школы: алгебра, дроби, экспоненты и многое другое!

1. М и математика

Используйте M&Ms для обучения математике! Предоставьте учащимся стопку M&Ms для подсчета и преобразования в дроби, десятичные числа и проценты. Вы также можете расширить это задание, предложив учащимся графически изобразить свои выводы.

• Необходимые материалы: M&Ms
• Тема: Дроби, десятичные числа, проценты и графики

Узнайте больше: Наше путешествие на запад

2. Что лучше купить?

В этом проекте ваши ученики станут экспертами в поиске наилучшего предложения. Работая с рядом сценариев, учащиеся получат много практики в расчете удельных ставок.

• Необходимые материалы: Распечатанные рабочие листы
• Тема: Стоимость единиц

Узнать больше: Что лучше купить?

3. Сэр Камференс и дракон числа Пи (Математическое приключение) Синди Нойшвандер

Расскажите своим ученикам об окружности кругов, прочитав эту книгу по математике и используя апельсины или бумажные тарелки, чтобы превратить круги в прямоугольники!

• Необходимые материалы: Книга сэра Камференса и острова Имметер, бумажные тарелки или апельсины
• Тема: Окружность

Подробнее: Почти школьники

4. Candy Bar Volume

Ваши ученики любят конфеты? Соблазните их этим сладким занятием. Студенты будут практиковаться в расчете и сравнении объема настоящих шоколадных батончиков. Предложите им использовать это задание, чтобы решить, какой шоколадный батончик им следует выбрать в следующий раз, когда им скажут: «Вы можете выбрать только один шоколадный батончик!»

• Необходимые материалы: Шоколадные батончики разного размера
• Тема: Том

Подробнее: Классная магия

5. Измерение объема твердого тела

В этом упражнении учащиеся будут вычислять объем различных твердых тел. В статье в блоге предлагается использовать камни, но вы можете использовать любые случайные предметы, которые сможете найти — коробку, iPad или даже пульт от телевизора!

• Необходимые материалы: любые твердые предметы
• Тема: Том

Узнайте больше: Сьюзен Эванс

6. Математика попкорна

Научите учащихся основам измерения и навыкам оценки, вместе приготовив попкорн, а потом наслаждайтесь его вместе!

• Необходимые материалы: бумага, ядра попкорна Тема: Емкость, измерение, сбор данных и сравнение

Подробнее: Наше путешествие на запад

7. Измерение объема коробок и сфер

Учащиеся могут отправиться на поиски сокровищ по классу или вашему дому в поисках предметов в форме коробки или сферы. После того, как учащиеся соберут ряд предметов, позвольте им подсчитать и сравнить объемы.

• Необходимые материалы: Коробки или сферические предметы
• Тема: Том

Узнайте больше: The Homeschool Scientist

8. Укладка Oreo

Приветствуем всех поклонников Oreo! Предложите учащимся складывать Oreos как можно выше в этом упражнении, чтобы узнать о сборе данных и средних значениях. Просто убедитесь, что ученики складывают больше, чем едят!

• Необходимые материалы: бумага, Oreos
• Тема: Сбор данных

Подробнее: Преподавание в аудитории 6

9. Сколько стоит тыква?

Это задание состоит из трех уроков. Ученикам дается воображаемая сумма денег, на которую они должны купить самую большую тыкву. Прекрасная возможность для студентов применить свои навыки расчета в реальном сценарии.

• Материалы: тыквы разных размеров
• Тема: Алгебра, вес, стоимость

Узнайте больше: Math Geek Mama

10. Процентная охота за мусором

Распечатайте подсказки, разместите их в школе или дома и отправьте своих учеников на охоту за мусором. Учащиеся будут так активно заняты, что забудут, что это урок математики!

• Материалы: подсказки, бумага, карандаши, планшеты (при наличии)
• Тема: Проценты

Узнать больше: Pinterest

11. Соотношение и выпечка

Дайте учащимся возможность применить свое понимание пропорций к реальной ситуации — масштабированию рецепта выпечки. Если вы действительно хотите пройти лишнюю милю, почему бы не попробовать настоящий рецепт и не приготовить вкуснейшее печенье!

• Материал: рабочий лист рецепта, ингредиенты (по желанию)
• Тема: Соотношение

Узнать больше: Pinterest

12. Графики бумажных самолетов

Дети могут научиться рисовать расстояние каждый раз, когда летают на бумажном самолетике. Это занятие требует небольшой подготовки, но это отличный способ увлечь учащихся.

• Необходимые материалы: Бумага
• Тема: Измерение, ведение учета, построение графиков, средние значения

Подробнее: Наше путешествие на запад

13. Путешествие на Луну

Предложите учащимся подготовиться к путешествию на Луну, используя коэффициенты для расчета своего «космического» веса. Отличное занятие для практики математических навыков и изучения увлекательных научных концепций.

• Материалы: распечатанные рабочие листы
• Тема: Графики, эквивалентные отношения

Узнать больше: Путешествие на Луну

14. Вращательная симметрия

Учащиеся могут использовать эту интерактивную игру, чтобы изучить поведение объектов при вращении вокруг центральной точки.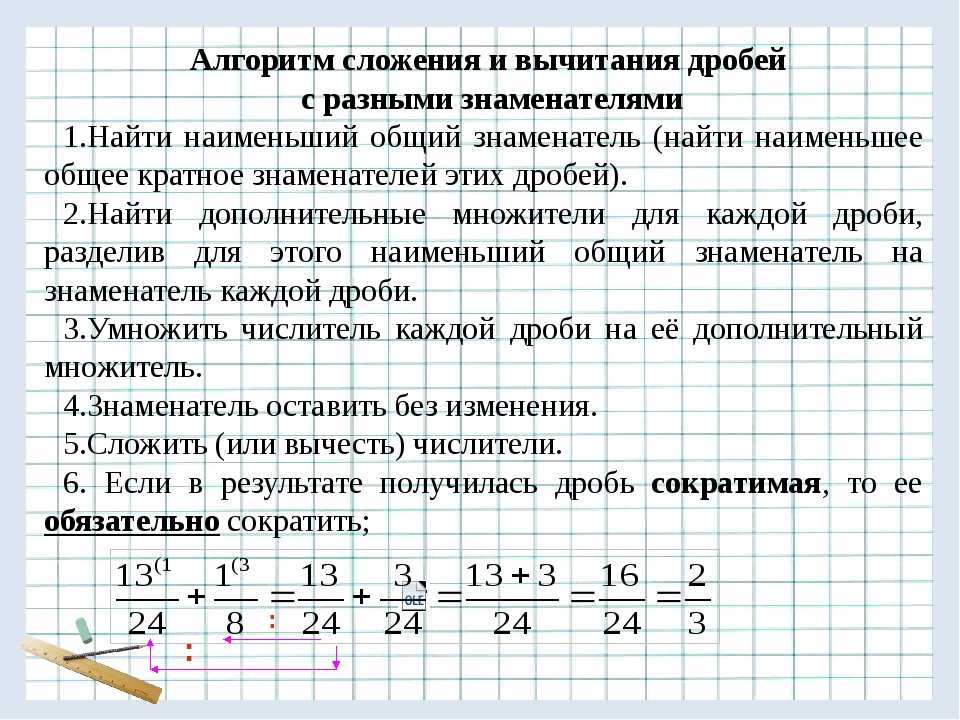

• Необходимые материалы: Доступ к компьютеру или устройству
• Тема: Вращательная симметрия

Узнайте больше: PBS Learning Media

15. Работа Франка Стеллы с транспортиром

Учащиеся могут проанализировать рисунок Фрэнка Стеллы, сделанный с помощью транспортира, и попытаться спроектировать и нарисовать свою собственную версию. Прекрасная возможность для студентов улучшить свои математические и художественные навыки.

• Материалы: Карандаш, транспортир, линейка, транспортир Фрэнка Стеллы
• Тема: Использование транспортира

Узнайте больше: Искусство — это то, чему я учу

16. Королевская шахматная доска: сила удвоения

Через эту историю учащиеся узнают о силе удвоения. После прочтения предложите своим ученикам подумать о том, как они могут использовать силу удвоения, чтобы получить больше карманных денег!

• Необходимые материалы: книга «Королевская шахматная доска»
• Тема: Удвоение

Подробнее: Наше путешествие на запад

17. Масштабируйте комикс

Пусть ваши ученики проявят свои творческие способности в этом упражнении. Студенты разработают и создадут свой собственный комикс, прежде чем научиться увеличивать или уменьшать его, чтобы он соответствовал кадру.

• Материалы: распечатанные рабочие листы
• Тема: Масштабирование

Узнайте больше: Масштабирование комиксов

18. Проект мозаики

Изучите различные методы создания потрясающих мозаичных изображений с использованием вращения, отражения и перемещения.

• Материалы: бумага, ручка, ножницы
• Тема: Вращение, отражение, перемещение

Подробнее: Тренер по геометрии

19. Пифагор с помощью Lego

Надоело постоянно рисовать треугольники, чтобы узнать о Пифагоре? Затем посмотрите это задание — учащиеся будут использовать детали Lego, чтобы доказать теорему Пифагора! Теперь это звучит веселее!

• Материалы: Лего
• Тема: Теорема Пифагора

Узнайте больше: Math Geek Mama

20. Геометрический снеговик

Если приближается Рождество, обязательно посмотрите это занятие. Сложив снеговика, школьники узнают о геометрии и получат новое украшение для елки!

• Материалы: шаблон снеговика, ножницы

Узнать больше: Mini Eco

21. Целочисленные точки

Обучение этому упражнению занимает всего 2-3 минуты, после чего учащиеся могут попрактиковаться в сложении и вычитании целых чисел. Это отличный способ наглядно научить учащихся правилам работы с целыми числами.

• Материалы: жетоны или пуфы двух разных цветов
• Тема: Целые числа

Узнайте больше: Математика в середине

22. Обзор квеста

Веселое занятие — отличная идея для повторения математики! В квесте студенты будут совместно решать задачи!

• Материалы: клей-карандаш, ножницы, линейка, манильские папки, металлическая застежка/скоба для бумаги, зеркало
• Тема: Повторение понятий 6 класса

Дополнительные сведения: Beyond the Worksheet

23. Сортировка карт

Это задание подходит для 7-го или 8-го класса математики. Учащимся даются разные словесные задачи с наборами карточек. Им нужно найти соответствующие карты для нахождения точек, наклона и графика, чтобы написать линейное уравнение.

• Тема: Наклон и линейные уравнения
• Материалы: клей-карандаш и цветная бумага

Узнать больше: Келли МакКаун

24. Игра GCF

Простая игра, в которой ученики решают найти наибольший общий множитель (НОД), чтобы расшифровать скрытое сообщение! Интересный способ попрактиковаться в поиске GCF.

• Тема: наибольший общий делитель
• Материалы: 3 разноцветные ручки, ножницы, клей

Подробнее: Математика в спросе

25. Математическая игра в уме

Используйте эту игру, чтобы развить математические способности в уме, используя целые числа с различными операциями. Он может быть адаптирован для работы только с одной операцией или со всеми и требует очень ограниченного количества материалов и подготовки.

• Темы: Операции с целыми числами
• Материалы: кости

Узнайте больше: Math Geek Mama

26. Сортировка

Эффективный математический обзор порядка операций. В этом упражнении учащиеся решают выражения и сортируют их по разным группам ответов.

• Темы: Порядок работы
• Материалы: цветная бумага, ножницы, клей

Подробнее: Мои математические ресурсы

27. Секретная фотография

Учащиеся будут упрощать радикалы, чтобы открывать цветовые коды. Затем они будут использовать разные цвета для создания загадочного изображения.

• Тема: Радикалы
• Материалы: цветные карандаши

Подробнее: Учителя платят учителям

29. Таблица процентных изменений

В этом рабочем листе используются примеры из реальной жизни, чтобы найти увеличение и уменьшение процента изменений.

• Тема: Процентное изменение в реальном мире
• Материалы: процентное изменение

Подробнее: Процентное изменение, Урок 1

30. Лестничные уравнения

Упражнение содержит математические уравнения, которые можно использовать по-разному — для домашней работы, которую необходимо уравнять, чтобы бросить вызов учащимся.

• Тема: 2 шага Уравнения
• Материалы: нет

Подробнее: Pret Homework

31. Кахут!

Веселая игра, в которую можно заинтересовать учащихся, — это Kahoot! Этот готовый Kahoot фокусируется на поиске площади поверхности трехмерных фигур.

• Тема: Площадь поверхности
• Материалы: компьютеры или телефоны

Узнать больше: Kahoot!

32. Зона складывания

Если вам нужно охватить основные математические понятия, интерактивные тетради отлично подойдут! В этом упражнении для интерактивной тетради рассказывается, как найти площадь треугольника.

• Тема: Площадь треугольника
• Материалы: ножницы, клей, цветная бумага

Узнайте больше: Caffeine Queen Teacher

33. Танцуй, танцуй!

Поднимите студентов-математиков со своих мест при обучении трансверсалам. Студенты будут двигаться, используя ленту на полу в качестве ориентира, чтобы танцевать в соответствии с указаниями для поперечного движения.

• Тема: Поперечные
• Материалы: цветная лента, динамики

Узнать больше: Тиффани Мозиер

34. 31-игра

Простая игра для первого дня или для первых игроков. Учащиеся должны составить ряды и столбцы, равные 31, из любых 25 карточек, которые они выберут.

• Тема: узоры и сложение

 

• Материалы: колоды карт

Узнать больше: Все гении

35. Дневные станции Пи

Учащиеся будут перемещаться по 6 различным станциям, выполняя различные действия, такие как чтение числа «пи» и применение числа «пи» в формуле.

• Тема: Пи
• Материалы: цветная бумага, круглые предметы, линейки

Подробнее: Math Giraffe

36. Художественные кружки Фибоначчи

Учащиеся узнают о последовательности и о том, как она встречается в природе. Затем они создадут свою собственную последовательность, используя компас и цветную бумагу.

• Тема: Последовательность Фибоначчи и использование компаса
• Материалы: линейка, циркуль, ножницы, клей-карандаш, карандаш, цветная бумага

Узнайте больше: Чем мы занимаемся весь день

37. Барби Банджи

Это упражнение представляет собой практическую симуляцию банджи-джампинг. Для каждого «прыжка» они будут измерять расстояние, пройденное куклой, добавлять данные в свою таблицу и подгонять резинки. Они будут продолжаться до тех пор, пока у них не будет достаточно данных, а затем использовать их для создания графиков.

Подробнее: Освещение

38. Соотношение Кубка мира Lego Man

Учащиеся будут использовать пропорции своего человечка Lego, чтобы определить и нарисовать мелом футбольное поле пропорционального размера на игровой площадке или на открытом воздухе.

• Тема: коэффициенты
• Материалы: мел, измерительные инструменты

Узнать больше: Math Pig

39. Недовольство

Grudgeball — это веселый, но не требующий подготовки способ повторения концепций со студентами в конце раздела. Учащиеся объединяются в группы и задают математические вопросы, если они ответят правильно, они уберут столько-то крестиков с доски и бросят мяч. Если они попадут в корзину, они могут поставить X другим группам. Выигрывает тот, кто первым избавится от своих крестиков.

• Тема: любая
• Материалы: баскетбольное кольцо
.

Подробнее: Привлечение их всех

40. Квадратичные крестики-нолики

Учащиеся будут практиковаться в решении и разложении на множители квадратных уравнений во время игры в крестики-нолики в парах. Рабочий лист включает в себя две игровые доски.

• Тема: квадратные уравнения
• Материалы: нет

Подробнее: Doc Player

41. Игра на запоминание неравенств

Учащиеся должны будут использовать свою память, чтобы сопоставить пары карточек с неравенствами. Карточки включают выражения, числовые ряды и различные операции.

• Тема: неравенства
• Материалы: печатные карты

Подробнее: Математик средней школы

42. Вероятностный эксперимент с игральными костями

В этом увлекательном эксперименте учащиеся будут использовать навыки критического мышления, гипотезы и определение вероятности.

• Тема: вероятность
• Материалы: 20-гранный кубик, доска для сухого стирания, маркеры (бумага/карандаш)

Узнать больше; STEAMsational

43. Головоломка-распределитель

Учащиеся будут использовать свойство распределения для решения выражений и сопоставления частей, чтобы собрать головоломку.

• Рубрика: Распределительное имущество
• Материалы: распечатать

Подробнее: Учителя платят учителям

44. Центры дробей

Эти центры охватывают многочисленные темы, связанные с дробями: сравнение, моделирование, использование дробей с операциями и многое другое.

• Тема: Дроби
• Материалы: кости, распечатки

Узнайте больше: Дженнифер Финдли

45. Математическое искусство

Учащиеся используют сетку 100 для создания иллюстраций с использованием математики. Они будут кодировать произведения цветом, определяя долю, десятичную дробь и процент для каждого цвета.

• Тема: дроби, десятичные знаки, проценты
• Материалы: краски и распечатка

Подробнее: проектное обучение Linden STEAM Academy

46. Экспонентная битва

Студентам будут розданы базовая карта и карта показателя. В этом раунде выигрывает тот, у кого был самый высокий продукт.

• Тема: Показатель степени и умножение
• Материалы: игральные карты

Узнайте больше: Учитесь с математическими играми

47. Площадь поверхности правых призм

Учащиеся будут использовать трехмерную бумажную форму для анализа поверхности и решения, чтобы найти площадь определенной формы.

• Тема: площадь поверхности
• Материалы: бумага, ножницы, карточки с заданиями

Узнать больше: я Кендалл Хант

48. Сюжет коробки с людьми

Это задание на основе шаблонов, в котором учащиеся будут использовать данные из реальной жизни для изучения диаграмм с ячейками и усами и изучения наборов данных.

• Тема: Диаграммы с ячейками и усами
• Материалы: 2 линейки и веревка или малярная лента

Подробнее: ETeams

49. Игра преобразования измерений

Если вам нужна простая игра на уроке математики, попробуйте эту игру-конверсию. Он отлично подходит для проверки преобразования измерений и не требует большой подготовки.

• Тема: метрическая и обычная система
• Материалы: распечатка, игровые фигуры

Узнайте больше: Учитель воображения

50. Пиксельная математика

Создайте цифровое искусство с помощью Google, решая математические задачи.

• Тема: умножение дробей
• Материалы: компьютер

Узнайте больше: Обучайте с Тиной

51. Упражнение со словами

Учащиеся будут использовать моделирование, числовые ряды и стандартный алгоритм для решения текстовых задач на деление дробей.

• Тема: Деление дробей
• Материалы: маркеры, распечатка

Узнайте больше: у вас есть эта математика

52. Две правды и одна ложь

Это увлекательное математическое задание на любую тему! Студенты должны создать свои собственные проблемы — 2 правильно решенных и 1 неправильно. Затем им нужно объяснить, почему. Отличный выходной билет или обменяться с другими студентами, чтобы увидеть, смогут ли они найти ложь.

• Тема: любая
• Материалы: распечатать

Подробнее: Математика равна любви

53. Геометрические отражения

Учащиеся будут создавать различные отражения многоугольника. Когда они создадут его, у них будет визуальное представление отражения для анализа.

• Тема: размышления
• Материалы: дырокол, миллиметровка, карандаш

Узнайте больше: Scaffolded Math and Science

54. Цифровые карточки с заданиями

Учащиеся будут решать биномы с помощью Google Forms. Цифровой контент доступен для редактирования, поэтому вы можете изменить действие по мере необходимости для вашего класса.

• Тема: умножение двучленов
• Материалы: компьютер

Узнайте больше: Линдси Боуден

55. Раскраска Уголок

Простой способ обучения ракурсам, который можно использовать в качестве вспомогательного средства визуальной памяти для учащихся, которым необходимо освежить знания. Цветовое кодирование помогает учащимся запомнить, какой тип угла имеет какое измерение.

• Тема: углы
• Материалы: краски, бумага, распечатка

Узнать больше: Scaffold Math

Последние мысли

Все вышеперечисленные математические задания были выбраны, чтобы помочь вашим ученикам повысить вовлеченность и прогресс в математике.

No related posts.