Мы пересадили свои деревца обратно на огород вместе с прочими не переносящими зимовку культурами, что заняло довольно много времени. Капризные растения привыкли к кадкам и теплу избы, поэтому отчаянно противились возвращению в холодную уличную землю. Хоть я и ворчал вслух, но размяться и сменить поднадоевшую деятельность было приятно. Кубик-калькулятор вышел довольно прихотливым. Акира на поддержание его работоспособности требовалось немало. Некоторые споровики порой отказывались сотрудничать или забывали заложенную программу. На такой случай я наделал запасных элементов в пазах. Замена и программирование новых не занимало так уж много времени, жаль только осколки ядра терялись навсегда. Но в целом артефакт-калькулятор того стоил. Также я немного проапгрейдил свою вычислительную машинку, что снова потребовало залезть в кубышку. А именно – заказал у местного кузнеца моток проволоки. Затем порезал на кусочки и проложил между всеми пазами, соединив в нечто вроде сети. Вечером девятого числа Возрождения я наконец закончил в полной мере обучение Лаки, как им пользоваться. Все-таки сложность расчетов на четвертый ранг из-за поправочных лунных коэффициентов возросла. Но сестренка дурочкой не была, и, даже не имея качественного образования, смогла разобраться. Тем самым я немного освободил себе времени, которое уходило ранее на расчеты ее парада лун. – Знаешь, братец, – заметила она задумчиво, наблюдая, как вспышик гоняет по заложенному алгоритму. – Ум… Мне кажется, ты соорудил нечто… потрясающее… – А ты разве во мне сомневалась? – спросил я с апломбом. – На то были веские причины, если учесть, как ты ве-ведешь себя. Наверное, только иномирянин способен создать нечто подобное… – Причем не каждый, – заметил я. – М-мы все равно не можем пока точно определять период вращения. – Вот-вот! Ты меня понимаешь, Лаки! – я радостно приобнял девчонку. – Не все… Но кое-каких простых вещей ты все-таки не понимаешь, – она отодвинулась, и я заметил следы смущения на ее лице. – Ты чего, стесняешься? Но мы же в одной постели не раз ночевали. – Это совершенно другое! – вспыхнула Лаки в момент. – Барах прав, не понять мне женщин. Но ты все равно милашка и умница у меня! А потому заслужила крепких обнимашек! Я придвинулся и сдавил сестренку в объятиях. – От-отпусти! – пискнула она. – Ишь чего удумали, охальники! При свете дня постыдились бы! Идите лучше огород полейте, раз силы остались! Бабушка Сурдхоба как всегда подкралась незаметно. – Да, баб Сур! – отсалютовал я и двинулся за ведрами. * * * Любит же братик поиграть с девичьим сердцем, сам того словно не замечая. Но долго дуться на него Лаки просто не могла, и уже к вечеру она снова залезла к нему на чердак и с любопытством следила, как Артур что-то дорабатывает в кубе. В последние дни он действительно очень часто с ним возился, но и польза от него была весомая. Лаки помнила слова Бараха о том, что расчеты на четвертый раз становятся чуть ли невозможными для просчета. Но вот призванный взял и нашел выход из ситуации. И если предыдущие его чудачества находились на вполне земном уровне, то данная штука ввела девочку в ступор, когда она осознала ее возможности. Когда Лаки представила, что у каждого практика, желающего стать сильнее в кратчайшие сроки, есть такое устройство, и он умеет им пользоваться, ей стало не по себе. В этот раз Лаки спустилась спать к себе, поскольку брат возился с кубом допоздна. По его словам, ему осталось совсем чуть-чуть до того, чтобы артефакт начал работать и с дробными числами. Это его «чуть-чуть» длилось с самого обеда. Улегшись в постель, девочка вспомнила о ее завтрашнем дне рождения и о ее подарке. Лаки сжала ингалятор в руке. – Пшу-ищ! – послышалось рядышком. – Ох, тебе не нравится дух воздуха внутри? Не ревнуй, сейчас я уберу его. Лаки положила артефакт на полку, и Пиджи по-хозяйски устроился подле, махнув кисточкой хвоста ей по носу. – Совсем разжирел на ядрах-то, – сквозь сон заметила девочка. – Скоро вдвоем не поместимся… – Пиу! – протестующе заметил хомяк-переросток. Шум и истошный крик выдернул Лаки из сонных оков. – … проклятущий демон, отцепись!!! – донесся до нее голос Сурдхобы. – Ч-что такое… – поднялась девочка, продирая глаза. – Отлично. Лаки присмотрелась и увидела в руках бабки знакомый прозрачный кубик, только на сей раз у него почему-то виднелись четыре конечности – маленькие пластикатовые ручки и ножки, коими он цеплялся за одежду Сурдхобы. – По-подождите, это же изобретение Тура! – Все ерундой мается, даром что до третьего ранга поднялся. Балбес окаянный. Вниз по лестнице спустился зевающий призванный. – Что за шум, а драки нет? – Сейчас будет. Ты зачем мне свою игрушку подсунул, ирод?! – вопросила Сурдхоба, подвесив кубик рядом с дымящей печкой. – Э-э?! Вы что с моей прелестью сотворить вздумали?! – Ты лучше объясни мне, почему я просыпаюсь, а эта штука у меня в волосах ползает?! – Не знаю! Может вы ему понравились. Верните сюда! Артур бесцеремонно выхватил артефакт, который беспомощно сучил ножками и ручками во всем стороны. – Есть! – послышался с его стороны тихий писк. Братец печально вздохнул, оглядев свое творение: – Значит так, Твейн, да? Совсем не дашь мне изобрести нечто выдающееся? Почему он ожил? – Нам почем знать? В печь его и всего делов! – рубанула старуха. – Еще чего! Да вы знаете, сколько я сил и средств в него вложил! Не смейте его трогать. И ты, чудо кубическое, не лазай где попало, если не хочешь, чтобы тебя на грилле поджарили. Я пойду досыпать. * * * Да уж, облом случился знатный. Мой калькулятор вдруг ни с того, ни с сего, обрел полуразумность. До Ляпки ему было далеко, и даже Пиджи понимал, казалось, намного больше. Но все равно это уже далеко не элементарный дух, способный даже произносить простые слова. Мое творение изменилось как внешне, так и внутренне. Находившееся ранее наверху главное ядро со вспышиком сместилось внутрь корпуса и теперь пульсировало периодически на манер сердца. Металлические стержни, ранее уложенные довольно ровно, теперь искривились и напоминали кровеносные сосуды, ведущие к хаотически размещенным ядрышкам со споровиками. Я при всем желании теперь не мог проследить созданные мной же алгоритмы. Все смешалось в какую-то непонятную мешанину, словно провода в коммуникационном шкафе у нерадивого сисадмина. – И каким образом мне теперь добавлять в тебя новые функции? – вздохнул я. – Еды? – Ладно, держи. Еще один проглот на мою голову, – поделился я акиром. Проверить что ли? Теперь непонятно, где у него устройство ввода. – Сколько будет 4321 умножить на 67777? Внутри кубика замелькали искры, причем не одна. Он что как-то смог распараллелить процессы? И каким теперь будет устройства вывода? – Два девять два восемь шесть четыре четыре один семь, – ответил тихий скрипучий голосок довольно быстро. – Ого! Похоже на правду, – воодушевился я. |
Powers of 10 without a Calculator
Powers of 10 without a Calculator Std 5f
A. Multiplication Powers of 10 alone
10 -3 x 10 +17 = 10 +14 Что мы сделали? Мы просто складываем показатели вместе.
B.
 Деление только на 10
Деление только на 10
10 -7
—— = 10 -7 x 10 +13 = 10 6
10 -13
Что мы сделали делать? Мы просто меняем знак показатель степени внизу и умножьте число, которое совпадает с пример умножения.
C. Степени умножения 10 и обычные номера с ними
2,5 х 10 -12 х 7,3 х 10 -4 = 18,25 х 10 -16 = 1,825 x 10 -15
А B C D AxC BxD
Что мы сделали
делать? Сначала относитесь к этому как к двум
проблемы. Сначала умножьте 2,5 х 7,3 = 18,25.
Далее умножьте 10 -12 x 10 -4 =
10 -16 . Теперь у нас есть проблема сделать
числа в научную запись. Так,
переместите десятичную единицу влево, чтобы получилось 1,825. Это изменит значение нашего ответа
если мы не изменим 10 -16 до другое значение, поэтому
чтобы не сделать другой номер.
Чтобы убедиться, что то, что я сделал на последнем шаге, было правильным, давайте используйте более простые номера:
32,5 x 10 -2 = 0,325
3,25 х 10 -1 = 0,325
Здесь мы уменьшили отрицательная сумма на 1 , потому что мы переместили десятичную дробь в слева по 1 .
Для того же причине также верно следующее:
0,0516 x 10 -2 = 0,000516
5,16 х 10 -4 = 0,000516
Здесь мы увеличено отрицательная сумма на 2 , потому что мы переместили десятичную дробь вправо по 2 .
D. Дивизия — степени 10 и обычные числа с ними
3,74 x 10 -18
—————- = 0,510 х (10 -18 х 10 +6 ) = 0,510 х 10 -12 = 5,10 х 10 -13
7,33 x 10 -6
Что мы сделали
делать? Разбейте это на две проблемы. Сначала разделите 3,74 на 7,33, чтобы получить 0,510. Далее делим 10 -18 на 10 -6 . Для этого меняем 10 -6 на
10 +6 при перемещении
к вершине дроби. Вот как
получаем 10 -12 . Теперь мы должны переместить десятичную дробь так, чтобы
научное обозначение, поэтому 0,510 нужно изменить на 5,10. Как с умножением
проблема выше в C. нам нужно настроить показатель степени 10, чтобы мы не меняли
значение числа.
Сначала разделите 3,74 на 7,33, чтобы получить 0,510. Далее делим 10 -18 на 10 -6 . Для этого меняем 10 -6 на
10 +6 при перемещении
к вершине дроби. Вот как
получаем 10 -12 . Теперь мы должны переместить десятичную дробь так, чтобы
научное обозначение, поэтому 0,510 нужно изменить на 5,10. Как с умножением
проблема выше в C. нам нужно настроить показатель степени 10, чтобы мы не меняли
значение числа.
Вы действительно хотите получить хорошее представление о том, что на самом деле означает величина степени десяти? НАСКОЛЬКО БОЛЬШОЙ БОЛЬШОЙ (10 10 ) и КАК МАЛЕНЬКИЙ МАЛЕНЬКИЙ (10 -10 )? Перейдите по этой ссылке:
Полномочия из 10 апплетов макро- и микровспышки, последовательность изображений с 10 по 16 по телефону 10 +23 .
Это очень весело и дает
вы действительно чувствуете, что это за сила 10 вещей
о. 9{-7}[/latex]
9{-7}[/latex]
При использовании отрицательных показателей, чем больше отрицательный показатель, тем меньше число.
Преобразование между научной и десятичной системой счисления
S научная система счисления используется учеными, математиками и инженерами при работе с очень большими или очень маленькими числами. Используя экспоненциальную запись, большие и маленькие числа можно записать так, чтобы их было легче читать.
Когда число записывается в экспоненциальном представлении, 9{n}[/latex], где коэффициент a равен [latex]1\leq{a}<10[/latex], а n – целое число.
Теперь давайте сравним некоторые числа, выраженные как в экспоненциальном представлении, так и в стандартном десятичном представлении, чтобы понять, как преобразовать из одной формы в другую. Взгляните на таблицы ниже. Обратите особое внимание на показатель степени в экспоненциальном представлении и положение десятичной точки в десятичном представлении.
Большие числа 9{5}\end{array}[/latex] Обратите внимание, что десятичная точка сдвинута на 5 знаков влево, а показатель степени равен 5. ПримерЗапишите следующие числа в экспоненциальном представлении.
Показать раствор Чтобы записать небольшое число (от 0 до 1) в экспоненциальном представлении, вы переместите десятичную дробь вправо , и показатель степени должен быть равен 9{-5}\end{array}[/latex] Вы можете заметить, что десятичная точка была перемещена на пять знаков вправо , пока вы не дошли до числа 4, которое находится между 1 и 10. Показатель степени равен [ латекс]-5[/латекс]. ПримерЗапишите следующие числа в экспоненциальном представлении.
Показать раствор Преобразование экспоненциального представления в десятичное представление 9{-8}=\underset{\longleftarrow}{0.00000005.}=0.00000005\end{массив}[/latex]Для каждой степени числа 10 вы перемещаете десятичную точку на одно место. Будьте осторожны и не увлекайтесь нулями — количество нулей после запятой всегда будет на 1 меньше 90 258, чем показатель степени, потому что требуется одна степень 10, чтобы сдвинуть это первое число влево от десятичной точки. . ПримерЗапишите следующее в десятичной системе счисления.
|

 Я уже ранее проверял: некоторые элементальные духи молнии действительно могут двигаться намного быстрее, частично сливаясь с металлом. Вспышик после апгрейда носился как угорелый, из-за чего скорость вычислений повысилась в разы.
Я уже ранее проверял: некоторые элементальные духи молнии действительно могут двигаться намного быстрее, частично сливаясь с металлом. Вспышик после апгрейда носился как угорелый, из-за чего скорость вычислений повысилась в разы. – Все-таки это была моя специальность в прошлом мире. Составлять алгоритмы и программировать я умею. Хотя создавать самому железо – таким я занимался впервые. Надо еще дополнить разветвление по работе с нецелыми числами. В принципе любое нецелое число можно представить произведением целого и десяткой в минус какой-то степени. Конечно, придется ограничиться несколькими знаками после запятой, но за точностью все равно гнаться глупо.
– Все-таки это была моя специальность в прошлом мире. Составлять алгоритмы и программировать я умею. Хотя создавать самому железо – таким я занимался впервые. Надо еще дополнить разветвление по работе с нецелыми числами. В принципе любое нецелое число можно представить произведением целого и десяткой в минус какой-то степени. Конечно, придется ограничиться несколькими знаками после запятой, но за точностью все равно гнаться глупо.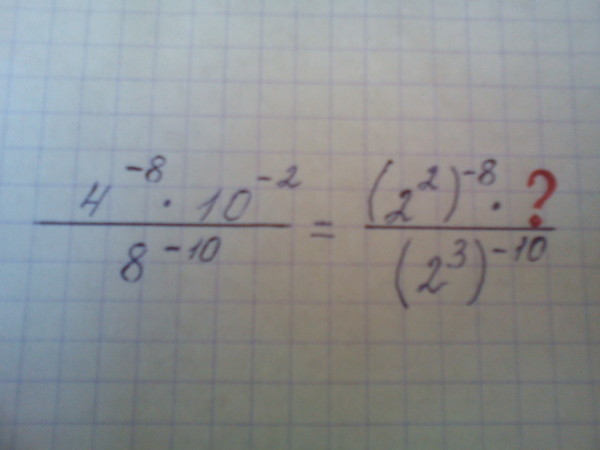
 Это ведь какая ценность на самом деле находится у них в доме?
Это ведь какая ценность на самом деле находится у них в доме?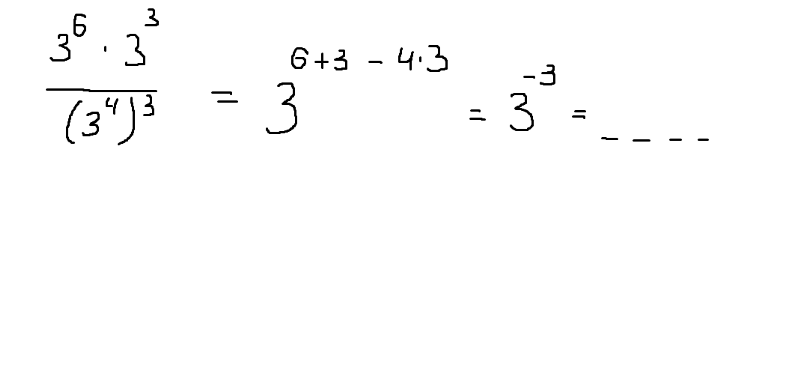 Помоги растопить печку, деточка. Сейчас мы расплавим это недоразумение!
Помоги растопить печку, деточка. Сейчас мы расплавим это недоразумение!
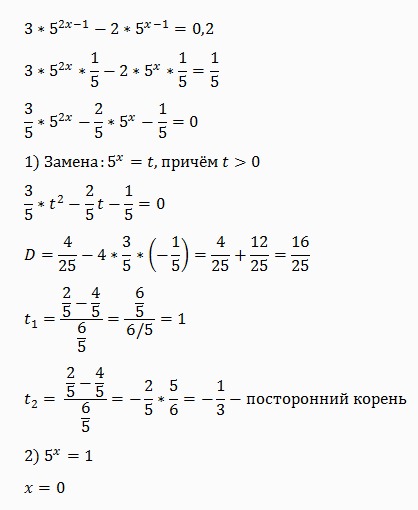
 000000000000000793[/латекс]
000000000000000793[/латекс]
 Если оно еще не представлено в экспоненциальной записи, вы преобразуете его, и все готово.
Если оно еще не представлено в экспоненциальной записи, вы преобразуете его, и все готово.