НОУ ИНТУИТ | Лекция | Комплексные корни n-й степени из единицы и решение уравнений
< Лекция 5 || Лекция 6: 123 || Лекция 7 >
Аннотация: В данной лекции рассматриваются комплексные корни n-й степени из единицы. Приведены формулы для решения уравнений третьей и четвертой степеней, доказан ряд теорем. Рассмотрен ряд характерных задач, а также приведены задачи для самостоятельного рассмотрения
Ключевые слова: Окружность, доказательство, группа, первообразная, пункт, ПО, дискриминант кубического многочлена, действительный, радиус, значение функции, функция, композиция, минимум, многочлен, многочлен неприводимый, поле, определение, умножение, кратность
Комплексные корни n-й степени из единицы
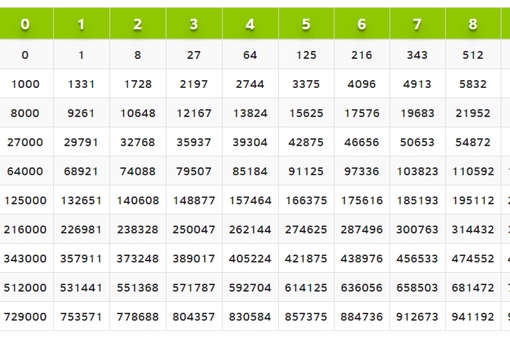
Так как , r=1, , то формула для корней n -й степени из 1 принимает вид
Точки wk являются вершинами правильного n -угольника, вписанного в окружность единичного радиуса с центром в начале координат, при этом одной из вершин этого многоугольника является 1. Например, при n=8
Например, при n=8
Теорема 2.9.1. Совокупность всех n корней n -й степени из 1 с операцией умножения является коммутативной группой (подгруппой в ).
Доказательство.
- Если , т. е. wn=1, zn=1, то , поэтому . Таким образом, на Tn определена операция умножения (очевидно, коммутативная и ассоциативная).
- Ясно, что 1
- Если , то wn=1, и поэтому .
Замечание 2.9.2. Группа Tn является циклической, т. е. все ее элементы являются степенями одного элемента, называемого циклическим образующим (в качестве одного из циклических образующих можно взять , так как wk=(w1)k для , т. е. все элементы wk группы Tn являются степенями корня w1, такие корни называются первообразными). Покажите, что является первообразным корнем тогда и только тогда, когда наибольший общий делитель чисел k и n равен 1.
е. все элементы wk группы Tn являются степенями корня w1, такие корни называются первообразными). Покажите, что является первообразным корнем тогда и только тогда, когда наибольший общий делитель чисел k и n равен 1.
Упражнение 2.9.3. Доказать, что сумма всех k -х степеней корней уравнения x n=1 равна
n, если k делится на n ;
0, если k не делится на n.
Задача 2.9.4. Если , то |z|=1, но z не является корнем из единицы (т. е. для любого ).
Задача 2.9.5. Доказать, что
а) ;
б) .
Указание. Пусть
(все корни степени 2n из 1 ). Тогда
Тогда
(так как xn=-1, x2n=1 ). Но , поэтому
Следовательно,
Полагая x=1, имеем
Дальше >>
< Лекция 5 || Лекция 6: 123 || Лекция 7 >
CHAINSAW MANFigZero 1/6 Power — магазин threezero
149,00 долларов США
Фигурки MAN CHAINSAW MAN от threezero — это следующий захватывающий выпуск в линейке продуктов FigZero. FigZero стал широко известен тем, что расширяет границы аниме-фигурок с помощью подвижных шарнирных фигурок в масштабе 1/6 с подробными скульптурами и индивидуальными костюмами.
Фигурка FigZero 1/6 Power имеет рост примерно 11,3 дюйма (28,8 см) и представляет собой полностью подвижную коллекционную фигурку с более чем 31 точкой артикуляции. Как и фигурка Денджи, все части были созданы известным японским скульптором Акинори Такаки.
Power включает в себя в общей сложности три сменных лицевых пластины (улыбка, крики и удивление) и две сменные накладки для волос (стандартные и движущиеся волосы). Торс для FigZero 1/6 Power — это совершенно новый дизайн, который включает в себя подкладки для груди, которые можно легко прикрепить или отсоединить с помощью магнита. Тканевый наряд персонажа включает тканевый жакет, белую рубашку, брюки и галстук. Дополнительные аксессуары включали кровавый меч, кровавый молот, шесть наборов сменных рук в разных позах и несочлененный кот-компаньон Мяуи в масштабе 1/6.
©Tatsuki Fujimoto/SHUEISHA, MAPPA
Цена предварительного заказа: 149 долларов США / 1 170 гонконгских долларов / 1 030 юаней / 20 880 йен
Ориентировочная поставка: 3-й квартал 2023 г.
※ Стоимость доставки зависит от веса/размера товара и места доставки .
※ Пошлины, налоги и любые другие сборы, связанные с таможенным оформлением, не включены в цену.
※ Все неоплаченные заказы будут отменены после продажи.