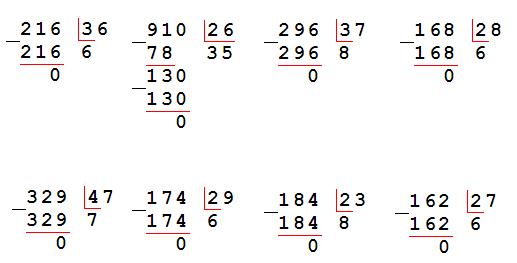648 разделить на 4 в столбик: Разделить столбиком 648 на 4

Содержание

Как правильно объяснить ребёнку деление в столбик. Деление в столбик 648 разделить на 6 в столбик объяснение

Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.

Деление – интересная операция, в чем мы и убедимся с вами в этой статье!

Деление чисел

Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.

Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.

Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».

Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.

Деление с остатком

Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.

Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).

Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).

Деление на 3 и 9

Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:

Найти сумму цифр делимого.

Поделить на 3 или 9 (в зависимости от того, что вам нужно).

Если ответ получается без остатка, то и число поделится без остатка.

Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.

Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.

Умножение и деление

Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.

Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.

Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.

Деление 3 класс

В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:

Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?

Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?

Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок.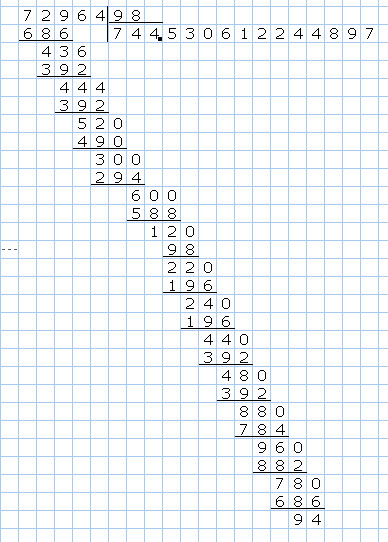 Сколько каждый получит яблок, если нужно поделить их одинаково?

Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?

Деление 4 класс

Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:

Деление в столбик

Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.

Рассмотрим пример, 512:8.

1 шаг . Запишем делимое и делитель следующим образом:

Частное будет записано в итоге под делителем, а расчеты под делимым.

2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:

3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:

Теперь 51 больше 8. Это неполное частное.

4 шаг . Ставим точку под делителем.

5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:

6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:

7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:

8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.

* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:

10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.

Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.

Деление трехзначных

Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.

Деление дробей

), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):

Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.

Деление числа на классы

Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.

Деление натуральных чисел

Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Деление презентация

Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное.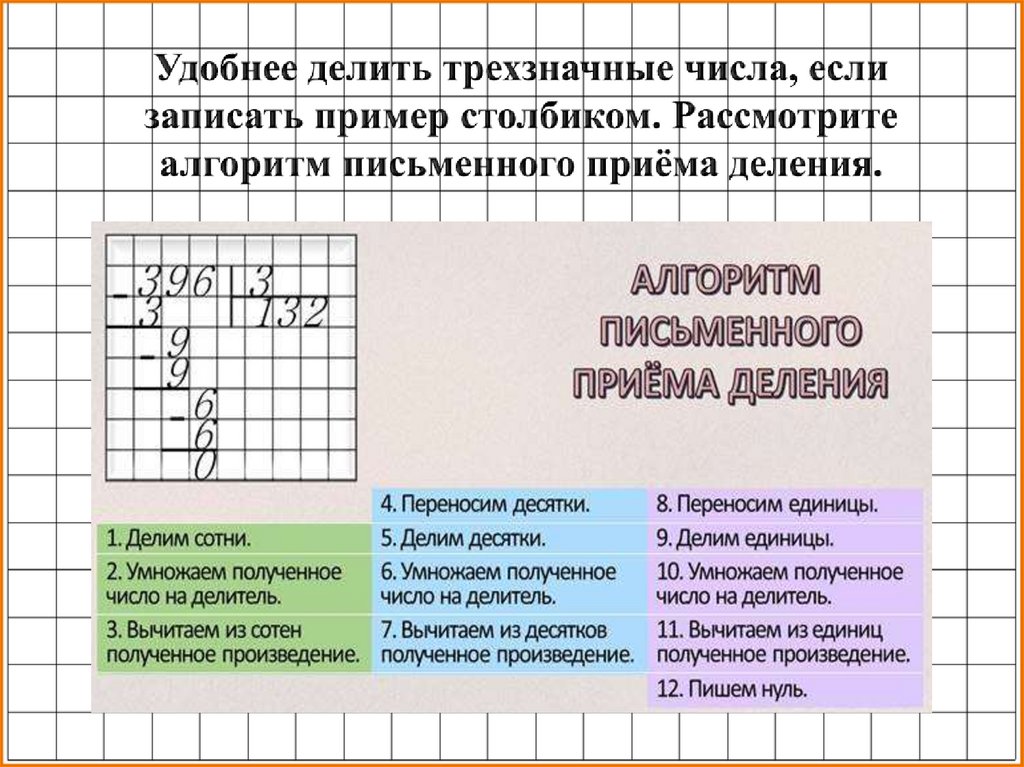 Время зря не потратите, а свои знания закрепите!

Примеры на деление

Легкий уровень

Средний уровень

Сложный уровень

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.

Игра «Угадай операцию»

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Упрощение»

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение»

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Визуальная геометрия»

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Копилка»

Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение перезагрузка»

Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.

Развитие феноменального устного счета

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.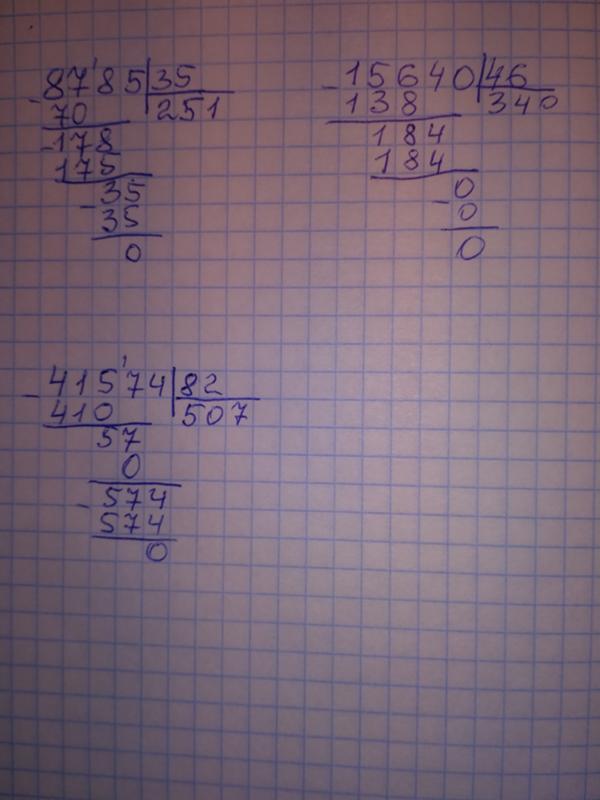

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

Развитие памяти и внимания у ребенка 5-10 лет

Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать.

После прохождения курса ребенок сможет:

В 2-5 раз лучше запоминать тексты, лица, цифры, слова

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Деньги и мышление миллионера

Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.

Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.

Для деления чисел из двух и более цифр (знаков) применяют деление в столбик .

По традиции, разбираться как делить столбиком будем на примере.

Вычислить:

Для начала запишем делимое и делитель в столбик. Выглядеть это будет так:

Их частное (результат) будем записывать под делителем. У нас это цифра «8 ».

Начинаем делить «512 » на «8 » следующим образом:

Определяем неполное частное . Для этого слева направо сравниваем цифры делимого и делитель.
Берём «5 ». Цифра «5 » меньше «8 », значит нужно взять еще одну цифру из делимого.
«51 » больше «8 ». Значит это неполное частное. Ставим точку в частном (под уголком делителя).
Запомните!
Для того, чтобы избежать ошибок, не забывайте определять количество цифр в частном.
Для этого посчитаем сколько цифр осталось в делимом, после неполного частного. У нас после «51 » стоит только одно цифра «2 ». Значит и добавляем в результат ещё одну точку.
Приступаем к делению. Вспоминая таблицу умножения на «8 », находим ближайшее к «51 » произведение.
«6 · 8 = 48 »
Записываем цифру «6 » в частное.
Записываем «48 » под «51 ».
Запомните!
При записи под неполном частным самая правая цифра неполного частного должна стоять над самой правой цифрой произведения.

Между «51 » и «48 » слева поставим «− » (минус). Вычтем по правилам вычитания в столбик «48 » и под чертой запишем результат.
В остатке получилось «3 ». Сравним остаток с делителем. «3 » меньше «8 ».

Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .

Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:

За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:

Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:

Под делимым будут записываться промежуточные вычисления:

Полностью форма записи деления столбиком выглядит следующим образом:

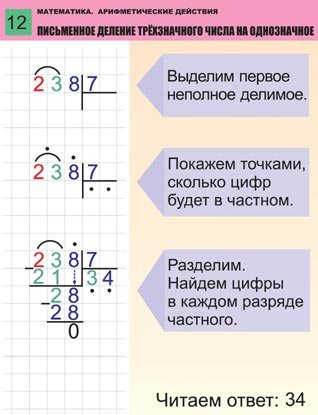
Как делить столбиком

Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:

Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:

это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:

В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.

Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.

Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:

Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:

Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.

К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:

Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.

Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:

Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:

Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:

Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:

Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:

Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.

Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:

Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:

Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:

Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:

Деление столбиком с остатком

Пусть нам требуется разделить 1340 на 23.

Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:

Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:

Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:

1340: 23 = 58 (остаток 6)

Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:

3: 10 = 0 (остаток 3)

Калькулятор деления столбиком

Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.

Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?

Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.

Я уже писала о том, Эта статья может стать для вас полезной.

Осваиваем операцию разделения (деления) на части в игровой форме

На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.

Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.

Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.

Умножаем и делим, используя таблицу умножения

Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.

Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.

Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.

Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!

По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.

Делим столбиком – приведем пример

Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.

Объясняем наглядно

Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.

Шаг 1 . Записываем числа, разделив их «уголком».

Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.

Шаг 3. Переходим к оформлению деления столбиком:

Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.

Записываем результат.

Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.

Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.

Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.

Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.

Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.

Как научить ребенка делению – закрепляем навык

Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.

«Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
«Деление. Уровень 4. Рабочая тетрадь» от Kumon
«Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров

Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.

Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей.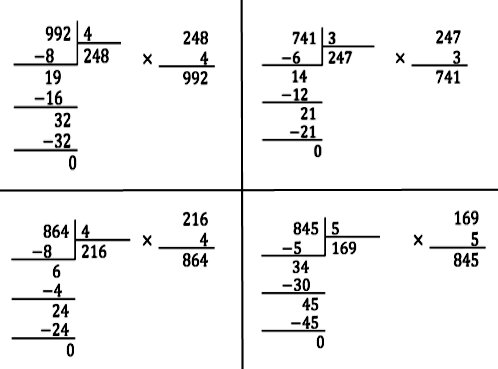 Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.

Для того чтобы легко научить ребёнка операции деления нужно:

Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.

Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.

Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т. д.) во время конструирования, игр и наблюдений за природой.

Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт

Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:

Математика. Деление уголком | Сайт Леонида Некина

Деление «уголком» — это, на мой взгляд, самая тяжелая, самая нудная тема во всей школьной математике. Тут нам придется всерьез поднапрячься. Пусть, однако, нас вдохновляет мысль, что весь последующий материал будет значительно легче и приятнее.

Прежде всего, рассмотрим деление на однозначное число. Допустим, мы хотим вычислить значение выражения

$648 / 2$.

Пользуясь свойствами умножения, мы можем расписать делимое таким образом:

$648 =$

$6$ $\,\cdot\,100~+$ $4$ $\,\cdot\,10~+~$ $8$ $~=$

$3$ $\,\cdot\,$ $2$ $\,\cdot\,100~+~$ $2$ $\,\cdot\,$ $2$ $\,\cdot\,10~+~$ $4$ $\,\cdot\,$ $2$ $~=$

$($ $3$ $\,\cdot\,100~+~$ $2$ $\,\cdot\,10~+~$ $4$ $)\,\cdot\,$ $2$ $~=$

$3$ $2$ $4$ $\,\cdot\,$ $2$ .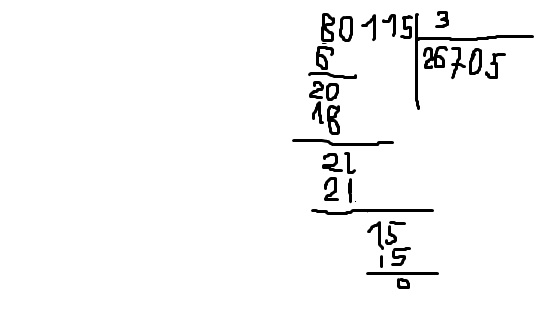

После этого становится очевидно, что частное от деления равно

$648 / 2 = 324$.

Но это мы взяли самый что ни на есть простейший случай, когда каждую отдельно взятую цифру делимого можно поделить на делитель. А вот пример несколько посложнее:

$156 / 2 =$ ?

Здесь первая цифра оказалась меньше делителя. Поэтому, расписывая делимое, мы не будем отрывать ее от второй цифры:

$156~=$

$15$ $\,\cdot\,10~+~$ $6$ .

Поскольку число $15$ не делится нацело на $2$, придется нам прибегнуть к делению с остатком. Представим результат такого деления в виде:

$15$ $~=~$ $7 \cdot 2$ $~+~$ $1$ $~=~$ $14$ $~+~$ $1$ .

Теперь мы можем продолжать расписывать наше делимое дальше:

$156 =$

$15$ $\,\cdot\,10~+~$ $6$ =

( $14$ $~+~$ $1$ )$\,\cdot\,10~+~$ $6$ $~=$

$14$ $\,\cdot\,10~+~$ $1$ $\,\cdot\,10~+~$ $6$ $~=$

$14$ $\,\cdot\,10~+~$ $16$ $~=$

$7$ $\,\cdot\,$ $2$ $\,\cdot\,10~+~$ $8$ $\,\cdot\,$ $2$ $~=$

( $7$ $\,\cdot\,10~+~$ 8 )$\,\cdot\,$ $2$ $~=$

$7$ $8$ $\,\cdot\,$ $2$ .

Отсюда моментально получаем ответ:

$156 / 2 = 78$.

Такого рода расчеты можно проводить в уме и сразу же писать ответ. Но мы сейчас перепишем их в виде краткой таблицы. Умение составлять такие таблицы нам пригодится, когда мы займемся делением на многозначные числа, когда всё окажется не так просто. Делимое и делитель запишем так:

$1$	$5$	$6$	$2$

При делении первых двух разрядов ( $15$ ) на двойку получается $7$ плюс еще какой-то остаток. С этим остатком мы разберемся чуть позже, а пока запишем семерку под чертой снизу от делителя (здесь у нас со временем будет выписан полный ответ):

$1$	$5$	$6$	$2$
			$7$

Умножаем на эту семерку наш делитель ( $2$ ) и записываем ответ ( $14$ ) под первыми двумя разрядами делимого ( $15$ ):

$1$	$5$	$6$	$2$
$1$	$4$		$7$

Теперь настало время вычислить остаток от деления $15$ на $2$ . Он равен, очевидно,

$15$ $~-~$ $2$ $\,\cdot\,$ $7$ $~=~$ $15$ $~-~$ $14$ .

У нас уже всё подготовлено, чтобы выполнить это вычитание «столбиком»:

$1$	$5$	$6$	$2$
$1$	$4$		$7$
	$1$

У нас получается единица , к которой мы приписываем шестерку из следующего разряда делимого:

$1$	$5$	$6$	$2$
$1$	$4$		$7$
	$1$	$6$

В результате такого приписывания у нас получается число $16$ . Мы делим его на наш делитеть ( $2$ ) и получаем $8$ . Эту восьмерку пишем в строке ответа, под чертой снизу от делителя:

$1$	$5$	$6$	$2$
$1$	$4$		$7$	$8$
	$1$	$6$

Ответ мы получили, однако правила составления таблицы таковы, что нам надо добавить в нее еще две строки. Мы должны формальным образом убедиться, что не потеряли остаток от деления. Умножаем делитель ( $2$ ) на последнюю цифру ответа ( $8$ ), приписываем результат ( $16$ ) снизу к нашей таблице в последние два разряда делимого:

$1$	$5$	$6$	$2$
$1$	$4$		$7$	$8$
	$1$	$6$
	$1$	$6$

Вычитаем последнюю строку из предпоследней и получаем $0$:

$1$	$5$	$6$	$2$
$1$	$4$		$7$	$8$
	$1$	$6$
	$1$	$6$
		$0$

Этот последний ноль есть не что иное, как остаток от деления, который образовался бы в том случае, если бы мы рассматривали деление с остатком:

$156 : 2 = 78~(\text{ост. }~0)$.

Чтобы получше это понять, возьмем похожий пример, в котором, однако, остаток не равен нулю:

$157 : 2 = 78~(\text{ост.}~1)$.

Таблица для этого примера выглядит так:

$1$	$5$	$7$	$2$
$1$	$4$		$7$	$8$
	$1$	$7$
	$1$	$6$
		$1$

Здесь, опять-таки, остаток стоит в последней строке. Для полноты картины распишем наше делимое в таком виде:

$157~=$

$14$ $\,\cdot\,10~+~$ $17$ $~=$

$7$ $\,\cdot\,$ $2$ $\,\cdot\,10~+~$ $8$ $\,\cdot\,$ $2$ $~+~1~=$

( $7$ $\,\cdot\,10~+~$ $8$ )$\,\cdot\,$ $2$ $~+~1~=$

$7$ $8$ $\,\cdot\,$ $2$ $~+~1$

Теперь мы готовы к тому, чтобы делить (нацело или с остатком) на многозначные числа. Это делается при помощи подобной же таблицы (именно из-за ее особого вида данная процедура получила название деление «уголком»). Допустим, требуется выполнить деление с остатком:

$135674 : 259~=~$?

Приступаем к заполнению таблицы:

	$1$	$3$	$5$	$6$	$7$	$4$	$2$	$5$	$9$

В данном случае, чтобы найти первую цифру частного, надо взять первые четыре цифры делимого ( $1356$ ) и получившееся число поделить (с остатком) на делитель ( $259$ ). Почему надо взять именно первые четыре цифры делимого? Потому что если бы мы взяли хотя бы на одну цифру меньше, то получившееся число ( $135$ ) оказалось бы меньше делителя ( $259$ ), а это не то, что нам надо. Итак, возьмем первые четыре цифры делимого и рассмотрим следующее деление с остатком:

$1356$ : $259$ = ?

Тут нам помогут приближенные вычисления, для которых, как мы знаем, вовсе необязательно, чтобы числа делились друг на друга нацело:

$1356$ / $259$ $~\approx 1356 / 300 \approx 1500 / 300 = 15 / 3~=~$ $5$ .

Зная результат приближенного деления, мы можем предположить, что, скорее всего,

$1356$ : $259$ = $5$ (остаток — пока неважно какой).

Конечно, абсолютной уверенности у нас нет. Здесь вместо пятерки вполне может стоять четверка или шестерка , однако вряд ли мы ошиблись больше, чем на одну единицу. Имея это в виду, тем не менее берем эту пятерку и заносим ее в нашу таблицу в строку ответа. После этого умножаем на нее делитель ( $259$ ) и при этом записываем ответ под делимым в подходящие разряды:

	$1$	$3$	$5$	$6$	$7$	$4$	$2$	$5$	$9$
	$1$	$2$	$4$
$259$ $~\cdot~$ $5$ =	$1$	$2$	$9$	$5$			$5$

Здесь «маленькие» цифры — это побочный продукт процедуры умножения: мы познакомились с ними, когда учились умножать «в столбик».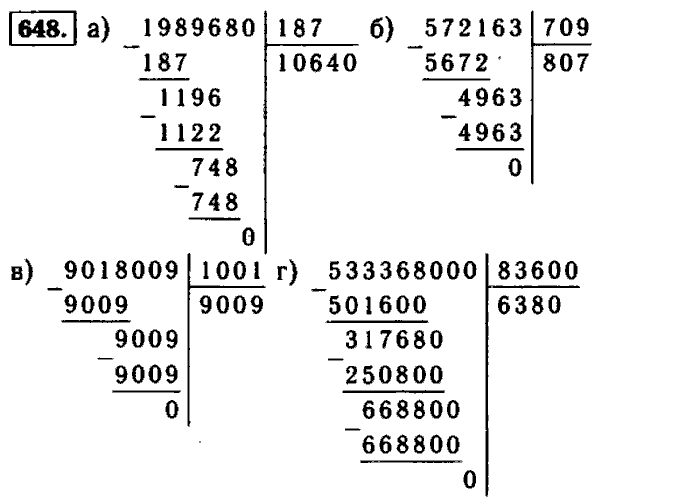 После того как умножение выполнено, они становятся больше не нужны: на них можно просто не обращать внимания. Выражение $259$ ∙ $5$ , написанное слева от таблицы, помещено сюда только ради пояснения того, что мы делаем. К таблице оно, собственно, не принадлежит, и в будущем мы такие пояснения выписывать не будем. Тут важно отметить, что результат нашего умножения $1295$ оказался меньше записанного над ним числа $1356$ , составленного из первых четырех цифр делимого. Если бы это было не так, то это означало бы, что приближенное деление дало нам завышенный результат. Нам надо было бы тогда зачеркнуть пятерку в строке ответа, на ее место поставить четверку — после чего зачеркнуть и переделать все наши последующие вычисления. Но нам на этот раз повезло, и ничего переделывать не требуется.

Теперь выполняем вычитание в столбик и получаем:

	$1$	$3$	$5$	$6$	$7$	$4$	$2$	$5$	$9$
	$1$	$2$	$4$
$259$ $~\cdot~$ $5$ =	$1$	$2$	$9$	$5$			$5$
			$6$	$1$

Внимательно приглядимся к полученной разности ( $61$ ). Очень важно, что она оказалась меньше делителя ( $259$ ). В противном случае мы пришли бы к выводу, что приближенное деление дало нам заниженный результат и нам пришлось бы теперь исправлять в строке ответа пятерку на шестерку , а также переделывать все последующие вычисления. К счастью, этого не случилось. Приближенное вычисление нас не подвело, и мы теперь совершенно точно знаем, что,

$1356$ : $259$ = $5$ (ост. $61$ ).

Возвращаемся к таблице. К нашему остатку ( $61$ ) приписываем семерку из следующего разряда делимого и приступаем к нахождению второй цифры ответа. Это делается с помощью точно такой же процедуры, что и раньше. Потом — очередь за третьей цифрой. В конце концов таблица принимает такой вид:

	$1$	$3$	$5$	$6$	$7$	$4$	$2$	$5$	$9$
	$1$	$2$	$4$
$259$ $~\cdot~$ $5$ =	$1$	$2$	$9$	$5$			$5$	$2$	$3$
			$6$	$1$	$7$
			$1$	$1$
$259$ $~\cdot~$ $2$ $~=~$			$5$	$1$	$8$
				$9$	$9$	$4$
				$1$	$2$
$259$ $~\cdot~$ $3$ $~=~$				$7$	$7$	$7$
				$2$	$1$	$7$

Можно выписывать окончательный ответ:

$135674 : 259 = 523~(\text{ост}. ~217)$.

Самая большая неприятность в делении «уголком» состоит в том, что приближенные вычисления, к которым приходится прибегать по ходу дела, не дают сразу гарантированно правильного результата и нуждаются иногда в последующей коррекции. Впрочем, по мере тренировки, у нас выработается особое чутье и мы будем уже сразу почти наверняка знать, какие цифры следует писать в строке ответа, чтобы потом ничего больше не надо было исправлять и переделывать.

Разумеется, нам будут попадаться случаи, когда частное содержит нули. Каждый такой ноль позволит сделать в таблице небольшие сокращения. Вот пример такой таблицы:

$2$	$6$	$2$	$7$	$4$	$0$	$8$	$7$
$2$	$2$
$2$	$6$	$1$				$3$	$0$	$2$	$0$
		$1$	$7$	$4$
		$1$	$1$
		$1$	$7$	$4$
				$0$

Как и в случае умножения «в столбик», для того чтобы было удобнее писать «маленькие» цифры, нам может понадобиться

лист со специальной линовкой для вычислений (формат pdf).

Теперь остается только тренироваться, тренироваться и тренироваться.

Конспект

Деление «уголком». Рассмотрим пример:

делимое : делитель = частное (остаток такой-то).

Наша задача — найти частное и остаток, если известны делимое и делитель. Решаем эту задачу в несколько шагов, на каждом из которых мы находим одну цифру частного.

Шаг первый. Берем в делимом столько цифр спереди, чтобы они составляли число, которое при делении на делитель дает однозначное число и еще какой-то (промежуточный) остаток. Выполнив такое деление, выписываем полученное однозначное число в качестве первой цифры частного, а к промежуточному остатку приписываем в конец первую из оставшихся цифр делимого. В результате такого приписывания мы получаем число, которое мы передаем для дальнейшей «обработки» во второй шаг.

Шаг второй. Число, поступившее для «обработки» из предыдущего шага, делим на делитель. В результате получаем однозначное число и какой-то еще промежуточный остаток. Однозначное число мы записываем в качестве следующей цифры частного, а к промежуточному остатку приписываем в конец первую из оставшихся цифр делимого и передаем получившееся число для дальнейшей «обработки» в следующий шаг.

Описание последующих шагов в точности совпадает с описанием второго шага. Мы останавливаемся, когда в делимом больше не остается цифр для приписывания к очередному промежуточному остатку. К этому времени частное оказывается полностью выписанным, а последний промежуточный остаток и есть окончательный остаток в нашем исходном примере.

Из «бесконечного» сборника типовых упражнений

Деление нацело на однозначное число

Деление с остатком на однозначное число

Деление с остатком на однозначное число с возможным «приписыванием» нулей

Деление нацело на двузначное число

Деление с остатком на двузначное число

Деление нацело на трехзначное число

Деление с остатком на трехзначное число

4 класс.

Моро. Учебник №2. Ответы к стр. 58

Числа от 1 до 1000

Деление на двузначное и трёхзначное число
Письменное деление на двузначное число
Ответы к стр. 58

При делении с остатком на двузначное число рассуждают также, как и при делении без остатка. Объясни, как выполнено деление с остатком.
_ 324 |62 _ 526 |74 _ 793 |83
310 |5 518 |7 474 |9
14 8 46

Надо 324 разделить на 62.
Разделю 324 не на 62, а на 60, чтобы легче было найти цифру частного. Для этого разделю 32 на 6, получу 5. Это пробная цифра, её нельзя сразу записать в частном — сначала надо проверить, подходит ли цифра 5.
Умножу 62 на 5, получится 310. Вычту: 324 — 310 = 14, 14 меньше 62, значит, цифра 5 подходит, а 14 — остаток. Теперь её можно записать в частном.

Надо 526 разделить на 74.
Разделю 526 не на 74, а на 70, чтобы легче было найти цифру частного. Для этого разделю 52 на 7, получу 7. Это пробная цифра, её нельзя сразу записать в частном — сначала надо проверить, подходит ли цифра 7.
Умножу 74 на 7, получится 518. Вычту: 526 — 518 = 8, 8 меньше 74, значит, цифра 7 подходит, а 8 — остаток. Теперь её можно записать в частном.

Надо 793 разделить на 83.
Разделю 793 не на 83, а на 80, чтобы легче было найти цифру частного. Для этого разделю 79 на 8, получу 9. Это пробная цифра, её нельзя сразу записать в частном — сначала надо проверить, подходит ли цифра 9.
Умножу 83 на 9, получится 747. Вычту: 793 — 747 = 46, 46 меньше 83, значит, цифра 9 подходит, а 46 — остаток. Теперь её можно записать в частном.

211. Найди частное и остаток, проверь решение.
156 : 48 278 : 62 346 : 56 445 : 73

_— 156 |48 Проверка:
144 |3 _×48
12 3
144

144 + 12 = 156

_— 278 |62 Проверка:
248 |4 _×62
30 4
248

248 + 30 = 278

_— 346 |56 Проверка:
336 |6 _×56
10 6
336

336 + 10 = 346

_— 445 |73 Проверка:
438 |6 _×73
7 6
438

438 + 7 = 445

212. Космонавты были в полёте 290 ч. Сколько это суток и часов?

1 сутки = 24 часа

_— 290 |24
24 |12 — суток
_50
48
2 — часа
О т в е т: 12 суток и 2 часа.

213. Площадь первого участка 120 м², второго 160 м². При одинаковой норме высева на 1 м² на первом участке высеяли семян ржи на 1 кг меньше, чем на втором. Объясни, что означают выражения.
160 — 120 1000 : (160 — 120) 1000 : (160 — 120) • 160

160 — 120 — разница между площадями участков
1000 : (160 — 120) — столько грамм семян высеяли на 1 м²
1000 : (160 – 120) • 160 – столько грамм семян высеяли на втором участке

214. В международном автопробеге участвовало 350 машин. Экипаж каждой машины состоял из трёх спортсменов. До финиша не дошли 105 машин. Сколько машин и сколько спортсменов прибыли к финишу?

1) 350 – 105 = 245 (м. ) — дошли до финиша
2) 245 • 3 = 735 (с.) — прибыли к финишу
О т в е т: 245 машин и 735 спортсменов.

215. Составь по задачам уравнения и реши их.
1) Какое число надо уменьшить на 28, чтобы получить число, равное сумме чисел 58 и 37?
2) Какое число надо увеличить в 8 раз, чтобы получить число, равное произведению чисел 80 и 12?
3) Какое число надо уменьшить в 28 раз, чтобы получить число, равное разности чисел 300 и 203?

1) x — 28 = 58 + 37
x — 28 = 95
x = 95 + 28
x = 123

2) x • 8 = 80 • 12
x • 8 = 960
x = 960 : 8
x = 120

3) x : 28 = 300 — 203
x : 28 = 97
x = 97 • 28
x = 2716

216. 384 : 96 192 : 48 648 : 72 352 • 46 — 5840 : 80

_— 384 |96 _— 192 |48
384 |4 192 |4
0 0

_— 648 |72
648 |9
0

352 • 46 — 5840 : 80 = 16192 — 73 = 16119
_×352_— 5840|80
46     560 |73
_{+ 2112   —}240    1408      240
16192    0

_16192
73
16119

217.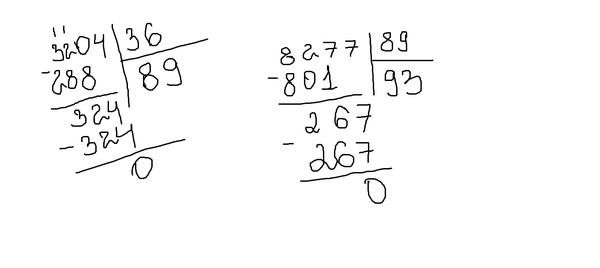 Найди значения выражений 360 : с и 360 • с, если с = 1; c = 3; c = 4; c = 6; c = 10.
Наблюдай, как при этом изменяется частное, как изменяется произведение.

360 : 1 = 360     360 • 1 = 360
360 : 3 = 120     360 • 3 = 1080
360 : 4 = 90      360 • 4 = 1440
360 : 6 = 60       360 • 6 = 2160
360 : 10 = 36     360 • 10 = 3600
Значение частного уменьшается, а значение произведения увеличивается.

218. Выложи из палочек такую фигуру. Какие углы в этой фигуре? Переложи 4 палочки так, чтобы получилось два остроугольных треугольника. Будут ли эти треугольники равнобедренными? равносторонними?

В этой фигуре все углы тупые.
Эти треугольники будут и равнобедренными и равносторонними. Равнобедренный треугольник — это треугольник, у которого две стороны равны по длине. Условие равенства двух сторон является необходимым и достаточным, чтобы считать треугольник равнобедренным.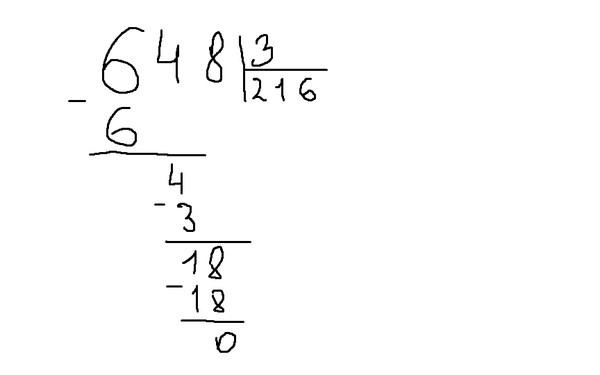 Это условие в равностороннем треугольнике выполняется всегда. Следовательно равносторонний треугольник всегда является равнобедренным.

399 : 57 236 : 59 475 : 95 609 • 27 — 4320 : 60

_— 399 |57 _— 236 |59
399 |7 236 |4
0 0

_— 475 |95
475 |5
0

609 • 27 — 4320 : 60 = 16443 — 72 = 16371
_×609_— 4320|60
27     420 |72
_{+ 4263   —}120    1218      120
16443        0

_16443
72
16371

ЗАДАНИЕ НА ПОЛЯХ
МАГИЧЕСКИЙ КВАДРАТ

ГДЗ по математике. Учебник. 4 класс. Часть 2. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.

Математика. 4 класс

Онлайн калькулятор. Умножение столбиком. — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7

Содержание

правило, примеры. Калькулятор умножения столбиком

Инструкция

Сначала проверьте навыки ребенка в умножении. Если ребенок нетвердо знает таблицу умножения, то с делением у него тоже могут быть проблемы. Тогда при объяснении деления можно разрешить подглядывать в шпаргалку, но таблицу все-таки придется выучить.

Запишите делимое и делитель через разделительную вертикальную черту. Под делителем вы будете записывать ответ — частное, отделив его горизонтальной чертой. Возьмите первую цифру числа 372 и спросите у ребенка, сколько раз число шесть «помещается» в тройке. Правильно, нисколько.

Тогда возьмите уже две цифры — 37. Для наглядности можно выделить их уголком. Снова повторите вопрос – сколько раз число шесть содержится в 37. Чтобы сосчитать быстро, пригодится . Подберите ответ вместе: 6*4 = 24 – совсем непохоже; 6*5 = 30 – близко к 37. Но 37-30 = 7 – шесть «поместится» еще раз. Наконец, 6*6 = 36, 37-36 = 1 – подходит. Первая цифра частного найдена – это 6. Напишите ее под делителем.

Запишите 36 под цифрой 37, подведите чертой. Для наглядности в записи можно использовать знак . Под чертой поставьте остаток – 1. Теперь «спустите» следующую цифру числа, двойку, к единице – получилось 12. Объясните ребенку, что цифры всегда «спускаются» по одной. Опять спросите, сколько «шестерок» содержит 12. Ответ – 2, на этот раз без остатка. Напишите вторую цифру частного рядом с первой. Окончательный результат – 62.

Также подробно рассмотрите случай деления . Например, 167/6 = 27, остаток 5. Скорее всего, ваш отпрыск про простые дроби пока ничего не слышал. Но если он будет задавать вопросы, что делать с остатком дальше, можно объяснить на примере яблок. 167 яблок разделили между шестью людьми.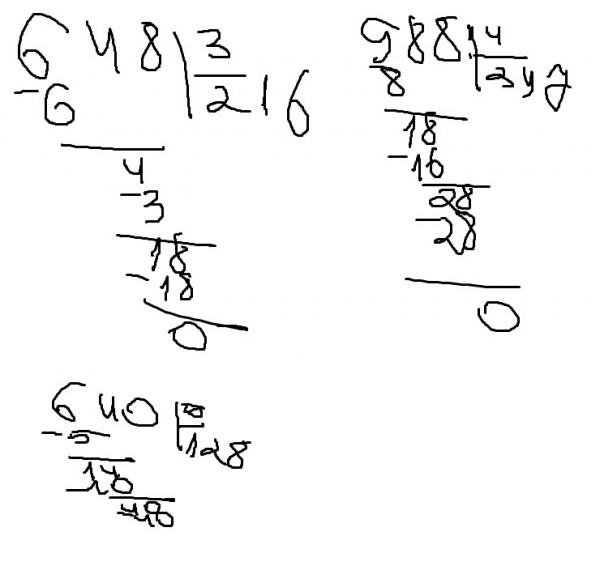 Каждому досталось 27 штук, и пять яблок остались неподеленными. Можно поделить и их, разрезав каждое на шесть долек и раздав поровну. Каждому человеку досталась одна долька от каждого яблока – 1/6. А так как яблок было пять штук, то и долек у каждого оказалось по пять – 5/6.

То есть результат можно записать так: 27 5/6.

Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.

Деление столбиком — удобный метод, часто применяемый для операции деления многозначных натуральных чисел. Именно этому методу и посвящена данная статья. Ниже мы рассмотрим, как выполнять деление столбиком. Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем — многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик.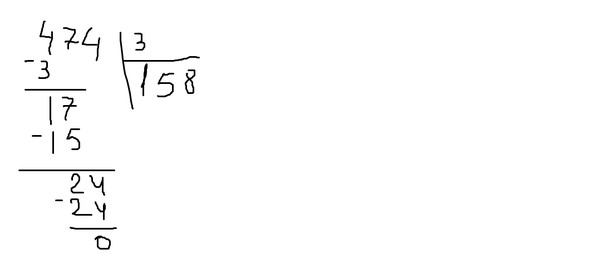

Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:

Пусть нам нужно разделить 6105 на 55 , запишем:

Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем. В общем случае схема деления столбиком выглядит так:

Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.

Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:

Практические навыки удобнее всего отрабатывать на простых примерах. Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8 ÷ 2 = 4 .

Итак, сначала запишем делимое и делитель согласно методу деления в столбик.

Следующим шагом нужно выяснить, сколько делителей содержит делимое. Как это сделать? Последовательно умножаем делитель на 0 , 1 , 2 , 3 . . Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.

Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.

Вернемся к примеру.

2 · 0 = 0 ; 2 · 1 = 2 ; 2 · 2 = 4 ; 2 · 3 = 6 ; 2 · 4 = 8

Итак, мы сразу получили число, равное делимому.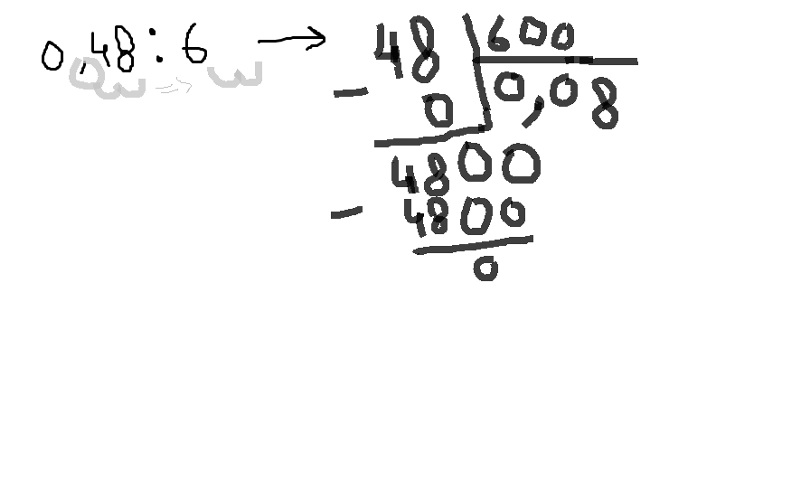 Записываем его под делимым, а число 4 , на которое мы умножали делитель, записываем на место частного.

Теперь осталось вычесть числа под делителем (также по методу столбика). В нашем случае 8 — 8 = 0 .

Данный пример — деление чисел без остатка. Число, получащееся после вычитания — это остаток деления. Если оно равно нулю, значит числа разделились без остатка.

Теперь рассмотрим пример, когда числа делятся с остатком. Разделим натуральное число 7 на натуральное число 3 .

В данном случае, последовательно умножая тройку на 0 , 1 , 2 , 3 . . получаем в результате:

3 · 0 = 0 7

Под делимым записываем число, полученное на предпоследнем шаге. По делителем записываем число 2 — неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили 6 .

В завершение операции вычитаем 6 из 7 и получаем:

Данный пример — деление чисел с остатком. Неполное частное равно 2 , а остаток равен 1 .

Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.

Алгоритм деления столбиком будем рассматривать на примере деления многозначного числа 140288 на число 4 . Сразу скажем, что понять суть метода гораздо легче на практических примерах, и данный пример выбран не случайно, так как иллюстрирует все возможные нюансы деления натуральных чисел столбиком.

1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14 , так как первая цифра делимого 1 меньше, чем делитель 4 .

2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x = 14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ , включая нуль: 0 , 1 , 2 , 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x . Когда в результате умножения получается число 14 , записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делителем. Если в результате умножения получается число, большее чем x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.

В соответствии с алгоритмом имеем:

4 · 0 = 0 14 .

Под выделенным числом записываем число 12 , полученное на предпоследнем шаге. На место частного записываем множитель 3 .

3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.

4. Число 2 меньше числа 4 , поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следующую цифру делимого — 0 . В итоге отмечаем новое рабочее число — 20 .

Важно!

Пункты 2 — 4 повторяются циклически до окончания операции деления натуральных чисел столбиком.

2. Снова посчитаем, сколько делителей содержится в числе 20 . Умножая 4 на 0 , 1 , 2 , 3 . . получаем:

Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение.

3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20 — 20 = 0 .

4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2 .

Принимаем это число за рабочее и снова выполняем пункты алгоритма.

2. Умножаем делитель на 0 , 1 , 2 , 3 . . и сравниваем результат с отмеченным числом.

4 · 0 = 0 2

Соответственно, под отмеченным числом записываем число 0 , и под делителем в следующий разряд частного также записываем 0 .

3. Выполняем операцию вычитания и под чертой записываем результат.

4. Справа под чертой добавляем цифру 8 , так как это следующая цифра делимого числа.

Таким образом, получаем новое работчее число — 28 . Снова повторяем пункты алгоритма.

Проделав все по правилам, получаем результат:

Переносим под черту вниз последнюю цифру делимого — 8 . В последний раз повторяем пункты алгоритма 2 — 4 и получаем:

В самой нижней строчке записываем число 0 . Это число записывается только на последнем этапе деления, когда операция завершена.

Таким образом, результатом деления числа 140228 на 4 является число 35072 . Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.

Приведем другие примеры деления чисел в столбик и примеры записи решений.

Пример 1. Деление натуральных чисел в столбик

Разделим натуральное число 7136 на натуральное число 9 .

После второго, третьего и четвертого шага алгоритма запись примет вид:

Повторим цикл:

Последний проход, и поучаем результат:

Ответ: Неполное неполное частное чисел 7136 и 9 равно 792 , а остаток равен 8 .

При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.

Пример 2. Деление натуральных чисел в столбик

Разделим число 7042035 на 7 .

Ответ: 1006005

Деление многозначных натуральных чисел столбиком

Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2 — 4 остаются неизменными.
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе. Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.

Перемножать большие числа, записывая их в строку, рано или поздно становится довольно сложным и утомительным процессом. Гораздо проще воспользоваться специальным алгоритмом по умножению в столбик: вам не придется держать числа в своей голове и что-либо запоминать. Вы можете делать пометки над столбиком, чтобы всегда видеть, как числа вам нужно перенести. Если вы пытаетесь обучить такому способу ребенка, то очень важно, чтобы таблица умножения отскакивала у него от зубов, иначе, процесс затянется надолго, а сам малыш совершит много ошибок, которые вереницей потянутся по всему примеру. Внимательно прочитайте статью и возьмите такой алгоритм себе на вооружение.

Запишите пример в строчку и посмотрите: какой из множителей меньше? Меньший окажется ниже в записи умножения в столбик, а большой множитель будет стоять наверху.

Запишите пример по такому принципу, как указано на картинке ниже.

Сверху напишите большее число.
Слева поставьте знак умножения в виде крестика.
Снизу запишите меньшее число.
Проведите прямую черту под примером.

Если в примере есть множитель, который оканчивается на ноль или несколько нолей, то его следует записывать так:

Ноли нужно выносить за пример.
Числа пишите под числами.

В таком случае, вы просто переносите это количество нолей сразу в ответ. Если ноли имеются и у первого множителя, и у второго, то сложите их количество и запишите в ответ.

Теперь начинайте расчёт по такому принципу:

Всё верхнее число вы умножаете на последнюю цифру нижнего. Помните, что на последние ноли умножение не производится.
Чтобы вам было удобнее, записывайте числа, которые нужно перенести, сверху над всем примером. Позднее вы можете их просто стереть, зато в процессе вам не придется запоминать числа переноса.
Как только вы закончите расчет, запишите полученное число под чертой.

Как только вы перемножите верхнее число на последнюю цифру нижнего и запишите свой ответ, начинайте перемножать следующее.

По такому же принципу умножьте всё верхнее число на вторую с конца цифру нижнего. Также записывайте числа переноса, однако, ответ вам следует записать под первым решением, но сдвинув запись на одну клеточку левее. У вас получится столбик с выступающей влево строкой.

Как вы уже догадались, вам нужно перемножить верхнее число на все цифры нижнего, начиная с конца. Каждый раз запись ответа переносится на одну клетку левее.

Перемножьте таким образом все числа между собой. Теперь снова проведите черту под столбиком. Между всеми решениями поставьте знак сложения.

Теперь вам осталось выполнить сложение в столбик, которое вы уже должны уметь делать:

Складывайте все числа, находящиеся на одной вертикальной линии.
Если число получается двухзначным, то число десятков вы переносите в следующую вертикальную полосу.

Под некоторыми числами вовсе не будет других – в таком случае, вы просто записываете это число в ответ. Не забывайте переносить в ответ все нули, которые стоят в конце множителей.

Выполнять умножение в столбик очень удобно и быстро, особенно, если требуется перемножить большие числа. Вы легко можете проверить правильность умножения, просто разделив ответ на один из множителей. Для этого используйте калькулятор, либо способ деления уголком. На первых порах такое умножение занимает значительную долю времени, но с опытом, всё действие происходит всего за пару секунд.

Азы деления столбиком и в уме дети изучают в начальной школе: в 3-м или 4-м классе. Но вникают в материал быстро и легко далеко не все третьеклассники. Дома нужно много практиковаться, решать тренировочные примеры. Но сначала лучше еще раз объяснить деление уголком, с остатком, выявить пробелы в детских знаниях.

Как стать суперучителем без специальной подготовки и помочь ребенку с этой трудной темой, расскажем подробнее.

Как научиться делить столбиком

Деление столбиком с остатком и без него нельзя начинать без подготовки. Сначала ребенок должен хорошо уметь и знать следующее:

Отработайте все обозначенные умения до автоматизма. Затем приступайте к делению маленьких цифр на примере таблицы умножения в уме. Например, ребенок выучил, как умножать цифру 6:

Смело предлагайте такие примеры:

Через пару уроков школьник будет выполнять такие задания легко. Можно разнообразить занятия по устному счету играми на деление.

На заметку! Все начальные математические навыки хорошо автоматизируются с помощью онлайн-тестов, где ребенок получает мгновенный результат своей работы.

Игровые задания

Интересные математические игры на деление помогают детям закрепить навык, узнать законы работы с цифрами, освоить устный счет.

Головоломки на развитие внимания. Напишите в тетради 3–5 примеров на деление с ответами. Все, кроме одного, должны быть решены неверно. Нужно быстро найти тот пример, который содержит правильный ответ. Затем исправить остальные с помощью устного счета.
Подбор примера по результату. Предлагайте малышу ответ без примера. Давайте задание придумать задачу. Например, ответ 8. Ребенок может придумать такую задачу: 48:6.
«Идем в магазин». Расставьте на полу игрушки с карточками. На листах написаны примеры: 6:2, 18:3, 42:7, 100:50. Игрушки — это «товар» в фантазийном магазине, частное после решения примера — их цена. Чтобы узнать стоимость покупки, нужно решить задания, а потом оплатить полученный результат в кассу. Играть лучше в небольшой команде — 2–3 человека.
«Молчуны». Ребенок получает карточки с цифрами от 1 до 100. Задавайте вопросы с примерами на деление, ученик должен отвечать без слов, показывая правильный ответ.
Небольшие самостоятельные работы с подарком за старательность. Распечатайте карточки с примерами в количестве 5–10 штук. Укажите время на решение, например 5 минут. Поставьте перед ребенком песочные часы. После выполнения контрольной верно поощрите школьника походом в зоопарк, кино, покупкой книги, сладостей.
«Ищем дерево». Нарисуйте небольшой сад с деревьями на картоне. Каждому растению дайте номер, пусть их будет 10. На листочке для ученика напишите 3 примера:

45:9 120:60 14:7

Школьник должен вычислять результат к каждому заданию, а потом складывать все числа между собой. Получится так:

Ребенок должен найти дерево под номером 9.

Для игры можно использовать цветные пуговицы и ставить их на занятые деревья. Развлечение подходит для командных соревнований.

После устной работы с делением натуральных чисел можно показать ребенку порядок записи примеров столбиком. Если педагогического опыта у вас нет, посмотрите видеоурок на эту тему, вспомните теорию сами.

Теперь можно приступать к объяснению сложного материала школьнику. Есть несколько методик домашнего обучения делению:

1.

Мама-учитель

Родителям придется ненадолго стать педагогами. Оборудовать доску, купить мел или маркеры. Заранее вспомнить школьный материал. Объяснить пошагово теорию и закрепить ее на практике с помощью большого количества самостоятельных, карточек, контрольных работ.

2. Посмотреть вместе с ребенком обучающее видео

Например, это:

Затем нужно обсуждать с малышом материал, закреплять навык на практике несколько недель.

3. Нанять репетитора

Деление не самая сложная тема в школьной программе. В начальных классах можно легко обойтись без платных уроков с педагогом. Этот вариант оставим на крайний случай.

На заметку! Обязательно противопоставляйте деление умножению. Проверяйте результат обоих действий противоположным.

Как объяснить деление столбиком

Сначала стоит доходчиво объяснить, что такое деление на простом примере. Суть математического действия — разложить число поровну. В 3-м классе дети хорошо учатся на доступных примерах: раздают кусочки торта гостям, рассаживают кукол по 2 машинам.

Когда малыш усвоит суть деления, покажите его запись на листке. Используйте уже знакомые задания с простыми числами:

Сначала запишите задачу обычным способом: 250:2=?
Каждому числу дайте название: 250 — делимое, 2 — делитель, результат после знака равно — частное.
Затем сделайте сокращенную запись столбиком (уголком):

Рассуждайте вместе так: сначала найдем неполное частное. Это будет 2, так как оно не меньше делителя, а вернее, равно ему. В этом числе помещается один делитель, значит, в частное записываем цифру 1 и умножаем ее на 2. Заносим полученный результат под делимым. Отнимаем 2-2. Получится ноль, поэтому сносим следующее число и опять подыскиваем частное. Совершаем математическое действие до тех пор, пока не получится ноль.
После получения окончательного результат сделайте проверку с помощью умножения: 125х2=250.

Желательно научить третьеклассника рассуждать в процессе вычисления вслух, выполнять действия на черновике. Сначала проговаривайте алгоритм вместе, потом только слушайте ученика и помогайте исправить ошибки.

На заметку! Приучайте малыша постоянно проверять себя. Школьник должен понимать, что величина остатка вычитания в столбике деления должен всегда быть меньше делителя.

Деление на однозначное число

Возьмите листок и ручку, посадите ребенка рядом. Сначала запишите пример уголком сами. Для деления на однозначное число выбирайте такие цифры, которые дают результат без остатка (полный ответ).

Первый урок можно построить так:

Положите перед ребенком картинку с образцом деления столбиком.
Придумайте собственный пример. Пусть это будет 254:2
Задание нужно записывать уголком. Доверьте это школьнику. Он может посмотреть, как делается запись на картинке.
Спросите третьеклассника: «Какое число нужно делить на 2 первым?». В этот момент важно объяснять, что делимое должно быть равно или большего делителя. Малыш выделит для деления первое число из данной цифры: 2… 54
Теперь определите вместе, сколько двоек поместится в числе 2. Ответ: 1.
Записываем частное под уголком.
Умножаем 1 на 2 и записываем результат под делимым.
Вычитаем.
Так как получился 0, сносим следующую цифру под линию после вычитания: 5.
Опять задаем вопрос: «Сколько двоек поместится в 5?» Малыш вспоминает таблицу умножения или подбирает частное с помощью логики. Отвечает: 2.
Записываем 2 в частное, умножаем на 2.
Результат (4) записываем под 5.
Отнимаем.
Остается 1. Единицу разделить на 2 нельзя, поэтому сносим остатки делимого вниз. Получается 14.
Делим 14 на 2. Записываем в частное 7.
Умножаем на 2. Записываем под чертой 14.
Отнимаем.
В конце всегда должен получаться 0.
В результате у ребенка сформируется такая запись:

Для закрепления запишите еще 3–5 примеров на деление на этом же листочке. Не отходите далеко от школьника, образец не прячьте, не превращайте урок в проверочную работу. Малыш только учится делить. На этом этапе помогайте ему, подсказывайте и наталкивайте на правильное решение для повышения уверенности в себе.

На заметку! Для автоматизации навыка деления столбиком можно составить небольшую памятку, где прописан каждый этап математического действия. Разрешайте школьнику смотреть в нее до тех пор, пока он сам не забудет об образце.

Деление на двузначное число

Когда ученик 3-го класса усвоил деление на однозначное число, можно приступать к следующему этапу — работе с двузначными цифрами. Начинайте с простых, явных примеров, чтобы малыш понял алгоритм действий. Например, возьмите числа 196 и 28 и объясните принцип:

Сначала подберите примерное число для ответа. Для этого выясните приблизительно, сколько цифр 28 поместится в 196. Для удобства можно округлять оба числа: 200:30. Получится не больше 6. Полученное число не нужно записывать, это только догадка.
Проверяем результат умножением: 28х6. Получается 196. Предположения оказались верными.
Запишите ответ: 196:28 =6.

Еще один вариант обучения: деление на двузначное число уголком. Такой способ больше подходит для работы с числами от четырех разрядов, то есть тысяч. Приведем простой пример:

Напишите на листе бумаги 4070, начертите уголок и подпишите делитель — 74.
Определите, с какого числа начнете делить. Спросите у ребенка, можно ли разделить 4 на 74, 40? В результате малыш поймет, что сначала нужно ограничиться числом 407. Очертите полученную цифру сверху полукругом. 0 останется в стороне.
Теперь нужно выяснить, сколько 74 поместится в 407. Действуем с помощью логики и проверки умножением. Получится 5. Записываем результат под уголком (под делителем).
Теперь умножаем 74 на 5 и записываем результат под делимым. Получится 370. Важно начинать запись с первого числа слева.
После записи нужно подвести горизонтальную черту и отнять 370 от 407. Получится 37.
37 разделить на 74 нельзя, поэтому вниз сносится оставшийся в верхнем ряду 0.
Теперь делим 370 на 74. Подбираем множитель (5) и записываем его под уголком.
Умножаем 5 на 74, записываем результат в столбик. Получится 370.
Опять получаем разность. Результат будет равен 0. Значит, деление считается завершенным без остатка. 4070:74=55. Частное смотрим под уголком.

Для проверки правильности решение произведите умножение: 74х55=4070.

Есть мнение! Иметь в доме решебник с ГДЗ многие родители считают недопустимым. А зря. С помощью готовых заданий ребенок может легко проверить себя. Главное — правильно объяснить школьнику назначение сборника ДЗ с ответами.

Многозначные числа

Сложнее всего детям даются задачи на трехзначные и четырехзначные числа. Четверокласснику тяжело оперировать тысячами и сотнями тысяч. У школьника возникают следующие проблемы:

Не может определить неполное число делимого для первого действия. Вернитесь к изучению разрядов натуральных чисел, поработайте над развитием внимания малыша.
Пропускает 0 в записи частного. Это самая распространенная проблема. В результате у ребенка получается число на несколько разрядов меньше правильного. Чтобы избежать этой ошибки, нужно распечатывать памятку с последовательностью действий в примерах, где в середине частного есть нули. Предложите ребенку тренажер с такими заданиями для отработки навыка.

При обучении решению задач с крупными числами действуйте поэтапно:

Объясните, что такое неполное делимое и зачем его выделять.
Потренируйтесь в поиске делимого устно без последующего решения задач. Например, дайте детям такие задания:

Найдите неполное частное в примерах: 369:28; 897:12; 698:36.

Теперь приступайте к решению на бумаге. Запишите столбиком: 1068:89.
Сначала нужно отделить неполное делимое. Можно использовать запятую сверху над числами.

На заметку! Примеры с семизначными цифрами с третьеклассниками решать не нужно. Это лишнее. Достаточно остановиться на заданиях с пятизначными числами (до 10 000). Деление миллионов дети проходят в старших классах.

Деление с остатком

Завершающим этапом уроков на закрепление навыка деления будет решение заданий с остатком. Они обязательно встретятся в решебнике для 3–4-го класса. В гимназиях с математическим уклоном школьники изучают не только неполные числа, но и десятичные дроби. Форма записи примера уголком останется прежней, отличаться будет только ответ.

Примеры на деление с остатком берите несложные, можно преобразовывать уже решенные задания с целым числом в ответе, прибавляя к делимому единицу. Это очень удобно для ребенка, он сразу увидит, чем примеры похожи и чем отличаются.

Урок может выглядеть так:

На заметку! Отделять целое число от остатка запятой, делать из него дробное на начальном этапе обучения делению не нужно. Записывайте остаток отдельно, чтобы школьник видел конечный результат разности в столбике.

Как делать проверку

Проверка деления производится с помощью умножения: делитель умножается на делитель. Делать это можно столбиком:

Теперь проверим:

Для проверки деления с остатком нужно:

Умножить полное частное на делитель.
Прибавить к результату остаток.

34+1 (остаток) =35

Алгоритм проверки правильности решения примера деления не изменяется от разрядности цифр.

Важно! Первое время просите ребенка расписывать проверку умножением подробно, чтобы проверить и закрепить знание таблицы.

Примеры для тренировки

Научиться быстро решать примеры с делением помогают тренировочные задания. Карточками может оканчиваться каждый урок после прохождения новой темы.

Однозначные

Двузначные

Многозначные

Скачать карточки

В качестве домашнего математического тренажера используйте карточки с примерами. В них включайте разные случаи: с однозначными и многозначными числами, деление с полным результатом и остатком. Скачать карточки можно бесплатно. Раздаточный материал обязательно следует напечатать для проверочной работы.

Ошибки с делением у детей в начальной школе встречаются довольно часто. Уделите этой теме максимум внимания и времени, чтобы усвоение последующего материала проходило без запинок. Используйте карточки, видеоуроки, постоянную тренировку навыка и повторение пройденных тем в игровой форме. Тогда домашние уроки не навеют на ребенку скуку и пройдут с максимальной пользой.

ВАЖНО ! *при копировании материалов статьи обязательно указывайте активную ссылку на перво

Деление – интересная операция, в чем мы и убедимся с вами в этой статье!

Деление чисел

Деление с остатком

Деление на 3 и 9

Найти сумму цифр делимого.

Поделить на 3 или 9 (в зависимости от того, что вам нужно).

Если ответ получается без остатка, то и число поделится без остатка.

Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.

Умножение и деление

Деление 3 класс

В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:

Деление 4 класс

Деление в столбик

Рассмотрим пример, 512:8.

1 шаг . Запишем делимое и делитель следующим образом:

Частное будет записано в итоге под делителем, а расчеты под делимым.

2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:

3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:

Теперь 51 больше 8. Это неполное частное.

4 шаг . Ставим точку под делителем.

7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:

8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.

* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:

10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.

Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.

Деление трехзначных

Деление дробей

Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):

Деление числа на классы

Деление натуральных чисел

Деление презентация

Примеры на деление

Легкий уровень

Средний уровень

Сложный уровень

Игры на развитие устного счета

Игра «Угадай операцию»

Игра «Упрощение»

Игра «Быстрое сложение»

Игра «Визуальная геометрия»

Игра «Копилка»

Игра «Быстрое сложение перезагрузка»

Развитие феноменального устного счета

Скорочтение за 30 дней

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Деньги и мышление миллионера

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Напомним, что разделить натуральное число a на натуральное число b – это значит представить число a в виде:

a = bc + r ,

где частное c и остаток r – целые неотрицательные числа, причем остаток r удовлетворяет неравенству:

Если друг на друга делить многочлены, то возникает похожая ситуация.

Действительно, при выполнении над многочленами операций сложения, вычитания и умножения результатом всегда будет многочлен. В частности, при перемножении двух многочленов, отличных от нуля, степень произведения будет равна сумме степеней сомножителей.

Однако в результате деления многочленов многочлен получается далеко не всегда.

Говорят, что один многочлен нацело (без остатка) делится на другой многочлен, если результатом деления является многочлен.

Если же один многочлен не делится нацело на другой многочлен, то всегда можно выполнить деление многочленов с остатком, в результате которого и частное, и остаток будут многочленами.

Определение. Разделить многочлен a(x) на многочлен b(x) с остатком – это значит представить многочлен a(x) в виде

a(x) = b(x) c(x) + r(x) ,

где многочлен c(x) – частное, а многочлен r(x) – остаток, причем, степень остатка удовлетворяет неравенству:

Очень важно отметить, что формула

a(x) = b(x) c(x) + r(x)

является тождеством, т. е. равенством, справедливым при всех значениях переменной x .

При делении (с остатком или без остатка) многочлена на многочлен меньшей степени в частном получается многочлен, степень которого равна разности степеней делимого и делителя.

Один из способов деления многочленов с остатком – это деление многочленов «уголком», что представляет собой полную аналогию с тем, как это происходит при делении целых чисел.

К описанию этого способа деления многочленов мы сейчас и переходим.

Пример. Заранее расположив многочлены по убывающим степеням переменной, разделим многочлен

2x⁴ – x³ + 5x² – 8x + 1

на многочлен

x² – x + 1 .

Решение. Опишем алгоритм деления многочленов «уголком» по шагам:

Делим первый член делимого 2x⁴ на первый член делителя x². Получаем первый член частного 2x² .
Умножаем первый член частного 2x² на делитель x² – x + 1, а результат умножения

2x⁴ – 2x³ + 2x²

пишем под делимым 2x⁴ – x³ + 5x² – 8x + 1 .

Вычитаем из делимого написанный под ним многочлен. Получаем первый остаток

x³ + 3x²– 8x .

Если бы этот остаток был равен нулю, или был многочленом, степень которого меньше, чем степень делителя ( в данном случае меньше 2), то процесс деления был бы закончен. Однако это не так, и деление продолжается.

Делим первый член остатка x³ на первый член делителя x². Получаем второй член частного x .
Умножаем второй член частного x на делитель x² – x + 1 , а результат умножения

x³ – x²+ x

пишем под первым остатком x³ + 3x²– 8x .

Вычитаем из первого остатка написанный под ним многочлен. Получаем второй остаток

4x² – 9x + 1 .

Если бы этот остаток был бы равен нулю, или был многочленом, степень которого меньше, чем степень делителя, то процесс деления был бы закончен. Однако это не так, и деление продолжается.

Делим первый член второго остатка 4x² на первый член делителя x². Получаем третий член частного 4.
Умножаем третий член частного 4 на делитель x² – x + 1 , а результат умножения

4x² – 4x + 4

пишем под вторым остатком.

Вычитаем из второго остатка написанный под ним многочлен. Получаем третий остаток
– 5x – 3 .
Степень этого остатка равна 1, что меньше, чем степень делителя. Следовательно, процесс деления закончен.
Таким образом,

2x⁴ – x³ + 5x² – 8x + 1 =
= (x² – x + 1) (2x² + x +
+ 4) – 5x – 3 ,

где

Запись изложенного процесса деления многочленов «уголком» имеет следующий вид:

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Калькулятор столбиком умножение деление вычитание прибавление. Как делить в столбик? Как объяснить ребенку деление столбиком? Деление на однозначное, двузначное, трехзначное число, деление с остатком

Как делить десятичные дроби на натуральные числа? Рассмотрим правило и его применение на примерах.

Чтобы разделить десятичную дробь на натуральное число, надо:

1) разделить десятичную дробь на число, не обращая внимания на запятую;

2) когда закончится деление целой части, в частном поставить запятую.

Примеры.

Разделить десятичные дроби:

Чтобы разделить десятичную дробь на натуральное число, делим, не обращая внимания на запятую. 5 на 6 не делится, поэтому в частном ставим нуль. Деление целой части окончено, в частном ставим запятую. Сносим нуль. 50 делим на 6. Берем по 8. 6∙8=48. От 50 вычитаем 48, в остатке получаем 2. Сносим 4. 24 делим на 6. Получаем 4. В остатке — нуль, значит, деление окончено: 5,04: 6 = 0,84.

2) 19,26: 18

Делим десятичную дробь на натуральное число, не обращая внимания на запятую. Делим 19 на 18. Берем по 1. Деление целой части окончено, в частном ставим запятую. Вычитаем от 19 18. В остатке — 1. Сносим 2. 12 на 18 не делится, в частном пишем нуль. Сносим 6. 126 делим на 18, получаем 7. Деление окончено: 19,26: 18 = 1,07.

Делим 86 на 25. Берем по 3. 25∙3=75. От 86 вычитаем 75. В остатке — 11. Деление целой части окончено, в частном ставим запятую. Сносим 5. Берем по 4. 25∙4=100. От 115 вычитаем 100. Остаток — 15. Сносим нуль. 150 делим на 25. Получаем 6. Деление окончено: 86,5: 25 = 3,46.

4) 0,1547: 17

Нуль на 17 не делится, в частном пишем нуль. Деление целой части окончено, в частном ставим запятую. Сносим 1. 1 на 17 не делится, в частном пишем нуль. Сносим 5. 15 на 17 не делится, в частном пишем нуль. Сносим 4. Делим 154 на 17. Берем по 9. 17∙9=153. От 154 вычитаем 153. В остатке — 1. Сносим 7. Делим 17 на 17. Получаем 1. Деление окончено: 0,1547: 17 = 0,0091.

5) Десятичная дробь может получиться и при делении двух натуральных чисел.

При делении 17 на 4 берем по 4. Деление целой части окончено, в частном ставим запятую. 4∙4=16. От 17 вычитаем 16. Остаток — 1. Сносим нуль. 10 делим на 4. Берем по 2. 4∙2=8. От 10 вычитаем 8. В остатке — 2. Сносим нуль. 20 делим на 4. Берем по 5. Деление окончено: 17: 4 = 4,25.

И еще пара примеров на деление десятичных дробей на натуральные числа:

В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.

Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.

Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.

Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.

Как умножаются в столбик натуральные числа?

Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:

До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.

Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.

Алгоритм умножения в столбик десятичных дробей

Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.

Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.

Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:

С чего начать обучение делению?

До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.

После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?

После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.

Алгоритм деления чисел в столбик

Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:

До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
Записать делимое. Справа от него — делитель.
Прочертить слева и снизу около последнего уголок.
Определить неполное делимое, то есть число, которое будет минимальным для деления. Обычно оно состоит из одной цифры, максимум из двух.
Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.
Записать результат от умножения этого числа на делитель.
Написать его под неполным делимом. Выполнить вычитание.
Снести к остатку первую цифру после той части, которая уже разделена.
Снова подобрать число для ответа.
Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.

Как решать деление в столбик, если в делителе больше одной цифры?

Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.

Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.

Рассмотреть такое деление можно на примере — 12082: 863.

Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
После вычитания получается остаток 345.
К нему нужно снести цифру 2.
В числе 3452 четыре раза умещается 863.
Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
Остаток после вычитания равен нулю. То есть деление закончено.

Ответом в примере будет число 14.

Как быть, если делимое заканчивается на ноль?

Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.

Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.

Что делать, если разделить нужно десятичную дробь?

Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.

Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.

Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.

Деление двух десятичных дробей

Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.

Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.

Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.

В качестве примера: 28,4 делим на 3,2:

Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.
Их полагается разделить. Причем сразу все число 284 на 32.
Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
Деление целой части закончилось, и в ответ полагается поставить запятую.
Снести к остатку 0.
Снова взять по 8.
Остаток: 24. К нему приписать еще один 0.
Теперь брать нужно 7.
Результат умножения — 224, остаток — 16.
Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.

Деление закончено. Результат примера 28,4:3,2 равен 8,875.

Что делать, если делитель равен 10, 100, 0,1, или 0,01?

Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.

Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.

Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.

При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).

Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.

Деление периодических дробей

В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.

Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.

Если в примере разные дроби…

Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.

Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.

Деление столбиком неотъемлемая часть школьной программы и необходимое знание для ребенка. Чтобы избежать проблем на уроках и с их выполнением, следует давать ребенку основные знания еще с маленького возраста.

Гораздо легче объяснять ребенку определенные вещи и процессы в игровой форме, а не в формате стандартного урока (хотя на сегодняшний день существует достаточно разнообразных методик обучения в разных формах).

Из этой статьи вы узнаете

Принцип деления для малышей
Дети постоянно сталкиваются с разными математическими терминами, даже не подозревая, откуда они. Ведь многие мамочки, в форме игры, объясняют ребенку, что папы больше тарелка, в садик ходить дальше, чем в магазин и другие незамысловатые примеры. Всё это представляет ребенку первоначальное впечатление о математике, еще до похода ребёнка в первый класс.
Чтобы научить ребёнка делить без остатка, а позже с остатком, необходимо прямо предложить поиграть малышу в игры с делением. Разделите, например, конфеты между собой, а затем по очереди добавляйте следующих участников.
Сначала ребенок будет делить конфеты, отдавая каждому участнику по одной. А в конце вместе сделаете вывод. Следует пояснить, что «разделить» — значит всем одинаковое число конфет.
Если Вам необходимо растолковать этот процесс с помощью цифр, то можно привести пример в форме игры. Можно сказать, что цифра – это конфета. Следует объяснить, что число конфет, которые нужно делить между участниками – делимое. А количество человек, на которых делят эти конфеты – это делитель.
Потом следует показать это все наглядно, привести «живые» примеры, чтобы быстрее научить кроху делить. Играя, он намного быстрее все поймет и усвоит. Пока алгоритм объяснить будет сложно, и сейчас это не нужно.
Как обучить малыша делению в столбик
Объяснение крохе разных математических действий – это хорошая подготовка к походу в класс, особенно математический класс. Если Вы решили перейти к обучению ребенка делению столбиком, значит такие действия как сложение, вычитание, и что такое таблица умножения он уже усвоил.
Если же это у него все еще вызывает некоторые сложности, то нужно подтянуть все эти знания. Стоит напомнить алгоритм действий предыдущих процессов, научить свободно пользоваться своими знаниями. В противном случае малыш просто запутается во всех процессах, и перестанет что-либо понимать.
Для облегчения понимания этого, сейчас есть таблица деления для малышей. Принцип у нее такой же, как и у таблиц умножения. Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя.
При формировании понятия «деление» нужно обязательно делать все в игровой форме, приводить все примеры на знакомых ребенку вещах и предметах.
Очень важно, чтобы все предметы были четного числа, чтобы малышу было ясно, что итогом являются равные части. Это будет правильно, поскольку позволит крохе осознать, что деление — процесс обратный умножению. Если предметы будут нечетного количества, то итог выйдет с остатком и малыш запутается.
Умножаем и делим с помощью таблицы
При объяснении малышу взаимосвязи между умножением и делением, необходимо это все наглядно показывать на каком-либо примере. Например: 5 х 3 = 15. Вспомните, что итог умножения это произведение двух чисел.
И только после этого, объясняйте, что это обратный процесс к умножению и продемонстрируйте это наглядно с помощью таблицы.
Скажите, что нужно поделить результат «15» — на какой-то из множителей («5»/ «3»), и итогом будет постоянно иной, не принимавший участие в делении, множитель.
Также необходимо растолковать малышу, как правильно называются категории, которые выполняют деление: делимое, делитель, частное. И снова с помощью примера покажите, что из них является конкретной категорией.
Деление столбиком вещь не очень сложная, у нее есть свой легкий алгоритм, которому малыша нужно научить. После закрепления всех этих понятий и знаний, можно переходить к дальнейшему обучению.
В принципе, родителям стоит выучить с любимым чадом таблицу умножения в обратном порядке, и наизусть ее запомнить, так как это будет нужным при обучении делению столбиком.
Это делать необходимо до похода в первый класс, чтобы ребенку в школе было намного легче освоиться, и успевать за школьной программой, и чтобы класс из-за небольших неудач не начал дразнить ребенка. Таблица умножения есть и в школе, и в тетрадях, поэтому носить отдельную таблицу в школу не придется.
Делим с помощью столбика
Прежде чем приступить к занятию, нужно вспомнить названия цифр при делении. Что такое делитель, делимое и частное. Ребенок должен без ошибок делить эти цифры на правильные категории.
Самое главное при обучении деления столбиком, это усвоить алгоритм, который, в общем, довольно простой. Но сначала объясните ребенку значение слова «алгоритм», если он забыл его или до этого не изучал.
В том случае, если кроха прекрасно разбирается в таблице умножения и обратного деления, у него не будет никаких сложностей.
Однако на полученном результате долго задерживаться нельзя, необходимо регулярно тренировать приобретенные умения и навыки. Двигайтесь далее, как только станет ясно, что малыш понял принцип метода.
Необходимо научить малыша делить столбиком без остатка и с остатком, чтобы ребенок не пугался, что у него что-то не получилось разделить правильно.
Чтобы было проще обучить малыша процессу деления необходимо:
в 2-3 года понимание отношения целое-часть.
в 6-7 лет малыш должен свободно уметь выполнять сложение, вычитание и осознавать сущность умножения и деления.
Нужно побуждать интерес малыша к математическим процессам, чтобы этот урок в школе приносил ему удовольствие и желание учиться, и не мотивировать его на одних на уроках, но и в жизни.
Ребенок должен носить разные инструменты для уроков математики, учиться ими пользоваться. Однако если ребенку тяжело все носить, то не стоит его перегружать.
Калькулятор в столбик для Андроид устройств станет замечательным помощником для современных школьников. Программа не только дает правильный ответ на математическое действие, но и наглядно демонстрирует его пошаговое решение. Если же вам нужны более сложные калькуляторы – можете посмотреть или же продвинутый инженерный калькулятор.
Особенности
Главной особенностью программы является уникальность расчета математических операций. Отображение процесса вычислений столбиком дает возможность школьникам более подробно с ним ознакомиться, понять алгоритм решения, а не просто получить готовый результат и переписать его в тетрадь. Эта особенность имеет огромное преимущество перед другими калькуляторами, т.к. достаточно часто в школе учителя требуют расписать промежуточные вычисления, чтобы удостовериться, что школьник производит их в уме и действительно понимает алгоритм решения задач. Кстати, у нас есть еще одна программа похожего рода – .
Чтобы начать пользоваться программой, необходимо скачать калькулятор в столбик на Андроид. Сделать это можно на нашем сайте абсолютно бесплатно без дополнительных регистраций и смс. После установки откроется главная страница в виде тетрадного листа в клетку, на котором, собственно, и будут отображаться результаты вычислений и их подробное решение. Внизу располагается панель с кнопками:
Цифры.
Знаки арифметических действий.
Удаление раннее введенных символов.
Ввод осуществляется по тому же принципу, что и на . Все отличие состоит только в интерфейсе приложения – все математические вычисления и их результат отображаются в виртуальной ученической тетради.
Приложение позволяет быстро и правильно выполнить стандартные для школьника математические вычисления столбиком:
умножение;
деление;
сложение;
вычитание.
Приятным дополнением в приложении является функция ежедневного напоминания о домашнем задании по математике. Хотите – делайте домашки. Для ее включения следует зайти в настройки (нажать кнопку в виде шестеренки) и установить галочку о напоминании.
Достоинства и недостатки
Помогает школьнику не просто быстро получить правильный результат математических вычислений, но и понять сам принцип расчета.
Очень простой, интуитивно понятный интерфейс для каждого пользователя.
Установить приложение можно даже на самое бюджетное Андроид устройство с операционной системой 2. 2 и более поздней версией.
Калькулятор сохраняет историю проведенных математических вычислений, которую можно в любой момент очистить.
Калькулятор ограничен в математических операциях, поэтому применить его для сложных расчетов, с какими мог бы справиться инженерный калькулятор, не получится. Однако учитывая назначение самого приложения – наглядно продемонстрировать учащимся младшей школы принцип расчета в столбик, считать это недостатком не стоит.
Приложение также станет отличным помощником не только для школьников, но и для родителей, которые желают заинтересовать своего ребенка математикой и научить его правильно и последовательно производить вычисления. Если Вы уже пользовались приложением Калькулятор в столбик, оставьте свои впечатления ниже в комментариях.
Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.

Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг . Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг . Ставим точку под делителем.
5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Копилка»
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение перезагрузка»
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Решение по действиям в столбик. Деление натуральных чисел столбиком, примеры, решения
Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.

Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию
Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям
Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.
Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».
Итак, как объяснить ребенку деление столбиком :
Постарайтесь сначала объяснить на маленьких цифрах. Возьмите счетные палочки, например, 8 штук
Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
Пусть ребенок сам разделит другое число, например, более сложное: 24:4
Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные
Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.
Начинайте с простого — деление на однозначное число:
Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.
Например, 256 разделить на 4:
Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам. Слева напишите первую цифру, а справа над чертой вторую
Спросите у малыша, сколько четверок помещается в двойке — нисколько
Тогда берем 25. Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
Опять спрашивайте: в единице сколько помещается четверок — нисколько. Тогда сносим к единице цифру «6»
Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»
Письменное деление на двузначное число
Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.
Важно: Снова начинайте объяснять с простых действий. Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.
Выполните вместе такое простое действие: 184:23 — как нужно объяснять:
Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе. Ответ будет 8
Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.
Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:
Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3. Записываем 3 в ответ под чертой справа
Под 76 записываем 72 и проводим линию, записываем разность — получилось 4. Эта цифра делится на 24? Нет — сносим 8, получается 48
Цифра 48 делится на 24? Правильно — да. Получается 2, записываем эту цифру в ответ
Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно
Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.
Например:
Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
Сносим 6. Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4. Умножаем 4 на 716, получается 2864
Запишите 2864 под 2864, получается в разности 0. Ответ 204
Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.
Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.
Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):
Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
Делится эта цифра на 8? Правильно — нет. Получается, остаток 3
После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:
В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375
Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.
Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.
Алгоритм деления чисел заключается в следующем:
Сделать прикидку числа, которое будет стоять в ответе
Найти первое неполное делимое
Определить число цифр в частном
Найти цифры в каждом разряде частного
Найти остаток (если он есть)
По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).
Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:
1428:42
2924:68
30296:56
136576:64
16514:718
Для закрепления результата можно использовать такие игры на деление:
«Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.
Условие для ребенка: Среди нескольких примеров, только один решен правильно. Найди его за минуту.
Видео: Игра арифметика для детей сложение вычитание деление умножение
Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2
Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.

Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг . Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг . Ставим точку под делителем.
5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Копилка»
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение перезагрузка»
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Деление многозначных или многоразрядных чисел удобно производить письменно в столбик . Давайте разберем, как это делать. Начнем с деления многоразрядного числа на одноразрядное, и постепенно увеличим разрядность делимого.
Итак, поделим 354 на 2 . Для начала разместим эти числа как показано на рисунке:
Делимое размещаем слева, делитель справа, а частное будем записывать под делителем.
Теперь начинаем делить делимое на делитель поразрядно слева на право. Находим первое неполное делимое , для этого берем первый слева разряд, в нашем случае 3 и сравниваем с делителем.
3 больше 2 , значит 3 и есть неполное делимое. Ставим точку в частном и определяем, сколько ещё разрядов будет в частном – столько же, сколько осталось в делимом после выделения неполного делимого. В нашем случае в частном столько же разрядов, сколько в делимом, то есть старшим разрядом будут сотни:
Для того чтобы 3 разделить на 2 вспоминаем таблицу умножения на 2 и находим число при умножении которого на 2 получим наибольшее произведение, которое меньше 3.
2 × 1 = 2 (2
2 × 2 = 4 (4 > 3)
2 меньше 3 , а 4 больше, значит, берем первый пример и множитель 1 .
Записываем 1 в частное на место первой точки (в разряд сотен), а найденное произведение записываем под делимым:
Теперь находим разность, между первым неполным делимым и произведением найденного разряда частного и делителем:
Полученное значение сравниваем с делителем. 15 больше 2 , значит, мы нашли второе неполное делимое. Для того чтобы найти результат деления 15 на 2 вновь вспоминаем таблицу умножения на 2 и находим наибольшее произведение, которое меньше 15 :
2 × 7 = 14 (14
2 × 8 = 16 (16 > 15)
Искомый множитель 7 , записываем его в частное на место второй точки (в десятки). Находим разность между вторым неполным делимым и произведением найденного разряда частного и делителя:
Продолжаем деление, для чего находим третье неполное делимое . Спускаем следующий разряд делимого:
Делим неполное делимое на 2, полученное значение ставим в разряд единиц частного. Проверим правильность деления:
2 × 7 = 14
Результат деления третьего неполного делимого на делитель пишем в частное, находим разность:
Разность мы получили равную нулю, значит деление произведено правильно .
Усложним задачу и приведем другой пример:
1020 ÷ 5
Запишем наш пример в столбик и определим первое неполное частное:
Разряд тысяч делимого составляет 1 , сравниваем с делителем:
1
Добавляем в неполное делимое разряд сотен и сравниваем:
10 > 5 – мы нашли неполное делимое.
Делим 10 на 5 , получаем 2 , записываем результат в частное. Разность между неполным делимым и результатом умножения делителя и найденного разряда частного.
10 – 10 = 0
0 мы не пишем, опускаем следующий разряд делимого – разряд десятков:
Сравниваем второе неполное делимое с делителем.
2
Нам следует добавить в неполное делимое ещё один разряд, для этого в частное, на разряд десятков ставим 0 :
20 ÷ 5 = 4
Записываем ответ в разряд единиц частного и проверяем: записываем произведение под второе неполное делимое и вычисляем разность. Получаем 0 , значит пример решён правильно .
И ещё 2 правила деления в столбик:
1. Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить, например:
Сколько нулей в младшем разряде делимого мы убираем, столько же нулей убираем в младших разрядах делителя.
2. Если в делимом после деления остались нули, то их следует перенести в частное:
Итак, сформулируем последовательность действий при делении в столбик.
Размещаем делимое слева, делитель справа. Помним, что делимое мы делим, поразрядно выделяя неполные делимые и деля их последовательно на делитель. Разряды в неполное делимое выделяются слева направо от старших к младшим.
Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить.
Определяем первый неполный делитель:
а) выделяем в неполный делитель старший разряд делимого;
б) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (в) , если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4 ;
в) добавляем в неполное делимое следующий разряд и переходим к пункту (б) .
Определяем сколько разрядов будет в частном, и ставим столько точек на месте частного (под делителем) сколько будет в нем разрядов. Одна точка (один разряд) за все первое неполное делимое и остальных точек (разрядов) столько же, сколько осталось разрядов в делимом после выделения неполного делимого.
Делим неполное делимое на делитель, для этого находим число, при умножении которого на делитель получилось бы число либо равное неполному делимому, либо меньше его.
Найденное число записываем на место очередного разряда частного (точки), а результат умножения его на делитель записываем под неполным делимым и находим их разность.
Если найденная разность меньше или равна неполному делимому значит, мы правильно поделили неполное делимое на делитель.
Если в делимом остались еще разряды, то продолжаем деление, иначе переходим к пункту 10 .
Опускаем к разности следующий разряд делимого и получаем очередное неполное делимое:
а) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (б), если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4;
б) добавляем к неполному делимому следующий разряд делимого, при этом в частное на место следующего разряда (точки) пишем 0;
в) переходим к пункту (а).
10. Если мы выполняли деление без остатка и последняя найденная разность равна 0 , то мы правильно выполнили деление .
Мы говорили о делении многоразрядного числа на одноразрядное. В случае, когда разрядность делителя больше, деление выполняется аналогично:

Как вычитать столбиком
Вычитание многозначных чисел обычно выполняют столбиком, записывая числа друг под другом (уменьшаемое сверху, вычитаемое снизу) так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т. д.). Слева между числами ставится знак действия. Под вычитаемым проводят черту. Вычисление начинают с разряда единиц: из единиц вычитают единицы, затем из десятков — десятки и т. д. Результат вычитания записывают под чертой:
Рассмотрим пример, когда в каком-либо разряде цифра уменьшаемого меньше цифры вычитаемого:
От 2 мы не можем отнять 9, что нам делать в этом случае? В разряде единиц у нас нехватка, но в разряде десятков у уменьшаемого аж 7 десятков, поэтому мы можем один из этих десятков перекинуть в разряд единиц:
В разряде единиц у нас было 2, мы перекинули десяток, стало 12 единиц. Теперь мы легко можем от 12 отнять 9. Записываем под чертой в разряде единиц 3. В разряде десятков у нас было 7 единиц, одну из них мы перекинули в простые единицы, осталось 6 десятков. Записываем под чертой в разряде десятков 6. В результате мы получили число 63:
Вычитание столбиком обычно не записывают так подробно, вместо этого, над цифрой разряда, у которого будет занята единица, ставят точку, чтобы не запоминать, у какого разряда надо будет дополнительно вычесть единицу:
При этом говорят так: из 2 вычесть 9 нельзя, занимаем единицу, из 12 вычитаем 9 — получим 3, пишем 3, в разряде десятков у нас было 7 единиц, мы одну перекинули, осталось 6, пишем 6 .
Теперь рассмотрим вычитание столбиком из чисел, содержащих нули:
Начинаем вычитать. От 7 отнимаем 3, пишем 4. От нуля мы не можем отнять 5, поэтому мы вынуждены занять единицу в старшем разряде, но в старшем разряде у нас тоже 0, поэтому и для этого разряда мы вынуждены занять в более старшем разряде. Занимаем единицу из разряда тысяч, получаем 10 сотен:
Одну из единиц разряда сотен мы занимаем в младший разряд, получаем 10 десятков. Из 10 вычитаем 5, пишем 5:
В разряде сотен у нас осталось 9 единиц поэтому, от 9 отнимаем 6, пишем 3. В разряде тысяч у нас была единица, но мы её потратили на младшие разряды, поэтому здесь остаётся нуль (его записывать не надо). В результате мы получили число 354:
Такая подробная запись решения была приведена, чтобы было проще понять, как выполняется вычитание столбиком из чисел содержащих нули. Как уже упоминалось, на практике решение обычно записывается так:
А все упомянутые действия выполняются в уме. Чтобы было легче выполнять вычитание, запомните простое правило:
Если при вычитании столбиком над нулём стоит точка, нуль превращается в 9.
Калькулятор вычитания столбиком
Данный калькулятор поможет вам выполнить вычитание чисел столбиком. Просто введите уменьшаемое и вычитаемое и нажмите кнопку Вычислить.
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340: 23 = 58 (остаток 6)
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3: 10 = 0 (остаток 3)
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
Математика. Деление уголком | Сайт Леонида Некина
Главная > Образование > Математика > МАТЕМАТИКА «С НУЛЯ» (учебник) >
<< Назад  |   Оглавление  |   Далее >>
Деление «уголком» — это, на мой взгляд, самая тяжелая, самая нудная тема во всей школьной математике. Тут нам придется всерьез поднапрячься. Пусть, однако, нас вдохновляет мысль, что весь последующий материал будет значительно легче и приятнее.
Прежде всего, рассмотрим деление на однозначное число. Допустим, мы хотим вычислить значение выражения
648 / 2.
Пользуясь свойствами умножения, мы можем расписать делимое таким образом:
648 =
6 ∙ 100 + 4 ∙ 10 + 8 =
3 ∙ 2 ∙ 100 + 2 ∙ 2 ∙ 10 + 4 ∙ 2 =
( 3 ∙ 100 + 2 ∙ 10 + 4 ) ∙ 2 =
324 ∙ 2 .
После этого становится очевидно, что частное от деления равно
648 / 2 = 324.
Но это мы взяли самый что ни на есть простейший случай, когда каждую отдельно взятую цифру делимого можно поделить на делитель. А вот пример несколько посложнее:
156 / 2 = ?
Здесь первая цифра оказалась меньше делителя. Поэтому, расписывая делимое, мы не будем отрывать ее от второй цифры:
156 =
15 ∙ 10 + 6 .
Поскольку число 15 не делится нацело на 2, придется нам прибегнуть к делению с остатком. Представим результат такого деления в виде:
15 = 7 ∙ 2 +  1 = 14 + 1 .
Теперь мы можем продолжать расписывать наше делимое дальше:
156 =
15 ∙ 10 + 6 =
( 14 + 1 ) ∙ 10 + 6 =
14 ∙ 10 + 1 ∙ 10 + 6 =
14 ∙ 10 + 16 =
7 ∙ 2 ∙ 10 + 8 ∙ 2 =
( 7 ∙ 10 + 8 ) ∙ 2 =
78 ∙ 2 .
Отсюда моментально получаем ответ:
156 / 2 = 78.
Такого рода расчеты можно проводить в уме и сразу же писать ответ. Но мы сейчас перепишем их в виде краткой таблицы. Умение составлять такие таблицы нам пригодится, когда мы займемся делением на многозначные числа, когда всё окажется не так просто. Делимое и делитель запишем так:

1
5
6
2






При делении первых двух разрядов ( 15 ) на двойку получается  7 плюс еще какой-то остаток. С этим остатком мы разберемся чуть позже, а пока запишем семерку под чертой снизу от делителя (здесь у нас со временем будет выписан полный ответ):

1
5
6
2




7

Умножаем на эту  семерку наш делитель ( 2 ) и записываем ответ ( 14 ) под первыми двумя разрядами делимого ( 15 ):

1
5
6
2

1
4

7

Теперь настало время вычислить остаток от деления 15-ти на 2 . Он равен, очевидно,
15 −  2 ∙ 7 = 15 − 14 .
У нас уже всё подготовлено, чтобы выполнить это вычитание «столбиком»:

1
5
6
2

1
4

7


1

У нас получается единица , к которой мы приписываем шестерку из следующего разряда делимого:

1
5
6
2

1
4

7


1
6

В результате такого приписывания у нас получается число 16 . Мы делим его на наш делитеть ( 2 ) и получаем 8 . Эту восьмерку пишем в строке ответа, под чертой снизу от делителя:

1
5
6
2

1
4

7
8

1
6

Ответ мы получили, однако правила составления таблицы таковы, что нам надо добавить в нее еще две строки. Мы должны формальным образом убедиться, что не потеряли остаток от деления. Умножаем делитель ( 2 ) на последнюю цифру ответа ( 8 ), приписываем результат ( 16 ) снизу к нашей таблице в последние два разряда делимого:

1
5
6
2

1
4

7
8

1
6

1
6

Вычитаем последнюю строку из предпоследней и получаем 0:

1
5
6
2

1
4

7
8

1
6

1
6

0

Этот последний нуль есть не что иное, как остаток от деления, который образовался бы в том случае, если бы мы рассматривали деление с остатком:
156 : 2 = 78 (ост. 0).
Чтобы получше это понять, возьмем похожий пример, в котором, однако, остаток не равен нулю:
157 : 2 = 78 (ост. 1).
Таблица для этого примера выглядит так:

1
5
7
2

1
4

7
8

1
7

1
6

1

Здесь, опять-таки, остаток стоит в последней строке. Для полноты картины распишем наше делимое в таком виде:
157 =
14 ∙ 10 + 17 =
7 ∙  2 ∙ 10 +  8 ∙  2 + 1 =
( 7 ∙ 10 + 8 ) ∙  2 + 1 =
7 8 ∙  2 + 1
Теперь мы готовы к тому, чтобы делить (нацело или с остатком) на многозначные числа. Это делается при помощи подобной же таблицы (именно из-за ее особого вида данная процедура получила название деление «уголком»). Допустим, требуется выполнить деление с остатком:
135674 : 259 = ?
Приступаем к заполнению таблицы:


1
3
5
6
7
4
2
5
9

В данном случае, чтобы найти первую цифру частного, надо взять первые четыре цифры делимого ( 1356 ) и получившееся число поделить (с остатком) на делитель ( 259 ). Почему надо взять именно первые четыре цифры делимого? Потому что если бы мы взяли хотя бы на одну цифру меньше, то получившееся число ( 135 ) оказалось бы меньше делителя ( 259 ), а это совсем не то, из чего можно было бы извечь полезную информацию. Итак, возьмем первые четыре цифры делимого и рассмотрим следующее деление с остатком:
1356 : 259 = ?
Тут нам помогут приближенные вычисления, для которых, как мы знаем, вовсе необязательно, чтобы числа делились друг на друга нацело:
1356 / 259 ≈ 1356 / 300 ≈ 1500 / 300 = 15 / 3 =  5 .
Зная результат приближенного деления, мы можем предположить, что, скорее всего,
1356 : 259 = 5 (остаток — пока неважно какой).
Конечно, абсолютной уверенности у нас нет. Здесь вместо  пятерки вполне может стоять  четверка или  шестерка , однако вряд ли мы ошиблись больше, чем на одну единицу. Имея это в виду, тем не менее берем эту  пятерку и заносим ее в нашу таблицу в строку ответа. После этого умножаем на нее делитель ( 259 ) и при этом записываем ответ под делимым в подходящие разряды:

1
3
5
6
7
4
2
5
9

   1
   2
   4

259 ∙ 5 =
1
2
9
5

5

Здесь «маленькие» цифры — это побочный продукт процедуры умножения: мы познакомились с ними, когда учились умножать «в столбик». После того как умножение выполнено, они становятся больше не нужны: на них можно просто не обращать внимания. Выражение 259 ∙ 5 , написанное слева от таблицы, помещено сюда только ради пояснения того, что мы делаем. К таблице оно, собственно, не принадлежит, и в будущем мы такие пояснения выписывать не будем. Тут важно отметить, что результат нашего умножения ( 1295 ) оказался меньше записанного над ним числа 1356 , составленного из первых четырех цифр делимого. Если бы это было не так, то это означало бы, что приближенное деление дало нам завышенный результат. Нам надо было бы тогда зачеркнуть  пятерку в строке ответа, на ее место поставить четверку — после чего зачеркнуть и переделать все наши последующие вычисления. Но нам на этот раз повезло, и ничего переделывать не требуется.
Теперь выполняем вычитание в столбик и получаем:

1
3
5
6
7
4
2
5
9

   1
   2
   4

259 ∙ 5 =
1
2
9
5

5

6
1

Внимательно приглядимся к полученной разности ( 61 ). Очень важно, что она оказалась меньше делителя ( 259 ). В противном случае мы пришли бы к выводу, что приближенное деление дало нам заниженный результат и нам пришлось бы теперь исправлять в строке ответа пятерку на  шестерку , а также переделывать все последующие вычисления. К счастью, этого не случилось. Приближенное вычисление нас не подвело, и мы теперь совершенно точно знаем, что,
1356 : 259 = 5 (ост. 61 ).
Возвращаемся к таблице. К нашему остатку ( 61 ) приписываем  семерку из следующего разряда делимого и приступаем к нахождению второй цифры ответа. Это делается с помощью точно такой же процедуры, что и раньше. Потом — очередь за третьей цифрой. В конце концов таблица принимает такой вид:

1
3
5
6
7
4
2
5
9

   1
   2
   4

259 ∙ 5 =
1
2
9
5

5
2
3

6
1
7

   1
   1

259 ∙ 2 =

5
1
8

9
9
4

   1
2

259 ∙ 3 =

7
7
7

2
1
7

Можно выписывать окончательный ответ:
135674 : 259 = 523 (ост. 217).
Самая большая неприятность в делении «уголком» состоит в том, что приближенные вычисления, к которым приходится прибегать по ходу дела, не дают сразу гарантированно правильного результата и нуждаются иногда в последующей коррекции. Впрочем, по мере тренировки, у нас выработается особое чутье и мы будем уже сразу почти наверняка знать, какие цифры следует писать в строке ответа, чтобы потом ничего больше не надо было исправлять и переделывать.
Разумеется, нам будут попадаться случаи, когда частное содержит нули. Каждый такой нуль позволит сделать в таблице небольшие сокращения. Вот пример такой таблицы:

2
6
2
7
4
0
8
7

   2
   2


2
6
1

3
0
2
0

1
7
4

   1
   1

1
7
4

0

Как и в случае умножения «в столбик», для того чтобы было удобнее писать «маленькие» цифры, нам может понадобиться
лист со специальной линовкой для вычислений (формат pdf). 2=(a-b)(a+b)\).

$(x-1)(x-2)(x-\sqrt{2})(x+\sqrt{2})≥0$

Вот сейчас все готово для применения метода интервалов.

Запишем ответ.

Ответ: $(-∞;-\sqrt{2}]∪[1;\sqrt{2}]∪[2;∞)$.
Скачать статью
Онлайн-калькулятор для деления в столбик десятичных дробей
Делить десятичные дроби в столбик немного сложнее, чем целые числа из-за плавающей точки, еще задачу усложняет надобность деления остатка. Поэтому если вы хотите упростить этот процесс или проверить свой результат, можно воспользоваться онлайн-калькулятором, который не только выведет ответ, но и покажет всю процедуру решения.
Читайте также: Конвертеры величин онлайн
Делим в столбик десятичные дроби с помощью онлайн-калькулятора
Подходящих под эту цель онлайн-сервисов существует большое количество, однако практически все они мало чем отличаются друг от друга. Сегодня мы подготовили для вас два разных варианта вычисления, а вы, ознакомившись с инструкциями, выберите тот, который будет наиболее подходящим.
Способ 1: OnlineMSchool
Сайт OnlineMSchool был разработан для изучения математики. Сейчас на нем присутствует не только множество полезной информации, уроков и задач, но и встроенные калькуляторы, один из которых мы сегодня задействуем. Деление в столбик десятичных дробей в нем происходит так:
Перейти на сайт OnlineMSchool
Откройте главную страницу сайта OnlineMSchool и перейдите в раздел «Калькуляторы».
Внизу вы найдете сервисы для теории чисел. Выберите там «Деление в столбик» или «Деление в столбик с остатком».
В первую очередь обратите внимание на инструкцию по использованию, представленную в соответствующей вкладке. Рекомендуем с ней ознакомиться.
Теперь вернитесь в «Калькулятор». Здесь вам следует еще раз убедиться, что выбрана правильная операция. Если нет, измените ее, воспользовавшись всплывающим меню.
Введите два числа, используя точку для обозначения целой части дроби, а также отметьте галочкой пункт, если необходимо делить остаток.
Для получения решения щелкните левой кнопкой мыши на знаке равно.
Вам будет предоставлен ответ, где подробно расписан каждый шаг получения конечного числа. Ознакомьтесь с ним и можете переходить к следующим вычислениям.
Перед тем как делить остаток, внимательно изучите условие задачи. Часто этого делать не нужно, иначе ответ могут засчитать неправильным.
Всего за семь простых шагов мы смогли поделить десятичные дроби в столбик с помощью небольшого инструмента на сайте OnlineMSchool.
Способ 2: Rytex
Онлайн-сервис Rytex также помогает в изучении математики, предоставляя примеры и теорию. Однако сегодня нас интересует присутствующий в нем калькулятор, переход к работе с которым осуществляется следующим образом:
Перейти на сайт Rytex
Воспользуйтесь ссылкой выше, чтобы перейти на главную страницу Rytex. На ней кликните по надписи «Онлайн калькуляторы».
Опуститесь в самый низ вкладки и на панели слева отыщите «Деление столбиком».
Перед началом выполнения основного процесса прочтите правила использования инструмента.
Теперь в соответствующие поля введите первое и второе число, а затем укажите, нужно ли делить остаток, отметив галочкой необходимый пункт.
Для получения решения нажмите на кнопку «Вывести результат».
Теперь вы можете узнать, как было получено итоговое число. Поднимитесь выше по вкладке, чтобы перейти к вводу новых значений для дальнейшей работы с примерами.
Как видите, рассмотренные нами сервисы практически не отличаются между собой, разве что только внешним видом. Поэтому можно сделать вывод – нет разницы, какой веб-ресурс использовать, все калькуляторы считают правильно и предоставляют развернутый ответ по вашему примеру.
Читайте также:
Сложение систем счисления онлайн
Перевод из восьмеричной в десятичную онлайн
Перевод из десятичной в шестнадцатеричную систему онлайн
Мы рады, что смогли помочь Вам в решении проблемы.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТ
Общий метод — Дивизион — Национальная версия 4 по математике
Разделите \ (8932 \) на \ (7 \) — \ ((8932 \ div 7) \).
Начните с деления \ (8 \) в столбце тысяч на \ (7 \). Это будет \ (1 \) остаток времени \ (1 \). Поместите \ (1 \) в ответ в столбце тысяч, а остаток рядом с \ (9 \) в столбце сотен (теперь \ (19 \)).
Разделите \ (7 \) на ‘\ (19 \)’ в столбце сотен. Он идет \ (2 \) раз остаток \ (5 \). Поместите \ (2 \) в ответ в столбце сотен и остаток рядом с \ (3 \) в столбце десятков (теперь \ (53 \)).
$2″> Разделите \ (7 \) на ‘\ (53 \)’ в столбце десятков. Он идет \ (7 \) раз остаток \ (4 \). Поместите \ (7 \) в ответ в столбце десятков и остаток рядом с \ (2 \) в столбце единиц (теперь \ (42 \)).
Разделите \ (7 \) на ‘\ (42 \)’ в столбце единиц. Он повторяется \ (6 \) раз без остатка. Поставьте \ (6 \) в ответ в столбце единиц.
Следовательно, \ (8932 \ div 7 = 1276 \)
Теперь попробуйте ответить на вопрос, приведенный ниже.
Вопрос
Разделите \ (346 \) на \ (8 \) — \ ((346 \ div 8) \)
Показать ответ
28hrcendayk.0.0.0.1:0.1.0.$0.$2.$1.3″>
Используйте ту же процедуру, что и выше, пока не дойдете до \ (6 \) в столбце единиц.
Получаем, что \ (8 \) в \ (26 \) идет \ (3 \) раз остаток \ (2 \). Поскольку после \ (6 \) нет цифр, вы должны теперь вставить \ (0 \) как цифру после десятичной точки. Теперь в ваш ответ также должна быть включена десятичная точка. Остаток \ (2 \) теперь помещается рядом с \ (0 \) после десятичной точки (теперь \ (20 \)).
Разделите \ (8 \) на ‘\ (20 \)’ в столбце десятых. Он идет \ (2 \) раз остаток \ (4 \).
\ (2 \) стоит в десятом столбце ответа. Введите \ (0 \) в сотый столбец и поместите остаток \ (4 \) рядом с этим (теперь \ (40 \)).
28hrcendayk.0.0.0.1:0.1.0.$0.$2.$1.3.$2.$4″> Мы получаем \ (8 \) в ‘\ (40 \)’ проходит \ (5 \) раз без остатка. \ (5 \) стоит в ответе в сотом столбце.
Следовательно \ (346 \ div 8 = 43 \ cdot 25 \)
Как обрабатывать деление на ноль в SQL
База данных:
Операторы:
NULLIF, WHERE
Проблема:
Вы хотите выполнить деление в своем SQL-запросе, но знаменатель — это выражение, которое может быть нулевым. База данных выдаст вам ошибку, когда знаменатель фактически равен нулю.
Пример:
В нашей базе данных есть таблица с именем investor_data с данными в следующих столбцах: id , investor_year , price_per_share , доход и расходы .
id investor_year price_per_share доход расходы
1 2016 20 3200 2300
2 2017 130 2000 2000
3 2018 40 200 100
4 2019 15 5900 4900
Давайте разделим цену за акцию на разницу между доходами и расходами, чтобы определить коэффициент P / E (соотношение цены и прибыли) для каждого года. Обратите внимание, что бывают случаи, когда доход равен расходам, поэтому их разница будет равна нулю. Таким образом, нам нужно найти способ избежать деления на ноль.
Решение:
ВЫБЕРИТЕ инвестор_год, price_per_share / NULLIF (доходы-расходы, 0) AS P_E_ratio ИЗ данных инвестора;
Этот запрос возвращает коэффициент P / E для каждого года, как описано в формулировке задачи:
инвестор_год P_E_ratio
2016 0.0222
2017 НЕТ
2018 0,4000
2019 0,0150
Если разница между доходами и расходами равна нулю (как в случае с 2017 годом), функция NULLIF изменяет ноль на значение NULL. Следовательно, деление на ноль дает результат NULL.
Обсуждение:
Если вы хотите изящно обрабатывать деление на ноль, вы можете использовать функцию NULLIF . NULLIF принимает два аргумента: интересующее выражение и значение, которое вы хотите переопределить. Если первый аргумент равен второму, то NULLIF возвращает NULL; в противном случае возвращается первый аргумент.
Эту функцию можно использовать для обработки потенциального деления на ноль, заключив знаменатель в обращение к NULLIF . В нашем примере, если разница между доходами и расходами равна нулю, это значение будет изменено на NULL, а знаменатель в делении будет NULL, а не ноль.
Решение 2. Используйте
ГДЕ
Конечно, в некоторых ситуациях вы можете использовать более простое решение: просто избегайте деления на ноль, используя WHERE с оператором сравнения. В нашем примере мы могли бы проверить, отличается ли доход-расходы от 0. Если это так, расчет будет возвращен.
ВЫБЕРИТЕ инвестор_год, price_per_share / (доходы-расходы) AS P_E_ratio ИЗ данных инвестора ГДЕ (доходы-расходы) 0;
Обратите внимание, что с решением WHERE вы получите меньше строк, чем в таблице investor_date . Строки, в которых доходы и расходы равны, в конечном результате отображаться не будут.
Знакомство с колоннами с перегородкой | AIChE
Перегородка может быть добавлена в дистилляционную колонну для повышения эффективности разделения трех или более продуктов.
▲ Рис. 1. Стандартная колонна с перегородкой (DWC) имеет стенку, разделяющую колонну на две части. Потоки пара и жидкости показаны синими стрелками и красными стрелками соответственно.
Колонны с перегородкой (DWC) — это тип дистилляционной колонны, которая может разделять смеси нескольких компонентов на три или более высокочистых потока (рис. 1). DWC требует гораздо меньше энергии, капиталовложений и производственного пространства, чем обычные колонны в последовательной или параллельной конфигурации. Фактически, требования к капитальным затратам для DWC могут быть на 20–30% ниже, чем у традиционных градирен (1–5) .
Обычные дистилляционные колонны являются неотъемлемой частью нефтеперерабатывающей и химической промышленности. Модернизация существующих колонн с помощью перегородки для повышения эффективности разделения является частью более масштабного стремления к интенсификации процессов в этих отраслях. Интенсификация процесса (PI) направлена на резкое повышение стоимости и энергоэффективности за счет переосмысления традиционных схем работы. DWC — один из примеров усовершенствованной технологии.
Концепция DWC хорошо известна, и большое количество литературы посвящено моделированию и контролю этих столбцов (1, 6, 7) . В нескольких публикациях обсуждались промышленные применения DWC в различных массовых и модернизированных приложениях (8, 9) .
Технология достаточно универсальна, и нет двух абсолютно одинаковых приложений DWC. Таким образом, сложно разработать стандартный протокол для проектирования этих столбцов. DWC используются в различных сферах, например, в газовых установках, в установках для разделения нафты и разделителях риформинга.
В этой статье описаны три основных типа DWC. Пример демонстрирует, как добавление перегородки может улучшить чистоту бокового потока без необходимости добавления второй колонны.
Как удалить # DIV / 0 в Excel • Портфолио производительности
Когда-нибудь в некоторых ваших электронных таблицах Microsoft Excel отображалась ошибка # DIV / 0 в различных ячейках? Ошибка Excel возникает, когда формула электронной таблицы пытается разделить на 0 или пустую ячейку. В этом руководстве я объясню, как можно предотвратить появление этих ошибок, добавив простой аргумент функции ЕСЛИ.
Что значит # DIV / 0! Имеете ввиду в Excel?
Это логическая ошибка, которая возникает, когда возникает одно из этих условий:
число делится на ноль (0)
ваша формула Excel относится к пустой или пустой ячейке
Предположим, вы должны были щелкнуть одну из # DIV / 0! ячеек вы увидите всплывающую подсказку Excel, которая гласит: « Используемая формула или функция — деление на ноль или пустые ячейки. ”Вы можете увидеть пример на скриншоте ниже, используя Microsoft Office 365.
Пример # DIV / 0! ошибка и всплывающая подсказка
Я получил ошибку Excel в ячейке E7 , потому что я попытался разделить свое значение Cost в C7 на мое Счетчик каталогов в D7 .
Я запустил объявление стоимостью 77,45 доллара и произвел 0 запросов в каталог. Другими словами, я просил Microsoft Excel разделить 77,45 доллара на ноль. Ой.
Вторая причина, по которой Excel отображает эту ошибку для ячейки E11 , заключалась в том, что ячейка D11 пуста.Трудно увидеть, потому что всплывающая подсказка перекрывает значение ячейки.
Хотя может показаться, что эта ошибка отображается только при делении, ее можно унаследовать от диапазона. В приведенном ниже примере я попытался ввести СУММ столбец E. Я также получаю сообщение об ошибке, потому что было # DIV / 0! в диапазоне ячеек.
# DIV / 0! в ячейках отображаются ошибки.
Добавьте простую логику в формулу Excel
Вероятно, вы задаетесь вопросом, как удалить ошибку # div / 0. В конце концов, пустые ячейки и нули — допустимые записи.Есть несколько способов исправить эту ошибку, включая функцию ЕСЛИОШИБКА. Однако я предпочитаю использовать функцию ЕСЛИ. ЕСЛИОШИБКА может замаскировать все ошибки, помимо этого раздражения.
Это логическая функция, в которой вы можете указать Excel выполнить одно действие IF , условие ИСТИНА и другое действие, если условие ЛОЖНО .
В этом случае я хочу, чтобы Excel выполнил другое действие, ЕСЛИ у меня счетчик каталога «0». В противном случае Excel может продолжить работу в обычном режиме.В частности, я хочу заменить сообщение об ошибке на 0,00 долларов США.
Как показать ноль вместо # DIV / 0!
Создайте столбец для формулы. (например, стоимость конв. в столбце E)
Щелкните следующую ячейку в этом столбце. (например, E2)
Щелкните вкладку Формулы на ленте Excel.
Нажмите кнопку Вставить функцию в крайнем левом углу.
В диалоговом окне Вставить функцию выберите IF .
Нажмите ОК .
В диалоговом окне «Аргументы функции » щелкните поле Logical_test .
Щелкните верхнюю ячейку столбца, на который вы делите. (например, D2)
В том же текстовом поле после типа ссылки на ячейку = 0 . (В поле должно отображаться что-то вроде D2 = 0)
Оставьте поле Value_if_true пустым, чтобы получить 0,00 долларов США.
В поле Value_if_false введите формулу, например C2 / D2.
Логический тест для ячейки = 0
Щелкните OK .
Скопируйте формулу Excel в каждую ячейку столбца.
Вы можете увидеть это в примере ниже. В каждом случае, когда у меня был «0» или пустая ячейка в столбце D (количество каталогов), Excel оставил значение Conv Cost в столбце E равным 0,00 долларов США. Эта функция также зафиксировала значение моей суммы в ячейке E14.
Обратите внимание, как # div / 0! ошибки исчезли
Вскоре вы начнете вводить эту функцию прямо в строке формул Excel, а не использовать диалоговое окно Вставить функцию .
Другие замены формул для # DIV / 0!
Точно так же, как некоторым людям не нравятся сообщения об ошибках деления на ноль, другие могут возражать против значений пустых ячеек или ссылки 0,00 доллара США. Они могут предпочесть что-то вроде текстового значения или даже содержимого другой ячейки.
Вы можете подставить текст или ссылку на ячейку вместо того, чтобы значение ячейки было 0,00 долларов США. Например, я мог бы использовать «NA». Обратите внимание на кавычки, иначе вы можете получить ошибки в формулах.
= ЕСЛИ (D2 = 0, "NA", C2 / D2)
или оставлено пустым
= ЕСЛИ (D2 = 0, "", C2 / D2)
или использовалось другое значение ячейки
= ЕСЛИ (D2 = 0, C2, C2 / D2)
В этом последнем примере Excel вместо этого вставит значение Cost в ячейку Conv Cost.В зависимости от вашей ситуации это может быть более точным. В моем примере стоимости преобразования каталога лучше использовать значение «Стоимость», чем «0» или пустое поле.
Другое решение от читателей упомянуло, что метод ERROR.TYPE работает хорошо. Корпорация Майкрософт присвоила этому примеру # DIV / 0 значение ошибки «2». Более подробную информацию об ERROR.TYPE можно найти на сайте Microsoft.
Как видите, есть несколько способов исправить ошибку деления на ноль в Excel. Скорее всего, какой бы метод вы ни выбрали, он будет меньше раздражать ваших пользователей, чем просмотр # DIV / 0!
Вам также могут понравиться эти учебные пособия по Excel
Заявление об отказе от ответственности: изображения из API рекламы продуктов Amazon. Я могу получить партнерскую комиссию за эти продукты, если вы их купите. Обновлено: 2021-05-05
3 способа умножения в Excel
Хотя «формулы умножения Excel» не существует, существует несколько способов умножения в Excel. Например, вы используете звездочку (*) для умножения, но ударяетесь о кирпичную стену, когда применяете другие арифметические операторы? А как насчет быстрых клавиш для умножения множества чисел за один шаг?
Прочтите, чтобы узнать о трех эффективных способах вычисления формулы умножения в Excel.
1.). В этих случаях помните, что Excel выполняет операции в порядке PEMDAS: сначала скобки, затем показатели, умножение, деление, сложение и вычитание.
В следующей формуле «= 2 * 3 + 5 * 6» Excel сначала выполняет две операции умножения, получая 6 + 30, и складывает произведения, чтобы получить 36.
Что делать, если вы хотите сложить 3 + 5 перед умножением? Используйте круглые скобки. Excel всегда будет оценивать все, что указано в скобках, прежде чем возобновить оставшиеся вычисления после PEMDAS. В случае «= 3 * (3 + 5) * 6» Excel сначала складывает 3 и 5, в результате получается 8. Затем он умножает 3 * 8 * 6 и достигает 144.
Если у вас возникли проблемы с запоминанием порядка PEMDAS, используйте мнемонический прием тети Салли: используйте первые буквы предложения: «Пожалуйста, извините мою дорогую тетю Салли».
2. Умножение с функцией ПРОДУКТ
Если вам нужно умножить несколько чисел, вы можете оценить сокращенную формулу ПРОДУКТ, которая умножает все числа, указанные в скобках.
Аргументы могут быть:
Числа или формулы, разделенные запятыми, например:
= ПРОДУКТ (3,5 + 2,8,3,14)
Это эквивалентно = 3 * (5 + 2) * 8 * 3,14.
Ссылки на ячейки, разделенные запятыми, например:
= ПРОДУКТ (A3, C3, D3, F3).
Это эквивалентно = A3 * C3 * D3 * F3.
Диапазон ячеек, содержащий числа или несколько диапазонов, разделенных запятыми, например:
= ПРОДУКТ (F3: F25),
, что эквивалентно = F3 * F4 * F5 * (и так далее, вплоть до) * F25, или:
= ПРОДУКТ (F3: F25, h5: h45).
Любая комбинация чисел, формул, ссылок на ячейки и ссылок на диапазоны.
В каждом случае Excel умножает все числа, чтобы найти произведение. Если ячейка в диапазоне пуста или содержит текст, Excel не учитывает значение этой ячейки в вычислениях. Если ячейка в диапазоне равна нулю, продукт будет равен нулю.
3. Умножение диапазонов с помощью функции СУММПРОИЗВ
Рассмотрим следующий счет. Формула в столбце E (с формулой, показанной справа от таблицы) умножает количество на цену, чтобы получить расширенную цену.Сумма в ячейке E7 суммирует расширенные цены.
Но что, если вы не хотите, чтобы расширенные цены отображались как отдельные расчеты? Что, если вы хотите сделать все за один шаг?
Попробуйте функцию СУММПРОИЗВ, которая умножает ячейки в двух диапазонах и суммирует результаты.
СУММПРОИЗВ (D2: D5, C2: C5) умножает D2 * C2, D3 * C3 и т. Д. И суммирует результаты. Обратите внимание, что результат 84,50 такой же, как в предыдущем примере.
Эта функция неоценима для расчета средневзвешенных значений, таких как оценки в классе или цены на основе переменного государственного налога, при котором диапазон значений умножается на диапазон, содержащий веса.
Следующие шаги
Это всего лишь три метода умножения чисел в формулах Excel. Когда вы освоите их, попробуйте формулу PRODUCTIF, которая умножает все числа в диапазоне, если выполняется условие.
А пока попробуйте смешать и сопоставить формулы умножения, используя любую комбинацию вместе с другими арифметическими функциями, чтобы создать сложные математические модели.
Как использовать функцию Excel MOD
Функция MOD выполняет операцию по модулю.Он принимает число и делитель и возвращает остаток после деления. В этой формуле мы вычитаем один результат MOD из другого. Для первого МОДа мы используем число …
.
Время в Excel — это дробное значение, равное 24 часам. Один час времени равен 1/24, а 1 минута времени составляет 1 / (24 * 60) = 1/1440. В результате, если у вас есть десятичное значение для 15 минут и время в A1, вы можете добавить 15 минут …
Время в Excel — это дробное значение числа 1.Итак, 12:00 — это 24.12 = 0,5, 6:00 — это 24.06 = 0,25 и так далее. Итак, чтобы преобразовать время по заданному числу, вам нужно разделить количество часов на 24, чтобы получить необходимое …
Формулы, в которых используется понятие «день недели», основаны на идее, что каждый день недели имеет определенное число. По умолчанию Excel присваивает 1 воскресенью и 7 субботе. В формуле примера B6 — это дата …
Первое, что делает эта формула, — сравнивает дату в столбце B с датой начала: = ЕСЛИ (B4> = начало Если дата не больше даты начала, формула возвращает ноль.Если дата больше или равна …
Ядром этой формулы является функция MOD. MOD принимает число и делитель и возвращает остаток после деления, что делает его полезным для формул, которые должны делать что-то каждый n-й раз. В этом случае …
Эта формула использует функции MOD и COLUMN для фильтрации значений не в n-м столбцах, а затем запускает MAX для результата. Ключ в этом фрагменте: MOD (COLUMN (B5: K5) -COLUMN (B5) + 1, L5) = 0 Здесь в формуле используется КОЛОНКА…
Порядковые номера представляют собой позицию или ранг в последовательном порядке. Обычно они пишутся с использованием номера + буквенного суффикса: 1-й, 2-й, 3-й и т. Д. Чтобы получить порядковый суффикс для небольшого набора чисел, вы можете использовать …
Когда вы используете формулу для применения условного форматирования, формула вычисляется для каждой ячейки в выделенном фрагменте. В этом случае в формуле нет адресов, поэтому для каждой ячейки в данных это СТРОКА и ЕДИНИЦА…
Функция СУММПРОИЗВ работает напрямую с массивами. Одна вещь, которую вы можете довольно легко сделать с помощью SUMPRODUCT, — это выполнить тест на массиве, используя один или несколько критериев, а затем подсчитать результаты. В этом случае мы запускаем …
Функция MOD возвращает остаток после деления. Если делитель равен 1, MOD вернет ноль для любого целого числа. Мы используем этот факт, чтобы построить простую формулу, которая проверяет результат MOD. Когда результат …
По сути, эта формула вычитает время начала из времени окончания, чтобы получить продолжительность в часах. Это делается для расчета рабочего времени и времени перерыва. MOD (C6-B6,1) // получаем время работы MOD (E6-D6,1) // получаем время перерыва Далее …
Сложность подсчета количества часов между двумя моментами времени проистекает из времени, которое пересекает полночь. Это потому, что время, которое пересекает полночь, часто имеет время начала позже, чем время окончания (т.е. начать с …
Excel обрабатывает даты и время, используя систему, в которой даты — это порядковые номера, а время — дробные значения. Например, 1 июня 2000 г. 12:00 представлено в Excel как число 36678,5, где 36678 — это дата …
Время в Excel — это дробное значение, равное 24 часам. Один час времени равен 1/24, а 1 минута времени составляет 1 / (24 * 60) = 1/1440. В результате, если у вас есть десятичное значение для 6 часов и время в A1, вы можете добавить 6 часов…
Pivot | Sisense | Документация
Применимо к Sisense в Linux
Windows и Linux используются разные версии виджета сводной таблицы. Sisense в Windows использует Pivot1, а Sisense в Linux использует Pivot2.В целом Pivot1 и Pivot2 одинаковы, но есть небольшие различия в функциях и поведении. Например, когда Sisense развернут в Linux, вы можете выбрать отображение HTML в ячейках Pivot2 в виде HTML или обычного текста (Pivot1 всегда отображает HTML). Это полезно, например, для отображения гиперссылок.
В разделе «Сводная таблица» установите переключатель «Разрешить отображение содержимого сводной таблицы в формате HTML».Когда переключатель включен, Sisense отображает HTML как HTML. Когда он отключен, Sisense отображает HTML как обычный текст.
На панели «Строки» нажмите «Добавить +», чтобы выбрать поля, значения которых будут помещены в строки сводной таблицы.
Примечание. Когда Sisense развернут в Linux, вы можете отображать HTML в ячейках Pivot 2 как HTML или обычный текст. Чтобы выбрать «Администратор»> «Управление системой», затем в области «Сводная таблица» установите переключатель «Разрешить отображение содержимого сводной таблицы в формате HTML». Когда переключатель включен, Sisense отображает HTML как HTML, а когда он отключен, Sisense отображает HTML как простой текст.
Если выбрано несколько строк, они разбиваются на подстроки (группы). Например, ниже показано условие, добавленное как вторая строка:
Щелкните меню строки на панели данных или щелкните правой кнопкой мыши заголовок строки в виджете и выберите «Общие итоги» или «Промежуточные итоги».
Примечание. Промежуточные итоги доступны только в том случае, если у вас более одной строки в таблице.
Если вы выбрали отображение промежуточных итогов, выберите метод их вычисления. Щелкните меню «Значение» на панели данных, затем щелкните «Подытог по» и выберите метод.
Примечание. В каждом поле можно выбрать разные промежуточные итоги. Для этого щелкните заголовок нужного значения в таблице, щелкните «Подытог по» и выберите метод.
Параметр по умолчанию — Авто, который объединяет все данные, отправляя отдельный запрос в модель данных.Это означает, что Sisense применяет одну и ту же формулу, заданную в мере, ко всем данным. Другие настраиваемые параметры (Sum, Min, Max и т. Д.) Вычисляют только значения в строках над промежуточным итогом на основе данных, представленных в сводной таблице, вместо исходной формулы, установленной в мере.
Если определено, на общие итоги влияют промежуточные итоги.В следующем примере общая сумма средних продаж равна 10, что соответствует средним продажам для двух регионов (Азии и Европы). В приведенном ниже примере для параметра «Средние продажи» для параметра «Промежуточный итог» (см. Выше) установлено значение «Сумма», поэтому общий итог — это сумма строк выше.
Промежуточный итог по среднему принимает значения в строках над ним, поэтому не может быть установлен для отображения взвешенного (многопроходного) среднего. Один из способов добиться этого — изменить формулу таким образом, чтобы при установке для параметра «Промежуточные итоги» значения «Авто» отображалось средневзвешенное значение.
Например, см. Нижеприведенный вариант использования (из Образца информационной панели Healthcare) с использованием взвешенного агрегирования:
Здесь используются два связанных поля: деление. ID и Rooms.Division_ID. Эти два поля используются из таблицы измерений в строке «Строки» и ее эквивалента в таблице фактов в формуле.
В этом примере мы подсчитываем койки в подразделении, суммируем результаты и делим этот результат на сумму комнат в подразделении. Рассматривая конкретное деление, это то же самое, что и подсчет коек / комнат, но в целом это 10/59 (сумма / сумма) — средневзвешенное значение.
Более подробный пример см. Здесь.
Sisense поддерживает экспорт сводных таблиц до 1,5 миллионов ячеек. Попытка экспортировать большее количество ячеек может привести к тайм-ауту. Следующие свойства сводной таблицы увеличивают вероятность достижения тайм-аута при работе с очень большими таблицами:
Промежуточные или общие итоги
Сложные формулы в значениях
Правила безопасности данных
Фильтры на уровне виджетов
Те, кто в школе относился к урокам математики с пренебрежением, наверняка хотя бы несколько раз в жизни бывали в неловкой ситуации. Как посчитать, сколько оставить на чай или сумму коммунального платежа? Если знать пару простых приёмов, это займёт у вас буквально секунду. А уж во время экзамена знание правил умножения больших чисел может помочь сэкономить критически недостающее время. «Мел» совместно с Creu делится простыми секретами вычислений.
Этот приём невероятно прост. Возьмите любое число и поделите пополам. Если в результате получилось целое число, припишите ноль в конце. Если нет, не обращайте внимание на запятую и в конце добавьте пять. Это срабатывает всегда:
Это просто. Чтобы умножить любое число от одного до девяти на девять, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например, 9×3 — загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 — это два), затем посчитайте после загнутого пальца (в нашем случае — семь). Ответ — 27.
Деление на пять
На самом деле делить большие числа на пять очень просто. Нужно просто умножить на два и перенести запятую:
195 / 5
1. 195 * 2 = 390
2. Переносим запятую: 39,0 или просто 39.
2978 / 5
1. 2978 * 2 = 5956
2. 595,6
9. Вычитание из 1000
Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом. Отнимите от девяти все цифры, кроме последней. А последнюю цифру отнимите от десяти:
1000-648
1. От 9 отнимите 6 = 3
2. От 9 отнимите 4 = 5
3. От 10 отнимите 8 = 2
Ответ: 352
10. Систематизированные правила умножения
Умножение на 5: Умножьте на 10 и разделите на 2.
Умножение на 6: Иногда проще умножить на 3, а потом на 2.
Умножение на 9: Умножьте на 10 и отнимите исходное число.
Умножение на 12: Умножьте на 10 и дважды прибавьте исходное число.
Умножение на 13: Умножьте на 3 и 10 раз прибавьте исходное число.
Умножение на 14: Умножьте на 7, а затем на 2.
Умножение на 15: Умножьте на 10 и 5 раз прибавьте исходное число, как в предыдущем примере.
Умножение на 16: Если хотите, 4 раза умножьте на 2. Или умножить на 8, а потом на 2.
Умножение на 17: Умножьте на 7 и 10 раз прибавьте исходное число.
Умножение на 18: Умножьте на 20 и дважды отнимите исходное число.
Умножение на 19: Умножьте на 20 и отнимите исходное число.
Умножение на 24: Умножьте на 8, а потом на 3.
Умножение на 27: Умножьте на 30 и 3 раза отнимите исходное число.
Умножение на 45: Умножьте на 50 и 5 раз отнимите исходное число.
Умножение на 90: Умножьте на 9 и припишите 0.
Умножение на 98: Умножьте на 100 и дважды отнимите исходное число.
Умножение на 99: Умножьте на 100 и отнимите исходное число.
БОНУС: проценты
Вычислить 7% от 300.
Сперва нужно понять значение слова «процент» (percent). Первая часть слова — про (per). Per = для каждого. Вторая часть — цент (cent), это как 100. Например, столетие = 100 лет. 100 центов в одном долларе и так далее. Итак, процент = для каждой сотни.
Итак, получается, что 7% от 100 будет семь. (Семь для каждой сотни, только одной сотни).
8% от 100 = 8.
35,73% от 100 = 35,73
Но как это может быть полезным? Вернёмся к задачке 7% от 300.
7% от первой сотни равно 7. 7% от второй сотни — то же 7, и 7% от третьей сотни — все те же 7. Итак, 7 + 7 + 7 = 21. Если 8% от 100 = 8, то 8% от 50 = 4 (половина от 8).
Дробите каждое число, если нужно вычислить проценты из 100, если же число меньше 100, просто перенесите запятую влево.
Примеры:
8%200 =? 8 + 8 = 16.
8%250 =? 8 + 8 + 4 = 20,
8%25 = 2,0 (Передвигаем запятую влево).
15%300 = 15+15+15 =45
15%350 = 15+15+15+7,5 = 52,5
Также полезно знать, что вы всегда можете поменять числа местами: 3% от 100 — то же самое, что 100% от 3. А 35% от 8 — то же самое, что и 8% от 35.
Источник: Creu
Контрольные и проверочные работы по математике 4 класс
Урок 9. Математический диктант.

Вычислите сумму чисел 45 и 60 и уменьшите её на 4 десятка.

Вычислите разность чисел 330 и 220 и уменьшите её на 50.

Найдите частное чисел 450 и 9.

Известна сумма 750 и первое слагаемое 200. Чему равно второе слагаемое?

Известна разность между числами — 300 и уменьшаемое 770. Чему равно вычитаемое?

Известно частное 6 и делитель 30. Чему равно делимое?

Найдите частное чисел 360 и 6.

Найдите второе слагаемое, если первое слагаемое 20, а сумма 900.

Произведение 720, первый множитель 8. Чему равен второй множитель?

Частное 6, делитель 50. Чему равно делимое?
Урок 10. Самостоятельная работа.1 вариант
2 вариант

Решить задачу:
В 6 одинаковых домах 24 подъезда. Сколько подъездов в 12 таких же домах?

Решить задачу:
От 4 коров получили за день 40 л молока, от каждой поровну. Сколько коров при том же надое дадут 90 л молока?

Выполни вычисления:
105 x 5 425 x 2 856 : 4 504 + 139
2 x 128 959 : 7 585 : 9 603 — 427

Выполни вычисления:
748 : 2 648 : 4 913 x 3 704 — 328
987 : 3 507 x 2 5 x 329 405 + 249

Найти значения выражений:
(30 + 160 : 4) : 2 280 — 40 : 2 + 100

Найти значения выражений:
(400 — 160 : 8) : 2 900 — 50 x 2 + 140

Найти периметр и площадь
прямоугольника со сторонами 5 см и 4 см.

Найти периметр и площадь
квадрата со стороной 6 см.
Урок 11. Входная контрольная работа. №1
Урок 13. Контрольный устный счёт.
92 : 23 84 : 6 200 x 4 + 200
68 : 17 91 : 7 900 — 400 : 2
57 : 19 75 : 3 1000 : 2 + 500
64 : 16 85 : 5 1000 : 5 — 200
Урок 15. Проверочная работа.
(Печатная тетрадь, стр. 4 — 7)
Урок 21. Контрольный устный счёт.
30 000 : 100 200 x 10 84 x 1 000 : 10
5 000 : 1 000 307 x 100 47 x 100 x 100
371 x 100 810 : 10 43 x 1 000 : 100
35 x 1 000 3 500 : 100 582 x 100 : 10
Урок 23. Проверочная работа.
(Печатная тетрадь, стр. 16 — 17)
Урок 24. Самостоятельная работа.Вариант

Решить задачу:
В 12 лодках можно перевезти 48 человек, размещая людей в лодках поровну в каждой. Сколько людей перевезли в 7 таких лодках ?

Решить задачу:
В санаторий привезли 100 кг картофеля в 5 одинаковых мешках. Сколько килограммов картофеля в 3 таких мешках?

Выполни вычисления:
328 + 243 984 — 638 215 x 4

739 + 1 10 000 — 1 843 972 — 3 000
546 x 1 000 849 600 : 10 67 800 + 90

Выполни вычисления:
436 + 259 792 — 456 828 : 3

69 + 1 30 000 — 1 709 318 — 300
680 x 1 000 95 800 : 100 138 000 + 45

Сравни : числа и поставь нужный знак(>,<,=):

039 и 270 039 12 650 и 12 065

Сравни : числа и поставь нужный знак(>,<,=):

0 и 405 070 25 390 и 25 309

Запиши наименьшее пятизначное
число и число, которое следует за ним при счёте.

Запиши наибольшее пятизначное
число и число, которое следует за ним при счёте.
5*. Запиши 2 числа, произведение
которых равно 100, а частное 1.
5*. Запиши 2 числа, произведение
которых равно 100, а разность 0.
Урок 25. Контрольная работа. №2вариант
2 вариант

Реши задачу:
Токарь за семичасовой рабочий день вытачивает 63 детали, а его ученик за 6 ч вытачивает 30 таких деталей. На сколько больше деталей вытачивает за 1 ч рабочий, чем его ученик?

Реши задачу:
Рабочий за семичасовой рабочий день изготавливает 56 деталей, а его ученик за 4 ч изготавливает 24 такие детали. Сколько всего деталей изготавливают за 1 ч рабочий и его ученик вместе?

Вычисли:

000 : 1 000 7 800 x 10
3 000 + 400 + 50 + 9 400 376 — 400 000 — 70
5 000 + 60 + 2 605 — 500 000 — 600
9 000 + 5 43 879 — 43 000 — 800

Вычисли:
84 000 : 1 000 5 300 x 100
7 000 + 500 + 60 + 3 800 231 — 800 000 — 1
6 000 + 500 + 1 657 908 — 600 000 — 50 000 7 000 + 7 65 997 — 65 000 — 70

Запиши числа 3 798 до 3 806.

Запиши числа 5 697 до 5 703.

Запиши число, в котором:
а) 15 единиц IV класса, 30 единиц III класса, 567
единиц II класса, 306 единиц I класса;
б) 168 миллионов 48 тысяч 30 единиц;
в) 27 миллионов 27 тысяч 27 единиц;
г) 3 миллиарда 430 миллионов 5 тысяч
50 единиц.

Запиши число, в котором:
а) 7 единиц IV класса, 31 единица III класса, 907 единиц II класса, 36 единиц I класса;
б) 22 миллиарда 40 миллионов 16 тысяч 20 единиц;
в) 118 миллионов 18 тысяч 80 единиц;
г) 35 миллионов 35 тысяч 35 единиц.

Реши уравнения:

: a = 9 b : 3 = 11 14 x c = 42

Реши уравнения:
96 : a = 8 b : 4 = 11 13 x c = 52
6*. Запиши двузначное число, в
котором единиц на 3 больше, чем десятков, а сумма цифр равна 15.
6*. Запиши двузначное число, в
котором единиц на 4 меньше, чем десятков, а сумма цифр равна 18.
Урок 26. Проект «Числа вокруг нас. Наш город в числах и величинах». (стр. 32)
Урок 30. Математический диктант.

800 кв. дм = . . . кв. м

60 000 кв. см = . . . кв. м

2 кв. км = . . . кв. м

2 кв. см 10 кв. мм = . . . кв. мм

6 кв. дм 05 кв. см = . . . кв. см

2 кв. м 50 кв. дм = . . . кв. дм

Сравнить: 1 кв. м и 99 кв. дм

Сравнить: 1 кв. км и 999 999 кв. м

Найти площадь прямоугольника со сторонами 10 см и 30 см.

Найти площадь квадрата со стороной 90 см.
Урок 38. Проверочная работа.
(Печатная тетрадь, п\р, стр. 28 — 29 )
Урок 39. Самостоятельная работа.
(Печатная тетрадь, п\р, стр. 30 — 31)
Урок 40. Контрольная работа. №3 (сборник к\р, синенькая)1 вариант
2 вариант

Реши задачу:
В магазин привезли 32 коробки конфет, по 9 кг в каждой, и 36 коробок вафель, по 8 кг в каждой. Каких сладостей привезли больше и на сколько килограммов больше?

Реши задачу:
Один мастер изготовил 6 ниток бус, по 38 бусинок в каждой, а другой — 7 ниток бус , по 36 бусинок в каждой. Какой мастер использовал больше бусинок и на сколько?

Вычисли:

618 + 4 536 7 518 x 3

879 — 19 586 16 002 : 7

Вычисли:
42 731 + 23 895 8 416 x 4

586 — 33 569 32 568 : 6

Выполни вычисления и сделай проверку:

км 640 м — 9 км 890 м

Выполни вычисления и сделай проверку:
29 т 350 кг + 18 т 980 кг

Реши уравнение:
X — 180 = 20 x 6

Реши уравнение:
X + 60 = 16 x 6
5*. Восстанови пропущенные цифры:
3 7 9
+ 6

6 5 8
5*.Восстанови пропущенные цифры:
2 8 6
+ 1
1 1 5 4
Урок 42. Тест. (Печатная тетрадь, п\р, стр. 32 — 35)
Урок 43. Контрольный устный счёт.
(учебник, 4 кл. I часть, стр. 58 — 59)
Урок 46. Математический диктант.

К какому числу прибавили 560 и получили 840?

Сумму чисел 370 и 630 разделите на 100.

Сколько вычли из 341, если получили 333?

Найдите произведение чисел 320 и 3.

Какое число в 5 раз больше числа 200?

Уменьшите 600 на 3.

Частное чисел 320 и 40 увеличьте в 5 раз.

Из какого числа нужно вычесть 135, чтобы получилось 70?

Из 100 000 вычтите 5.

900 разделите на 100.
Урок 50. Математический диктант.
— Запишите цифрами числа.

Шесть тысяч триста восемьдесят шесть. (6 386)

Семь миллионов двести пятьдесят четыре тысячи сорок восемь. (7 254 048)

Пятнадцать миллионов две тысячи триста двадцать. (15 002 320

Двести четырнадцать миллионов пятьдесят шесть. (214 000 056)

Шесть миллиардов четыре миллиона семь. (6 004 000 007)
— Увеличьте каждое число на 7 000.
(13 386, 7 261 048, 15 009 320, 214 007 056, 6 004 007 007).
— Уменьшите каждое из полученных чисел на 200.
(13 186, 7 260 848, 15 009 120, 214 006 856, 6 004 006 807).
Урок 51. Проверочная работа.
(Печатная тетрадь, п\р, стр. 36 — 39 )
Урок 52. Контрольная работа. №4 (методичка, с. 376)вариант
2 вариант

Реши задачу:
На комбинате в декабре изготовили 7 163 л сока, а в январе — на 678 литров меньше. Из всего сока 9 789 литров разлили в пакеты, а остальной сок — в бутылки. Сколько литров сока разлили в бутылки?

Реши задачу:
Зимой в магазине продали 3 486 кукол, весной — на 697 кукол меньше. Из всех проданных кукол 4 486 кукол были в платьях, а остальные — в спортивных костюмах. Сколько было кукол в спортивных костюмах?

Выполни вычисления и сделай проверку:
700 000 — 24 618 312 879 — 179 542
804 608 + 96 395 730 406 + 1 962

Выполни вычисления и сделай проверку:
600 600 — 24 863 529 631 — 181 479
143 807 + 57 296 320 504 + 5 893

Вычисли, записывая вычисления в столбик :
28 км 640 м — 9 км 890 м
18 т 360 кг + 16 т 740 кг

Вычисли, записывая вычисления в столбик:
16 т 230 кг — 9 т 750 кг

км 560 м — 19 км 540 м

Реши уравнения:
290 + X = 640 — 260 b x 13 = 78

Реши уравнения:
400 — X = 275 + 25 а : 5 = 90
5*. Вставь пропущенные цифры:
3 7 9
+ 4 3 1
5 6 0
5 6 8
5*.Вставь пропущенные цифры:
6 7 1
+ 5 8 3
7 6 9
6 2 6
6*.Вставь пропущенные цифры:
а : b — c x d + k x m : n
6*.Вставь пропущенные цифры:
а : (b — c) x d + k x (m : n)
Урок 53. Тест. (учебник, 4 кл. I часть, стр. 74 — 75)
Урок 60. Контрольный устный счёт.
0 : 145 400 x 8 0 дес. x 5 + 3 дес.
312 x 1 1 x 19 050 4 тыс. + 0 тыс. x 7
0 x 195 375 : 375 4 800 : = 60
805 x 10 4 200 : 3 x 10 = 3 500
Урок 62. Самостоятельная работа.
(Печатная тетрадь, п\р, стр. 48 — 49)
Урок 65. Математический диктант.

Запишите число, которое на 1 единицу больше, чем 85 699, 50 000 009.

Запишите число, которое на 1 единицу меньше, чем 555 500, 10 000, 999 999.

Запишите число, которое состоит из 3 542 десятков.

Из цифр 9, 8, 7, 5, 0 составьте наименьшее число.

Запишите число 50 000, а рядом число в 50 раз меньше его.

Сколько всего сотен в числе 6 668 956?

Сколько цифр надо для записи числа 5 591 116?

Найди двадцатую часть от 840.

Выразите в сутках 360 часов.

Выразите в тоннах 336 000 кг.
Урок 67. Проверочная работа.
(Печатная тетрадь, п\р, стр. 44 — 47)
Урок 68. Контрольная работа. №5
(учебник, 4 кл. I часть, стр. 96 — 99) иливариант

вариант

Реши задачу:
С одного поля собрали 1 т 800 кг картофеля, а с другого — в 3 раза меньше. Весь картофель разложили в мешки, по 40 кг в каждый. Сколько мешков с картофелем получили?

Реши задачу:
В первый день в санаторий приехало 900 человек, а во второй — в 9 раз меньше, чем в первый. Всех отдыхающих поселили в комнаты, по 2 человека в каждой. Сколько комнат заняли все отдыхающие?

Выполни вычисления:
6 234 x 2 8 334 : 6
32 542 x 7 6 985 : 5
80 020 x 5 1 520 : 4
907 x 9 — 852 : 3

Выполни вычисления:
5 124 x 2 9 522 : 6
23 452 x 7 2 367 : 3
20 080 x 9 1 806 : 6
840 x 6 — 795 : 3

Вычисли периметр и площадь
прямоугольника со сторонами 2 см и 4 см.

Вычисли периметр и площадь
прямоугольника со сторонами 7 см и 3 см.

Реши уравнения:
90 + X = 1 800 : 10

Реши уравнения:
470 — X = 30 x 4
Урок 72. Самостоятельная работавариант

вариант

Реши задачу:
Какое расстояние проедет всадник за 3 ч, если скорость его движения 13 км/ч?

Реши задачу:
За 2 ч велосипедист проехал 28 км. С какой
скоростью ехал велосипедист?

Выполни вычисления:
234 x 600 2 380 x 40 3 405 x 300
500 x (2 357 — 2 000)

Выполни вычисления:
457 x 500 3 160 x 30 2 608 x 400

400 + 600 x 1 358
3. Реши задачу:
Слон и слонёнок начали двигаться одновременно навстречу друг другу. Скорость слона 60 м/мин, скорость слонёнка 20 м/мин. Слоны встретились через 10 мин. Какое расстояние было между ними сначала?
3. Реши задачу:
Две черепахи начали двигаться одновременно навстречу друг другу, когда находились на расстоянии 66 м. Скорость одной черепахи 5 м/мин, а другой — 6 м/мин. Через сколько минут черепахи встретятся?
4*. Периметр квадрата равен 16 см.
Из трёх таких квадратов сложили один прямоугольник. Найди периметр и площадь этого прямоугольника.
4*. Периметр квадрата равен 24 см. Из
трёх таких квадратов сложили один прямоугольник. Найди периметр и площадь этого прямоугольника.
Урок 73. Контрольный устный счёт.

Скорость грузового поезда 35 км/час. Поезд был в пути 2 часа. Какое расстояние он прошёл?

Велосипедист проехал 36 км за 2 часа. С какой скоростью он двигался?

Охотник верхом на лошади проехал 28 км со скоростью 14 км/час. Сколько времени он потратил на дорогу?

Расстояние от города до посёлка 30 км. Сколько времени потребуется пешеходу, чтобы пройти это расстояние со скоростью 6 км/час?

Мальчик пробежал 20 м за 10 сек. С какой скоростью бежал мальчик?

Крейсер проплыл 80 км со скоростью 40 км/час. Сколько времени он затратил?

Муха летела со скоростью 5 м/сек 15 секунд. Какое расстояние она пролетела?

Грач пролетел 100 м со скоростью 10 м/сек. Сколько времени он был в пути?

За 3 сек сокол пролетел 78 м. Какова скорость сокола?

Орёл летел со скоростью 30 м/сек 6 секунд. Сколько метров пролетел орёл?
Урок 74. Проверочная работа.
(Печатная тетрадь, п\р, стр. 54 — 55)
Урок 83. Контрольная работа. №61 вариант

вариант

Реши задачу:
От двух пристаней, находящихся на рас-стоянии 90 км друг от друга, одновремен-но отправились навстречу друг другу два теплохода и встретились через 2 ч. Скорость одного из них 21 км/ч. С какой скоростью шёл второй теплоход?

Реши задачу:
Две девочки одновременно вышли из своих домов навстречу друг другу и встретились через 3 мин. Скорость первой девочки 60 м/мин, а второй девочки — 70 м/мин Каково расстояние между их домами?

Вычисли, выполнив запись столбиком:

00 x 5 540 x 700
3 400 x 30 80 x 356

Вычисли, выполнив запись столбиком :
2 300 x 90 640 x 800
64 000 x 3 70 x 365

Вырази в указанных единицах измерения:
45 м 2 дм = . . . дм 8 т 5 ц = . . . кг
7 сут. 14 ч = . . . ч 20 000 кв.см = . . . кв.м

Вырази в указанных единицах измерения:
34 000 кв.дм = . . . кв.м 36 ц 5 кг = . . . кг
7 кв.м 14 кв.см = . . . кв.см 4 ч 23 мин = . . . мин

Реши уравнения:
X — 546 = 35 + 64 X x (500 : 100) = 125

Реши уравнения:
376 — X = 7 x 9 у : 3 = 720 : 9
5*. Запиши такое числовое равенство, в котором произведение будет равно одному из множителей.
5*. Запиши такое числовое равенство, в котором делитель будет равен частному.
Урок 86. Контрольный устный счёт.
— Ответ предыдущего примера является первым числом следующего.
2 000 : 2 = 30 000 : 1 000 = 9 000 : 1 000 =
x 7 = x 10 = x 100 =
: 100 = : 3 = : 9 =
: 7 = x 60 = x 50 =
x 50 = : 100 = : 5 =
: 100 = x 10 = x 8 =
x 1 000 = : 6 = : 8 =
Урок 90. Самостоятельная работавариант

вариант

Реши задачу:
От одной платформы одновременно в противоположных направлениях отошли два поезда. Скорость движения одного поезда 40 км/ч, а другого — 30 км/ч. Через сколько часов расстояние между поездами будет 280 км ?

Реши задачу:
Из одной деревни одновременно в разных направлениях выехали велосипедист и мотоциклист. Скорость велосипедиста 12 км/ч, а мотоциклиста 38 км/ч. Какое расстояние будет между ними через 3 ч ?

Выполни вычисления:
44 820 : 60 269 100 : 900 72 800 : 700

x (2 357 — 2 000)

Выполни вычисления:
12 700 : 50 248 800 : 800 98 100 : 900

400 + 600 x 1 358

Реши уравнение:

: X = 99 : 9

Реши уравнение:
у x 40 = 640 + 560
4*. Запиши 2 числа, при умножении которых получается 105. Найди
3 варианта.
4*. Запиши 2 числа, при умножении которых получается 104. Найди
3 варианта.
Урок 92. Математический диктант.

Найдите произведение чисел 700 и 4.

Делимое 800, делитель 80. Чему равно частное?

Какое число меньше, чем число 560, в 80 раз?

Во сколько раз 4 тысячи больше 2 сотен?

Чему равно частное от деления чисел 3 200 и 800?

Увеличьте число 22 в 30 раз.

Первый множитель 400, второй 30. Чему равно произведение?

Уменьшите число 7 200 в 80 раз.

Произведение чисел 15 и 400 уменьшите в 100 раз.

Делимое 560, делитель 70. Найти частное.
Урок 93. Проверочная работа.
(Печатная тетрадь, п\р, стр. 64 — 65)
Урок 94. Контрольная работа. №7вариант

вариант

Реши задачу:
Из двух городов, расстояние между которыми 330 км, одновременно навстречу друг другу выехали два автобуса и встретились через 3 ч. Первый автобус ехал со средней скоростью 60 км/ч. С какой средней скоростью ехал второй автобус?

Реши задачу:
Из двух городов, расстояние между которыми 560 км, одновременно навстречу друг другу выехали два поезда и встретились через 4 ч. Первый поезд ехал со средней скоростью 65 км/ч. С какой средней скоростью ехал второй поезд?

Выполни вычисления:
65 700 : 900 36 200 : 40
2 374 x 50 843 x 600

Выполни вычисления :

800 : 800 18 270 : 30
3 643 x 70 659 x 700

Выполни деление с остатком:
7 360 : 800 11 970 : 400

Выполни деление с остатком:
3 380 : 600 13 590 : 300

Найди ширину прямоугольника,
если известно, что его площадь равна 7 200 кв. дм, а длина — 80 дм.

Найди длину прямоугольника, если
известно, что его площадь равна 4 800 кв. дм, а ширина — 80 дм.
5*. Вставь пропущенные знаки
арифметических действий и расставь скобки так, чтобы равенство стало верным.
6 6 6 6 6 6 6 =100
5*. Вставь пропущенные знаки
арифметических действий и расставь скобки так, чтобы равенство стало верным.
5 5 5 5 5 = 100
Урок 100. Проверочная работа.
(Печатная тетрадь, п\р, стр. 70 — 71)
Урок 101. Контрольный устный счёт.
360 : 3 560 : 80 2 300 : 100
120 x 6 770 : 7 99 x 10
780 : 6 5 200 : 260 3 200 : 800
35 x 20 450 : 9 63 x 2
25 x 30 85 x 2 240 : 120
9 000 : 30 68 x 3 1 000 — 1
Урок 103. Математический диктант.

Какое число надо разделить на 1 000, чтобы получить 527

Увеличьте 9 789 в 100 раз.

Найдите произведение чисел 1300 и 5.

На сколько надо разделить 15 300, чтобы получить 5 100?

Запишите все числа от 55 068 до 55 498, которые делятся на 100 без остатка.

Найдите шестую часть от числа 4 800.

Найдите одну восьмую от разности чисел 600 и 40.

Какое число уменьшили в 120 раз и получили 40?

Из 6000 вычтите произведение чисел 150 и 20.

Составьте наибольшее четырёхзначное число при помощи цифр 1, 0, 8, 4. Цифры в числе не повторяются.
Урок 107. Контрольная работа. №8вариант

вариант

Реши задачу:
Из двух городов, расстояние между которыми 200 км, одновременно в противоположных направлениях выехали два автомобиля. Скорость одного 65 км/ч, а другого — 35 км/ч . Какое расстояние будет между ними через 2 ч?

Реши задачу:
Из двух посёлков, расстояние между которыми 40 км, одновременно в противоположных направлениях вышли два пешехода. Скорость одного 5 км/ч, а другого — 6 км/ч . Какое расстояние будет между ними через 3 ч?

Выполни вычисления:
654 x 98 8 104 x 65
738 x 52 7 415 x 32

x 780 3 004 x 401

Выполни вычисления :
357 x 48 5 702 x 37
812 x 64 6 814 x 820

x 702 8 003 x 231

Реши уравнение:
а + 120 = 4 000 : 5

Реши уравнение:
а + 970 = 69 x 32

Найди значение выражения.

000 — 424 x 76 : 4

Найди значение выражения.
8 000 — 568 x 14 : 2
5*. Реши задачу.
Оля вышла на прогулку на 3 мин раньше, чем Алёша. Алёша вышел на 2 мин позже, чем Саша. Кто из детей вышел раньше всех и на сколько минут?
5*. Реши задачу.
Врач прописал больному 5 уколов — по
уколу через каждые полчаса. Сколько потребуется времени, чтобы сделать все уколы?
Урок 114. Математический диктант.

Сколько нулей нужно записать после цифры 3, чтобы она обозначала десятки тысяч?

Увеличьте в 2 раза разность чисел 880 и 630.

Запишите число, которое состоит из 45 десятков, и увеличьте его в 100 раз.

Наибольшее трёхзначное число увеличьте в 1 000 раз?

Не выполняя деления, определите, сколько цифр будет в частном при делении числа 308 на 28.

Найдите одну седьмую часть от числа 4 200.

Какое число увеличили в 120 раз, если получили 9 600?

Произведение двух чисел равно 8 844. Одно из чисел 4. Чему равно второе число?

Во сколько раз уменьшили 8 004, если получили 2 001?

Какое число может быть частным от деления числа 486 на 54 - 6, 8 или 9?
Урок 117. Проверочная работа.
(Печатная тетрадь, п\р, стр. 77 — 76)
Урок 118. Контрольный устный счёт.
360 : 18 600 : 15 810 : 27
520 : 13 880 : 22 480 : 12
960 : 80 715 : 15 700 : 35
770 : 77 780 : 26 680 : 17
270 : 27 320 : 16 840 : 21
510 : 17 500 : 25 930 : 31
Урок 121. Самостоятельная работавариант

вариант

Реши задачу:
Если в каждом зале помещать по 28 картин, то все картины займут 48 залов. Сколько залов займут все эти картины, если в каждый зал помещать по 24 картины?

Реши задачу:
Если на каждую страницу помещать 32 строки, то весь текст займёт 52 страницы. Сколько страниц займёт этот текст, если на каждую страницу помещать 26 строк?

Выполни деление:
288 648 : 72 243 452 : 503
61 983 : 97 166 520 : 724

Выполни деление:
25 543 : 89 760 518 : 253
27 360 : 38 985 312 : 328

Сравни : числа и поставь нужный знак(>,<,=):
430дм 34м 3т 917кг 3т 719кг

Сравни : числа и поставь нужный знак(>,<,=):
72 т 720 ц 3 км 615 м 4 651 м
4*. Восстанови пропущенные числа.
X 2 8 7 9
9 6
4*. Восстанови пропущенные числа.
X 5 7
3 6 3 6
Урок 124. Контрольная работа. №9вариант

вариант

Реши задачу:
Из питомника привезли 3 600 луковиц тюльпанов, а луковиц ирисов — в 5 раз меньше. Двенадцатую часть всех ирисов посадили на городские клумбы, а остальные отдали в детские сады. Сколько ирисов посадят в детских садах?

Реши задачу:
В теплице собрали 2 352 кг помидоров, а огурцов — в 7 раз меньше. Седьмую часть всех огурцов отправили на консервный завод, а остальные продали. Сколько килограммов огурцов продали?

Вычисли значения выражений и сделай проверку:
654 x 209 2 844 840 : 471

Вычисли значения выражений и сделай проверку:
898 x 306 760 760 : 364

Реши уравнение:
112 : x = 48 : 6

Реши уравнение:
112 : x = 48 : 8

Выполни действия, вставь пропущенные числа.
33 м 49 см + 22 м 68 см = м см
8 мин 10 с — 7 мин 45 с = мин с
3 т 2 ц 75 кг — 8 ц 98 кг = т ц кг

Выполни действия, вставь пропущенные числа.
8 м 7 см — 5 дм 9 см = м дм см
2 мин 52 с + 43 с = мин с
2 т 2 ц 88 кг + 7 ц 86 кг = т ц кг
5*. Реши задачу.
Сколько нужно досок длиной 3 м и шириной 2 дм, чтобы настелить пол в квадратной комнате, сторона которой 6 м?
5*. Реши задачу.
Сколько нужно досок длиной 4 м и шириной 4 дм, чтобы настелить пол в квадратной комнате, сторона которой 8 м?
Урок 125. Самостоятельная работавариант

вариант

Реши задачу:
В 7 одинаковых по массе пакетах 28 кг мандаринов. Сколько потребуется таких пакетов, чтобы так же разложить 64 кг мандаринов?

Реши задачу:
За 5 одинаковых коробок пластилина заплатили 70 р. Сколько таких коробок пластилина можно купить на 98 р.?

Выполни вычисления:
65 000 — 8 679 5 098 X 27
56 387 + 47 918 19 712 : 64
150 131 — 25 942 : 7 X 27

Выполни вычисления:
60 079 — 7 385 6 098 X 45
59 346 + 18 958 35 958 : 78

100 — 18 534) : 6 X 25

Реши уравнение:
456 — x = 7 X 8

Реши уравнение:
у : 12 = 42 + 58

Длина участка прямоугольной
формы 8 м, а ширина в 2 раза меньше. Найди площадь этого участка.

Ширина парника прямоугольной
формы 6 м, а длина на 2 м больше его ширины. Найди площадь этого парника.
5*. Представь число 60 000 в виде
произведения двух множителей, каждый из которых делится на 100.
5*. Представь число 40 000 в виде
произведения двух множителей, каждый из которых делится на 100.
Урок 127. Математический диктант.

Увеличьте число 569 в 1 000 раз.

Найдите частное чисел 8 000 и 50.

Найдите сумму чисел 8 300 и 1 700. Уменьшите её в 1 000 раз.

Найдите произведение чисел 140 и 50.

Найдите одну третью часть от суммы чисел 240 и 360.

Сколько сантиметров в пяти метрах трёх дециметрах?

Запишите пятизначное число, сумма цифр которого равна 8.

Чему равна половина от числа 740?

Сколько центнеров в 90 000 килограммов?

Сколько часов в двух сутках и десяти часах?
Урок 130. Проверочная работа.
(Печатная тетрадь, п/р, стр. 78 — 79)
Урок 131. Итоговая контрольная работа.вариант

вариант

Реши задачу:
Из двух городов одновременно навстречу друг другу отправились скорый и товарный поезда. Они встретились через 13 ч. Каково расстояние между городами, если известно, что скорость скорого поезда 100 км/ч, а скорость товарного поезда составляет половину от его скорости?

Реши задачу:
Из двух городов, расстояние между которыми 918 км, выехали одновременно навстречу друг другу два скорых поезда. Скорость одного поезда 65 км/ч. Какова скорость другого поезда, если поезда встретились через 6 ч?

Вычисли значения выражений:
654 x 204 — (8 963 + 68 077) : 36
9 676 + 12 237 — 8 787 x 2 : 29

Вычисли значения выражений:
587 x 706 + (213 956 — 41 916) : 34
735 148 — 86 499 + 56 763 : 9 x 45

Реши уравнение:
x — 8 700 = 1 700

Реши уравнение:

500 — у = 1 500

Сравни величины.
5 400 кг 54 ц 4 ч 20 мин 420 мин
970 см 97 м 3 кв. дм 7кв. см 307 кв.см

Сравни величины.
4 т 56 кг 456 кг 4 мин 30с 430 с
870 см 8дм 7см 8 кв. см 6 кв. мм 86 кв.мм

Реши задачу.
Участок прямоугольной формы, ширина которого в 2 раза меньше длины, засеяли овсом. Периметр участка 1 140 м. Чему равна его площадь?

Реши задачу.
Длина поля 130 м, ширина 70 м. Две пятые части участка засеяны картофелем. Сколько квадратных метров площади засеяно картофелем?
5*. Оля и Алёша познакомились 7 лет
назад. Сколько лет тогда было Оле, если через 5 лет Алёше будет 17 лет и он старше Оли на 2 года?
5*. Аня и Ира познакомились 5 лет
назад. Сколько лет тогда было Ире, если через 6 лет Ане будет 18 лет и она младше Иры на 2 года?
Урок 133. Контрольный устный счёт.
860 : 430 2 500 : 125 555 000 : 555
660 : 330 66 000 : 220 77 700 : 111
936 : 234 8 400 : 210 32 000 : 160
780 : 260 5 400 : 108 60 000 : 150
848 : 212 7 400 : 185 6 000 : 400
968 : 121 52 500 : 105 640 000 : 320
Сколько 648 разделить на 4 с использованием длинного деления?
Запутались в длинном делении? К концу этой статьи вы сможете разделить 648 на 4, используя деление в длинную сторону, и сможете применить ту же технику к любой другой задаче на деление в длинную сторону! Давайте взглянем.
Хотите быстро научиться или показать учащимся, как решать число 648, разделенное на 4, с помощью деления в большую сторону? Включи это очень быстрое и веселое видео прямо сейчас!
Итак, первое, что нам нужно сделать, это уточнить термины, чтобы вы знали, что представляет собой каждая часть деления:
Первое число, 648, называется делимым.
Второе число 4 называется делителем.
Здесь мы разберем каждый шаг процесса длинного деления на 648, разделенного на 4, и объясним каждый из них, чтобы вы точно поняли, что происходит.
648 разделить на 4 пошаговое руководство
Шаг 1
Первым шагом является настройка нашей задачи деления с делителем в левой части и делимым в правой части, как показано ниже:
Шаг 2
Мы можем выяснить, что делитель (4) входит в первую цифру делимого (6), 1 раз. Теперь, когда мы это знаем, мы можем поставить 1 вверху:
Шаг 3
Если мы умножим делитель на результат предыдущего шага (4 x 1 = 4), то теперь мы можем добавить этот ответ под делимым:
1
4 6 4 8
8
4
Шаг 4
Далее из второй цифры делимого (6 — 4 = 2) вычтем результат предыдущего шага и запишем этот ответ ниже:
0 1 4 6 4 8 — 4 2
Step 5
Move the second digit of the dividend (4) down like so:
1
4 6 4 8
— 4
2 4
40035
40032 (Diving 6). (s), поэтому мы можем поставить 6 сверху:
1 6
4 6 4 8
— 4
2 4
Шаг 7
Если мы умножим делитель на результат предыдущего шага (4 x 6 = 24), то теперь мы можем добавить этот ответ под делимым:
1 6
4 6 4 8
— 4
2 4
2 4
Шаг 8
Далее отнимаем результат предыдущего шага от третьей цифры делимого2 (20 — :
1 6
4 6 4 8
— 4
2 4
— 2 4
0 0 . 0002 Move the third digit of the dividend (8) down like so:
1 6
4 6 4 8
— 4
2 4
— 2 4
8
Шаг 10
Делитель (4) входит в нижнее число (8), 2 раза, поэтому мы можем поставить 2 сверху:
5 6 2
4 6 4 8
— 4
2 4
— 2 4
8
Шаг
. can now add that answer below the dividend:
1 6 2
4 6 4 8
— 4
2 4
— 2 4
8
8
Шаг 12
Далее вычтем результат предыдущего шага из четвертой цифры делимого (8 — 8 = 0) и запишем этот ответ ниже:
1 6 2
4 6 4 8
— 4
2 4
— 2 4
8
— 8
0
Чему равно число 4, разделенное на 4?
Если вы дочитали до этого урока, молодец! Больше не осталось цифр, чтобы двигаться вниз от делимого, а это значит, что мы решили задачу деления в длинную сторону.
Ваш ответ — это верхнее число, а любой остаток будет нижним числом. Итак, для 648, разделенных на 4, окончательное решение:
162
Остаток 0
Дополнительные вычисления для вас
Теперь вы изучили метод деления 648 на 4, вот несколько других способов, которыми вы можете выполнить вычисления:
С помощью калькулятора, если вы набрали 648 разделить на 4, вы получите 162.
Вы также можете представить 648/4 в виде смешанной дроби: 162 0/4
Если вы посмотрите на смешанную дробь 162 0/4, вы увидите, что числитель совпадает с остатком (0), знаменатель — это наш первоначальный делитель (4), а целое число — это наш окончательный ответ (162 ).
Калькулятор деления на длинное деление
Введите еще одну задачу на деление на длинное деление
Следующая задача на деление на длинное деление
Хотите еще больше деления на длинное деление, но не хотите вводить два числа в калькулятор выше? Без проблем. Вот следующая задача, которую вам нужно решить:
Чему равно 648, разделенное на 5 в длинное деление?
Случайные задачи на длинное деление
Если вы добрались до этого конца страницы, значит, вы ДЕЙСТВИТЕЛЬНО любите задачи на длинное деление, а? Ниже приведена куча случайно сгенерированных вычислений для вашего долгого деления удовольствия:
Чему равно 445, разделенное на 477 в длинное деление?
Чему равно 235, разделенное на 274 в длинное деление?
Чему равно 597, разделенное на 751 в длинном делении?
Чему равно 26, разделенное на 452 в длинное деление?
Чему равно 560, разделенное на 725 с использованием длинного деления?
Сколько 274 разделить на 465 с помощью деления в большую сторону?
Чему равно 877, разделенное на 929 в длинное деление?
Чему равно 671, разделенное на 701 с использованием длинного деления?
Чему равно 267, разделенное на 816 в длинное деление?
Чему равно 775, разделенное на 781 с использованием длинного деления?
Чему равно 40, разделенное на 480 в длинное деление?
Чему равно 550, разделенное на 617 с использованием длинного деления?
Чему равно 81, разделенное на 311 в длинное деление?
Чему равно 521, разделенное на 628 с использованием длинного деления?
Чему равно 417, разделенное на 653 в длинное деление?
Сколько 104 разделить на 954 в длинное деление?
Чему равно 872, разделенное на 886 с использованием длинного деления?
Сколько 32 разделить на 153 с помощью деления в длинное число?
Чему равно 975, разделенное на 988 с помощью деления в большую сторону?
Чему равно 365, разделенное на 695 в длинное деление?
Чему равно 835, разделенное на 912 с использованием длинного деления?
Чему равно 788, разделенное на 983 в длинное деление?
Чему равно 414, разделенное на 527 с использованием длинного деления?
Чему равно 669, разделенное на 998 в длинное деление?
Чему равно 472, разделенное на 728 в длинное деление?
Чему равно 556, разделенное на 783 в длинное деление?
Что такое 279разделить на 865 с использованием длинного деления?
Чему равно 144, разделенное на 263 в длинном делении?
Чему равно 921, разделенное на 963 в длинное деление?
Сколько 908 разделить на 923 в длинное деление?
Чему равно 128, разделенное на 731 в длинном делении?
Чему равно 785, разделенное на 794 в длинное деление?
Чему равно 958, разделенное на 997 в длинное деление?
Чему равно 716, разделенное на 802 с использованием длинного деления?
Сколько 132 разделить на 539?используя длинное деление?
Чему равно 620, разделенное на 674 в длинное деление?
Чему равно 542, разделенное на 592 в длинное деление?
Чему равно 65, разделенное на 850 с использованием длинного деления?
Чему равно 232, разделенное на 822 в длинное деление?
Чему равно 596, разделенное на 818 в длинном делении?
Чему равно 946, разделенное на 952 в длинное деление?
Чему равно 879, разделенное на 900 с использованием длинного деления?
Чему равно 710, разделенное на 862 с использованием длинного деления?
Чему равно 75, разделенное на 313 с использованием длинного деления?
Чему равно 490, разделенное на 934 в длинное деление?
Чему равно 921, разделенное на 959 с использованием длинного деления?
Чему равно 785, разделенное на 931 с использованием длинного деления?
Чему равно 710, разделенное на 731 с использованием длинного деления?
Чему равно 705, разделенное на 902 с использованием длинного деления?
Чему равно 398, разделенное на 582 с использованием длинного деления?
Чему равно 69, разделенное на 545 в длинное деление?
Чему равно 645, разделенное на 814 с использованием длинного деления?
Чему равно 909, разделенное на 931 с использованием длинного деления?
Чему равно 350, разделенное на 735 с использованием длинного деления?
Сколько 122 разделить на 732 в длинное деление?
Чему равно 607, разделенное на 657 в длинное деление?
Чему равно 480, разделенное на 594 с использованием длинного деления?
Сколько 512 разделить на 973 в длинное деление?
Чему равно 977, разделенное на 986 в длинное деление?
Чему равно 95, разделенное на 884 с использованием длинного деления?
Чему равно 641, разделенное на 654 в длинное деление?
Чему равно 138, разделенное на 929 в длинное деление?
Чему равно 567, разделенное на 935 в длинное деление?
Чему равно 737, разделенное на 966 с использованием длинного деления?
Чему равно 451, разделенное на 834 с использованием длинного деления?
Чему равно 928, разделенное на 932 в длинное деление?
Сколько 912 разделить на 919 в длинное деление?
Чему равно 932, разделенное на 987 с использованием длинного деления?
Чему равно 931, разделенное на 932 с использованием длинного деления?
Что такое 963 разделить на 971 с использованием длинного деления?
Чему равно 344, разделенное на 367 в длинное деление?
Чему равно 285, разделенное на 456 в длинном делении?
Чему равно 204, разделенное на 882 в длинное деление?
Чему равно 927, разделенное на 981 с использованием длинного деления?
Чему равно 588, разделенное на 596 в длинное деление?
Чему равно 506, разделенное на 669 в длинное деление?
Чему равно 378, разделенное на 889 в длинное деление?
Сколько будет 221 разделить на 900 с использованием длинного деления?
Чему равно 975, разделенное на 984 с использованием длинного деления?
Чему равно 679, разделенное на 795 в длинное деление?
Чему равно 719, разделенное на 734 с использованием длинного деления?
Чему равно 224, разделенное на 532 в длинном делении?
Сколько 313 разделить на 437 в длинное деление?
Сколько 369 разделить на 391 с помощью деления в большую сторону?
Сколько 321 разделить на 372 в длинное деление?
Чему равно 355, разделенное на 406 с использованием длинного деления?
Сколько 178 разделить на 270 в длинное деление?
Чему равно 876, разделенное на 968 в длинное деление?
Чему равно 482, разделенное на 886 в длинное деление?
Чему равно 412, разделенное на 952 с использованием длинного деления?
Чему равно 805, разделенное на 980 с использованием длинного деления?
Сколько 804 разделить на 927 с помощью деления в большую сторону?
Чему равно 716, разделенное на 828 с использованием длинного деления?
Чему равно 966, разделенное на 969 в длинное деление?
Чему равно 588, разделенное на 824 в длинное деление?
Чему равно 675, разделенное на 968 в длинное деление?
Чему равно 414, разделенное на 574 в длинное деление?
Чему равно 241, разделенное на 550 в длинное деление?
Чему равно 740, разделенное на 865 с использованием длинного деления?
Чему равно 920, разделенное на 997 с использованием длинного деления?
Чему равно 962, разделенное на 993 в длинное деление?
§ 25-2-648.
НОРМЫ ПОКАЗАТЕЛЕЙ ТЕРРИТОРИИ ПЛАНИРУЕМОЙ ЗАСТРОЙКИ (ТРЗ)., Раздел 5. Объединение и наложение районов., Статья 3. ДОПОЛНИТЕЛЬНЫЕ ТРЕБОВАНИЯ К ОТДЕЛЬНЫМ РАЙОНАМ., Подглава С. ПРАВИЛА ИСПОЛЬЗОВАНИЯ И ЗАСТРОЙКИ., Глава 25-2. ЗОНИРОВАНИЕ., Раздел 25. ЗЕМЕЛЬНОЕ РАЗВИТИЕ., Кодекс землеустройства, Остин
(А)
Этот раздел применяется к соглашению о запланированной зоне застройки или району зонирования. требования этого раздела заменяют противоречащие положения запланированного развития территориальное соглашение или постановление, если таковые имеются.
(Б)
Планируемая застройка территории не может создавать опасных или нежелательных элементов, т.к. описанных в этом разделе или административном регламенте города.
(С)
Опасные или нежелательные элементы включают опасные, вредные, вредные или нежелательные шум, дым, пыль, запах, загрязнение воздуха, жара, влажность, жидкие или твердые отходы или отходы, свет или блики или другое вещество, состояние, излучение или элемент, которые неблагоприятно затрагивает имущество или использование имущества в непосредственной близости. Это исключает восстановление ресурсов системы, использующие твердые отходы.
(Д)
Опасный или нежелательный элемент измеряется в порядке, установленном настоящим подраздел.
(1)
Шум, вибрация, свет, блики, запах или излучение измеряются в точке на линия исходного свойства, которая имеет самые высокие показания, или в любой другой точке, где существование элементов может быть более очевидным. Уровни шума определяются в соответствии с информацией об уровнях шума в окружающей среде, необходимых для защиты здоровья населения и благосостояние с достаточным запасом прочности, Агентство по охране окружающей среды, 1974.
(2)
Дым или токсичные или вредные вещества измеряются в месте выброса в атмосферу.
(3)
Для открытых промышленных операций, описанных в подразделе (E)(6), концентрация пыли измеряется на уровне земли или на жилой высоте, а также на границе участка или за его пределами, в зависимости от того, что приводит к наивысшему измерению.
(Е)
Опасный или нежелательный элемент не может превышать пределы, установленные настоящим подраздел.
(1)
За исключением шума от транспортного средства или строительных работ, шум не может превышать 55 децибел по локальной сети в светлое время суток и 45 децибел по локальной сети в ночное время часы.
(2)
Колебания земли не должны превышать:
(а)
пределы в колонке I ниже; или же
(б)
если точка измерения является границей жилого района или находится в пределах 80 футов линии границы жилой застройки, расположенной на полосе отчуждения улицы, пределы в колонке II ниже.
Колонка I Колонка II
Частота циклов в секунду Рабочий объем (дюймы) Рабочий объем (дюймы)
от 0 до 1 . 0020 .0008
от 1 до 10 .0010 .0004
от 10 до 20 .0008 .0002
от 20 до 30 . 0005 .0001
от 30 до 40 .0004 .0001
40 лет и старше .0003 .0001

(3)
Легкая или прямая сварочная вспышка не может превышать 0,4 фут-свечи поперек источника. линия собственности. Свет от этих источников должен быть экранирован от соседней собственности.
(4)
Дымить нельзя:
(а)
таким же темным или более темным по оттенку, как обозначенный № 0 на диаграмме Ринглеманна, как опубликован Горным бюро США; или же
(б)
непрозрачности, которая затемняет поле зрения наблюдателя до степени, равной или превышающей дым, описанный в подразделе (E)(4)(a).
(5)
Выбросы твердых частиц на каждый акр земли в запланированной застройке площадь не может превышать:
(а)
для частиц размером 44 микрона или меньше — один фунт в течение любого часа; а также
(б)
для частиц размером более 44 микрон – 0,05 фунта в течение любого часа.
(6)
Открытые промышленные операции с пылеобразующим оборудованием, включая пескоструйную обработку, распыление краски, дозирование гравия и бетона и подобные операции могут не производить пыль в концентрации, превышающей один миллион частиц на каждый кубический фут в точка измерения.
(Ф)
Планируемая территория застройки должна соответствовать требованиям по хранению, использованию, и производство взрывчатых веществ и опасных материалов в Главе 6-2 ( Опасные материалы ) а также Глава 25-12, Статья 7 ( Единый пожарный кодекс ).
Отделы и услуги | Hamilton County NY
Alcoholism & Substance Abuse Prevention-Education & Referral — Four Rivers Alliance
HFM Prevention Council
88 Bridge Street — Suite 5
Johnstown, N.Y. 12095
Office: (518) 736-8188 доб. 107
Электронная почта: [email protected]
Координатор грантов …………………………………………Патрик Крауз
Офис: (518) 774-0372
Электронная почта: [email protected]
Преподаватель по профилактике ……………………………….. … Лора Ли Лаурия
Офис: (518) 921-8113
Эл. ……………………..Эванджелин Уэллс
Офис: (518) 648 -5355

Государственный защитник
102 County View Drive
Lake Pleasant, NY 12108
Офис: (518) 548-6810 или (518) 251-2702
Электронная почта: Defender@hamiltoncountyny. gov
Государственный защитник ……………………………….. ……………….Стерлинг Гудспид
Помощник государственного защитника……………………. ……………. Мартин Позефски
_________________________________________________________________________
Совет по этике
Почтовый индекс Box 205
Lake Pleasant, NY 12108
(518) 548-6651
Председатель …………………. …………..Джек Фиттерер – Индиан Лейк
Секретарь ………………………………………………………. ………. Лаура Абрамс, Ариетта
Роберт Лимперт — Ариетта
Шон Карри — Лонг Лейк
Дэвид Скрэнтон — Инлет
Манро Колли Смит — Спекулянт
НАЖМИТЕ ЗДЕСЬ, чтобы ознакомиться с Кодексом этики
НАЖМИТЕ ЗДЕСЬ, чтобы ознакомиться с формой жалобы на нарушение этических норм

Сотрудник по бюджету
P.O. Box 168
Lake Pleasant, NY 12108
(518)548-5531
Офицер . ………………………………. ……………………………….. Барри Л. Бейкер

Предотвращение злоупотребления психоактивными веществами
143 White Birch Lane
Indian Lake, NY 12842
Офис: (518) 648-5355
Электронная почта: [email protected]
Директор ………………………………… ……………………….. Роберт Клеппанг

Клерк, округ Гамильтон
102 County View Drive, P.O. Box 204
Lake Pleasant, New York 12108
Телефон: (518) 548-7111
Факс: (518) 548-9740
Электронная почта: [email protected]
[email protected]
Автомобиль — лицензии, регистрация и сделки. Сделки с землей — подача и запись. Судебные документы — верховный, окружной и уголовный. Залоги и судебные решения. Лицензии на охоту, рыбалку, отлов. Карты обследования. Лицензии на пистолет. Нотариальная информация и документы. «Ведение бизнеса как» и корпоративные документы. Обзор оценки мелких претензий
Посетите веб-сайт www.dmv.ny.gov
Важные формы:
MV-44 Заявление о выдаче водительского удостоверения, водительского удостоверения или удостоверения личности
MV-44EDL Заявление о выдаче расширенного/реального удостоверения личности, водительского удостоверения или удостоверения личности
ID-44 Как подать заявление на получение нового York Learner Permit, Driver License, Non-Driver ID
MV-619 Отчет о проверке зрения
MV-82 Заявление о регистрации транспортного средства/право собственности
MV-82B Заявление о регистрации лодки
ID-82 Удостоверение личности
DTF-802 Налоговая форма
DTF -803 Форма 9 освобождения от налога с продаж0003
Для получения записей о рождении, браке или смерти, а также разрешений на использование собак обращайтесь к своему секретарю в ГОРОД.
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ СКАЧАТЬ СЧЕТ
НАЖМИТЕ ЗДЕСЬ — Отчет о передаче недвижимого имущества RP-5217
Персонал:
Джейн С. Зареки, клерк округа
Хизер А. Фарбер, заместитель клерка округа
Эйлин Хиггинс, помощник заместителя клерка — Автомобили с 8:30 до 16:00
Records Room с 8:30 до 16:30

Комиссар присяжных заседателей
Здание суда округа Гамильтон
102 County View Drive, PO Box 701
Lake Pleasant, NY 12108
Телефон: (518) 285-6188
Комиссия по электронной почте: swilt.0gover91 …………………………………………. ………………… Сэди С. Уилт

Общественные службы
143 White Birch Lane
Indian Lake, NY 12842
Часы работы: с понедельника по пятницу с 8:30 до 16:30
Психиатрическая служба: Кризисная служба и служба «горячей линии». Психиатрические услуги. Психологические службы. Индивидуальная, семейная, парная и групповая терапия
. Службы управления делами. Службы поддержки семьи. Консультирование по созависимости. Дневные услуги/отдых. Координация CCSI. Детская СПОА. Услуги по профилактике психического здоровья. Услуги по профилактике употребления алкоголя, табака и других наркотиков (химической зависимости). Программа Trailblazer. Информационно-просветительская деятельность. Справочные услуги для домашней и общественной программы Wavier. Помощь амбулаторному лечению. Оценки, назначенные судом. Услуги молодежного совета. Передышка. Направление на услуги, не предоставляемые в округе (например, жилье, RTF, дневное лечение и программы проживания, SPOA для взрослых). Направление для лечения химической зависимости, лечения от азартных игр и услуг OMRDD.
Директор ……………………………………………… ………… Роберт Клеппанг, LMSW, ACSW
Кризисная служба: 24/7 1-800-533-8443
Телефон: (518) 648-5355 Факс (518) 648-6437
E- почта: [email protected]

Расширение кооператива Корнелла
«Помогая людям помочь себе»
Просветительская деятельность и образование в следующих областях: Дом и территория – Выбор и идентификация растений, идентификация вредителей, включая насекомых и животных, тестирование почвы и рекомендации по исправлению положения.
Овощеводство.
Энергетическое образование.
Растущие здоровые дети.
Большой подсчет птиц на заднем дворе.
Урожай Адирондака.
Неместные инвазивные виды.
Старший руководитель отдела ……………………………………… Джамиля Пейдж
Часы работы: Пн-Пт — с 8:30 до 16:30
Телефон (518) 548-6191   Факс (518) 548-7803

Коронеры:
Район № 1
Мэтью Дж. Миллер
PO Box 76, Inlet, NY 13360
Домашний: (315) 357-3418 или сотовый: (315) 369-5432
Электронная почта: [email protected]
Район № 2
Тимоти Смит
P.O. Box 667, Lake Pleasant, NY 12108
Домашний: (518) 548-3634 или сотовый: (757)705-9081
Электронная почта: [email protected]
District #3
John Anderson
141 Little Amsterdam Road
P.O. Box 87, Wells, NY 12190
Мобильный: (518) 332-0941
Электронная почта: coroner3@hamiltoncountyny. gov
District #4
Carl E. Turner
1188 Main Street
Long Lake, NY 12847-2204
Мобильный телефон: (518) 636-8808
Эл.
Окружной прокурор и помощник окружного прокурора
Окружной прокурор
Charles R. Getty, Jr.
320 North George Street
P.O. Box 950
Rome, NY 13442-0950
Офис: (315) 336-3900
Факс (315)336-3239
Электронная почта: [email protected]
Помощник прокурора округа
Кристин Э. Николелла, эсквайр
PO Box 395
Delanson, NY 12053
Телефон: (518) 895-2111
Эл.
Судебные канцелярии и палаты
Офис секретаря суда — Суд по семейным делам, окружной и суррогатный суд
139 White Birch Lane, P.O. Box 780
Indian Lake, NY 12842
Телефон: (518) 648-5411
Адреса электронной почты:
[email protected] hamiltonfamily@nycourts. gov [email protected]

Главный клерк ………………………………………….. …….. Ариана К. Элдридж
Заместитель главного клерка………………….. ……… Мишель ДеШо
*Все судебные заседания проходят по адресу: Lake Pleasant Courthouse, 102 County View Drive, Lake Pleasant, NY 12108
Судья по семейным делам, окружным и суррогатным судам
P.O.Box 780 139 White Birch Lane
Indian Lake, NY 12842
Телефон: (518)648-5966
Судья…………………………………………… ………… Достопочтенный. Татьяна Н. Коффингер
Электронная почта: [email protected]
Главный прокурор суда…………………………….. Линн Пуччарелли
Секретарь судьи…. ……………………………… Наташа Гэдвей

Окружной прокурор
139 Уайт Берч Лейн, П.О. Box 277
Indian Lake, NY 12842
Телефон: (518) 648-5113 Факс: (518) 648-5724
Эл. …………………………………………. Кристофер С. Шамбо
Ассистент Окружной прокурор ……………………………….. Сьюзан Хартманн
ДОРОЖНЫЕ БИЛЕТЫ:
Если вам было предъявлено обвинение в нарушении правил дорожного движения, отличном от вождения в состоянии алкогольного опьянения или вождения в состоянии инвалидности, вы можете иметь право на снижение суммы обвинения.
Чтобы подать заявку на возможное снижение штрафа за нарушение правил дорожного движения, нажмите на ссылку ниже и Следуйте всем инструкциям.
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ запросить снижение стоимости транспортных средств и дорожного движения

Экономическое развитие
102 County View Drive
P.O. Box 57
Lake Pleasant, NY 12108
Офис: (518) 548-3078 Факс: (518) 548-3091
E-mail: [email protected]
Директор . ……………………………………………………… …………..Кристи Л. Уилт
Помощник ……………………………… …………………………..РаШель Мартц
Агентство промышленного развития округа Гамильтон
102 County View Drive
Lake Pleasant, NY 12108
Телефон: (518) 548-3078 Факс: (518) 548-3091
Поддержка малого бизнеса. Стартапы. Расширение. Финансирование. Кредиты. Совет. Бизнес и маркетинговые планы. Государственное агенство. Регуляторная помощь.
www.hamiltoncounty.com/economic-development/ida
www.adirondackgoodlife.com
Электронная почта: [email protected]
Исполнительный директор ………………………………………… ….Кристи Л. Уилт

Выборы, Совет
102 County View Drive
P.O. Box 175
Lake Pleasant, NY 12108
Телефон: 518-548-4684
Зарегистрироваться для голосования, Изменить регистрацию партии, Адрес (почтовый) Изменить,
баллотирование на политические посты, подача петиций о назначении и независимых петиций, раскрытие финансовой информации, проверка выборов и обучение хранителей машины для голосования в день выборов, заочное голосование, посещение средних школ для регистрации (18 лет).
ОТЧЕТ ОБ УЧАСТОКЕ ИЗБИРАТЕЛЬСТВА
ЧТОБЫ ЗАГРУЗИТЬ РЕГИСТРАЦИОННУЮ ФОРМУ, ФОРМУ ИЗМЕНЕНИЯ РЕГИСТРАЦИИ И ИЛИ АДРЕСА, НАЗНАЧЕНИЕ/НЕЗАВИСИМУЮ ПЕТИЦИЮ, ЗАКОН О ВЫБОРАХ NYS OPEN HOW TO ALL IN OFFICE, ФОРМУ ОТСУТСТВУЮЩЕГО ЗАЯВЛЕНИЯ, ПОСЕТИТЕ СЛЕДУЮЩИЙ ВЕБ-САЙТ: www.elections.ny.gov
Персонал:
Джейд Шерман, комиссар по выборам демократов
Гейл П. Тил, комиссар по выборам республиканцев
Виктория Э. Фиш, заместитель комиссара по выборам республиканцев
Избирательная комиссия округа Гамильтон, информация
Управление по чрезвычайным ситуациям
2558 State Route 8
Lake Pleasant, NY 12108
План уменьшения опасности округа Гамильтон нажмите ЗДЕСЬ
Что вы знаете о планах по уменьшению опасности вашего округа? Что ж, мы случайно знаем, где можно узнать больше! Присоединяйтесь к Департаменту по чрезвычайным ситуациям округа Гамильтон в партнерстве с Отделом внутренней безопасности и служб экстренной помощи штата Нью-Йорк и лабораторией AVAIL Университета в Олбани, когда мы разрабатываем законопроект округа Гамильтон 9. 1064 Мультиюрисдикционный план смягчения последствий всех опасностей (HMP). Проект плана находится по адресу https://hamilton.mitigateny.org/. Пожалуйста, расскажите нам о своем опыте борьбы со стихийными бедствиями и о том, как лучше всего справляться с этими опасностями, приняв участие в опросе общественного мнения. Заранее спасибо за участие в опросе! Вы вносите свой вклад в обеспечение безопасности вашего сообщества! Вопросы можно направлять по адресу:[email protected].
Персонал:
Директор аварийно-спасательных служб ……………… Джилл Данхэм
Электронная почта: [email protected]
Координатор службы неотложной помощи ……………………………..Avis Warner
Электронная почта: [email protected]
Координатор пожарной охраны ……………………………….. Джей Гриффин
Электронная почта: [email protected]
Телефон: (518) 548-6223   Факс: (518) 548-3392
Для экстренных случаев используйте: 518-548-6111 (депеша шерифа)
Консультативный совет по пожарной безопасности
P. O. Box 44
Lake Pleasant, NY 12108
Президент ……………………………….. Винс Лаурия
Телефон: (518)924-4401 или Электронная почта: [email protected]
Вице-президент…………………….. Мэтт О’Брейн
Секретарь……… …………………………… Крис Хейс
Электронная почта: [email protected]
Консультативный совет по пожарной безопасности
Бенсон Джеймс Льюек
Озеро Блу Маунтин Шеф Грег Джордж, заместитель начальника Чарльз Брузо
Надежда Ass’t Chief Эрик Робинсон, Гарри Даунинг
Индиан Лейк Крис Митчелл
Вход Шеф Деннис Хадсон, Тодд Марло
Лейк-Плезант Шеф Билл Уортон, заместитель начальника Крис Хейс
Лонг Лейк Шеф Мартин Пирс, первый заместитель начальника Джон Уокер
Морхаус Шеф Джеймс Лак, Брайан Тейлор
Писеко Стивен Воэрле, Дон Пинкертон
Ракетт Лейк Майкл Лэмпхер
Спекулянт Мэтт О’Брайен, Майк Трейси
Колодцы Шеф Винс Лаурия, Тимоти О’Нил
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ ПОЛУЧИТЬ ПРАВИЛА И ПОЛОЖЕНИЯ

Встречи проводятся по телефонам:
Департамент добровольной пожарной охраны Лейк-Плезант, 114 S Shore Rd Lake Pleasant, NY 12108
(518) 548-3760
и:
Byron Park Building — 8284 NY IndianLake
(518)-648-6483
Все собрания открыты для публики и начинаются в 19:00

Историк
Генеалогические файлы. Карты, книги и тематические файлы. Фотографии
102 County View Drive
P.O. Box 205, Lake Pleasant, NY 12108
Информацию об услугах, ресурсах, коллекциях и часах работы можно найти на веб-сайте историка округа: www.hamiltoncountyhistorian.org
ЧАСЫ — четверг с 9:00 до 11:10: 00:00 и с 13:00 до 16:00
* Если что-то нужно в любой другой день, просто оставьте сообщение на рабочем телефоне или отправьте электронное письмо *

Окружной историк …………………………………………. ………….. Эрнест Д. Вирджил
Телефон: (518) 548-5526
Cell: (518) 420-8339
Электронная почта: историксы @hamiltoncountyny.gov
Жилищная помощь
Joseph E. Mastrianni, Inc.
11 Federal Street
Saratoga Springs, NY 12866
Телефон: (518) 372-4739

Услуги по охране психического здоровья
148 White Birch Lane
Indian Lake, N. Y. 12842
Телефон: (518) 648-5355    Факс: (518) 648-6437
Электронная почта: [email protected]
Директор ……………………………………………… …………………………..Роберт Клеппанг

Департамент транспортных средств
102 County View Drive
P.O. Box 204
Lake Pleasant, NY 12108
Телефон: (518) 548-7111 Факс: (518) 548-9740
Электронная почта: [email protected]
Офис для пожилых людей
1340 State Route 9, Lake George, NY 12845
Телефон: (518) 761-6347
Факс: (518) 761-6344
Директор ……………………………………………… …. Дина Парк
Бухгалтерский учет ……………………………….. ….. Джеффри Хейнс
Официальная газета
Гамильтон Каунти Экспресс
PO Box 659, 2942 State Route 28
Old Forge, NY 13420
Телефон: (315) 369-2237
Эл. …………………………………………. ……………….. Джефф Дилонг

Единый рабочий источник
Округ Гамильтон OneWorkSource предлагает широкий спектр услуг, помогающих поддерживать как работодателей, так и сотрудников. Это универсальный центр карьеры, предоставляющий услуги предприятиям и соискателям округа Гамильтон.
Почтовый индекс Box 725
Indian Lake, NY 12842
Телефон: (518) 648-6131 Факс: (518) 648-5257
Часы работы: с понедельника по пятницу, с 8:30 до 15:30
Для получения информации о нашей универсальной карьере Щелкните по центру ЗДЕСЬ

Отдел кадров
Заявление о приеме на государственную службу:
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ СКАЧАТЬ (Заявка на обследование)
Прием заявлений для:
Уборщица в Индиан-Лейк
Полицейский
Сертифицированный медицинский помощник на дому
Заместитель шерифа
Бухгалтерский клерк
Социальный работник
Координатор семейных медицинских услуг
Координатор общественного здравоохранения и готовности к чрезвычайным ситуациям
Зарегистрированная медсестра
Директор общественных служб
Cleaner-Lake Clinic1 Социальный работник (MHSA)
Директор по обслуживанию пациентов
Объявленные осмотры:
Заместитель шерифа
Полицейский
Справочник сотрудника округа Гамильтон
Офицер. ………………………………………….. ………………….Кимберли Бирн
Клерк………………….. ……………………………………… Хайде Томсон
Почтовый индекс Box 174
102 County View Drive Route 8,
Court House Lake Pleasant, NY 12108
Телефон: (518) 548-6375 Факс: (518) 548-3108
Электронная почта: [email protected]
Hours of Рабочий:
с понедельника по пятницу с 8:30 до 16:30
Экзамены проводятся по субботам в течение года.
Отдел пробации
Подготовка досудебных расследований. Отчеты для уголовных судов. Надзор за преступниками, осужденными на условный срок.
Директор ………………………………………………………. …….. Эми Грейнджер,
, сотрудник службы пробации………………….. …. John Boya
Телефон: (518) 648-5040 Факс: (518) 648-0359
Электронная почта: probation@hamiltoncountyny. gov
Часы работы: Пн-Пт – Обычно с 8:30 до 16:30
P.O. Box 666
Indian Lake, NY 12842
Доступность офиса может меняться в зависимости от надзора на местах и обязанностей суда.

Общественное здравоохранение
     Сестринские услуги
Агентство по охране здоровья на дому
Телефон: (518) 648-6141
Дети с особыми медицинскими потребностями
Телефон: (518) 648-6497
0 Сестринские услуги Box 250, White Birch Lane
Indian Lake, NY 12842
Телефон: (518) 648-6497   Факс: (518) 648-6143
Эл. ……… Эрика Махони
Электронная почта: [email protected]
Директор по работе с пациентами …………………………..Carriann Grexa-Allen
E-mail: Carriann.Grexaallen [email protected]
Программы общественного здравоохранения — (518) 648-6497
Сертифицированное агентство по охране здоровья на дому — (518) 648-6141
DSS Public Health & Community Services:
Веб-сайт: www. hamiltoncounty.com/health-human-services
Департамент общественных работ
Главный офис — 2558 State Route 8
P.O. Box 56
Lake Pleasant, NY 12108
Офис: (518) 548-7141        Факс: (518) 548-4308
Электронная почта: highway@ hamiltoncountyny.gov
Суперинтендант……………….. .. ……… ………… … Трейси Дж. Элдридж
Административный менеджер… …………………. …. …… ……….Лиза Джонсон
Road Supervisor III ………………….. …………………………..Кристофер Митчелл
ОТДЕЛ ШОССЕ:
Техническое обслуживание дорог округа. Удаление снега и льда. Ремонт мостов и техническое обслуживание водопропускных труб на всех дорогах города и округа.
Позвоните по номеру 518-548-7141, чтобы сообщить о любом небезопасном мусоре на дорогах округа.
Чтобы получить Карты Графства — Стоимость $4,00 каждая.
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ ПОЛУЧИТЬ: Заявление о разрешении на проезд. Это должно быть
представлено и одобрено суперинтендантом шоссе округа до 9.1064 действительно.
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ ПОЛУЧИТЬ ИНСТРУКЦИЮ ПО РАЗРЕШЕНИЮ НА РАБОТУ
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ РАЗРЕШИТЬ НА РАБОТУ
Гараж на озере Плезант…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………… ..…Грегг Бойер
Гараж в Индиан-Лейк……………………………..(518) 648-6128
Дорожный инспектор II………………………….. ..…..Роберт Берджесс
Гараж Лонг-Лейк………………………………..(518) 624-2186
Дорожный инспектор II……………………… ..……….Джон Уокер
ОТДЕЛ ТВЕРДЫХ ОТХОДОВ:
Предприятия, расположенные в Индиан-Лейк и Лейк-Плезант, принимают твердые отходы и материалы для вторичной переработки от жителей и городов округа Гамильтон.
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ Ознакомиться с Правилами и положениями станции перегрузки твердых отходов
Справочный лист рекомендаций по переработке
Пересадочная станция Лейк-Плезант
Часы работы с 8:00 до 16:00 с понедельника по субботу
2297 State Route 8 Lake Pleasant, NY 12108
Джозеф Блэквуд, техник полигона
Телефон: (518) 548-3867
Перегрузочная станция Индиан-Лейк
Часы работы: с 8:00 до 4:00 с четверга по понедельник
Чейн-Лейк-роуд, Индиан-Лейк, Нью-Йорк 12842
Рэнди Делонг, техник полигона
Телефон: (518) 648-0223
Щелкните здесь, чтобы ознакомиться с Законом штата Нью-Йорк о переработке аккумуляторов
Нажмите здесь, чтобы ознакомиться с Законом штата Нью-Йорк о переработке и повторном использовании электронного оборудования
НАЖМИТЕ ЗДЕСЬ, чтобы ознакомиться с проектом плана обращения с твердыми отходами
ЗДАНИЯ ОТДЕЛ:
Руководитель строительных проектов…………………………. Марк Стюарт
(518) 548-5200
Служба налогообложения недвижимости
Информация об оценке: инвентаризация имущества, оценочная стоимость, выравнивающие ставки и т. д.
Налоговая информация: налоговые ставки, налоговые сборы, городские/окружные/школьные/деревенские налоги и т. д.
История участка. Данные о продажах
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ — Загрузить платежную ведомость
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ — Поиск Parcel & GIS
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ — информация о том, как оспорить оценку
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ — Отчет о передаче недвижимого имущества RP-5217
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ — Данные и информация о недвижимости
Директор ………………………………………………………. ……………………..Barry L. Baker
Тел.: (518) 548 — 5531
Факс: (518) 548-7064 P.
8
8. Box 168, Lake Pleasant, NY 12108
Электронная почта: [email protected]
Карты ГИС: www.hamcomaps.net
www.hamiltoncounty.com/municipalities/town-assessment-rolls

Департамент шерифа
     Тюрьма
102 County View Drive
P.O. Box 210
Lake Pleasant, NY 12108
Тюрьма: (518) 548-3113   Факс: (518) 548-4619
Офис: (518) 548-3113   Факс: (518) 548-10604 .gov
Электронная почта: [email protected]
Шериф ………………………………………………………. …………………….. Карл Г. Абрамс
Младший шериф ………………………………………… Кевин Брауниус
Электронная почта: [email protected]
Отдел социальных услуг
Временная помощь (TA), талоны на питание (FS), медицинская помощь (MA), программа пособий по планированию семьи, Family Health Plus, сберегательная программа Medicare (Buy-IN), программа помощи в оплате электроэнергии на дому (HEAP), отдел сбора алиментов ( SCU), услуги для взрослых, уход за приемными родителями, услуги по усыновлению, защита детей, профилактика детей, насилие в семье, домохозяйка/услуги по уходу за собой (PC), расширенные услуги на дому для пожилых людей (EISEP), информационный и справочный уход за детьми, летняя молодежная программа (SYP) и Программа трудоустройства и базовых навыков (JOBS).
Персонал:
Комиссар ……………………………………… ……………Роберта А. Блай
Эшли Сноу, социальный работник (обслуживание взрослых и детей)
Эбигейл Эйхлер, старший социальный работник (DV, EISEP, ПК)
ЭваДжин Андерссон, социальный работник
Эллисон Махони (HEAP)
Бет Кинг, эксперт по социальному обеспечению (MA &FS)
Виктория Мур, эксперт по социальному обеспечению
Дайан Кротти, координатор CSE (SCU и IT)
Стефани Хатчинс, главный бухгалтер
Конни Махони, эксперт по социальному обеспечению (TA/трудоустройство/уход за детьми)
PO Box 725, 139 White Birch Lane
Indian Lake, New York 12842-0725
Телефон: (518) 648-6131 Факс: (518) 648-5257
Часы работы: с 8:00 до 16:30
Конфиденциальная телефонная линия по борьбе с мошенничеством
Если вы подозреваете, что совершается мошенническое действие, позвоните на горячую линию конфиденциальной информации о мошенничестве по телефону:
.
1-866-448-6662. Звонящие могут оставаться анонимными

DSS округа Гамильтон предоставляет субсидию по уходу за детьми , чтобы помочь покрыть расходы по уходу за детьми для квалифицированных семей, пока родитель/опекун занят работой. Эта субсидия зависит от дохода. Дополнительную информацию можно получить на веб-сайте Управления по делам детей и семьи (OCFS.ny.gov) или связавшись с Конни по телефону DSS округа Гамильтон (518) 648-6131.
Для получения помощи по программе HEAP или SNAP — https://www.mybenefits.ny.gov
Скидка на широкополосный доступ.. . Программа экстренной помощи широкополосной связи (getemergencybroadband.org)
Веб-сайт службы здравоохранения и социальных служб округа Гамильтон: НАЖМИТЕ ЗДЕСЬ

Федеральные и государственные правила проживания в домах престарелых и престарелых
Район охраны почв и водных ресурсов
Мониторинг качества озерной и паровой воды. Информационно-просветительская работа по инвазивным видам и управление ими. Борьба с эрозией отложений, включая гидропосев. Продажа деревьев и кустарников. Помощь в управлении озером и береговой линией. Техническая поддержка. Стабилизация береговой эрозии. Частные испытания скважин в течение всего лета. Образовательная программа по охране природы среди студентов и местных сообществ. День охраны окружающей среды Энвиротон. Студенческий опыт обучения на свежем воздухе. Информация о ливневых и альтернативных септических системах. Ежемесячный уголок охраны природы и ежегодный информационный бюллетень.
Для получения дополнительной информации о наших программах посетите веб-сайт Округа охраны почв и водных ресурсов округа Гамильтон по адресу: www.hcswcd.com
Найдите нас на Facebook и Vimeo
Персонал:
Районный менеджер …………………………………………. ..Кейтлин Стюарт
Техник по консервации……………………………. Ленни Крут
Часы работы: понедельник – Пятница: с 8:00 до 16:30
103 County View Drive
Lake Pleasant, NY 12108
Телефон: (518) 548-3991   Факс: (518) 548-5602
Электронная почта: [email protected]

Остановка D.W.I. Программы
Почтовый индекс Box 210
Lake Pleasant, NY 12108
Телефон: (518) 548-3113 Факс: (518) 548-5407
Координатор ………………….. ………………….Шериф Карл Г. Абрамс
Туризм
102 County View Drive
P.O. Box 57
Lake Pleasant, NY 12108
Офис: 518-548-3076 Факс: 518-548-3091
Электронная почта: [email protected]
Веб-сайт — www.AdirondackExperience.com
Директор ………………………………………………………. ……………………..Кристи Л. Уилт
Помощник……………… ………………………………. ………… ……..RaChelle Martz
Маркетинг — Региональное управление устойчивого туризма (ROOST) …….. 518-523-2445
Казначей, графство Гамильтон
102 County View Drive
P.O. Box 206
Lake Pleasant, NY 12108
Телефон: (518) 548-7911
Факс: (518) 548-4519
Эл. …………………………………………. Бет Хант
Заместитель казначея…………………………………………… …… Джоди Смолл
Электронная почта: [email protected]
ДЛЯ ОПЛАТЫ СБОРОВ НАЖМИТЕ ЗДЕСЬ.1064 Оплатите налоги на имущество моей просроченной задолженности
Оплатите налоги Центральной школы Лейк-Плезант за 2018/2019 годы здесь:
Оплатите налоги Центральной школы Лейк-Плезант за 2018/2019 годы

Veteran’s Service Agency
(контракт с Fulton Co.)
102 County View Drive
Lake Pleasant, NY 12108
Телефон: (518) 548-6651 или (518) 736-5651 Факс 9104:5688 -7608
Электронная почта: ветераны@fultoncountyny. gov

Меры и весы
Почтовый индекс Box 392
Inlet, NY 13360
Домашний: (315) 357-3309 Сотовый: (315) 369-8771
Электронная почта: [email protected]
Директор…………… ……………………………….. Герберт В. Шмид

Найдите контактное лицо по Закону о свободе информации в Министерстве юстиции | OIP
Найдите контактное лицо по Закону о свободе информации в Министерстве юстиции | ОИП | Департамент правосудия Перейти к основному содержанию
You are here
Home » Office of Information Policy » Подайте запрос по Закону о свободе информации в DOJ
Переключение видов
Антимонопольный отдел
Антимонопольный отдел
Кеннет Хендрикс
Начальник отдела FOIA/PA
Антимонопольный отдел
Министерство юстиции
Здание Liberty Square
Suite 1000, 450 5th Street, N. W.
Washington, DC 20530-0001
Телефон: (202) 514-2692
Факс: (202) 616-4529
Электронная почта: [email protected]
Центр обслуживания запросов по Закону о свободе информации: (202) 514-2692
Представитель по связям с общественностью по Закону о свободе информации: Уэйн Фостер, (202) 514-2692
Бюро алкоголя, табака, огнестрельного оружия и взрывчатых веществ
Бюро по алкоголю, табаку, огнестрельному оружию и взрывчатым веществам
Адам С. Сайпл
Начальник отдела управления информацией и конфиденциальностью
Бюро по алкоголю, табаку, огнестрельному оружию и взрывчатым веществам
Министерство юстиции
Комната 4.E-301
99 Нью-Йорк Авеню, Н.В.
Вашингтон, округ Колумбия 20226
Телефон: (202) 648-8740
Портал FOIA: https://www.securerelease.us/
Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 648-8740
Представитель по связям с общественностью по Закону о свободе информации: Зина Корнегай, (202) 648- 7390
Гражданский отдел
Гражданский отдел
Элизабет А. Вуд
Закон о свободе информации и конфиденциальности
Гражданский отдел
Министерство юстиции
Комната 8314
1100 L Street, NW
Вашингтон, округ Колумбия 20530-0001
Телефон: (202) 514-2319 Факс: 910 (202) 514-2319 Факс: (910) 202) 514-7866
Электронная почта: [email protected]
Центр обслуживания запросов по Закону о свободе информации: (202) 514-2319
Представитель по связям с общественностью по Закону о свободе информации: Стефани Б. Логан, (202) 514-2319
Отдел гражданских прав
Отдел гражданских прав
Килиан Б. Кагл, начальник
4CON, комната 6.153
950 Pennsylvania Ave., N.W.
Washington, DC 20530
Телефон: (202) 514-4210
Эл. Служба по связям с общественностью
Служба по связям с общественностью
Шон Голидей
Координатор Закона о свободе информации/PA
Служба по связям с общественностью
Министерство юстиции
145 N Street NE
Suite 5E300
Вашингтон, округ Колумбия 20530
Телефон: (202) 3095-10645 CRSFOIA @ usdoj. gov
Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 305-2935
Представитель по связям с общественностью по Закону о свободе информации: Шон Голидей, (202) 431-1277
Уголовный отдел
Криминальный отдел
Кристина Батлер
Исполняющий обязанности начальника, FOIA/PA Unit
Отдел уголовных преступлений
Министерство юстиции
Комната 803, здание Кини
Вашингтон, округ Колумбия 20530-0001
Телефон: (202) 616-0307
Факс: (202) 514-6117
Электронная почта: [email protected]
3
2 Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 616-0307
Представитель по связям с общественностью по Закону о свободе информации: Сара Вестенберг, (202) 616-0307
отдел по борьбе с наркотиками
Управление по борьбе с наркотиками
Келли Миллер, начальник
Закон о свободе информации и конфиденциальности, раздел
Drug Enforcement Administration
8701 Morrissette Drive
Springfield, Virginia 22152
Телефон: (571) 776-2300
Эл. : Дешелия Уоллес, (571) 776-2300
Отдел окружающей среды и природных ресурсов
Отдел окружающей среды и природных ресурсов
Чарльз Смиролдо
Координатор Закона о свободе информации
Министерство юстиции
Отдел окружающей среды и природных ресурсов
Law and Policy Section
950 Pennsylvania Avenue, NW
Washington, DC 20530-0001
Телефон: (202) 514-0424
Эл.
Представитель по связям с общественностью по Закону о свободе информации: Эмбер Блаха, (202) 616-5515
Исполнительный офис иммиграционного контроля
Исполнительный отдел иммиграционного контроля
Джозеф Р. Шааф
Главный юрисконсульт
Административно-правовой отдел
Исполнительный отдел иммиграционного контроля
Департамент юстиции
Suite 1903, 5107 Leesburg Pike
Falls Church, VA 22041
Телефон: (703) 605-1297
Факс: (703) 605-0570
Электронная почта: [email protected]
FOIA 900 Центр:
(703) 605-1297
Связь с общественностью по Закону о свободе информации:
Crystal Souza, (703) 605-1297
Целевые группы Исполнительного управления по борьбе с организованной преступностью по борьбе с наркотиками
Административное управление по борьбе с организованной преступностью Целевые группы по борьбе с наркотиками
Кристин Бруди-Эверетт
Целевые группы по борьбе с организованной преступностью по борьбе с наркотиками
Министерство юстиции США
441 G Street NW
Suite 6B13
Washington, DC 20530
Отправить запрос: ocdetf. [email protected]
FOIA Представитель по связям с общественностью: Кристин Бруди-Эверетт, ) 514-0296
Исполнительный офис прокуроров США
Исполнительный офис прокуроров США
Арла Витте-Симпсон
Служба связи с общественностью
Исполнительный офис прокуроров США
Министерство юстиции
175 N Street, N.E.
Suite 5.400
Вашингтон, округ Колумбия 20530-0001
Телефон: (202) 252-6036
Форма онлайн-запроса
Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 252-6020
Связь с общественностью по Закону о свободе информации)05 36-6022)05 36-6022 Исполнительный офис попечителей США
Исполнительный офис попечителей США
Randi Meth
Советник по Закону о свободе информации
Офис главного юрисконсульта
Исполнительный офис попечителей США
Министерство юстиции
441 G Street, NW, Suite 6150
Washington, DC 20530
Телефон: (202) 307-1399
Факс: (202) 307-2397
Эл. : (202) 307-1399
Представитель по связям с общественностью по Закону о свободе информации: Елизавета Ференцевич, (202) 307-1399
Федеральное Бюро Расследований
Федеральное бюро расследований
Майкл Г. Зайдель, начальник отдела
Отдел документации/распространения информации
Отдел управления документами
Федеральное бюро расследований
Министерство юстиции
200 Конституция Драйв
Винчестер, Вирджиния 22602
Телефон: (540) 868-4593
Факс: (540) 868-4997
Онлайн-форма запроса: https://efoia.fbi.gov
Центр обслуживания запросов по Закону о свободе информации: (540) 868-1535
Представитель по связям с общественностью по Закону о свободе информации: Джозеф Бендер, (540) 868-2101
Федеральное бюро тюрем
Федеральное бюро тюрем
Юджин Байме
Надзорный прокурор
Запросы Закона о свободе информации/Закона о конфиденциальности
Федеральное бюро тюрем
Министерство юстиции
Комната 924, здание HOLC
320 First Street, N. W.
Washington, DC 20534
Телефон: (202) 514-6655
Эл. 202) 616-7750
Комиссия по урегулированию иностранных претензий США
Комиссия США по урегулированию иностранных претензий
Джереми Р. ЛаФрансуа
Главный административный советник
Комиссия по урегулированию иностранных претензий
Министерство юстиции
441 G Street, NW Room 6330
Washington, DC 20579
Телефон: (202) 616-6975
Факс: (202) 616-6993
Электронная почта: info.fcc @usdoj.gov
Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 616-6975
Представитель по связям с общественностью по Закону о свободе информации: Джереми Р. ЛаФрансуа, (202) 616-6975
ИНТЕРПОЛ (Национальное центральное бюро США)
ИНТЕРПОЛ (Национальное центральное бюро США)
Дэниел Дембковски
Специалист по правительственной информации
Офис главного юрисконсульта
Интерпол-Национальное центральное бюро США
Министерство юстиции
Вашингтон, округ Колумбия 20530
Телефон: (202) 616-0201
Электронная почта: Interpol-USNCB. [email protected]
Центр обслуживания запросов по Закону о свободе информации: (202) 616-0201
Представитель по связям с общественностью по Закону о свободе информации: Даниэль Дембковски, (202) 616-0201
Отдел управления правосудием
Отдел управления правосудием
Карен Макфадден
FOIA Контактное лицо
Управление юстиции
Министерство юстиции
Комната 1111 RFK, 950 Pennsylvania Avenue, N.W.
Вашингтон, округ Колумбия 20530-0001
Телефон: (202) 514-3101
Электронная почта: [email protected]
Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 514-3101
Представитель по связям с общественностью по Закону о свободе информации: Карен Макфадден, 5 (202) -3101
Отдел национальной безопасности
Отдел национальной безопасности
Арнетта Мэллори
Специалист по правительственной информации
Отдел национальной безопасности
Министерство юстиции
3 Площадь Конституции
175 N Street N. E., 12th Floor
Вашингтон, округ Колумбия 20530-0001
Телефон: (202) 233-2639
Эл. : (202) 233-2639
Представитель по связям с общественностью по Закону о свободе информации: Патрисия Мэтьюз, (202) 233-2639
Управление общественной полицейской службы
Управление общественной полицейской службы
Николь Ли, сотрудник Закона о свободе информации
Юридический отдел
Управление общественной полиции
Министерство юстиции
Площадь Две Конституции
145 N Street. Н.Э.
Washington, DC 20530-0001
Телефон: (202) 514-1873
Факс: (202) 514-3456
Эл. Представитель FOIA по связям с общественностью: Мелисса Фиери-Фетров, (202) 514-1873
Управление информационной политики
Управление информационной политики
Дуглас Хиббард
Начальник отдела первоначального запроса
Управление информационной политики
Министерство юстиции
6-й этаж
441 G St NW
Вашингтон, округ Колумбия 20530
Телефон: (202) 514-FOIA
Форма онлайн-запроса
FO 9000 Служба запроса Центр: (202) 514-3642
FOIA Представитель по связям с общественностью: Валери Вильянуэва, (202) 514-3642
Управление программ юстиции
Управление программ юстиции
Моника Поттер-Джонсон
Специалист по правительственной информации
Управление программ юстиции
Министерство юстиции
Комната 5400, 810 7th Street, N. W.
Washington, DC 20531
Телефон: (202) 307-6235
Факс: (202) 307-1419
Эл. Чандрия Слотер, (202) 307-6235
Офис юрисконсульта
Офис юрисконсульта
Мелисса Голден
Ведущий помощник юриста и специалист FOIA
Министерство юстиции
, комната 5517, Пенсильвания-авеню, 950, северо-запад.
Washington, DC 20530-0001
Телефон: (202) 514-2053
Эл. ) 514-2053
Управление правовой политики
Управление правовой политики
Дуглас Хиббард
Начальник отдела первоначального запроса
Управление информационной политики
Министерство юстиции
6-й этаж
441 G St NW
Вашингтон, округ Колумбия 20530
Телефон: (202) 514-FOIA
Форма онлайн-запроса
Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 514-3642
Представитель по связям с общественностью по Закону о свободе информации: Валери Вильянуэва, 5, (20) -3642
Управление по законодательным вопросам
Управление по законодательным вопросам
Дуглас Хиббард
Начальник отдела первоначального запроса
Управление информационной политики
Министерство юстиции
6-й этаж
441 G St NW
Вашингтон, округ Колумбия 20530
Телефон: (202) 514-FOIA
Форма онлайн-запроса
Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 514-3642
Представитель по связям с общественностью по Закону о свободе информации: Валери Вильянуэва, (202) 514-3642
Управление профессиональной ответственности
Управление профессиональной ответственности
Кармен Смит Картер, помощник советника по законам о свободе информации и конфиденциальности
Управление профессиональной ответственности
Министерство юстиции
950 Pennsylvania Avenue, N. W.
Suite 3241
Вашингтон, округ Колумбия 20530
Телефон: (202) 514-3365
Факс: (202) 514-5050
Эл.
Представитель по связям с общественностью по Закону о свободе информации: Аннетт Уормли, (202) 514-3365
Управление по связям с общественностью
Управление по связям с общественностью
Дуглас Хиббард
Начальник отдела первоначального запроса
Управление информационной политики
Министерство юстиции
6-й этаж
441 G St NW
Вашингтон, округ Колумбия 20530
Телефон: (202) 514-FOIA
Онлайн-форма запроса
Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 514-3642
Представитель по связям с общественностью по Закону о свободе информации: Валери Вильянуэва, (202) 514-36042
2
2 Канцелярия помощника генерального прокурора
Офис помощника генерального прокурора
Дуглас Хиббард
Начальник отдела первоначального запроса
Управление информационной политики
Министерство юстиции
6-й этаж
441 G St NW
Вашингтон, округ Колумбия 20530
Телефон: (202) 514-FOIA
Форма онлайн-запроса
Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 514-3642
Представитель по связям с общественностью по Закону о свободе информации: Валери Вильянуэва, (202) 514-3642
Генеральная прокуратура
Генеральная прокуратура
Дуглас Хиббард
Начальник отдела первоначального запроса
Управление информационной политики
Министерство юстиции
6-й этаж
441 G St NW
Вашингтон, округ Колумбия 20530
Телефон: (202) 514-FOIA
0002 Онлайн-форма запроса
Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 514-3642
Представитель по связям с общественностью по Закону о свободе информации: Валери Вильянуэва, (202) 514-3642
Канцелярия заместителя Генерального прокурора
Канцелярия заместителя Генерального прокурора
Дуглас Хиббард
Начальник отдела первоначального запроса
Управление информационной политики
Министерство юстиции
6-й этаж
441 G St NW
Вашингтон, округ Колумбия 20530
Телефон: (202) 514-3 FOIA
Форма онлайн-запроса
Центр обслуживания запросов по Закону о свободе информации: (202) 514-3642
Представитель по связям с общественностью по Закону о свободе информации: Валери Вильянуэва, (202) 514-3642
Офис Генерального инспектора
Офис Генерального инспектора
Дебора Уоллер
Специалист по правительственной информации
Офис Генерального инспектора
Министерство юстиции
Комната 4726
950 Pennsylvania Avenue, N. W.
Washington, DC 20530-0001
Телефон: (202) 616-0646
Факс: (202) 616-9152
Электронная почта: [email protected]
Центр обслуживания запросов по Закону о свободе информации: (202) 616-0646
Представитель по связям с общественностью по Закону о свободе информации: Дебора М. Уоллер, (202) 616-0646
Офис прокурора по помилованию
Прокуратура по помилованию
Лиза Поркари, советник прокурора
Прокуратура по помилованию
Министерство юстиции
950 Pennsylvania Avenue, N.W.
Washington, DC 20530
Телефон: (202) 616-6070
Факс: (202) 616-6069
Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 616-6070
Представитель по связям с общественностью по Закону о свободе информации: Малави Уэллс, (202) 616-6070
Офис генерального солиситора
Office of the General Solicitor
Valerie H. Yancey
Сотрудник по Закону о свободе информации и исполнительный директор
Office General Solicitor
Министерство юстиции
950 Pennsylvania Avenue, N. W., Room 6627
Washington, DC 20530-0001
Телефон: (2022020202020202020202020202020202020202020300001
) 616-9406
Электронная почта: [email protected]
Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 616-9406
Представитель по связям с общественностью по Закону о свободе информации: Валери Х. Янси, (202) 514-2203
Управление племенной юстиции
Управление племенного правосудия
Арла Витте-Симпсон
Служба по связям с общественностью по Закону о свободе информации
Исполнительный офис прокуроров США
Министерство юстиции
175 N Street, N.E.
Suite 5.400
Вашингтон, округ Колумбия 20530-0001
Телефон: (202) 252-6036
Факс: (202) 252-6048
Онлайн-форма запроса
Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 259-60200003
Связь с общественностью по Закону о свободе информации: (202) 252-6036
Управление по борьбе с насилием в отношении женщин
Управление по борьбе с насилием в отношении женщин
Кэтрин Постон
Советник адвоката
145 N Street NE
Suite 10W. 121
Вашингтон, округ Колумбия 20530
Телефон: (202) 307-6026
Эл. Центр обслуживания заявителей: (202) 307-6026
Представитель по связям с общественностью по Закону о свободе информации: Кэтрин Постон, (202) 307-6026
Консультативный офис по профессиональной ответственности
Консультативный отдел по вопросам профессиональной ответственности
Маргерит А. Дриссен
Адвокат-консультант
Консультативный отдел по вопросам профессиональной ответственности
Министерство юстиции
441 G Street, NW
6-й этаж
Вашингтон, округ Колумбия 20530
Телефон: (202) 5814-00 202) 353-7483
Электронная почта: [email protected]
Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 514-0458
Представитель по связям с общественностью по Закону о свободе информации: Квадира Зелеке, (202) 514-0458
Налоговый отдел
Налоговый отдел
Кармен М. Банерджи
Старший юрисконсульт отдела по вопросам Закона о свободе информации и Федерального закона
Налоговый отдел
Министерство юстиции
Почтовый ящик 227
Ben Franklin Station
Washington, DC 20044
Телефон: (202) 307-10643 9 : TaxDiv. [email protected]
Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 307-6423
Представитель по связям с общественностью по Закону о свободе информации: Кармен М. Банерджи, (202) 307-6423
Поверенные США
Адвокаты США
Арла Витте-Симпсон
Отдел по связям с общественностью по Закону о свободе информации
Исполнительный офис прокуроров США
Министерство юстиции
175 N Street, N.E.
Suite 5.400
Вашингтон, округ Колумбия 20530-0001
Телефон: (202) 252-6036
Форма онлайн-запроса
Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 252-6020
Связь с общественностью по Закону о свободе информации)05 36-6022)05 36-6022 Служба маршалов США
Служба маршалов США
Шарлотта М. Лакстон
Офицер Закона о свободе информации
Служба маршалов США
Офис главного юрисконсульта
CG-3 15th Floor
Washington, DC 20530-0001
Телефон: (703) 740-3943
Эл. 703) 740-3943
Связь с общественностью по Закону о свободе информации: (703) 740-3943
Комиссия США по условно-досрочному освобождению
Комиссия США по условно-досрочному освобождению
Анисса Бэнкс
Специалист по Закону о свободе информации/PA
Комиссия США по условно-досрочному освобождению
Министерство юстиции
90 K Street NE
3rd Floor
Washington, DC 20530
Телефон: (202) 346-7030
Эл. 202) 346-7030
Была ли эта страница полезной?
Была ли эта страница полезной?
Да №
Другие полезные истории от ИТ-директора — стр. 648
Как выбрать правильные ИТ-проекты
I.T. проектные решения и то, как они принимаются, неизбежно формируют нашу судьбу. Сделайте их правильно, и мы поднимем бизнес…
Джек Кин, 15 мая 2003 г.
Последние разработки в волоконной оптике
НЕ СМОТРИТЕ СЕЙЧАС, но новое оптическое волокно с низкими потерями — с зеркальной сердцевиной — может проводить интенсивный поток лазерного света, который…
Джон Эдвардс, 15 мая 2003 г.
Знакомство с услугами с оплатой по факту использования перед регистрацией
Разочарованный генеральный менеджер быстрорастущего подразделения фармацевтической компании из списка Fortune 100 решил поиграть с ИТ своей корпорации …
Майкл Шраге, 15 мая 2003 г.
Профиль Томаса Джарретта, секретаря Департамента технологий и информации и директора по информационным технологиям
Возраст: 51 год Зарплата: 133 660 долларов Предыдущее место работы: 30 лет работал в Verizon в штате Делавэр, занимая должность директора правительство, образование …
Трейси Мэйор, 1 мая 2003 г. оп, Бисмарк, Н.Д. Взяли на работу…
Трейси Мэйор, 1 мая 2003 г.
Представлено Microsoft
Новый подход к оценке ERP
В этом техническом документе представлена структура для оценки современной ERP и того, как она может улучшить результаты бизнеса.
Доступ сейчас
Вопросы и ответы с Дэном Ариели: почему хорошие ИТ-директора принимают плохие решения
Как ИТ-директору вам знаком следующий сценарий: вы вложили 900 000 долларов в систему прогнозирования, которая, как ожидается, будет стоить 1 доллар… Меридит Левинсон, 1 мая 2003 г.
База данных отпечатков пальцев ФБР помогла раскрыть дело об убийстве 45-летней давности
В среду, 29 января 2003 г., полиция арестовала 69-летнего Джеральда Ф. Мейсона за убийство двух патрульных из Эль-Сегундо, Калифорния. …
Бен Уортен, 1 мая 2003 г.
Почему стоит управлять ИТ как портфелем
Управление портфелем позволяет получить целостный взгляд на ИТ-портфель компании. В нем сравниваются инвестиции в технологии с точки зрения риска и …
Автор Lorraine Cosgrove WareMay, 1 2003
Оповещение для сотрудников
С ростом аутсорсинга ИТ-директора находятся в центре морального кризиса. Они видят, как многие их работники борются со стрессом на работе. Лучшие лидеры учатся помогать сотрудникам сейчас и удерживать их в будущем.
Стефани Оверби, 1 мая 2003 г.
Использование смарт-карт в Париже
В Париже трудно представить день без смарт-карт. Маленькие пластиковые карты, изобретенные во Франции в 1979 году…
By Susannah Patton May, 1 May, 2003
Европейские фирмы не сосредотачиваются на расходах на ИТ-безопасность
Безопасность является главной заботой повсюду, но в Европе эта забота не отражается в решениях по бюджетированию. Безопасность заняла третье место в …
Кэтлин Карр, 1 мая 2003
Правильное управление портфелем
Рон Кифер, вице-президент по управлению программами в DHL Americas, является ветераном типичного планирования проектов и портфелей? или …
Тодд Datz, 1 мая 2003 г.
Перемещение ИТ-директора, май 2003 г.
Алексей Зоглин (слева) отправился в путь. В прошлом месяце он покинул свой пост технического директора Orbitz после трехлетнего …
By Meridith Levinson, 1 мая 2003
FTC создаст реестр «Не звонить»
Нет ничего более раздражающего, чем незнакомец, звонящий во время ужина, чтобы продать вас
Джули Хэнсон, 1 мая 2003 г.
Отзывы читателей Февраль, март 2003 г. Выпуски журнала CIO Magazine: Cigna, Передовой опыт в области ИТ, Открытый исходный код
Статья Cigna не соответствует действительностиВаша статья от 15 марта [«Самостоятельные раны Cigna»] об инициативе Cigna HealthCare по преобразованию для интеграции службы поддержки клиентов…
By CIO Staff, 1 мая 2003 г. Охотники
Луи Фриссор управляет дата-центрами. Александр Седроне, менеджер хранилища данных, обеспечивает работу CRM. Сьюзен Брэдли — специалист по кадрам …
Майкл Голдберг, 1 мая 2003 г.
Экономическое обоснование управления ИТ-портфелем
По данным исследования AMR Research, 75% компаний не имеют четкого постоянного контроля над портфелями своих ИТ-проектов…
Автор Richard Pastore, 1 мая 2003 г.
ВОЗМОЖНО, вы узнаете знаменитые телефоны Polycom с треугольным динамиком, серые коммуникаторы, которые сидят на столах в конференц-залах по всему миру.
…
Дебби Янг, 1 мая 2003 г.
Как сохранить удовлетворенность ваших ИТ-клиентов
Точно так же, как удовлетворенность клиентов является ключевой целью для компаний, обеспечение удовлетворенности конечных пользователей является важной обязанностью …
Моханбир Сохни, 1 мая 2003 г. утечки ниже и ответьте «верно», если они соответствуют описанию, или «ложно», если они… ориентироваться в меняющемся ландшафте новых законодательных и нормативных директив, влияющих на ИТ и …
Эбби Лундберг, 15 апреля 2003 г.
Индустрия развлечений против музыкального и кинопиратства
До сих пор ИТ-директор уважаемой исследовательской организации в Калифорнии понятия не имеет, как кто-то взломал его …
By Sarah D ScaletApr, 15 2003
Широкополосный доступ в Интернет скоро появится в ближайшей к вам розетке?
ШИРОКОПОЛОСНЫЙ ИНТЕРНЕТ через каждую электрическую розетку? Технология существует. Но индустрия широкополосной связи по линиям электропередач все еще сталкивается с внедрением, регулированием …
Кристофер Линдквист, 15 апреля 2003 г.
Долгосрочные результаты служебных вычислений
Служебные вычисления — скромный термин для большой идеи: архитектуры, в которой управление сетью сведено к …
Автор Фред Хэпгуд, 15 апр. Страница не найдена [404] | Расширение сотрудничества UGA
Публикации
4-H Молодежное развитие Встречи округов и клубов, экологическое просвещение, программы животноводства, достижения проекта, летний лагерь
Животноводство Аквакультура, говядина, пчелы, молочные продукты, лошади, мелкие жвачные, птица и яйца, свиноводство
Окружающая среда и природные ресурсы Инвазивные виды, предотвращение загрязнения, лесное хозяйство, вода и засуха, погода и климат, дикая природа
Деньги, семья и дом Развитие взрослых и семьи, развитие младенцев, детей и подростков, деньги, жилье и домашняя среда
Полевые культуры, производство кормов и газонов Кукуруза, хлопок, фураж, конопля, арахис, мелкозерновые, соевые бобы, табак, газонная трава
Еда и здоровье Сохранение пищевых продуктов, коммерческая и домашняя безопасность пищевых продуктов, пищевая наука и производство, питание и здоровье
Производство фруктов, овощей и декоративных растений Черника, виноград, декоративное садоводство, лук, персики, орехи пекан, мелкие фрукты, овощи
Газон, сад и ландшафт Домашние сады, уход за газонами, декоративные растения, ландшафтный дизайн
Сорняки, болезни и вредители Болезни животных и паразиты, муравьи, термиты, вши и другие вредители, вредные животные, борьба с вредителями и болезнями растений, сорняки
Актуальные и актуальные темы Последние обновления, инициативы и программы от UGA Extension.
Избранные программы
4-H Встречи округов и клубов
Волонтерская программа Master Gardener Extension
Образовательная программа по безопасности пестицидов
Учебная программа школьного сада
Обучение ServSafe®
Услуги по тестированию почвы и воды
Классы, семинары и клубные встречи UGA Extension предлагает множество персонализированных услуг как семинары, классы, консультации, сертификаты, лагеря и педагог Ресурсы.
No related posts.
Навигация по записям
Предыдущая статьяСколько в 18 месяцах дней: Сколько дней в 18 месяцах
Следующая статья4 умножить на 4 плюс 4: 4 ПЛЮС 4 УМНОЖИТЬ НА 4 ПОМОГИТЕ
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Найти:
Рубрики
Геометрия
Математика
Физика
Химия
Школьная жизнь
Разное
© 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»
Карта сайта