ГЛАВА 1. ОБЩИЙ ЗНАМЕНАТЕЛЬ. Как выбирать своих людей
ГЛАВА 1. ОБЩИЙ ЗНАМЕНАТЕЛЬ
«Человек по своей природе не плохой. Он хороший. Но между ним и хорошими качествами лежат страх, гнев и подавления».
Л. Рон Хаббард, «Свободный Человек», журнал «Способность», № 232
Один мудрый человек однажды сказал, что нет двух абсолютно одинаковых людей. За это мы можем быть во век ему благодарны.
Люди бывают высокие, низкие и разного цвета. Разные биографии, жизненный опыт и есть такие, которым нравится ставить пластмассовых фламинго в своих палисадниках.
Однако, несмотря на очевидную уникальность личности, Рон Хаббард столкнулся с общим знаменателем в каждом: эмоции. Эмоции!
Он, должно быть, имеет в виду нервную женщину, визжащую при виде мыши, ребенка закатывающего истерики, когда не может получить булочку, напуганного солдата, который не возвращается на поле боя, жену, истерично рыдающую из-за того, что муж ее не любит.
Однако, по мере того как я читала книгу Рона Хаббарда, я наблюдала за всеми людьми, которых я знала (и когда это было неизбежно, я даже смотрела на себя). Его выводы представляются правдивыми. Каждый человек придерживается какого-то мнения относительно жизни — он находит ее жестокой, пугающей, полной раскаяния, сводящей с ума или прекрасной — но его точка зрения обусловлена не рассуждениями или интеллектом.
Она определяется эмоцией. Это знаменательное открытие Рона Хаббарда выявило три важных факта об эмоциях:
1. Есть набор неизменных реакций соответствующих каждой эмоции.
2. Эмоции идут в определенном порядке — от плохих к хорошим.
3. Есть слои сдерживаемых эмоций, ранее неизвестных.
НАБОР ЭМОЦИЙ
Каждой эмоции сопутствует полный, неизменный набор отношений и поведения. Поэтому, как только мы понимаем, что этот человек в горе (временно или хронически) мы ожидаем, что он будет горестно жаловаться: «Меня предали.
ПОСЛЕДОВАТЕЛЬНОСТЬ ЭМОЦИЙ
Именно в процессе исследований методов улучшения духовного здоровья Рон Хаббард обнаружил закономерность реакций по мере продвижения людей. Помогая индивидуумам убирать воздействия болезненного прошлого, он обнаружил, что в процессе работы они часто сначала проявляли апатию и, при продолжении работы, они проходили через определенные эмоциональные ступени, которые всегда появлялись в одном и том же неизменном порядке для каждого человека: горе, страх, скрытая враждебность, гнев (или воинственность), антагонизм, скука, удовлетворенность и хорошее состояние.
Затем он понял, что можно нарисовать эти эмоциональные реакции в виде шкалы, с более радостными наверху и скверными внизу. Вскоре стало очевидно, что каждый человек в любой момент находится где-то на этой шкале, хотя он двигается вверх и вниз по ней, в зависимости от того испытывает ли он удачу или неудачу.
Также стало ясно, что чем выше положение человека на эмоциональной Шкале Тонов, тем лучше он выживает. Он более способен достигать необходимого для жизни. Он более счастлив, более жив, более уверен и компетентен. Он побеждает. Наоборот, чем ниже падает человек по Шкале Тонов, тем ближе он к смерти. Он проигрывает, более несчастен, готов стать жертвой.
Если мы планируем трудное путешествие по дикой, необитаемой местности, эмоциональная шкала подсказывает нам, что не следует выбирать в компаньоны того, кто тоскливо слоняется, жалуясь, что все это звучит ужасно. Нам лучше взять парня, который с нетерпением ожидает эту поездку.
Нам лучше взять парня, который с нетерпением ожидает эту поездку.
Люди, находящиеся низко на этой шкале, ничего с нетерпением не ожидают. Чем меньше человек думает о будущем, тем ниже его шансы на выживание.
Для того чтобы отличать их друг от друга, Рон Хаббард дал различным эмоциям название и номер, по мере того как классифицировал их. Законченную последовательность он назвал Эмоциональная Шкала Тонов. Каждая эмоциональная позиция называется «тон». Как каждому музыкальному тону соответствует звук определенной высоты и вибрации, так и каждый тон на эмоциональной шкале содержит в себе присущие только ему характеристики. Было бы довольно трудно играть на пианино, если бы клавиши были не в последовательности, а перемешаны. И также почти невозможно понять людей и помочь им улучшиться без правильной шкалы, которая скажет нам точно насколько высоко или низко находится этот человек на клавиатуре эмоций.
Разделяющая линия шкалы тонов — это 2.0. Выше этой точки человек хорошо выживает. Ниже этого уровня его жизненные надежды довольно ничтожны. Используя эту линию, мы называем людей выше как «высоко-тонных». Людей ниже 2.0 как «низко-тонных».
Ниже этого уровня его жизненные надежды довольно ничтожны. Используя эту линию, мы называем людей выше как «высоко-тонных». Людей ниже 2.0 как «низко-тонных».
Там, где высоко-тонный человек разумен, низко-тонный человек действует нерационально. Чем ниже его тон, тем больше решения и поведение человека находятся под управлением эмоциональных чувств, несмотря на его образование или интеллект.
СДЕРЖИВАЕМЫЕ ЭМОЦИИ
Когда мы слышим об уравновешенном, «респектабельном» президенте банка с преданной семьей, который внезапно присваивает сто тысяч долларов и сматывается в Южную Америку с молоденькой танцовщицей, мы можем задать вопрос: «О чем он думал?» В этом то, конечно, и проблема. Он не думал. Он чувствовал. Эмоции руководили им, как и почти каждым. Вероятно, такие люди застают нас врасплох только из-за того, что их эмоциональный тон был сдерживаемым. Некоторые эмоции очевидны, потому что они выраженные. Но Рон Хаббард обнаружил, что под каждой выраженной эмоцией существует полоса сдерживаемых эмоций:
(энтузиазм) 4. 0 ЭНТУЗИАЗМ-выраженный
0 ЭНТУЗИАЗМ-выраженный
(интерес) 3.5
(консерватизм) 3.0 ЭНТУЗИАЗМ-сдерживаемый
(скука) 2.5
(антагонизм) 2.0
(боль) 1.8 ВРАЖДЕБНОСТЬ-выраженная
(гнев) 1.5
(отсутствие сочувствия) 1.2 ВРАЖДЕБНОСТЪ-сдерживаемая
(скрытая враждебность) 1.1
(страх) 1.0 СТРАХ-выраженный
(сочувствие) 0.9 СТРАХ-сдерживаемый
(задабривание) 0.8
(горе) 0.5 ГОРЕ-выраженное
(заглаживание вины) 0.375 ГОРЕ-сдерживаемое
(апатия) 0.05
С открытием этих, едва различимых, сдерживаемых эмоций, лежащих точно между выраженными эмоциями, как слои в «клубном» бутерброде[1], мы теперь имеем новую классификацию многих позиций человека по отношению к жизни.
Ничто из этого не означает, что человек постоянно фиксируется в какой-либо определенной позиции. Люди могут меняться. И иногда высоко-тонный человек может резко упасть на короткий период. Но если он достаточно высоко-тонный, он восстановится.
КАК ВЫ МОЖЕТЕ ИСПОЛЬЗОВАТЬ ЭТОТ МАТЕРИАЛ
Так как мы знаем основные характеристики каждой эмоции, мы можем встретить человека в первый раз и, в течение минут, можем понять его теперешнее расположение духа.
Глава 4. Общий анализ изображения конструктивной фигуры человека. Интерпретация третьего уровня
Глава 4. Общий анализ изображения конструктивной фигуры человека. Интерпретация третьего уровня Интерпретация третьего уровня осуществляется по всем четырем рисункам. Как было показано в предыдущей главе, первый рисунок имеет важное значение для диагностики и
Общий адаптационный синдром
Общий адаптационный синдром
Решив, что его эксперименты с крысами не привели к успеху (в конце концов, новый гормон он не открыл), Ганс Селье принялся искать другие возможные причины обнаруженных им симптомов. Но через несколько лет, уже будучи студентом-медиком
Но через несколько лет, уже будучи студентом-медиком
Глава VIII. Классификация выражений. Общий очерк всех мимических явлений
Глава VIII. Классификация выражений. Общий очерк всех мимических явлений Рассматривая какое-нибудь явление природы в качестве наблюдателей или художников, мы можем гордиться своим уменьем подмечать в нем существенные черты, тени и полутени, и в особенности – возможностью
8.1. Общий обзор
8.1. Общий обзор Термин «дефицит» происходит от латинского глагола «deficio», что означает буквально «не хватать, недоставать, оказываться недостаточным». Так что часто задаваемый врачами своим пациентам вопрос «На что жалуетесь?» в скрытой форме подразумевает именно то, что
Общий множитель
Общий множитель
В первый раз, когда я пошел на прием к Хорхе, я знал, что он не совсем обычный психотерапевт. Клаудиа, порекомендовавшая мне его, предупредила, что «Толстяк», как она его называла, был «немного специфическим» типом (sic)[1].Мне уже надоела привычная
Клаудиа, порекомендовавшая мне его, предупредила, что «Толстяк», как она его называла, был «немного специфическим» типом (sic)[1].Мне уже надоела привычная
Глава 4. Общий Реестр двадцати основных мужских сексуальных фобий в начале любовных отношений
Глава 4. Общий Реестр двадцати основных мужских сексуальных фобий в начале любовных отношений Внимание! Данная глава является продолжением и по сути даже приложением к предшествующей главе №3 «Тридцать основных объяснений мужской сексуальной сдержанности в начале
ЕСТЬ ЛИ ОБЩИЙ РЕЦЕПТ?
ЕСТЬ ЛИ ОБЩИЙ РЕЦЕПТ? Кажется, сейчас я поведу традиционные речи о спортивном образе жизни, свежем воздухе, режиме, воздержанности…Все это для человека то же, что для растения почва, тепло, вода, солнечный свет. Все это необходимо. Но… недостаточно и, увы, не всегда
МАЗОХИЗМ.
 ОБЩИЙ ОБЗОР
ОБЩИЙ ОБЗОРМАЗОХИЗМ. ОБЩИЙ ОБЗОР С моей точки зрения, к мазохизму относится широкий спектр феноменов, как нормальных, так и патологических, имеющих общее качество аутодеструктивности и получения сознательного или бессознательного удовольствия от страдания. Границы этой области
Глава 4. Общий подход к нейтрализации замечаний
Глава 4. Общий подход к нейтрализации замечаний Мы привели краткий перечень возможных возражений и замечании собеседников. Замечаний чаще всего неприятных. Но и нам самим приходится, в свою очередь, предъявлять претензии, критиковать, уличать в неблаговидных поступках,
Глава 11 Общий выигрыш – миф, или Обойдемся без поражений
Глава 11 Общий выигрыш – миф, или Обойдемся без
Глава 7 Наименьший общий знаменатель Институциональная Тень
Глава 7
Наименьший общий знаменатель
Институциональная Тень
Всякий, кто может заставить вас поверить в нелепицу, может и убедить совершать злодеяния. Вольтер
Видите ли, в этом мире есть одна ужасная вещь, а именно что каждый имеет на все свое объяснение.
Жан Ренуар
Самые
Вольтер
Видите ли, в этом мире есть одна ужасная вещь, а именно что каждый имеет на все свое объяснение.
Жан Ренуар
Самые
Какой общий знаменатель у дробей 7/45, 11/27, 5/18… -reshimne.ru
Новые вопросы
Ответы
У этих дробей общий знаменатель равен 270
Похожие вопросы
Сумма длин всех рёбер прямоугольного параллелепипеда равна 220 см, два его измерения- 25 см и 27 см. Найдите третье измерение параллелепипеда…
Найдите значение выражения: а) 1целая 1/6 + 1целая 1/3x + 2целых 2/9, если x= 0,5 Б) 4,8 😡 + 3,27 : x ,если x=0,3…
Знайдіть середнє арифметичне чисел 32,35,44,22. ..
..
Помогите пж очень нужно первое и второе…
6 задание.Пожалуйста помогите!Заранее спасибо….
Решите пожалуйста дам 20 баллов…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Как привести к общему знаменателю большие числа.
 Приведение дробей к наименьшему общему знаменателю, правило, примеры, решения
Приведение дробей к наименьшему общему знаменателю, правило, примеры, решенияЗнаменателем арифметической дроби a / b называют число b, показывающее размеры долей единицы, из которых составлена дробь. Знаменателем алгебраической дроби A / B называют алгебраическое выражение B. Для выполнения арифметических действий с дробями их необходимо привести к наименьшему общему знаменателю.
Вам понадобится
- Для работы с алгебраическими дробями при нахождении наименьшего общего знаменателя необходимо знать методы разложения многочленов на множители.
Инструкция
Рассмотрим приведение к наименьшему общему знаменателю двух арифметических дробей n/m и s/t, где n, m, s, t – целые числа. Понятно, что эти две дроби можно привести к любому знаменателю, делящемуся на m и на t. Но стараются привести к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей m и t данных дробей. Наименьшее кратное (НОК) чисел – это наименьшее , делящееся одновременно на все заданные числа. 2. Для
2. Для
Чтобы привести дроби к наименьшему общему знаменателю, надо: 1) найти наименьшее общее кратное знаменателей данных дробей, оно и будет наименьшим общим знаменателем. 2) найти для каждой из дробей дополнительный множитель, для чего делить новый знаменатель на знаменатель каждой дроби. 3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Примеры. Привести следующие дроби к наименьшему общему знаменателю.
Находим наименьшее общее кратное знаменателей: НОК(5; 4)=20, так как 20 — самое меньшее число, которое делится и на 5 и на 4. Находим для 1-й дроби дополнительный множитель 4 (20: 5=4). Для 2-й дроби дополнительный множитель равен 5 (20: 4=5). Умножаем числитель и знаменатель 1-й дроби на 4, а числитель и знаменатель 2-й дроби на 5. Мы привели данные дроби к наименьшему общему знаменателю (20 ).
Наименьший общий знаменатель этих дробей — число 8, так как 8 делится на 4 и на само себя. Дополнительного множителя к 1-й дроби не будет (или можно сказать, что он равен единице), ко 2-й дроби дополнительный множитель равен 2 (8: 4=2). Умножаем числитель и знаменатель 2-й дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (8 ).
Дополнительного множителя к 1-й дроби не будет (или можно сказать, что он равен единице), ко 2-й дроби дополнительный множитель равен 2 (8: 4=2). Умножаем числитель и знаменатель 2-й дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (8 ).
Данные дроби не являются несократимыми.
Сократим 1-ю дробь на 4, а 2-ю дробь сократим на 2. (см. примеры на сокращение обыкновенных дробей: Карта сайта → 5.4.2. Примеры сокращения обыкновенных дробей ). Находим НОК(16; 20)=2 4 · 5=16· 5=80. Дополнительный множитель для 1-й дроби равен 5 (80: 16=5). Дополнительный множитель для 2-й дроби равен 4 (80: 20=4). Умножаем числитель и знаменатель 1-й дроби на 5, а числитель и знаменатель 2-й дроби на 4. Мы привели данные дроби к наименьшему общему знаменателю (80 ).
Находим наименьший общий знаменатель НОЗ(5; 6 и 15)=НОК(5; 6 и 15)=30. Дополнительный множитель к 1-й дроби равен 6 (30: 5=6), дополнительный множитель ко 2-й дроби равен 5 (30: 6=5), дополнительный множитель к 3-ей дроби равен 2 (30: 15=2). Умножаем числитель и знаменатель 1-й дроби на 6, числитель и знаменатель 2-й дроби на 5, числитель и знаменатель 3-ей дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (30 ).
Умножаем числитель и знаменатель 1-й дроби на 6, числитель и знаменатель 2-й дроби на 5, числитель и знаменатель 3-ей дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (30 ).
Страница 1 из 1 1
В данном материале мы разберем, как правильно приводить дроби к новому знаменателю, что такое дополнительный множитель и как его найти. После этого сформулируем основное правило приведения дробей к новым знаменателям и проиллюстрируем его примерами задач.
Понятие приведения дроби к другому знаменателю
Вспомним основное свойство дроби. Согласно ему, обыкновенная дробь a b (где a и b – любые числа) имеет бесконечное количество дробей, которые равны ей. Такие дроби можно получить, умножив числитель и знаменатель на одинаковое число m (натуральное). Иными словами, все обыкновенные дроби могут быть заменены другими вида a · m b · m . Это и есть приведение исходного значения к дроби с нужным знаменателем.
Привести дробь к другому знаменателю можно, умножив ее числитель и знаменатель на любое натуральное число. Главное условие – множитель должен быть одинаков для обоих частей дроби. В итоге получится дробь, равная исходной.
Главное условие – множитель должен быть одинаков для обоих частей дроби. В итоге получится дробь, равная исходной.
Проиллюстрируем это примером.
Пример 1
Привести дробь 11 25 к новому знаменателю.
Решение
Возьмем произвольное натуральное число 4 и умножим обе части исходной дроби на него. Считаем: 11 · 4 = 44 и 25 · 4 = 100 . В итоге получилась дробь 44 100 .
Все подсчеты можно записать в таком виде: 11 25 = 11 · 4 25 · 4 = 44 100
Выходит, любую дробь можно привести к огромному количеству разных знаменателей. Вместо четверки мы могли бы взять другое натуральное число и получить еще одну дробь, эквивалентную исходной.
Но не любое число может стать знаменателем новой дроби. Так, для a b в знаменателе могут стоять только числа b · m , кратные числу b . Вспомните основные понятия деления – кратные числа и делители. Если число не кратно b , но делителем новой дроби оно быть не может. Поясним нашу мысль примером решения задачи.
Пример 2
Вычислить, возможно ли приведение дроби 5 9 к знаменателям 54 и 21 .
Решение
54 кратно девятке, которая стоит в знаменателе новой дроби (т.е. 54 можно разделить на 9). Значит, такое приведение возможно. А 21 мы разделить на 9 не можем, поэтому такое действие для данной дроби выполнить нельзя.
Понятие дополнительного множителя
Сформулируем, что такое дополнительный множитель.
Определение 1
Дополнительный множитель представляет собой такое натуральное число, на которое умножают обе части дроби для приведения ее к новому знаменателю.
Т.е. когда мы выполняем это действие с дробью, мы берем для нее дополнительный множитель. Например, для приведения дроби 7 10 к виду 21 30 нам потребуется дополнительный множитель 3 . А получить дробь 15 40 из 3 8 можно с помощью множителя 5 .
Соответственно, если мы знаем знаменатель, к которому необходимо привести дробь, то мы можем вычислить для нее и дополнительный множитель. Разберем, как это сделать.
Разберем, как это сделать.
У нас есть дробь a b , которую можно привести к некоторому знаменателю c ; вычислим дополнительный множитель m . Нам надо произвести умножение знаменателя исходной дроби на m . У нас получится b · m , а по условию задачи b · m = c . Вспомним, как связаны между собой умножение и деление. Эта связь подскажет нам следующий вывод: дополнительный множитель есть не что иное, как частное от деления c на b , иначе говоря, m = c: b .
Таким образом, для нахождения дополнительного множителя нам нужно разделить требуемый знаменатель на исходный.
Пример 3
Найдите дополнительный множитель, с помощью которого дробь 17 4 была приведена к знаменателю 124 .
Решение
Используя правило выше, мы просто разделим 124 на знаменатель первоначальной дроби – четверку.
Считаем: 124: 4 = 31 .
Выполнять расчеты такого типа часто требуется при приведении дробей к общему знаменателю.
Правило приведения дробей к указанному знаменателю
Перейдем к определению основного правила, с помощью которого можно привести дроби к указанному знаменателю. Итак,
Итак,
Определение 2
Для приведения дроби к указанному знаменателю нужно:
- определить дополнительный множитель;
- умножить на него и числитель, и знаменатель исходной дроби.
Как применить это правило на практике? Приведем пример решения задачи.
Пример 4
Выполните приведение дроби 7 16 к знаменателю 336 .
Решение
Начнем с вычисления дополнительного множителя. Разделим: 336: 16 = 21 .
Полученный ответ умножаем на обе части исходной дроби: 7 16 = 7 · 21 16 · 21 = 147 336 . Так мы привели исходную дробь к нужному знаменателю 336 .
Ответ: 7 16 = 147 336 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Для решения примеров с дробями необходимо уметь находить наименьший общий знаменатель. Ниже приведена подробная инструкция.
Как найти наименьший общий знаменатель – понятие
Наименьший общий знаменатель (НОЗ) простыми словами – это минимальное число, которое делится на знаменатели всех дробей данного примера. Другими словами его называют Наименьшим Общим Кратным (НОК). НОЗ используют только в том случае, если знаменатели у дробей различны.
Другими словами его называют Наименьшим Общим Кратным (НОК). НОЗ используют только в том случае, если знаменатели у дробей различны.
Как найти наименьший общий знаменатель – примеры
Рассмотрим примеры нахождения НОЗ.
Вычислить: 3/5 + 2/15.
Решение (Последовательность действий):
- Смотрим на знаменатели дробей, убеждаемся, что они разные и выражения максимально сокращены.
- Находим наименьшее число, которое делится и на 5, и на 15. Таким числом будет 15. Таким образом, 3/5 + 2/15 = ?/15.
- Со знаменателем разобрались. Что будет в числителе? Помочь выяснить это нам поможет дополнительный множитель. Дополнительный множитель – это число, получившееся при делении НОЗ на знаменатель конкретной дроби. Для 3/5 дополнительный множитель равен 3, так как 15/5 = 3. Для второй дроби дополнительным множителем будет 1, так как 15/15 = 1.
- Выяснив дополнительный множитель, умножаем его на числители дробей и складываем получившиеся значения.
 3/5 + 2/15 = (3*3+2*1)/15 = (9+2)/15 = 11/15.
3/5 + 2/15 = (3*3+2*1)/15 = (9+2)/15 = 11/15.
Ответ: 3/5 + 2/15 = 11/15.
Если в примере складываются или вычитаются не 2, а 3 или больше дробей, то НОЗ нужно искать уже для стольких дробей, сколько дано.
Вычислить: 1/2 – 5/12 + 3/6
Решение (последовательность действий):
- Находим наименьший общий знаменатель. Минимальным числом, делящимся на 2, 12 и 6 будет 12.
- Получим: 1/2 – 5/12 + 3/6 = ?/12.
- Ищем дополнительные множители. Для 1/2 – 6; для 5/12 – 1; для 3/6 – 2.
- Умножаем на числители и приписываем соответствующие знаки: 1/2 – 5/12 + 3/6 = (1*6 – 5*1 + 2*3)/12 = 7/12.
Ответ: 1/2 – 5/12 + 3/6 = 7/12.
Наименьший общий знаменатель — базовая арифметика
Все ресурсы по базовой арифметике
6 диагностических тестов 75 практических тестов Вопрос дня Карточки Learn by Concept
Справка по основам арифметики » Фракции » Линейные уравнения с дробями » Наименьший общий знаменатель
Какой наименьший общий знаменатель у следующих дробей: ?
Возможные ответы:
Правильный ответ:
Объяснение:
Правильный ответ — 36. Лучший способ решить эту задачу — взять каждый знаменатель и перечислить его кратные. Затем вы можете найти общее кратное между каждым знаменателем.
Лучший способ решить эту задачу — взять каждый знаменатель и перечислить его кратные. Затем вы можете найти общее кратное между каждым знаменателем.
Кратно 6: 6, 12, 18, 24, 30, 36 , 42, 48
Кратно 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33 , 36 , 39, 42
Кратность 12: 12, 24, 36 , 48, 60
Кратные 36: 36 , 72, 108
Кратные 18: 18, 36 , 54, 72
равно 36.
Сообщить об ошибке
Найдите наименьший общий знаменатель:
Возможные ответы:
Правильный ответ:
5 Объяснение:
Наименьший общий знаменатель — это наименьшее число, у которого каждый знаменатель является потенциальным множителем.
1. Умножьте два наименьших знаменателя:
2. Проверьте, могут ли другие знаменатели быть факторами в этом знаменателе:
Итак, 24 — ваш наименьший общий знаменатель. (48 также является общим знаменателем всех этих дробей, но не наименьшим)
(48 также является общим знаменателем всех этих дробей, но не наименьшим)
Сообщить об ошибке
Какой наименьший общий знаменатель у дробей и ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти наименьший общий знаменатель, перечисляйте кратные обоих знаменателей, пока не найдете наименьшее кратное, общее для обоих знаменателей.
4: 4, 8, 12, 16, 20, 24, 28 , 32
7: 7, 14, 21, 28 , 35
это должен быть наименьший общий знаменатель для этих двух дробей.
Сообщить об ошибке
Что такое наименьший общий знаменатель для дробей и ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти наименьший общий знаменатель, перечисляйте кратные обоих знаменателей, пока не найдете наименьшее кратное, общее для обоих знаменателей.
4: 4, 8, 12, 16, 20 , 24
5: 5, 10, 15, 20 , 25
Поскольку 20 является первым общим кратным 4 и 5, оно должно быть наименьший общий знаменатель этих двух дробей.
Сообщить об ошибке
Найдите наименьший общий знаменатель следующих дробей:
Возможные ответы:
Правильный ответ:
5 Объяснение:
Наименьший общий знаменатель — это наименьшее общее кратное знаменателей.
Кратность 27: 27 , 54, 81, 108, 135, 162, 189, 216, 243, 270 , 81, 90
Сообщить об ошибке
Определите наименьший общий знаменатель между следующими дробями: .
Возможные ответы:
Правильный ответ:
Объяснение:
Первый шаг при поиске ЖК-дисплея набора дробей — убедиться, что каждая из дробей упрощена. и уже упрощены. Однако можно сократить до . Это значительно упрощает задачу, потому что теперь у нас есть только два разных знаменателя для работы. Отсюда мы просто умножаем каждый знаменатель, увеличивая целые числа, пока не получим общий знаменатель. Важно всегда увеличивать меньший из двух знаменателей. Например, в этой задаче у нас есть 4 и 3 в знаменателях. Поскольку 3 меньше, мы умножим его на 2, получив 6. Теперь у нас есть 4 и 6. 4 меньше, поэтому мы умножаем его на 2, чтобы получить 8. Теперь у нас есть 8 и 6. 6 меньше, поэтому мы умножаем исходный знаменатель 3 на 3, в результате чего знаменатели 8 и 9. Следуя этой тенденции, мы получаем: 12 и 9, затем 12 и 12. Следовательно, 12 будет наименьшим общим знаменателем.
и уже упрощены. Однако можно сократить до . Это значительно упрощает задачу, потому что теперь у нас есть только два разных знаменателя для работы. Отсюда мы просто умножаем каждый знаменатель, увеличивая целые числа, пока не получим общий знаменатель. Важно всегда увеличивать меньший из двух знаменателей. Например, в этой задаче у нас есть 4 и 3 в знаменателях. Поскольку 3 меньше, мы умножим его на 2, получив 6. Теперь у нас есть 4 и 6. 4 меньше, поэтому мы умножаем его на 2, чтобы получить 8. Теперь у нас есть 8 и 6. 6 меньше, поэтому мы умножаем исходный знаменатель 3 на 3, в результате чего знаменатели 8 и 9. Следуя этой тенденции, мы получаем: 12 и 9, затем 12 и 12. Следовательно, 12 будет наименьшим общим знаменателем.
Хотя простое умножение всех знаменателей дает общий знаменатель дробей, это не всегда дает ЖК-дисплей.
Сообщить об ошибке
Какой наименьший общий знаменатель между и ?
Возможные ответы:
Правильный ответ:
Объяснение:
Самый быстрый способ найти наименьший общий знаменатель — перемножить числа.
В этом случае и оба являются простыми числами и не имеют общих делителей, кроме .
Мы можем перемножить их, чтобы получить окончательный ответ.
Другой подход состоит в том, чтобы перечислить все множители каждого числа и сначала посмотреть, какой множитель входит в оба набора.
Уведомление стоит в обоих наборах перед любым другим числом, следовательно, это наименьший общий знаменатель.
Сообщить об ошибке
Какой наименьший общий знаменатель у и ?
Возможные ответы:
Правильный ответ:
Объяснение:
При нахождении наименьшего общего знаменателя самым быстрым способом является перемножение чисел.
В этом случае и общий коэффициент, отличный от , который равный . Мы можем разделить эти числа на получение и остаток.
Так вот, у них нет общего множителя, поэтому просто умножьте их на общий множитель. Ответ
Ответ
Другой подход состоит в том, чтобы перечислить множители обоих чисел и найти множитель, который появляется в обоих наборах первым.
Мы видим, что в обоих наборах стоит перед любым другим числом, таким образом, это наш ответ.
Сообщить об ошибке
Какой наименьший общий знаменатель у и ?
Возможные ответы:
Правильный ответ:
Объяснение:
Самый быстрый способ найти наименьший общий знаменатель — перемножить числа. В этом случае и общий фактор, отличный от , который . Мы можем разделить эти числа на получение и остаток. Теперь у них нет общего множителя, поэтому просто умножьте их на общий множитель. Ответ
Другой подход состоит в том, чтобы перечислить факторы каждого числа. Множитель, который появляется первым в обоих наборах, является наименьшим общим знаменателем.
Мы видим, что появляется первым в обоих наборах и, таким образом, является наименьшим общим знаменателем.
Сообщить об ошибке
Какой наименьший общий знаменатель между , и ?
Возможные ответы:
Правильный ответ:
Объяснение:
При нахождении наименьшего общего знаменателя самым быстрым способом является перемножение чисел. В случае нахождения наименьших общих знаменателей среди трех или более чисел очень важно, чтобы между двумя знаменателями и, конечно, всеми тремя не было общих делителей. Это гарантирует, что ответ всегда будет наименьшим общим знаменателем.
Скажем, мы только что перемножили числа. Это в основном или . Это число кажется большим, но давайте сократим его пополам и проверим равномерное деление на , и . Давай проверим . не делится поровну на таков и ответ.
Итак, это восходит к утверждению: «В случае нахождения наименьших общих знаменателей среди трех или более чисел очень важно, чтобы между двумя знаменателями и, конечно, всеми тремя не было общих делителей». Если я умножил а, я могу уменьшить и и, но не . Это нормально. Теперь оставшимися значениями являются , и . У них есть только общий коэффициент . Итак, давайте умножим оставшиеся значения и факторизованное значение, чтобы получить
Сообщить об ошибке
Уведомление об авторских правах
Все основные арифметические ресурсы
6 Диагностические тесты 75 практических тестов Вопрос дня Карточки Learn by Concept
Наибольший общий делитель и наименьшее общее кратное
В математике наибольший общий делитель (GCF) — это наибольшее число, которое можно без остатка разделить на два или более чисел. У людей также есть другое название GCF, и вы, возможно, слышали его: некоторые люди называют GCD наивысшим общим фактором (HCF). Это то же самое. А множитель — это меньшее число, которое можно без остатка разделить на это число.
Это то же самое. А множитель — это меньшее число, которое можно без остатка разделить на это число.
Наименьшее общее кратное (НОК) — это наименьшее общее число, когда вы перечисляете кратные двух или более чисел. , кратное , — это большее число, на которое можно разделить число, не оставляя остатка.
Теперь, когда мы разобрались с этим, давайте займемся математикой.
Как найти наибольший общий делитель
Найти самый большой общий делитель не так сложно, как найти самый лучший пункт в длинном меню ресторана, так что не волнуйтесь.
Вы можете найти наибольший общий делитель, составив список всех делителей каждого числа. Затем вы просматриваете все числа в своем списке и находите самое большое целое число, которое является общим между ними.
Найдем наибольший общий делитель между 6 и 12.
Делители 6:
1, 2, 3, 6
Почему? Потому что вы можете разделить 6 без остатка на эти числа.
Теперь перечислим множители числа 12:
1, 2, 3, 4, 6, 12
Почему? Потому что на эти числа можно разделить 12 без остатка.
Теперь давайте посмотрим на оба ваших списка для чисел 6 и 12. Какое наибольшее число общего между этими двумя списками? Из всех этих чисел число, которое было наибольшим между ними, — это число 6 , так что 6 — это 9.0011 GCF или наибольший общий множитель.
Помните, что наибольший общий делитель должен быть целым числом. Здесь нет десятичных дробей и дробей!
Когда мы используем GCF?
Вам когда-нибудь приходилось уменьшать дроби ? Вот когда вам нужно будет знать наибольший общий множитель! Когда вам нужно упростить или уменьшить дробь, вы должны найти наибольший общий множитель между числителем и знаменателем. Если наибольший общий делитель больше 1, дробь можно уменьшить или упростить.
Можно ли упростить эти дроби?
7/11 и 4/8 .
Давайте посмотрим на 7/11 . Ни 7, ни 11 не имеют много делителей, так как являются простыми числами.
Мы можем умножить 7 на 1, чтобы получить 7. И мы можем умножить 11 на 1, чтобы получить 11. Вот и все. Наибольший общий делитель между 7 и 11 — это число 1.
Это означает, что 7/11 нельзя уменьшить.
Теперь давайте посмотрим на 4/8 .
Делители числа 4 равны 1, 2 и 4.
Делители числа 8 равны 1, 2, 4 и 8.
Как мы видим, наибольшим общим делителем чисел 4 и 8 является число 4 .
Круто! Это означает, что мы можем уменьшить дробь, разделив и числитель, и знаменатель на 4.
Итак, 4/8 можно упростить до 1/2.
Понятно? Право на!
Нахождение наибольшего общего делителя также является отличным строительным блоком для разложения на множители полиномиальных выражений!
Наименьшие общие кратные
Еще один термин, который вы можете часто слышать в паре с НОД, — это наименьшее общее кратное (НОК). Найти наименьшее общее кратное тоже не сложно. Наименьшее общее кратное — это наименьшее общее число, когда вы перечисляете числа, кратные двум или более числам. , кратное , — это большее число, на которое можно разделить число, не оставляя остатка.
Найти наименьшее общее кратное тоже не сложно. Наименьшее общее кратное — это наименьшее общее число, когда вы перечисляете числа, кратные двум или более числам. , кратное , — это большее число, на которое можно разделить число, не оставляя остатка.
Пример:
Перечислите числа, кратные 4:
4, 8, 12, 16, 20, 24, 28, 32, 36, 40 и так далее, считая до 4 s…
Наименьшее общее кратное равно наименьшее общее число, когда вы перечисляете числа, кратные двум или более числам.
Упражнение:
Сможете ли вы потренироваться находить наименьшее общее кратное между числами 4 и 6?
Сначала перечислите кратные:
Кратные 4:
4, 8, 12, 16, 20, 24, 28, 32, 36, 40 и так далее, считая до 4s …
Кратность 6:
, 4, 8, 12 , 30, 36, 42, 48 и так далее, считая до 6s …
Сможете ли вы найти наименьшее число общего между двумя составленными вами списками?
Верно, 12 — это наименьшее общее кратное 4 и 6. 0005
0005
Наибольший общий делитель: Наибольшее число, которое можно без остатка разделить на два или более чисел
Наибольший общий делитель: Другое причудливое название для наибольшего общего делителя без остатка
Наименьшее общее кратное: Наименьшее общее число при перечислении кратных двух или более чисел.
Обзор:
Наибольший общий делитель — это наибольший делитель, который является общим для двух чисел.
Наименьшее общее кратное — это наименьшее общее число, разделяемое между двумя числами.
Как происходит нахождение общих знаменателей
Общие знаменатели
Линда С.
спросил 05.02.143/12 + 7/8 =
Подписаться І 6
Подробнее
Отчет
5 ответов от опытных наставников
Лучший Новейшие Самый старыйАвтор: ЛучшиеНовыеСамыеСтарые
Кеннет Г. ответил 05.02.14
ответил 05.02.14
Репетитор
Новое в Византе
Опытный репетитор по математике и статистике
Смотрите таких репетиторов
Смотрите таких репетиторов
Линда,
Когда вам нужно найти общий знаменатель для двух или более дробей, первое, что вам нужно сделать, это найти наименьшее общее кратное всех знаменателей, которое называется НОК. LCM будет вашим наименьшим общим знаменателем.
В этой задаче нужно сложить дроби 3/12 и 7/8. Итак, сначала найдите НОК 12 и 8. Есть несколько способов сделать это. Если вы знаете, как разбить числа 8 и 12 на простые множители, есть простой способ найти это, или, в качестве альтернативы, вы можете просто посмотреть на числа, кратные 8 и 12
Множество 8 равен 8, 16, 24 , 32 ..
Клажу 12 — 12, 24 , 36, ..
Мы видим, что 24 — самое низкое число, которое является кратное как 12, так и 8 (это называется НОК 12 и 8), поэтому мы можем использовать 24 в качестве общего знаменателя для двух дробей. Этот метод также работает при добавлении 3 или 4 фракций.
Этот метод также работает при добавлении 3 или 4 фракций.
Итак, 3/12 = 6/24 при умножении числителя и знаменателя на 2,
И 7/8 = 21/24 при умножении числителя и знаменателя на 3.
3/12 + 7/8 = 6/24 + 21/24 = 27/24
Голосовать за 1 Понизить
Подробнее
Отчет
Джаред М. ответил 27.04.14
Репетитор
Новое в Византе
Терпеливый, опытный и знающий репетитор по математике и бухгалтерскому учету
См. таких репетиторов
Смотрите таких репетиторов
Сначала нужно найти наименьший общий знаменатель или наименьшее общее кратное. Кратные 12 равны 12, 24, 36, 48, 60, 72… Кратные 8 равны 8, 16, 24, 32, 40, 48… Когда вы перечисляете кратные каждому из них, вы можете видеть, что LCM равно 24.
Замените обе дроби так, чтобы знаменатель был равен 24, и соответственно измените числители. Теперь у вас есть 6/24 + 21/24. Оставьте знаменатель как есть и добавьте числители, и вы получите ответ 27/24. Однако, когда ваш ответ представляет собой дробь, вы должны представить ее в простейшей форме. Вы можете уменьшить дробь, разделив каждое число на 3, чтобы ваш ответ был ….?
Голосовать за 0 Понизить
Подробнее
Отчет
Парвиз Ф. ответил 05.02.14
Репетитор
4,8 (4)
Профессор математики в местных колледжах
Смотрите таких репетиторов
Смотрите таких репетиторов 92 = 4
НОК = 12 . 8 / 4 = 96/ 4 = 24
Уравнение (1) становится очень полезным в теории чисел и высшей математике.
Голосовать за 0 Понизить
Подробнее
Отчет
Стив С. ответил 05.02.14
Репетитор
5 (3)
Обучение предварительному исчислению, тригонометрическому исчислению и дифференциальному исчислению
См. таких репетиторов
Смотрите таких репетиторов
Мне нравится делать это на месте, поэтому я держу всю работу вместе (тогда, если я буду искать ошибку позже, мне не придется искать работу). Кроме того, я просто думаю о простых множителях и о том, сколько их у меня в каждом знаменателе; затем отрегулируйте, чтобы получить тот же набор во всех знаменателях. Это концепция, и я думаю, что она теряется среди всех слов, определенных для ее описания.
3/12 + 7/8 =
3/(2*2*3) + 7/(2*2*2) =
3*2/(2*2*2 *3) + 7*3/(2*2*2*3) =
(3*2 + 7*3)/(2*2*2*3) =
(6 + 21 )/(8*3) =
27/24
Голосовать за 0 Понизить
Подробнее
Отчет
Вивиан Л. ответил 05.02.14
ответил 05.02.14
Репетитор
3 (1)
Microsoft Word/Excel/Outlook, составление эссе, математика; Я ЛЮБЛЮ УЧИТЬ
Смотрите таких репетиторов
Смотрите таких репетиторов
Привет, Линда;
Самый быстрый метод — перемножить знаменатели вместе…
(8)(12)=96
(3/12) + (7/8) =
[(3/12)(8 /8)]+[(7/8)(12/12)]=
(24/96)+(84/96)=
108/96
54/48
27/24
Однако вы также можете заметить, что знаменатели…
(8)(3)=25 и
12)(2)=24
Следовательно, 24 — наименьший общий знаменатель…
[(3/12)(2/2)]+[(7/8)(3/3)]
( 6/24)+(21/24)
27/24
Голосовать за 0 Понизить
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
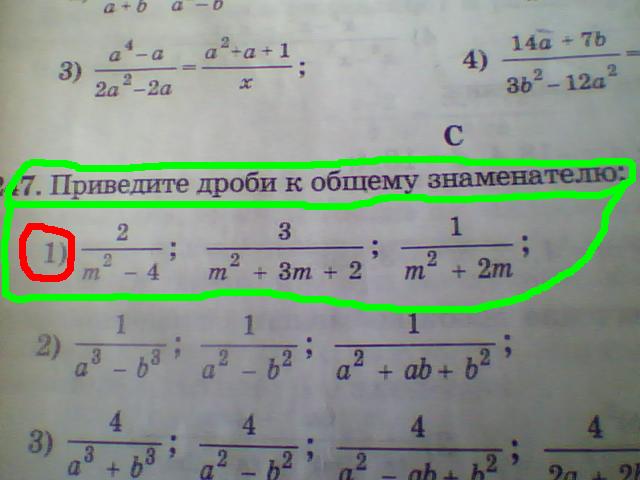

 3/5 + 2/15 = (3*3+2*1)/15 = (9+2)/15 = 11/15.
3/5 + 2/15 = (3*3+2*1)/15 = (9+2)/15 = 11/15.