9 число четное или нечетное число: Чётные и нечётные числа — урок. Математика, 2 класс.

Натуральные числа. Четные и нечетные числа. Действия над натуральными числами – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД

Запомнить

Восстановить пароль

Регистрация

Конспект

Числа, употребляемые при счете предметов или для указания порядкового номера того или иного предмета среди однородных предметов, называются натуральными. Любое натуральное число можно записать с помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Такую запись чисел называют десятичной.

Например: 24; 3711; 40125.

Наименьшим натуральным числом является единица.

Натуральные числа, расположенные в порядке возрастания, начиная с 1 и до бесконечности, называются натуральным рядом.

Например: 1; 2; 3; 4; 5; 6; 7;…

Множество натуральных чисел обозначают знаком «N» (от лат. naturalis – естественный).

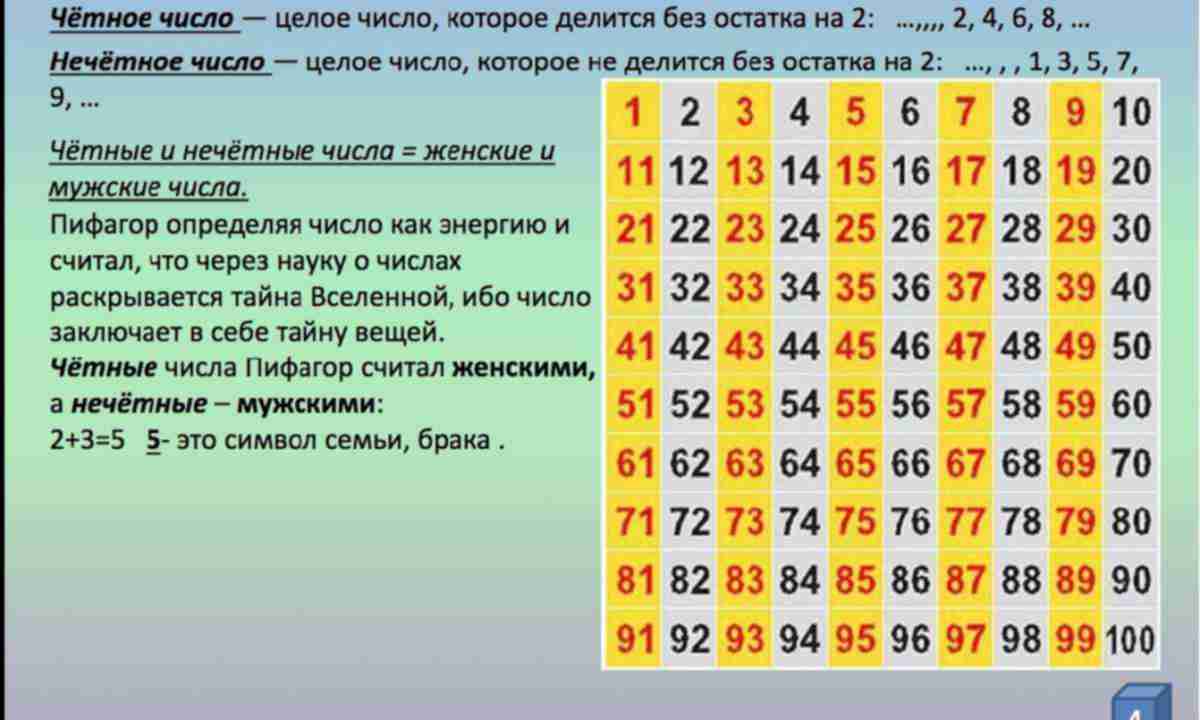
Натуральные числа бывают четными и нечетными. Четные числа – это те числа, которые оканчиваются цифрами 0; 2; 4; 6; 8. Нечетные числа – это те числа, которые оканчиваются цифрами 1; 3; 5; 7; 9.

Четные и нечетные числа обладают следующими свойствами:

1. сумма двух четных чисел четна;
2. сумма двух нечетных чисел четна;
3. сумма трех нечетных чисел нечетна;
4. сумма четного и нечетного числа – нечетное число.

В множестве натуральных чисел определены операции сложения и умножения; обратные операции (вычитание и деление) применимы не ко всем натуральным числам.

1. Сложение: a + b = c, a и b – слагаемые, с – сумма.
2. Умножение: a · b = c, a и b – множители, с – произведение.
3. Вычитание: a – b = c, а – уменьшаемое, b – вычитаемое, с – разность, где a > b.
4. Деление: a : b = c, а – делимое, b – делитель, с – частное, где a > b.

Сложение и умножение натуральных чисел обладают следующими свойствами:

1. Переместительное свойство сложения: a + b = b + a.
2. Сочетательное свойство сложения: (a + b) + c = a + (b + c).
3. Переместительное свойство умножения: a · b = b · a.
4. Сочетательное свойство умножения: (a · b) · c = a · (b · c).
5. Распределительное свойство умножения относительно сложения: a · (b + c) = a · b + a · c.

Примечание: переместительное, сочетательное и распределительное свойства кратко называются еще соответственно коммутативностью, ассоциативностью и дистрибутивностью.

Вопросы

1. Вычислите рациональным способом.

   626 · 16 + 243 · 19 + 374 · 16 + 257 · 19 =

2. Вычислите.

   (49 + 36) : 5 =

3. Значение выражения (221 + 169) : 39 + 190 равно

4. Вычислите.

   (196 : 7 – 576 : 24) · 4 =

5. Найдите значение выражения.

   (4723 + 1062) : 89 =

6. Вычислите рациональным способом.

   41 · 80 – 25 · 41 + 55 · 29 =

7. Вычислите, используя распределительное свойство умножения.

   114 · 25 =

8. Выполните действия.

   684 : (111 – 75) · 4 =

9. Выполните действия.

   41 · (109 – 58) : 17 =

10. Значение выражения 224 · 3 – 332 : 2 равно

11. Для нумерации страниц в книге использовали 354 цифры. Сколько страниц в этой книге?

Сообщить об ошибке

Обязательные

Математическая грамотность

Грамотность чтения

История Казахстана

Предметы по профилю

Биология

Химия

Английский язык

Французский язык

География

Немецкий язык

Информатика

Основы права

Русская литература

Математика

Физика

Русский язык

Всемирная история

Укажите предмет *

Скопируйте и вставьте вопрос задания *

Опишите подробнее найденную ошибку в задании *

Прикрепите скриншот

Объем файла не должен превышать 1МБ

Казахский

Русский

Обратите внимание! По выбранным Вами предметам ГРАНТЫ не предоставлены. В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.

1. Скачайте приложение iTest, используя QR-код или строку поиска в AppStore или Play Market

2. Авторизуйтесь в приложении и готовьтесь к экзаменам вместе с нами

Нечетное число | это… Что такое Нечетное число?

ТолкованиеПеревод

Нечетное число

Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет — нечётным (примеры: 1, 3, 75, −19). Нуль считается чётным числом. ^[1]

Чётное число — целое число, которое делится без остатка на 2:   …−4, −2, 0, 2, 4, 6, 8…

Нечётное число — целое число, которое не делится без остатка на 2:   …−3, −1, 1, 3, 5, 7, 9…

Иными словами, чётные и нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.

Содержание 1 Признак чётности 2 Арифметика 3 История и культура 4 Примечания

Признак чётности

Если в десятичной форме записи числа

последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число так же является чётным, в противном случае — нечётным.
42, 104, 11110, 9115817342 — чётные числа.
31, 703, 78527, 2356895125 — нечётные числа.

Арифметика

• Сложение и вычитание:
  • Чётное ± Чётное = Чётное
  • Чётное ± Нечётное = Нечётное
  • Нечётное ± Чётное = Нечётное
  • Нечётное ± Нечётное = Чётное
• Умножение:
  • Чётное × Чётное = Чётное
  • Чётное × Нечётное = Чётное
  • Нечётное × Нечётное = Нечётное
• Деление:
  • Чётное / Чётное — однозначно судить о чётности результата невозможно (если результат целое число, то оно может быть как чётным, так и нечётным)
  • Чётное / Нечётное = если результат целое число, то оно Чётное
  • Нечётное / Чётное — результат не может быть целым числом, а соответственно обладать атрибутами чётности
  • Нечётное / Нечётное = если результат целое число, то оно Нечётное

История и культура

Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. Так, в древнекитайской мифологии нечётные числа соответствовали Инь, а чётные — Ян.

В разных странах существуют связанные с количеством даримых цветов традиции, например в США, Европе и некоторых восточных странах считается что чётное количество даримых цветов приносит счастье. В России чётное количество цветов принято приносить лишь на похороны умершим; в случаях когда в букете много цветов, чётность или нечётность их количества уже не играет такой роли.

Примечания

1. ↑ «Чётные числа» в БСЭ.

Wikimedia Foundation. 2010.

Игры ⚽ Поможем сделать НИР

Синонимы:

нечет

• Нечетная функция
• Нечеткое множество

Полезное

Четные и нечетные арифметические правила

Четное число:

Четное число — это целое число, кратное 2.

Примеры:

2, 4, 6, 8, 10

Нечетное число: 9 0011

Ан нечетное число – это целое число, не кратное 2.

Примеры:

1, 3, 5, 7

Примечание:

В двузначном, трехзначном или четырехзначном числе, чтобы проверить, четное или нечетное, посмотрите на цифру на месте единиц.

Если на месте единицы стоит цифра 0, 2, 4, 6 или 8, то число четное.

Примеры:

138, 28596, 325670

Если в разряде единиц стоит цифра 1, 3, 5 или 7, то число нечетное.

Примеры:

261, 39485, 150867

1. Сумма или разность двух четных чисел всегда является четным числом.

4 + 8 = 12

16 — 10 = 6

2. Сумма или разность двух нечетных чисел всегда является четным числом.

3 + 7 = 10

13 — 7 = 6

3. Сумма или разность нечетного числа и четного числа всегда является нечетным числом.

3 + 8 = 11 6 + 7 = 13

13 — 6 = 7 8 — 5 = 3

4. Произведение двух четных чисел всегда четное число.

2 x 6 = 12

5. Произведение четного числа на нечетное всегда четное число.

3 х 6 = 18

4 x 7 = 28

6. Произведение двух нечетных чисел всегда нечетное число.

3 х 7 = 21

Дополнение нечетный + нечетный = четный четный + четный = четный нечетный + четный = нечетный четный + нечетный = нечетный

Умножение нечетное x нечетное = нечетное четное x четное = четное нечетное x четное = четное четное x нечетное = четное

Пример 1 :

9 + 49 четно или нечетно?

Решение:

9 = нечетное число

49 = нечетное число

Правило:

нечетное + нечетное = четное

Более того,

9 + 49 = 58

(58 — четное число)

Итак, 9 + 49 четно.

Пример 2 :

36 + 120 четно или нечетно?

Решение:

36 = четное число

120 = четное число

Правило:

четное + четное = четное

Кроме того,

36 + 120 = 156

(156 — четное число)

Итак, 36 + 120 — четное.

Пример 3 :

5 + 114 четно или нечетно?

Решение:

5 = нечетное число

114 = четное число

Правило:

нечетное + четное = нечетное

Кроме того,

5 + 11 4 = 119

(119 — нечетное число)

Итак, 5 + 114 нечетно.

Пример 4 :

146 + 289 четно или нечетно?

Решение:

146 = нечетное число

289 = четное число

Правило:

четное + нечетное = нечетное

Кроме того:

146 + 289 = 435

(435 — нечетное число)

Итак, 146 + 289 нечетно.

Пример 5 :

120 x 146 четное или нечетное?

Решение:

120 = четное число

146 = четное число

Правило:

четное x четное = четное

Кроме того,

120 х 146 = 17520

(17520 — четное число)

Итак, 17520 — четное число.

Пример 6:

Является ли 121 x 14 четным или нечетным?

Решение:

121 = нечетное число

14 = четное число

Правило:

нечетное x четное = четное

Кроме того,

121 x 14 = 1694

(1694 — четное число)

Итак, 121 х 14 четно.

Пример 7 :

Является ли 151 x 17 четным или нечетным?

Решение:

151 = нечетное число

17 = нечетное число

Правило:

нечетное x нечетное = нечетное

Кроме того,

151 x 17 = 2567

(2567 — нечетное число)

Итак, 151 х 17 нечетно.

Пример 8 :

Является ли 160 x 7 четным или нечетным?

Решение:

160 = четное число

7 = нечетное число

Правило: 

четное x нечетное = четное

Кроме того,

160 x 7 = 1120

(1120 — четное число)

Итак, 160 х 7 четно.

Пример 9 :

Является ли 2x ² четным или нечетным?

Решение:

В 2x ² ‘x’ является переменной и может принимать любое значение.

Какое бы значение мы ни подставили вместо x, когда x ²  умножается на 2, оно становится кратным 2.

Итак, 2x ² четно.

Пример 10 :

Является ли 2x ²  + 3 четным или нечетным?

Решение:

Из приведенного выше примера 9 видно, что 2x ²  четно.

А 3 — нечетное число.

2x ²  + 3 = четное + нечетное

Правило:

четное + нечетное = нечетное

Итак, 2x ²  + 3 нечетное.

Пожалуйста, отправьте ваш отзыв на [email protected]

Мы всегда ценим ваши отзывы.

©Все права защищены. onlinemath5all.com

Что такое четные и нечетные числа? Полное руководство

Возможно, вы много слышали о четных и нечетных числах, но что это такое? В этом блоге мы рассмотрим это более подробно и рассмотрим примеры нечетных и четных чисел от 1 до 100.

В этом блоге перейдите к:

• Что такое нечетные и четные числа?
• Нечетные числа от 1 до 100
• Четные числа от 1 до 100
• Каковы преимущества изучения нечетных и четных чисел?
• Когда дети узнают о нечетных и четных числах?
• Какие числа четные и нечетные?
• Является ли 0 четным числом?
• Является ли 1 нечетным числом?
• Во всех ли нечетных числах есть буква «е»?
• Все ли простые числа нечетные?
• Действия с нечетными и четными числами

---

Что такое четные и нечетные числа?

Четные числа делятся на 2, а нечетные — нет.

Это означает, что если вы разделите четное число на 2, вы всегда получите целое число (например, 10/2 = 5). С другой стороны, если вы разделите нечетное число на 2, вы получите дробный результат (например, 9)./2 = 4,5).

Помните об этом правиле, и это может быть очень полезно, когда дело доходит до сложения, вычитания, умножения и деления.

Фактически, это правило делимости можно применить к любому четному или нечетному числу, а не только к числам от 1 до 100!

Готовы проверить свои знания? Попробуйте наши интерактивные практические вопросы!

Попробуйте ответить на несколько вопросов

---

Примеры нечетных и четных чисел

Нечетные числа от 1 до 100

1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47 , 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97 , 99

Четные числа от 1 до 100 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100.

---

Часто задаваемые вопросы о нечетных и четных числах

Каковы преимущества изучения нечетных и четных чисел?

Знание того, является число нечетным или четным, может быть полезным во многих ситуациях. Например, при сложении или вычитании чисел вы можете объединять нечетные числа с нечетными и четные числа с четными, чтобы упростить расчеты.

В вопросах на умножение и деление вы также можете использовать тот факт, что нечетные числа всегда дают нечетные результаты при умножении, а четные числа всегда дают четные результаты (кроме 0, который является нейтральным).

Когда дети узнают о нечетных и четных числах?

Как указано в национальной учебной программе, учащиеся начинают знакомиться с нечетными и четными числами на ключевом этапе 1: 

«Они тренируются в счете, произнося числа, и в счете, перечисляя предметы и считая двойками, пятерками и десятками от разных кратных до развивать распознавание образов в системе счисления (например, нечетных и четных чисел)».

Какие числа четные и нечетные?

Некоторые числа одновременно четные и нечетные. Например, 2 четно, но также и нечетно, потому что его можно разделить на 1 и 2. 

3 также четно и нечетно, потому что его можно разделить на 1 и 3. Вы запутались? Мы тоже, но перечитайте последние несколько предложений, пока не впитаетесь!

Является ли 0 четным числом?

0 — особенный номер! Оно ни четное, ни нечетное. Это связано с тем, что при делении числа на 0 результат всегда будет неопределенным.

Является ли 1 нечетным числом?

Да, 1 нечетное число (или нет?)! Все числа, которые не делятся на 2, являются нечетными числами. Это включает в себя 1, 3, 5, 7, 9, 11, 13 и так далее.

Однако! Можно сказать, что 1 не является четным или нечетным числом. Это потому, что когда вы делите число на 1, результат всегда будет одним и тем же числом. Вы решаете его судьбу!

Во всех ли нечетных числах есть буква «е»?

Как это круто?! Нечетные числа должны заканчиваться на 1, 3, 5, 7, 9, и в результате у каждого числа есть буква «е». Разум = Взорван!

Все ли простые числа нечетные?

Все простые числа нечетные. Это связано с тем, что простое число можно разделить только на 1 и само на себя, поэтому результатом всегда будет нечетное число.

Некоторые примеры простых чисел:

3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47. много вещей, которые вы можете сделать, чтобы исследовать нечетные и четные числа с вашим ребенком или учениками.

• Узнать о них можно, посчитав разные предметы
  
• Вы можете попробовать считать 2 с, 5 с и 10 с
  
• Вы можете узнать, что происходит, когда вы делите нечетные и четные числа друг на друга

Наконец, вы можете заняться чем-нибудь интересным вместе с другом или членом семьи.

Вот некоторые упражнения с четными и нечетными числами, которые вы можете попробовать

1. Посмотрите, сможете ли вы найти шаблоны с нечетными и четными числами

2. Устройте соревнование с другом или членом семьи, чтобы узнать, кто наберет 100 сначала добавляя только нечетные или четные числа

3. Посмотрите, кто может составить самое большое нечетное или четное число, используя цифры 1-9

4. Попробуйте найти как можно больше различных нечетных и четных чисел

5. Посмотрите, сможете ли вы составить числовое предложение, используя нечетные и четные числа (например, 3+5=8 или 9+1=10)

6. Поиграйте в игру «Нечетный аут»; для этого вам понадобится партнер. Один человек загадывает нечетное число от 1 до 100, а другой должен угадать, что это такое! Отгадывающий может только спросить, четное или нечетное число. Человек, который думает о числе, может сказать только «да» или «нет».

7. Попробуйте отгадать загадки; например:

Я нечетное число. Убери одну букву, и я расквитаюсь. Какой я номер?

Надеемся, вам понравятся эти нечетные и четные числа!

---

Заключение

Несмотря на то, что нечетные и четные числа кажутся достаточно простыми, полезно иметь общее представление о том, что они из себя представляют. Эти знания становятся особенно полезными при выполнении таких действий, как сложение, вычитание, умножение и деление.