подкоренное число и показатель корня
- Квадратный корень
- Арифметический квадратный корень
Корень n-ой степени из числа a — это число, n-ая степень которого равна a. Например, корнем второй степени из 36 будет число 6, так как:
62 = 36.
Для записи корня используется знак √
(знак корня или радикал). Под чертой знака записывается подкоренное число, а над знаком, в левом верхнем углу, показатель корня:
2√36.
Подкоренное число — это степень, показатель корня — это показатель степени, корень — основание степени. Если
,
то
.
Эта запись читается так: корень n-ой степени из числа a равен x
.
Извлечение корня — это действие, обратное возведению в степень, с помощью которого по данной степени и по данному показателю степени находят основание степени.
Примеры:
3√125 = 5, так как 53 = 125;
2√81 = 9, так как 92 = 81;
5√32 = 2, так как 25 = 32.
Квадратный корень
Квадратным корнем из числа a называется число, квадрат которого равен a.
Например, квадратными корнями из числа 16 являются числа 4 и -4:
2√16 = 4 или 2√16 = -4.
Рассмотрим уравнение
x2 = a
при различных значениях a:
- a < 0:
В данном случае уравнение не будет иметь решений, так как квадрат любого числа всегда является положительным числом или нулём. Следовательно, x2 не может быть равен отрицательному числу.
- a = 0:
В этом случае уравнение имеет единственное решение:
x = 0.
- a > 0:
В этом случае уравнение имеет два корня: положительный и отрицательный, модули которых равны.
Так как вторая степень отрицательного числа является числом положительным:x = ±√a .
Так как вторая степень отрицательного числа является числом положительным:Из рассмотренного примера можно сделать вывод, что для того чтобы из числа можно было извлечь квадратный корень, необходимо, чтобы оно было числом положительным или нулём.
Арифметический квадратный корень
Арифметический квадратный корень из положительного числа a — это положительное число x, квадрат которого равен a:
2√a = x, следовательно x2 = a.
При обозначении квадратного корня показатель корня опускается, то есть квадратный корень обозначается знаком корня без показателя. Например:
√a — квадратный корень из a.
Обратите внимание, что при чтении выражения слово арифметический
опускается.
Действие, с помощью которого вычисляется квадратный корень, называется извлечением квадратного корня.
Извлечение квадратного корня — действие обратное возведению в квадрат (или возведению числа во вторую степень). При возведении в квадрат известно число, требуется найти его квадрат. При извлечении квадратного корня известен квадрат числа, требуется по нему найти само число.
Поэтому для проверки полученного результата можно найденный корень возвести во вторую степень, если степень будет равна подкоренному числу, значит корень был найден правильно.
Рассмотрим извлечение арифметического квадратного корня и его проверку на примере. Найдём √36, для этого надо найти число, при возведении которого во вторую степень получится 36. Таким числом является 6, так как
62 = 36.
Значит, √36 = 6. Корень -6 мы не рассматриваем, потому что арифметический корень является положительным числом.
3-8Квадратные корни без калькулятора!
Убийственная математика: квадратные корни без калькулятора!Многие люди спрашивали нас, как получить квадратный корень без калькулятора, и многие другие присылали нам разные способы сделать это! Вы найдете классический метод, описанный для вас в Easy Question Evil Answers. На этой странице есть и другие способы извлечения квадратных корней. Первые методы, показанные здесь, вероятно, лучше всего подходят для целых чисел, но есть и правильный метод для десятичных дробей. Внизу этой страницы описано, как найти квадратный корень по построению! | |||||||||||||||||||
Мы очень благодарны Фрэнку Лафонтену из Австралии, который связался с нами и объяснил метод, которому он научился в школе 60 лет назад! Конечно, самое замечательное в математике то, что метод Фрэнка прекрасно работает и сегодня. Вот его объяснение с его собственных слов — мы представили его здесь именно так, как он прислал его нам, потому что мы не видим, как мы могли бы сделать его еще лучше!
| |||||||||||||||||||
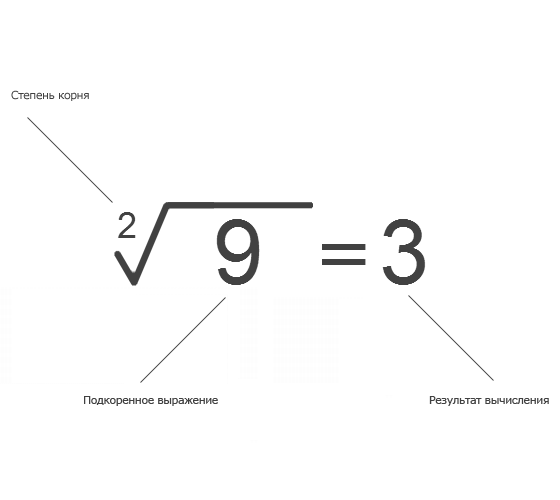.. и так далее.
Это (8,5 + 8,8235)/2 = 8,66175. Это очень близкий ответ! 
(например, 7 см)