А b в квадрате: а в квадрате b в квадрате (а+b)

Содержание

таблица, примеры использования с ответами по алгебре для 7 класса

В математике есть формулы, которые просто необходимо держать всегда в памяти, так как большинство заданий ЕГЭ не могут обойтись без их применения. Это формулы сокращенного умножения. Изучать ФСУ начинают в 7-м классе. Тема считается непростой, но знание их поможет избежать утомительных вычислений и снизить вероятность ошибки.

Что такое формула сокращенного умножения

Из названия следует, что эти формулы позволяют проводить умножение, возведение в степень чисел и многочленов сокращенно, то есть быстрее при более компактной записи решения. Эти тождества служат для разложения многочленов на множители, упрощения выражений и приведения многочленов к стандартному виду.

Таблица формул сокращенного умножения

Для удобства мы собрали все формулы сокращенного умножения в одну таблицу. Ее можно использовать при выполнении домашних заданий по алгебре. При решении задач вы можете заменить буквы a и b числами, переменными или даже целыми выражениями.

Квадрат суммы	(a + b)²= a² + 2ab + b²
Квадрат разности	(a – b)²= a² – 2ab + b²
Разность квадратов	a² – b²=(a – b)·(a + b)
Сумма кубов	a³ + b³=(a + b)·(a² – ab + b²)
Разность кубов	a³ – b³=(a – b)·(a² + ab + b²)
Куб суммы	(a + b)³= a³ + 3a²b + 3ab² + b³
Куб разности	(a – b)³= a³ – 3a²b + 3ab² – b³

Формулы сокращенного умножения следует выучить. Без первой тройки формул о «тройке» и мечтать нельзя, без остальных — о «четверке» и «пятерке».

Как запомнить все эти, на первый взгляд, сложные формулы? Можно использовать метод аналогии. Присмотритесь к ФСУ внимательнее и вы увидите, что формула квадрата суммы очень похожа на формулу квадрата разности: здесь нужно запомнить только одно отличие — «плюс» меняется на «минус».

Также легко запомнить куб суммы и куб разности: их формулы практически одинаковы, снова поменялись только знаки. Сумма кубов и разность кубов тоже похожи, к тому же они напоминают первые две формулы.

И еще: научитесь правильно проговаривать формулы сокращенного умножения. Очень частая ошибка учеников — говорить «формула суммы квадратов». Такой формулы не существует!

Дополнительные формулы сокращенного умножения

Не будем ограничиваться курсом 7-го класса по алгебре и добавим еще несколько формул.

Формула возведения в квадрат суммы трех, четырех и большего количества слагаемых:

(a₁+a₂+…+a_n)²=a₁²+a₂²+…+a_n−1²+a_n²+2·a₁·a₂+2·a₁·a₃+2·a₁·a₄+…+2·a₁·a_n−1+2·a₁·a_n+ +2·a₂·a₃+2·a₂·a₄+…+2·a₂·a_n−1+2·a₂·a_n+…+2·a_n−1·a_n.

Квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых. Для примера возведем в квадрат с использованием этой формулы сумму трех слагаемых x, y и z. Имеем: (x+y+z)²=x²+y²+z²+2·x·y+2·x·z+2·y·z. В частном случае при n=2 эта формула становится уже известной нам формулой квадрата суммы двух слагаемых.

Формула возведения в квадрат суммы трех, четырех и большего количества слагаемых:

aⁿ−bⁿ=(a−b)·(aⁿ⁻¹+aⁿ⁻²·b+aⁿ⁻³·b²+…+a²·bⁿ⁻³+a·bⁿ⁻²+bⁿ⁻¹)

Частными случаями этой формулы являются: разность квадратов (при n=2), разность кубов (при n=3) и сумма кубов (при n=3 и если b заменить на −b).

Важно!

При выполнении заданий необходимо знать некоторые свойства формул:

(a – b)²ⁿ = (b – a)²ⁿ, где n ∈ N
(a – b)²ⁿ⁺¹ = –(b – a)²ⁿ⁺¹, где n ∈ N

N – множество натуральных чисел

Примеры использования формул сокращенного умножения

Лучше всего формулы запоминаются на практике. Решайте как можно больше примеров, и все формулы запомнятся сами собой, а вы избавитесь от скучной и малоэффективной зубрежки. Итак, рассмотрим примеры и их решения с помощью формул сокращенного умножения.

Пример №1

Упростим выражение:

Применим формулу разности квадратов и получим:

Пример №2

Найдем значение выражения:

Применим формулы квадрата разности и квадрата суммы, раскроем скобки, приведем подобные слагаемые, сократим дробь и получим:

это интересно

Тригонометрические формулы

Таблица с основными тригонометрическими формулами, которые помогут при решении задач на ЕГЭ

ПОДРОБНЕЕ

Формулы сокращенного умножения. Разность квадратов, квадрат суммы, разность кубов, бином Ньютона.

Откровенно говоря, эти формулы должен помнить любой ученик седьмого класса. Изучать алгебру даже на школьном уровне и не знать формулу разности квадратов или квадрата суммы просто невозможно. Они постоянно встречаются при упрощении алгебраических выражений, при сокращении дробей и даже могут помочь в арифметических вычислениях. Ну, например, вам нужно вычислить в уме: 3,16² — 2 • 3,16 • 1,16 + 1,16². Если вы начнете считать это «в лоб», получится долго и скучно, а если воспользуетесь формулой квадрата разности, ответ получите за 2 секунды!
Итак, семь формул «школьной» алгебры, которые должны знать все:

Название Формула
Квадрат суммы (A + B)² = A² + 2AB + B²
Квадрат разности (A — B)² = A² — 2AB + B²
Разность квадратов (A — B)(A + B) = A² — B²
Куб суммы (A + B)³ = A³ + 3A²B + 3AB²+ B³
Куб разности (A — B)³ = A³ — 3A²B + 3AB² — B³
Сумма кубов A³ + B³ = (A + B)(A² — AB + B²)
Разность кубов A³ — B³ = (A — B)(A² + AB + B²)
Версия для печати в формате png
Обратите внимание: никакой формулы суммы квадратов не существует! Не позволяйте своей фантазии заходить слишком далеко.
Как проще всего запомнить все эти формулы? Ну, скажем, увидеть определенные аналогии. Например, формула квадрата суммы похожа на формулу квадрата разности (отличие лишь в одном знаке), а формула куба суммы — на формулу куба разности. Далее, в составе формул разности кубов и суммы кубов мы видим нечто похожее на квадрат суммы и квадрат разности (только коэффициента 2 не хватает).
Но лучше всего эти формулы (как и любые другие!) запоминаются на практике. Решайте больше примеров на упрощение алгебраических выражений, и все ф-лы запомнятся сами собой.
Любознательным школьникам будет, вероятно, интересно обобщить приведенные факты. Вот, скажем, существуют формулы квадрата и куба суммы. А что, если рассмотреть выражения типа (A + B)⁴, (A + B)⁵ и даже (A + B)ⁿ, где n — произвольное натуральное число? Можно ли увидеть здесь какую — либо закономерность?
Да, подобная закономерность существует. Выражение вида (A + B)ⁿ называется биномом Ньютона. Я рекомендую пытливым школьникам самим вывести формулы для (A + B)⁴ и (A + B)⁵, а далее попытаться увидеть общий закон: сравнить, например, степень соответствующего бинома и степень каждого из слагаемых, которые получаются при раскрытии скобок; сравнить степень бинома с количеством слагаемых; попытаться найти закономерности в коэффициентах. Мы не будем сейчас углубляться в эту тему (для этого нужен отдельный разговор!), а лишь запишем готовый результат:
(A + B)ⁿ = Aⁿ + C_n¹A^n-1B + C_n²A^n-2B² + … + C_n^kA^n-kB^k + … + Bⁿ.
Здесь C_n^k = n!/(k! • (n-k)!).
Напоминаю, что n! — это 1 • 2 • … • n — произведение всех натуральных чисел от 1 до n. Называется это выражение факториалом числа n. Например, 4! = 1 • 2 • 3 • 4 = 24. Факториал нуля считается равным единице!
А что можно сказать по поводу разности квадратов, разности кубов и т.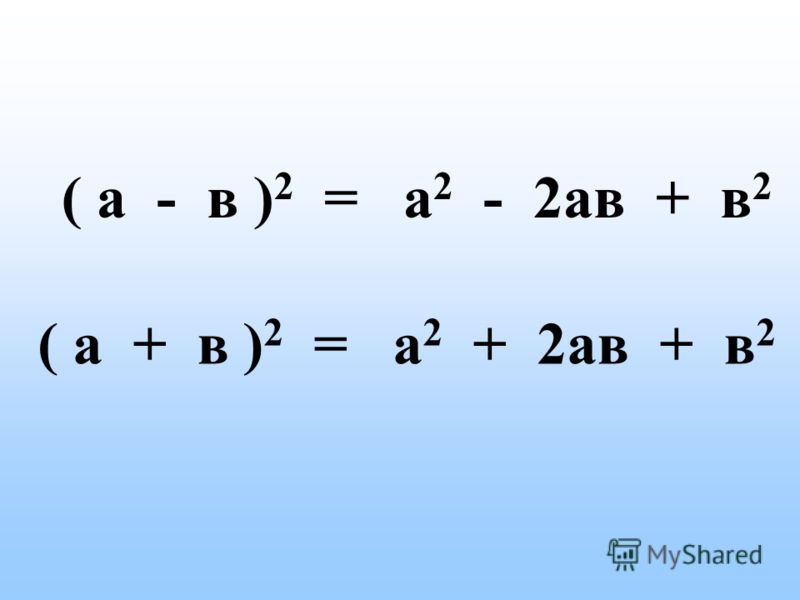 п.? Существует ли здесь какая-либо закономерность? Можно ли привести общую формулу для Aⁿ — Bⁿ?
Да, можно. Вот эта формула:
Aⁿ — Bⁿ = (A — В)(A^n-1 + A^n-2B + A^n-3B² + … + B^n-1).
Более того, для нечетных степеней n существует аналогичная ф-ла и для суммы:
Aⁿ + Bⁿ = (A + В)(A^n-1 — A^n-2B + A^n-3B² — … + B^n-1).
Мы не будем сейчас выводить эти формулы (кстати, это не очень сложно), но знать об их существовании, безусловно, полезно.

Возможно, вам будут интересны другие материалы:
Тест по математике для 7 класса
Тест по математике для 8 класса
Проценты. Задачи «на проценты». Часть I
Четность. Задачи: от элементарных до «олимпиадных»
ОГЭ по математике — пробный тест № 1
Подготовка к ОГЭ-2021 по математике

Math, Eloquently: a Plus b, Squared
Давай, попробуй это: спроси школьного учителя математики о единственной ошибке учащегося во всех классах, которая вызывает наибольшее раздражение. Бьюсь об заклад, что самый распространенный ответ, который вы получаете, — это некоторая версия того, как учащиеся неправильно возводят в квадрат сумму двух чисел (например, ( a + b ) ²), чтобы получить сумму квадратов отдельных чисел. числа (как в a ² + b ² ). Однако на самом деле эти выражения не равны; это не то, как возведение в квадрат работает. Действительно, по моему опыту, студенты, которые могут усвоить интуицию о том, почему они не равны, с гораздо большей вероятностью преуспеют в будущем. В этом уроке мы попытаемся разобраться в этом неравенстве:

Прежде чем объяснять, почему это неправда, я думаю, важно понять, почему так много людей думают, что
— это правда. Есть несколько причин, по которым учащийся может думать, что это правда, и у каждой из этих причин есть своя логика.
(1) Я знаю, что это верно для умножения:
, так почему же это не так, если вместо них стоит символ сложения?

Это классический случай, когда учащийся уделяет больше внимания обозначениям, чем тому, что на самом деле означают символы означает . Возведение в квадрат означает умножение выражения на само себя: ( ab ) ² означает ( ab )( ab ). Но самое главное, это целая куча умножений. А мы все знаем, что перемножаемые элементы можно перегруппировывать и переставлять по своему желанию (формально мы говорим, что умножение ассоциативно и коммутативно). И когда вы перегруппируете и перегруппируете, вы увидите, что два
a и два b перемножены вместе; таким образом а ² б ² . Но посмотрите, что ( a + b ) ² означает: ( a + b )( a + b ). Где возможность так просто переставить? Это не там. Смесь плюс и умножить на усложняет работу с этим выражением, чем если бы это было все умножение.
(2) Я знаю, что это законно делать то, что называется «распространением»:
, так почему я не могу распространять показатель степени так же, как я могу распространять этот забавный символ? (В любом случае, что это за штука?)
Эта штука — заглавная греческая буква «пси», и я использовал ее, чтобы продемонстрировать, как все можно распределять, даже если это выглядит сложно (эта идея понадобится нам в минута).
Но многие студенты не знают, что слово «распределить» на самом деле является прозвищем для гораздо более длинного описания процесса, показанного выше: это «распределительное свойство умножения над сложением». Распространение листовок на парковке означает, что каждый человек на парковке получает листовку, а распределение умножения на сложение означает, что каждый элемент сложения ( a и b ) умножаются. Это просто факт о нашей системе счисления, что вы можете добавить два числа, прежде чем умножать сумму на третье число (левая часть приведенного выше уравнения), или вы можете сначала умножить каждое из двух чисел на третье число по отдельности. (правая сторона), затем добавьте продукты, и вы получите тот же результат. На самом деле уравнение в (1) выше является демонстрацией другого дистрибутивного свойства: «дистрибутивного свойства показателей степени при умножении». И это верно, потому что умножение ассоциативно и коммутативно.

Но «распределительное свойство показателей степени над сложением» просто неверно. Различные дистрибутивные свойства — это разные математические процессы (тонкость, которую вы можете упустить, если не знаете их полных названий), и не все они должны быть действительными. На самом деле, большинство из них таковыми не являются; любой, который является действительным , особенный и важный.
(3) Но… кажется, что они должны быть равны!
Ну… только сначала может быть. Это распространенное заблуждение, что математические процессы, которые выглядят прямо на странице или кажутся правильными в вашей голове, должны быть правдой. Математики подходят к этому в совершенно противоположном направлении — в некотором смысле ничто не должно быть истинным, пока вы не докажете, что это правда. И равенство в данном случае просто… не верно! Очень жаль! Повезло! Ну что ж, научимся с этим справляться!

Как только вы внимательно посмотрите на эту ситуацию, используя примеры и различные математические интерпретации, вы обнаружите, что вы, вероятно, даже не верите, что две стороны могут быть равны. У вас уже есть знания, чтобы убедить себя в этом. Давайте посмотрим на некоторые из этих примеров.
Если вы находитесь в кондитерской, набираете конфеты в пакет и покупаете полтора фунта конфет по цене 1,50 доллара за фунт, сколько с вас возьмут? Вы можете не знать ответ сразу, но держу пари, вы знаете, что 1,25 доллара — смехотворный ответ. Вы покупаете больше фунта конфет, поэтому цена будет всего имеют больше 1,50 доллара. Тем не менее, если вы думаете, что квадрат суммы — это сумма отдельных квадратов, вам придется поверить, что 1,25 доллара — это правильно:
Полтора фунта умножить на полтора доллара за фунт. не равняется одной с четвертью долларов. Обратите внимание на ключевое расположение знака «не равно». Убедитесь, что вы понимаете причину каждого шага этой математической строки.

Держу пари, ты, вероятно, можешь возвести в квадрат число 20 в уме. 2 умножить на 20 будет 40, поэтому 20 умножить на 20 будет 400. Возможно, вы не так быстро возведете 21 в квадрат. Фактический ответ не важен, но есть ли у вас интуиция, что это не 401? Что ж, эта интуиция исходит из глубокой интуиции, что квадрат суммы не является суммой отдельных квадратов:
Опять же, какая-то часть вашего мозга уже знает, что (20 + 1) ² не одно и то же. как 20 ² + 1 ² .
Чему тогда соответствует ( a + b ) ² ? Или, другими словами, существует ли выражение без круглых скобок, которое всегда имеет одно и то же значение? Формальная алгебра ниже. Он использует распределительное свойство умножения вместо сложения, которое мы видели выше. Популярный термин для процесса, который вы, возможно, знаете, — FOILing:

Опять же, убедитесь, что вы понимаете каждый шаг в этом процессе.
Теперь a ² + 2 ab + b ² не совсем очевидный способ переписать ( a + b 90 004 ) ² , но у него есть преимущество быть правильным! Однако, если вы попытаетесь интерпретировать это по-другому (например, геометрически), это может иметь гораздо больше смысла. Естественный способ понять концепцию возведения в квадрат — посмотреть на площадь квадрата, которая рассчитывается путем возведения в квадрат. Итак, ниже изображен квадрат, каждая сторона которого равна a + b длинный. Чтобы было понятнее, эти стороны разбиты на отдельные части
a и b .
Спрашивать о ( a + b ) ² то же самое, что спрашивать о площади всего квадрата. Но весь квадрат разбит на меньшие квадраты и прямоугольники, и мы знаем достаточно информации, чтобы рассчитать каждую из этих меньших частей по отдельности. Площади двух меньших квадратов рассчитаны ниже.
Обратите внимание, что площади двух меньших квадратов вместе взятые далеки от общей площади большого квадрата. В терминах алгебры мы должны были бы сказать, что ( a + b ) ² просто должно быть больше, чем a ² + b ² . Конечно, это означает, что они не могут быть равны, что мы и пытались понять! Однако на самом деле эта картина говорит нам даже больше.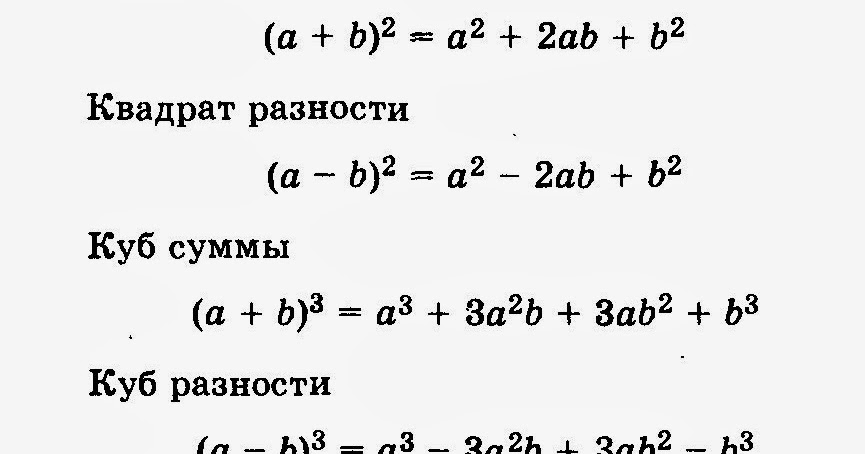 Это говорит нам, насколько больше. Каждый из синих прямоугольников имеет длину
a и ширина b , поэтому каждый из них имеет площадь a умножить на b . И их два. Это означает, что ( a + b ) ² = a ² + 2 ab + b ² , как мы видели в алгебре.
Наконец, я покажу еще один способ понять исходное неравенство. Последний способ требует, чтобы вы знали, что говорит теорема Пифагора, и я предполагаю, что вы знаете (если нет, вы можете пропустить эту часть). Обратите внимание на квадрат, построенный на гипотенузе треугольника ниже:
Квадрат имеет площадь c ² , что по теореме Пифагора равно a ² + b ² . Но это как раз правая часть нашего исходного неравенства. Поэтому имеет смысл спросить о квадрате, представленном левой стороной. Квадрат с площадью и площадью должен иметь длину стороны a + b . Но из треугольника видно, что a + b должно быть больше, чем c (прогулка по гипотенузе должна требовать меньше шагов, чем прогулка по сторонам треугольника — технически это называется «неравенство треугольника»). То есть две стороны неравенства геометрически представляют площадь квадрата, но эти квадраты не могут быть одного размера, поэтому два выражения не могут быть равными.
Надеюсь, этого достаточно, чтобы убедить вас.
Видео-урок: Обратное утверждение теоремы Пифагора
Расшифровка видео
Что мы будем делать в этом уроке? Посмотрите на обратную теорему Пифагора. Но какова обратная сторона Теорема Пифагора?
Ну, обратная сторона Теорема Пифагора — это то, где мы используем теорему Пифагора, чтобы доказать, является ли треугольник прямоугольный или нет. Ну, во-первых, нам нужно напомним себе, что такое теорема Пифагора. А теорема Пифагора 𝑎 в квадрате плюс 𝑏 в квадрате равно 𝑐 в квадрате, где 𝑐 — гипотенуза, т.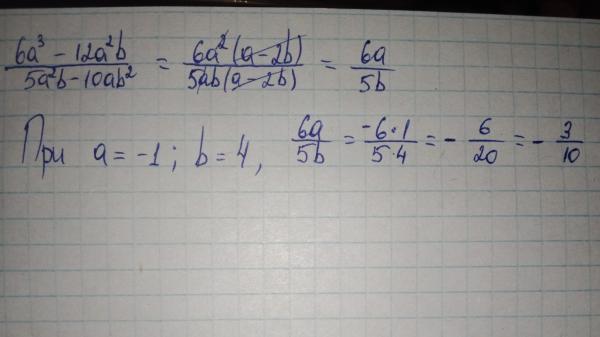 е. длинная сторона против прямого угла. А 𝑎 и 𝑏 — два других стороны. И неважно, какой из них который. И стоит отметить, что Теорема Пифагора работает только в прямоугольном или прямоугольном треугольнике.
Итак, что это значит? Ну, это означает, что сумма площади квадратов на двух более коротких сторонах или катетах равны площади квадрат, образованный наибольшей стороной, гипотенузой. Таким образом, если мы имеем треугольник, в котором это не работает, поэтому 𝑎 в квадрате плюс 𝑏 в квадрате не равно 𝑐 в квадрате, то можно сделать вывод, что это не будет прямоугольный треугольник.
Хорошо, отлично. Итак, теперь мы знаем, что это такое и как мы собираемся использовать его. Давайте немного посмотрим, как это все работает.
Теорема Пифагора утверждает что в прямоугольном треугольнике площадь квадрата на гипотенузе равна сумма площадей квадратов на катетах. Означает ли это, что треугольник где 𝑐 в квадрате равно 𝑎 в квадрате плюс 𝑏 в квадрате обязательно является правильным треугольник? Предположим, что треугольник 𝐴𝐵𝐶 имеет длины сторон 𝑎, 𝑏 и 𝑐, где 𝑐 в квадрате равно 𝑎 в квадрате плюс 𝑏 в квадрате. Пусть треугольник 𝐷𝐵𝐶 прямоугольный. треугольник со сторонами 𝑎, 𝑏 и 𝑑. Часть (1) Использование Пифагора Теорема, что вы можете сказать о связи между 𝑎, 𝑏 и 𝑑?
В этой задаче имеем вопрос, означает ли это, что треугольник, где 𝑐 в квадрате равно 𝑎 в квадрате плюс 𝑏 квадрат обязательно является прямоугольным треугольником? И что мы собираемся делать, мы собираюсь ответить на этот вопрос через каждый из этапов этой проблемы. Ну, как говорится в вопросе, Теорема Пифагора гласит, что 𝑐 в квадрате равно 𝑎 в квадрате плюс 𝑏 в квадрате. Ну, вот где 𝑐 гипотенуза. А гипотенуза самая длинная сторону, противоположную прямому углу.
Ну вот, в этой оранжевой стороне, это 𝑑 наша гипотенуза, потому что она противоположна прямому углу и является самой длинной сторона. Поэтому, как нам говорят, что треугольник 𝐷𝐵𝐶 — прямоугольный треугольник, это может дать нам отношение. И это то, что 𝑑 в квадрате будет равно 𝑎 в квадрате плюс 𝑏 в квадрате, что означает, что мы ответили на первый часть вопроса.
Итак, теперь давайте перейдем к вторая часть вопроса.
Мы знаем, что для треугольника 𝐴𝐵𝐶, 𝑐 в квадрате равно 𝑎 в квадрате плюс 𝑏 в квадрате. Какой вывод вы делаете о 𝑑?
Ну, если у нас есть 𝑐 в квадрате равно 𝑎 в квадрате плюс 𝑏 в квадрате, что мы можем сделать, так это использовать некоторые замена. Потому что то, что мы можем сделать, это то, что мы можем sub в 𝑑 в квадрате для 𝑎 в квадрате плюс 𝑏 в квадрате, потому что мы знаем, что 𝑑 в квадрате равно 𝑎 в квадрате плюс 𝑏 в квадрате. Итак, что мы собираемся есть 𝑐 в квадрате равно 𝑑 в квадрате. Итак, теперь мы можем сформировать отношения между 𝑐 и 𝑑. И это если мы возьмем квадрат корень из обеих частей уравнения, то, что у нас останется, это 𝑐 равно 𝑑. И мы можем игнорировать негатив значения, потому что мы смотрим на длины. Ну так мы и ответили в этой части вопроса мы пришли к выводу о 𝑑, что 𝑑 равно 𝑐.
Итак, давайте перейдем к следующему часть.
Ну и следующая часть, из вопрос, можно ли построить различные треугольники с стороны одинаковой длины?
Ну, нет. И это потому, что если два треугольника имеют стороны одинаковой длины, и они фактически конгруэнтны. Это потому, что это один из способы, которыми мы пользуемся для доказательства конгруэнтности. Потому что это называется SSS, и это значит бок-бок-бок. И если две вещи совпадают, это означает, что они точно такие же. Итак, мы ответили на эту часть вопрос.
Переходим к следующей части.
Итак, заключительная часть вопрос, что вы думаете о треугольнике 𝐴𝐵𝐶?
Ну, мы знаем этот треугольник 𝐷𝐵𝐶 и треугольник 𝐴𝐵𝐶 имеют одинаковую длину 𝑎. Оба имеют одинаковую длину 𝑏. И мы уже заявили, что 𝑑 равно 𝑐. Поэтому, прежде всего, мы должен сказать, что он конгруэнтен треугольнику 𝐷𝐵𝐶. И это потому, что все стороны одинаковы. Поэтому, если они равны, то мы можем сказать, что треугольник 𝐴𝐵𝐶 имеет прямой угол при 𝐶.
Итак, что мы здесь сделали, так это показан один из способов демонстрации теоремы Пифагора. И мы также ответили на вопрос, означает ли это, что треугольник, где 𝑐 в квадрате равно 𝑎 в квадрате плюс 𝑏 квадрат обязательно является прямоугольным треугольником? И ответ — да, это так. И мы показали, что с каждым из наши шаги. Таким образом, наш полный вывод о треугольнике 𝐴𝐵𝐶 заключается в том, что он конгруэнтен треугольнику 𝐷𝐵𝐶. Значит, угол прямой при 𝐶.
Итак, отлично, теперь мы показали Теорема Пифагора. Но то, что мы хотим сделать сейчас, это посмотреть, как мы можем использовать его, чтобы доказать, действительно ли треугольник прямоугольный. Итак, что мы будем делать в этом проблема в том, что мы собираемся использовать обратную теорему Пифагора, чтобы показать, треугольник на самом деле может быть прямоугольным или прямоугольным треугольником.
Банка длиной 7,9 см, 8,1 см и 5,3 см образуют прямоугольный треугольник?
Ну, первое, что мы могли бы сказать об этих трех длинах заключается в том, что мы определенно можем образовать из них треугольник. И это потому, что когда мы добавляем вместе две более короткие стороны, мы получаем 13,2. И 13,2 больше, чем 8,1, что это другая сторона. Таким образом, мы знаем, что могли бы образуют треугольник, потому что если бы он был меньше 8,1, то мы не могли бы их соединить вместе. Таким образом, мы не могли сформировать треугольник. А если бы он был равен 8,1, то это будет просто прямая линия. Хорошо, отлично. Мы знаем, что можем составить треугольник, но давайте посмотрим, сможем ли мы образовать прямоугольный или прямоугольный треугольник.
Итак, первое, что мы сделаем Вспомните теорему Пифагора. И это говорит о том, что 𝑐 в квадрате равно 𝑎 в квадрате плюс 𝑏 в квадрате, где 𝑐 — наша самая длинная сторона или гипотенуза. И так, то, что это говорит о том, что сумма площадей квадратов на двух меньших сторонах равна сумме площадь квадрата по большей стороне. Таким образом, в нашем вопросе мы можно сказать, что если возвести в квадрат 5,3 и 7,9и сложить их вместе, должно быть равно квадрат 8,1, если мы хотим, чтобы это был прямоугольный треугольник. И доказательство этого таким образом использует то, что называется обратной теоремой Пифагора.
Итак, первым делом вычислить 7,9 в квадрате плюс 5,3 в квадрате, что дает нам 62,41 плюс 28,09, то есть равно 90,5. Итак, теперь, что мы хотим сделать, мы хотите вычислить квадрат наибольшей стороны, которая равна 8,1. Ну, мы уже можем оценить видеть, что это не будет таким же, как 90,5. Потому что если мы подумаем о 8.1 в квадрате, ну, это почти равно восьми в квадрате. А восемь в квадрате равно 64. Итак, поэтому наша ценность определенно будет ниже 90,5, потому что это 65,61. Таким образом, мы можем сделать вывод, что сумма квадратов на двух более коротких сторонах не будет равна сумме квадрат на большей стороне, потому что 90,5 не равно 65,61. Таким образом, мы не можем сформировать прямоугольный треугольник или прямоугольный треугольник с этими тремя длинами.
И мы могли бы догадаться об этом по начало. Потому что, если мы посмотрим на значения, которые у нас есть, мы получили 7,9 и 5,3. Ну 7.9 очень близко к восемь. Поэтому, если у нас будет восемь в квадрате добавить 5,3 в квадрате будет больше, чем 8,1 в квадрате, потому что, опять же, 8,1 в квадрате очень близко к восьми в квадрате. Так что это было бы хорошо гипотеза, которую мы могли иметь с самого начала.
Хорошо, отлично. Итак, мы показали, что можем использовать обратная теорема Пифагора, чтобы показать, является ли треугольник прямоугольным или нет. Но теперь, что мы собираемся сделать, это мы собираемся взглянуть на вопрос, который немного сложнее. Итак, мы можем использовать еще некоторые навыки наряду с нашей теоремой Пифагора.
В прямоугольнике 𝐴𝐵𝐶𝐷 предположим 𝐴𝐸 равно восьми, 𝐷𝐸 равно двум и 𝐷𝐶 равно четырем. Является ли треугольник 𝐵𝐸𝐶 правильным? под углом?
Итак, первым делом сделать в этом вопросе добавить информацию, что мы знаем. Ну, во-первых, мы знаем, что 𝐴𝐸 это равно восьми. Тогда мы знаем, что 𝐷𝐸 равно два. А потом нам говорят, что 𝐷𝐶 равно до четырех. Хорошо, отлично. Это вся информация, которая у нас есть было сказано. Но также мы можем использовать это для заключить еще немного информации. Ну, во-первых, 𝐴𝐵 тоже должен быть четыре. Потому что это прямоугольник. Итак, 𝐴𝐵 должно быть равно 𝐷𝐶. А 𝐵𝐶 должно быть равно двум плюс восемь, потому что эти два значения, сложенные вместе, дают то же самое, что и длины 𝐴𝐸 и 𝐷𝐸 вместе. Итак, это будет иметь длину 10.
Итак, мы пометили все наши стороны. И что мы можем сделать, так это отметить на пара прямых углов, которые окажутся полезными. И мы могли бы сделать это, потому что мы знать, что это прямоугольник. Таким образом, прямоугольник будет иметь право угла в каждом из его углов. Итак, что нас просят сделать в этом вопрос в том, чтобы выяснить, является ли треугольник 𝐵𝐸𝐶 прямоугольным или прямым треугольник. И способ, которым мы можем это сделать, заключается в используя обратную теорему Пифагора. А теорема Пифагора утверждает что 𝑐 в квадрате равно 𝑎 в квадрате плюс 𝑏 в квадрате, где 𝑐 — это наша гипотенуза.
И что мы подразумеваем под обратным что если это не так, то, следовательно, он не может быть прямым или прямоугольным треугольника, поскольку теорема Пифагора верна только для прямоугольных треугольников. Ну, для того, чтобы сделать это и использовать это чтобы увидеть, является ли треугольник 𝐵𝐸𝐶 на самом деле прямоугольным, ну, что мы нужно будет сделать, это узнать каждую из длин. И поскольку мы не знаем длины 𝐶𝐸 или 𝐵𝐸, мы должны выяснить это в первую очередь.
Ну, что мы собираемся сделать, так это начнем со стороны 𝐶𝐸. И мы можем узнать это, сформировав треугольник 𝐶𝐷𝐸. И это причина прямоугольного треугольника как мы показали, в левом верхнем углу есть прямой угол. Итак, что мы можем сделать, так это использовать теорема Пифагора, чтобы узнать длину 𝐶𝐸. Таким образом, мы можем сказать, что 𝐶𝐸 квадрат будет равен двум в квадрате плюс четыре в квадрате. И это потому, что 𝐶𝐸 это наш гипотенуза, потому что она противоположна прямому углу и самой длинной стороне. Следовательно, 𝐶𝐸 в квадрате равно будет равно четырем плюс 16, что будет равно 20.
Теперь, по сути, нам не нужно на самом деле узнать, что такое 𝐶𝐸. Потому что, когда мы будем работать в следующей части мы рассмотрим треугольник 𝐵𝐸𝐶. У нас будет каждая из сторон в квадрате. Итак, мы можем сохранить этот ответ, который мы иди туда. Если бы мы хотели выяснить, что 𝐶𝐸 было, мы просто возьмем квадратный корень из обеих частей этого уравнения, вот что мы получили. И если мы это сделаем, мы получим два значения, потому что мы могли получить отрицательное или положительное значение. Но мы могли бы игнорировать негатив значение, потому что мы смотрим на длину. Итак, нам понадобится позитив ценности.
Хорошо, отлично. Итак, теперь у нас есть информация, которую мы нужно, потому что мы знаем, что 𝐶𝐸 — ну, что более важно, что такое 𝐶𝐸 в квадрате — равно. Итак, теперь давайте двигаться дальше и узнать 𝐵𝐸. И чтобы сделать это, что мы можем сделать, это посмотрите на этот прямоугольный треугольник, который у нас есть на правой стороне нашего прямоугольника, потому что у нас получился треугольник 𝐴𝐵𝐸. Итак, что мы можем сказать, так это что 𝐵𝐸 в квадрате будет равно восьми в квадрате плюс четыре в квадрате. Следовательно, 𝐵𝐸 в квадрате равно будет равно 64 плюс 16. Следовательно, 𝐵𝐸 в квадрате равно будет равно 80. Итак, как и прежде, это все, что нам нужно для этой проблемы. Тем не менее, мы могли бы сделать то же самое как в последний раз и брал корень с обеих сторон, чтобы узнать, что такое 𝐵𝐸.
Итак, теперь мы можем использовать все информация, которая у нас есть, чтобы выяснить, является ли треугольник 𝐵𝐸𝐶 прямоугольным треугольник. Потому что если это так, то 𝐶𝐸 в квадрате плюс 𝐵𝐸 в квадрате будет равно 𝐵𝐶 в квадрате, потому что 𝐵𝐶 самое длинное сторона. Ну, во-первых, что мы Собираюсь сделать, это работать 𝐶𝐸 в квадрате плюс 𝐵𝐸 в квадрате. Ну, это будет 20 плюс 80 потому что я показал, что у нас уже есть 𝐶𝐸 в квадрате и 𝐵𝐸 в квадрате.
Однако, если у нас есть только длины корень 20 и корень 80, мы могли бы решить это, потому что корень 20 в квадрате будет 20, а корень из 80 в квадрате будет просто 80. И это потому, что у нас есть правило это говорит нам, что если у нас есть корень 𝑎, умноженный на корень 𝑎, он просто равен 𝑎. Итак, корень 𝑎 все в квадрате просто равно 𝑎. Итак, следовательно, мы знаем, что 𝐶𝐸 в квадрате плюс 𝐵𝐸 в квадрате будет 100, потому что 20 добавить 80 будет 100.
Итак, что мы хотим сделать, так это хотите выяснить, каким будет 𝐵𝐶 в квадрате, потому что, если это то же самое, что и 𝐶𝐸 в квадрате плюс 𝐵𝐸 в квадрате, тогда у нас есть прямоугольный треугольник. Ну и квадрат самой длинной сторона 𝐵𝐶 будет равна 10 в квадрате. Следовательно, 𝐵𝐶 в квадрате равно будет равно 100. Ну, это то же самое, что и значение мы получили, когда мы сложили квадраты двух более коротких сторон. Итак, что мы сделали, так это мы выполнили критерии теоремы Пифагора, потому что 𝑎 в квадрате плюс 𝑏 квадрат фактически равен 𝑐 в квадрате. Таким образом, мы можем сказать, что да, треугольник 𝐵𝐸𝐶 прямоугольный или прямоугольный.
Итак, в этом уроке мы рассмотрели различные различные примеры, демонстрирующие различные навыки. Итак, мы рассмотрели, как Формулируется теорема Пифагора. Мы также ознакомились с обратная теорема Пифагора и как ее можно использовать, чтобы показать, являются ли три линии могут образовывать прямоугольный или прямоугольный треугольник. Мы также рассмотрели это в этом вопрос в другом формате, который включал прямоугольник и разные треугольники.
А дальше посмотрим в некоторой координатной геометрии.
Две прямые пересекаются в точке 𝐴: три, минус один. Через точку 𝐵 проходит одна линия: пять, один и другой проходят через точку 𝐶: минус два, шесть. Найдите длины линии сегменты 𝐴𝐵, 𝐴𝐶 и 𝐵𝐶.
Итак, что я сделал в первую очередь для помогите нам понять, что происходит, я нарисовал набросок трех точек, которые нам дали. Итак, чтобы найти длины наших три отрезка, то, что мы собираемся использовать, называется расстоянием между формула очков. Итак, что такое формула расстояния утверждает, что это расстояние между двумя точками равно квадратному корню из 𝑥 два минус 𝑥 один в квадрате плюс 𝑦 два минус 𝑦 один в квадрате. Итак, квадратный корень из изменение нашей 𝑥-координаты в квадрате плюс изменение нашей 𝑦-координаты в квадрате.
Но откуда взялась эта формула от? Ну вообще-то это адаптация по теореме Пифагора. Потому что если у нас есть два очка 𝑥 один, 𝑦 один и 𝑥 два, 𝑦 два, ну и расстояние между этими двумя точками равно, в На самом деле, это будет гипотенуза прямоугольного треугольника. И это потому, что если у нас есть посмотрите сюда, если мы образуем прямоугольный треугольник, у нас будет изменение 𝑥 будет нижняя длина и изменение 𝑦 будет нашей вертикальной длиной. Следовательно, наша гипотенуза будь нашим 𝑑. Итак, в таком случае, если бы мы подумали о теореме Пифагора это гласит, что 𝑐 в квадрате равно 𝑎 в квадрате плюс 𝑏 в квадрате. Ну, у нас бы наш 𝑑 был бы нашим 𝑐. И тогда мы могли бы иметь наши 𝑥 два минус 𝑥 один. Итак, наше изменение в 𝑥 может быть нашим 𝑎. А наши 𝑦 два минус 𝑦 можно было бы будь нашим 𝑏.
Таким образом, мы можем видеть, что в на самом деле это будет нахождение 𝑑, нашего расстояния, с помощью теоремы Пифагора. Потому что, если бы мы хотели узнать что было 𝑐 или 𝑑, на самом деле это был бы просто квадратный корень из 𝑎 в квадрате плюс 𝑏 в квадрате, что у нас и было наверху. Великолепно! Хорошо, теперь мы знаем расстояние формула и откуда она взялась, найдем длины отрезков 𝐴𝐵, 𝐴𝐶 и 𝐵𝐶.
Итак, используя это, мы можем сказать, что что 𝐴𝐵 будет равно квадратному корню из пяти минус три в квадрате плюс один минус минус один в квадрате, что и будет изменением в нашем 𝑥-координата в квадрате плюс изменение нашей 𝑦-координаты в квадрате. Стоит отметить, что это не независимо от того, с какой стороны они будут, потому что в любом случае это даст нам то же самое результат, потому что они в квадрате. Так, например, пять минус три это два. Два в квадрате четыре. Три минус пять минус два. Отрицательные два в квадрате также четыре. Это даст нам root 𝑎, что упростит до двух корней два. Мы сделали это с помощью surd отношение.
Итак, если мы перейдем к 𝐴𝐶, это будет равно квадратному корню из трех минус минус два все в квадрате плюс минус один минус шесть все в квадрате. И это даст нам корень 74. И потом, 𝐵𝐶 тоже можно найти используя тот же метод, и это также будет root 74.
Итак, теперь мы ответили на эти части, давайте перейдем к следующим частям вопроса.
Итак, используя теорему Пифагора, решить, что треугольник 𝐴𝐵𝐶 прямоугольный треугольник. Отсюда и две строки перпендикуляр?
Как я уже говорил, Теорема Пифагора гласит, что 𝑐 в квадрате равно 𝑎 в квадрате плюс 𝑏 в квадрате, где 𝑐 это наша самая длинная сторона, гипотенуза. Ну, если мы посмотрим на три длин, составляющих наш треугольник, мы видим, что самая короткая длина должна быть равна двум корень два. Значит, самая длинная сторона должно быть 𝐴𝐶 или 𝐵𝐶, но на самом деле они одинаковой длины. Таким образом, мы не можем иметь гипотенуза или наибольшая сторона этого треугольника.
Таким образом, мы можем сказать, что треугольник 𝐴𝐵𝐶 не является прямоугольным, потому что теорема Пифагора не может быть встречались, потому что два корня два все в квадрате плюс корень 74 все в квадрате не могут быть равны корень 74 все в квадрате.
No related posts.