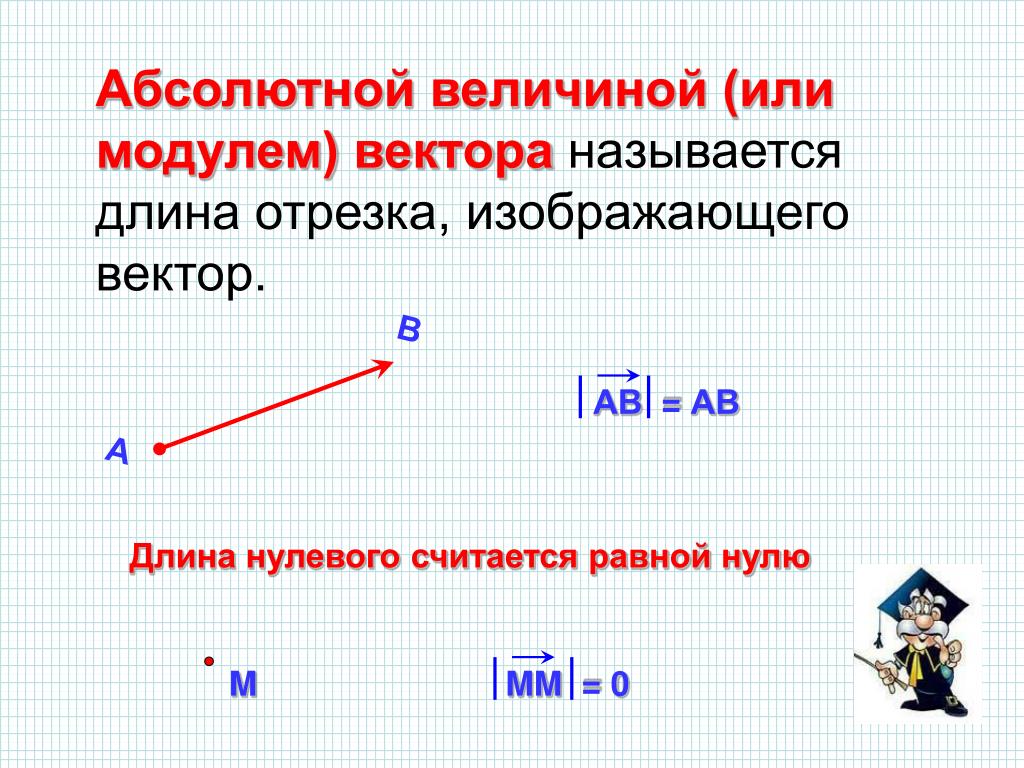
Модуль (абсолютная величина)
Модуль (абсолютная величина)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Краткий курс высшей математики
Краткий курс высшей математики
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. МЕТОД КООРДИНАТ. ПОНЯТИЕ ФУНКЦИИ § 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. КООРДИНАТЫ ТОЧКИ НА ПРЯМОЙ 2. Геометрическое изображение действительных чисел. Координаты точки на прямой 3. Абсолютная величина действительного числа 4. Расстояние между двумя точками на прямой § 2. КООРДИНАТЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ 2. Расстояние между двумя точками на плоскости 3. Деление отрезка в данном отношении 4. Координаты точки в пространстве 5. Расстояние между двумя точками в пространстве § 3.  УГОЛ МЕЖДУ ДВУМЯ ОСЯМИ. ПОЛЯРНЫЕ КООРДИНАТЫ УГОЛ МЕЖДУ ДВУМЯ ОСЯМИ. ПОЛЯРНЫЕ КООРДИНАТЫ2. Полярные координаты 3. Зависимость между декартовыми и полярными координатами § 4. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ 2. Понятие функции 3. График функции 4. Способы задания функций 5. Основные элементарные функции и их графики 6. Сложные функции. Элементарные функции 7. Целые и дробно-рациональные функции 8. Функции четные и нечетные. Периодические функции § 5. УРАВНЕНИЕ ЛИНИИ 2. Нахождение уравнения линии по ее геометрическим свойствам § 6 ПРЕОБРАЗОВАНИЕ КООРДИНАТ 2. Поворот осей координат ГЛАВА II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ § 1. ПРЯМАЯ 2. Уравнение прямой с угловым коэффициентом 3. Уравнение прямой, параллельной оси ординат 4. Общее уравнение прямой и его частные случаи 5. Точка пересечения прямых. Построение прямой по ее уравнению 7. Уравнение прямой, проходящей через данную точку в заданном направлении 8.  Пучок прямых Пучок прямых9. Уравнение прямой, проходящей через две данные точки 10. Расстояние от точки до прямой § 2. КРИВЫЕ ВТОРОГО ПОРЯДКА 2. Окружность 3. Эллипс 4. Гипербола 5. Парабола 6. Окружность, эллипс, гипербола и парабола как конические сечения 7. Упрощение уравнения кривой второго порядка. График квадратного трехчлена 8. Уравнение равносторонней гиперболы, асимптоты которой приняты за оси координат 9. График дробно-линейной функции 10. Преобразование уравнения кривой второго порядка, не содержащего члена с произведением координат ГЛАВА III. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ И ВЕКТОРНОЙ АЛГЕБРЫ § 1. ЭЛЕМЕНТЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ 2. Определитель третьего порядка 3. Понятие об определителях высших порядков § 2. СИСТЕМЫ УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ 2. Однородная система двух уравнений первой степени с тремя неизвестными 3. Система трех уравнений первой степени с тремя неизвестными 4. Однородная система трех уравнений первой степени с тремя неизвестными § 3.  ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ2. Линейные операции над векторами 4. Проекция вектора на ось и составляются вектора по оси 5. Разложение вектора на составляющие по осям координат 6. Направляющие косинусы вектора 7. Условие коллинеарности двух векторов 8. Скалярное произведение 9. Выражение скалярного произведения через проекции перемножаемых векторов 10. Косинус угла между двумя векторами 11. Векторное произведение 12. Выражение векторного произведения через проекции перемножаемых векторов 13. Смешанное произведение трех векторов 15. Условие компланарности трех векторов § 4. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ 2. Равенство матриц. Действия над матрицами 3. Обратная матрица 4. Матричная запись и матричное решение системы уравнений первой степени § 5. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ 2. Преобразование координат 3. Приведение квадратичной формы к каноническому виду 4. Упрощение общего уравнения кривой второго порядка ГЛАВА IV.  АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ§ 1. ПЛОСКОСТЬ 2. Нормальный вектор плоскости. Уравнение плоскости, проходящей через данную точку 3. Общее уравнение плоскости и его частные случаи 4. Построение плоскости по ее уравнению 5. Угол между плоскостями. Условия параллельности и перпендикулярности двух плоскостей 6. Точка пересечения трех плоскостей § 2. ПРЯМАЯ В ПРОСТРАНСТВЕ 2. Общие уравнения прямой 3. Векторное уравнение прямой. Параметрические уравнения прямой 4. Канонические уравнения прямой 5. Уравнения прямой, проходящей через две точки 6. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых § 3. Прямая и плоскость в пространстве 2. Точка пересечения прямой с плоскостью 3. Расстояние от точки до плоскости 4. Пучок плоскостей § 4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА 2. Цилиндрические поверхности 3. Конические поверхности 4. Поверхность вращения 6. Гиперболоиды 7. Параболоиды ГЛАВА V.  ТЕОРИЯ ПРЕДЕЛОВ ТЕОРИЯ ПРЕДЕЛОВ§ 1. ПРЕДЕЛ ФУНКЦИИ 2. Предел функции при х -> -оо 3. Предел функции при х->х0 4. Бесконечно малые функции. Ограниченные функции 5. Бесконечно большие функции и их связь с бесконечно малыми функциями 6. Основные теоремы о пределах 7. Предел функции при x -> 0 9. Натуральные логарифмы 10. Сравнение бесконечно малых функций § 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ 2. Операции над непрерывными функциями. Непрерывность элементарных функций 3. Свойства функций, непрерывных на сегменте 4. Понятие об обратной функции 5. Обратные тригонометрические функции 6. Показательная и логарифмическая функции 7. Понятие о гиперболических функциях ГЛАВА VI. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ 1. Приращение аргумента и приращение функции 2. Определение непрерывности функции с помощью понятии приращения аргумента и приращения функции 3. Задачи, приводящие к понятию производной 4.  Определение производной и ее механический смысл Определение производной и ее механический смысл5. Дифференцируемость функции 6. Геометрический смысл производной 7. Производные некоторых основных элементарных функций 8. Основные правила дифференцирования 9. Производная обратной функции 10. Производные обратных тригонометрических функций 11. Производная сложной функции § 12. Производные гиперболических функций 13. Производная степенной функции с любым показателем 14. Сводная таблица формул дифференцирования 15. Неявные функции и их дифференцирование 16. Уравнения касательной а нормали к кривой 17. Графическое дифференцирование § 2. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ 1. Нахождение производных высших порядков 2. Механический смысл второй производной § 3. ДИФФЕРЕНЦИАЛ ФУНКЦИИ 2. Производная как отношение дифференциалов 3. Дифференциал суммы, произведения и частного функций 4. Дифференциал сложной функции. Инвариантность формы дифференциала 5. Применение дифференциала к приближенным вычислениям 6.  Дифференциалы высших порядков Дифференциалы высших порядков§ 4. ФУНКЦИИ, ЗАДАННЫЕ ПАРАМЕТРИЧЕСКИ, И ИХ ДИФФЕРЕНЦИРОВАНИЕ 2. Дифференцирование функций, заданных параметрически § 5. ВЕКТОРНАЯ ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА 2. Векторная функция скалярного аргумента и ее производная 3. Уравнения касательной прямой и нормальной плоскости к пространственной кривой 4. Механический смысл первой и второй производных векторной функции скалярного аргумента § 6. НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ 2. Теорема Ролля 3. Теорема Лагранжа 4. Правило Лопиталя § 7. ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ПОСТРОЕНИЮ ГРАФИКОВ 2. Максимум и минимум функции 3. Достаточный признак существования экстремума, основанный на знаке второй производной 4. Отыскание наибольшего и наименьшего значений функции 5. Применение теории максимума и минимума к решению задач 6. Выпуклость и вогнутость графика функции. Точки перегиба 7. Асимптоты графика функции 8. Общая схема исследования функции и построение ее графика § 8.  ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ2. Уточнение найденных значений корней методом хорд и касательных § 9. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА ГЛАВА VII. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА 2. Геометрический смысл неопределенного интеграла 3. Таблица основных интегралов 4. Основные свойства неопределенного интеграла § 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ 2. Интегрирование методом замены переменной 3. Интегрирование по частям § 3. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ 2. Рациональные дроби. Выделение правильной рациональной дроби 3. Интегрирование простейших рациональных дробей 4. Разложение правильной рациональной дроби на простейшие дроби 5. Метод неопределенных коэффициентов 6. Интегрирование рациональных дробей § 4. Интегрирование тригонометрических функций 2. Рациональные функции двух переменных 3. Интегралы вида § 5. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ 2. Интеграл вида 3.  Интегралы видов Интегралы видов4. Интегралы вида § 6. ОБЩИЕ ЗАМЕЧАНИЯ О МЕТОДАХ ИНТЕГРИРОВАНИЯ. ИНТЕГРАЛЫ, НЕ БЕРУЩИЕСЯ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ 2. Понятие об интегралах, не берущихся в элементарных функциях ГЛАВА VIII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. ЗАДАЧИ, ПРИВОДЯЩИЕ К ОПРЕДЕЛЕННОМУ ИНТЕГРАЛУ 2. Задача о работе переменной силы § 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 2. Свойства определенного интеграла 3. Производная интеграла по переменной верхней границе 4. Формула Ньютона—Лейбница 5. Замена переменной в определенном интеграле 6. Интегрирование по частям в определенном интеграле § 3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 2. Вычисление площади в полярных координатах 3. Вычисление объема тела по известным поперечным сечениям 4. Объем тела вращения 5. Длина дуги кривой 6. Дифференциал дуги 7. Площадь поверхности вращения 8. Общие замечания о решении задач методом интегральных сумм § 4. КРИВИЗНА ПЛОСКОЙ КРИВОЙ 2.  Вычисление кривизны Вычисление кривизны3. Радиус кривизны. Круг кривизны. Центр кривизны 4. Эволюта и эвольвента § 5. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 2. Интегралы от разрывных функций 3. Признаки сходимости несобственных интегралов § 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 2. Метод трапеций 3. Метод параболических трапеций (метод Симпсона) ГЛАВА IX. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 2. График функции двух переменных 3. Функции трех и большего числа переменных § 2. Предел функции нескольких переменных. Непрерывность функции. Точки разрыва 2. Непрерывность функции нескольких переменных 3. Понятие области 4. Точки разрыва 5. Свойства функций, непрерывных в ограниченной замкнутой области § 3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ 2. Геометрический смысл частных производных функции двух переменных 3. Частные производные высших порядков § 4. ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 2.  Полный дифференциал функции Полный дифференциал функции3. Приложение полного дифференциала к приближенным вычислениям § 5. Дифференцирование сложных и неявных функций 2. Инвариантность формы полного дифференциала 3. Дифференцирование неявных функций § 6. СКАЛЯРНОЕ ПОЛЕ 2. Производная по направлению 3. Градиент 4. Касательная плоскость а нормаль к поверхности 5. Геометрический смысл полного дифференциала функции двух переменных § 7. ЭКСТРЕМУМ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ 2. Наибольшее и наименьшее значения функции двух переменных ГЛАВА X. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ § 1. ДВОЙНОЙ ИНТЕГРАЛ 2. Двойной интеграл. Теорема существования 3. Свойства двойного интеграла 4. Вычисление двойного интеграла в декартовых координатах 5. Вычисление двойного интеграла в полярных координатах 6. Приложения двойного интеграла § 2. ТРОЙНОЙ ИНТЕГРАЛ 2. Тройной интеграл и его свойства 3. Вычисление тройного интеграла в декартовых координатах 4. Вычисление тройного интеграла в цилиндрических координатах 5.  Приложения тройного интеграла Приложения тройного интеграла§ 3. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ 2. Задача о работе. Криволинейный интеграл 3. Вычисление криволинейного интеграла 4. Формула Остроградского — Грина 5. Независимость криволинейного интеграла от пути интегрирования 6. Отыскание первообразной по полному дифференциалу 7. Криволинейный интеграл по длине дуги ГЛАВА XI. РЯДЫ § 1. ЧИСЛОВЫЕ РЯДЫ 2. Геометрическая прогрессия 3. Простейшие свойства числовых рядов 4. Необходимый признак сходимости ряда 5. Достаточные признаки сходимости знакоположительных рядов 6. Знакопеременные ряды 7. Остаток ряда и его оценка § 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ 2. Правильно сходящиеся функциональные ряды и их свойства § 3. СТЕПЕННЫЕ РЯДЫ 2. Свойства степенных рядов 3. Ряды по степеням разности х-а 4. Разложение функций в степенные ряды. Ряд Тейлора 5. Разложение некоторых элементарных функций в ряды Тейлора и Маклорена § 4. ПРИЛОЖЕНИЕ РЯДОВ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ 2.  Приближенное вычисление интегралов Приближенное вычисление интегралов§ 5. ПОНЯТИЕ О ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ. СТЕПЕННЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ 2. Числовые ряды с комплексными членами 3. Степенные ряды в комплексной области § 6. РЯДЫ ФУРЬЕ 2. Ряд Фурье 3. Сходимость ряда Фурье 4. Ряды Фурье для четных и нечетных функций 5. Разложение в ряд Фурье функций с периодом 2l ГЛАВА XII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 2. Дифференциальные уравнения первого порядка 3. Уравнения с разделяющимися переменными 4. Однородные уравнения 5. Линейные уравнения 6. Уравнение в полных дифференциалах 7. Особые решения 8. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера § 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 2. Простейшие уравнения второго порядка, допускающие понижение порядка 3. Понятие о дифференциальных уравнениях высших порядков § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 2.  Линейные однородные дифференциальные уравнения второго порядка Линейные однородные дифференциальные уравнения второго порядка3. Линейные неоднородные дифференциальные уравнения второго порядка 4. Метод вариации произвольных постоянных § 4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ 2. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами 3. Приложение линейных дифференциальных уравнений второго порядка к изучению механических и электрических колебаний § 5. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ 2. Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами § 6. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ РЯДОВ § 7. ПОНЯТИЕ О СИСТЕМАХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 2. Системы линейных дифференциальных уравнений с постоянными коэффициентами ПРИЛОЖЕНИЕ 1. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА ПРИЛОЖЕНИЕ 2. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ |
Python Absolute Value — abs() для действительных и комплексных чисел — LearnDataSci
Автор: Alfie Grace
Data Scientist
Math
Абсолютное значение числа относится к величине этого значения, независимо от того, является ли оно положительное или отрицательное. Например, абсолютное значение -5 равно 5.
Например, абсолютное значение -5 равно 5.
Ниже приведен синтаксис использования функции abs() для определения абсолютного значения числа в Python:
abs(-5)
Сегодня мы рассмотрим несколько примеров того, где можно применить функцию abs() , уделяя особое внимание действительным и комплексным числам.
Применение функции abs() к действительному числу возвращает величину этого числа. Мы можем определить действительное число как находящееся на прямой числовой линии, представленной на изображении ниже. Величина действительного числа относится к его расстоянию по прямой от начала координат.
Знак числа указывает, в каком направлении на линии находится число; положительные значения располагаются вдоль положительной оси, а отрицательные — вдоль отрицательной оси. В кратком примере, показанном во введении, -5 — действительное число.
Что касается Python, действительные числа — это числа, которые являются целыми числами или числами с плавающей запятой. Следующий пример демонстрирует, как мы можем применить функцию abs к списку целых чисел:
список_реальных_чисел = [-12, -6, 0, 4, 8]
для числа в real_number_list:
абсолютное_значение = абс (число)
print(f'Число: {число}, Абсолютное значение: {absolute_value}') Вывод:
Число: -12, Абсолютное значение: 12 Число: -6, Абсолютное значение: 6 Число: 0, Абсолютное значение: 0 Число: 4, Абсолютное значение: 4 Число: 8, Абсолютное значение: 8
Использование функции abs() преобразовало отрицательные числа в положительные. Для положительных чисел изменений не произошло.
Помните, что абсолютное значение действительного числа относится к его расстоянию от 0 и называется величиной. Поскольку величина — это просто расстояние, она всегда будет положительной.
Поскольку величина — это просто расстояние, она всегда будет положительной.
Мы также можем использовать функцию abs() для чисел с плавающей запятой. См. пример ниже:
real_number_list = [-4.16, -3.12, 11.88, 16.32]
для числа в real_number_list:
абсолютное_значение = абс (число)
print(f'Число: {число}, абсолютное значение: {absolute_value}') Выход:
Число: -4,16, абсолютное значение: 4,16 Число: -3,12, абсолютное значение: 3,12 Число: 11,88, абсолютное значение: 11,88 Число: 16,32, абсолютное значение: 16,32
Мы также можем применить функцию abs() к комплексным числам.
Комплексное число представляет собой комбинацию действительных и мнимых чисел. Мы можем определить мнимое число как выражение квадратного корня из отрицательного числа. Обычно они выражаются через значение $i$ или $j$, что означает квадратный корень из -1.
Мнимые числа помогают заполнить множество пробелов в математике. В результате они довольно часто используются в отраслях, связанных с математикой, особенно в электротехнике. На изображении ниже показан пример комплексного числа:
В следующем коде показано, как можно создать комплексное число в Python, а затем применить функцию abs() для получения его величины:
c = (6 + 7j) abs(c)
Out:
9.219544457292887
В Python мы используем 92} \приблизительно 9.22$$
Получить абсолютное значение значения в Python можно быстро и легко, используя функцию abs() . Функция abs() работает с целыми числами, числами с плавающей запятой и комплексными числами, поэтому она поможет вам в любой ситуации, когда вам может понадобиться ее применить.
Начать обучение бесплатно
Познакомьтесь с авторами
Алфи Грейс Специалист по данным
Алфи получила степень магистра машиностроения в Университетском колледже Лондона. В настоящее время он работает специалистом по данным в Square Enix. Найдите его в LinkedIn.
В настоящее время он работает специалистом по данным в Square Enix. Найдите его в LinkedIn.
Редактор: Брендан
Основатель LearnDataSci
Вернуться к оглавлению блога
Как получить абсолютное значение чисел в Python? · Kodify
В Python существует множество способов работы с положительными и отрицательными значениями. Но иногда нам просто нужно убедиться, что наше значение не имеет отрицательного знака. Давайте посмотрим, как помогает абсолютное значение.
В ЭТОЙ СТАТЬЕ:
# Два способа получить абсолютные значения в Python
В математике абсолютное значение — это неотрицательное значение числа без учета его знака (Википедия, 2019). То есть абсолютное значение — это значение, которое описывает, насколько далеко число от нуля.
Например, абсолютное значение -12 равно 12 . А абсолютное значение 33 равно просто 33 . Наша программа использует абсолютные значения, когда нам не важен знак, а просто нужно значение.
У Python есть два способа получить абсолютное значение числа:
- Встроенная функция
abs()возвращает абсолютное значение. - Функция
math.fabs()также возвращает абсолютное значение, но в виде значения с плавающей запятой.
Стандартная функция abs() — это то, что вам нужно в 95% случаев. Итак, давайте начнем с этого.
# Получить абсолютные значения с помощью функции Python
abs() Встроенная функция abs() возвращает абсолютное значение (Lutz, 2013). Для выполнения своей работы функции требуется один аргумент, который должен быть числом (Python Docs, nd a). Затем он возвращает абсолютное значение этого аргумента.
Чтобы использовать функцию, просто вызовите abs() всякий раз, когда вам нужно абсолютное значение:
abs(-23,43) # Возвращает: 23,43
Функция abs() возвращает различные типы значений (Python Docs, nd a):
- Когда мы передаем
abs()целое число или значение с плавающей запятой, мы получаем в ответ абсолютное целое число или значение с плавающей запятой.
- Но если мы зададим
abs()комплексное число, то функция вернет величину этого числа.
# Получить абсолютное значение целых чисел в Python
Итак, чтобы получить абсолютное значение целого числа, мы просто передаем это целое число в функцию abs() . Вот пример:
# Несколько случайных целых чисел
переменнаяA = 28
переменнаяB = -101
переменнаяC = 0
переменнаяD = -9116439
# Получить абсолютные значения этих целых чисел
абсА = абс(переменнаяА)
абсВ = абс(переменнаяB)
абсC = абс(переменнаяC)
абсD = абс(переменнаяD)
# Выводим результаты
print("Абсолютные значения целых чисел с помощью `abs()`:")
print("|", переменнаяA, "| = ", absA, sep="")
print("|", переменнаяB, "| = ", absB, sep="")
print("|", переменнаяC, "| = ", absC, sep="")
print("|", переменнаяD, "| = ", absD, sep="")
Эта мини-программа сначала создает четыре целочисленные переменные (от переменнаяA до переменнаяB ). Есть положительное значение, два отрицательных и ноль. Теперь мы хотим получить их абсолютное значение.
Есть положительное значение, два отрицательных и ноль. Теперь мы хотим получить их абсолютное значение.
Итак, мы вызываем функцию abs() для каждой следующей переменной. Это дает нам значение, которое говорит, насколько далеко конкретное число от нуля. Мы помещаем эти значения в четыре новые переменные, от absA до absD .
Затем мы выводим как исходное число, так и его абсолютное значение с помощью Python 9.0014 функция печати() . Вот как выглядит этот вывод:
Абсолютные значения целых чисел с помощью `abs()`: |28| = 28 |-101| = 101 |0| = 0 |-9116439| = 9116439
# Получить абсолютное значение значений с плавающей запятой в Python
Конечно, мы также можем получить абсолютное значение чисел, которые имеют дробное значение. Для этого мы просто вызываем abs() для этого значения. Вот быстрый пример:
# Несколько случайных значений с плавающей запятой переменнаяA = -12,34 переменнаяB = -1,8457425364 переменнаяC = -0,00000000001 переменнаяD = 9424.5895279095 # Получить абсолютное значение каждой переменной абсVarA = абс (переменнаяA) абсVarB = абс (переменнаяB) абсVarC = абс(переменнаяC) абсVarD = абс(переменнаяD) # Выводим результаты print("Абсолютные значения значений с плавающей запятой с помощью `abs()`:") print("|", переменнаяA, "| = ", absVarA, sep="") print("|", variableB, "| = ", absVarB, sep="") print("|", переменнаяC, "| = ", absVarC, sep="") print("|", variableD, "| = ", absVarD, sep="")
Эта мини-программа создает четыре переменные с плавающей запятой. Мы называем их переменнаяA от до переменнаяD .
Затем мы получаем их абсолютные значения. Для этого мы вызываем функцию abs() для каждой переменной. Мы сохраняем результат функции в новой переменной (от absVarA до absVarD ).
Затем мы отображаем результаты с помощью нескольких операторов print() . Каждый выводит исходную переменную и ее абсолютное значение:
|-12,34| = 12,34 |-1,8457425364| = 1,8457425364 |-1e-11| = 1e-11 |9424,5895279095| = 9424,5895279095
# Получить абсолютные значения с плавающей запятой с помощью функции Python
math. fabs()
fabs() В дополнение к стандартной функции abs() , Python также имеет функцию math.fabs() . Эта функция также нуждается в одном аргументе. Затем он возвращает абсолютное значение этого аргумента в виде значения с плавающей запятой (Python Docs, nd b).
Это поведение похоже на abs() , но вот ключевое отличие: мы всегда возвращаем значение с плавающей запятой — даже когда мы даем math.fabs() целое число для начала.
Чтобы использовать math.fabs() , мы просто делаем:
import math math.fabs(-8) # Возвращает: 8.0
# Пример: получение абсолютных значений в виде значений с плавающей запятой
Итак, чтобы получить абсолютное значение в виде значения с плавающей запятой, мы вызываем math.fabs() для числового значения. Вот пример:
импортировать математику # Несколько случайных значений значениеА = -4 значениеB = -56 значениеC = 26 значениеD = -2,992474203 # Получить абсолютное значение с плавающей запятой из каждого fabs_A = math.fabs(valueA) fabs_B = math.fabs(valueB) fabs_C = math.fabs(valueC) fabs_D = math.fabs(значениеD) # Выводим результаты print("Абсолютные значения с плавающей запятой с `fabs()`:") print("|", valueA, "| = ", fabs_A, sep="") print("|", valueB, "| = ", fabs_B, sep="") print("|", valueC, "| = ", fabs_C, sep="") print("|", valueD, "| = ", fabs_D, sep="")
Эта мини-программа сначала импортирует математический модуль . Затем мы объявляем четыре переменные, от valueA до valueB . Их значения включают как положительные, так и отрицательные числа.
Чтобы получить их абсолютное значение, мы выполняем функцию math.fabs() для каждой переменной. Это дает нам абсолютное значение с десятичной составляющей. Мы сохраняем эти результаты в переменных от fabs_A до fabs_D .
Последняя часть имеет Функция print() отображает как исходное, так и абсолютное значение. Как видно из вывода, каждое значение возвращается как значение с плавающей запятой:
Абсолютные значения с плавающей запятой с помощью fabs(): |-4| = 4,0 |-56| = 56,0 |26| = 26,0 |-2,992474203| = 2,992474203
# Получить абсолютные значения из списка или массива Python
В приведенных выше примерах у нас было abs() и math., которые возвращали абсолютное значение одного значения. Но что, если у нас есть последовательность значений? Давайте взглянем.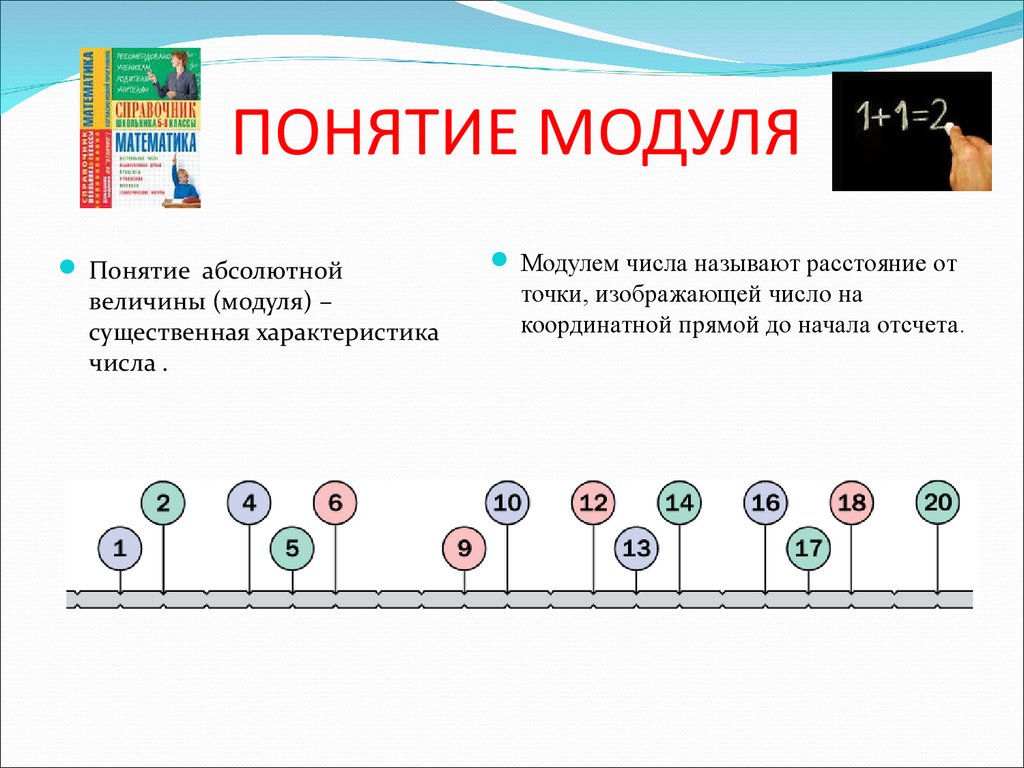 fabs()
fabs()
# Получить абсолютное значение чисел в списке Python
В Python есть несколько способов получить абсолютное значение каждого значения списка. Одним из вариантов является выражение понимания списка. Это обеспечивает чистый и эффективный способ преобразования полного списка в абсолютные значения.
Вот пример:
# Несколько случайных чисел
значения = [-40, 58, -69, -84, 51, 76, -12, 36]
# Получить абсолютное значение для каждого числа
absValues = [abs(число) для числа в значениях]
# Выходные данные
print("Исходные числа:\n", значения)
print("Абсолютные значения:\n", absValues) В этой мини-программе мы сначала создаем список с именем значений . Его значения являются как положительными, так и отрицательными целыми числами.
Затем мы кодируем понимание списка. Между квадратными скобками ( [ и ] ) функция abs() получает абсолютное значение каждого числа значения. Эта переменная
Эта переменная число происходит из нашего списка значений . Мы генерируем его с помощью встроенного выражения для : для числа в значениях . Это создает новый список с абсолютным значением каждого исходного значения списка.
Затем функция print() выводит как исходный список, так и список с абсолютными значениями. Вот как выглядит этот вывод:
Исходные номера: [-40, 58, -69, -84, 51, 76, -12, 36] Абсолютные значения: [40, 58, 69, 84, 51, 76, 12, 36]
Кстати, если вам не нужно сохранять исходные значения списка, просто установите исходный список на результат понимания списка. Например:
# Некоторые примеры значений значения = [-40, 58, -69, -84, 51, 76, -12, 36] # Замените исходные числа абсолютными значениями значения = [абс (число) для числа в значениях]
# Получение абсолютных значений из списка с помощью цикла Python
Хотя понимание списка полезно, его нельзя использовать в любой ситуации. Особенно, если мы также хотим обрабатывать значения помимо простого получения абсолютного значения, тогда обычный цикл
Особенно, если мы также хотим обрабатывать значения помимо простого получения абсолютного значения, тогда обычный цикл для часто является лучшим выбором.
Допустим, мы хотим получить абсолютное значение отрицательных значений в нашем списке, но умножить положительные на 2. Вот как мы можем запрограммировать это с помощью цикла Python:
# Некоторые положительные и отрицательные значения
значения = [-40, 58, -69, -84, 51, 76, -12, 36]
# Берем абсолютное значение отрицательных значений, но
# умножить положительные значения на 2
обработано = []
для числа в значениях:
если число < 0:
обработано.append (абс (число))
еще:
обработано.добавлять(число * 2)
# Выходные данные
print("Исходные числа:\n", значения)
print("Обработанные числа:\n", обработано) Здесь мы сначала составляем список с номерами. Этот список значений содержит как положительные, так и отрицательные целые числа.
Потом делаем новый список, обработано . Этот список изначально пуст (но заполняется внутри цикла). Затем делаем цикл
Этот список изначально пуст (но заполняется внутри цикла). Затем делаем цикл на . Этот цикл проходит через список значений . Переменная числа цикла представляет собой значение списка во время каждого цикла цикла.
Внутри цикла оператор if/else оценивает эту переменную. Когда он ниже нуля, Функция abs() принимает абсолютное значение. Затем мы используем метод списка append() , чтобы добавить значение в наш обработанный список .
Когда переменная цикла равна нулю или больше, выполняется предложение else . Там мы умножаем переменную на 2 и добавляем в список.
В последнем фрагменте кода функция Python print() выводит исходный и обработанный список. Вот что выдает:
Исходные номера: [-40, 58, -69, -84, 51, 76, -12, 36] Обработанные номера: [40, 116, 69, 84, 102, 152, 12, 72]
Если вам не нужны исходные значения списка, вы также можете перезаписать список циклом для . Удобной функцией, которая может помочь в этом, является функция Python
Удобной функцией, которая может помочь в этом, является функция Python enumerate() . Вот как это выглядит:
# Некоторые положительные и отрицательные значения
значения = [-40, 58, -69, -84, 51, 76, -12, 36]
# Проходим по списку и заменяем
# каждое число с его абсолютным значением
для индекса значение в перечислении (значения):
значения [индекс] = абс (значение)
# Получить абсолютные значения из массива Python
Если ваши положительные и отрицательные значения находятся в массиве Python, то получение их абсолютных значений аналогично работе со списками. Вот пример: массив импорта
# Создаем массив со случайными значениями
значения = массив.массив('i', [-40, 58, -69, -84, 51, 76, -12, 36])
# Создаем новый массив с абсолютными значениями
absValues = array.array('i', [abs(значение) для значения в значениях])
# Выводим результаты
print("Исходные значения массива:\n", значения)
print("Абсолютные значения:\n", absValues) Сначала мы импортируем модуль массива . Затем мы создаем массив с помощью конструктора
Затем мы создаем массив с помощью конструктора array.array() . Этот массив имеет как положительные, так и отрицательные целые числа.
Затем мы строим второй массив на основе абсолютных значений первого. Чтобы это произошло, мы создаем массив со списком. Это выражение принимает абсолютное значение ( abs(value) ) из каждого числа, которое генерирует встроенное выражение для ( для значения в значениях ). При этом мы проходим по исходному списку и в процессе собираем абсолютные значения.
В последнем бите кода функция print() выводит массив исходных и абсолютных значений. Вот как это выглядит:
Исходные значения массива:
массив('i', [-40, 58, -69, -84, 51, 76, -12, 36])
Абсолютные значения:
массив('i', [40, 58, 69, 84, 51, 76, 12, 36])
Если вам не нужны исходные данные, вы можете перезаписать этот массив его абсолютными значениями. Например:
значений = array.array('i', [-40, 58, -69, -84, 51, 76, -12, 36]) # Перезаписать существующий массив абсолютными значениями values = array.array('i', [абс(значение) для значения в значениях])
# Получить абсолютные значения из массива NumPy
Если вы работаете с пакетом числового программирования NumPy для Python, у вас может быть массив NumPy, из которого вы хотите получить абсолютные значения. Вот как мы это делаем:
import numpy
значения = numpy.array ([-40, 58, -69, -84, 51, 76, -12, 36])
# Создать новый массив абсолютных значений
absValues = numpy.abs (значения)
print("Исходные значения массива NumPy:\n", значения)
print("Абсолютные значения:\n", absValues) Этот код сначала импортирует модуль numpy . Затем мы создаем массив с именем значений с положительными и отрицательными целыми числами.
Чтобы получить их абсолютные значения, мы вызываем функцию numpy.abs() и передаем этот массив в качестве аргумента. В результате NumPy возвращает новый массив с абсолютным значением каждого числа в исходном массиве. Мы называем этот массив
В результате NumPy возвращает новый массив с абсолютным значением каждого числа в исходном массиве. Мы называем этот массив absValues .
Последние операторов print() отображают оба массива. Как видно из вывода, numpy.abs() дал нам абсолютное значение для каждого из исходных значений массива:
Исходные значения массива NumPy: [-40 58 -69 -84 51 76 -12 36] Абсолютные значения: [40 58 69 84 51 76 12 36]
Если вам не нужно сохранять исходные данные, вы также можете перезаписать существующий массив абсолютными значениями. Вот как:
значений = numpy.array([-40, 58, -69, -84, 51, 76, -12, 36]) # Перезаписать массив, чтобы получить только абсолютные значения значения = numpy.abs (значения)
# Сводка
Функция Python abs() возвращает абсолютное значение для целых чисел и чисел с плавающей запятой. Чтобы использовать его, мы вызываем функцию и предоставляем ей аргумент, абсолютное значение которого нам нужно.



 5895279095
# Получить абсолютное значение каждой переменной
абсVarA = абс (переменнаяA)
абсVarB = абс (переменнаяB)
абсVarC = абс(переменнаяC)
абсVarD = абс(переменнаяD)
# Выводим результаты
print("Абсолютные значения значений с плавающей запятой с помощью `abs()`:")
print("|", переменнаяA, "| = ", absVarA, sep="")
print("|", variableB, "| = ", absVarB, sep="")
print("|", переменнаяC, "| = ", absVarC, sep="")
print("|", variableD, "| = ", absVarD, sep="")
5895279095
# Получить абсолютное значение каждой переменной
абсVarA = абс (переменнаяA)
абсVarB = абс (переменнаяB)
абсVarC = абс(переменнаяC)
абсVarD = абс(переменнаяD)
# Выводим результаты
print("Абсолютные значения значений с плавающей запятой с помощью `abs()`:")
print("|", переменнаяA, "| = ", absVarA, sep="")
print("|", variableB, "| = ", absVarB, sep="")
print("|", переменнаяC, "| = ", absVarC, sep="")
print("|", variableD, "| = ", absVarD, sep="")
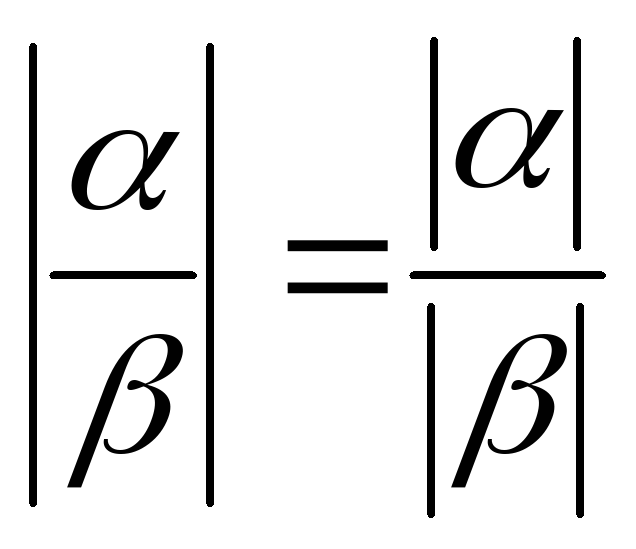 fabs()
fabs()  fabs(valueA)
fabs_B = math.fabs(valueB)
fabs_C = math.fabs(valueC)
fabs_D = math.fabs(значениеD)
# Выводим результаты
print("Абсолютные значения с плавающей запятой с `fabs()`:")
print("|", valueA, "| = ", fabs_A, sep="")
print("|", valueB, "| = ", fabs_B, sep="")
print("|", valueC, "| = ", fabs_C, sep="")
print("|", valueD, "| = ", fabs_D, sep="")
fabs(valueA)
fabs_B = math.fabs(valueB)
fabs_C = math.fabs(valueC)
fabs_D = math.fabs(значениеD)
# Выводим результаты
print("Абсолютные значения с плавающей запятой с `fabs()`:")
print("|", valueA, "| = ", fabs_A, sep="")
print("|", valueB, "| = ", fabs_B, sep="")
print("|", valueC, "| = ", fabs_C, sep="")
print("|", valueD, "| = ", fabs_D, sep="")
 array('i', [-40, 58, -69, -84, 51, 76, -12, 36])
# Перезаписать существующий массив абсолютными значениями
values = array.array('i', [абс(значение) для значения в значениях])
array('i', [-40, 58, -69, -84, 51, 76, -12, 36])
# Перезаписать существующий массив абсолютными значениями
values = array.array('i', [абс(значение) для значения в значениях])