Алгоритм построения графика квадратичной функции: Построение графика квадратичной функции — урок. Алгебра, 8 класс.

2+ q» | Математика

Автор: Кибирева Ирина Валерьевна

Организация: МБОУ «Дульдургинская СОШ»

Населенный пункт: Забайкальский край, с. Дульдурга

Урок по теме «Преобразование графика функции у=ах² в график функции

у = а(х + р)²+ q»

Цель урока: Обеспечить выявление алгоритма построения графика квадратичной функции с помощью преобразований графика у=ах².

Задачи:

Обучающие: актуализировать опорные знания по теме, рассмотреть преобразование графика функции у=ах² в график функции у =а(х + р)²+ q используя исследовательский метод, получить алгоритм построения графиков функций вида y =а(х + р)²+ q, провести первоначальный контроль знаний с помощью тренажера «Перемещение параболы» на образовательном портале интерактивной платформы для обучения детей UCHI.RU.

Развивающие

: развитие математического мышления (умений обобщать, сравнивать, анализировать, делать выводы).

Воспитательные: воспитание культуры общения, умения слушать и вступать в диалог, строить сотрудничество с учителем и учениками.

Тип урока: Урок усвоения новых знаний

Место урока в системе уроков: По теме график функции у = ax²+bx+cотводится 4 урока, первый из которых по рекомендациям автора УМК является преобразование графика функции у=ах² в график функции у =а(х + р)²+ q.

Формы работы организации познавательной деятельности: фронтальная, групповая, индивидуальная.

Технологии: информационно-коммуникативная, развивающего обучения.

Время проведения занятия 45 минут.

На данном уроке основополагающим является деятельностный подход, использование ИКТ и работа над формированием универсальных учебных действий.

Урок направлен на достижение следующих результатов:

Предметные: оперировать понятиями: функция, график функции, строить график квадратичной функции и на ее примере использовать преобразования графика функции y=f(x) для построения графиков функций у = af(kx+b)+c.

Метапредметные: способности самостоятельно ставить цели, планировать пути достижения, представлять информацию в различной форме (словесной, табличной, графической) и умения организовывать совместную деятельность с учителем и сверстниками.

Личностные: способность обучающихся к самообразованию, заинтересованность в приобретении и расширении математических знаний и способов действий.

Урок состоит из следующих этапов:

Вводно-мотивационный этап

, который состоит из трех составляющих.

1.Самоопределение к деятельности: целью которого является мотивация учащихся к учебной деятельности с помощью психологического настроя на успешную деятельность на уроке.

2.Создание тупиковой ситуации, формулирование темы урока, постановка учебной задачи: целью которого является создание ситуации требующей дальнейшего изучения квадратичной функции. Формулировка темы урока и учебной задачи. Используемые средства обучения презентация и наводящие вопросы учителя. На данном этапе развиваются умения ставить цели и задачи (метапредметные результаты – овладение способами организации учебной деятельности).

3.Актуализация опорных знаний. Цель: Подготовить учащихся к деятельности через повторение. Средства обучения: программа для построения графиков Аdvanced Grapher, вопросы учителя.

Операционно-содержательный этап:

Открытие новых знаний:

Цель данного этапа: Создание условий для выполнения творческой работы в группах, в ходе которой учащиеся получат новые знания о преобразовании графика квадратичной функции.

Класс делится на три группы. Каждой группе предлагается выполнить ряд заданий:

1. Заполнить предложенные таблицы.

2. Построить графики и выявить закономерность.

3. Составить таблицу изменения графика функции в зависимости от чисел а, р и q.

Для этого учащиеся используют карточки с порядком действий, ватман, клей, ножницы, цветную бумагу, документ-камеру, программу для построения графиков Аdvanced Grapher.

В результате чего приходят к алгоритму преобразования графика функции у=ах² в график функции у =а(х + р)²+ q.

Первичное закрепление проводится с помощью построения схемы цепочки преобразований графика функции и построения алгоритма для графика у =а(х + р)

2+ q.

Рефлексивно-оценочный этап проходит с использованием тренажера «Перемещение параболы» на образовательном портале интерактивной платформы для обучения детей UCHI.RU. Основная цель которого провести первоначальный контроль знаний. Тренажер содержит пять заданий на движения графиков. В ходе работы за тренажером учащиеся закрепляют преобразования согласно полученному алгоритму.

Для оценивания деятельности учащихся заполняется лист оценивания.

Планируемые результаты:

Учащиеся получат возможность оперировать понятиями: функция, график функции, строить график квадратичной функции и на ее примере использовать преобразования графика функции y=f(x) для построения графиков функций у = af(kx+b)+c.

В повседневной жизни и при изучении других предметов учащиеся получат возможность иллюстрировать с помощью графика реальную зависимость или процесс по их характеристикам; использовать график квадратичной функции при решении задач из других учебных предметов.

Личностные УУД: Осознанное, уважительное и доброжелательное отношение к другому человеку, его мнению.

Регулятивные УУД: Умение самостоятельно определять цели обучения, планировать решение учебной задачи, осуществлять итоговый контроль деятельности, анализировать собственную работу и работу товарищей.

Познавательные УУД: Умение строить логические рассуждения, применять алгоритмы и схемы для решения учебных задач.

Коммуникативные УУД: Умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, работать индивидуально и в группе, отстаивать свою точку зрения.

Литература, источники информации:

1. Г. К. Муравин, К.С.Муравин., Муравина О.В. Алгебра 9 класс. Учебник. – М.:Дрофа, 2010.

Г.К. Муравин, Муравина О.В. Алгебра 9 класс. Методическое пособие. – М.:Дрофа, 2010.

Ход урока:

1. Вводно-мотивационный этап

 

Здравствуйте ребята! Я рада вас видеть сегодня на уроке в хорошем настроении. Посмотрите друг другу в глаза, улыбнитесь, пожелайте хорошего рабочего настроения на уроке. Я тоже вам желаю сегодня отличной работы.

Перед вами КИМы OГЭ. Посмотрите на задание №10. Как вы думаете, с чем будет связан наш урок? (С графиками функций)

А с графиками, каких функций вы узнаете, если соотнесете формулу с рисунком

Какая это функция? (Квадратичная)

Что является ее графиком? (Парабола)

С помощью, каких преобразований можно получить график этой функции из графика функции (необходимо растянуть график от оси абсцисс в а раз, если а >1, и сжать к оси абсцисс если а <1)

 

Формулировка темы урока и постановка учебной задачи

 

А чем отличается функция у = а(х + р)²+ q от функции у = ах²? Будет ли ее графиком парабола (возможно да).

От чего будет зависеть ее расположение? (предположение: От р и q)

Что нам предстоит сегодня узнать на уроке? (Версии учащихся, приходим к преобразованию графика функции у=ах² в график функции у = а(х + р)²+ q)

Тема урока: Преобразование графика функцииу=ах² в график функции у = а(х + р)²+ q.

 

Актуализация опорных знаний

Вспомним основные свойства графика функции . (Используя построенный график)

Будут ли отличаться свойства графика от свойств графика ?

Будут ли отличаться свойства зеленого и красного графиков? (да, так как разное направление ветвей, а значит, меняются некоторые свойства)

 

 

Операционно-содержательный этап

 

Открытие новых знаний

Деление класса на три группы. Каждой группе предлагается выполнить ряд заданий:

1. Заполнить предложенные таблицы.

2. Построить графики и выявить закономерность.

3. Составить таблицу изменения графика функции в зависимости от чисел а, р и q, используя ватман, клей, шаблоны графика функции y=аx², программу для построения графиков на выбор.

Задания первой группе:

1. Заполнить таблицу значений

№	x	—2	—1,5	—1	—0,5	00	00,5	11,5	12
1
2
3
4

2. Построить график функции в тетради и на отдельном листе (на отдельном листе вырезать в качестве шаблона)

3.Построить график функции и подумать над вопрсом «Чем отличается этот график от первого?» и «Можно ли получать график второй функции из графика первой и как?»

4. Построить график функции и подумать над вопросом «Чем отличается этот график от первого?» и «Можно ли получить график третьей функции из графика первой и как?»

5. Построить график функции . Подумать над вопросом «Чем отличается этот график от второго?» и «Как его получить?»

6. Построить график функции с помощью шаблона . Подумать «Чем отличается этот график от третьего? Что надо сделать с третьим графиком, чтобы получить пятый?

7. Построить график функции и с помощью шаблона . В каждом случае укажите координаты вершины параболы.

8. Составить таблицу изменения графика функции в зависимости от чисел а, р и q используя ватман, клей и шаблоны графика функции y=2x²_.

 

Исходная функция	Последующая функция	График	Преобразование
2	2
2
2
2
2

Задания второй группе (См. приложение 1)

Задания третьей группе (См. приложение 1)

• Защита проделанной работы учащимися с использованием документ-камеры и проделанной работы учащимися на ватманах. Разъяснение всех шагов полученных преобразований.
• Коллективное обсуждение полученных результатов.
• Формулировка выводов.
• Как получается график функции ?

Вывод: График функции получается сдвигом параболы р единиц влево при р > 0 и на — р единиц вправо при .

Как получается график функции ?

Вывод: График функции получается сдвигом параболы вдоль оси абсцисс, а затем вдоль оси ординат на q единиц вверх, если q>0 и на q единиц вниз q<0

Вывод: График функции получается из параболы y=ax²с помощью двух сдвигов вдоль осей координат.

Составить цепочку преобразований, с помощью которой можно из графика функции получить график функции .

Пояснения:

1. Вытянуть график функции

2. Сдвиг вправо на 3 единицы

3. Сдвиг вниз таким образом, координаты вершины параболы (3;-2)).

Формулируется алгоритм и записывается алгоритм построения графика функции по шагам.

 

3. Рефлексивно-оценочный этап

Работа с тренажером на образовательном портале UCHI.RU.

Последующие задания тренажера (См. в приложении 2).

 

Ребята, что нового вы узнали сегодня на уроке?

Давайте вернемся к началу урока. Чем отличается функция у = а(х + р)²+ q от функции у =ах² и что будет ее графиком?

Чему научились сегодня на уроке?

Посмотрите еще раз на КИМы ОГЭ и скажите есть ли еще не знакомые нам вопросы? (Да) Какой же вывод мы можем сделать?

 

Каждой группе предлагается оценить участие членов группы и работу с тренажером по пятибалльной шкале.

Лист оценивания

 

Работа в группе (от 0-5 баллов)
Работа с тренажером (от 0-5 баллов)
Итого: 5-6 баллов – «3», 7-8 баллов – «4», 9-10 баллов – «5»

 

Домашнее задание: п.14(учебник Г.К. Муравин Алгебра 9) №193, 200

 

 

 

Приложения:

1. file0.docx.. 435,6 КБ
2. file1.docx.. 1,3 МБ

Опубликовано: 10.03.2020

Сопоставление спектральных графов и регуляризованные квадратичные релаксации: алгоритм и теория

Чжоу Фань, Ченг Мао, Йихонг Ву, Цзямин Сюй

Материалы 37-й Международной конференции по машинному обучению , PMLR 119:2985-2995, 2020.

Аннотация

Сопоставление графов, также известное как выравнивание сети, направлено на восстановление скрытого соответствия вершин между двумя немаркированными взвешенными графами с корреляцией ребер. Для решения этой задачи мы предлагаем спектральный метод GRAph Matching by Pairwise eigen-Alignments (GRAMPA), который сначала строит матрицу подобия как взвешенную сумму внешних произведений между всеми парами собственных векторов двух графов, а затем выводит сопоставление с помощью простой процедуры округления. Для класса универсальности коррелированных моделей Вигнера GRAMPA обеспечивает точное восстановление скрытого соответствия между двумя графами с реберной корреляцией $1 — 1/\mathrm{polylog}(n)$ и средней степенью не менее $\mathrm{polylog}(n) $. Это соответствует современным гарантиям для алгоритмов с полиномиальным временем, установленным для коррелированных графов Эрдёша-Реньи, и значительно превосходит существующие спектральные методы. Превосходство GRAMPA также продемонстрировано на множестве синтетических и реальных наборов данных с точки зрения как статистической точности, так и вычислительной эффективности.

Процитировать эту статью

---

БибТекс

@InProceedings{pmlr-v119-fan20a, title = {Сопоставление спектральных графов и регуляризованные квадратичные релаксации: алгоритм и теория}, автор = {Фань, Чжоу и Мао, Чэн и Ву, Ихун и Сюй, Цзямин}, booktitle = {Материалы 37-й Международной конференции по машинному обучению}, страницы = {2985--2995}, год = {2020}, редактор = {III, Хэл Дауме и Сингх, Аарти}, объем = {119}, серия = {Материалы исследования машинного обучения}, месяц = ​​{13--18 июля}, издатель = {PMLR}, pdf = {http://proceedings.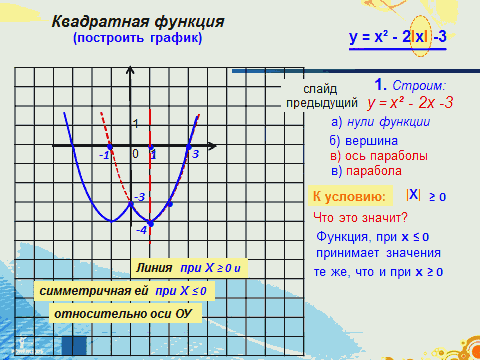 mlr.press/v119/fan20a/fan20a.pdf}, URL = {https://proceedings.mlr.press/v119/fan20a.html}, abstract = {Сопоставление графов, также известное как сетевое выравнивание, направлено на восстановление скрытого соответствия вершин между двумя немаркированными взвешенными графами с корреляцией ребер. Для решения этой задачи мы предлагаем спектральный метод GRAph Matching by Pairwise eigen-Alignments (GRAMPA), который сначала строит матрицу сходства как взвешенную сумму внешних произведений между всеми парами собственных векторов двух графов, а затем выводит сопоставление с помощью простой процедуры округления. Для класса универсальности коррелированных моделей Вигнера GRAMPA достигает точного восстановления скрытого соответствия между двумя графами с реберной корреляцией $1 - 1/\mathrm{polylog}(n)$ и средней степенью не менее $\mathrm{polylog}(n) $. Это соответствует современным гарантиям для алгоритмов с полиномиальным временем, установленным для коррелированных графов Эрдёша-Реньи, и значительно превосходит существующие спектральные методы. Превосходство GRAMPA также продемонстрировано на множестве синтетических и реальных наборов данных с точки зрения как статистической точности, так и вычислительной эффективности.} }

Сноска

%0 Документ конференции Сопоставление спектральных графов %T и регуляризованные квадратичные релаксации: алгоритм и теория %A Чжоу Фан %А Ченг Мао %A Ихонг Ву % А Цзямин Сюй %B Материалы 37-й Международной конференции по машинному обучению %C Материалы исследования машинного обучения %D 2020 %E Хэл Доме III %E Арти Сингх %F пмлр-v119-fan20a %I PMLR %Р 2985--2995 %U https://proceedings.mlr.press/v119/fan20a.html %V 119 Сопоставление графов %X, также известное как сетевое выравнивание, направлено на восстановление скрытого соответствия вершин между двумя немаркированными взвешенными графами с корреляцией ребер. Для решения этой задачи мы предлагаем спектральный метод GRAph Matching by Pairwise eigen-Alignments (GRAMPA), который сначала строит матрицу подобия как взвешенную сумму внешних произведений между всеми парами собственных векторов двух графов, а затем выводит сопоставление с помощью простой процедуры округления. Для класса универсальности коррелированных моделей Вигнера GRAMPA обеспечивает точное восстановление скрытого соответствия между двумя графами с реберной корреляцией $1 - 1/\mathrm{polylog}(n)$ и средней степенью не менее $\mathrm{polylog}(n) $. Это соответствует современным гарантиям для алгоритмов с полиномиальным временем, установленным для коррелированных графов Эрдёша-Реньи, и значительно превосходит существующие спектральные методы. Превосходство GRAMPA также продемонстрировано на множестве синтетических и реальных наборов данных с точки зрения как статистической точности, так и вычислительной эффективности.

АПА

Фань, З., Мао, К., Ву, Ю. и Сюй, Дж.. (2020). Сопоставление спектральных графов и регуляризованные квадратичные релаксации: алгоритм и теория. Proceedings of the 37th International Conference on Machine Learning , in Proceedings of Machine Learning Research 119:2985-2995 Доступно по адресу https://proceedings. mlr.press/v119/fan20a.html.

---

Сопутствующий материал

Алгоритмический анализ

Алгоритмический анализ

Алгоритм анализа

Эта лекция посвящена анализу алгоритмов с упором на следующие цели обучения:

• 17: Учащийся может правильно связать проблемы и потенциальные алгоритмические решения.
• 18: Студент может оценивать алгоритмы аналитически и эмпирически.

Введение

Правильность алгоритма относится к тому, содержит ли он ошибки. О процедурах тестирования мы поговорим ниже.

Ясность алгоритма относится к тому, насколько хорошо он выражен и описан. Можете ли вы понять, что он делает и как он это делает? Мы начнем использовать комментариев для документирования нашего кода.

Эффективность алгоритма обычно относится к тому, как эффективно использует два ключевых ресурса: time и space — то есть процессор или центральный процессор (CPU), и оперативная память компьютера , часто называемый произвольным доступом память (ОЗУ).

Чем быстрее алгоритм — чем быстрее он завершает свою задачу — тем эффективнее он является по отношению ко времени.

Чем меньше памяти он использует, тем эффективнее он использует пространство.

Алгоритмы сортировки и поиска

При обсуждении этой темы мы поговорим о сортировке и поиске алгоритмы. Алгоритм сортировки сортировки упорядочивает данные в определенном порядке, например, в числовом порядке. или в алфавитном порядке. А 9Алгоритм 0059 search ищет некоторые целевые данные, например, имя в телефонной книге. Вы можете думать, что данные содержатся в списке .

Эффективность и размер ввода

Проблемы с эффективностью возникают только при наличии больших объемов из данных . Размер ввода алгоритма часто сокращается с N . По мере роста N различия между эффективными и становятся очевидными неэффективные алгоритмы.

Например, в этой таблице показаны различия во времени работы в секунд для одного и того же алгоритма сортировки при разных размерах ввода.

List Size, N	Older Computer	Newer Computer
125	12.5	2.8
250	49.3	11.0
500	195.8	43.4
1000	780,3	172,9
2000	3114,9	690,5

Компьютерщики любят абстрагироваться от различий в эффективности, которые вызваны разным аппаратным и программным обеспечением — например, более быстрым или медленным компьютером.

Вот некоторые старые данные, полученные на разных машинах при сортировке 2000 целых чисел по тому же алгоритму:

Тип компьютера	Время
Домашний ПК	51.915
Desktop PC	11.508
Minicomputer	2. 382
Mainframe	0.431
Supercomputer	0.087

Эмпирический анализ: Данные в обеих этих таблицах были собрал опытным путем или опытным путем — т.е. запуск и синхронизация фактической программы на разных машинах и входах.

Абстрактный анализ

Мы также можем анализировать эффективность алгоритма более абстрактно, сравнение алгоритма с хорошо известными математическими функциями.

Рассмотрим следующий график с четырьмя функциями: логарифмическая , линейная , квадратичная и экспоненциальная функции:

Логарифмическая функция:   y = log 2 x Линейная функция:         г = 5x Квадратичная функция:    y = x 2 Экспоненциальная функция: y = 2 x

Как видите, с увеличением X время работы увеличивается. Но посмотрите на различия. Посмотрите, как медленно увеличивается время работы для логарифмической функции по сравнению с экспоненциальной функцией.

С точки зрения этих четырех типов функций мы организуем в следующем порядке в зависимости от того, насколько быстро они увеличиваются по мере увеличения размера x :

logarithmic		linear		quadratic		exponential
log 2 x		x		x 2		2 x

Эффективность алгоритма

Ученые-компьютерщики любят характеризовать эффективность алгоритма с точки зрения того, насколько быстро время выполнения будет увеличиваться по мере увеличения размера входных данных, n .

Чтобы увидеть существенные различия, рассмотрим некоторые числа для этих типов функций:

Входы	Время работы алгоритма (секунды)
n	logarithmic log 2 n	linear n	quadratic n 2	exponential 2 n
8	3	8	64	256
16	4	16	256	65,536
32	5	32	1,024	4,296,967,296
64	6	64	4,096	1. 84 x 10 19
128	7	128	16,384	3.40 x 10 38
256	8	256	65,536	1,15 x 10 77
512		512	262,144	1,3444914949494949491494914914949149149491494914949498	949494949149491494914949491449298	949149149149149149149149149149149149149491449тели. Итак, для 512 входов линейный алгоритм может выполнять некоторые задание за 512 секунд. В то время как экспоненциальный алгоритм будет занимает 1,34 х 10 154 секунд. Алгоритмы и задачи Ученые-компьютерщики любят анализировать проблемы, задавая какой тип алгоритма нам нужно решить эту проблему? Или что быстрее тип алгоритма, который может решить эту проблему? Алгоритм линейного поиска Например, чтобы найти число 100 в следующих списках номера, нам пришлось бы пройтись по каждому номеру в списке, начиная с слева направо. Список 1 (16 номеров): (15 20 4 2 1 17 19 25 100 65 78 19 20 15 0 72) Список 2 (16 номеров): (15 20 4 2 1 17 19 25 65 78 19 20 15 0 72 75) Мы можем использовать алгоритм линейного поиска : # Ищем X в списке L и возвращаем его индекс, indx, в L # Или вернуть -1, если X нет в списке Чтобы найти X в списке L, СДЕЛАЙТЕ: Установите глобальный индекс в 1 За каждое число номер , в списке L : Если число = X : Возврат индекс Установить индекс на индекс + 1 Return -1 # Номер отсутствует в списке, поэтому return -1 TODO: Вручную отследите этот алгоритм в списке 1 и списке 2 и подсчитайте, сколько раз вам нужно пройти через петлю. Вопрос: Допустим, в нашем списке 512 номеров. В наихудший случай — т.е. когда X нет в списке — как много раз мы будем проходить через цикл while? Этот алгоритм (и задача, которую он решает) называется линейным потому что в худшем случае требуется N итераций цикла, чтобы найти что-то в списке из N элементов. Алгоритм логарифмического поиска Если бы наш список был отсортирован, например, как телефонная книга, то он не имеет смысла выполнять линейный поиск, т. е. начинать со страницы 1. Список 1 (16 номеров): (1 2 5 6 9 12 15 16 32 64 100 128 256 299 512 568) Список 2 (16 номеров): (1 2 5 6 9 12 15 16 32 64 99 128 256 299 512 568) Вместо этого мы могли бы угадать приблизительное расположение числа в список и посмотри там. В самом общем случае можно предположить что X было средним значением в списке. Если бы X было больше (или меньше) среднего значения, мы бы поиск в верхней (нижней) половине списка. Это известно как алгоритм двоичного поиска . Например, угадать секретное число от 1 до N: Угадайте среднее значение в диапазоне 1..N Если догадка слишком высока, отрезать верхнюю часть диапазона. Если догадка слишком мала, обрезать нижнюю часть диапазона. Повторяйте, пока не останется только 1 число. ВОПРОС: Сколько попыток найти секретное число от 1 до 100? От 1 до 500? Вы должны видеть это как N увеличивается, двоичный search будет расти очень медленно, как логарифмическая функция . Алгоритм квадратичной сортировки Давайте рассмотрим пример алгоритма, который работает как квадратичная функция . Сортировка списка номеров N от младшего слишком высоко с помощью пузыря Сортировать. Список 1 (5 номеров): (10 5 4 4 1) ПРИМЕЧАНИЕ. Пузырьковая сортировка, вероятно, является худшим алгоритмом сортировки в мире. И есть много алгоритмов сортировки, которые намного эффективнее. Но вот пузырьковая сортировка: # Отсортировать N чисел в списке L в порядке возрастания Для списка из N элементов повторите N-1 раза. # N-1 шагов Для каждой соседней пары предметов # N-1 пар Если пара не по порядку, поменять местами номера Этот алгоритм содержит вложенных циклов . Внешний цикл повторяется N-1 раза. И при каждом повторении внутренняя петля делает N-1 сравнений соседних чисел. Так что N 2 — 2N + 1 сравнения. Это квадратичное . Аналогия с часами : Подумайте о соотношении секунд стрелка и минутная стрелка на часах. Секундная стрелка тикает 60 раз каждую минуту. Чтобы отсчитать 1 час, минутная стрелка тикает 60 раз, что составляет 3600 секунд. TODO: Вручную отследите этот алгоритм в списке 1 и подсчитайте, сколько раз вы выполняете оператор IF? Вопрос: Предположим, что в списке 512 номеров и он потребовалась 1 секунда, чтобы сравнить и поменять местами пару чисел. Примерно как сколько секунд потребуется, чтобы отсортировать список? Эффективная сортировка Пузырьковая сортировка — это пример алгоритма сортировки на месте . Он не требует намного больше памяти, чем сам список. Наиболее эффективные алгоритмы сортировки на месте могут отсортировать N чисел за время, пропорциональное логарифму n n функция. Для 512 номеров, которые потребуют пропорционального времени до 512 × 8 = 8 192 секунды вместо 512 × 512 = 262 144 секунды. Алгоритм линейной сортировки Что, если бы мы не заботились об экономии места? Как быстро мы могли сортировать N номеров? # Отсортировать список из N чисел в списке L в порядке возрастания. Предполагать # список содержал числа, значения которых находились в диапазоне от 1 до M . # Например, числа могут быть между 1 и 1000. (1) Составьте список LL из M «сегментов», каждый из которых содержит пустой список. (2) Для каждого из N номеров в списке L поместите его в соответствующее ведро. (3) Пройдите по списку, LL, и опорожните ведра обратно в список, L. Например, для нашего исходного списка (10 5 4 4 1) и при условии, что числа диапазон от 1 до 10: (0) L = ( 10 5 4 4 1) (1) LL = ( () () () () () () () () () () ) (2) LL = ( (1) () () (4 4) (5) () () () () (10) ) (3) L = ( 1 4 4 5 10 ) Вопросы: Пространственная эффективность: С точки зрения пространства, этот алгоритм требует места для N числа в L и M ковша, значит N + M . Как это намного больше места? Линейно больше? Квадратично больше? Эффективность использования времени: С точки зрения наших входов N , это алгоритм растет линейно по мере роста размера N . Это показывает, что для данной задачи разные алгоритмы могут иметь разная эффективность. Экспоненциальный алгоритм Задача коммивояжера является примером проблема, которую можно решить только с помощью экспоненциальный алгоритм . Учитывая N городов, найдите кратчайший путь (наименее затратный путь) через все N городов. Единственный известный способ решения этой проблемы — методом полного перебора . Перечислите все возможные пути через города. Для 3 городов мы можем легко сделать это: А Б В А В Б Б А С Б В А С Б А ТАКСИ Вообще есть N! способа обустроить N городов. Здесь есть 3 × 2 × 1 = 6 способов расположить 3 города. И вообще Н! намного больше, чем 2 N : Н Н! 2 N 3 6 8 4 24 16 5 120 32 6 720 64 Задачи, которые можно решить только с помощью экспоненциальных алгоритмов известны как неразрешимые проблемы . Нет общего, оптимального решения для задачи коммивояжера. Существует эвристических решений. Эвристика — это эмпирическое правило, которое дает довольно хорошее (но не всегда оптимальное) решение. Для коммивояжера проблемы, мы можем использовать эвристику ближайшего соседа , т. е. выбрать ближайший соседний город как следующий город. Вычислимость Теоретически говоря, а не практически, есть проблемы, которые в принципе не могут быть вычисляться? Мы не говорим здесь о практические пределы вычислений. Ответ «Нет». В 1936 году британский Математик Алан Тьюринг доказал, что существует ряд проблем, которые не могут быть решены. решается любым алгоритмом или вычислительной процедурой. Пример: Проблема с остановкой. Дано описание компьютерной программы, определить, останавливается ли программа или продолжает работать вечно. В другими словами, учитывая программу и набор входных данных, решить, будет ли программа в конечном итоге остановится, учитывая этот набор входных данных. Тьюринг доказал, что не существует общего алгоритма, способного решить проблема остановки для любой программы и любых входных данных. Мы не будем здесь вдаваться в подробности, но важно, чтобы вы знали что у компьютеров есть это ограничение. Работа в классе Решения Выполните следующие упражнения и добавьте свои ответы на страницу портфолио. на сегодняшнее домашнее задание. Для каждой из следующих задач решите, может ли она быть решена с помощью линейный алгоритм и кратко объясните, почему или почему нет. Вычислить сумму списка, содержащего N случайных целых чисел. Определение повторяющихся чисел в списке из N случайных целых чисел. Для каждой из следующих задач решите, может ли она быть решена с помощью логарифмический алгоритм и кратко объясните, почему или почему нет. Угадывание числа от 1 до 100, если ваши догадки характеризуются как «слишком высоко» или «слишком низко». Угадывание числа от 1 до 100, если ваши предположения характеризуются как «неправильные» или вправо». Для каждой из следующих проблем решите, является ли она неразрешимой и объясните кратко, почему или почему нет. Вычисление суммы всех чисел в квадратной матрице размером N × N . Существует ли для данных n целых чисел такое подмножество, что сумма именно на Б? Например, предположим, что целые числа равны {4, 5, 8, 13, 15, 24, 33}. Если B = 36, то ответ — да (а 4, 8, 24 — это решение). No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт