Алгоритм решения систем уравнений методом подстановки: Решите систему методом подстановки x+y=5 3x+y=7

Математика: апреля 2020

Урок 30.04

Тема: Системы линейных уравнений с двумя переменными. Метод сложения.

Задание на урок:
1. Внимательно пересмотреть видеоуроки в предыдущих уроках.
2. Прочитать теорию §16, п.44.
3. Повторить алгоритм решения систем методом сложения.
4. Разобрать образец «Оформление решения систем методом сложения».

Дом задание: §16, п.43, 44, алгоритмы. Решить пять систем (в прикрепленном файле) строго по образцу!

Фотографии домашней работы выслать на эл. почту [email protected]

Урок 29.04

Тема: Прямоугольные  треугольники.

Задание на урок:
1. Повторить теорию §3 п.34-35.
2. Выучить свойства прямоугольных треугольников, признаки равенства прямоугольных треугольников.

 Домашнее задание: Решить задачи  из прикрепленного файла по вариантам.

Фотографию домашней работы выслать на эл. почту [email protected]

Урок 28.04

Тема: Системы линейных уравнений с двумя переменными. Метод сложения.

Задание на урок:
1. Внимательно пересмотреть видеоуроки в предыдущих уроках.
2. Прочитать теорию §16, п.44.
3. Повторить алгоритм решения систем методом сложения.
4. Разобрать образец «Оформление решения систем методом сложения».

Дом задание: §16, п.43, 44, алгоритмы. № 1082, 1083, строго по образцу!

Фотографии домашней работы выслать на эл. почту [email protected]

Урок 27.04

Тема: Системы линейных уравнений с двумя переменными. Метод сложения и подстановки.

Задание на урок:
1. Внимательно пересмотреть видеоуроки в предыдущих уроках.
2. Повторить теорию §16, п.43, 44. Повторить алгоритмы решения систем методом подстановки и сложения

Дом задание: §16, п. 43, 44, алгоритмы. Выполнить задание на Учи.ру  (задание активно только до 30.04)

Урок 23.04

Тема: Системы линейных уравнений с двумя переменными. Метод сложения.

Задание на урок:
1. Внимательно просмотреть 4 видеоурока.
     В каждом видео разобран один из возможных способов метода сложения.
     Смотрим по порядку сверху вниз.
     Оформление решения систем методом сложения дам позже.
2. Прочитать теорию §16, п.44.
3. Выучить алгоритм решения систем методом сложения.

Урок 22.04

Тема: Прямоугольные  треугольники.

Задание на урок:
1. Повторить теорию §3 п.34-35.
2. Выучить свойства прямоугольных треугольников.

3. Выполнить тест на блоге.
 Домашнее задание: Решить задачи  из прикрепленного файла.

Фотографию домашней работы выслать на эл. почту [email protected]
не позднее 29.04 12.00.

Урок 21.04

Тема: Системы линейных уравнений с двумя переменными. Метод подстановки.

Задание на урок:
1. Внимательно пересмотреть видеоурок (в предыдущем уроке).
2. Прочитать теорию §16, п.43.
3. Повторить алгоритм решения систем методом подстановки.
4. Разобрать образцы оформления решения систем методом подстановки. ОБЯЗАТЕЛЬНО!

Дом задание: §16, п.43, алгоритм, № №1071, 1072(а,б).

Фотографию домашней работы выслать на эл. почту [email protected]
не позднее 23.04 14.00.

Р.S. Системы оформляем как в образцах, а не списываем с ГДЗ. Решение систем уравнений записываем, так же как уравнения, в столбик. Ответ записывается в виде координат точки (х, у).

Урок 20.04

Тема: Системы линейных уравнений с двумя переменными. Метод подстановки.

Задание на урок:
1. Внимательно пересмотреть видеоурок (в предыдущем уроке).
2. Прочитать теорию §16, п.43.
3. Повторить алгоритм решения систем методом подстановки.
4. Разобрать образцы оформления решения систем методом подстановки.

Дом задание: §15, п. 42, §16, п.43, алгоритм., № 1069(а,б), №1070

Фотографию домашней работы выслать на эл. почту [email protected]
не позднее 21.04 14.00.

Урок 16.04

Тема урока: Системы линейных уравнений c двумя переменными. Метод подстановки.

Задание на урок: 

1. Внимательно просмотреть и разобрать видеоуроки.
2. Прочитать теорию §15, п. 42, §16, п.43. 

3. Выучить алгоритм решения систем методом подстановки.

Дом задание: §15, п. 42, §16, п.43, алгоритм.

Урок 15.04

Тема: Соотношение между сторонами и углами треугольника. Прямоугольные  треугольники.

Задание на урок:

1. Повторить теорию §1,2,3 п. 30-35.
2. Выполнить тест на блоге по теории.

 Домашнее задание: Решить задачи  из прикрепленного файла.

Фотографию домашней работы выслать на эл. почту [email protected]
не позднее 24.04 12.00.

Урок 14.04

Тема урока: Системы линейных уравнений с двумя переменными.

Задание на урок: 

1. Прочитать теорию §15, п. 42 + конспект урока.
2. Выучить определение, разобрать примеры в параграфе.

Дом задание:  № 1060 (б-г), с. 210; № 1062 (а, в), с. 210 (обратите внимание на разбор примеров 1-3 на страницах 208-209 учебника).

Фотографии домашней работы выслать на эл. почту [email protected] не позднее 15.04  14.00

Урок 13.04

Тема урока: Линейное уравнение с двумя переменными и ее график.

Задание на урок: 

1. Внимательно пересмотреть видеоурок (в предыдущем уроке)
2. Повторить теорию §15, п. 40, 41 + конспект урока.
3. Выполнить задание на Учи.ру, время выполнения с 13.04 по 16.04

Дом задание:  Выполнить самостоятельную работу.

Фотографии домашней работы выслать на эл. почту [email protected] не позднее 14.04 12.00

P.S. Ребята, огромная просьба не присылать по несколько раз одну и ту же домашнюю работу. И домашние работы за третью четверть не ПРОВЕРЯЮ!

Урок 11.04

Тема урока: Линейное уравнение с двумя переменными и ее график

Задание на урок: Повторение

1. Внимательно просмотреть видеоурок (в предыдущем уроке)
2. Прочитать §15, п. 40, 41 + конспект урока.
3. Выучить определения.

Дом задание:  К понедельнику выполнить Вариант № 375583 (ВПР-7) с сайт «Сдам ГИА» (math7-vpr.sdamgia.ru), для тех, кто еще не выполнил.
На сайте вводите ответы и подгружаете свои ответы во второй части/

Не забудьте в войти под своим логином

, иначе программа не засчитает вам решение.

Урок 9.04

Тема урока: Линейное уравнение с двумя переменными и ее график

Задание на урок:

1. Внимательно просмотреть видеоурок
2. Прочитать §15, п. 40, 41 + конспект урока.
3. Выучить определения.

4. Разобрать все номера в конспекте урока.

Дом задание:  № 1031, № 1037, № 1048 (а, в, д), (построить графики уравнений в одной координатной плоскости).

Обратная связь:  Фотографии  домашней работы выслать на эл. почту [email protected]  не позднее 11.04 12.00

УРОК 8.04

Тема: Соотношение между сторонами и углами треугольника. Прямоугольные  треугольники.

Задание на урок:

1. Повторить теорию §2, п. 32, 33.
2. Решить № 248, №249.
3. Выучить теорию §3 п. 34, 35.

 Домашнее задание: №252, №253 готовимся к сам. работе по теории.

Фотографию самостоятельной  работы выслать на эл.

почту [email protected]
не позднее 09.04 12.00.
Проверяю наличие домашней работы.

Урок 07.04

Тема урока: Контрольная работа «Разложение многочлена на множители»

Задание на урок:

1. Повторить способы разложения на множители. Учебник п. 28, 30, 33, 35, 36.

Вспоминаем, что начинаем раскладывать на множители сначала используя вынесение общего множителя за скобки (если такой имеется), затем формулы сокращенного умножения или способ группировки).
2. Повторить формулы сокращенного умножения. 

3. Выполнить контрольную работу по вариантам.

Дом задание:  выполнить дом. самостоятельную работу

Обратная связь:  Фотографии контрольной работы и домашней работы выслать на эл. почту [email protected]  не позднее 08.04 12.00

Урок 6.04.

Тема урока: Применение различных способов для разложения на множители .

Задание на урок:

1. Повторить способы разложения на множители. Учебник п. 28, 30, 33, 35, 36.

Вспоминаем, что начинаем раскладывать на множители сначала используя вынесение общего множителя за скобки (если такой имеется), затем формулы сокращенного умножения или способ группировки).
2. Повторить формулы сокращенного умножения. 

3. Выполнить задание на Учи.ру.

Дом задание:  № 969,  №979, № 1007.

Обратная связь:  Фотографию домашней работы выслать на эл. почту [email protected] или в Сетевом городе не позднее 07.04 12.00

Проверяю наличие дом.работы

Ребята, вынужденные каникулы подошли к концу, плавно переходим к дистанционному обучению.
Повторяем формулы сокращенного умножения, выполняем задание на Учи.ру, время выполнения пять дней с 06.04 до 10.04. Оценка будет выставлена на 6.04.

Напоминаю, что не все выполнили работу ВПР № 375583   на сайте Сдам ГИА

Домашнее задание будет согласно расписанию уроков, дублирую и здесь и в эл. дневниках.

Следующие Предыдущие Главная страница

Подписаться на: Сообщения (Atom)

Решение систем линейных уравнений методом сложения / Системы линейных уравнений с двумя переменными / Алгебра / Справочник по математике 5-9 класс

Алгоритм решения системы линейных уравнений методом сложения:

1) подобрав «выгодные» множители (если это необходимо), преобразовать одно или оба уравнения системы так, чтобы коэффициенты при одной из переменных стали противоположными числами;

2) сложить почленно левые и правые части уравнений, полученных на первом шаге;

3) решить уравнение с одной переменной, полученное на втором шаге;

4) подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы;

5) вычислить значение другой переменной;

6) записать ответ.

Пример 1:

Решите систему уравнений методом сложения:

Решение:

В исходной системе коэффициенты при переменной — противоположные числа, значит, можно получить уравнение с одной переменной, сложив почленно левые и правые части уравнений системы:

В левой части полученного уравнения приводим подобные слагаемые, учитывая то, что сумма противоположных чисел равна нулю, получаем:

Мы получили линейное уравнение, которое имеет единственный корень или, разделив числитель на знаменатель,

Подставим найденное значение переменной в любое из уравнений системы, например в первое. Получим:

Перенесем слагаемое 10 из левой части уравнения в правую, изменив при этом его знак:

 или

Мы получили линейное уравнение, которое имеет единственный корень: или, разделив числитель на знаменатель,

Пара чисел (1; 10) — искомое решение системы.

Обратите внимание, при записи решения системы в скобках на первом месте пишут значение , на втором — значение .

Пример 2:

Решите систему уравнений методом сложения:

Решение:

Если мы сложим почленно левые и правые части уравнений системы, то у нас получится уравнение с двумя переменными. Следовательно, исходную систему еще нельзя решить методом сложения.

Умножим обе части первого уравнения на 4. Получим систему, решения которой совпадают с решениями исходной системы:

Для такой системы метод сложения уже будет эффективным, т.к. коэффициенты при переменной — противоположные числа, значит, можно получить уравнение с одной переменной, сложив почленно левые и правые части уравнений системы:

В левой части полученного уравнения приводим подобные слагаемые, учитывая то, что сумма противоположных чисел равна нулю, получаем:

Мы получили линейное уравнение, которое имеет единственный корень: или, разделив числитель на знаменатель,

Подставим найденное значение переменной в любое из уравнений системы, например в первое.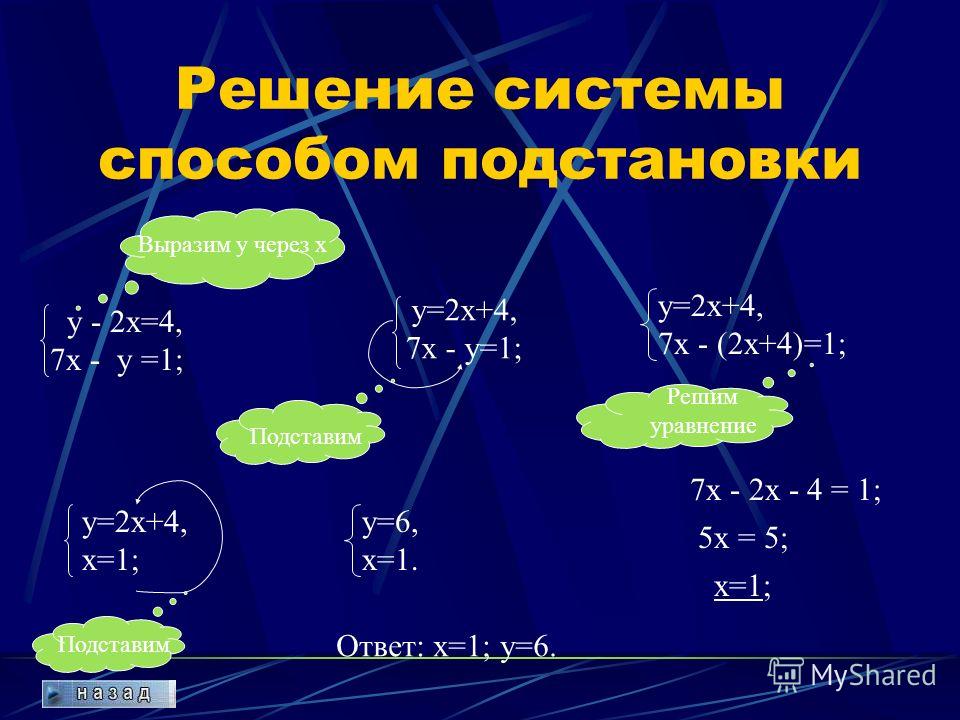 Получим:

или, выполнив умножение,

Перенесем слагаемое 4 из левой части уравнения в правую, изменив при этом его знак:

или

Мы получили линейное уравнение, которое имеет единственный корень: или, раздели числитель на знаменатель,

Пара чисел (1; 2) — искомое решение системы.

Решение систем линейных уравнений | by Yaşar Yücel Yeşilbağ

Существует множество методов решения систем линейных уравнений. Кратко объясним некоторые из них, их плюсы и минусы, а также определим алгоритм выбора метода.

В этой статье мы не будем углубляться в детали методов или примеры кодирования, так как уже есть много источников, освещающих теоретические и практические аспекты.

(Изображение создано jcomp — www.freepik.com)

Некоторые определения

[1] В математике система линейных уравнений представляет собой набор линейных уравнений с одинаковым набором переменных. Решением этой системы является набор значений переменных, при котором все уравнения выполняются одновременно.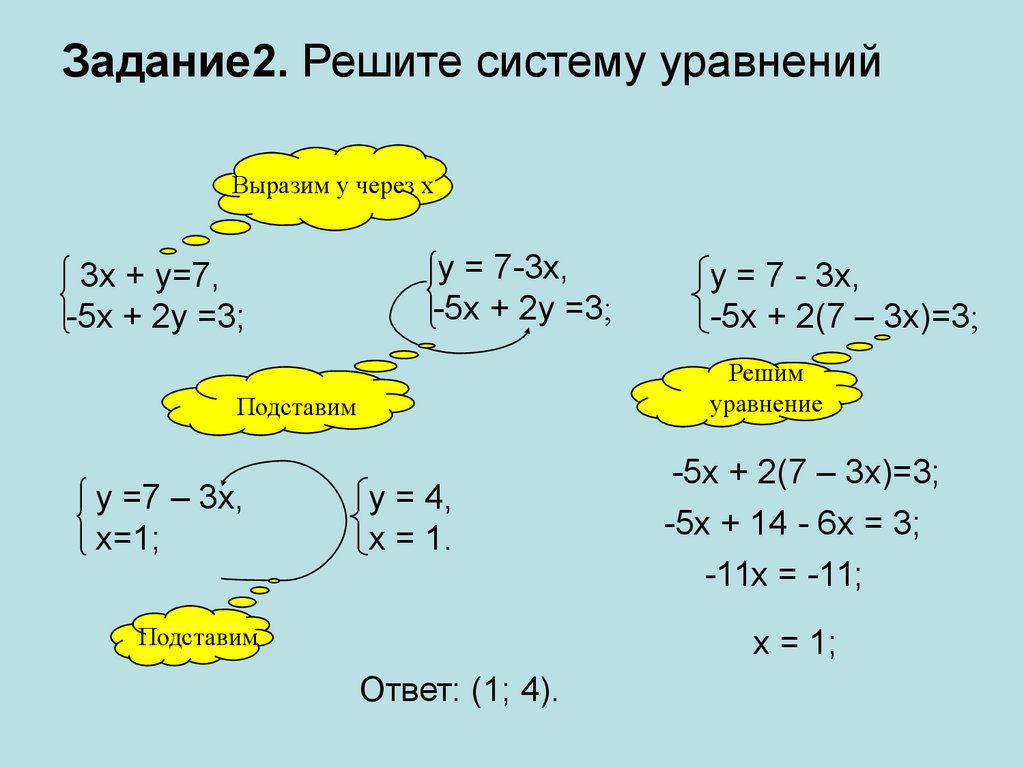

Общая система m линейных уравнений с n неизвестными может быть записана следующим образом. Обратите внимание, что для того, чтобы иметь единственное уникальное решение, m должно быть равно n, а уравнения должны быть независимыми (не могут быть получены друг из друга).

Эту систему также можно записать в матричной форме , как показано ниже, где A — матрица коэффициентов, а b — матрица констант.

[2] Треугольная матрица — это особый вид квадратной матрицы. Квадратная матрица называется нижнетреугольной, если все ее элементы выше главной диагонали равны нулю, и верхней треугольной, если все элементы ниже главной диагонали равны нулю.

Матричное уравнение в форме Lx=b или Ux=b легко решить с помощью процесса, называемого прямой подстановкой или обратная замена соответственно. Сначала вычисляют x1, затем подставляют его в следующее уравнение для решения x2 и повторяют до xn.

Исключение Гаусса

[3] Этот метод сначала увеличивает матрицу коэффициентов и матрицу констант.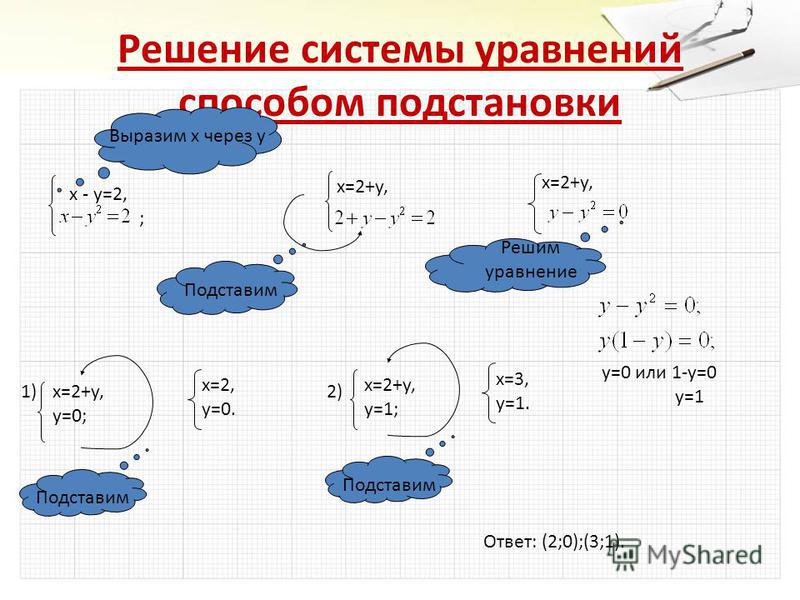 Затем использует последовательность элементарных операций со строками, чтобы изменить матрицу, пока она не станет треугольной (гауссовой) или единичной (гауссовской) матрицей.

Плюсы: это быстро, набор решений будет получен путем выполнения исключения Гаусса и замены или путем выполнения исключения Гаусса-Жордана. Поскольку операции выполняются на месте, дополнительная память не требуется.

Минусы: Если требуется много решений с разными постоянными матрицами, но с одной и той же матрицей коэффициентов, весь процесс следует выполнять каждый раз с самого начала. [6]

Решение матрицы

[1] Этот метод требует вычисления обратной матрицы коэффициентов. Это обратное можно получить с помощью исключения Гаусса – Джордана, как показано ниже. Затем решение вычисляется как x=A⁻¹b.

Плюсы: После вычисления обратной матрицы многие решения с различными постоянными матрицами могут быть вычислены очень быстро с помощью простого матричного произведения.

Минусы: Поскольку задействована другая матрица того же размера, требуется двойной объем памяти.

LU Разложение

[4] Этот метод разлагает матрицу коэффициентов на произведение нижней треугольной матрицы и верхней треугольной матрицы, A=LU.

Итак, Ax=b становится LUx=b. Пусть Ux=y. Метод сначала решает Ly=b для y с помощью прямой подстановки, а затем решает Ux=y для x с помощью обратной подстановки.

Плюсы: после вычисления матриц L и U многие решения с различными постоянными матрицами можно быстро вычислить с помощью прямых и обратных подстановок.

Минусы: Разложение LU занимает больше времени, чем обращение матрицы [7]. И 2 замены медленнее, чем простое матричное произведение при матричном решении.

Разложение Холецкого

[5] Этот метод разлагает симметричную матрицу коэффициентов на произведение нижней треугольной матрицы и ее транспонирования, A=LL*.

Итак, Ax=b становится LL*x=b. Пусть L*x=y. Метод сначала решает Ly=b для y с помощью прямой подстановки, а затем решает L*x=y для x с помощью обратной подстановки.

Вариантом этого метода является разложение LDL с преимуществом, позволяющим избежать извлечения квадратных корней, A=LDL*.

Таким образом, Ax=b становится LDL*x=b. Пусть DL*x=y. Метод сначала решает Ly=b для y с помощью прямой подстановки, а затем решает DL*x=y для x с помощью обратной подстановки. Обратите внимание, что L*x=D⁻¹y можно рассчитать как L*x=y/D, поскольку D⁻¹=1/D для диагональных матриц.

Плюсы: Декомпозиция генерирует только одну треугольную матрицу, а схема доступа позволяет встраивать матрицу L в матрицу коэффициентов, поэтому требования к памяти очень низкие. Вычисляется меньшее количество матричных элементов, поэтому он более эффективен, а его численная устойчивость выше.

Минусы: Требуется, чтобы матрица коэффициентов была симметричной. Поскольку его формула содержит квадратные корни, она немного загружает процессор. Хотя это можно преодолеть, используя его вариант LDL, который полностью исключает вычисление квадратного корня.

Метод Выбор Алгоритма

 если( матрица коэффициентов симметрична ){ 
  выбрать разложение Холецкого  
 }иначе если( много решений с одинаковой матрицей коэффициентов ){ 
 если( предпочтительна эффективность использования памяти )  выберите LU Decomposition  
 if( эффективность процессора предпочтительнее)  выберите Matrix Solution  
 }else  выберите Gaussian Elimination  

Ссылки

Systemarlinear_equations_org_wiki_org_wiki_ofpedia.
[2]: https://en.wikipedia.org/wiki/Triangular_matrix
[3]: https://en.wikipedia.org/wiki/Gaussian_elimination
[4]: ​​https://en.wikipedia.org /wiki/LU_decomposition
[5]: https://en.wikipedia.org/wiki/Cholesky_decomposition
[6]: https://math.stackexchange.com/questions/266355/necessity-advantage-of-lu-decomposition-over-gaussian-elimination
[7]: https://math. stackexchange.com/questions /2010045/What-the-the-Advantage-of-Lu-Factorization

Эффективность генетического алгоритма в решении одновременных уравнений

• DOI: 10.5120/1900-2534
• ID: 7715608

 @Artus abiodcee. ,
  title={Эффективность генетического алгоритма при решении одновременных уравнений},
  автор = {М. Икотун Абиодун, Нурудин Олавале и П. Аделокун Адебовале},
  journal={Международный журнал компьютерных приложений},
  год = {2011},
  объем = {14},
  страницы = {38-41}
} 

• М. Абиодун, Н. Олавале, П. А. Адебовале
• Опубликовано 28 февраля 2011 г.
• Информатика
• Международный журнал компьютерных приложений

Существует несколько известных традиционных алгоритмов решения системы линейных уравнений, основанных на некоторые теоретические положения. Поиск решения этой системы уравнений посредством эволюционного процесса генетического алгоритма является новой и развивающейся областью исследований. Подход с генетическим алгоритмом следует концепции эволюции решения путем стохастического развития поколений популяции решений с использованием определенной функции пригодности для определения наилучшего решения для… 

Просмотр через Publisher

ijcaonline.org

Анализ производительности моделирования отжига и генетического алгоритма на системах линейных уравнений

• М. Ислам, Мост Тахамина Хатун, К. Сиддики, Вонг Хин Йонг, М. Н. Худа

• 5 900 Компьютер Наука

  F1000Research

• 2021

Решение задач и моделирование с использованием традиционных методов замещения в больших масштабах для систем, использующих наборы одновременных уравнений, требует много времени. Для такой крупномасштабной задачи глобальной оптимизации…

Решение дифференциального уравнения с помощью модифицированных генетических алгоритмов

• E. A. Hussain, Yahya Mourad Abdul — Abbass

• , Математика

  Журнал Университета Вавилона для чистых и прикладных Sciences

Journal of Wabylon для Pure и Applied Scierences

Журнал Университета Вавилона для Pure и Applied Scierences

Journal of Wabylon. на методе, который предлагает полином для решения обыкновенного дифференциального уравнения (ОДУ) второго порядка и с использованием эволюционного алгоритма, чтобы найти коэффициенты предлагаемого полинома.

Solving Linear Systems of Equations using a Memetic Algorithm

• Liviu Octavian Mafteiu-Scai, Emanuela Mafteiu-Scai

• Computer Science, Mathematics

• 2012

This paper proposes a memetic algorithm (MA) to solve linear системы уравнений путем преобразования линейной системы уравнений в задачу оптимизации и находит как можно больше решений внутри заданного интервала.

Исследование алгоритма оптимизации поиска пищи бактериями и его приложений для решения одновременных уравнений

• Гаутам Махапатра, С. Банерджи

• Информатика

• 2013

бактерии, такие как E.Coli, могут быть использованы для решения такой системы уравнений с рангом меньше или равным n.

Улучшение сходимости итерационных методов решения систем уравнений методами меметики

• Liviu Octavian Mafteiu-Scai

• Информатика

• 2013

Предлагается метод, вдохновленный меметическим алгоритмом (MA), для улучшения сходимости итерационных методов решения систем уравнений, как линейных, так и нелинейных.

Улучшенная сходимость итерационных методов решения систем уравнений методами меметики

• Ливиу Октавиан Мафтейу-Скай

• Информатика

• 2013

Предлагается метод, вдохновленный меметическим алгоритмом (МА), для улучшения сходимости итерационных методов решения систем уравнений, как линейных, так и нелинейных.

Решение систем уравнений с помощью методов искусственного интеллекта

• И. М. Терфалоага

• Информатика, математика

• 2015

уравнения.

Алгоритмы оптимизации головного шторма для решения систем уравнений

• Liviu Octavian Mafteiu-Scai, Emanuela Mafteiu, Roxana Mafteiu-Scai

• Компьютерная наука

  Algorithms

• Brain Smourmization Algorithms

• Brain Smourshiz алгоритмов Brain Storm Optimization (BSO) при решении систем уравнений (СУ). Алгоритм BSO — это алгоритм роевого интеллекта, который имитирует мозговой штурм человека…

  Изменение параметров для линейного решателя уравнений с использованием генетического алгоритма

  • A. M. Ikotun, A. Akinwale, O. Arogundade

  • Компьютерная наука

  • 2017

  . уравнения, которые представляют собой реалистичные проблемы, такие как природные явления или инженерные проблемы в области науки и техники.

  Новый подход к решению систем уравнений, вдохновленный мозговым штурмом

  • Ливиу Октавиан Мафтейу-Скай

  • Информатика

  • 2015

  Предлагаемый метод способен находить решения заданной системы уравнений даже в тех случаях, когда традиционные методы не работают, и в случаях, когда нет точных решение существует, приближенное решение хорошее и может быть получено предложенным методом.

  ПОКАЗАНЫ 1-10 ИЗ 13 ССЫЛОК

  СОРТИРОВАТЬ ПОРелевантности Наиболее влиятельные документыНедавность

  Представления для генетических и эволюционных алгоритмов

  В этой монографии изучается ряд критических элементов теории представлений для ГПЗ и применяется к эмпирическому изучению различных важных идеализированных тестовых функций и задач коммерческого значения.

  Генетические алгоритмы в оптимизации поиска и машинном обучении

  • Д. Голдберг

  • Информатика

  • 1988

  В этой книге собраны компьютерные методы, математические инструменты и результаты исследований, которые помогут как студентам, так и практикам применять генетические алгоритмы к задачам во многих областях.

  Генетические алгоритмы + структуры данных = Программы эволюции

  • Z. Michalewicz

  • Компьютерная наука, экономика

    Springer Berlin Heidelberg

  • 1996

• 1996
• 1996

1996

1996

EVOLERS и EVOLERSE ANDOLERALE и EVOLERSER ANGELERSTER. Эвристика и выводы.

Адаптация в естественных и искусственных системах

• Дж. Холланд

• Информатика

• 1975

Названия основополагающих работ в области адаптации и модификации, целью которых является имитация биологической оптимизации и некоторых (не GA) направлений ИИ.