Arccos и arcsin таблица: arcsin, arccos, arctg arcctg, .

Главные значения: arcsin, arccos, arctg и arctg: расчет, свойства

Данный тип функций решают задачу вычисления и определения угловых значений по известному заданному значению тригонометрической функции.

 Например, синус какого угла будет иметь значение \[\frac{1}{2}\]

Напрашивается ответ,  что это угол 60° или \[\frac{\pi}{3}\] , однако вспоминая о периоде значений косинуса, делаем вывод:  углы, при которых косинус равен \[\frac{1}{2}\], существует достаточно много.

Данные тригонометрические функции являются обратными по значению. Они имеют множество характерных свойств:

Проведем доказательство перечисленных свойств на примере значения арксинуса. Значение угла данной функции равняется числу a. И данное значение находится на промежутке чисел от -1 до +1.

sin(arcsin a)=a

Все остальные функции доказываются аналогично, согласно их определения.

Определение значений обратных функций, будет иметь смысл при условии, что неизвестное число a будет делать в пределах от -1 до +1.

Противоположные значения для обратных значений функций арксинус, арккосинус, арктангенс, арккотангенс

Взаимосвязь функций противоположных чисел можно записать в следующем виде:

Перейдем к доказательству записанных выражений.

Доказательство арксинусов:

\[\text { Если }-1 \leq a \leq 1 \Rightarrow \arcsin (-a)=-\arcsin a .\]

Данная тригонометрическая функция имеет предел значений от \[-\frac{\pi}{2} \text { до } \frac{\pi}{2}\] и синус его равен -a.

Докажем, что — arcsin a находится в пределах \[-\frac{\pi}{2} до \frac{\pi}{2}\] и обоснуем, что sin (-arcsin a)=-a.

Для функции арксинус справедливо неравенство, следующего вида:\[-\frac{\pi}{2} \leq \arcsin a \leq \frac{\pi}{2}\].

Для того чтобы получить эквивалентное неравенство, нужно обе части равенства умножить на значение-1. После вычислений получим:\[-\frac{\pi}{2} \leq-\arcsin \mathrm{a} \leq \frac{\pi}{2}\].

Докажем, что sin ( − arcsin   a ) = − a sin(-arcsin a)=-a.

Применим свойство противоположных углов и составим уравнение:

 sin ( − a r c sin   a ) = − sin ( a r c sin   a )=-sin arcsin a.

Арккосинус доказывается следующим образом:

Записываем выражение: \[\arccos (-a)=\pi-\arccos a \text { при } a \in(-1,1)\]

Для этой функции принимает равенство \[0 \leq \arccos a \leq \pi\] обе части равенства нужно перемножить на значение равное -1 и изменить знаки на противоположные. Выполнив вычисления получим равенство: \[\pi \geq \pi-\arccos a \geq \pi\].

Чтобы доказать оставшиеся две функции, применяются аналогичные свойства и правила.

Правило противоположных чисел позволяет упростить процесс решения и исключает все операции при вычислении с отрицательными числами.

Например:

Принцип сложения обратных тригонометрических функций

Для тригонометрических функций, прямых или обратных, характерны простые математические свойства, а именно: сложение данных.

Составим доказательство функций для арксинуса и арккосинуса. Формулы arcsin и arccos в виде суммы, можно представить как  \[\arcsin a=\frac{\pi}{2}-\arccos a\]. Затем применить определение, из которого следует, что арксинус — это число, которое относится пределу значений  от \[-\frac{\pi}{2} \text { до } \frac{\pi}{2}\] , синус равняется  a.

Обе части неравенства \[0 \leq \arccos a \leq \pi\] умножим на значение -1 и прибавим \[\frac{\pi}{2}\].

Выполнив все необходимые операции по вычислению заданного равенства, получим следующие выражения:

Для завершения доказательства запишем формулу: \[\sin \left(\frac{\pi}{2}-\arccos a\right)=\cos (\arccos a)=a\]

Сформулируем свойства рассматриваемых значений  функций относительно  синуса, косинуса, тангенса и котангенса.

Значение  arcsin (sin a) имеет смысл в том случае, если a относится к пределам \[-\frac{\pi}{2} ; \frac{\pi}{2}\] и выполняется условие \[-\frac{\pi}{2} \leq a \leq \frac{\pi}{2}\].

Аналогичные условия характерны и для других функций. 

Пример: \[\arcsin \left(\sin \frac{8 \pi}{3}\right)=\frac{8 \pi}{3}\], является неверной, потому что \[\frac{8 \pi}{3}\], не удовлетворяет условию. 

Главные значения: arcsin, arccos, arctg и arctg

Применяя таблицы определения значений прямых функций, мы имеем точные числовые значения для следующих углов \[0, \pm 30,45,60,90,120 \ldots \ldots \ldots \ldots \ldots \pm 180\] градусов.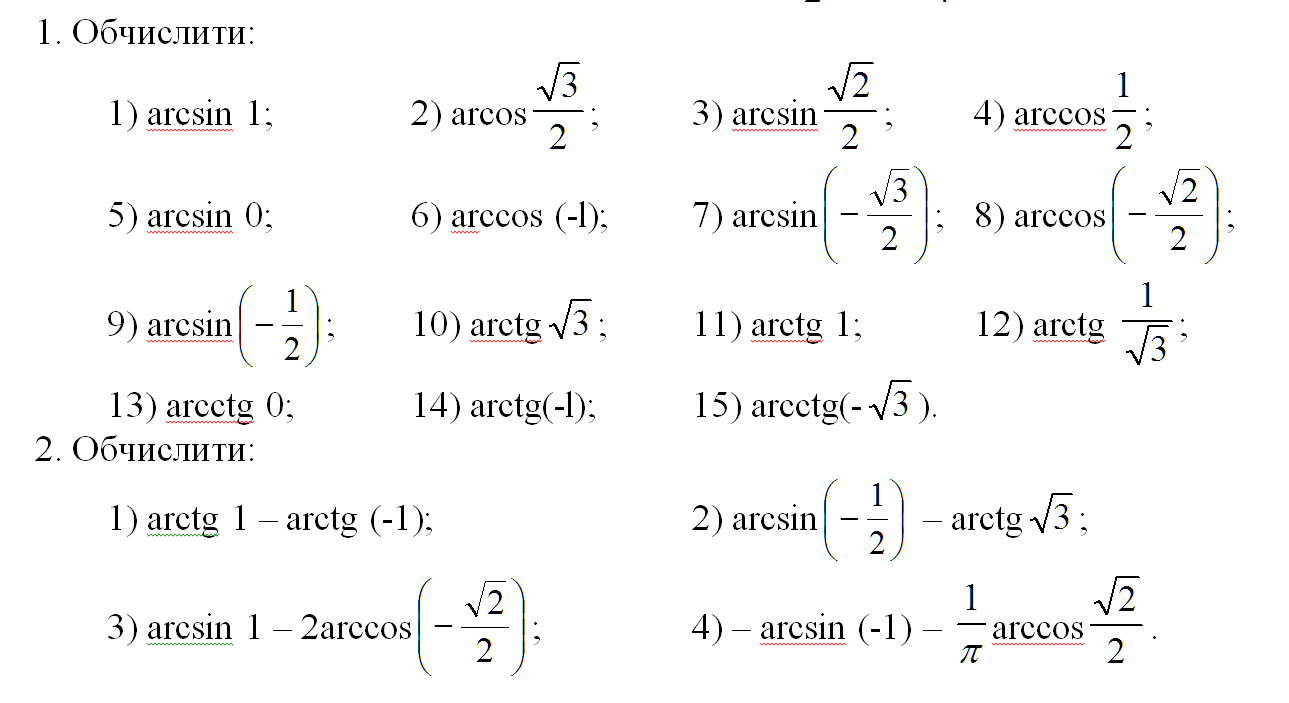 Таблица является очень простой и понятной для применения при выполнении необходимых расчетов.

Продолжение таблицы 1

Вычисленные значения принято сводить в таблицу, показанную выше. Особенно рекомендуются, ее заучивать наизусть, для более хорошего восприятия.

Учитывая данные вышеприведенной таблицы, можно вычислить необходимые для нас значения функций. 

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Для более практичного применения сведем все данные арксинуса в таблицу. Их необходимо запомнить, а лучше всего выучить наизусть. Так ка к ним придется возвращаться на постоянной основе.

Далее определимся с основными значения арккосинуса. Для вспомнить функцию прямую по значению к данной.

Далее определяем нужные нам значения арккосинуса и сводим их в таблицу.

И напоследок остается вычислить значения арктангенса и арккотангенса.

Выведем значения основных прямых функций и получим следующие значения для каждого значения в градусах:

\[\operatorname{tg} 90^{\circ}, 270^{\circ}\] — данные угловые значения, не определяются, согласно основным законам геометрии и математики. {\circ}\]- для перечисленных угловых значений по законам математики и всех технических наук в целом, значения не определяются

Далее все данные запишем в виде табличной формы.

Первая таблица для арктангенса

Вторая таблица  для арккотангенса

Рассмотрим, также значения для нестандартных угловых значений и сведем их в таблицу.

В данной таблице приведены значения углов, которые считаются нестандартными. Также таблица необходима, чтобы облегчить жизнь, в первую очередь, школьной программе. 

Например:

Основные способы, которые помогут заполнить таблицу функций тригонометрии.

Необходимо изобразить простую таблицу, где будет несколько столбцов и строк, необходимых для заполнения данных. Следующая задача, состоит в том, что нужно пустые графы заполнить. Записываем в первом столбике значение математических функций, ранее нами изученных.

В начальной строке, должны отображаться самые часто используемые значения углов: от нуля до девяноста градусов и так далее.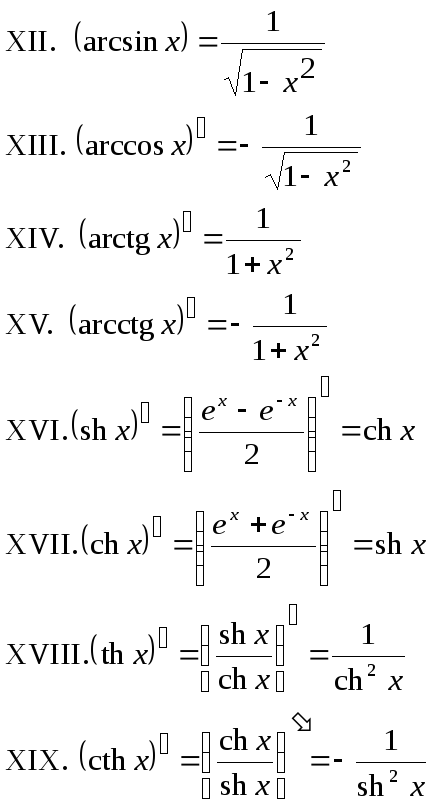  

Оставшиеся ячейки нужно оставить незаполненными, для следующих действий. Чтобы понять тригонометрию, нужно изучать не только основные функции. Стоит уделить внимание и таким функциях как: косеканс (cosec) и секанс(sec).

На практике решений, обычно требуется точность в три-четыре знака, после запятой, но не более. Для расчета, с такой точностью, значение синуса, в формуле достаточно трех известных слагаемых, а иногда и двух.  Произвести простых четыре перемножения.  

Дважды разделить, умножить и отнять. 

Если производить действия инженерным калькулятором, становится понятно, что все вышеперечисленные действия, уже запрограммированы в его микросхеме.  

В таблице представлены следующие данные:

• число в квадратной и кубической степени;
• числа квадратных корней;
• логарифмические функции и значение;
• функции тригонометрии, представленный в градусах и радианах;
• обратные функции.

Мы показали, что представляет таблица, какие данные и значения отображает.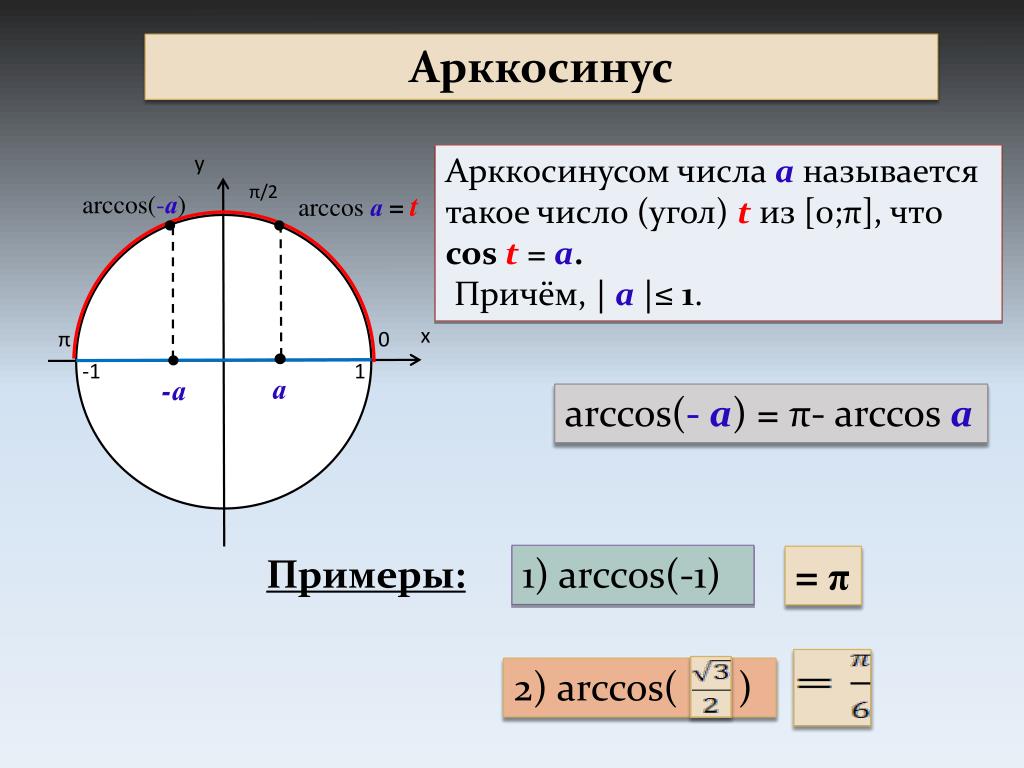 {\prime}=4,102 .\]

Тригонометрические функции являются периодическими. Функции, которые, являются обратными к ним будут иметь многозначное значение.  Другим словами это множество угловых значений, для которых соответствующая функция является заданным числом.

Арксинус (y = arcsin x )  – это функция, обратная к синусу ( x = sin y ).

Свойства функции	Функции y=arcsin х
E(f)	\[-1 \leq x \leq-1\]
D(f)	\[-\frac{\pi}{2}<y<\frac{\pi}{2}\]
наличие четности	Нечётная, т.к. arcsin(-x)= — arcsin x
характер графика направление	возрастание

Арккосинус ( y = arccos x )  – это функция, обратная к косинусу ( x = cos y).

Свойства	Функции y=arccos х
E(f)	\[-1 \leq x \leq-1\]
D(f)	\[0 \leq y \leq \pi\]
Чётности	Данное свойство ей не характерно. Иными словами отсутствует.
Монотонность	Убывающая

Арктангенс ( y = arctg x )  – характеризуется, как обратное значение функции относительно тангенса.

Следовательно арккотангенс имеет такие свойства по отношению к тангенсу.

Свойства	y=arctg х	y=arcctg х
E(f)	R	R
D(f)	\[\left(-\frac{\pi}{2} ; \frac{\pi}{2}\right)\]	\[(0 ; \pi)\]
Характер функции	Нечётная	Нечётная
Периоды	Возрастающая	Убывающая

Формулы arcsin arccos. Вывод формул обратных тригонометрических функций

Урок и презентация на темы: «Арксинус. Таблица арксинусов. Формула y=arcsin(x)»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.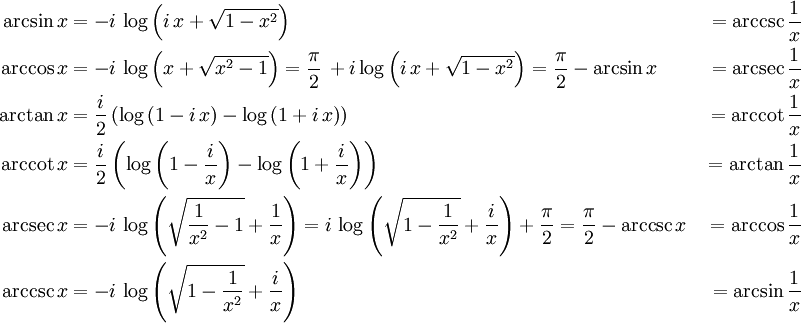

Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Программная среда «1С: Математический конструктор 6.1»
Решаем задачи по геометрии. Интерактивные задания на построение в пространстве

Что будем изучать:
1. Что такое арксинус?

2. Обозначение арксинуса.
3. Немного истории.
4. Определение.

6. Примеры.

Что такое арксинус?

Ребята, мы с вами уже научились решать уравнения для косинуса, давайте теперь научимся решать подобные уравнения и для синуса. Рассмотрим sin(x)= √3/2. Для решения этого уравнения требуется построить прямую y= √3/2 и посмотреть: в каких точках она пересекает числовую окружность. Видно, что прямая пересекает окружность в двух точках F и G. Эти точки и будут решением нашего уравнения. Переобозначим F как x1, а G как x2. Решение этого уравнения мы уже находили и получили: x1= π/3 + 2πk,
а x2= 2π/3 + 2πk.

Решить данное уравнение довольно просто, но как решить, например, уравнение
sin(x)= 5/6. Очевидно, что это уравнение будет иметь также два корня, но какие значения будут соответствовать решению на числовой окружности? Давайте внимательно посмотрим на наше уравнение sin(x)= 5/6.
Решением нашего уравнения будут две точки: F= x1 + 2πk и G= x2 + 2πk,
где x1 – длина дуги AF, x2 – длина дуги AG.
Заметим: x2= π — x1, т.к. AF= AC — FC, но FC= AG, AF= AC — AG= π — x1.
Но, что это за точки?

Столкнувшись с подобной ситуацией, математики придумали новый символ – arcsin(x). Читается, как арксинус.

Тогда решение нашего уравнения запишется так: x1= arcsin(5/6), x2= π -arcsin(5/6).

И решение в общем виде: x= arcsin(5/6) + 2πk и x= π — arcsin(5/6) + 2πk.
Арксинус — это угол (длина дуги AF, AG) синус, которого равен 5/6.

Немного истории арксинуса

История происхождения нашего символа совершенно такая же, как и у arccos. Впервые символ arcsin появляется в работах математика Шерфера и известного французского ученого Ж.Л. Лагранжа. Несколько ранее понятие арксинус рассматривал Д. Бернули, правда записывал его другими символами.

Общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка «arc» происходит от латинского «arcus» (лук, дуга). Это вполне согласуется со смыслом понятия: arcsin x — это угол (а можно сказать и дуга), синус которого равен x.

Определение арксинуса

Если |а|≤ 1, то arcsin(a) – это такое число из отрезка [- π/2; π/2], синус которого равен а.

Если |а|≤ 1, то уравнение sin(x)= a имеет решение: x= arcsin(a) + 2πk и
x= π — arcsin(a) + 2πk

Перепишем:

x= π — arcsin(a) + 2πk = -arcsin(a) + π(1 + 2k).

Ребята, посмотрите внимательно на два наших решения. Как думаете: можно ли их записать общей формулой? Заметим, что если перед арксинусом стоит знак «плюс», то π умножается на четное число 2πk, а если знак «минус», то множитель — нечетный 2k+1.
С учётом этого, запишем общую формула решения для уравнения sin(x)=a:

Есть три случая, в которых предпочитают записывать решения более простым способом:

sin(x)=0, то x= πk,

sin(x)=1, то x= π/2 + 2πk,

sin(x)=-1, то x= -π/2 + 2πk.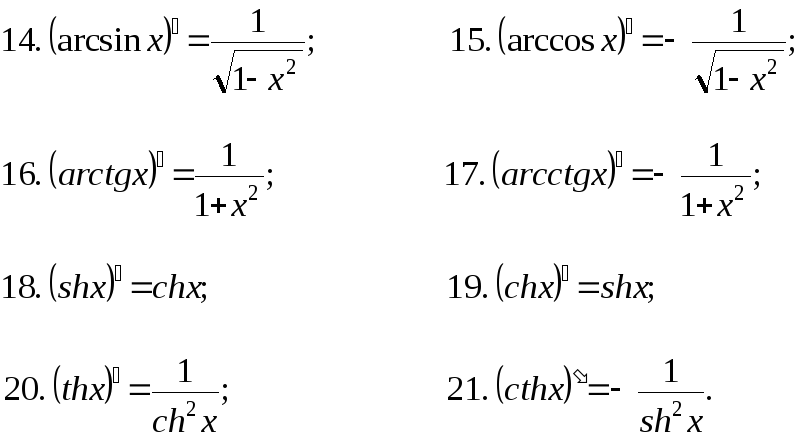

Для любого -1 ≤ а ≤ 1 выполняется равенство: arcsin(-a)=-arcsin(a).

Напишем таблицу значений косинуса наоборот и получим таблицу для арксинуса.

Примеры

1. Вычислить: arcsin(√3/2).
Решение: Пусть arcsin(√3/2)= x, тогда sin(x)= √3/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= π/3, т.к. sin(π/3)= √3/2 и –π/2 ≤ π/3 ≤ π/2.
Ответ: arcsin(√3/2)= π/3.

2. Вычислить: arcsin(-1/2).
Решение: Пусть arcsin(-1/2)= x, тогда sin(x)= -1/2. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: x= -π/6, т.к. sin(-π/6)= -1/2 и -π/2 ≤-π/6≤ π/2.
Ответ: arcsin(-1/2)=-π/6.

3. Вычислить: arcsin(0).
Решение: Пусть arcsin(0)= x, тогда sin(x)= 0. По определению: — π/2 ≤x≤ π/2. Посмотрим значения синуса в таблице: значит x= 0, т.к. sin(0)= 0 и — π/2 ≤ 0 ≤ π/2. Ответ: arcsin(0)=0.

4. Решить уравнение: sin(x) = -√2/2.

x= arcsin(-√2/2) + 2πk и x= π — arcsin(-√2/2) + 2πk.
Посмотрим в таблице значение: arcsin (-√2/2)= -π/4.
Ответ: x= -π/4 + 2πk и x= 5π/4 + 2πk.

5. Решить уравнение: sin(x) = 0.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(0) + 2πk и x= π — arcsin(0) + 2πk. Посмотрим в таблице значение: arcsin(0)= 0.
Ответ: x= 2πk и x= π + 2πk

6. Решить уравнение: sin(x) = 3/5.
Решение: Воспользуемся определением, тогда решение запишется в виде:
x= arcsin(3/5) + 2πk и x= π — arcsin(3/5) + 2πk.
Ответ: x= (-1) n — arcsin(3/5) + πk.

7. Решить неравенство sin(x) Решение: Синус — это ордината точки числовой окружности. Значит: нам надо найти такие точки, ордината которых меньше 0.7. Нарисуем прямую y=0.7. Она пересекает числовую окружность в двух точках. Неравенству y Тогда решением неравенства будет: -π – arcsin(0.7) + 2πk

Задачи на арксинус для самостоятельного решения

1) Вычислить: а) arcsin(√2/2), б) arcsin(1/2), в) arcsin(1), г) arcsin(-0.8).
2) Решить уравнение: а) sin(x) = 1/2, б) sin(x) = 1, в) sin(x) = √3/2, г) sin(x) = 0. 25,
д) sin(x) = -1.2.
3) Решить неравенство: а) sin (x)> 0.6, б) sin (x)≤ 1/2.

Представлен способ вывода формул для обратных тригонометрических функций. Получены формулы для отрицательных аргументов, выражения, связывающие арксинус, арккосинус, арктангенс и арккотангенс. Указан способ вывода формул суммы арксинусов, арккосинусов, арктангенсов и арккотангенсов.

Основные формулы

Вывод формул для обратных тригонометрических функций прост, но требует контроля за значениями аргументов прямых функций. Это связано с тем, что тригонометрические функции периодичны и, поэтому, обратные к ним функции многозначны. Если особо не оговорено, то под обратными тригонометрическими функциями подразумевают их главные значения. Для определения главного значения, область определения тригонометрической функции сужают до интервала, на котором она монотонна и непрерывна. Вывод формул для обратных тригонометрических функций основывается на формулах тригонометрических функций и свойствах обратных функций как таковых.

Свойства обратных функций можно разбить на две группы.

В первую группу входят формулы, справедливые на всей области определения обратных функций:
sin(arcsin x) = x
cos(arccos x) = x
tg(arctg x) = x (-∞ ctg(arcctg x) = x (-∞

Во вторую группу входят формулы, справедливые только на множестве значений обратных функций.
arcsin(sin x) = x при
arccos(cos x) = x при
arctg(tg x) = x при
arcctg(ctg x) = x при

Если переменная x не попадает в указанный выше интервал, то ее следует привести к нему, применяя формулы тригонометрических функций (далее n — целое):

sin x = sin(- x-π) ; sin x = sin(π-x) ; sin x = sin(x+2 πn) ;
cos x = cos(-x) ; cos x = cos(2 π-x) ; cos x = cos(x+2 πn) ;
tg x = tg(x+πn) ; ctg x = ctg(x+πn)

Например, если известно, что то
arcsin(sin x) = arcsin(sin( π — x )) = π — x .

Легко убедиться, что при π — x попадает в нужный интервал. Для этого умножим на -1 : и прибавим π : или Все правильно.

Обратные функции отрицательного аргумента

Применяя указанные выше формулы и свойства тригонометрических функций, получаем формулы обратных функций отрицательного аргумента.

arcsin(- x) = arcsin(-sin arcsin x) = arcsin(sin(-arcsin x)) = — arcsin x

Поскольку то умножив на -1 , имеем: или
Аргумент синуса попадает в допустимый интервал области значений арксинуса. Поэтому формула верна.

Аналогично для остальных функций.
arccos(- x) = arccos(-cos arccos x) = arccos(cos(π-arccos x)) = π — arccos x

arctg(- x) = arctg(-tg arctg x) = arctg(tg(-arctg x)) = — arctg x

arcctg(- x) = arcctg(-ctg arcctg x) = arcctg(ctg(π-arcctg x)) = π — arcctg x

Выражение арксинуса через арккосинус и арктангенса через арккотангенс

Выразим арксинус через арккосинус.

Формула справедлива при Эти неравенства выполняются, поскольку

Чтобы убедиться в этом, умножим неравенства на -1 : и прибавим π/2 : или Все правильно.

Аналогично выражаем арктангенс через арккотангенс.

Выражение арксинуса через арктангенс, арккосинуса через арккотангенс и наоборот

Поступаем аналогичным способом.

Формулы суммы и разности

Аналогичным способом, получим формулу суммы арксинусов.

Установим пределы применимости формулы. Чтобы не иметь дела с громоздкими выражениями, введем обозначения: X = arcsin x , Y = arcsin y . Формула применима при
. Далее замечаем, что, поскольку arcsin(- x) = — arcsin x, arcsin(- y) = — arcsin y, то при разных знаках у x и y , X и Y также разного знака и поэтому неравенства выполняются. Условие различных знаков у x и y можно написать одним неравенством: . То есть при формула справедлива.

Теперь рассмотрим случай x > 0 и y > 0 , или X > 0 и Y > 0 . Тогда условие применимости формулы заключается в выполнении неравенства: . Поскольку косинус монотонно убывает при значениях аргумента в интервале от 0 , до π , то возьмем косинус от левой и правой части этого неравенства и преобразуем выражение:
;
;
;
.
Поскольку и ; то входящие сюда косинусы не отрицательные. Обе части неравенства положительные. Возводим их в квадрат и преобразуем косинусы через синусы:
;
.
Подставляем sin X = sin arcsin x = x :
;
;
;
.

Итак, полученная формула справедлива при или .

Теперь рассмотрим случай x > 0, y > 0 и x 2 + y 2 > 1 . Здесь аргумент синуса принимает значения: . Его нужно привести к интервалу области значения арксинуса :

Итак,

при и.

Заменив x и y на — x и — y , имеем

при и.
Выполняем преобразования:

при и.
Или

при и.

Итак, мы получили следующие выражения для суммы арксинусов:

при или ;

при и ;

при и .

Что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс?

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!

Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.

Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов… Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.

Итак, удивляемся, но запоминаем: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Бывает угол, скажем 30°. А бывает угол arcsin0,4. Или arctg(-1,3). Всякие углы бывают.) Просто записать углы можно разными способами. Можно записать угол через градусы или радианы. А можно — через его синус, косинус, тангенс и котангенс…

Что означает выражение

arcsin 0,4 ?

Это угол, синус которого равен 0,4 ! Да-да. Это смысл арксинуса. Специально повторю: arcsin 0,4 — это угол, синус которого равен 0,4.

И всё.

Чтобы эта простая мысль сохранилась в голове надолго, я даже приведу разбивочку этого ужасного термина — арксинус:

arc sin 0,4
угол, синус которого равен 0,4

Как пишется, так и слышится.) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.

Что такое arccos 0,8 ?
Это угол, косинус которого равен 0,8.

Что такое arctg(-1,3) ?
Это угол, тангенс которого равен -1,3.

Что такое arcctg 12 ?
Это угол, котангенс которого равен 12.

Такая элементарная расшифровка позволяет, кстати, избежать эпических ляпов. ) Например, выражение arccos1,8 выглядит вполне солидно. Начинаем расшифровку: arccos1,8 — это угол, косинус которого равен 1,8… Скока-скока!? 1,8!? Косинус не бывает больше единицы!!!

Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)

Элементарно, как видите.) У каждого угла имеется свой персональный синус и косинус. И почти у каждого — свой тангенс и котангенс. Стало быть, зная тригонометрическую функцию, можно записать и сам угол. Для этого и предназначены арксинусы, арккосинусы, арктангенсы и арккотангенсы. Далее я всю эту семейку буду называть уменьшительно — арки. Чтобы печатать меньше.)

Внимание! Элементарная словесная и осознанная расшифровка арков позволяет спокойно и уверенно решать самые различные задания. А в непривычных заданиях только она и спасает.

А можно переходить от арков к обычным градусам или радианам? — слышу осторожный вопрос.)

Почему — нет!? Легко. И туда можно, и обратно. Более того, это иногда нужно обязательно делать. Арки — штука простая, но без них как-то спокойнее, правда?)

Например: что такое arcsin 0,5?

Вспоминаем расшифровку: arcsin 0,5 — это угол, синус которого равен 0,5. Теперь включаем голову (или гугл)) и вспоминаем, у какого угла синус равен 0,5? Синус равен 0,5 у угла в 30 градусов . Вот и все дела: arcsin 0,5 — это угол 30°. Можно смело записать:

arcsin 0,5 = 30°

Или, более солидно, через радианы:

Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.

Если вы осознали, что такое арксинус, арккосинус… Что такое арктангенс, арккотангенс… То легко разберётесь, например, с таким монстром.)

Несведущий человек отшатнётся в ужасе, да…) А сведущий вспомнит расшифровку: арксинус — это угол, синус которого… Ну и так далее. Если сведущий человек знает ещё и таблицу синусов… Таблицу косинусов. Таблицу тангенсов и котангенсов, то проблем вообще нет!

Достаточно сообразить, что:

Расшифрую, т.е. переведу формулу в слова: угол, тангенс которого равен 1 (arctg1) — это угол 45°. Или, что едино, Пи/4. Аналогично:

и всё… Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что и является правильным ответом.

Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!

Частенько, в подобных примерах, внутри арков стоят отрицательные значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8)… Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:

Нужно вам, скажем, определить значение выражения:

Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно.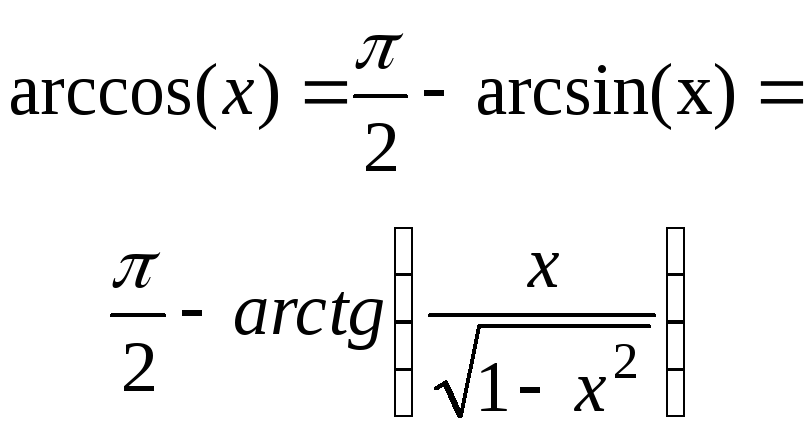 Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:

Внутри арккосинуса справа уже положительное значение. То, что

вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:

Вот и всё.

Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.

С примерами 7 — 9 проблема? Ну да, есть там некоторая хитрость.)

Все эти примеры, с 1-го по 9-й, тщательно разобраны по полочкам в Разделе 555. Что, как и почему. Со всеми тайными ловушками и подвохами. Плюс способы резкого упрощения решения. Кстати, в этом разделе много полезной информации и практических советов по тригонометрии в целом. И не только по тригонометрии. Очень помогает.

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Даны определения обратных тригонометрических функций и их графики. А также формулы, связывающие обратные тригонометрические функции, формулы сумм и разностей.

Определение обратных тригонометрических функций

Поскольку тригонометрические функции периодичны, то обратные к ним функции не однозначны. Так, уравнение y = sin x , при заданном , имеет бесконечно много корней. Действительно, в силу периодичности синуса, если x такой корень, то и x + 2πn (где n целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны . Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin x . Если ограничить аргумент x интервалом , то на нем функция y = sin x монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin y .

Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями.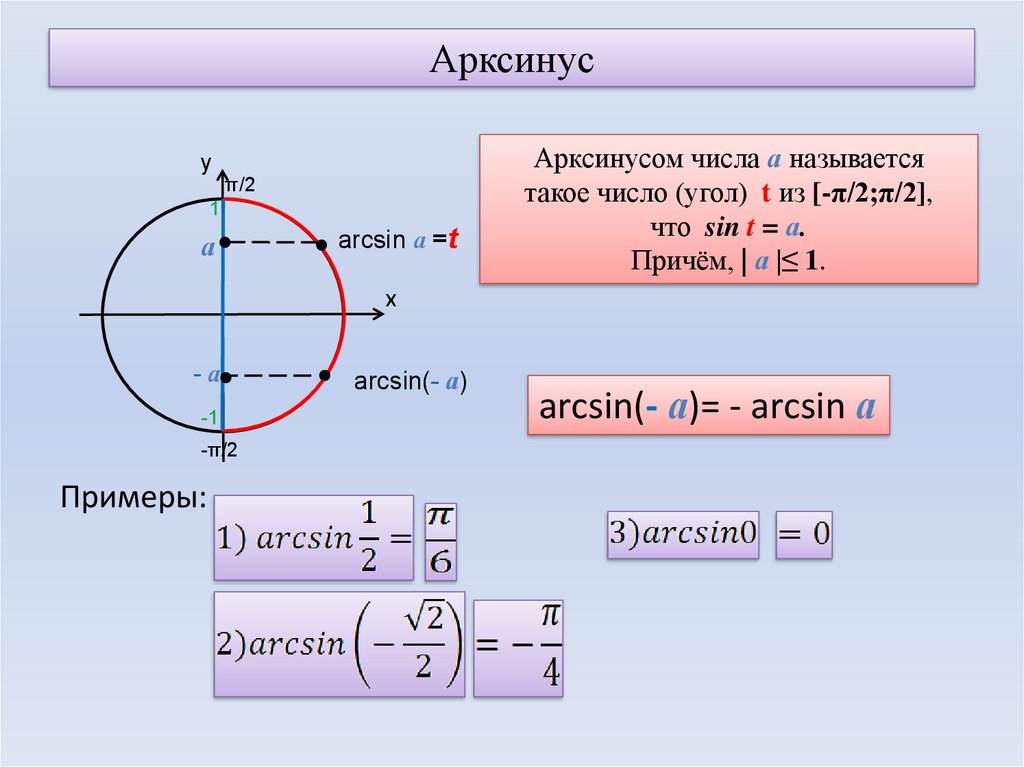

Арксинус (y = arcsin x ) — это функция, обратная к синусу (x = sin y

Арккосинус (y = arccos x ) — это функция, обратная к косинусу (x = cos y ), имеющая область определения и множество значений .

Арктангенс (y = arctg x ) — это функция, обратная к тангенсу (x = tg y ), имеющая область определения и множество значений .

Арккотангенс (y = arcctg x ) — это функция, обратная к котангенсу (x = ctg y ), имеющая область определения и множество значений .

Графики обратных тригонометрических функций

Графики обратных тригонометрических функций получаются из графиков тригонометрических функций зеркальным отражением относительно прямой y = x . См. разделы Синус, косинус , Тангенс, котангенс .

y = arcsin x

y = arccos x

y = arctg x

y = arcctg x

Основные формулы

Здесь следует особо обратить внимание на интервалы, для которых справедливы формулы.

arcsin(sin x) = x при
sin(arcsin x) = x
arccos(cos x) = x при
cos(arccos x) = x

arctg(tg x) = x при
tg(arctg x) = x
arcctg(ctg x) = x при
ctg(arcctg x) = x

Формулы, связывающие обратные тригонометрические функции

Формулы суммы и разности

при или

при и

при и

при или

при и

при и

при

при

при

при

Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом и арккотангенсом. Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями.

Рассмотрим рисунок единичной окружности, на котором графически отображено значений тригонометрических функций.

Если вычислить arcs OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α. Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков.

Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График имеет вид асимметричной кривой, проходящей через центр координат.

Свойства арксинуса:

Если сопоставить графики sin и arcsin , у двух тригонометрических функций можно найти общие закономерности.

Арккосинус

Arccos числа а — это значение угла α, косинус которого равен а.

Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.

Рассмотрим функцию арккосинуса более подробно:

1. Функция определена на отрезке [-1; 1].
2. ОДЗ для arccos — .
3. График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
4. Y = 0 при x = 1.
5. Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.

Некоторые свойства арккосинуса совпадают с функцией косинуса.

Возможно, школьникам покажется излишним такое «подробное» изучение «арков». Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.

Задание 1. Укажите функции изображенные на рисунке.

Ответ: рис. 1 – 4, рис.2 — 1.

В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать вид кривой, если ее всегда можно построить по расчетным точкам. Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий.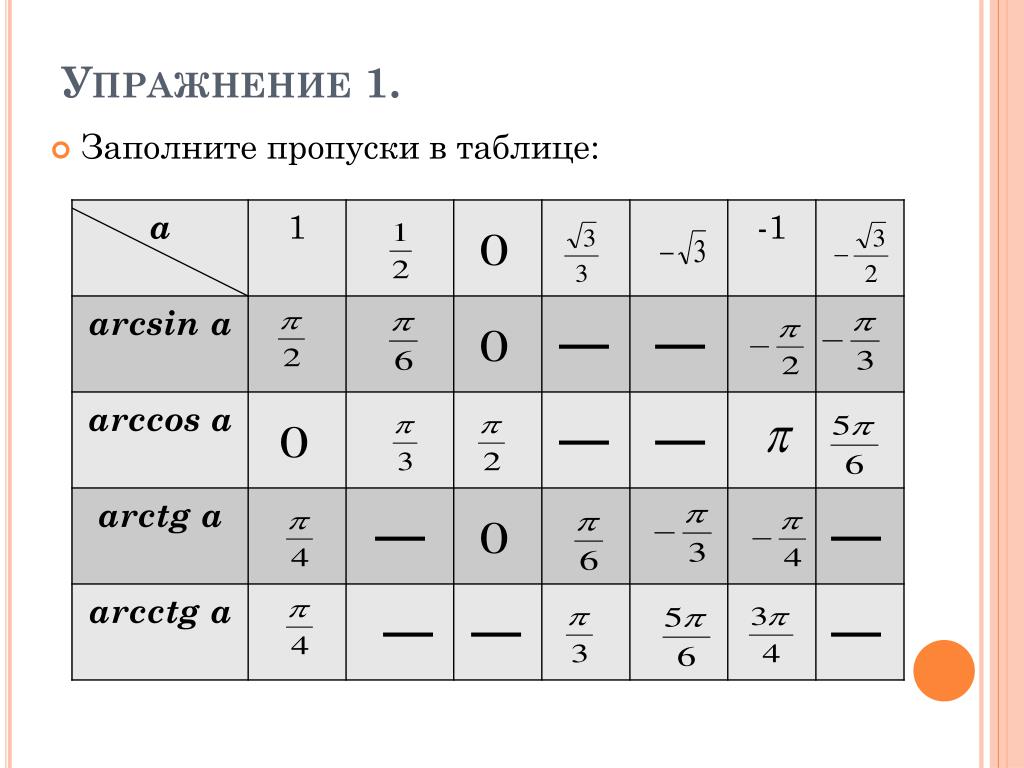

Арктангенс

Arctg числа a – это такое значение угла α, что его тангенс равен а.

Если рассмотреть график арктангенса, можно выделить следующие свойства:

1. График бесконечен и определен на промежутке (- ∞; + ∞).
2. Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.
3. Y = 0 при x = 0.
4. Кривая возрастает на всей области определения.

Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.

Арккотангенс

Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.

Свойства функции арккотангенса:

1. Интервал определения функции – бесконечность.
2. Область допустимых значений – промежуток (0; π).
3. F(x) не является ни четной, ни нечетной.
4. На всем своем протяжении график функции убывает.

Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.

Задание 2. Соотнести график и форму записи функции.

Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,

Ответ: рис. 1 – 1, рис. 2 – 4.

Тригонометрические тождества arcsin, arcos, arctg и arcctg

Ранее нами уже была выявлена взаимосвязь между арками и основными функциями тригонометрии. Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров.

Также существуют соотношения для arctg и arcctg:

Еще одна полезная пара формул, устанавливает значение для суммы значений arcsin и arcos, а также arcctg и arcctg одного и того же угла.

Примеры решения задач

Задания по тригонометрии можно условно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить график данной функции, найти ее область определения или ОДЗ и выполнить аналитические преображения для решения примера.

При решении первого типа задач необходимо придерживаться следующего плана действий:

При работе с графиками функций главное – это знание их свойств и внешнего вида кривой. Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания.

Допустим в ЕГЭ необходимо найти ответ для уравнения типа:

Если правильно преобразовать выражение и привести к нужному виду, то решить его очень просто и быстро. Для начала, перенесем arcsin x в правую часть равенства.

Если вспомнить формулу arcsin (sin α) = α , то можно свести поиск ответов к решению системы из двух уравнений:

Ограничение на модель x возникло, опять таки из свойств arcsin: ОДЗ для x [-1; 1]. При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1.

19.1: Функции arcsin, arccos и arctan

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

49073

• Томас Тредлер и Холли Карли
• CUNY Городской технологический колледж Нью-Йорка через New York City College of Технологии в CUNY Academic Works

Обратные тригонометрические функции — это обратные функции функций \(y=\sin x\), \(y=\cos x\) и \(y=\tan x\), ограниченные соответствующими областями.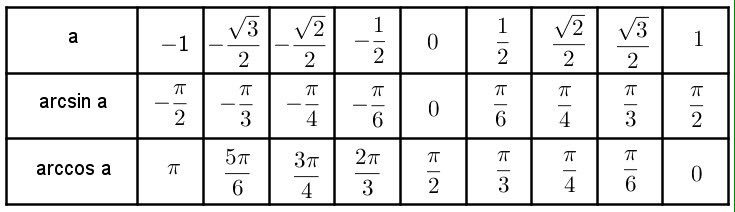 В этом разделе мы даем точное определение этих функций.

Функция арктангенса

Начнем с обратной функции тангенса \(y=\tan(x)\). Напомним, что график \(y=\tan(x)\) выглядит следующим образом:

Он имеет вертикальные асимптоты в точках \(x=\pm\dfrac{\pi}{2}, \pm\dfrac{ 3\pi}{2}, \pm\dfrac{5\pi}{2}, \dots\). Обратите внимание, что \(y=\tan(x)\) не является взаимно однозначной функцией в смысле определения [DEF:1-to-1] на стр. . (Например, горизонтальная линия \(y=1\) пересекает график в точках \(x=\dfrac{\pi}{4}\), \(x=\dfrac{\pi}{4}\pm\ pi\), \(x=\dfrac{\pi}{4}\pm2\pi\) и т. д.) Однако, когда мы ограничиваем функцию областью \(D=(\dfrac{-\pi}{ 2},\dfrac{\pi}{2})\) ограниченная функция 9{-1}(x)\)

Далее мы определяем функцию обратного синуса. Для этого снова сначала вспомним график функции \(y=\sin(x)\) и заметим, что он тоже , а не взаимно-однозначный.

Однако при ограничении синуса областью \(\left[\dfrac{-\pi}{2},\dfrac{\pi}{2}\right]\) ограниченная функция равна один к одному.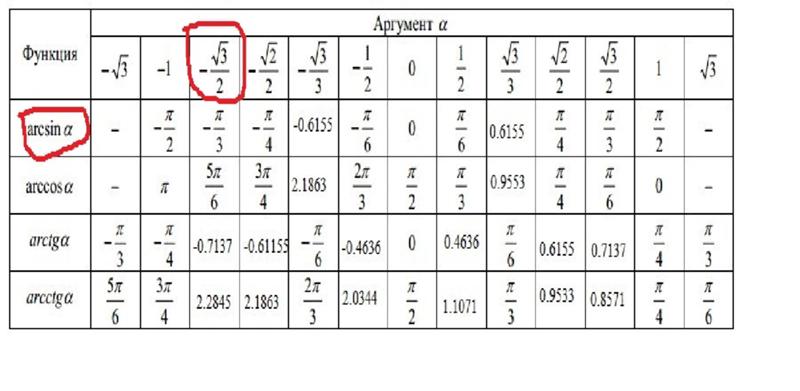 {-1}(x)} \номер\] 9{-1}(x)\)

Наконец, мы определяем арккосинус. Вспомните график \(y=\cos(x)\) и снова заметьте, что функция , а не взаимно однозначна.

В этом случае способ ограничить косинус однозначной функцией не так ясен, как в предыдущих случаях для синуса и тангенса. По соглашению косинус ограничен областью определения \([0,\pi]\). Это обеспечивает функцию, которая является взаимно однозначной, которая используется для определения арккосинуса.

Определение: арккосинус или арккосинус 9{-1}(17) \text{ is undefined} \nonumber \]

Другие входные значения можно получить с помощью калькулятора, нажав \(\boxed {\text{2nd}}\)\(\boxed {\ текст{cos}}\) ключи. Например, мы получаем следующие значения функции (здесь с использованием измерения в радианах).

---

Эта страница с заголовком 19.1: Функции arcsin, arccos и arctan используются совместно в соответствии с лицензией CC BY-NC-SA 4.0. Ее авторами, ремикшированием и/или кураторами являются Томас Тредлер и Холли Карли (Нью-Йоркский городской колледж технологии в CUNY Academic Works) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.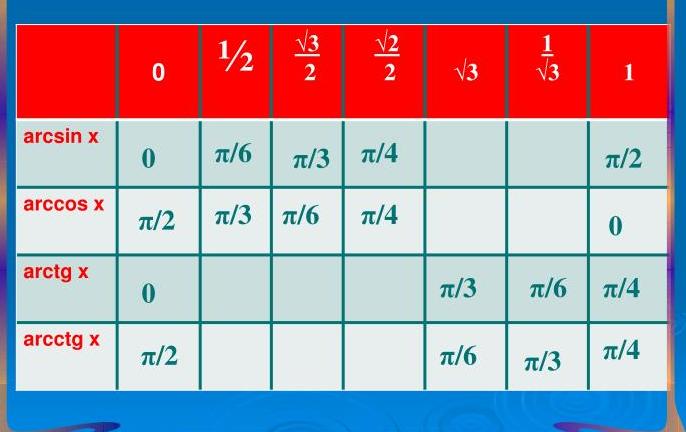

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Томас Тредлер и Холли Карли

   Лицензия

   СС BY-NC-SA

   Версия лицензии

   4,0

   Показать страницу TOC

   нет

2. Теги

   1. арктангенс
   2. арктангенс
   3. источник@https://academicworks. cuny.edu/ny_oers/1

Арксин, Арккос, Арктан — Тригонометрия

Все ресурсы по тригонометрии

6 Диагностические тесты 155 практических тестов Вопрос дня Карточки Learn by Concept

Помощь по тригонометрии » Тригонометрические операции » Arcsin, Arccos, Arctan

Что такое  если и ?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти, нам нужно использовать данную информацию в задаче. Даны противолежащая и прилежащая стороны. Затем мы можем, по определению, найти число и его меру в градусах, используя функцию.

Теперь найдем меру угла с помощью функции  .

Если вы рассчитали меру угла как  , значит, ваш калькулятор настроен на радианы, а его необходимо установить на градусы.

Сообщить об ошибке

Что такое треугольник выше  если и ?

Возможные ответы:

Правильный ответ:

Объяснение:

Нам нужно использовать тригонометрическую функцию, чтобы найти . Нам даны противоположная и смежная стороны, поэтому мы можем использовать функции  и  .

Сообщить об ошибке

Для треугольника выше, что такое  если  и ?

Возможные ответы:

Правильный ответ:

Объяснение:

Нам нужно использовать тригонометрическую функцию, чтобы найти . Нам даны противолежащая сторона и гипотенуза, поэтому мы можем использовать функции  и  .

Сообщить об ошибке

Что из следующего является эквивалентом степени обратной тригонометрической функции

?

Возможные ответы:

Правильный ответ:

Объяснение:

Это обращение функции косинуса. Это означает, что если , то .

Следовательно,

 

Сообщить об ошибке

Приняв угол в градусах, определите значение .

Возможные ответы:

Правильный ответ:

Объяснение:

Для оценки необходимо знать существующий домен и диапазон для этих обратных функций.

Арксинус:

Арккосинус:

Арктангенс:

9 0031

Оцените каждый термин. Окончательные ответы должны возвращать угол.

Сообщить об ошибке

Если 

,

, какие значения принимает?

Предположим, что   

Возможные ответы:

Реального решения нет.

Правильный ответ:

Объяснение:

Если , то мы можем применить обратный косинус к обеим сторонам:

Так как косинус и обратный косинус отменяют друг друга; затем мы можем применить обратные функции синуса и секущей, чтобы получить решение.

  и                                             и                                                                                   

 

 

Сообщить об ошибке

Рассчитать .

Возможные ответы:

Правильный ответ:

Объяснение:

Функция арксеканс принимает тригонометрическое отношение на единичной окружности в качестве входных данных и возвращает угол в качестве выходного значения. Таким образом, данная функция может быть переписана как

и является мерой угла, которая при применении к функции косинуса дает . Обратите внимание, что функция арксеканса, выраженная в условии задачи, написана с большой буквы; следовательно, мы ищем «главную» угловую меру, или ту, которая лежит между  и . Так как , и поскольку  лежит между  и ,

.

 

Сообщить об ошибке

Рассчитать .

Возможные ответы:

Правильный ответ:

Объяснение:

Домен в аргументе  для     –

 .