ОглавлениеВВЕДЕНИЕЧасть первая.  Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА 2. Простые и составные числа. Признаки делимости. 3. Наибольший общий делитель и наименьшее общее кратное. 4. Целые числа. Рациональные числа. 5. Десятичные дроби. Представление рациональных чисел десятичными дробями. 6. Иррациональные числа. Действительные числа. 7. Действия с приближенными числами. 8. Числовая ось. Координаты точки на плоскости. § 2. Степени и корни 9. Степени с натуральными показателями. 10. Степени с целыми показателями. 11. Корни. 12. Степени с рациональными показателями. Степени с действительными показателями. 13. Алгоритм извлечения квадратного корня. § 3. Комплексные числа 14. Основные понятия и определения. 15. Рациональные действия с комплексными числами. 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа. 17. Действия с комплексными числами, заданными в тригонометрической форме. 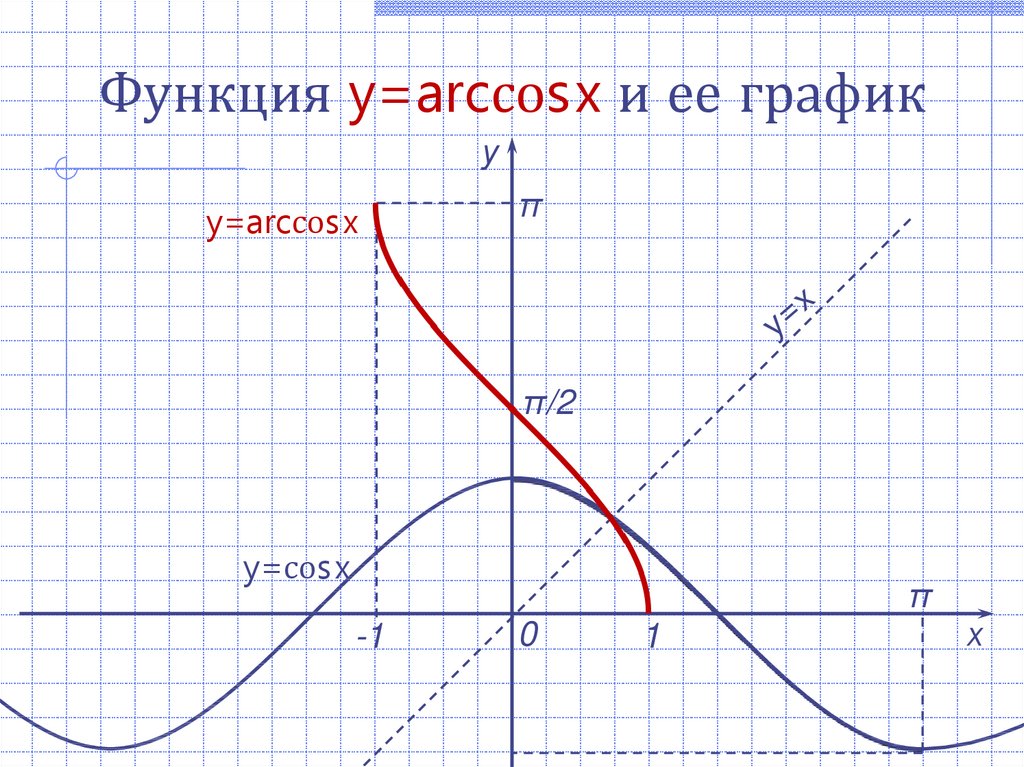 Формула Муавра. Формула Муавра.18. Извлечение корня из комплексного числа. Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ 19. Алгебраические выражения. Одночлены и многочлены. 20. Формулы сокращенного умножения. 21. Бином Ньютона. 22. Разложение многочлена на множители. 23. Дробные алгебраические выражения. § 2. Иррациональные алгебраические выражения 24. Радикалы из алгебраических выражений. 25. Освобождение от иррациональности в знаменателе дроби. Глава III. ЛОГАРИФМЫ 26. Определение и свойства логарифмов. 27. Логарифмы по различным основаниям. Модуль перехода. § 2. Десятичные логарифмы 28. Характеристика и мантисса десятичного логарифма. 29. Применение десятичных логарифмов к вычислениям. Глава IV. ФУНКЦИИ И ГРАФИКИ 30. Величина. Числовые множества. 31. Определение функции. 32. График функции. Способы задания функций. 34. Сложная функция. 35. Обратная функция. 36.  n. n.41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени. 42. Показательная функция. 43. Логарифмическая функция. § 3. Преобразование графиков 44. Параллельный сдвиг графика. 45. График квадратного трех члена. 46. График дробно-линейной функции. 47. Преобразование симметрии. Сжатие и растяжение графика. 48. Построение графиков функций. 49. Сложение графиков. § 4. Некоторые сведения о рациональных функциях 50. Целые и дробные рациональные функции. Деление многочленов. 51. Схема Горнера. Теорема Безу. 52. Нули многочлена. Разложение многочлена на множители. Глава V. УРАВНЕНИЯ 53. Уравнение. Корни уравнения. 54. Равносильные уравнения. 55. Системы уравнений. 56. Графическое решение уравнений. §. 2. Алгебраические уравнения с одной неизвестной 57. Число и кратность корней. 58. Уравнения первой степени (линейные уравнения). 59. Уравнения второй степени (квадратные уравнения). 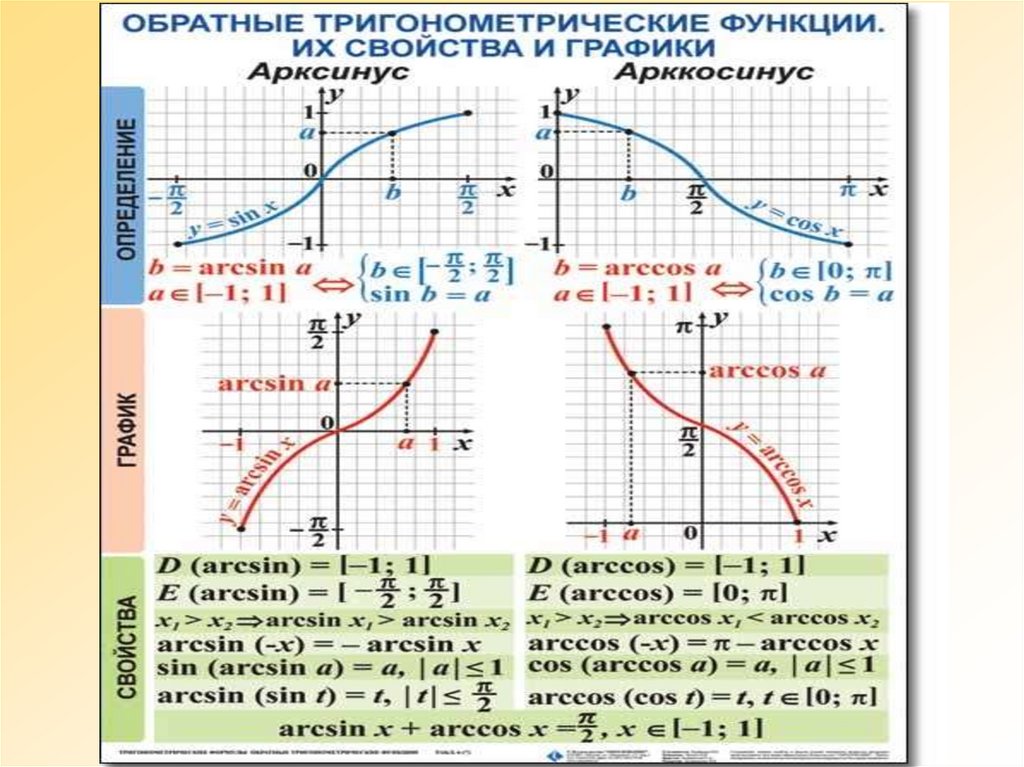 60. Формулы Виета. Разложение квадратного трехчлена на множители. 61. Исследование квадратного уравнения. 62. Уравнения высших степеней. Целые корни. 63. Двучленные уравнения. 64. Уравнения, сводящиеся к квадратным. 65. Возвратные уравнения. § 3. Системы алгебраических уравнений 66. Линейные системы. 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными. 68. Системы, состоящие из уравнения второй степени и линейного уравнения. 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней. 70. Иррациональные уравнения. 71. Показательные уравнения. 72. Логарифмические уравнения. 73. Разные уравнения. Системы уравнений. Глава VI. НЕРАВЕНСТВА 74. Свойства неравенств. Действия над неравенствами. 75. Алгебраические неравенства. § 2. Решение неравенств 76. Множество решений неравенства. 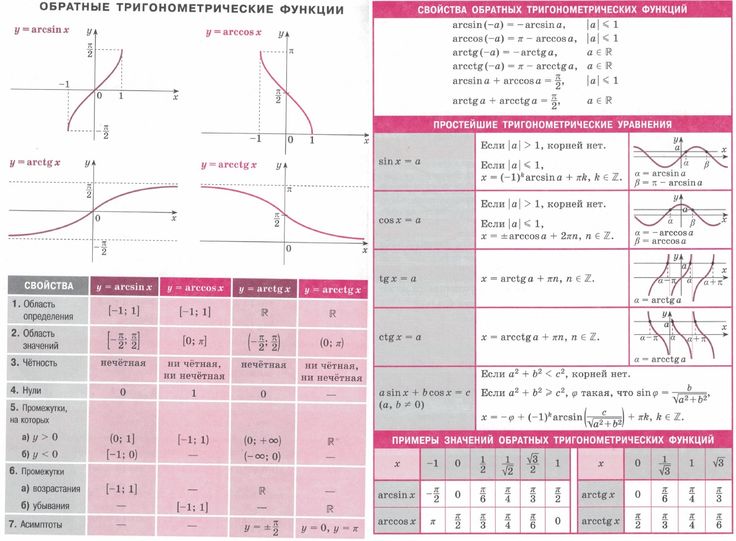 Равносильные неравенства. Равносильные неравенства.77. Графическое решение неравенств. 79. Квадратные неравенства. 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х. 81. Иррациональные, показательные и логарифмические неравенства. 82. Неравенства с двумя неизвестными. Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ 83. Числовая последовательность. 84. Предел числовой последовательности. 85. Бесконечно малые. Правила предельного перехода. § 2. Арифметическая прогрессия 86. Арифметическая прогрессия. Формула общего члена. 87. Свойства арифметической прогрессии. 88. Формула для суммы n членов арифметической прогрессии. § 3. Геометрическая прогрессия 89. Геометрическая прогрессия. Формула общего члена. 90. Свойства геометрической прогрессии. 91. Формулы для суммы n членов геометрической прогрессии. 92. Бесконечно убывающая геометрическая прогрессия. Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ) 93. Вектор, проекция вектора.  94. Положительные углы и дуги, меньшие 360°. 95. Углы и дуги, большие 360°. 96. Отрицательные углы. Сложение и вычитание углов. § 2. Тригонометрические функции произвольного угла 97. Определение основных тригонометрических функций. 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi. § 3. Соотношения между тригонометрическими функциями одного и того же угла 100. Вычисление значений тригонометрических функций по значению одной из них. 101. Значения тригонометрических функций некоторых углов. § 4. Четность, нечетность и периодичность тригонометрических функций 102. Четность и нечетность. 103. Понятие периодической функции. 104. Периодичность тригонометрических функций. § 5. Формулы приведения 105. Зависимость между тригонометрическими функциями дополнительных углов. 106. Формулы приведения. Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ § 1.  Тригонометрические функции числового аргумента Тригонометрические функции числового аргумента108. Области определения и области изменения значений тригонометрических функций. 109. Некоторые неравенства и их следствия. § 2. Графики тригонометрических функций 110. Первоначальные сведения о таблицах тригонометрических функций. 111. Основные графики. 112. Примеры построения графиков некоторых других тригонометрических функций. 113. Дальнейшие примеры построения графиков функций. Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ 114. Расстояние между двумя точками на плоскости. 115. Косинус суммы и разности двух аргументов. 116. Синус суммы и разности двух аргументов. 117. Тангенс суммы и разности двух аргументов. 118. О формулах сложения для нескольких аргументов. § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a 119. Тригонометрические функции двойного аргумента. 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n.  121. Тригонометрические функции половинного аргумента. 122. Выражение основных тригонометрических функций аргумента а через tg(a/2). § 4. Преобразование в произведение сумм вида § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента 127. Преобразование в произведение выражения a•sina + b•cosa. 128. Преобразование в произведение выражений a•sina+b и a•cosa+b 129. Преобразование в произведение выражения a•tga+b. Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ 130. Функция у = arcsin x (арксинус). 131. Функция y = arccos x (арккосинус). 132. Функция y = arctg x (арктангенс). 133. Функция y = arcctg x (арккотангенс). 134. Пример. § 2. Операции над обратными тригонометрическими функциями 135. Тригонометрические операции. 136. Операции сложения (вычитания). § 3. Обратные тригонометрические операции над тригонометрическими функциями 137.  Функция у = arcsin (sin x). Функция у = arcsin (sin x).138. Функция y = arctg (tg x). Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 139. Уравнение sin х = а. 140. Уравнение cos х = a. 141. Уравнение tg x = a. 142. Уравнение ctg x = a. 143. Некоторые дополнения. § 2. Способ приведения к одной функции одного и того же аргумента 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента. 146. Способ разложения на множители. 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t. § 3. Некоторые частные приемы решения тригонометрических уравнений и систем 148. Введение вспомогательного аргумента. 149. Преобразование произведения в сумму или разность. 150. Переход к функциям удвоенного аргумента. 151. Решение уравнения типа… 152. Применение подстановок sinx ± соsx = y. § 4. Решение тригонометрических неравенств  155. Примеры тригонометрических неравенств, сводящихся к простейшим. Часть вторая. ГЕОМЕТРИЯ 156. Точка. Прямая. Луч. Отрезок. 157. Плоскость. Фигуры и тела. 160. Равенство фигур. Движение. 161. Равенство тел. § 2. Измерение геометрических величин 162. Сложение отрезков. Длина отрезка. 163. Общая мера двух отрезков. 164. Сравнительная длина отрезков и ломаных. 165. Измерение углов. 166. Радианная мера угла. 167. Измерение площадей. 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда. Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ 169. Перпендикуляр и наклонные. 170. Свойство перпендикуляра, проведенного к отрезку в его середине. 171. Параллельные прямые. 172. Углы, образованные двумя параллельными прямыми и секущей. 173. Углы с параллельными или перпендикулярными сторонами. § 2. Геометрические места точек. Окружность 174. Геометрическое место точек. 175. Свойство биссектрисы угла.  176. Окружность. 177. Взаимное расположение прямой и окружности. Касательная и секущая. 178. Хорда и диаметр. Сектор и сегмент. 179. Взаимное расположение двух окружностей. § 3. Основные задачи на построение 181. Деление отрезка пополам. Построение перпендикуляров. 182. Построение углов. 183. Другие задачи на построение. Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ 184. Стороны и углы треугольника. 185. Биссектрисы треугольника. Вписанная окружность. 186. Оси симметрии сторон треугольника. Описанная окружность. 187. Медианы и выcоты треугольника. 188. Равенство треугольников. 189. Построение треугольников. 190. Равнобедренные треугольники. 191. Прямоугольные треугольники. § 2. Параллелограммы 192. Четырехугольники. 193. Параллелограмм и его свойства. 194. Прямоугольник. § 3. Трапеция 196. Трапеция. 197. Средняя линия треугольника. 198. Средняя линия трапеции. 199. Деление отрезка на равные части.  § 4. Площади треугольников и четырехугольников 200. Площадь параллелограмма. 201. Площадь треугольника. 202. Площадь трапеции. Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР 203. Пропорциональные отрезки. 204. Свойства биссектрис внутреннего и внешнего углов треугольника. § 2. Подобное преобразование фигур (гомотетия) 205. Определение гомотетичных фигур. 206. Свойства преобразования подобия. § 3. Общее подобное соответствие фигур 207. Подобные фигуры. 208. Периметры и площади подобных треугольников. 209. Применение подобия к решению задач на построение. Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ 210. Углы с вершиной на окружности. 211. Углы с вершиной внутри и вне круга. 212. Угол, под которым виден данный отрезок. 213. Четырехугольники, вписанные в окружность. 214. Пропорциональные отрезки в круге. 215. Задачи на построение. § 2. Метрические соотношения в треугольнике 216. Пропорциональные отрезки в прямоугольном треугольнике.  Теорема Пифагора. Теорема Пифагора.218. Теорема синусов. Формула Герона. 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов. 218. Теорема синусов. Формула Герона. 219. Радиусы вписанной и описанной окружностей. § 3. Решение треугольников 220. Таблицы функций. 221. Решение треугольников. Сводка основных формул. 222. Решение прямоугольных треугольников. 223. Решение косоугольных треугольников. Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА 224. Выпуклые многоугольники. 225. Правильные многоугольники. 226. Соотношения между стороной, радиусом и апофемой. 227. Периметр и площадь правильного n-угольника. 228. Удвоение числа сторон правильного многоугольника. § 2. Длина окружности. Площадь круга и его частей 229. Длина окружности. 230. Площадь круга и его частей. Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ 231. Взаимное расположение двух прямых в пространстве.  232. Взаимное расположение прямой линии и плоскости. 233. Взаимное расположение двух плоскостей. 234. Свойства параллельных прямых и плоскостей. 235. Построения в стереометрии. § 2. Перпендикулярность прямых и плоскостей 236. Перпендикуляр к плоскости. 237. Перпендикуляр и наклонные. 238. Угол между прямой и плоскостью. 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей. 240. Общий перпендикуляр двух скрещивающихся прямых. § 3. Двугранные и многогранные углы 241. Двугранный угол. 242. Взаимно перпендикулярные плоскости. 243. Трехгранные углы. 244. Многогранные углы. § 4. Многогранники 245. Многогранники. 246. Правильные многогранники. Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА 247. Цилиндры и призмы. 248. Параллелепипеды. 249. Объемы призм и цилиндров. 250. Площадь боковой поверхности призмы. 251. Площадь поверхности цилиндра. § 2. Пирамида. Конус 252. Свойства пирамиды и конуса.  253. Объем пирамиды и конуса. 254. Площадь боковой поверхности правильной пирамиды и конуса. 255. Усеченный конус и усеченная пирамида. § 3. Шаровая поверхность. Шар 256. Шар и шаровая поверхность. 257. Объем шара и его частей. 258. Площадь поверхности шара и ее частей. 259. Понятие телесного угла. Ответы к упражнениям Приложения |
arcsin (x) | функция обратного синуса
arcsin (x) | функция обратного синусаГлавная страница / Математика / Тригонометрия /Arcsin
arcsin (x), sin -1 (x), функция обратного синуса .
- Определение слова arcsin
- График arcsin
- Правила Arcsin
- Таблица Arcsin
- Калькулятор Arcsin
Определение Arcsin
Арксинус x определяется как функция, обратная синусу x, когда -1≤x≤1.
Когда синус y равен x:
грех у = х
Тогда арксинус x равен функции обратного синуса x, которая равна y:
arcsin x = грех -1 x = y
пример
arcsin 1 = sin -1 1 = π / 2 рад = 90 °
График arcsin
Правила Arcsin
| Название правила | Правило |
|---|---|
| Синус арксинуса | грех (arcsin x ) = x |
| Арксинус синуса | arcsin (sin x ) = x +2 k π, когда k ∈ℤ ( k целое) |
| Арксин отрицательного аргумента | arcsin (- x ) = — arcsin x |
| Дополнительные углы | arcsin x = π / 2 — arccos x = 90 ° — arccos x |
| Сумма арксина | arcsin α + arcsin ( β ) = arcsin ( α√ (1- β 2 ) + β√ (1- α 2 ) ) |
| Arcsin разница | arcsin α — arcsin ( β ) = arcsin ( α√ (1- β 2 ) — β√ (1- α 2 ) ) |
| Косинус арксинуса | |
| Касательная к арксинусу | |
| Производная арксинуса | |
| Неопределенный интеграл от арксинуса |
Таблица Arcsin
| х | arcsin (x) (рад) | arcsin (x) (°) |
|---|---|---|
| -1 | -π / 2 | -90 ° |
| -√ 3 /2 | -π / 3 | -60 ° |
| -√ 2 /2 | -π / 4 | -45 ° |
| -1/2 | -π / 6 | -30 ° |
| 0 | 0 | 0 ° |
| 1/2 | π / 6 | 30 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 3 | 60 ° |
| 1 | π / 2 | 90 ° |
- Функция синуса
- Функция арккосинуса
- Функция арктана
- Калькулятор Arcsin
- Конвертер градусов в радианы
- Арксин из 0
- Арксин из 1
- Арксин бесконечности
- Граф Арксин
- Производная Arcsin
- Интеграл Арксина
- Грех арчсина
- Cos of arcsin
- Загар арчсина
Advertising
ТРИГОНОМЕТРИЯ
- Функция Arccos
- Функция Arcsin
- Функция арктана
- Функция косинуса
- Функция синуса
- Касательная функция
БЫСТРЫЕ ТАБЛИЦЫ
- Рекомендовать сайт
- Отправить отзыв
- О нас
Обратная тригонометрическая функция: арксинус
Перед изучением этого раздела рекомендуется прочитать
Попытка «отменить» тригонометрические функции.
Чтобы функция имела обратную, каждый выход должен иметь ровно один соответствующий вход .
Таким образом, только взаимно однозначные функции имеют обратные.
Функция синуса не имеет true обратная, потому что функция синуса не является взаимно однозначной.
Итак, чтобы попытаться определить «функцию обратного синуса», мы делаем все возможное, как описано ниже.
Функция арксинуса (точное определение ниже) — это лучшее, что мы можем сделать , пытаясь получить обратную функцию
синусоидальная функция.
Функция арксинуса равна на самом деле обратная сторона зеленой фигуры, показанной выше!
Вот функциональная панель того, что происходит:
| Функция синуса принимает действительное число . 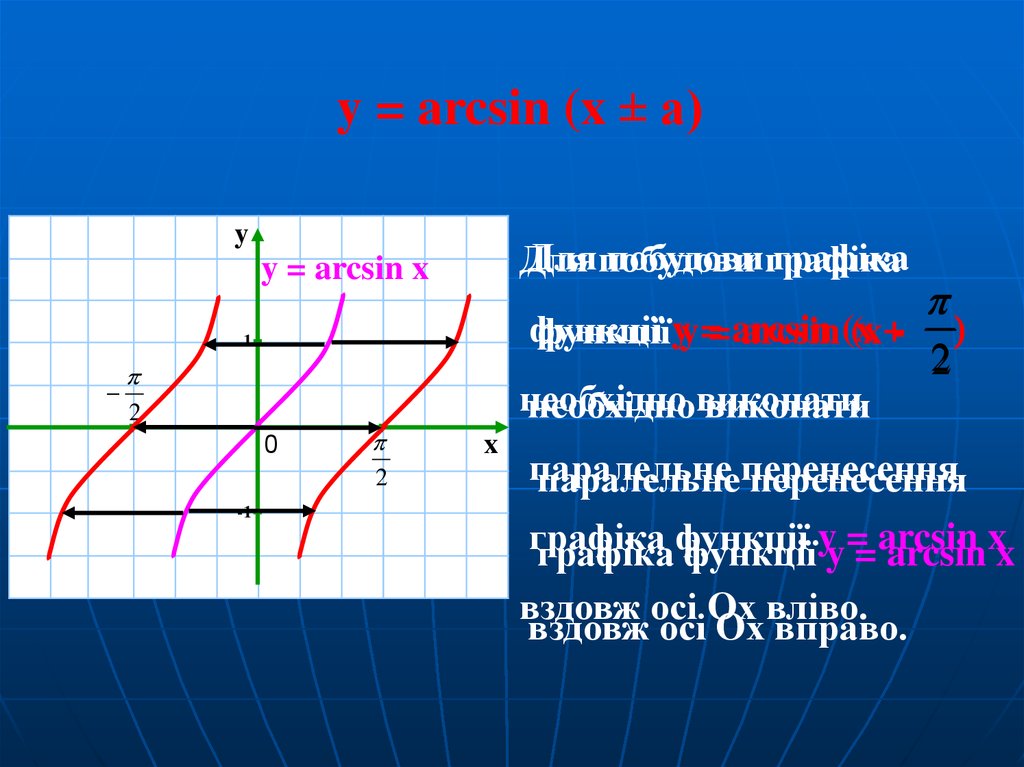 в качестве входа. в качестве входа. Он дает результат в интервале $\,[-1,1]\,$. Например (как показано ниже), | Когда мы пытаемся использовать поле функции синуса «назад»,
мы попадаем в беду. Вывод $\,0.5\,$ мог прийти | Однако,
когда мы используем зеленый кусок синусоида, проблема решена! Теперь их работает только один вход . Обратите внимание, что $\,\color{green}{x}\,$ находится в интервале $\,[- \frac{\pi}2,\frac{\pi}2]\,$. |
Это немного неправильное название, но функция арксинуса (точное определение ниже) часто упоминается как
как «функция обратного синуса».
Лучшее название было бы что-то вроде «инверсия соответствующим образом ограниченной синусоидальной функции».
(Однако неудивительно, что люди не говорят ничего такого длинного и громоздкого.)
Итак, что же такое $\,\arcsin 0.5\,$?
$\,\arcsin 0,5\,$ — число из интервала $\,[-\frac{\pi}{2},\frac{\pi}{2}]\,$, синус которого равен $\,0,5. \,$
Что такое $\,\arcsin x\,$?
В более общем случае пусть $\,x\,$ будет любым числом в интервале $\,[-1,1]\,$.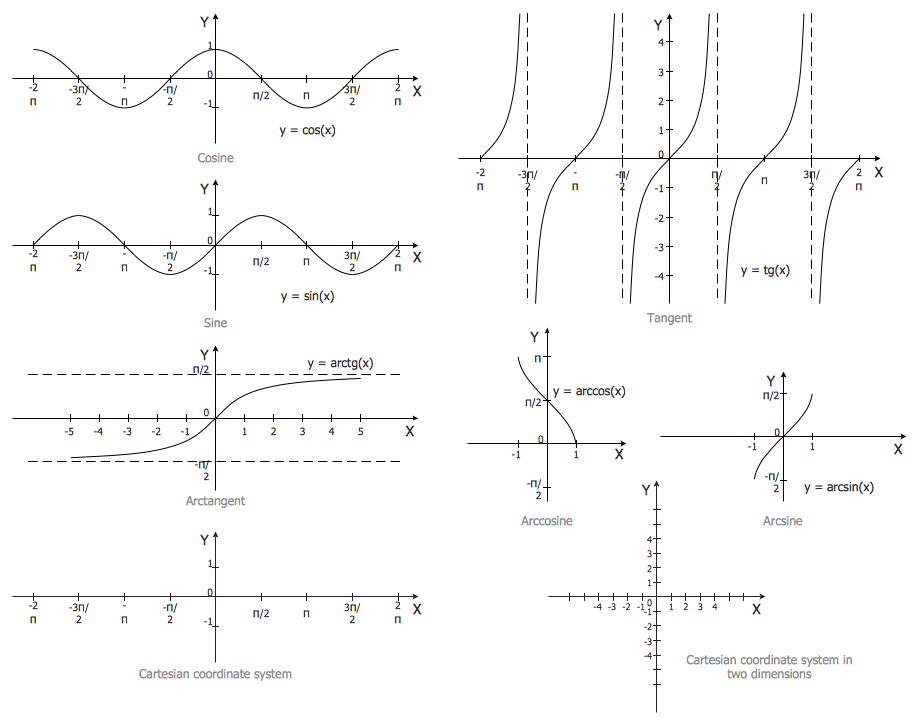
Затем:
$\,\arcsin x\,$ — число в интервале $\,[-\frac{\pi}{2},\frac{\pi}{2}]\,$, синус которого равен $\,x \,$
В моем собственном уме (здесь говорит автор доктор Кэрол Бернс) я произношу следующие слова:
$\,\arcsin x\,$ — это число между $\,-\frac{\pi}{2}\,$ и $\,\frac{\pi}{2}\,$, синус которого равен $\ ,х\,$
Я лично знаю конечные точки включая , так что это меня не смущает.
Однако слово «между» неоднозначно — оно может включать или не включать конечные точки, в зависимости от контекста.
Можно уточнить, сказав:
$\,\arcsin x\,$ — это число между $\,-\frac{\pi}{2}\,$ и $\,\frac{\pi}{2}\,$ (включая конечные точки) синус которого равен $\,x\,$
.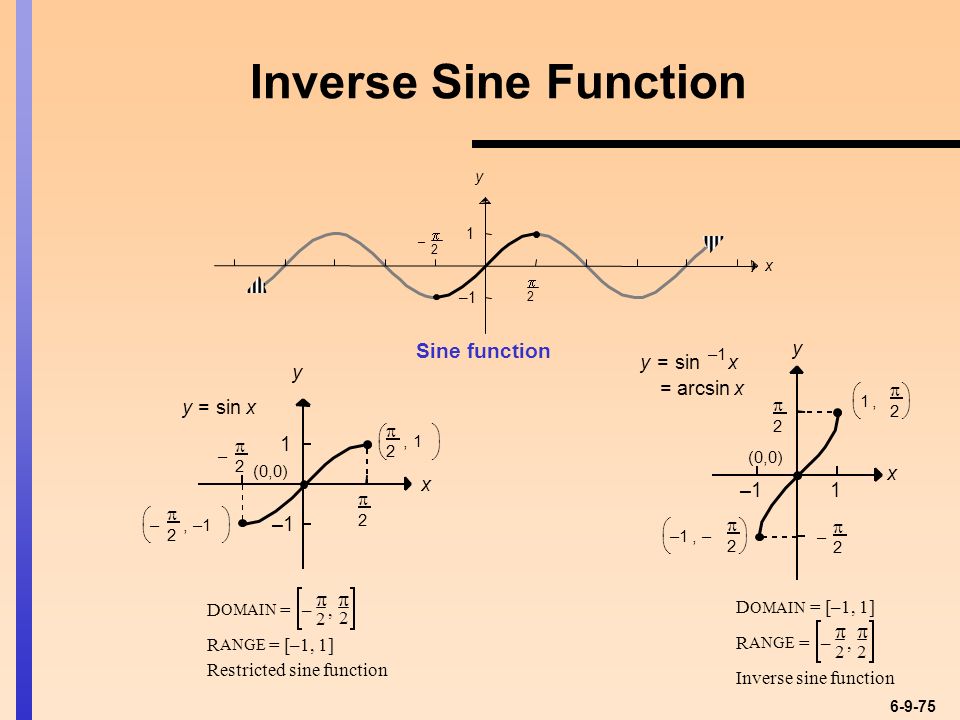 {-1} x}\ \ \ \ \
\cssId{s67}{\text{если и только если}}\ \ \ \
\cssId{s68}{\bigl(\\sin y = x\\\text{AND}\ \ -\frac{\pi}{2} \le y\le \frac{\pi}{2}\ \ больше)}
$$
{-1} x}\ \ \ \ \
\cssId{s67}{\text{если и только если}}\ \ \ \
\cssId{s68}{\bigl(\\sin y = x\\\text{AND}\ \ -\frac{\pi}{2} \le y\le \frac{\pi}{2}\ \ больше)}
$$
Примечания к определению функции арксинуса:
Ваш браузер не поддерживает аудио элементы.
ПРОЧТЕНИЕ, ЧАСТЬ 2
- ОФИЦИАЛЬНОЕ НАЗВАНИЕ В ОТНОШЕНИИ ФУНКЦИИ ОБОЗНАЧЕНИЯ СОКРАЩЕНИЯ:
Формальное название функции, обсуждаемой в этом разделе, — «арксинус».
Он имеет букву «е» на конце и произносится как ARC-sine (с длинным «i» в слове «sine»). 9{-1}\,$’ вводит в заблуждение и дает себя к ошибкам.
Этот автор настоятельно предпочитает обозначение ‘$\,\arcsin\,$’. - АЛЬТЕРНАТИВНОЕ ОПРЕДЕЛЕНИЕ, С ИСПОЛЬЗОВАНИЕМ ГРАДУСОВ ВМЕСТО РАДИАНОВ:
Входные данные для тригонометрических функций можно рассматривать как действительные числа (радианы) или градусы.
Например, $\,\sin \frac{\pi}{2} = 1\,$: здесь $\,\frac{\pi}{2}\,$ — мера в радианах. 9\circ]\,$, синус которого равен $\,x\,$ - НАВЫКИ КАЛЬКУЛЯТОРА:
Если калькулятор находится в режиме градусов, то $\,\arcsin x\,$ сообщается в градусах.
Если калькулятор работает в радианном режиме, то значение $\,\arcsin x\,$ отображается в радианах. - ГРАФИК ФУНКЦИИ АРКСИНУСА: 9{-1}\,$,
находится путем отражения графика $\,f\,$
относительно прямой $\,y = x\,$.
Ниже этот прием используется для построения графика функции арксинуса:Вот кусок синусоиды
который используется для определения функции арксинуса:
домен: $\,[-\frac{\pi}{2},\frac{\pi}{2}]\,$диапазон: $\,[-1,1]\,$
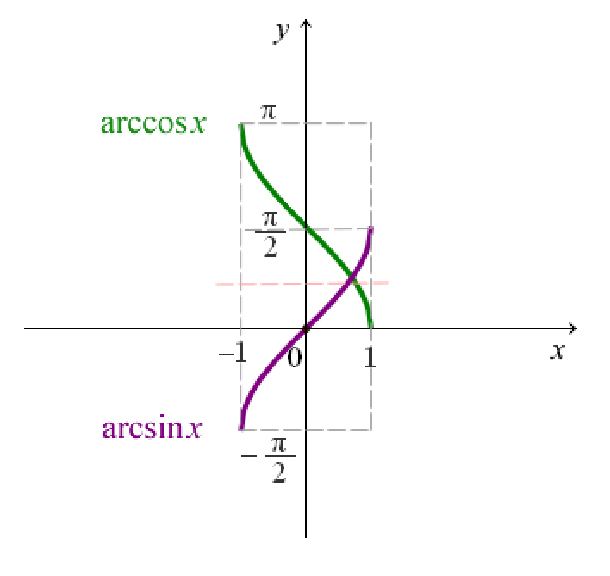
Вот та же кривая,
вместе со своим отражением относительно прямой $\,\color{red}{y = x}\,$График функции арксинуса
домен: $\,[-1,1]\,$диапазон: $\,[-\frac{\pi}{2},\frac{\pi}{2}]\,$
Обратите внимание, что домен и область значений функции и ее обратной функции меняются местами!
Домен одного является диапазоном другого.
Диапазон одного является доменом другого. 9{-1}\,$ что-то делает, а $\,f\,$ отменяет действие Поскольку функции синуса и арксинуса являются , а не истинными инверсиями друг друга,
отношения между ними немного сложнее.Вот направление, в котором они делают красиво «отменяют» друг друга: начните с числа, сначала примените функцию арксинуса, затем примените функцию синуса, и в конечном итоге там, где вы начали. Подробности:
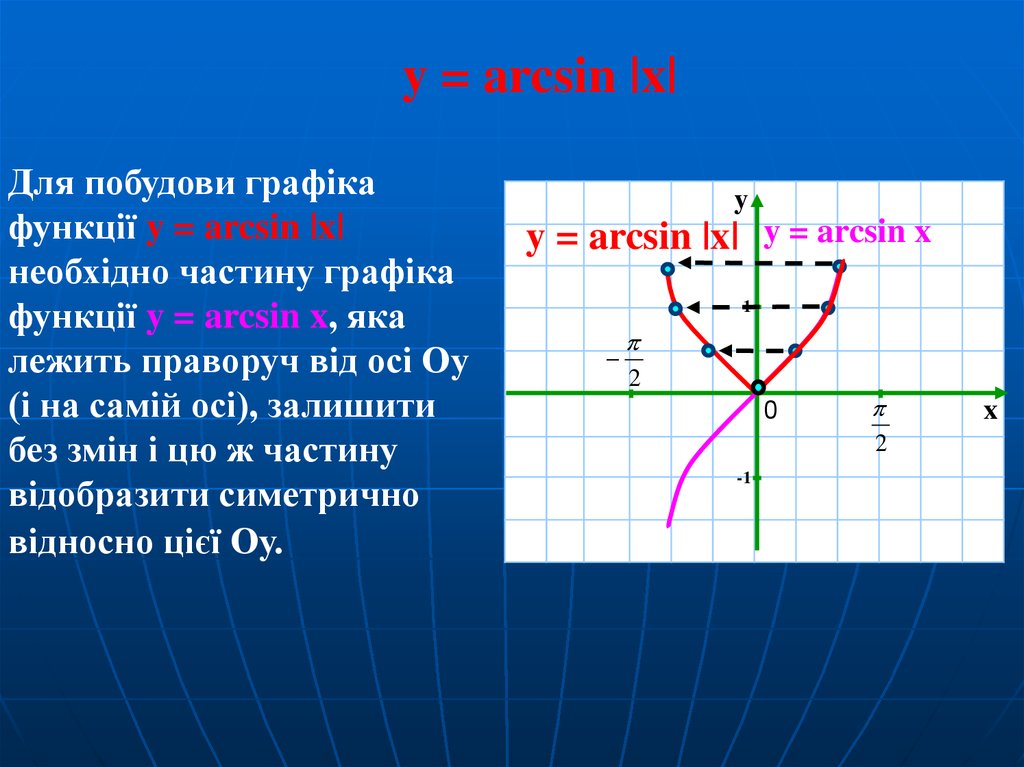
Для всех $\,x\in [-1,1]\,$, $$ \cssId{sb67}{\sin(\arcsin x) = x} $$
- начните с $\,\color{red}{x}\in [-1,1]\,$
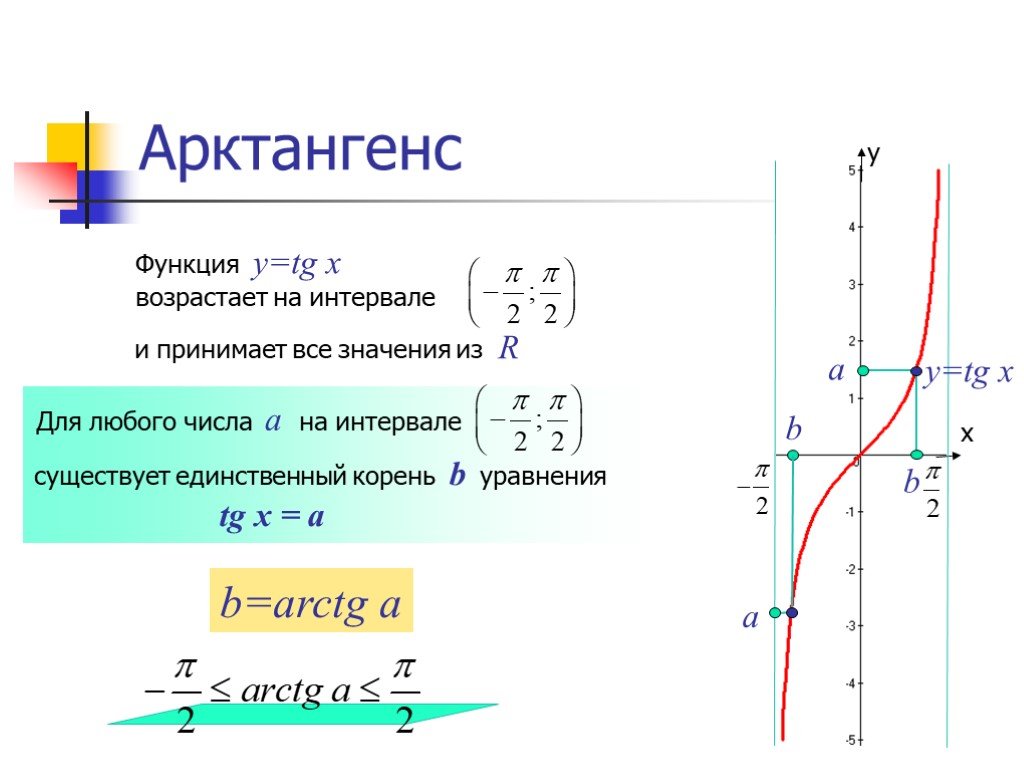
- функция арксинуса переводит $\,\color{red}{x}\,$ в $\,\color{green}{\arcsin x}\,$ в интервале $\,[-\frac{\pi}2 ,\frac{\pi}2]\,$
- функция синуса возвращает
$\,\color{green}{\arcsin x}\,$ обратно в $\,\color{red}{x}\,$
Вот направление, где они не обязательно красиво «отменять» друг друга: начните с числа, сначала примените функцию синуса, затем примените функцию арксинуса.  Если число, с которого вы начали, находится вне интервала $\,[-\frac{\pi}2,\frac{\pi}2]\,$,
тогда вы не окажетесь там, где начали!
Если число, с которого вы начали, находится вне интервала $\,[-\frac{\pi}2,\frac{\pi}2]\,$,
тогда вы не окажетесь там, где начали!Вот подробности:
Для всех $\,x\in [-\frac{\pi}2,\frac{\pi}2]\,$, $$ \cssId{sb77}{\arcsin(\sinx) = x} $$
(См. верхний график справа.) Для всех $\,x\not\in [-\frac{\pi}2,\frac{\pi}2]\,$, $$ \cssId{sb80}{\arcsin(\sin x) \ne x} $$
(См. нижний график справа.) Пример: найти точное значение $\,\arcsin(-0.
 5)\,$ 9\circ\,$, синус которой равен $\,-\frac 12\,$.
5)\,$ 9\circ\,$, синус которой равен $\,-\frac 12\,$.- Напомним: синус — это $y$-значение точек на единичной окружности.
- Нарисуйте единичный круг.
Отметьте $\,-\frac 12\,$ на оси $y$.
Отметьте уникальный угол между $\,-9\цирк\,$.- Используя радианную меру, $\,\arcsin(-\frac 12) = -\frac{\pi}6\,$.
Модуль 4 — Параметрические уравнения, тригонометрические и обратные тригонометрические функции
Модуль 4 — Параметрические уравнения, тригонометрические и обратные тригонометрические функции — Урок 4Модуль 4.  Параметрические уравнения, тригонометрические и обратные тригонометрические функции
Параметрические уравнения, тригонометрические и обратные тригонометрические функции Введение | Урок 1 | Урок 2 | Урок 3 | Урок 4 | Самооценочный тест Урок 4.4. Обратные тригонометрические функции На уроке 4.1 вы построили параметрический график функции и ее обратной зависимости. В этом уроке вы будете использовать тот же метод для построения графика обратной зависимости синусоидальной функции. Ограничивая значения Tmin и Tmax, вы определяете обратное отношение, поэтому оно также является функцией.
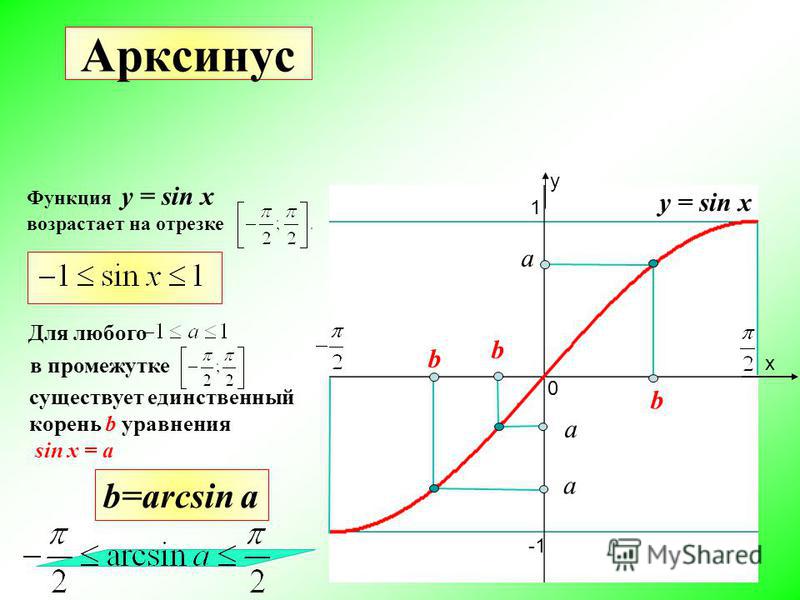
Обратный синус
Исследуйте обратную функцию синуса, одновременно строя график функции синуса и ее обратной функции с помощью параметрических уравнений.
- Отключите все активные графики рассеяния.
- Выберите параметрический и одновременный режимы в меню РЕЖИМ.

- Очистите все уравнения в редакторе Y= и введите функцию синуса, , и его обратная функция, , делая синусоиду толще.
- Отображение графиков в [-2 , 2 , 0,1] х [-9,5, 9,5, 1] х [-2 , 2 , 1] окно.
Обратите внимание, что синусоидальная функция колеблется вокруг оси x , а ее обратная волна колеблется вокруг оси y . Поскольку существует более одного значения y , связанного с некоторыми значениями x , обратное отношение не является функцией.
Ограничение домена синуса
Функция, обратная синусу, не является функцией. Но если вы ограничите область определения функции синуса так, чтобы каждое значение y в [-1, 1] встречалось только один раз, то обратная функция этой ограниченной функции также будет функцией.
- Измените значения Tmin и Tmax на значения, показанные ниже.
- Отобразите графики как функции синуса, так и ее инверсии, но используйте обычный стиль линии для функции синуса.

Обратной этой ограниченной функции является функция, однако смотровое окно не очень хорошее.
- Введите следующие значения окна:
Отобразите только обратную функцию, отменив выбор X 1T и Y 1T , как описано ниже.
- Нажимать затем переместите курсор на знак «=» рядом с X 1T и нажмите .
Знаки «=» для X 1T и Y 1T больше не должны выделяться. Это означает Х 1T и Y 1T больше не выбираются для построения графика и не будут отображаться. - Отобразите график обратного синуса, нажав
Ограничение домена y = sin( x ) также ограничило диапазон обратного отношения, что заставило каждый вход обратного отношения иметь ровно один выход. В результате инверсия равна 9Функция 0349 y = sin -1 x , что также записывается как y = arcsin x .




 Если число, с которого вы начали, находится вне интервала $\,[-\frac{\pi}2,\frac{\pi}2]\,$,
тогда вы не окажетесь там, где начали!
Если число, с которого вы начали, находится вне интервала $\,[-\frac{\pi}2,\frac{\pi}2]\,$,
тогда вы не окажетесь там, где начали!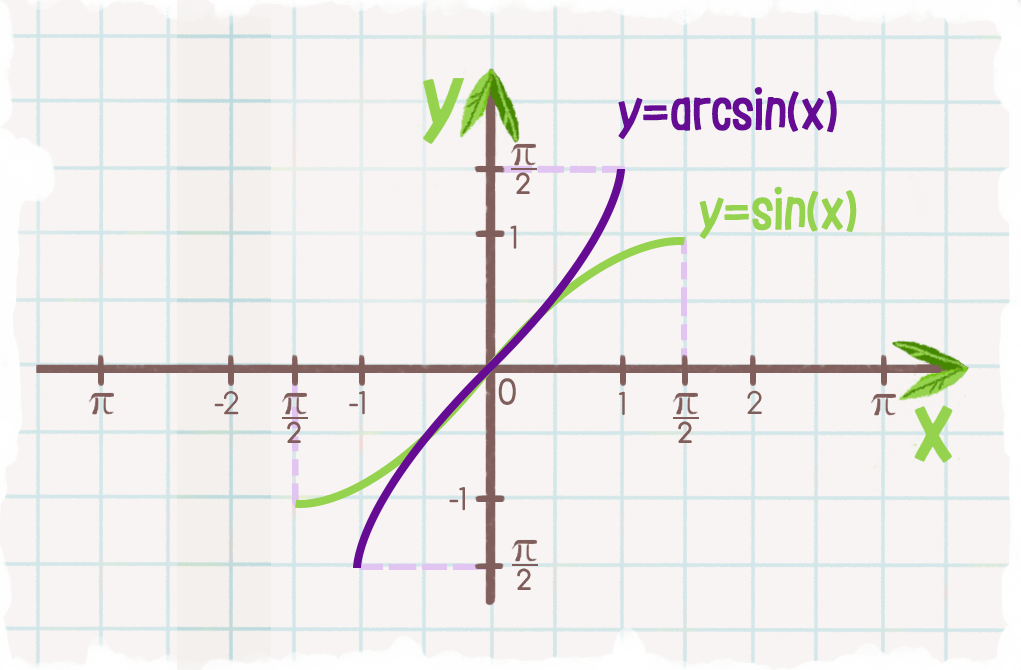 5)\,$ 9\circ\,$, синус которой равен $\,-\frac 12\,$.
5)\,$ 9\circ\,$, синус которой равен $\,-\frac 12\,$. Параметрические уравнения, тригонометрические и обратные тригонометрические функции
Параметрические уравнения, тригонометрические и обратные тригонометрические функции