Блог для уроків інформатики: февраля 2015
Тригонометричні рівняння
Арктангенс
Арктангенс, y = arcsin x, определен при и имеет множество значений .
График функции арктангенс
График функции y = arctg xГрафик арктангенса получается из графика тангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, множество значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арктангенса.
Арккотангенс
Арккотангенс, y = arcctg x, определен при и имеет множество значений .
График функции арккотангенс
График функции y = arcctg xГрафик арккотангенса получается из графика котангенса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккотангенса.
Четность
Функция арктангенс является нечетной:
arctg(–x) = arctg(–tg arctg x) = arctg(tg(–arctg x)) = – arctg xФункция арккотангенс не является четной или нечетной:
Свойства — экстремумы, возрастание, убывание
Основные свойства арктангенса и арккотангенса представлены в таблице.
| y = arctg x | y = arcctg x | |
| Область определения | – ∞ ≤ x ≤ ∞ | – ∞ ≤ x ≤ ∞ |
| Множество значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы, минимумы | нет | нет |
| Нули, y = 0 | x = 0 | нет |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
| – | π | |
| 0 |
Таблица арктангенсов и арккотангенсов
В данной таблице представлены значения арктангенсов и арккотангенсов, в градусах и радианах, при некоторых значениях аргумента.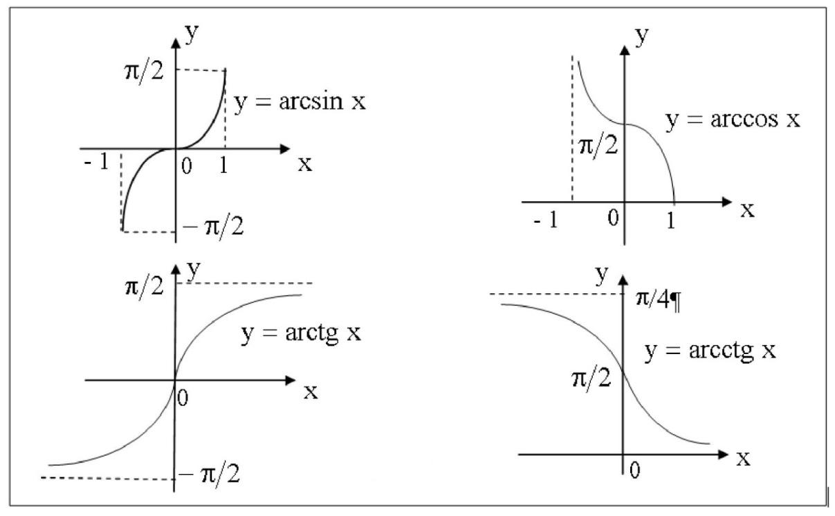
| x | arctg x | arcctg x | ||
| град. | рад. | град. | ||
| – ∞ | – 90° | – | 180° | π |
| – | – 60° | – | 150° | |
| – 1 | – 45° | – | 135° | |
| – | – 30° | – | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 1 | 45° | 45° | ||
| 60° | 30° | |||
| + ∞ | 90° | 0° | 0 | |
Арксинус
Арксинус, y = arcsin x определен при и имеет множество значений .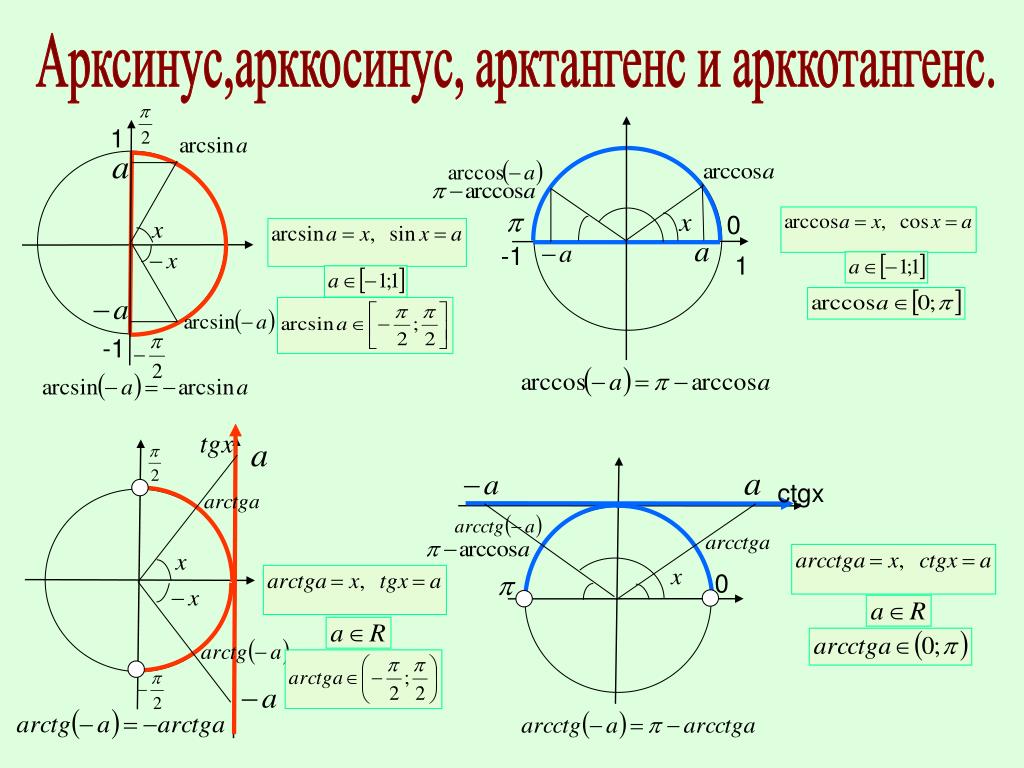
График функции арксинус
График функции y = arcsin xГрафик арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арксинуса.
Арккосинус
Арккосинус, y = arccos x определен при и имеет множество значений .
График функции арккосинус
График функции y = arccos xГрафик арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккосинуса.
Функция арксинус является нечетной:
arcsin(–x) = arcsin(–sin arcsin x) = arcsin(sin(–arcsin x)) = – arcsin xФункция арккосинус не является четной или нечетной:
arccos(–x) = arccos(–cos arccos x) = arccos(cos(π–arccos x)) =π – arccos x ≠ ± arccos x Свойства — экстремумы, возрастание, убывание
Основные свойства арксинуса и арккосинуса представлены в таблице.
| y = arcsin x | y = arccos x | |
| Область определения | – 1 ≤ x ≤ 1 | – 1 ≤ x ≤ 1 |
| Область значений | ||
| Возрастание, убывание | монотонно возрастает | монотонно убывает |
| Максимумы | ||
| Минимумы | ||
| Нули, y = 0 | x = 0 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = π/2 |
Таблица арксинусов и арккосинусов
В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.
| x | arcsin x | arccos x | ||
| град. | рад. | град. | рад. | |
| – 1 | – 90° | – | 180° | π |
| – | – 60° | – | 150° | |
| – | – 45° | – | 135° | |
| – | – 30° | – | 120° | |
| 0 | 0° | 0 | 90° | |
| 30° | 60° | |||
| 45° | 45° | |||
| 60° | 30° | |||
| 1 | 90° | 0° | 0 | |
Следующие Главная страница
Подписаться на: Сообщения (Atom)
Уравнение касательной к графику функции f(X) в точке х0
Таблица производных
Функция f (х) | Производная f ‘ (х) |
С, где С — любое число | 0 |
хп, где п – любое число | пхп-1 |
ех | ех |
aх | ахlnа |
ln х | |
lоg a x | |
sin х | cosх |
cos х | -sinх |
tg х | |
ctgх |
y = f(x0) + f ‘(x0)(x – x0)
Обратные тригонометрические функции
Функция | Область определения | Область значений |
y = arcsinx | [-1;1] | [-/2; /2] |
y = arccosx | [-1;1] | [0; ] |
y = arctgx | x – любое | (-/2; /2) |
y = arcctgx | x – любое | (0; ) |
sin(arcsin x) = x
cos(arccos x) = x
tg(arctg x) = x
ctg(arcctg x) = x arcsin(-x) = — arcsinx
sin(arсcos x)= arccos(-x)= -arccos x
cos(arcsin x) = arctg(-x) = — arctg x
tg (arcctg x) = arcctg(-x) = -arcctgx
ctg (arctg x) =
Значения тригонометрических функций
a | 0o | 30o | 45o | 60o | 90o | 120o | 135o |
a | 0 | /6 | /4 | /3 | /2 | 2/3 | 3/4 |
sin | 0 | 1 | |||||
cos | 1 | 0 | |||||
tg | 0 | 1 | — | — 1 | |||
ctg | — | 1 | 0 | — 1 |
Формулы
90o— | 90o+ | 270o- | 270o+ | |
/2 — | /2 + | 3/2- | 3/2+ | |
sin | cos | cos | -cos | -cos |
cos | sin | -sin | -sin | sin |
tg | ctg | -ctg | ctg | -ctg |
ctg | tg | -tg | tg | -tg |
sin(-x) = -sinx cos(-x) = cos x
sin(x-y) = — sin(y-x) cos(x-y) = cos(y-x)
для некоторых углов
150o | 180o | 210o | 225o | 270o | 300o | 330o | 360o |
5/6 | | 7/6 | 5/4 | 3/2 | 5/3 | 11/6 | 2 |
0 | — 1 | 0 | |||||
-1 | 0 | 1 | |||||
0 | 1 | — | 0 | ||||
— | 1 | 0 | — |
приведения
180o- | 180o+ | 360o- | 360o+ | |
— | + | 2 — | 2 + | |
sin | sin | -sin | -sin | sin |
cos | -cos | -cos | cos | cos |
tg | -tg | tg | -tg | tg |
ctg | -ctg | ctg | -ctg | ctg |
tg(-x) = — tgx ctg(-x) = — ctg x
tg(x-y) = — tg(y-x) ctg(x-y) = — ctg(y-x)
Рассмотрим функцию y=arctan x а) Заполните таблицу с помощью графической утилиты.
(b) Нанесите точки из таблицы в части (a) и нарисуйте график функции. (Не используйте графическую утилиту.)
(c) Используйте графическую утилиту для построения графика функции арктангенса и сравните результат с нарисованным от руки графиком в части (b).
г) Найдите горизонтальные асимптоты графика.Вопрос
Рассмотрим функцию $y=\arctan x$ а) Заполните таблицу с помощью графической утилиты. (b) Нанесите точки из таблицы в части (a) и нарисуйте график функции. (Не используйте графическую утилиту.) (c) Используйте графическую утилиту для построения графика функции арктангенса и сравните результат с нарисованным от руки графиком в части (b). г) Найдите горизонтальные асимптоты графика.
Мгновенный ответ:
Шаг 1/2
(a) Мы можем использовать графический калькулятор, чтобы заполнить таблицу. Мы можем использовать следующие значения $x$: $-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5$.
Получаем следующую таблицу:
\begin{табличный}{|c|c|} \hline
$x$ & $\arctan x$ \\ \hline
$-5$ & $-1,3734$ \\ \hline
$-4$ & $-1.3258$ \\ \hline
$-3$ & $-1.2490$ \\ \hline
$-2$ & $-1.1071$ \\ \hline
$-1$ и $-0,7854$ \\ \hline
$0$ & $0$ \\ \hline
$1$ & $0,7854$ \\ \hline
$2$ & $1.1071$ \\ \hline
3$ и 1,249$0$ \\\hline
$4$ и $1,3258$ \\ \hline
$5$ и $1,3734$ \\ \hline
\end{tabular}
Рекомендация видео с лучшим совпадением:
Решено проверенным экспертом
У нас нет заданного вами вопроса, но вот рекомендуемое видео, которое может помочь.
Вопрос о лучшем совпадении
Пошаговый ответ
Рассмотрим функцию $y=\arctan x$
а) Заполните таблицу с помощью графической утилиты.
(b) Нанесите точки из таблицы в части (a) и нарисуйте график функции. (Не используйте графическую утилиту.)
(c) Используйте графическую утилиту для построения графика функции арктангенса и сравните результат с нарисованным от руки графиком в части (b).
г) Найдите горизонтальные асимптоты графика.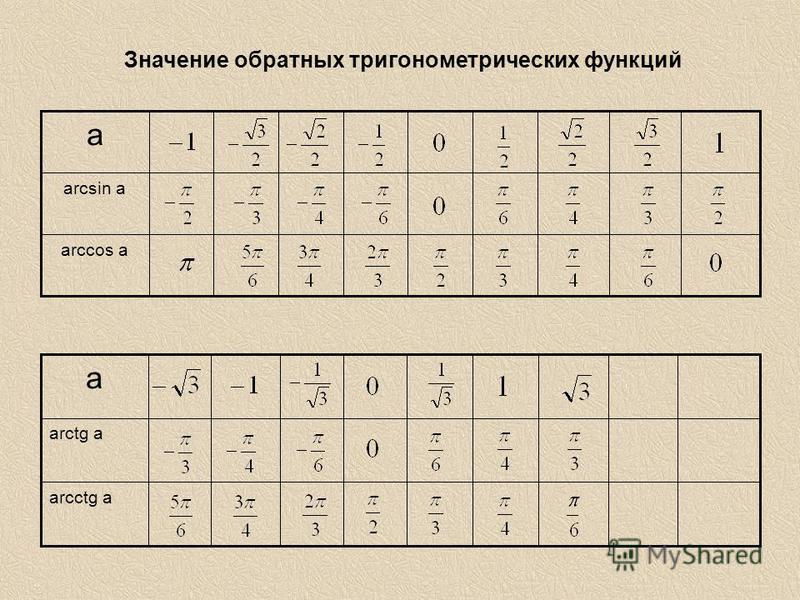
Рекомендуемые видео
Стенограмма
Мы можем написать Штейну, когда у нас будет две статьи о панике. Мы знаем, что tangles X определяется, когда X со мной, и мы можем принять все ex, принадлежащие нашему, за избыток с нулевым toe, то есть пятью toe do. Ехал по трассе две и пауза глубокая и это было не включительно, но надо придерживаться этого. Нам нужно найти графическую утилиту, чтобы заполнить таблицу, потому что этот x принят в ответ на этот вопрос. Это x нет, и в то же время здесь мы должны выделить ось y, поэтому мы будем использовать графические люди, которые вы на графике напишете Почему равно двум функция выберет Tang хуже, Это x нет, и в то же время здесь мы должны выделить ось у. Там, где Льюис и в стихах встанем было выключено, ось X отметит от минус 10 два плюс 10. Так давайте сейчас шагнем, когда это? Это будет нами отмечено. Таким образом, мы видим, что это больше, чем мы думаем. Мы должны ограничить его до минус два плюс 10 минус 10, чтобы благословить 10.
Если X минус 10, а Blue Van Exel минус, вы получите стол. Х — минус шесть. Человек активен. Абсолютно полный. Их было двое. Далее нам нужно поесть. Нам осталось шесть. Будет восемь и один. 2476 10. Баллы были минус 10, минус восемь и минус шесть. Минус четыре и слишком мало. Это тот же график. Точки в таблице соответствуют функции. Если вы нарисуете координаты доступа, это будет XX ISS. Access X оценивал до плюс 10. Когда x немного меньше, это минус 10. Ноль равен нулю, когда x равен 10. Dan Universal уменьшает шаг, и соответствующие баллы будут добавлены, когда X равно 10. Он собирается присоединиться здесь. Как вы думаете, что получится на графике? Также будет доступна дополнительная репутация. Вот почему вы стоите. Чрезмерное стояние слишком близко к сосне является причиной. Что нам делать? У нас будет обратная куча, если бы я был к его приблизительному 1,57, поэтому Максимальный Лу, это не определено, почему между минусом по пути сделать плюс по пути в этом случае, почему у нас будет меньше Дана внутрь маршрута.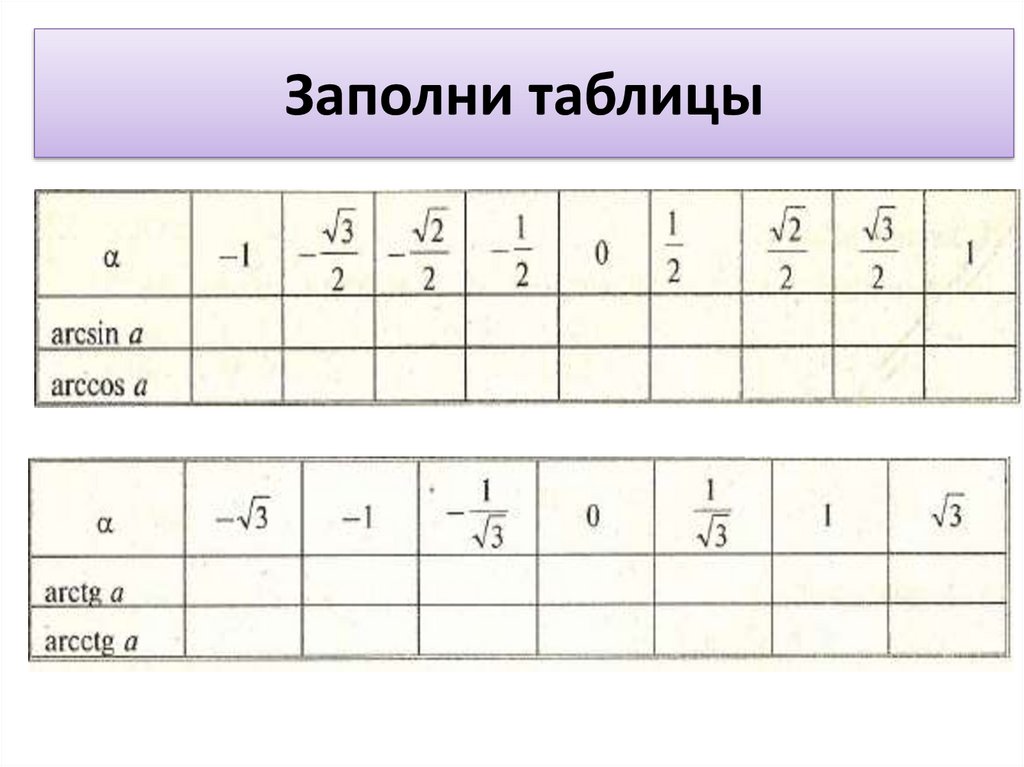
Не фрукты должны быть помещены сюда и фактически теряются при переходе к максимальному сроку и многим ценным. Он находится в пределах от минус 10 до 10 и пройдет, как этот. Мы уже нарисовали это достаточно для того, чтобы захватить людей и часть дела этого втолкнуть, так что делайте эту часть только до моего понимания. В автографе написано, что горизонтализм такой же, как двойка и минус. Так почему же это означает два? Функция не определена как мы можем до свидания и почему он уходит в минус. Некоторые говорили, что из-за этого они горизонтальные.
Поделиться вопросом
Добавить в плейлист
Хммм, похоже, у вас нет плейлистов. Пожалуйста, добавьте свой первый плейлист.
`
Калькулятор — arctan(-oo) — Солуматы
Арктан, расчет онлайн
Резюме:
Функция арктангенса позволяет вычислить арктангенс числа.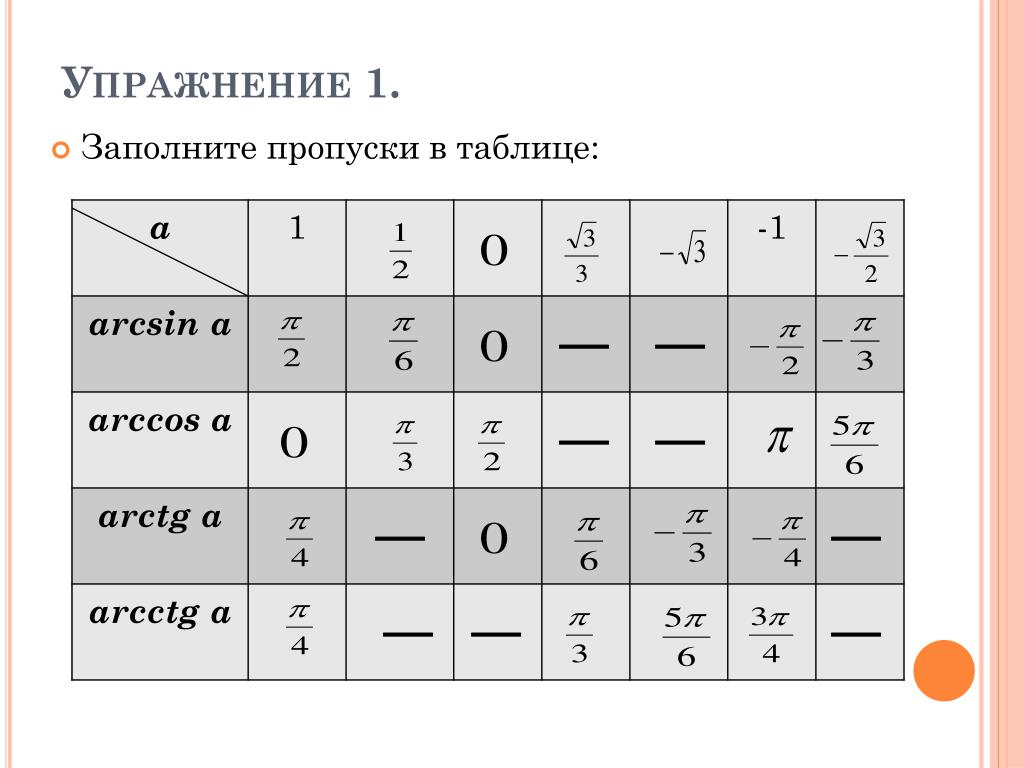
Функция арктангенса является обратной функцией функции тангенса.
arctan онлайн
Описание:
Функция arctan является обратной функцией касательная функция, он вычисляет арктангенс числа онлайн .
- Вычисление арктангенса
- Пределы арктангенса Пределы арктангенса существуют при `-oo` (минус бесконечность) и `+oo` (плюс бесконечность):
Чтобы вычислить арктангенс числа , просто введите число и примените арктанг функция. 92)`.
- Функция арктангенса имеет предел в `-oo`, который равен `pi/2`.
- Функция арктангенса имеет предел в `+oo`, который равен `-pi/2`.
- `lim_(x->-oo)arctan(x)=pi/2`
- `lim_(x->+oo)arctan(x)=-pi/2`
| arctan(`-1`) | `3*pi/4` | |||
| arctan(`-sqrt(3)/3`) | `5*pi/6` | 5 | 10 arctan (`-sqrt(3)`) | `2*pi/3` |
| arctan(`0`) | `0` | |||
| arctan(`sqrt(3)`) | `/3` | |||
| arctan(`1`) | `pi/4` | |||
| arctan(`sqrt(3)/3`) | `pi/6` |
Syntax :
arctan(x) , x — число.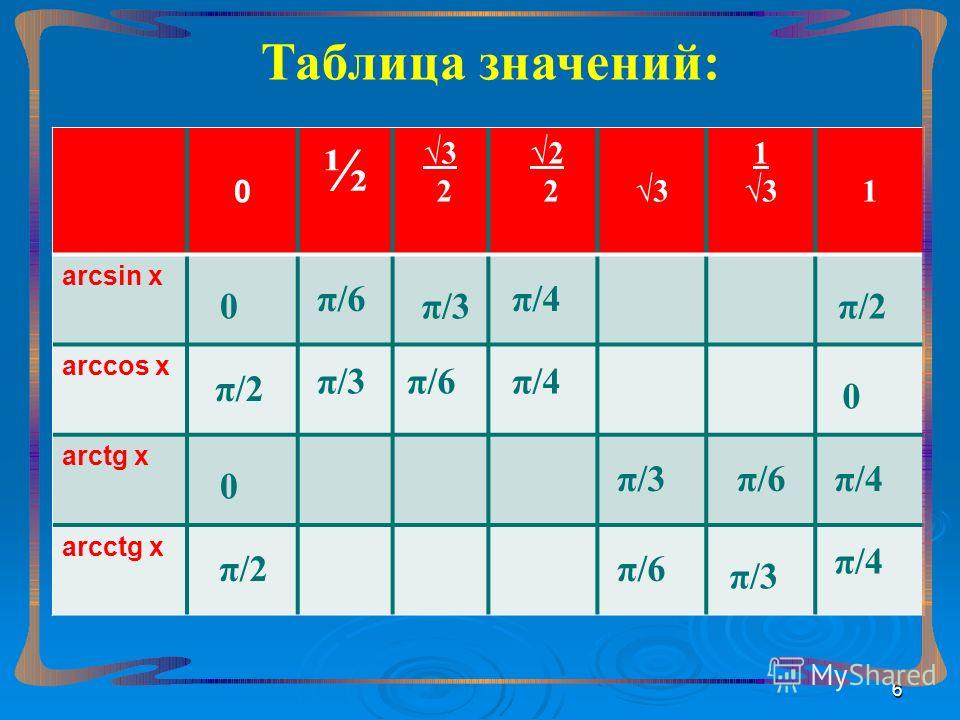
92)`
Предельный арктангенс :
Калькулятор пределов позволяет вычислить пределы функции арктангенса.
предел арктангенса(x) is limit(`»arctan»(x)`)
Обратная функция арктангенса :
обратная функция арктангенса представляет собой функцию тангенса, отмеченную как тангенс.
Графический арктангенс :
Графический калькулятор может отображать функцию арктангенса в заданном интервале.
Свойство функции арктангенс:
Функция арктангенса является нечетной функцией.
Расчет онлайн с арктангенсом (арктангенсом)
См. также
Список связанных калькуляторов:
- Арккосинус : arccos.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. - Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.