Арифметическая и геометрическая прогрессии — презентация онлайн
Изучена данная тема,
Пройдена теории схема,
Вы много новых формул узнали,
Задачи с прогрессией решали.
И вот в этот урок
Нас красивый лозунг
поведет:
“ПРОГРЕССИО — ВПЕРЕД”
3. Основная цель: Повторить и закрепить умения и вычислительные навыки использования основных формул прогрессий при решении задач.
Содержание— Прогрессии
— Математический диктант
— Карточки для индивидуального
пользования
— Самостоятельная работа
Прогрессии
АРИФМЕТИЧЕСКАЯ
ПРОГРЕССИЯ
ГЕОМЕТРИЧЕСКАЯ
ПРОГРЕССИЯ
5
Определения
Числовая
последовательность а1, а2,
а3, …,аn, … называется
арифметической
прогрессией, если для всех
натуральных n выполняется
равенство an+1 = an + d, где d
– некоторое число.
Числовая
последовательность
b1, b2, b3, …, bn, … называется
геометрической
прогрессией, если для всех
натуральных n
выполняется равенство
bn+1 = bnq, где bn≠0, q –
некоторое число, не
равное нулю.
прогрессии
6
Сравните графики
Разность двух рядом стоящих
членов остается одна и та же,
вследствие чего члены
прогрессии возрастают
(убывают) равномерно.
Разность двух соседних членов
увеличивается по мере удаления
их от начала ряда: вследствие
этого, члены такой прогрессии,
по мере их удаления от начала
ряда, возрастают всё быстрее и
быстрее, что наглядно
изображено на рисунке.
Свойство членов прогрессий
Каждый член
арифметической прогрессии,
начиная со второго, равен
среднему арифметическому
двух соседних с ним членов,
при n>1.
an 1 an 1
an
2
Если все члены прогрессии
положительны, то каждый
член геометрической
прогрессии, начиная со
второго, равен среднему
геометрическому двух
соседних с ним членов, при
n>1.
bn bn 1 b n 1
прогрессии
8
Формулы n–ого члена
прогрессий
АРИФМЕТИЧЕСКАЯ ГЕОМЕТРИЧЕСКАЯ
ПРОГРЕССИЯ
ПРОГРЕССИЯ
àn a1 (n 1)d bn b1 q
n 1
9
Сумма n первых членов
прогрессий
АРИФМЕТИЧЕСКАЯ
ПРОГРЕССИЯ
ГЕОМЕТРИЧЕСКАЯ
ПРОГРЕССИЯ
a1 a2
Sn
n
2
b1 (1 q )
Sn
,q 1
1 q
n
10
Математический диктант
арифметическая прогрессия d = 3
1) 2; 5; 8; 11;14; 17;…
геометрическая прогрессия q = 3
2) 3; 9; 27; 81; 243;…
последовательность чисел
3) 1; 6; 11; 20; 25;…
геометрическая прогрессия q = 2
4) –4; –8; –16; –32; …
последовательность чисел
5) 5; 25; 35; 45; 55;…
арифметическая прогрессия d = – 2
6) –2; –4; – 6; – 8; …
Истинно или ложно
каждое высказывание
1.
В арифметической прогрессии2,4; 2,6;… разность равна 2.
2. В геометрической прогрессии
0,3; 0,9;… третий член равен 2,7
3. 11-ый член арифметической прогрессии, у
которой a1 4,2; d 0,4 равен 0,2
4. Сумма 5 первых членов
геометрической прогрессии,
у которой
b1 1, q 2,
равна 11.
5. Последовательность чисел, кратных 5,
является геометрической прогрессией.
6. Последовательность степеней числа 3
является арифметической прогрессией.
Проверь себя!
1. В арифметической прогрессии
2,4; 2,6;… разность равна 2.
d = 2,6 – 2,4 = 0,2 высказывание ложно
2. В геометрической прогрессии
0,3; 0,9;… третий член равен 2,7
b3 0,3 3 2,7 высказывание истинно
2
3. 11-ый член арифметической прогрессии, у которой
равен 0,2
a1 4,2; d 0,4
a11 4,2 0,4 10 4,2 4 0,2
высказывание ложно
4. Сумма 5 первых членов геометрической прогрессии,
у которой b1 1, q 2,
равна 11.
1 2 1 33
S5
11
2 1
3
5
высказывание истинно
5.
Последовательность чисел, кратных 5, являетсягеометрической прогрессией.
высказывание ложно, т.к.
xn 5n
5; 10; 15;… — арифм. прогрессия
6. Последовательность степеней числа 3 является
арифметической прогрессией
высказывание ложно, т.к. xn 3
3; 9; 27;…- геометрическая прогрессия
n
Карточки для
индивидуального
пользования
1) Дано: (а n ) арифметическая прогрессия
а1 = 5 d = 3
Найти: а6 ; а10.
Решение: используя формулу
а n = а 1+( n -1) d
а6 = а1 +5 d = 5+ 5 . 3 = 20
а10 = а1 +9 d = 5+ 9 . 3 = 32
Ответ: 20; 32
Решение
2) Дано: (b n ) геометрическая
прогрессия
b1= 5 q = 3
Найти: b3 ; b5.
Решение: используя формулу b
n = b1 q n-1
b3 =b1q2 = 5 . 32 =5 . 9=45
b5 =b1q4 = 5 . 34 =5 . 81=405
Ответ:45; 405.
Решение
3) Дано: (а n ) арифметическая
прогрессия
а4 = 11 d = 2
Найти: а1 .
Решение: используя формулу
а n= а 1+ ( n – 1) d
а4 = а1 +3 d ; а1= а4 – 3 d =11 – 3 .
2=5
Ответ: 5.
Решение
4) Дано: (b n ) геометрическая
прогрессия
b4= 40 q = 2
Найти: b1.
Решение: используя формулу b n = b1 q
n-1
b4 =b1q3 ; b1 = b4 : q3 =40:23 =40 :8=5
Ответ: 5.
Решение
5) Дано: (а n ) арифметическая
прогрессия
а4=12,5; а6=17,5
Найти: а5
6) Дано: (b n ) геометрическая
прогрессия
b4=12,5; b6=17,5
Найти: b5
b5 b4 b6 6 24 144 12
Самостоятельная работа
24. Самостоятельная работа
1)Дано: (а n ), а1 = – 3, а2 = 4.Найти: а16 – ?
2)Дано: (b n ) , b 12 = – 32, b 13 = – 16. Найти: q – ?
3)Дано: (а n ), а21 = – 44, а22 = – 42.Найти: d — ?
4)Дано: (b n ) , bп > 0, b2 = 4, b4 = 9.Найти: b3 – ?
5)Дано: (а n ), а1 = 28, а21 = 4. Найти: d — ?
6) Дано: (b n ) , b5 = 8 q = 2. Найти: b1 – ?
7) Дано: (а n ), а7 = 16, а9 = 30.Найти: а8 –?
Ответы:
1) 102
2) 0,5
3) 2
4) 6
5) – 1,2
6) 0,5
7) 23
26. Ответы:
Урок сегодня завершён,Но каждый должен знать:
Познание, упорство, труд
К прогрессу в жизни
приведут.
Вся элементарная математика — Средняя математическая интернет-школа
Числовая последовательность. Арифметическая прогрессия.
Разность прогрессии. Геометрическая прогрессия. Знаменатель
прогрессии. Бесконечно убывающая геометрическая прогрессия.
Обращение периодической десятичной дроби в обыкновенную.
Последовательности. Рассмотрим ряд натуральных чисел:
1, 2, 3, … , n – 1, n , … .
Если заменить каждое число n в этом ряду некоторым числом u n , следуя некоторому закону, мы получим новый ряд чисел:
u
называемый числовой
последовательностью .
Число u n называется общим членом числовой последовательности.
П р и м е р ы числовых последовательностей:
2, 4, 6, 8, 10, … , 2 n , … ;
1, 4, 9, 16, 25, … , n ² , … ;
1, 1/2, 1/3, 1/4, 1/5, … , 1/ n , … .
Арифметическая прогрессия. Числовая
последовательность,
каждый член которой, начиная со
второго, равен предыдущему, сложенному с постоянным для этой последовательности
числом d , называется арифметической прогрессией . Число d называется разностью
прогрессии .
Любой член ариф
метической
прогрессии вычисляется по формуле:
Сумма n первых членов арифметической прогрессии вычисляется как:
П р и м е р . Найти сумму первых ста нечётных чисел.
Р е ш е н и е . Применим последнюю формулу. Здесь a 1 = 1, d = 2 . Тогда
Геометрическая прогрессия. Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на постоянное для этой последовательности число q , называется геометрической
прогрессией .
Число q называется знаменателем
прогрессии . Любой член
геометрической прогрессии вычисляется
по формуле:
b n = b 1 q n — 1 .
Сумма n первых членов геометрической прогрессии вычисляется как:
Бесконечно убывающая геометрическая прогрессия.
которому неограниченно приближается
сумма n первых членов рассматри
ваемой
прогрессии при неограниченном возрастании числа n .
Сумма
членов бесконечно убывающей геометрической прогрессии
П р и м е р . Найти сумму членов бесконечно убывающей геометрической прогрессии:
Р е ш е н и е . Применим последнюю формулу. Здесь b 1 = 1, q = 1/2. Тогда:
Обращение периодической
десятичной дроби в обыкновенную. Предположим, мы хотим обратить
периодическую десятичную дробь 0.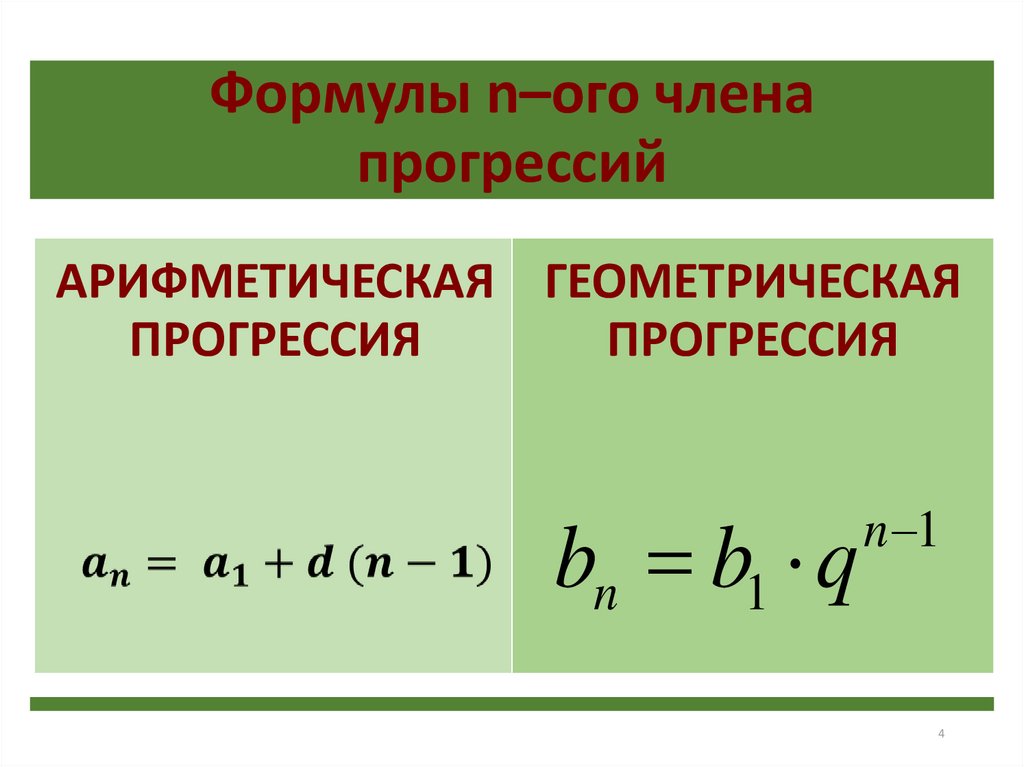
Это бесконечно убывающая геометрическая прогрессия, первый член которой равен 3/10, а разность q = 1/10. В соответствии с выше приведенной формулой эта сумма равна:
Таким образом , 0.(3) = 1/3.
Назад
Понимание арифметических и геометрических рядов
Все ресурсы по математике для старших классов
8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept
Справка по математике для старших классов » Предварительный расчет » Последовательности и серии » Понимание арифметических и геометрических рядов
Оценка:
Возможные ответы:
Ни один из других ответов не является правильным.
Правильный ответ:
Объяснение:
Эту сумму можно определить по формуле суммы бесконечного геометрического ряда с начальным членом и знаменателем:
Сообщить об ошибке
Четвертый член арифметической прогрессии равен -20, а восьмой член равен -10. Какой сотый член последовательности?
Возможные ответы:
110
105
210
220
55
Правильный ответ:
220
5 Объяснение:
Арифметическая последовательность — это последовательность, в которой есть общая разница между последовательными элементами. Например, последовательность {2, 5, 8, 11} является арифметической последовательностью, потому что каждый член можно найти, прибавив три к члену перед ним.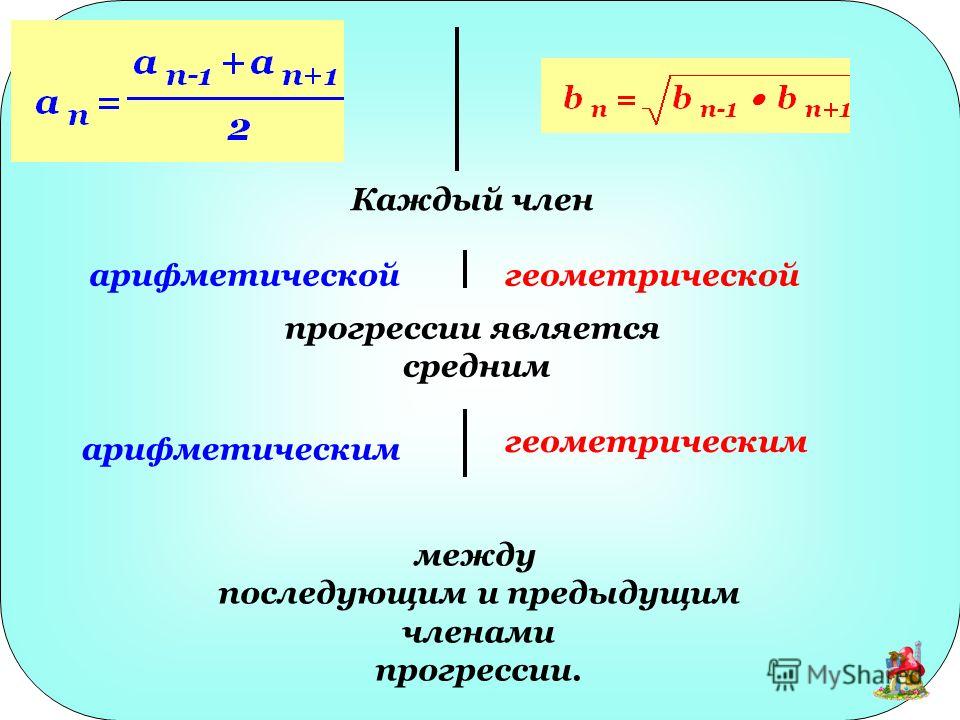
Обозначим n-й член последовательности. Тогда для арифметических последовательностей вообще можно использовать следующую формулу:
, где d — общая разница между двумя последовательными терминами.
Нам даны 4-й и 8-й члены последовательности, поэтому мы можем написать следующие уравнения:
.
Теперь у нас есть система двух уравнений с двумя неизвестными:Решим эту систему, вычитая уравнение из уравнения. Результат этого вычитания
.
Это означает, что d = 2,5.
Используя уравнение, мы можем найти первый член последовательности.
В конечном итоге нас просят найти сотый член последовательности.
Ответ составляет 220.
Отчет о ошибке
Найдите сумму, если возможно,:
Возможные ответы:
Правильный ответ:
Правильный ответ:
Ответ:
Объяснение:
Формула суммирования бесконечного геометрического ряда:
,
, где – первый член ряда, а – скорость изменения между последовательными членами.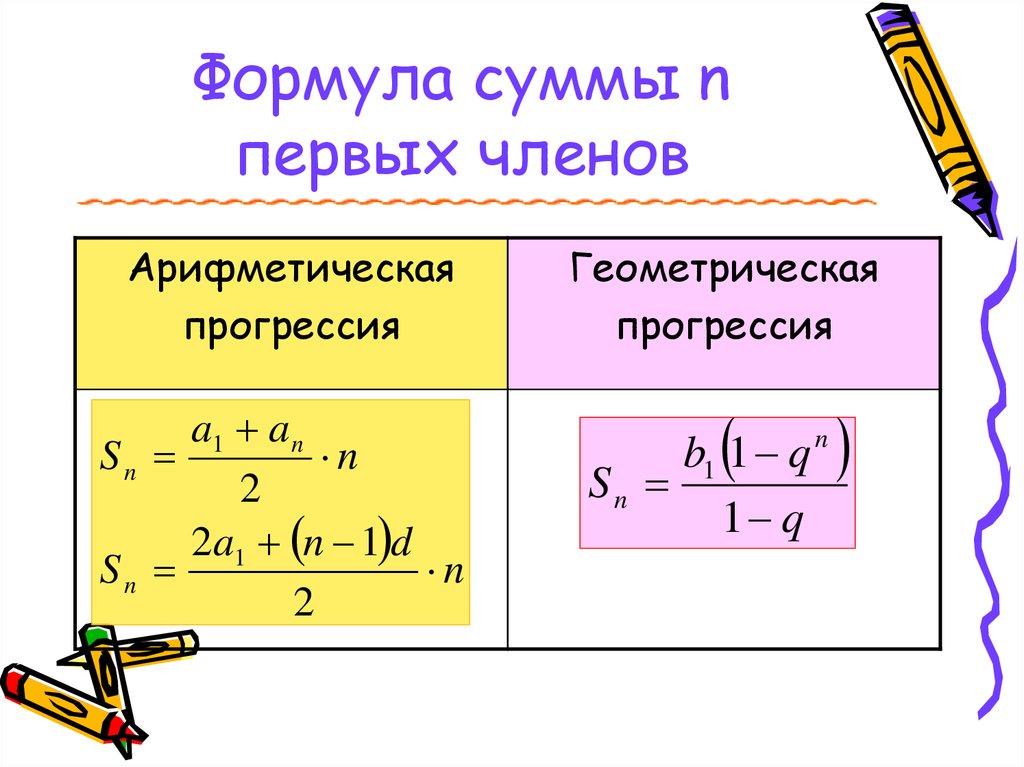
Ключевым моментом здесь является нахождение скорости или шаблона между терминами. Поскольку это геометрическая последовательность, скорость является константой, на которую умножается каждый новый член.
Подключение наших значений, мы получаем:
Отчет о ошибке
Найдите сумму, если возможно:
Возможные ответы:
Правильный ответ:
0. Правильный ответ:
0Объяснение:
Формула суммирования бесконечного геометрического ряда:
,
где – первый член ряда, а – скорость изменения между последовательными членами ряда
Так как члены меняют знак, мы знаем, что скорость должна быть отрицательной.
Подключение наших значений, мы получаем:
Отчет о ошибке
Найдите сумму, если возможно:
Возможные ответы:
94 9000Правильный ответ:
Нет решения
Пояснение:
Формула суммирования бесконечного геометрического ряда
,
где – первый член в ряду, а – скорость изменения между последовательными элементами в ряду.
Чтобы бесконечный геометрический ряд имел сумму, должно быть больше и меньше , т.е.
Поскольку решения нет.
Сообщить об ошибке
Уведомление об авторских правах
Все математические ресурсы средней школы
8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Учитесь по концепции
Арифметическая геометрическая последовательность
Последовательность означает порядок. Теперь дело в том, что такое последовательность и как она связана с предметом математики. Арифметическая последовательность — это числа, которые можно складывать или вычитать. Геометрическая прогрессия идет от одного члена к другому, умножается или делится. Результатом является общая ценность. См. рисунок ниже, в арифметической последовательности разность (d) всегда является стандартным значением 7. В геометрической последовательности общее значение всегда равно 2. Арифметическая последовательность представляет собой сложение (или вычитание) в установленном порядке.
Геометрическая последовательность — это умножение (или деление) в заданном порядке.
Изображение скоро будет загружено
Формула арифметической последовательности
Давайте разберемся с формулой арифметической последовательности. В арифметической последовательности один член всегда идет к следующему члену путем прибавления, например, 1, 2, 3, 4, 5….10 и так далее. Здесь в этой последовательности каждое число переходит ко второму числу путем прибавления (или вычитания 1). Давайте возьмем несколько примеров, чтобы лучше понять. 2, 5, 8, 11, 14… это арифметическая последовательность, так как каждый шаг добавляет 3. То же самое верно для обратного порядка (при вычитании). Например. 7, 3, -1, -5 … представляет собой арифметическую последовательность, так как на каждом шаге вычитается 4.
Важно отметить, что число, которое прибавляется или вычитается на каждом уровне арифметической последовательности, называется разностью (d).
Причина в том, что если вы сложите или вычтете (что также известно как поиск разницы), вы всегда получите одно и то же общее значение. См. рис. 2 ниже
Изображение будет загружено в ближайшее время
Формула геометрической последовательности
Геометрическая последовательность или геометрическая последовательность представляет собой геометрический порядок. Мы получаем результаты, умножая члены геометрической прогрессии. Проще говоря, геометрическая последовательность переходит от одного члена к другому, всегда умножая (или делея) на одно и то же общее значение или число. Например, 2, 4, 8, 16, 32… — это геометрический ряд. Причина в том, что каждый шаг умножается на два. Возьмем другой пример, 81, 27, 9., 3, 1 … это геометрическая последовательность, так как каждый шаг делится (или умножается) на число 3.
Важно отметить, что обычное число, которое умножается или делится на каждом шаге геометрической последовательности, называется отношением r .
Это связано с тем, что если разделить или найти соотношение последовательных членов, то получится обычное или стандартное соотношение. См. рис. 3 ниже.
Изображение будет добавлено в ближайшее время
Арифметическая геометрическая прогрессия
Арифметическая прогрессия представляет собой ряд или последовательность чисел, в которой каждый член получается из следующего путем сложения или вычитания фиксированного или обычного числа, называемого общей разностью d. Например, серия 9., 6, 3, 0, -3 и так далее — это арифметическая прогрессия со стандартной разностью -3. Прогрессия -3, 0, 3, 6, 9 является примером арифметической прогрессии (АП), в которой три являются общей разностью d.
Установленная форма АР: а, а + d, а + 2d, а + 3d и ….и так далее. N-й член будет
an = a + (n -1)d
Геометрическая прогрессия — это ряд, в котором каждый член получается умножением или делением следующего члена на фиксированное или обычное число.
Например, ряд 8, 4, -2, 1, -1/2… является геометрической прогрессией (ГП), для которой -1/2 является обыкновенным отношением.
Общепринятая форма GP: a, ar, ar2, ar3, ar4….и так далее. N-й член будет иметь вид an = ar (n-1)
Пример -1
Найдите общую разность и следующий член следующего ряда:
3, 11, 19, 27, 35 …
Имеем найти общую разность d. Вы можете подобрать любую пару. Начнем с вычитаний.
11 — 3 = 8
19 -11 = 8
27 -19 = 8
35 — 27 = 8
Везде разность равна 8, поэтому общая разность равна 8,
У нас есть 5 терминов. Нам нужно найти следующий или шестой член. Это можно узнать, добавив обыкновенную разность к пятому члену, 35 + 8 = 43.
шестой член = 43 и обычная разность =8
Пример -2
Найдите знаменатель и 7-й член следующей последовательности
2/9, 2/3, 2, 6, 18.