Арифметические задачи для дошкольников | Картотека по математике:
Арифметические задачи.
Любую задачу нужно внимательно прочитать (может быть и не один раз!) и после этого уяснить, что любая задача состоит из четырех частей:
1. Условие.
2. Вопрос.
3. Решение.
4. Ответ.
Образец:
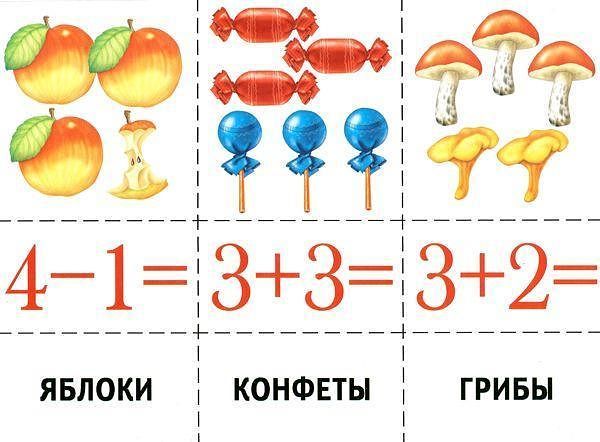
1. Задача на нахождение суммы:
а) Миша и Витя ходили на рыбалку. Миша поймал 4 рыбки, а Витя – 2. (Условие задачи)
б) Сколько всего рыб поймали мальчики вместе?
(Вопрос к задаче)
в) Решение: 4+2=6
(Решение задачи)
г) Ответ: вместе мальчики поймали 6 рыб.
(Ответ)
2. Задача на нахождение остатка:
В вазе было 5 яблок. Маша съела 2 яблока. (Условие)
Сколько яблок осталось в вазе? (Вопрос)
Решение: 5–2=3 (Решение)
Ответ: в вазе осталось 3 яблока. (Ответ)
Задачи на нахождение неизвестных компонентов
1. Задача на нахождение первого слагаемого:
Нина вылепила из пластилина несколько ягод и 1 мишку. Всего она вылепила 5 фигур. Сколько ягод вылепила Нина?
Всего она вылепила 5 фигур. Сколько ягод вылепила Нина?
Решение: 5–1=4
Ответ: Нина вылепила 4 ягоды.
2. Задача на нахождение второго слагаемого:
Витя вылепил 4 медведей и несколько зайчиков. Всего он вылепил 7 фигур. Сколько зайчиков вылепил Витя?
Решение: 7–4=3
Ответ: Витя вылепил 3 зайчиков
3. Задача на нахождение уменьшаемого:
Дети сделали на ёлку несколько гирлянд. Одну из них уже повесили на ёлку, у них осталось 3 гирлянды. Сколько всего гирлянд сделали дети?
Решение: 3+1=4
Ответ: Дети сделали 4 гирлянды.
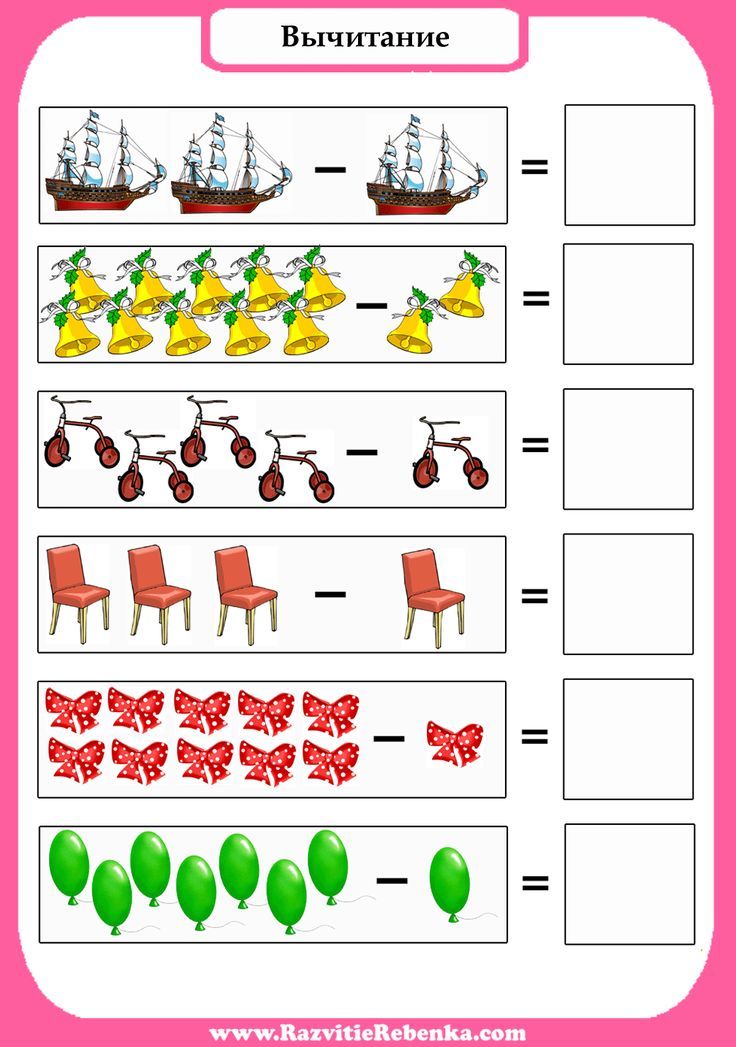
4. Задача на нахождение вычитаемого:
Дети сделали 7 гирлянд на ёлку. Когда они повесили на ёлку несколько гирлянд, у них осталась 1 гирлянда. Сколько гирлянд повесили на ёлку?
Решение: 7–1=6
Ответ: На ёлку повесили 6 гирлянд.
Задачи на нахождение больше (меньше) на несколько единиц
1. Задача на нахождение больше на несколько единиц:
На тарелке лежали сливы и персики. Слив было 6, а персиков – на 2 больше. Сколько персиков лежало на тарелке?
Сколько персиков лежало на тарелке?
Решение: 6+2=8
Ответ: на тарелке лежало 8 персиков.
2. Задача на нахождение меньше на несколько единиц:
Лена накрывала на стол. Голубых чашек было 3, а желтых на 1 меньше. Сколько желтых чашек стояло на столе?
Решение: 3–1=2
Ответ: на столе стояло 2 желтых чашки.
Задачи на разностороннее сравнение
1. На сколько больше:
К празднику Миша вырезал 4 флажка, а Маша – 6 флажков. На сколько больше флажков вырезала Маша?
Решение: 6–4=2
Ответ: Маша вырезала на 2 флажка больше, чем Миша.
2. На сколько меньше:
Бабушка и мама ходили в магазин. Бабушка купила 5 апельсинов, а мама – 4. На сколько меньше апельсин купила мама.
Решение: 5–4=1
Ответ: Мама купила на 1 апельсина меньше, чем бабушка.
Взаимообратные задачи
1. У Вовы было 6 красных марок 4 синих. Сколько всего марок было у Вовы?
Решение: 6+4=10
Ответ: У Вовы было 10 марок.
2. У Вовы было 10 марок. 6 марок красного цвета, остальные синего. Сколько синих марок было у Вовы?
6 марок красного цвета, остальные синего. Сколько синих марок было у Вовы?
Решение: 10–6=4
Ответ: У Вовы было 4 марки синего цвета.
3. У Вовы было 10 марок. Несколько марок были красного цвета и 4 марки синего цвета. Сколько марок красного цвета было у Вовы?
Решение: 10–4=6
Ответ: У Вовы было 6 марок красного цвета
Косвенные задачи
9 детей разместилось в двух лодках: несколько детей село в большую лодку, а 4 ребёнка село в маленькую. Сколько детей село в большую лодку?
Решение: 9–4=5
Ответ: В большую лодку село 5 детей.
§ 2. Понятие арифметической задачи. Её структура
Под арифметической задачей будем понимать один из видов заданий, в котором есть словие, требование, но нет указания на то арифметическое действие, которое нужно осуществить над данными в условии числами, чтобы выполнить требование.
Условие
арифметической задачи включает: множества
и их численности, либо величины и их
значения, либо «отвлеченные числа»;
связи между данными и искомым, либо
между данными, на основе которых
выбираются арифметические действия.
В требовании указывается на искомое. Требование может быть сформулировано в вопросительной или повествовательной форме.
Структура арифметической задачи может быть различной.
1. Стандартная структура задачи: сначала условие, потом требование.
Например: «С аэродрома сначала улетело 6 самолетов, а затем 4 самолета. Сколько всего самолетов улетело?»
2. Нестандартная структура задачи:
а) Сначала требование, потом условие (Сколько всего самолетов улетело с аэродрома, если сначала улетело 6 самолетов, а потом 4 самолета?).
б) Условие разъединено требованием (С аэродрома улетело сначала 6 самолетов. Сколько всего самолетов улетело, если потом улетело 4 самолета?).
В
традиционных школьных учебниках
большинство арифметических задач
(примерно 90%) имеют стандартную структуру
текста. Такими же, как правило, являются
задачи, составляемые учителями и
представленные в различных дидактических
материалах. Результатом такого подбора
задач в практике работы массовой школы
является следующий факт: в конце учебного
года при работе с простой арифметической
задачей со стандартной структурой
текста правильно выделили условие и
требование 96,6% первоклассников,
участвующих в эксперименте, с нестандартной
структурой текста — 61% (а), 58% (б).
Результатом такого подбора
задач в практике работы массовой школы
является следующий факт: в конце учебного
года при работе с простой арифметической
задачей со стандартной структурой
текста правильно выделили условие и
требование 96,6% первоклассников,
участвующих в эксперименте, с нестандартной
структурой текста — 61% (а), 58% (б).
Значительная часть детей, не выделивших правильно составные части задачи, не смогли решить арифметическую задачу.
В зависимости от числа арифметических действий, выполняемых при решении задачи, все арифметические задачи делятся на две группы: простые арифметические задачи и составные арифметические задачи.
К простым арифметическим задачам относятся задачи, для решения которых арифметическое действие нужно выполнить только один раз. Все остальные задачи относятся к составным арифметическим задачам.
Существуют
классификации простых арифметических
задач по различным основаниям. Например,
по виду арифметического действия,
которым решается задача. Выделяются в
соответствии с этим простые арифметические
задачи на сложение, вычитание, умножение,
деление. Однако в методическом отношении
наиболее удобной является классификация,
имеющая своим основанием математические
положения, лежащие в основе выбора
арифметического действия (их называют
теоретической основой выбора
арифметического действия). Классификация
предложена М.А. Бантовой [1].
Например,
по виду арифметического действия,
которым решается задача. Выделяются в
соответствии с этим простые арифметические
задачи на сложение, вычитание, умножение,
деление. Однако в методическом отношении
наиболее удобной является классификация,
имеющая своим основанием математические
положения, лежащие в основе выбора
арифметического действия (их называют
теоретической основой выбора
арифметического действия). Классификация
предложена М.А. Бантовой [1].
Она выделяет три группы задач.
I группа — задачи, теоретической основой выбора арифметического действия в которых является его конкретный смысл. К этой группе относятся следующие виды задач:
1) на нахождение суммы,
2) на нахождение остатка,
3) на нахождение произведения,
4) на деление по содержанию,
5) на деление на равные части.
До
того времени, пока задачи не решаются
с помощью составления уравнения, в эту
группу входят также задачи на нахождение
неизвестных слагаемого, уменьшаемого,
вычитаемого, делимого, делителя,
множителя, т.
II группа — задачи, теоретической основой выбора арифметического действия в которых являются связи между компонентами и результатами арифметических действий. Это задачи, являющиеся обратными по отношению к задачам 1-5 первой группы, когда они решаются с помощью составления уравнения.
III группа — задачи, теоретической основой выбора арифметического действия в которых является связь отношений «больше», «меньше» с соответствующими арифметическими действиями: задачи на увеличение (уменьшение) числа на несколько единиц (прямая и косвенная формы), на увеличение (уменьшение) числа в несколько раз (прямая и косвенная формы), на разностное и кратное сравнение (по два вида).
Все составные задачи, решаемые в начальных классах, делятся на две группы:
I группа — составные нетиповые задачи,
II группа — составные типовые задачи.
Ко
второй группе относятся задачи, связанные
с пропорциональными величинами: на
нахождение четвертого пропорционального,
на пропорциональное деление, на нахождение
неизвестного по двум разностям, задачи
на движение.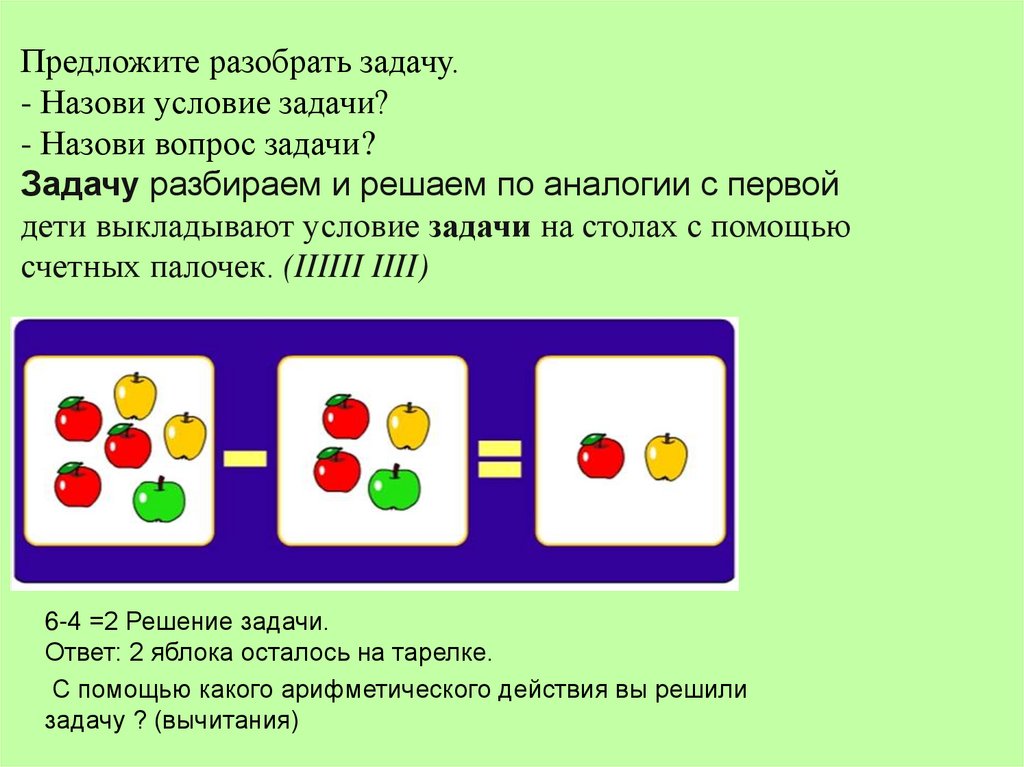
Все остальные составные арифметические задачи, решаемые в начальных классах, относятся к составным нетиповым задачам.
Сколько стоит 2 × 4? Понимание того, как мозг решает арифметические задачи. Границы для юных умовAbstract Сколько будет 2 × 4? Звучит как простой вопрос, но задумывались ли вы когда-нибудь о том, как решить эту проблему? В этой статье вы узнаете о двух разных стратегиях, которые мы используем для решения арифметических задач. Введение Поскольку математика является одним из самых важных навыков, которые необходимо освоить, понимание того, как решаются арифметические задачи, может оказать очень большое влияние. Вам нужна математика не только каждый день в школе, но и во взрослом возрасте. Если вы хотите стать программистом, инженером или ученым, вы будете ежедневно иметь дело с числами. Существуют ли разные способы решения арифметической задачи? Для изучения арифметики детей и взрослых обычно просят решать арифметические задачи как можно быстрее и точнее. Задачи обычно представляются на экране компьютера одна за другой (см. рис. 1). Как только участник дает ответ, появляется следующая задача. Чтобы изучить различные стратегии, которые мы используем в арифметике, ученые обычно используют сочетание различных арифметических операций разной сложности.
Используя эти методы, ученые обнаружили, что арифметические задачи можно разделить на две категории: маленькие и большие задачи. Небольшие задачи решаются очень быстро, и участники делают меньше ошибок при решении этих задач. Хорошим примером может быть «2 × 4». Большие проблемы обычно немного сложнее решить. Участникам требуется больше времени, чтобы решить эти проблемы, а также сделать больше ошибок. Хорошим примером может быть «12 × 3». Ученые иногда расходятся во мнениях относительно того, где провести черту между малыми и большими проблемами. Насколько сложно решить проблему, зависит от вашего возраста и способностей. Однако различия в скорости и ошибках между маленькими и большими задачами предполагают, что мы используем две основные стратегии для их решения [2]. Первая стратегия, вычисление ответа, часто используется с большими задачами. Это называется процедурной стратегией, потому что поиск ответа включает в себя несколько шагов или несколько процедур. Например, чтобы решить «12 × 3», вы можете разделить задачу на две более простые, например «10 × 3 = 30» и «2 × 3 = 6». После этого вы можете сложить результаты, чтобы получить ответ «36». Но добавление дополнительных шагов имеет свои недостатки. Это занимает больше времени, и каждый шаг также увеличивает вероятность совершения ошибок. Однако вы не всегда используете одну и ту же стратегию для решения одной и той же проблемы. После того, как вы решите это несколько раз, правильный ответ 1 день просто придет вам в голову. Это показывает, что способ решения этой проблемы изменился. Теперь вы используете вторую стратегию: знать ответ наизусть — это часто называют поиском фактов. Решая одну и ту же задачу несколько раз, вы сохраняете ее ответ в своей долговременной памяти. Переход от использования процедурных стратегий к использованию поиска фактов является важным шагом в развитии арифметических способностей [3].
Какие области мозга участвуют в решении арифметических задач? Попытка понять, как работает мозг, иногда может показаться решением сложной головоломки. Подобно тому, как головоломка состоит из разных частей, ваш мозг состоит из разных 9 частей.
Первая часть головоломки — внутритеменная борозда. Он расположен в теменной коре и отвечает за понимание значения чисел [4]. Первым шагом при решении арифметической задачи является понимание величины числа. Например, вы должны знать, что «4 собаки» — это больше, чем «2 собаки». Вам также необходимо понимать порядок чисел (например, «1» предшествует «2», «2» предшествует «3» и так далее). При расчете вы используете свое понимание величины и порядка, чтобы найти правильное решение. Следующие части головоломки включают в себя три области мозга в лобной коре. Вентролатеральная префронтальная кора работает с областями теменной коры, чтобы сгладить отвлекающие факторы, такие как мечты о следующей поездке на велосипеде с друзьями. Дорсолатеральная префронтальная кора необходима для манипулирования числами, например, для разделения большой задачи на более простые этапы. Установлено, что нижняя лобная извилина играет важную роль в игнорировании подобных, но неправильных ответов [5]. Последние части нашей головоломки — это гиппокамп и угловая извилина. Гиппокамп расположен глубоко внутри вашего мозга. Он играет важную роль в хранении арифметических фактов [6]. Гиппокамп — это кнопка «сохранения» вашего мозга. Когда дело доходит до математики, она работает с лобной корой, чтобы помочь вам сохранить ответы на арифметические задачи в виде арифметических фактов в вашей долговременной памяти. Затем угловая извилина участвует в поиске этих фактов при решении арифметических задач. Как меняется решение арифметических задач с возрастом? Вы когда-нибудь вместе с друзьями решали сложную головоломку? Если это так, вы, вероятно, работали вместе, чтобы решить эту проблему. Ваш мозг работает аналогичным образом. Различные области мозга работают вместе при решении проблемы. Последняя часть нашей головоломки — понимание того, как эти области мозга работают вместе, когда вы считаете. Как вы теперь знаете, способ решения арифметических задач меняется по мере того, как вы становитесь старше. Вместо того, чтобы в основном использовать процедурные стратегии для решения арифметических задач, вы начинаете чаще использовать поиск фактов. Но это не единственное, что меняется. Ученые обнаружили, что во время этого процесса меняется и способ совместной работы различных областей мозга. Например, пока вы молоды, лобная кора играет очень важную роль. Он управляет вашим рабочая память и внимание, потому что способ решения арифметических задач включает в себя несколько шагов (процедурные стратегии). Все области мозга работают вместе, общаясь друг с другом. Это общение происходит по широкой сети путей (называемых белым веществом), которые соединяют все области мозга. Эти сети похожи на то, как дороги соединяют разные города. Одна из этих дорог в головном мозге называется верхним продольным пучком. Эта дорога соединяет префронтальную кору с теменной корой (где находится IPS) [8]. Поскольку в процессе решения арифметических задач в определенные моменты вашей жизни задействованы разные области мозга, связи между этими областями также меняются. Ученые до сих пор пытаются полностью понять, как и почему эти связи меняются по мере взросления. Это означает, что хотя мы уже много знаем о том, как решать арифметические задачи, нам все еще нужно провести дополнительные исследования, чтобы решить загадку вычислительного мозга. РезюмеДаже если на первый взгляд это кажется простым процессом, решение арифметической задачи на самом деле включает в себя много шагов. Не только это, но и по мере того, как вы становитесь старше, вы используете разные стратегии для их решения. Почти каждая часть вашего мозга меняется. Сначала многие области мозга работают вместе, чтобы решить арифметическую задачу. Некоторые части позволяют вам сосредоточиться на задаче, другие отслеживают и запоминают результаты ваших вычислений. Гиппокамп сохраняет правильный результат в вашей долговременной памяти. Когда вы становитесь старше, вам нужно всего несколько специализированных областей мозга для решения одной и той же задачи. Теперь ваш мозг работает очень эффективно. В следующий раз, когда вы будете делать домашнюю работу по математике, найдите минутку и подумайте обо всех задействованных областях мозга! Глоссарий Дискалькулия развития : ↑ Трудность в изучении или понимании арифметики. Электроэнцефалография (ЭЭГ) : ↑ Нейробиологический инструмент для измерения электрических сигналов, производимых мозгом. Этот метод может сказать нам с высокой точностью, в какой момент времени области мозга выполняют определенную задачу. Функциональная магнитно-резонансная томография (фМРТ) : ↑ Инструмент для измерения разницы кислорода в мозге. Поскольку во время работы активным областям требуется больше кислорода, мы можем с высокой точностью сказать, какие части выполняют эту работу. Области мозга : ↑ Мозг можно разделить на четыре основные части: лобная кора, теменная кора, височная кора и затылочная кора. Каждая кора содержит области мозга с уникальными функциями. Рабочая память : ↑ Важнейшая функция вашего мозга. Конфликт интересовАвторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов. БлагодарностиМы хотели бы искренне поблагодарить тех, кто помогал в переводе статей из этого сборника, чтобы сделать их более доступными для детей за пределами англоязычных стран, а также Фонд Джейкобса за предоставление средств, необходимых для перевода статей. . В этой статье мы особенно хотели бы поблагодарить Ниенке ван Аттевельдт и Сабину Петерс за перевод на голландский язык. Каталожные номера[1] ↑ Bugden, S., and Ansari, D. 2014. Когда ваш мозг не может сделать 2 + 2: случай дискалькулии развития. Фронт. Молодые умы 2:8. doi: 10.3389/frym.2014.00008 [2] ↑ Зиглер, Р. [3] ↑ Де Смедт, Б. 2016. «Индивидуальные различия в арифметическом поиске фактов», в Mathematical Cognition and Learning , редакторы Д. Б. Берч, Д. К. Гири и К. М. Кёпке (Сан-Диего, Калифорния: Academic Press). п. 219–43. doi: 10.1016/B978-0-12-801871-2.00009-5 [4] ↑ Vogel, S.E., Goffin, C., and Ansari, D. 2015. Специализация развития левой теменной коры для семантического представления арабских цифр: исследование адаптации fMR. Дев. Познан. Нейроски . 12, 61–73. doi: 10.1016/j.dcn.2014.12.001 [5] ↑ Де Вишер, А., Фогель, С.Э., Райсхофер, Г., Хасслер, Э., Кошутниг, К., Де Смедт, Б., и др. 2018. Эффект интерференции и размера задачи при решении фактов умножения: индивидуальные различия в активации мозга и арифметической производительности. | |||||||||||||||||||||||||||||||||||



 Вы также познакомитесь с различными областями мозга, такими как внутритеменная борозда, которые работают вместе, когда вы используете эти разные стратегии. Какая стратегия и какие области мозга вы используете, меняется со временем по мере того, как вы лучше знакомитесь с арифметикой. Этот переход особенно заметен в том, как области мозга работают и взаимодействуют друг с другом — одни области становятся более активными, а другие — менее активными. Прочитав эту статью, вы узнаете больше о методах, которые мы используем для решения арифметических задач, и об областях мозга, необходимых для поиска ответов на ваше следующее домашнее задание по математике.
Вы также познакомитесь с различными областями мозга, такими как внутритеменная борозда, которые работают вместе, когда вы используете эти разные стратегии. Какая стратегия и какие области мозга вы используете, меняется со временем по мере того, как вы лучше знакомитесь с арифметикой. Этот переход особенно заметен в том, как области мозга работают и взаимодействуют друг с другом — одни области становятся более активными, а другие — менее активными. Прочитав эту статью, вы узнаете больше о методах, которые мы используем для решения арифметических задач, и об областях мозга, необходимых для поиска ответов на ваше следующее домашнее задание по математике. Поскольку математика важна почти на каждой работе, людям, которые плохо разбираются в математике, иногда трудно найти работу. Некоторые из них могут даже страдать от чего-то под названием 9.0185 дискалькулия развития . Поэтому понимание того, что происходит в мозгу, когда вы считаете, может быть очень полезным для детей, у которых проблемы с математикой. Понимание причин этих трудностей позволяет учителям строить свои уроки таким образом, чтобы детям было легче учиться. И, конечно же, просто любопытство о том, как все устроено, всегда является достаточной причиной для проведения эксперимента!
Поскольку математика важна почти на каждой работе, людям, которые плохо разбираются в математике, иногда трудно найти работу. Некоторые из них могут даже страдать от чего-то под названием 9.0185 дискалькулия развития . Поэтому понимание того, что происходит в мозгу, когда вы считаете, может быть очень полезным для детей, у которых проблемы с математикой. Понимание причин этих трудностей позволяет учителям строить свои уроки таким образом, чтобы детям было легче учиться. И, конечно же, просто любопытство о том, как все устроено, всегда является достаточной причиной для проведения эксперимента!

 Вместо вычисления ответа теперь вы можете его запомнить. Кроме того, становясь лучше в решении более простых задач, вы также становитесь лучше в решении более сложных задач. Чтобы лучше понять эти изменения, нам нужно заглянуть внутрь нашего мозга, пока он решает арифметические задачи. Для этого ученые используют различные инструменты, такие как электроэнцефалография (ЭЭГ) и функциональная магнитно-резонансная томография (фМРТ, см. рис. 2).
Вместо вычисления ответа теперь вы можете его запомнить. Кроме того, становясь лучше в решении более простых задач, вы также становитесь лучше в решении более сложных задач. Чтобы лучше понять эти изменения, нам нужно заглянуть внутрь нашего мозга, пока он решает арифметические задачи. Для этого ученые используют различные инструменты, такие как электроэнцефалография (ЭЭГ) и функциональная магнитно-резонансная томография (фМРТ, см. рис. 2). 0185 областей мозга (см. рисунок 3). Понимание функции каждой области мозга даст вам более четкое представление о том, как она вписывается в головоломку.
0185 областей мозга (см. рисунок 3). Понимание функции каждой области мозга даст вам более четкое представление о том, как она вписывается в головоломку.
 Когда вы становитесь старше и начинаете использовать поиск фактов, роль вашей лобной коры меняется. Когда вы смотрите на лобную кору с помощью фМРТ или ЭЭГ, вы можете видеть, что она становится менее активной по мере того, как вы становитесь старше. Он по-прежнему участвует в процессе поиска правильного ответа, но ему уже не приходится работать так усердно, как раньше. Возможно, вы сталкивались с чем-то подобным, когда сотрудничали со своими друзьями. Поначалу кому-то из вас, возможно, приходилось следить за прогрессом каждого и давать инструкции, что делать дальше (аналогично лобной коре). После того, как вы успешно решили несколько головоломок вместе, вы сможете работать вместе, не нуждаясь в том, чтобы кто-то всегда проверял прогресс. Меняется и роль гиппокампа. При поиске фактов он более активен у детей раннего возраста, чем у взрослых [7]. Это потому, что когда вы молоды, гиппокамп все еще усердно работает, чтобы сохранить ответы на арифметические задачи в вашей долговременной памяти.
Когда вы становитесь старше и начинаете использовать поиск фактов, роль вашей лобной коры меняется. Когда вы смотрите на лобную кору с помощью фМРТ или ЭЭГ, вы можете видеть, что она становится менее активной по мере того, как вы становитесь старше. Он по-прежнему участвует в процессе поиска правильного ответа, но ему уже не приходится работать так усердно, как раньше. Возможно, вы сталкивались с чем-то подобным, когда сотрудничали со своими друзьями. Поначалу кому-то из вас, возможно, приходилось следить за прогрессом каждого и давать инструкции, что делать дальше (аналогично лобной коре). После того, как вы успешно решили несколько головоломок вместе, вы сможете работать вместе, не нуждаясь в том, чтобы кто-то всегда проверял прогресс. Меняется и роль гиппокампа. При поиске фактов он более активен у детей раннего возраста, чем у взрослых [7]. Это потому, что когда вы молоды, гиппокамп все еще усердно работает, чтобы сохранить ответы на арифметические задачи в вашей долговременной памяти. По мере того, как вы становитесь старше, вашему гиппокампу приходится работать все меньше и меньше, потому что вы сталкиваетесь с меньшим количеством новых ответов, которые нужно сохранить.
По мере того, как вы становитесь старше, вашему гиппокампу приходится работать все меньше и меньше, потому что вы сталкиваетесь с меньшим количеством новых ответов, которые нужно сохранить.
 Хороший обзор можно найти в статье Young Minds; Когда ваш мозг не может сделать 2 + 2: случай дискалькулии развития [1].
Хороший обзор можно найти в статье Young Minds; Когда ваш мозг не может сделать 2 + 2: случай дискалькулии развития [1].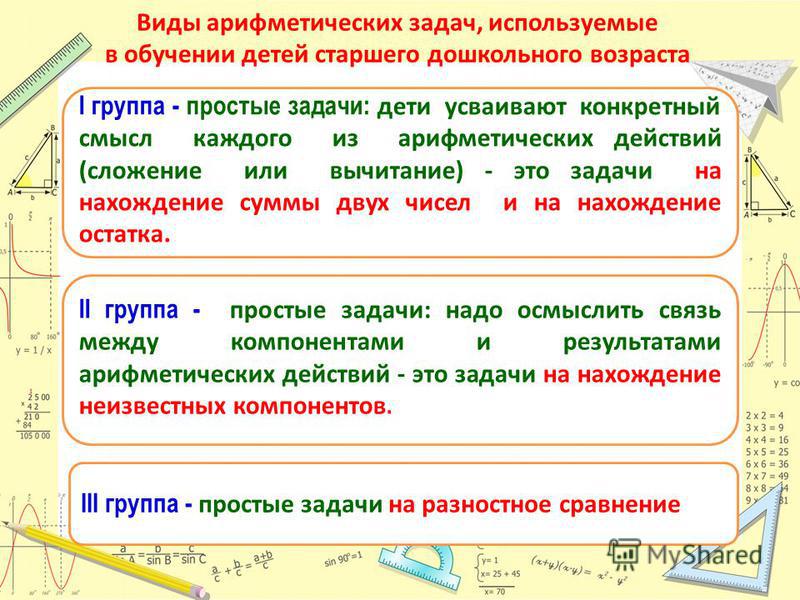 Подобно рабочей памяти компьютера, она хранит информацию в вашем уме, чтобы работать с ней, когда она вам нужна.
Подобно рабочей памяти компьютера, она хранит информацию в вашем уме, чтобы работать с ней, когда она вам нужна. С. 1996. Развивающиеся умы: процесс изменения детского мышления . Нью-Йорк, штат Нью-Йорк: Издательство Оксфордского университета. doi: 10.5860/выбор.34-5984
С. 1996. Развивающиеся умы: процесс изменения детского мышления . Нью-Йорк, штат Нью-Йорк: Издательство Оксфордского университета. doi: 10.5860/выбор.34-5984