Арксинус минус 1 2: Чему равен arccos(-1/2) ? — ответ на Uchi.ru

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )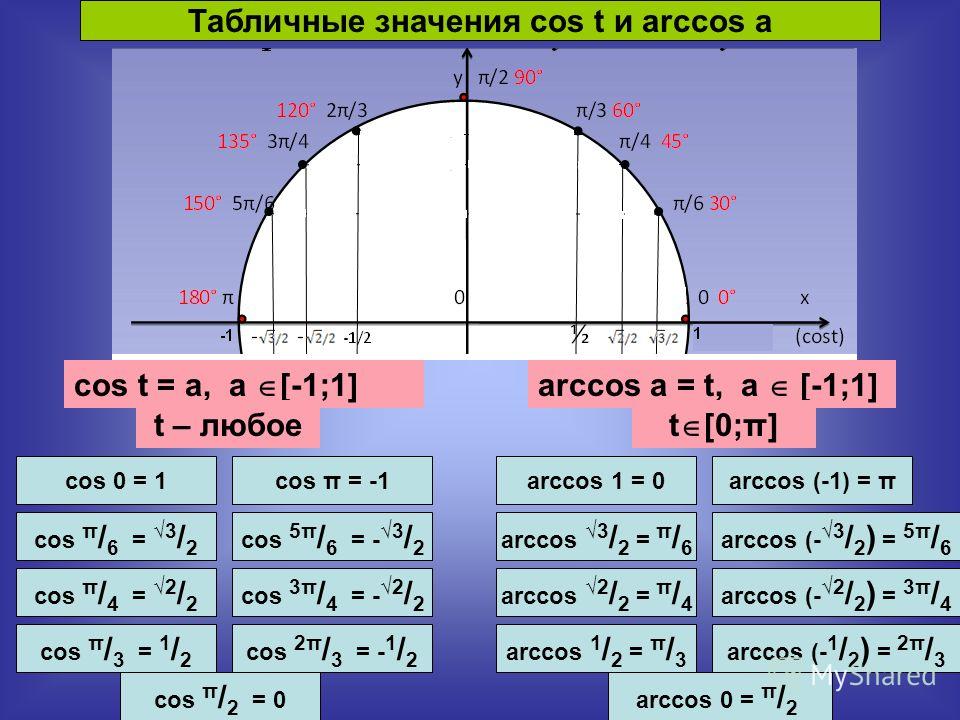
87Найти точное значение
sin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Формулы с арксинусом, арккосинусом, арктангенсом и арккотангенсом

Сферы применения правил обратных тригонометрических функций

Определение

Тригонометрия — раздел математики, объясняющий зависимость между сторонами и углами треугольника, правила используют для расчета углов.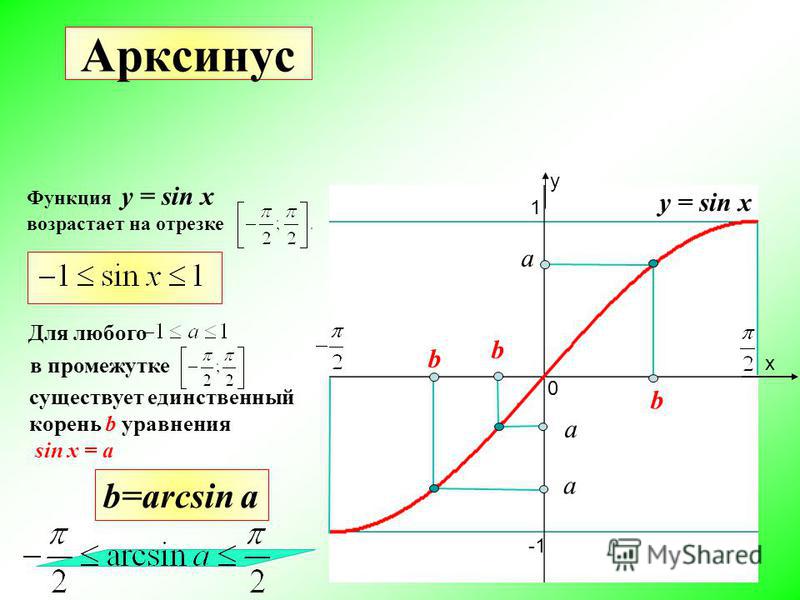

Изучая постулаты тригонометрических функций, ученики и студенты часто задаются вопросом, где эти знания могут пригодиться. Сфер применения достаточно много. Астрономы используют понятия для расчёта положения небесных объектов, тригонометрия помогает выполнять чертежи и создавать архитектурные шедевры, выстраивать модель биологических ритмов. В морской и воздушной навигации, акустике и оптике, в анализе финансового рынка, статистике, медицине, химии, во многих областях используются тригонометрические вычисления. Поэтому так важно научиться применять и выводить формулы самостоятельно.

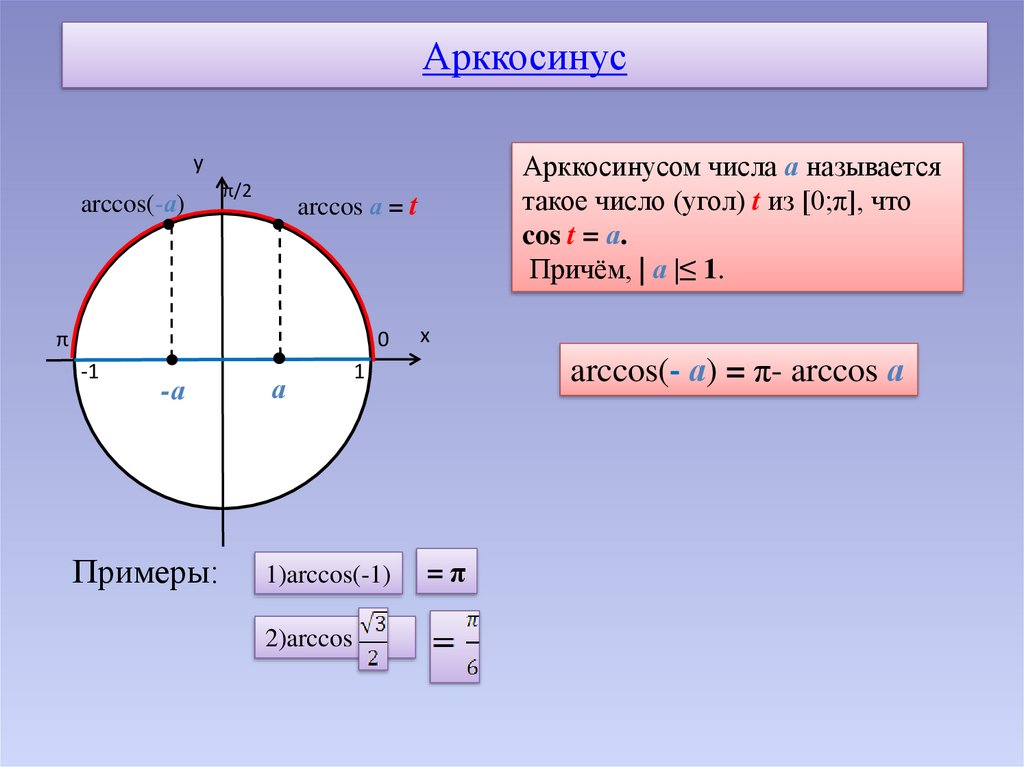
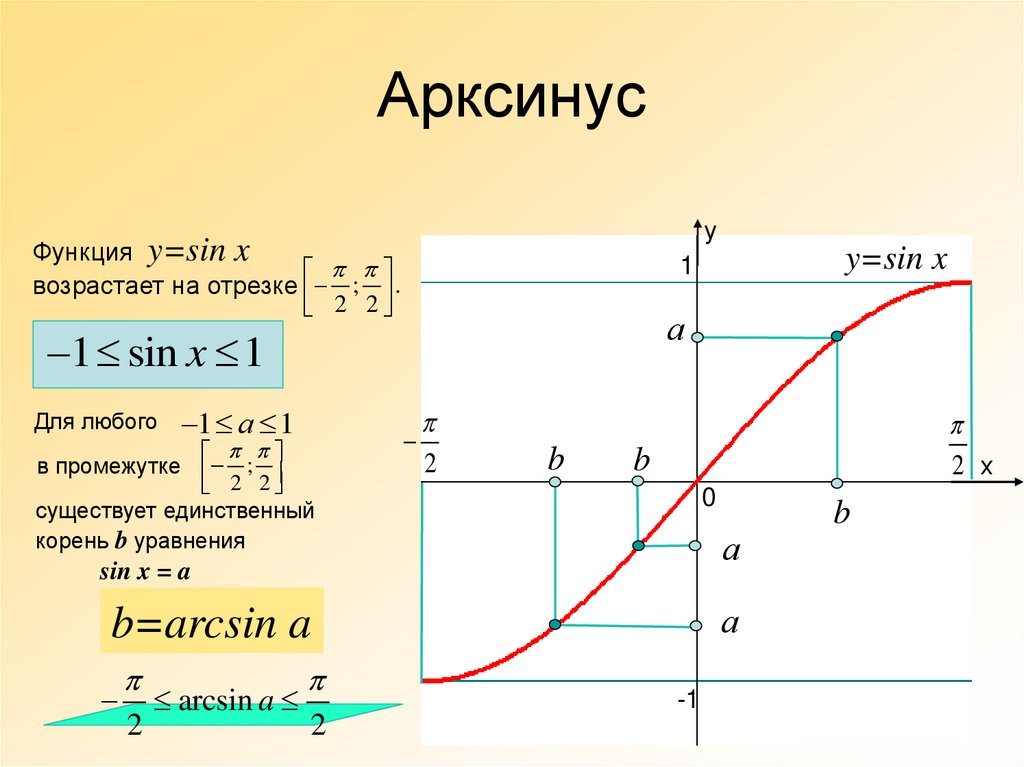
Обратные функции тригонометрии

Обратными называются функции, которые ещё называют арксинус, арккосинус, арктангенс, арккотангенс.

Название данный вид тригонометрической зависимости, получил от соответствующей прямой функции с приставкой арк — дуга. Взаимосвязь просматривается между длиной дуги единичной окружности и соответствующим определённым отрезком.

Правила обратной функции справедливы в пределах интервалов, например,

формула арксинуса возможна при:

\[\arcsin (\sin \mathrm{x})=\mathrm{x} \text { при }-\frac{\pi}{2} \leq \mathrm{x} \leq \frac{\pi}{2}\]

\[\arccos (\cos \mathrm{x})=\mathrm{x} \text { при } 0 \leq \mathrm{x} \leq \pi\]

и так далее.

Формулы с обратными функциями тригонометрии

Уже были рассмотрены обратные тригонометрические функции. Они, как и другие функции имеют между собой связи и зависимости, которые можно выразить в виде формул и использовать для решения задач.

В данной работе мы рассмотрим основные формулы, в которых применяются функции тригонометрии. Разберём их виды, деление на группы, доказательства и способы решения задач с их помощью.

Группировка основных понятий

Сначала проведём группировку формул, для того чтобы сделать более понятной логику объяснений. И объединим все правила и доказательства в одну статью.

Синус от арксинуса для \[\alpha \in(-1 ; 1) \sin (\arcsin \alpha)=\alpha, \cos (\arccos \alpha)=\alpha\]

Тангенса от арктангенса для \[\alpha \in(-\infty, \infty) \operatorname{tg}(\operatorname{arctg} \alpha)=\alpha, \operatorname{ctg}(\operatorname{arctg} \alpha)=\alpha\].

Указанное в данных выражениях легко выводится из самих определений обратных функций тригонометрии. При необходимости найти arcsin tg, можно использовать приведённые формулы.

Тангенс, арктангенс, котангенс, арккотангенс, синус, арксинус, косинус, арккосинус и формулы

\[\text{Для }-\frac{\pi}{2} \leq \alpha \leq \frac{\pi}{2} \arcsin (\sin \alpha)=\alpha\],

\[\text{Для } \leq \alpha \leq \pi \arccos (\cos \alpha)=\alpha\],

\[\text{Для }-\frac{\pi}{2}<\alpha<\frac{\pi}{2} \operatorname{arctg}(\operatorname{tg} \alpha)=\alpha\],

\[\text{Для } 0<\alpha<\pi \operatorname{arcctg}(\operatorname{ctg} \alpha)=\alpha\].

В данном примере собраны тригонометрические выражения, достаточно очевидные, которые можно вывести из определений функций тригонометрии. Необходимо обратить внимание, на то, что высказывания будут верны, если «а» (угол, или числовое значение) будет входить в определённый предел. Если условие не выполняется, расчёт будет не верен и формулу использовать нельзя.

Соотношение между собой обратных тригонометрических функций противоположных чисел

Рассмотрим важное определение:

Обратные функции тригонометрии можно выразить через аркфункции противоположного положительного числа.

\[\text{Для }\alpha \in \operatorname{open}-1,1] \text { arccis }(-\alpha)= -\operatorname{arc} \sin \alpha, \quad \operatorname{arc} \cos (-\alpha)=\pi -a r c \cos \alpha\]

\[\text { Для } \alpha \in(-\infty, \infty) \operatorname{arctg}(-\alpha)= -\operatorname{arctg} \alpha, \operatorname{arcctg}(-\alpha)=\pi-\operatorname{arcctg} \alpha\]

Это значит, если расчёты имеют функции отрицательного числа, от них можно избавиться. Для этого необходимо преобразовать их в аркфункции положительных чисел. Такие вычисления проводить проще.

Формулы суммы: arcsin + arccos, arctg +arcctg

Правила суммы выглядят так:

Для \[\alpha \in[-1,1] \arcsin \alpha+\arccos \alpha=\frac{\pi}{2}\],

Для \[\alpha \in[-\infty, \infty] \operatorname{arctg} \alpha+\operatorname{arctg} \alpha=\frac{\pi}{2}\].

Отсюда видно, что arcsin определённого числа можно выразить через его arccos , и наоборот. Тоже правило касается и arctg и arcctg, которые выражаются аналогично.

Формулы связи между обратными и прямыми тригонометрическими функциями

Чтобы иметь возможность решить множество задач, требуется знание связей между прямыми тригонометрическими функциями, и их аркфункциями. {2}}}{\alpha}\] при условии \[\alpha \in(-1,0) \cup(0,1)\].

  • Исходя из \[\operatorname{tg} \alpha=\frac{1}{\operatorname{ctg} \alpha}, \alpha \in\left(0, \frac{\pi}{2}\right) \cup\left(\frac{\pi}{2}, \pi\right)\] получаем \[\operatorname{tg}(\operatorname{arcctg} \alpha)=\frac{1}{\operatorname{ctg}(\operatorname{arcctg} \alpha)}=\frac{1}{\alpha}\] при условии, что \[\alpha \neq 0\].

    • Далее нам понадобятся понятия котангенсов арксинуса, арккосинуса, арктангенса. Напомним такое тригонометрическое равенство:

    \[\operatorname{ctg} \alpha=\frac{1}{\operatorname{tg} \alpha}\]

    Применяя данное выражение можно вывести необходимые формулы, вставляя выражения тангенса обратных функций тригонометрии. Практически необходимо поменять местами числитель и знаменатель.

    Выражение арксинуса с помощью арккосинуса, арктангенса и арккотангенса

    Прямые и обратные функции в тригонометрии связаны между собой. Полученные в результате выведения формулы помогут найти связь и между обратными функциями тригонометрии, выразив одни аркфункции через другие. {2} \frac{\alpha}{2}=\sqrt{\frac{1-\cos \alpha}{2}}\]

    Если представленный угол имеет значение больше нуля, но меньше Пи, то получаем:

    \[\sin \frac{\arccos \alpha}{2}=\sqrt{\frac{1-\cos (\arccos \alpha)}{2}}\]

    \[\Leftrightarrow \sin \frac{\arccos \alpha}{2}=\frac{\sqrt{1-\alpha}}{2}\]

    Здесь мы выводим следующую готовую формулировку, арксинус которой выведен через арккосинус:

    \[\frac{\arccos \alpha}{2}=\arcsin \sqrt{\frac{1-\alpha}{2}}\]

    В тексте рассмотрены лишь некоторые, самые популярные виды связей между прямыми и обратными функциями тригонометрии. Главное не выучить наизусть данные постулаты, а научиться их применять и выводить, исходя из уже известных определений.

    Удобно использовать инженерный вид калькулятора, на котором есть, необходимые для вычислений тригонометрические формулы и функции.

    Мэтуэй | Популярные задачи

    92
    1 Найти точное значение грех(30)
    2 Найти точное значение грех(45)
    3 Найти точное значение грех(30 градусов)
    4 Найти точное значение грех(60 градусов)
    5 Найти точное значение загар (30 градусов)
    6 Найти точное значение угловой синус(-1)
    7 Найти точное значение грех(пи/6)
    8 Найти точное значение cos(pi/4)
    9 Найти точное значение грех(45 градусов)
    10 Найти точное значение грех(пи/3)
    11 Найти точное значение арктан(-1)
    12 Найти точное значение cos(45 градусов)
    13 Найти точное значение cos(30 градусов)
    14 Найти точное значение желтовато-коричневый(60)
    15 Найти точное значение csc(45 градусов)
    16 Найти точное значение загар (60 градусов)
    17 Найти точное значение сек(30 градусов)
    18 Найти точное значение cos(60 градусов)
    19 Найти точное значение cos(150)
    20 Найти точное значение грех(60)
    21 Найти точное значение cos(pi/2)
    22 Найти точное значение загар (45 градусов)
    23 Найти точное значение arctan(- квадратный корень из 3)
    24 Найти точное значение csc(60 градусов)
    25 Найти точное значение сек(45 градусов)
    26 Найти точное значение csc(30 градусов)
    27 Найти точное значение грех(0)
    28 Найти точное значение грех(120)
    29 Найти точное значение соз(90)
    30 Преобразовать из радианов в градусы пи/3
    31 Найти точное значение желтовато-коричневый(30)
    32
    35 Преобразовать из радианов в градусы пи/6
    36 Найти точное значение детская кроватка(30 градусов)
    37 Найти точное значение арккос(-1)
    38 Найти точное значение арктан(0)
    39 Найти точное значение детская кроватка(60 градусов)
    40 Преобразование градусов в радианы 30
    41 Преобразовать из радианов в градусы (2 шт. )/3
    42 Найти точное значение sin((5pi)/3)
    43 Найти точное значение sin((3pi)/4)
    44 Найти точное значение тан(пи/2)
    45 Найти точное значение грех(300)
    46 Найти точное значение соз(30)
    47 Найти точное значение соз(60)
    48 Найти точное значение соз(0)
    49 Найти точное значение соз(135)
    50 Найти точное значение cos((5pi)/3)
    51 Найти точное значение cos(210)
    52 Найти точное значение сек(60 градусов)
    53 Найти точное значение грех(300 градусов)
    54 Преобразование градусов в радианы 135
    55 Преобразование градусов в радианы 150
    56 Преобразовать из радианов в градусы (5 дюймов)/6
    57 Преобразовать из радианов в градусы (5 дюймов)/3
    58 Преобразование градусов в радианы 89 градусов
    59 Преобразование градусов в радианы 60
    60 Найти точное значение грех(135 градусов)
    61 Найти точное значение грех(150)
    62 Найти точное значение грех(240 градусов)
    63 Найти точное значение детская кроватка(45 градусов)
    64 Преобразовать из радианов в градусы (5 дюймов)/4
    65 Найти точное значение грех(225)
    66 Найти точное значение грех(240)
    67 Найти точное значение cos(150 градусов)
    68 Найти точное значение желтовато-коричневый(45)
    69 Оценить грех(30 градусов)
    70 Найти точное значение сек(0)
    71 Найти точное значение cos((5pi)/6)
    72 Найти точное значение КСК(30)
    73 Найти точное значение arcsin(( квадратный корень из 2)/2)
    74 Найти точное значение загар((5pi)/3)
    75 Найти точное значение желтовато-коричневый(0)
    76 Оценить грех(60 градусов)
    77 Найти точное значение arctan(-( квадратный корень из 3)/3)
    78 Преобразовать из радианов в градусы (3 пи)/4 
    79 Найти точное значение sin((7pi)/4)
    80 Найти точное значение угловой синус(-1/2)
    81 Найти точное значение sin((4pi)/3)
    82 Найти точное значение КСК(45)
    83 Упростить арктан(квадратный корень из 3)
    84 Найти точное значение грех(135)
    85 Найти точное значение грех(105)
    86 Найти точное значение грех(150 градусов)
    87 Найти точное значение sin((2pi)/3)
    88 Найти точное значение загар((2pi)/3)
    89 Преобразовать из радианов в градусы пи/4
    90 Найти точное значение грех(пи/2)
    91 Найти точное значение сек(45)
    92 Найти точное значение cos((5pi)/4)
    93 Найти точное значение cos((7pi)/6)
    94 Найти точное значение угловой синус(0)
    95 Найти точное значение грех(120 градусов)
    96 Найти точное значение желтовато-коричневый ((7pi)/6)
    97 Найти точное значение соз(270)
    98 Найти точное значение sin((7pi)/6)
    99 Найти точное значение arcsin(-( квадратный корень из 2)/2)
    100 Преобразование градусов в радианы 88 градусов

    Обратные триггерные уравнения.

    Наверное, это самое сложное и… | Соломон Се | Вся математика перед колледжем

    Вероятно, это самая сложная и сложная тема во всей математике средней школы.

    Пререквизиты:

    • Блок Круг
    • Угол контрольного угла и угол в стандартной позиции
    • Обратные функции
    • Radian & Degraphing
    • .

      На самом деле он просит вас использовать обратную триггерную функцию навыков.

      Самая сложная для понимания часть — это множество решений. И не все действительны.

      напр. sin⁻¹(1/2) означает, что мы знаем, что значение синуса равно 1/2 , и мы хотели бы получить меру угла дуги . Но есть несколько дуговых углов, могут иметь одно и то же значение синуса:

      • Против часовой стрелки: 30°, 150°
      • По часовой стрелке: -330°, -210°.

      Но чтобы сделать функцию действительной, мы должны сделать ее равной 1-ВХОД-1-ВЫХОД .
      Таким образом, мы должны отфильтровать их и оставить только одно решение, ограничив меру угла .

      Мера угла в синусоидальной функции ограничена ДОМЕНОМ , но в обратной функции она стала ДИАПАЗОНОМ .

      Путем фильтрации с помощью ДИАПАЗОНА мы должны получить ответ ТОЛЬКО ОДИН И ДОЛЖЕН ТОЛЬКО ОДИН .

      Таким образом, после фильтрации всех других решений у нас есть только ОДНО решение, мы называем его:
      Принципиальное значение обратной триггерной функции,
      которое отображается в любом калькуляторе при вводе.

      • Сначала использовал КАЛЬКУЛЯТОР , чтобы получить основное значение в качестве нашего базового решения .
      • Найдите зеркальное решение каждой тригонометрической функции с помощью Тождеств тригонометрической симметрии :
      • sin(θ) = sin(π - θ) , если θ ПОЛОЖИТЕЛЬНОЕ.
      • sin(θ) = sin(-π - θ) , если θ ОТРИЦАТЕЛЬНО.
      • cos(θ) = cos(-θ)
      • tan(θ) = tan(-π + θ) , если θ ПОЛОЖИТЕЛЬНОЕ.
      • tan(θ) = tan(π + θ) , если θ ОТРИЦАТЕЛЬНО.
      • Добавьте к решению периодичность для представления всех периодических решений: x = θ + 2πn

      Пример:

      sin(x) = 0,65
      • Используйте калькулятор и получите 9092. основное значение: 0,71 Рад .
      • Применить идентификатор триггера sin(θ) = sin(π-θ) , чтобы получить зеркальное решение: arcsin(0,65) = π - arcsin(0,65) , что будет: 2,43 Rad .
      • With two solutions 0.71 Rad and 2.43 Rad and add periodicity, we’ll get two full solutions:
      • x = 0.71 + 2πn
      • x = 2.43 + 2πn

      Example:

      sin(x) = −0,25
      • Используйте калькулятор , чтобы сделать arcsin(-0,25) и получить основное значение: -0,25 Рад .
      • Примените тождество триггера sin(θ) = sin(-π-θ) , чтобы получить зеркальное решение: arcsin(-0,25) = -π - arcsin(-0,25) , что будет: -2,89 Рад .
      • с двумя решениями -0,25 RAD и 3,39 RAD и ADD PEORICICION, мы получим два полных решения:
      • x = -0,25 + 2πn
      • x = -2,89 + 2πn
      • x = -2,89 + 2πn
      • x = -2,89 + 2πn
      • x = -2,89 + 29930
      • x = -2,89 +
      • . Пример: cos(x) = −0,7
        • Используйте калькулятор сделать arccos(-0.7) и получить основное значение: 2.35 Rad .
        • Примените тождество триггера cos(θ) = cos(-θ) , чтобы получить зеркальное решение: arccos(-0.7) = - arcsin(-0.7) , что будет: -2.35 Rad .
        • С двумя решениями 2,35 Рад и -2,35 Рад и добавлением периодичности мы получим два полных решения:
        • x = 2,35 + 2πn
        • + 9π 9350 x = -2,35016

        Пример:

        cos(x)=0,4
        • Используйте калькулятор , чтобы вычислить arccos(0,4) и получить основное значение: 1,16 Rad .
        • Примените тождество триггера cos(θ) = cos(-θ) , чтобы получить зеркальное решение: arccos(0.4) = - arcsin(0.4) , что будет: -1,16 Rad .
        • С двумя растворами 1,16 Рад и -1,16 Рад и добавлением периодичности мы получим два полных решения:
        • x = 1,16 + 2πn
        • x = -1,16 + 2πn

        означает, что угол существует только в Q.1 и Q.4

      • Arccos(x)=θ : 0° < θ < 180°, означает, что угол существует только в Q.1 и Q.2
      • Arctan(x) =θ : -90° < θ < 90°, угол существует только в Q.1 и Q.40909 90 and -90 ,
        just to think about the         CLOCKWISE and COUNTER-CLOCKWISE .

        С специальными триггерными значениями нам вообще не нужен калькулятор, а только для того, чтобы посмотреть на изображение полного единичного круга. Или даже не это, если вы можете это вспомнить.

        Примечание:
        Полная единичная окружность показывает только против часовой стрелки угловых мер, что означает ТОЛЬКО ПОЛОЖИТЕЛЬНЫЕ УГЛЫ ,
        , поэтому вам нужно сделать свою собственную математику, чтобы получить ОТРИЦАТЕЛЬНЫХ УГЛОВ , иначе. Угол по часовой стрелке равен .

        См. YouTube: Оценка обратных тригонометрических функций, Основное введение, Примеры и практические задачи: sin⁻¹(1/2), sin⁻¹(√3/2), [[sin⁻¹(-1/2)] ](https://youtu.be/aRVWs1tDarI?t=4m1s), sin⁻¹(-√3/2), sin⁻¹(0), sin⁻¹(1), sin⁻¹(-1), cos⁻¹(1/2), cos⁻¹(-√3/2), cos⁻¹(-√2/2), cos⁻¹(0), tan⁻¹(0), tan⁻¹(1 ), загар⁻¹(-1), загар⁻¹(√3), загар⁻¹(-√3/3), просмотреть все.

        Пример: Решите

        sin⁻¹(1/2)
        • Глядя на единичную окружность , мы знаем, что существует несколько мер дуги, которые могут получить синусоидальное значение 1/2 , равное 30°. , 150°, -210°, -330°.
        • Отфильтруйте все остальные по диапазону [-90°, 90°] , мы получим 30° — это ЕДИНСТВЕННЫЙ и ДОЛЖЕН ТОЛЬКО ОДИН ответ.

        Пример: Решите

        sin⁻¹(-1/2)
        • Посмотрите на единичный круг , мы знаем, что ответ: 210°, 330°, -30°, -150°
        • С фильтрацией по диапазону [-90°, 90°] , поэтому -30° — единственный ответ.

        Пример: Решите

        cos⁻¹(√2/2)

        Как только вы поймете, как решить исходное решение функций, с этим базовым решением будет очень просто.
        Ниже приведены пошаговые решения:

        • Упростите уравнение до sin(θ)=?? Форма .
        • Решите θ с помощью ДВУХ решений в виде θ = ?? + 2πn 909:30 .
        • Замените θ выражением x и решите уравнение для x .

        Практика хана.

        No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *