Python Atan2
Функция atan2(y, x) в математическом модуле Python часто используется для вычисления арктангенса y/x в радианах. Математический модуль предоставляет множество констант, таких как значения «пи» и «тау». Мы можем сэкономить время, не записывая значение каждой константы каждый раз, когда мы хотим ее использовать, и мы можем сделать это с большой точностью.
Atan() можно рассматривать как atan(y/x), где y и x не что иное, как два целых числа. Импортируя математический модуль, мы можем его использовать. Сначала мы должны импортировать математический модуль, а затем использовать статический объект для вызова этой функции.
Содержание
- Синтаксис Atan2
- Пример 1
- Пример 2
- Пример 3
- Пример 4
- Пример 5
- Atan или Atan2: в чем разница?
- Заключение
Синтаксис Atan2
Функция Python atan2 имеет следующий синтаксис.
Он принимает два параметра, оба имеют числовой тип данных; если какой-либо другой тип данных указан в качестве параметра, это вызовет ошибку типа. Он возвращает значение арктангенса числа типа данных float. Здесь «x» представляет декартову координату X и может быть целым числом или допустимым числовым выражением. ’y’, с другой стороны, может представлять декартову координату Y как целое число или допустимое числовое выражение.
Он возвращает значение арктангенса числа типа данных float. Здесь «x» представляет декартову координату X и может быть целым числом или допустимым числовым выражением. ’y’, с другой стороны, может представлять декартову координату Y как целое число или допустимое числовое выражение.
Давайте рассмотрим несколько примеров, чтобы лучше понять концепцию функции Python math.atan2 и ее работу.
Пример 1
Вот программа Python3, которая показывает, как использовать метод atan2(). Мы начали с импорта математического модуля. После этого было напечатано тета-значение двух отрицательных координат (-0,7 и −0,7). Точно так же отображается тета-значение двух положительных координат (1,4 и 2,2). Наконец, код написан для получения значения тета. Значения 1,2 и −1,5.
import math
theta_one = math.atan2(—0.7, —0.7)
print(«atan2(-0.7, -0.7) : «, theta_one)
theta_two = math.atan2(1.4, 2.2)
print(«atan2(1.2, 1.5) : «, theta_two)
theta_three = math.
atan2(1.2, —1.5)
print(«atan2(1.2, -1.5):», theta_three)
На следующем изображении вы можете видеть, что отображается тета-значение двух отрицательных значений (первая строка), двух положительных (вторая строка) и одной положительной и одной отрицательной координаты (третья строка).
Пример 2
Вот еще один программный код Python3, в котором используется метод atan(). Мы импортировали математический модуль и построили два списка (a и b) в первой строке кода. Список «a» имеет значения [2, 3, 4, 5], а список «b» имеет значения [7, 4, 6, 3]. Как вы можете видеть в последних строках кода, мы начали обход диапазона, чтобы получить тета-значения для всех местоположений «b», а также «a».
import math
a = [2, 3, 4, 5]
b = [7, 4, 6, 3]
for i in range(len(a)):
theta_result = math.atan2(b[i], a[i])
print(theta_result)
Ниже вы можете видеть, что отображаются тета-значения всех заданных чисел.
Пример 3
Программный код Python3 для объяснения ошибки TypeError в функции atan() можно найти ниже. Как видно из кода, мы передали целочисленные значения после загрузки математического модуля, и программа выдала TypeError.
import math
b, a = 2, 4
theta_result = math.atan2([b], [a])
print(theta_result)
Вот ошибка TypeError, сгенерированная после того, как мы передали целочисленные значения в программу.
Пример 4
Мы будем использовать функцию math.atan2, чтобы получить наклон в радианах, когда в этом примере заданы координаты Y и X. В коде видно, что после импорта нужного модуля math мы будем определять наклон, когда заданы координаты X и Y. Мы определили наклон в радианах с помощью функции math.atan2. Как видите, мы напечатали результат в последней строке кода.
import math
X = 4; Y = 4
theta_result = math.atan2(Y, X)
print(theta_result)
Вот полученный скриншот для вашей помощи.
Пример 5
Вот последний пример, более подробный, чтобы помочь вам понять концепцию. В Python функция atan2 возвращает угол (в радиусе) между осью X и заданной точкой (y, x). Мы найдем то же самое с разными типами данных и отобразим результаты в этом примере atan2.
Во-первых, мы напрямую использовали функцию atan2 как для положительных, так и для отрицательных целых чисел. Следующие операторы вычисляют угол (в радиусе) для соответствующих значений.
Затем функция atan2 была применена к элементам Python Tuple & List. Python Tuple обозначается как «Tup_one», а элемент списка отображается в коде как «Lis_one». Как видите, данный код (изображение прикреплено ниже) прекрасно работает на них.
Затем математическая функция была применена к нескольким значениям. Мы использовали функцию atan2 для строкового значения в предыдущем операторе, и она вернула TypeError в качестве вывода.
Здесь все приведенные выше операторы из кода выполняются идеально, за исключением последней строки, которая сгенерировала TypeError.
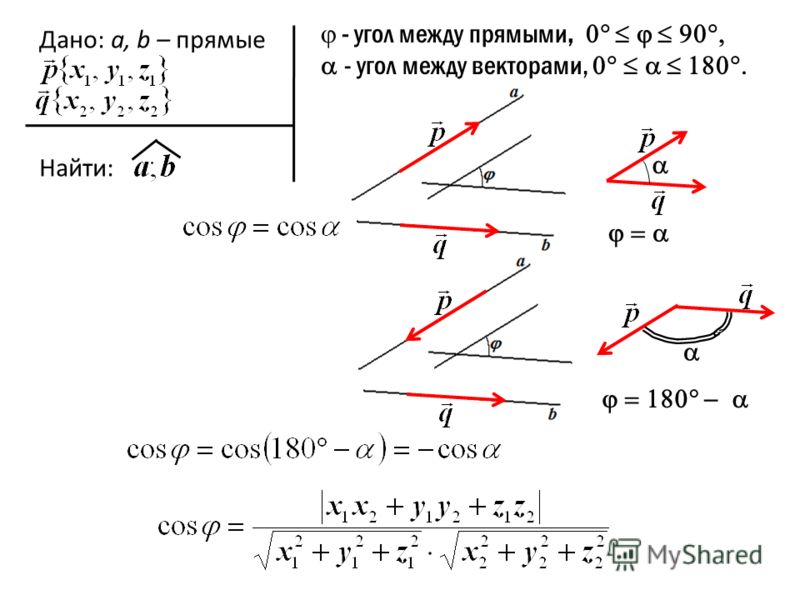
Atan или Atan2: в чем разница?
Почти каждый язык программирования включает математический модуль с многочисленными тригонометрическими функциями, включая atan и atan2.
В математике Atan — это просто арктангенс, арктангенс. Когда мы вычисляем atan(x,y) для вектора «v» с координатами [x,y]. Наименьший угол между вектором v и осью X определяется абсолютным значением этого результата. Atan2 — не что иное, как более мягкая вариация Atan. Угол между вектором «v» и «угловым началом» на единичной окружности возвращается atan2.
Заключение
Математический модуль включает процедуру atan2(). Эта функция используется для вычисления арктангенса y/x, что дает результат в радианах. Atan() можно рассматривать как atan(y/x), где y и x — два целых числа. Импортируя математический модуль, мы можем его использовать. Сначала мы должны импортировать математический модуль, а затем использовать статический объект для вызова этой функции. Эта стратегия была представлена в этом посте с многочисленными примерами, чтобы вы могли легко понять и применить эту концепцию к своим программам.
Угол между векторами : Чулан (М)
| The DEADman |
| ||
27/08/10 |
| ||
| |||
| mihailm |
| ||
19/05/10 |
| ||
| |||
| The DEADman |
| ||
27/08/10 |
| ||
| |||
| ShMaxG |
| |||
11/04/08 |
| |||
| ||||
Алексей К. |
| ||
29/09/06 |
| ||
| |||
| ShMaxG |
| |||
11/04/08 |
| |||
| ||||
| mihailm |
| ||
19/05/10 |
| ||
| |||
| The DEADman |
| ||
27/08/10 |
| ||
| |||
Алексей К. |
| ||
29/09/06 |
| ||
| |||
| The DEADman |
| ||
27/08/10 |
| ||
| |||
Алексей К. |
| ||
29/09/06 |
| ||
| |||
| The DEADman |
| ||
27/08/10 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 12 ] |
Модераторы: Модераторы Математики, Супермодераторы
Угол между векторами
Угол между векторами Джеймс Уокер
9 декабря 2014 г. , пересмотрено 5 июня 2016 г. . В течение многих лет я делал это, используя знакомую формулу для угла через скалярное произведение и функцию арккосинуса:
, пересмотрено 5 июня 2016 г. . В течение многих лет я делал это, используя знакомую формулу для угла через скалярное произведение и функцию арккосинуса:
$$\theta = \mathrm{acos}\left(\frac{\mathbf{u}•\mathbf {v}}{\left\|\mathbf{u} \right\|\;\left\|\mathbf{v} \right\|}\right)$$
Для машинных вычислений вы можете записать его с одним квадратным корнем:
$$\theta = \mathrm{acos}\left(\frac{\mathbf{u}•\mathbf{v}}{\ sqrt{\strut(\mathbf{u}•\mathbf{u})\,(\mathbf{v}•\mathbf{v})}}\right)$$
Однако недавно я обратил на это внимание (например, через сообщение в блоге Джона Блэкберна), что это не самая точная формула, особенно для векторов, которые почти параллельны или противоположны. Рассмотрим график арккосинуса, показанный справа. Его особенности при 1 и -1 вызывают проблему. Рассмотрим векторы \(\mathbf{u} = (1, 0, 0)\) и \(\mathbf{v} = (1, x, 0)\) и посмотрим, что происходит, когда \(x\ ) мало относительно 1. В этом случае формула угла принимает вид: 92\;.\]
Напомним, что машинное представление чисел с плавающей запятой имеет параметр \(\эпсилон\) (машинный эпсилон), такой что числа \(1\) и \(1 + z\) имеют одно и то же представление всякий раз, когда \(|z| < \epsilon\).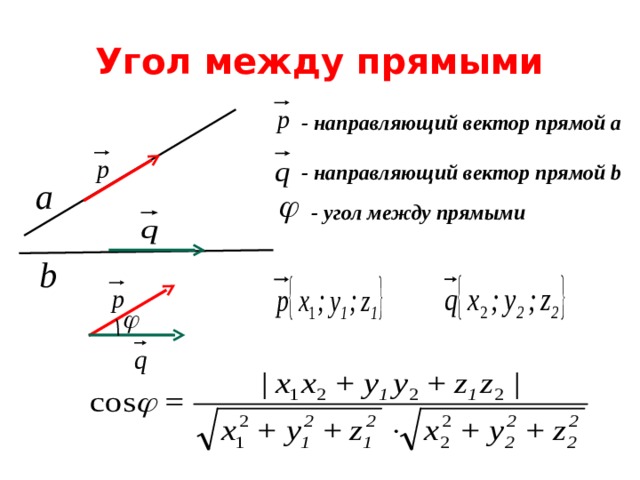 2} \; .
\end{выравнивание}
\] 92|\; < \; 9999.5 \,\epsilon\;.\]
2} \; .
\end{выравнивание}
\] 92|\; < \; 9999.5 \,\epsilon\;.\]
Улучшенная формула
Так как мы пытаемся вычислить угол, неизбежна какая-то обратная тригнометрическая функция. Функция обратного синуса имеет те же особенности, что и арккосинус. Но арктангенс хорош и гладок во всей действительной области, поэтому мы могли бы искать формулу, используя арктангенс.
Из двух известных формул
\[\mathbf{u}•\mathbf{v} = \|\mathbf{u}\| \, \|\mathbf{v}\| \cos(\тета)\; \mbox{и}\]
\[\|\mathbf{u}\times\mathbf{v}\| = \|\mathbf{u}\| \, \|\mathbf{v}\| \ грех (\ тета) \; \mbox{,}\]
мы можем сделать вывод, что
\[\tan(\theta) = \frac{\|\mathbf{u}\times\mathbf{v}\|}{\mathbf{u} •\mathbf{v}}\;.\]
Мы должны быть немного осторожны, превращая это в функцию, включающую арктангенс, так как мы ищем угол в интервале \([0, \pi] \), но стандартный арктангенс имеет диапазон \([-\pi/2, \pi/2]\). Однако в стандартной библиотеке функций C есть версия арктангенса, которая делает именно то, что нам нужно:
\[\theta = \operatorname{atan2}\left( \|\mathbf{u}\times\mathbf{v}\|, \mathbf{u}•\mathbf{v} \right)\]
Между прочим, использование atan2 также означает, что нам не нужно беспокоиться о делении на ноль.
Еще лучше?
Если векторы \(\mathbf{u}\) и \(\mathbf{v}\) имеют одинаковую длину, легко проверить, что \(\mathbf{u} + \mathbf{v}\ ) и \(\mathbf{u} — \mathbf{v}\) ортогональны, и что тангенс половины угла между \(\mathbf{u}\) и \(\mathbf{v}\) равен \ (\left\|\mathbf{u} — \mathbf{v}\right\| / \left\|\mathbf{u} + \mathbf{v}\right\|\). Следовательно, угол между \(\mathbf{u}\) и \(\mathbf{v}\) равен \(2\,\operatorname{atan2}\left(\left\|\mathbf{u} — \mathbf{ v}\right\|, \left\|\mathbf{u} + \mathbf{v}\right\|\right)\). Чтобы справиться с более общим случаем, мы можем масштабировать \(\mathbf{u}\) и \(\mathbf{v}\) по длинам друг друга, чтобы получить векторы одинаковой длины:
\[ \theta = 2\, \operatorname{atan2}\left( \влево\| \, \|\mathbf{v}\|\,\mathbf{u} — \|\mathbf{u}\|\,\mathbf{v}\, \right\|, \left\|\, \|\mathbf{v}\|\,\mathbf{u} + \|\mathbf{u}\|\,\mathbf{v}\,\right\| \Правильно) \]
Я читал размахивающие руками аргументы в пользу того, что эта формула лучше, чем формула, включающая перекрестное произведение, из-за сокращений, связанных с вычислением перекрестного произведения.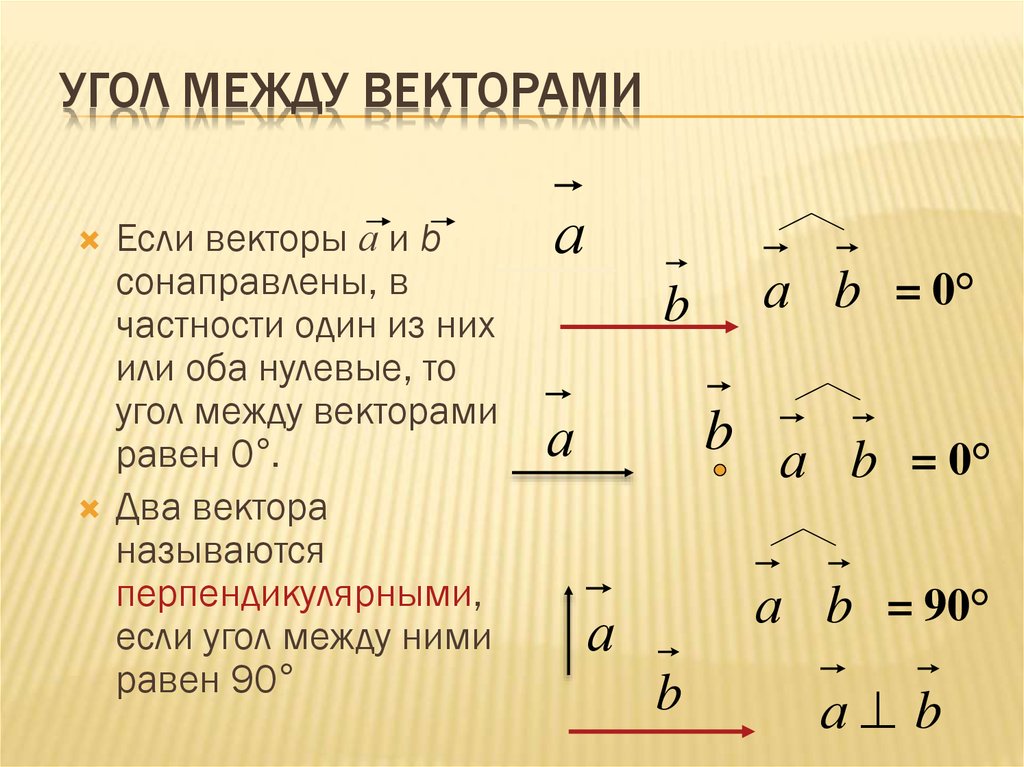

 atan2(1.2, —1.5)
atan2(1.2, —1.5)
 03.2011, 14:38
03.2011, 14:38  03.2011, 14:41
03.2011, 14:41 
 03.2011, 14:51
03.2011, 14:51 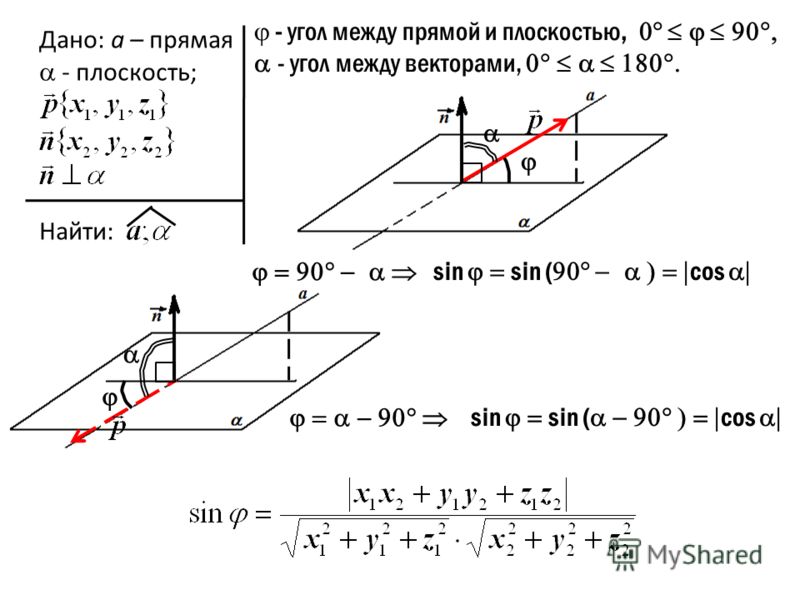 03.2011, 14:54
03.2011, 14:54  03.2011, 17:05
03.2011, 17:05  03.2011, 17:55
03.2011, 17:55