Эквивалентные бесконечно малые функции и их
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 6 из 13Следующая ⇒ применение для вычисления пределов Определение. Бесконечно малые функции называются эквивалентными бесконечно малыми при , если Пишут так: при .
Теорема. Пусть в окрестности точки , за исключением, быть может, ее самой, задана функция и бесконечно малые функции . Тогда Это равенство понимается в смысле: если существует предел его правой части, то существует равный ему предел левой части (и обратно). Отсюда же следует, что если один из пределов не существует, то не существует и другой. Доказательство. Пусть тогда Аналогично доказывается обратное утверждение.
Пары эквивалентных бесконечно малых, которые используют при вычислении пределов:
9) при
Монотонные функции. И непрерывности обратной функции Определение. Функция называется неубывающей (невозрастающей) на отрезке , если для любых выполняется неравенство . Неубывающие и невозрастающие функции называются монотонными. Если неравенства строгие, то функция называется возрастающей (убывающей) на отрезке. Возрастающие и убывающие функции называются строго монотонными. Теорема. Рассмотрим непрерывную строго возрастающую функцию на отрезке , причем Тогда существует обратная к f функция , однозначная, строго возрастающая и непрерывная на .
Доказательство существования. Поскольку каждому значению соответствует только одно значение , то любому значению y из можно поставить в соответствие именно то значение x, для которого обозначим это соответствие так: .
Доказательство возрастания. Из условия возрастания следует: если Верно и обратное утверждение: если Но и получаем: если т.е. обратная функция – возрастающая.
Доказательство непрерывности обратной функции. Докажем непрерывность обратной функции в произвольной точке . Обозначим и выберем произвольное , такое, что . Пусть
Выберем Тогда, очевидно, а . (*) Пусть теперь , т.е. . С учетом (*) можно записать, что . В силу возрастания функции следует, что Но , поэтому или А это и означает, что функция непрерывна в точке Разрывы первого и второго рода
Определение. 
Рассмотрим график . Кружок в точке А означает, что эта точка входит в область значений , т.е. . Стрелка в точке В означает, что точка В в область значений функции не входит. Поскольку , функция имеет разрыв в точке с.
Другие возможные случаи разрывов.
Если функция f имеет конечные пределы и , но , то функция имеет в точке разрыв I рода. Если , то в точке устранимая особенность. Если доопределить так, что , то получим непрерывную функцию.
Пример разрывной функции (функция Кронекера): Точка является точкой разрыва I рода.
Если у функции не существует ни левого, ни правого предела, либо одного из них, либо эти пределы бесконечны в точке С, то функция имеет разрыв II рода.
Пример 1.
;
–точка разрыва II рода. Пример 2. Ее график имеет вид:
Эта функция не имеет в точке ни левого, ни правого предела. – точка разрыва II рода.
Пример 3.
Точки , – точки разрыва II рода. В них не определена, а пределы слева и справа бесконечны.
Функции, непрерывные на отрезке
Определение. Функция называется непрерывной на отрезке , если она непрерывна во всех точках интервала , непрерывна справа в точке a, слева в точке b. Теорема 1. Если функция непрерывна на отрезке , то она ограничена на нем, т.е. существует число , такое, что для всех . Теорема 2 (теорема Вейерштрасса). Если функция непрерывна на отрезке , то она достигает минимума и максимума на , т.е. существуют точки , такие, что для всех .
Теорема 3. Если функция непрерывна на и числа не равны нулю и имеют противоположные знаки, то на интервале имеется по крайней мере одна точка c, такая, что .
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
⇐ Предыдущая12345678910Следующая ⇒ Читайте также: Где возникла философия и почему? Относительная высота сжатой зоны бетона Сущность проекции Гаусса-Крюгера и использование ее в геодезии Тарифы на перевозку пассажиров |
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 2098; Нарушение авторского права страницы; Мы поможем в написании вашей работы!  su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.014 с.) su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.014 с.)
|
Эквивалентные бесконечно малые функции. Сравнение бесконечно больших функций.
Среди б.м. функций одного порядка особое место в приложениях занимают эквивалентные б.м. функции. Определение 10.5. Б.м. при х а функции а(х) и Р(х) называют эквивалентными при х а и обозначают ), если предел их отношения при х а равен единице, или Эквивалентные бесконечно малые функции. Главная часть бесконечно малой функции. Сравнение бесконечно больших функций Свойство эквивалентности б.м. функций симметрично, поскольку из (10.8) следует lim Транзитивность свойства эквивалентности вытекает с учетом (10.8) непосредственно из (10.2). Запись вида ot(x)x~аР(х) иногда называют асимптотическим равенством функций а(х) и 0(х) в окрестности точки а. Для того чтобы две б.м. при х а функции а(х) и 0(х) были эквивалентными при а, необходимо и достаточно, чтобы их разность а(х) — 0(х) была б.м. более высокого порядка по сравнению с каждой из них, т.е. Пусть а(х) Х~а0{х). Тогда с учетом определения 10.5 и, согласно определению ). Аналогично можно доказать, что а(ж) — /3(я)х5ао(а(а;)). Обратно, при ) с учетом определения 10.2 имеем .. а это, по определению 10.5, означает, что а(х) X~afi{x). Из предположения а(х) — х=ао(а(х)) следует такой же результат. Теорема 10.3. Если б.м. при х -у а функции а(х) и 0(х) являются эквивалентными при х а, а функция x(t) в Эквивалентные бесконечно малые функции. Главная часть бесконечно малой функции.
Возможно вам будут полезны данные страницы:
В силу непрерывности функции In у в точке с учетом (9.12) получим ИЛИ Поскольку loge(l + x) = (ln(l + x))/lna, согласно (10.14) имеем 6. В силу непрерывности функции Согласно (10.14) можно записать — 1. Возвращаясь к обозначению аргумента через х, получим Эквивалентные бесконечно малые функции. Главная часть бесконечно малой функции. Сравнение бесконечно больших функций 7. С учетом (10.16) вычислим Следовательно, (1 -f x)* — или при s £ R \ {0} В частности, при Из полученных соотношений (10. Тогда, если существует предел при х а произведения (или частного f(x)/a(x)), он не изменится при замене а(х) на эквивалентную при х-ча б.м. функцию /?(х), или Действительно, с учетом Из этой теоремы следует удобное для использования (10.18) правило: предел отношения б.м. при i-4a функций равен пределу отношения эквивалентных им при х -»а б.м. функций. Пример 10.4. Вычислим с учетом (10.18) Главная часть бесконечно малой функции Согласно утверждению 7.4 сумма конечного числа функций, б.м. при х а, есть снова б.м. при х а функция.
Если для n = 2, N orn(x)x=eo(ai(x)), то ai(x) называют главной частью суммы б.м. при х а функций. Инаг че, главная часть суммы б.м. — это слагаемое более низкого порядка малости по сравнению с каждым из остальных слагаемых. Ясно, что если в сумме есть несравнимые слагаемые (см. Когда для каждого слагаемого в сумме б.м. при х а функций можно указать порядок к относительно х — а, главной частью такой суммы будет слагаемое (если оно единственное) низшего порядка. В сумме б.м. при х -> оо функций главной частью будет слагаемое низшего порядка относительно 1/х при условии, что оно единственное, и для каждого слагаемого можно указать порядок малости. Теорема 10.6:Сумма конечного числа б.м. при х а функций эквивалентна своей главной части, или 4 Если ai(s) — главная часть суммы a(x), то с учетом свойства (7.22) суммы функций, имеющих конечные пределы) и определения 10.2 найдем I что, согласно (10.8), означает эквивалентность при х а суммы б.м. функций и ее главной части. Следствие 10.1. В некоторой проколотой окрестности о U (а) точки а сумма конечного числа б.м. при х а функций сохраняет знак своей главной части, или В ходе доказательства теоремы 10. Процедура выделения главной части в виде А(х — а)к для б.м. при х-ьа, функции а(х) связана с рассмотрением предела и подбором значений А: и Л, так, чтобы этот предел оказался равным единице. После выделения главной части ее можно использовать для приближенного вычисления значений функции ог(х) при значениях х в некоторой окрестности точки а. Возникающая при этом абсолютная |7(х)| и относительная |7(я)/а(х)| погрешности будут стремиться к нулю при х -4 а. Если требуется более высокая точность вычисления значений или представления функции в окрестности точки а, то следует попытаться выделить главную часть из б.м. при х а функции 7(ж). Эту процедуру можно продолжить. Такую процедуру уточнения называют построением асимптотического разложения функции в окрестности данной точки. Пример 10.7. Пусть точность замены по (10.17) при s = = 1/2 и х->0 функции \Л + х -1 на функцию х/2 недостаг точна. Если потребуется еще более высокая точность, то наступит очередь выделять главную часть из б.м. при х-» О функции £(х) и т.д. # Если для двух б.м. при х а функций а(х) и /3(х) известны их главные части, соответственно А(х-а)к и J9(x-a)m, то что можно сказать о главной части суммы а(х) 4-/?(х) ? При к ф т главной частью суммы будет то из слагаемых А(х — а)* и В(х — а)т, в котором показатель степени меньше. Если же к = т, то главная часть суммы есть (Л-f В)(х — а)* при условии, что А + В ф 0. В противном случае главные части слагаемых взаимно уничтожаются, и сумма а(х) + 0(х) оказывается при х а б.м. функцией более высокого порядка, чем каждое из слагаемых. В этом случае приходится выделять из нее б.м. функцию вида С (х- а)4 при q > к. Пример 10.8. а. Функции а(х) = у/1 + х — 1 и (3(х) = = у/1-х -1 являются б.м. при х 0. Из примера 10.7 следует, что при х —> 0 2. Отсюда где , и главной частью суммы заданных функций при х 0 будет -х2/4. б. Рассмотрим теперь функции а(х) = 1п(1 + Зх + х2) и /?(х) = 1п(1 — Зх + х2), являющиеся б. Дело в том, что из (10.18) непосредственно следует лишь эквивалентность ln(l + z) т.е., согласно теореме 10.2, справедлива запись . На основании теоремы 10.3 полагаем z равным либо Зх + х2,либо —Зх + х2, и тогда После сложе- ния заданных б.м. функций получим но два последних слагаемых в правой части сами могут содержать слагаемые вида Ах2, которые обязаны войти в главную часть суммы ot(x)+0(x) при х 0. Поэтому для выделения главной части суммы исходных б.м. функций преобразуем эту сумму к виду где е(х)x=qo(-7×2 + х4). Вот теперь вполне определенно и обоснованно можно сказать, что при х 0 главная часть этой суммы равна -7х2. Сравнение бесконечно больших функцийДля 6.6. функций можно ввести классификацию, аналогичную классификации б. При с = 0 v(x) называют б.б. функцией более низкого порядка роста по сравнению с w(x) при х а и записывают а в случае бесконечного предела отношения v(x)/w(x) — б.б. функцией более высокого порядка роста по сравнению с w(x) при х а и записывают w(x)x=eo(t;(a;)) (слово „роста» часто опускают). Наконец, если не существует ни бесконечного, ни конечного предела этого отношения, то и(х) и ги(х) называют несравнимыми при х а б.б. функциями. Пример 10.9. а. Функции 2х2 и х2 + х являются б.б. одного порядка при , так как б. Функция ах (а > 1) является б.б. более высокого порядка роста по сравнению с хк {к> 0) при х +оо, так как согласно (7. Аналогично, если в сумме конечного числа б.б. функций при х а можно указать для каждого слагаемого порядок роста к относительно 1/(х — а), слагаемое высшего порядка будет также главной частью такой суммы при хча, если это слагаемое единственное. Например, в сумме l/sin2g+ctgz двух б.б. функций при х 0 согласно (10.18) первое слагаемое имеет второй порядок относительно 1/х, а второе — первый порядок. Поэтому главной частью этой суммы при х —>0 будет l/sin2x. Утверждение 10.2. Сумма конечного числа б.б. функций эквивалентна своей главной части. Пример 10.10. Функция /(ж) = yj 1/х — 1 определена в полуинтервале (0, 1] и как элементарная функция — непрерывна в этом промежутке (см. 3.6 и 9.5). Так как при х +0 эта функция является б.б., а прямая х = 0 будет вертикальной асимптотой графика . Найдем главную часть f(x) при х->+0 в виде А/хк из условия (10.27) эквивалентности б.б. функции и ее главной части: limQf{x)/(A/xk) = = 1. Отсюда Ясно, что предел в правой части этого равенства будет конечным и отличным от нуля, если к = 1/2. Тогда А = 1, и главной частью f(x) при х->+0 будет 1/у/х (рис. 10.1). Поскольку lim fix) = lim — 1 = 0, г-И-0 v ‘ г-fl-O V х при х 1 — 0 , f(x) является б.м. функцией. Найдем главную часть }(х) при z-4 1-О в виде А(1-х)к Рис. 10.1 из условия (10.8) эквивалентности б.м. функции и ее главной части: lim q f(x)/(A(l — х)*) = 1. Отсюда Эквивалентные бесконечно малые функции. Главная часть бесконечно малой функции. Сравнение бесконечно больших функций (1 — х)к Предел в правой части этого равенства будет конечным и отличным от нуля, если А: = 1/2. Тогда А = 1, и главной частью f(x) при х-» 1-0 будет у/1 -х (см. рис. 10.1). |
Помогите решить / разобраться (М)
| anpetrobul |
| ||
21/01/17 |
| ||
| |||
| Metford |
| |||
06/04/13 |
| |||
| ||||
| anpetrobul |
| ||
21/01/17 |
| ||
| |||
| bot |
| |||
21/12/05 |
| |||
| ||||
| deep blue |
| ||
23/11/09 |
| ||
| |||
| sergei1961 |
| ||
25/08/11 |
| ||
| |||
| bot |
| |||
21/12/05 |
| |||
| ||||
| anpetrobul |
| ||
21/01/17 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 8 ] |
Модераторы: Модераторы Математики, Супермодераторы
Math Tutor — Функции — Обзор методов
Math Tutor — Функции — Обзор методов — Ограничения Это метод, который помогает оценить некоторые ограничения. Его можно рассматривать как
простой хитрый трюк, или можно создать историю об этом, что приводит нас к
название. Слово «бесконечно малый» определенно не относится к
бесконечно малое dx , как мы его знаем из дифференцируемости или непрерывности
по Лейбницу. Значение другое, и мы объясним его ниже.
Сначала рассмотрим простой способ.
Его можно рассматривать как
простой хитрый трюк, или можно создать историю об этом, что приводит нас к
название. Слово «бесконечно малый» определенно не относится к
бесконечно малое dx , как мы его знаем из дифференцируемости или непрерывности
по Лейбницу. Значение другое, и мы объясним его ниже.
Сначала рассмотрим простой способ.
Следующий предел хорошо известен, и, используя замена мы легко выводим другие версии:
Мы можем использовать их для упрощения других ограничений следующим образом (мы показываем процесс в подробно, чтобы оправдать это):
Сравните первый предел и последний во второй строке. Мы по существу
заменил синус на x — 1, то есть
трюк, о котором мы хотим поговорить.
Конечно, мы могли бы решить этот предел, используя
правило Лопиталя, но есть
ситуации, когда подход замены быстрее или удобнее. Мы можем дистиллировать
основная идея замены одного выражения другим в следующем
утверждение.
Теорема.
Пусть a — действительное число, ∞ или −∞. Пусть f , g , h — функции, определенные на некотором приведенном окрестности и . Еслитогда
Заметим, что мы уже обсуждали ситуацию, когда отношение двух функций f и h сходится к 1 на a в разделе на порядок функций и ввел следующие обозначения: f ∼ h at a . Мы также столкнулись с идеей замены раньше. А именно, в разделе о интуитивная оценка мы заменяли многочлены и подобные выражения их доминирующими условия. Эта теорема показывает, что подобная идея может быть использована и в других случаях. предельные точки и . Мы можем выразить это следующим образом:
• Если f ∼ h at a ,
чем мы можем заменить f на h в выражениях вида f / g и г / f при оценке пределов при и .
Обратите внимание на ограничение на тип выражения. В общем, мы не можем заменить где угодно, как мы обсудим ниже.
Бесконечно малые
Мы часто оцениваем пределы в a = 0. Некоторые люди любят придумывать истории о замене в таких пределах с использованием специальной терминологии. Под бесконечно малым они подразумевают любую функцию, которая имеет предел в нуле, равный нулю. Типичные бесконечно малые были бы грех( x ), пер(1 + x ), или мощности x B . Два бесконечно малые f , h считаются эквивалентными if f ∼ h at 0. Эти эквиваленты бесконечно малые тогда можно свободно обменивать всякий раз, когда они образуют числитель знаменатель дроби в пределе при 0.
Вот список самых популярных эквивалентных бесконечно малых.
Обратите внимание, что n в последней формуле может быть любым положительным вещественным числом,
например дробь. Таким образом, формула помогает также с корнями.
Таким образом, формула помогает также с корнями.
Пример: Мы решим следующий предел, используя эквивалентные бесконечно малые числа.
Это было значительно проще, чем использовать правило Лопиталя. Однако можно использовать его в школе (на экзамене) только в том случае, если эквивалентные бесконечно малые были правильно установлены в классе.
Приведенные выше формулы также могут помочь с ограничениями в других точках, кроме 0, используя подходящие замены.
Пример:
Пример:
Основное ограничение этого метода заключается в том, что мы можем безопасно заменить только знаменатель или числитель в целом. Действительно, рассмотрим следующий пример.
Пример:
Этот результат неверен, правильный ответ
Замена Тейлора
Глядя на приведенную выше таблицу эквивалентных бесконечно малых, можно заметить, что
во всех случаях член справа на самом деле является первым членом Тейлора
расширение функции слева. Это не случайно. В общем, когда
оценка предела в a , мы можем заменить функции их расширениями
с центром и . Если мы используем полное разложение (степенной ряд), мы можем сделать
как мы хотим, предполагая, что степенной ряд сходится к исходной функции
в каком-то районе и .
Это не случайно. В общем, когда
оценка предела в a , мы можем заменить функции их расширениями
с центром и . Если мы используем полное разложение (степенной ряд), мы можем сделать
как мы хотим, предполагая, что степенной ряд сходится к исходной функции
в каком-то районе и .
Однако работа с серией может быть затруднена.
Часто лучше использовать просто ненулевой полином Тейлора некоторого
степень. Тогда мы должны быть осторожны, чтобы не ошибиться. Мы определенно можем
сделайте это, если функция, которую мы хотим заменить, является точно числителем или
знаменатель в дроби, которую мы исследуем. Если мы хотим заменить
в других местах, то мы должны выбрать степень так, чтобы мы
не потерять важную информацию. Интуитивно мы можем заменить часть
исследуемое выражение с его тейлоровским разложением определенной степени по
ситуации, когда замена полностью не отменяется в
процесс. Это не совсем правильное математическое утверждение, оно было бы
трудно дать полное и точное описание, учитывая, насколько разнообразны пределы
проблемы могут быть. Когда вы решите использовать замену, большой опыт и
необходимо хорошее понимание.
Когда вы решите использовать замену, большой опыт и
необходимо хорошее понимание.
В качестве примера вернемся к расчету выше, который не сработал. Мы покажет дважды.
Поскольку эквивалентные бесконечно малые обычно не изучаются, мы не будем использовать их в официальных решениях здесь, в Math Tutor. Начнем с того, что заметим, что когда мы заменили синус полиномом первой степени, он отменился. Таким образом, он был слишком коротким. Пробуем следующую доступную длину, то есть третью полином степени, потому что часть его должна остаться в числителе.
Назад к обзору методов — Лимиты
анализ — Алгебра эквивалентных бесконечно малых
Вопрос
Изменено 5 лет, 7 месяцев назад
Просмотрено 182 раза
$\begingroup$
Вопрос:
Верна ли алгебра на эквивалентных бесконечно малых?
Пример:
$$\sqrt{1+x} — 1 \sim_0 \frac{x}{2} \longrightarrow \sqrt{1+x} \sim_0 \frac{x}{2} + 1$$
Я зная, что и левое, и правое равенство верны, но это просто совпадение, что похоже, что я добавил $ 1 $ к обеим сторонам левого равенства, чтобы получить правильное?
- алгебра-предварительное исчисление
- анализ
- пределы
- бесконечно малые
$\endgroup$
5
$\begingroup$ 92$$
В самом деле, попробуйте это, и вы увидите, что это верно, что позволяет вам показать, что
$$\sqrt{1+x}\sim_01+\frac x2$$
В любом случае, в общем, когда вы пишете что-то вроде
$$\sqrt{1+x}-1\sim_0\frac x2$$
Это означает, что они оба имеют одинаковые скорости роста (их разница ограничена чем-то, что стремится к нулю быстрее, чем их), и оттуда легко показать, что сложение и умножение можно перемещать.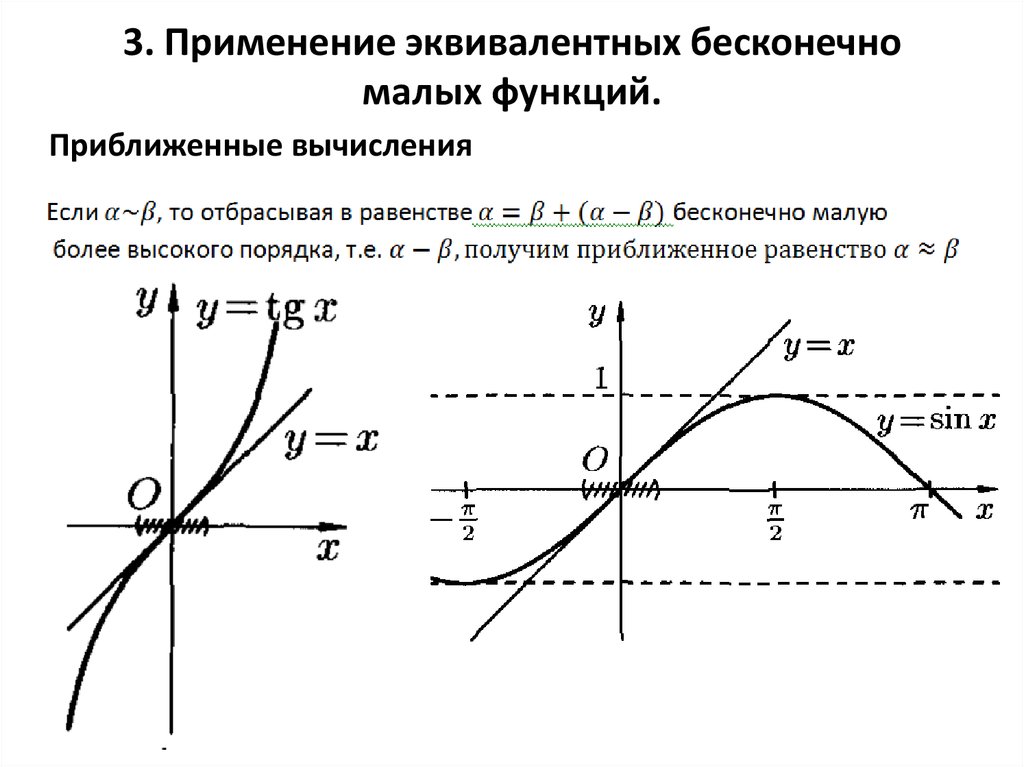 2 x}\right)} \neq 1$$ 92 x}\right)$, что означает, что вы не можете делать все, что хотите, для эквивалентности бесконечно малых и при этом поддерживать эквивалентность.
2 x}\right)} \neq 1$$ 92 x}\right)$, что означает, что вы не можете делать все, что хотите, для эквивалентности бесконечно малых и при этом поддерживать эквивалентность.
Однако я подозреваю, что если $h$ является достаточно «хорошей» функцией, то $f \sim g$ подразумевает $h\circ f \sim h \circ g$
Я разместил аналогичный вопрос здесь. В моем вопросе эквиваленты не бесконечно малы, а скорее бесконечны , но концепция аналогична.
$\endgroup$
$\begingroup$
В некоторых комментариях была небольшая путаница относительно того, должно ли отношение $a\sim_0 b$ определять аддитивное отношение, означающее, что $a-b$ бесконечно мало, или мультипликативное отношение, означающее, что $\frac {a}{b}$ бесконечно близко к $1$, т. е. $1-\frac{a}{b}$ бесконечно мало. Невыполнение различий между двумя отношениями, безусловно, может привести к ошибке, как указал пользователь Bernard в комментарии.
Поэтому было бы безопаснее ввести разные обозначения для этих двух отношений. Таким образом, $a\приблизительно b$ означает, что $a-b$ бесконечно мала, тогда как $a\;_{\ulcorner\!\urcorner}\;b$ (аналогично обозначению равенства Лейбница) означает, что $1-\frac{a }{b}$ бесконечно мала, т. е. $1-\frac{a}{b}\ приблизительно0$.
Если вы хотите использовать отношение $a\;_{\ulcorner\!\urcorner}\;b$, то, строго говоря, ваш вывод требует дальнейшего обоснования, поскольку отношение сохраняется не аддитивно, а только мультипликативно.
Подробнее об отношениях Лейбница см. в этом ответе.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Бесконечно малое определение и значение | Dictionary.com
- Основные определения
- Викторина
- Связанный контент
- Примеры
- Британский
- Научный
Показывает уровень оценки в зависимости от сложности слова.
[ in-fin-i-tes-uh-muhl ]
/ ˌɪn fɪn ɪˈtɛs ə məl /
Сохранить это слово!
См. синонимы для: бесконечно малый / бесконечно малый / бесконечно малый на Thesaurus.com
Показывает уровень оценки в зависимости от сложности слова.
прилагательное
неопределенно или чрезвычайно мало; минута: бесконечно малые сосуды в системе кровообращения.
неизмеримо мал; меньше присваиваемой величины: в бесконечно малой степени.
Математика. из бесконечно малых величин, относящихся к ним или связанных с ними.
существительное
бесконечно малая величина.
Математика. переменная, имеющая нуль в качестве предела.
ВИКТОРИНА
Сыграем ли мы в «ДОЛЖЕН» ПРОТИВ. «ДОЛЖЕН» ВЫЗОВ?
Следует ли вам пройти этот тест на «должен» или «должен»? Это должно оказаться быстрым вызовом!
Вопрос 1 из 6
Какая форма используется для указания обязательства или обязанности кого-либо?
Происхождение бесконечно малого
Впервые записано в 1645–1655 гг.; от нового латинского infinītēsim(us), эквивалентного латинскому infinīt(us) бесконечный + -ēsimus суффикс порядковых числительных + -al 1
ДРУГИЕ СЛОВА ИЗ Infinitisimal
in·fin·i·tes·i·mal·i ·ty, in·fin·i·tes·i·mal·ness, существительное·fin·i·tes·i·mal·ly, наречиеСлова рядом с бесконечно малым
бесконечное десятичное число, бесконечное расстояние, бесконечное произведение, бесконечный регресс , бесконечный ряд, бесконечно малый, исчисление бесконечно малых, инфинитив, инфинитив, инфинитивное предложение, маркер инфинитива
Dictionary. com Полный текст
На основе Random House Unabridged Dictionary, © Random House, Inc., 2022
com Полный текст
На основе Random House Unabridged Dictionary, © Random House, Inc., 2022
Слова, относящиеся к бесконечно малому
незаметный, незначительный, микроскопический, крошечный, незначительный, маленький, миниатюрный, минутный, атомарный, незначительный, незначительный, крошечный, крошечный, незаметный
Как использовать бесконечно малый в предложении
Он изучает бесконечно малые колебания света из космоса в надежде найти чужие планеты, способные поддерживать жизнь.
Только что получивший Пулитцеровскую премию за «The Overstory», Ричард Пауэрс представляет еще одну оду окружающей среде|Рон Чарльз|21 сентября 2021 г.|Washington Post яркость в несколько частей на миллион — и вычисление невидимых тел, которые затемняют их при прохождении.
Что такое жизнь? — Выпуск 106: Разумная жизнь|Калеб Шарф|16 сентября 2021 г.|Наутилус
Вы услышите все эти истории обо всех людях, обо всех людях, которые добились успеха, но они будут подобны бесконечно малой части всех остальных, пытающихся сделать то же самое и не способных сделать это.
 .
.Банда Гиллмора: Социальное восхождение|Стив Гиллмор|30 июля 2021 г.|TechCrunch
Открытие и определение энтропии Клаузиусом — одно из чудес науки — полностью основывались на бесконечно малых изменениях от одного состояния равновесия замкнутой системы к другому .
Время течет к порядку — Выпуск 93: Предшественники|Джулиан Барбур|2 декабря 2020|Наутилус
Результатом является то, что даже бесконечно малой неточности в любом измерении турбулентности достаточно, чтобы опровергнуть любой анализ того, как это может развиваться.
Неожиданный поворот раскрывает секреты турбулентности|Дэвид Х. Фридман|3 сентября 2020 г.|Журнал Quanta
Но, конечно, процент американцев, которые знают об этом, бесконечно мал.
Пять самых больших лжи об Obamacare|Майкл Томаски|17 августа 2014 г.|DAILY BEAST
«Разница между щелчком и отсутствием щелчка часто бесконечно мала, и слишком много не щелчков», — вспоминает он.

Величайшее шоу Нью-Йорка, или Как они не облажались с «Парнями и куколками»|Росс Ветцстеон|6 апреля 2014 г.|DAILY BEAST
Спорная территория велика в воображении истории и бесконечно мала в географии.
Каирская речь Барака Обамы и его израильская проблема|Марти Перец|25 февраля 2013 г.|DAILY BEAST
Квантовая теория объясняет мелочи, когда материя и энергия делятся на бесконечно малые частицы.
Горячие чтения этой недели: 5 июня 2012 г. | Николас Манкузи, Джимми Со | 6 июня 2012 г. | DAILY BEAST
Но так мало времени до начала фактического голосования, что вероятность ошибки бесконечно мала.
Не делай этого, Крис!|Мэтт Латимер|30 сентября 2011|DAILY BEAST
И Леки говорит: «Только бесконечно малая часть земли принадлежит потомкам тех, кто владел ею до Кромвеля».
Верен ли Ольстер?|Анонимно
Обычный Джонс очень увлекся удалением крошечной пылинки из левой манжеты.

Средний Джонс|Сэмюэл Хопкинс Адамс
Часть можно назвать удовлетворением, а мельчайший остаток, бесконечно малую часть, назвать — если в жизни есть такая вещь — радостью.
Тирания Бога|Джозеф Льюис
Эти бесконечно малые различия между человеком и человеком слишком ничтожны для Всемогущего существа.
Дракула|Брэм Стокер
В лучшем случае это лишь описание бесконечно малой частички реальности.
By the Christmas Fire|Samuel McChord Crothers
British Dictionary definitions for infinitesimal
infinitesimal
/ (ˌɪnfɪnɪˈtɛsɪməl) /
adjective
infinitely or immeasurably small
maths of, relating to, or involving a небольшое изменение значения переменной, стремящееся к нулю в качестве предела
существительное
математика бесконечно малая величина
Производные формы бесконечно малой
бесконечно малая, наречие Collins English Dictionary — Complete & Unabridged 2012 Digital Edition
© William Collins Sons & Co.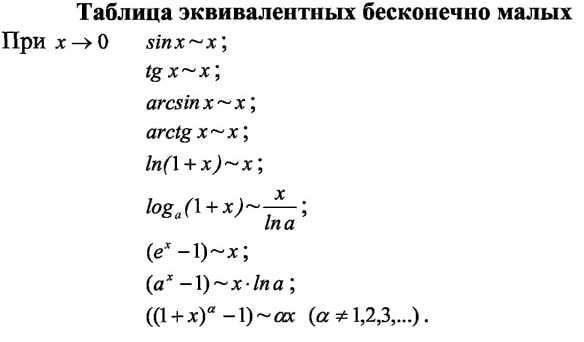

 Все правила по сольфеджио
Все правила по сольфеджио
 Теорема о существовании
Теорема о существовании




 cosx-1. Теорема 10.4. Пусть a(x) и /(х) — некоторая функция, определенная в проколотой окрестности точки а.
cosx-1. Теорема 10.4. Пусть a(x) и /(х) — некоторая функция, определенная в проколотой окрестности точки а. /х б.м. при х 0 функций главной частью будет f/xy поскольку с учетом (10.18) и теоремы 10.4 согласно определению.
/х б.м. при х 0 функций главной частью будет f/xy поскольку с учетом (10.18) и теоремы 10.4 согласно определению. ao((x-a)m), то, согласно теореме 10.2, что возможно в силу (10.8) лишь при В = А и т = к.
ao((x-a)m), то, согласно теореме 10.2, что возможно в силу (10.8) лишь при В = А и т = к. o(x2).
o(x2). м. при х 0. Из (10.18) с учетом теоремы 10.3 получим Теперь, казалось бы, можно сказать, что главной частью суммы а(х) + /3(х) при х 0 будет 2х2. Но такой вывод является поспешным и поверхностным, а потому, как часто бывает, неверным.
м. при х 0. Из (10.18) с учетом теоремы 10.3 получим Теперь, казалось бы, можно сказать, что главной частью суммы а(х) + /3(х) при х 0 будет 2х2. Но такой вывод является поспешным и поверхностным, а потому, как часто бывает, неверным. м. функций (см. 10.1), также связанную с пределом их частного. Пусть v(s) и w(x) — функции, б.б. при х а (см. определение 7.11), где а — конечная или бесконечная точка расширенной числовой прямой. Если существует lim v(x)/w(x) = с6 R \ {0}, то в этом х—¥а случае v(x) и w(x) называют б.б. функциями одного порядка при х а и записывают v(x)x=aO(u;(a;)) или t0(s)r=aO(v(a:)).
м. функций (см. 10.1), также связанную с пределом их частного. Пусть v(s) и w(x) — функции, б.б. при х а (см. определение 7.11), где а — конечная или бесконечная точка расширенной числовой прямой. Если существует lim v(x)/w(x) = с6 R \ {0}, то в этом х—¥а случае v(x) и w(x) называют б.б. функциями одного порядка при х а и записывают v(x)x=aO(u;(a;)) или t0(s)r=aO(v(a:)). 32) в. Функции x(2 + sinx) и х являются несравнимыми б.б. при х оо, поскольку при х —> оо не существует предела отношения z(2 + sina:)/x = 2 +sin а: (ни конечного, ни бесконечного). является суммой б.б. при х оо функций, причем порядок роста к относительно х каждого слагаемого совпадает с соответствующим показателем степени. Поэтому слагаемое а$хп высшего порядка роста (к = п), поскольку оно единственно, и будет главной частью этой суммы при х оо.
32) в. Функции x(2 + sinx) и х являются несравнимыми б.б. при х оо, поскольку при х —> оо не существует предела отношения z(2 + sina:)/x = 2 +sin а: (ни конечного, ни бесконечного). является суммой б.б. при х оо функций, причем порядок роста к относительно х каждого слагаемого совпадает с соответствующим показателем степени. Поэтому слагаемое а$хп высшего порядка роста (к = п), поскольку оно единственно, и будет главной частью этой суммы при х оо. В общем случае можно говорить о главной части не только алгебраической суммы конечного числа б.б. при х а (или при х оо) функций, но и произвольной по структуре функции f(x)y эквивалентной при х а степенной функции А/(х — а)* (при х оо —степенной функции Ахк), Аф 0, к > 0. Эта степенная функция и будет главной частью б.б. функции соответственно при х —у а или при х оо. Путь нахождения коэффициента А и показателя степени к основан на использовании определения 10.7 и утверждения 10.2 и подобен процедуре выделения главной части б.м. функции.
В общем случае можно говорить о главной части не только алгебраической суммы конечного числа б.б. при х а (или при х оо) функций, но и произвольной по структуре функции f(x)y эквивалентной при х а степенной функции А/(х — а)* (при х оо —степенной функции Ахк), Аф 0, к > 0. Эта степенная функция и будет главной частью б.б. функции соответственно при х —у а или при х оо. Путь нахождения коэффициента А и показателя степени к основан на использовании определения 10.7 и утверждения 10.2 и подобен процедуре выделения главной части б.м. функции.
 01.2017, 13:59
01.2017, 13:59  01.2017, 15:50
01.2017, 15:50 
 01.2017, 12:20
01.2017, 12:20  01.2017, 12:33
01.2017, 12:33 

 Кроме того полезно понимать куда стремится x в этих эквивалентностях.
Кроме того полезно понимать куда стремится x в этих эквивалентностях. .
.
