Частица массой м несущая заряд q движется в однородном магнитном поле: Частица массой m, несущая заряд q, движется в однородном магнитном поле с индукцией В по окружности радиусом R со скоростью v. Как изменятся радиус траектории, период обращения и кинетическая энергия частицы при увеличении скорости её движения

Тренажер по физике по заданиям «В» ЕГЭ | Материал для подготовки к ЕГЭ (ГИА) по физике по теме:

Тренажер по физике  по заданиям  «В»  ЕГЭ

по теме: «Движение по окружности»

В задачах по элементарному курсу электромагнетизма можно выделить основные группы:

а) задачи о силовом действии ЭМ-поля на проводники с током и

б) задачи о силовом действии ЭМ-поля на движущиеся в нем заряженные частицы.

Плоское движенце заряженной частицы в однородном магнитном поле.

При движении заряженной частицы в магнитном поле на нее действует сила Лоренца, которая, как известно, направлена перпендикулярно вектору скорости частицы, поэтому эта сила работы не совершает. Следовательно, при движении частицы в любом стационарном магнитном поле кинетическая энергия и модуль скорости частицы сохраняются — изменяется только направление вектора скорости частицы.

Рассмотрим движение заряженной частицы в однородном магнитном поле, когда вектор скорости частицы направлен перпендикулярно вектору индукции магнитного поля. Так как модуль скорости частицы сохраняется, сила Лоренца перпендикулярна вектору индукции поля, то вектор скорости все время будет перпендикулярен вектору индукции поля. Итак, модули векторов скорости и индукции постоянны, векторы перпендикулярны, следовательно, модуль силы Лоренца также будет оставаться постоянным и равным Fл = qυB. Сила Лоренца является центростремительной, она приводит к искривлению траектории, а, так ее модуль постоянен, то кривизна траектории частицы будет постоянна, то есть траекторией частицы будет окружность. Радиус этой окружности R можно найти на основании уравнения второго закона Ньютона.

из которого находим:

Найдем период обращения частицы в магнитном поле: .

Задача 1.

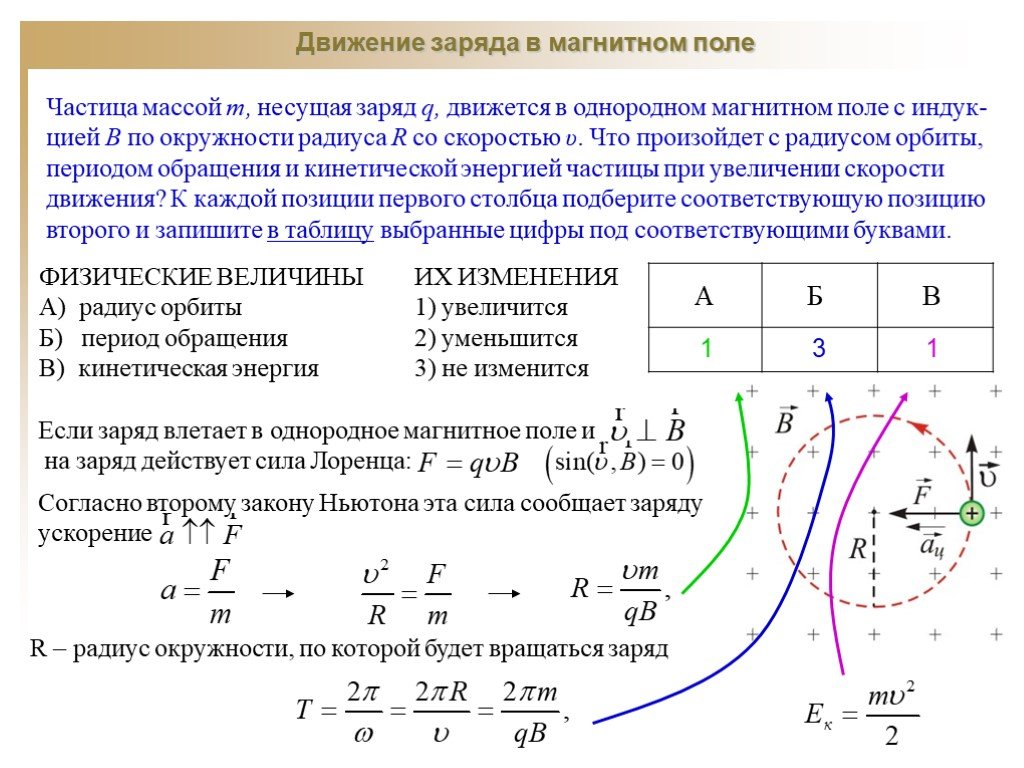
Частица массой m, несущая  заряд q, движется в однородном магнитном  поле с индукцией В по окружности радиуса R со скоростью υ. Что произойдет с радиусом орбиты, периодом обращения и кинетической энергией частицы при увеличении скорости движения?  

К каждой позиции первого столбца подберите соответствующую позицию  второго и запишите в таблицу выбранные цифры под соответствующими  буквами.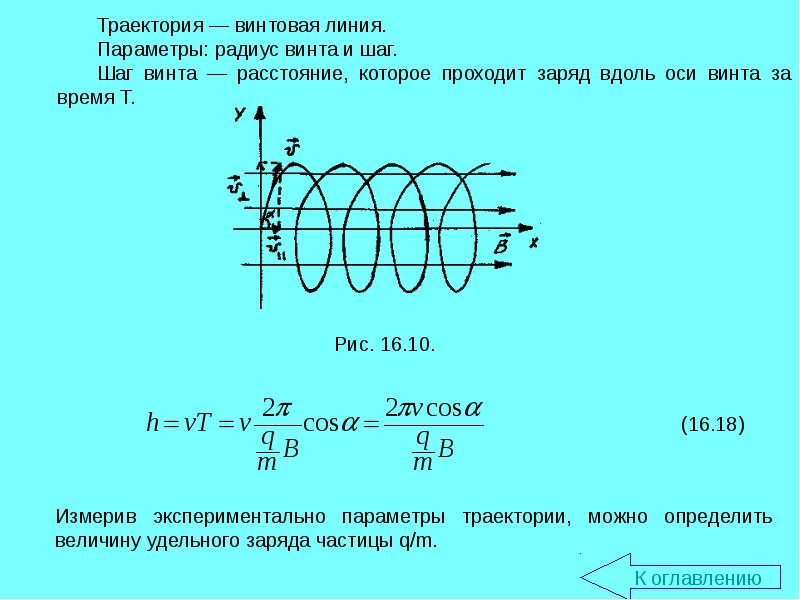

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ	ИХ ИЗМЕНЕНИЯ
А)   радиус орбиты	1) увеличится
Б)  период обращения	2) уменьшится
В)  кинетическая энергия	3) не изменится

Решение:

• Радиус окружности по которой движется  частицы зависит от скорости: . При увеличении скорости частицы радиус увеличится.
• Период обращения частицы в магнитном поле не зависит от скорости частицы: , значит период останется прежним.
• Кинетическая энергия зависит от скорости: , при увеличении скорости кинетическая энергия возрастает.

А	Б	В
1	3	1

Задача 2.

Частица массой m, несущая  заряд q, движется в однородном магнитном  поле с индукцией В по окружности радиуса R со скоростью υ. Что произойдет с радиусом орбиты, периодом обращения и кинетической энергией частицы при увеличении заряда частицы, если ее скорость не изменилась?

 К каждой позиции первого столбца подберите соответствующую позицию  второго и запишите в таблицу выбранные цифры под соответствующими  буквами.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ	ИХ ИЗМЕНЕНИЯ
А)   радиус орбиты	1) увеличится
Б)  период обращения	2) уменьшится
В)  кинетическая энергия	3) не изменится

Решение:

• Радиус окружности по которой движется  частицы зависит от заряда частицы: . При увеличении  заряда частицы радиус уменьшится.
• Период обращения частицы в магнитном поле зависит от заряда частицы: , чем больше заряд частицы, тем период обращения меньше.
• Кинетическая энергия зависит от скорости:  от заряда не зависит.

А	Б	В
2	2	3

Задача 3.

   Частица массой m, несущая  заряд q, движется в однородном магнитном  поле с индукцией В по окружности радиуса R со скоростью υ. Что произойдет с радиусом орбиты, периодом обращения и кинетической энергией частицы, если в этом поле с такой же скоростью движется частица массой 2m и зарядом q?  

К каждой позиции первого столбца подберите соответствующую позицию  второго и запишите в таблицу выбранные цифры под соответствующими  буквами.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ	ИХ ИЗМЕНЕНИЯ
А)   радиус орбиты	1) увеличится
Б)  период обращения	2) уменьшится
В)  кинетическая энергия	3) не изменится

Решение:

• Радиус окружности по которой движется  частицы зависит от массы частицы: . При увеличении массы частицы в 2 раза радиус увеличится в 2 раза.
• Период обращения частицы в магнитном поле зависит от массы частицы: , чем больше масса частицы, тем период обращения больше.
• Кинетическая энергия зависит от скорости и массы частицы:  , для частицы большей массы кинетическая энергия больше.

А	Б	В
1	1	1

Задача 4.

Частица массой m, несущая  заряд q, движется в однородном магнитном   поле с индукцией В по окружности радиуса R со скоростью υ. Что произойдет со скоростью этой частицы, радиусом ее орбиты и периодом обращения в данном поле при увеличении ее кинетической энергии?

К каждой позиции первого столбца подберите соответствующую позицию  второго и запишите в таблицу выбранные цифры под соответствующими  буквами.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ	ИХ ИЗМЕНЕНИЯ
А)   радиус орбиты	1) увеличится
Б)  период обращения	2) уменьшится
В)  скорость	3) не изменится

Решение:

Кинетическая энергия увеличивается при увеличении скорости.

• Радиус окружности по которой движется  частицы зависит от скорости: . При увеличении скорости частицы радиус увеличится.
• Период обращения частицы в магнитном поле не зависит от скорости частицы: , значит период останется прежним.
• Скорость частицы увеличится.

А	Б	В
1	3	1

Физическое тело выходит на круговую орбиту вокруг Земли и становится ее  спутником, если ему сообщить первую космическую скорость. В этом случае  центростремительная сила  равна силе притяжения спутника Землей.

, ,

 Без учета других факторов, влияющих на поведение спутника на орбите, уравнение состояния динамического равновесия спутника имеет вид:

где m — масса спутника; M — масса Земли, равная М = 5,98*1024 килограмм массы; γ — гравитационная постоянная, равная γ=6,67*10-11 м³/кгс²; R — средний радиус Земли, равный R=6371 км, h- высота спутника над поверхностью Земли

Для высот, значительно меньших радиуса Земли (h

mg ∼ mv²/R,    

где g = γM/R² ∼ 9,81 м/с² — ускорение свободного падения у поверхности Земли.

Скорость, необходимая для того, чтобы движущееся тело превратилось в спутника Земли, определяется из соотношения:

Задача 1.

В результате перехода с одной круговой орбиты на другую центростремительное ускорение спутника Земли увеличивается. Как изменяются в результате этого перехода радиус орбиты спутника, скорость его движения  по орбите и период обращения вокруг Земли?  

Для каждой величины определите соответствующий характер изменения

1) увеличивается  

2) уменьшается  

3) не изменяется    

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.  

Решение:

При увеличении центростремительного ускорения  возрастает действующая сила, значит радиус орбиты уменьшается.

Скорость    зависит от высоты h и при ее уменьшении скорость спутника возрастает.

Период обращения   уменьшается.

Радиус орбиты	Скорость движения по орбите	Период обращения вокруг Земли
2	1	2

Задача 2.

В результате перехода с одной круговой орбиты на другую центростремительное ускорение спутника Земли уменьшается. Как изменяются в результате этого перехода радиус орбиты спутника, скорость его движения  по орбите и период обращения вокруг Земли?  

Для каждой величины определите соответствующий характер изменения

1) увеличивается  

2) уменьшается  

3) не изменяется    

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.  

Решение:

При  уменьшении центростремительного ускорения  действующая сила уменьшается, значит радиус орбиты увеличивается.

Скорость    зависит от высоты h и при ее увеличении скорость спутника уменьшается.

Период обращения   увеличивается.

Радиус орбиты	Скорость движения по орбите	Период обращения вокруг Земли
1	2	1

Задача 3

В результате перехода с одной круговой орбиты на другую скорость движения спутника Земли увеличивается. Как изменяются в результате перехода радиус орбиты спутника, его центростремительное ускорение период обращения вокруг Земли?

Для каждой величины определите соответствующий характер изменения:  

1) увеличивается  

2) уменьшается  

3) не изменяется    

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.  

Решение:

Скорость    зависит от высоты h, если скорость спутника увеличивается то высота должна уменьшиться.

При уменьшении радиуса орбиты сила тяжести, а значит и центростремительное ускорение увеличивается.

Период обращения   уменьшается.

Радиус орбиты	Центростремительное ускорение	Период обращения вокруг Земли
2	1	2

Задача 4.

В результате перехода с одной круговой орбиты на другую скорость движения спутника Земли уменьшается. Как изменяются в результате перехода радиус орбиты спутника, его центростремительное ускорение период обращения вокруг Земли?

Для каждой величины определите соответствующий характер изменения:  

1) увеличивается  

2) уменьшается  

3) не изменяется    

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.  

Решение:

Скорость    зависит от высоты h, если скорость спутника уменьшается, то высота должна увеличиться.

При увеличении радиуса орбиты сила тяжести, а значит и центростремительное ускорение уменьшается.

Период обращения   увеличивается.

Радиус орбиты	Центростремительное ускорение	Период обращения вокруг Земли
1	2	1

Движение тела, брошенного горизонтально,  можно  рассматривать как сложное, складывающееся из двух движений: равномерного  движения в горизонтальном направлении с начальной скоростью Vо и одновременного  свободного падения вниз. Вниз тело падает с постоянным ускорением g=9,8 м/с2.

Высота ,

Поскольку в горизонтальном направлении никакие силы не действуют (сопротивление воздуха не учитывать), то скорость в горизонтальном направлении изменяться не будет.

L=V0.t.

Эти соотношения показывают, что расстояние, пройденное телом в вертикальном направлении, не зависит от величины начальной скорости — ведь ее значение не входит в формулу для расчета высоты Н. А дальность полета в горизонтальном направлении будет тем больше, чем больше начальная скорость.

Задача 1.

Шарик , брошенный горизонтально с высоты H с начальной скоростью  υ0,  за время  t пролетел в  горизонтальном направлении  υ0  расстояние L (см. рисунок). В другом опыте на этой же установке  начальная  скорость шарика  равна 2υ0. Что  произойдет  при  этом с временем полета, дальностью полета и ускорением шарика?

Для каждой величины определите соответствующий характер ее изменения:  

1) увеличилась    

2) уменьшилась  

3) не изменилась  

Решение:

Время полета зависит только от высоты:  , и при увеличении скорости не изменится.

Дальность полета увеличится в 2 раза.

Ускорение шарика постоянно и равно g.

Время полета	Дальность полета	Ускорение шарика
3	1	3

Задача 1.

Шарик , брошенный горизонтально с высоты H с начальной скоростью  υ0,  за время  t пролетел в  горизонтальном направлении  υ0  расстояние L (см. рисунок). В другом опыте на этой же установке  начальная  скорость шарика  равна υ0/2. Что  произойдет  при  этом с временем полета, дальностью полета и ускорением шарика?

Для каждой величины определите соответствующий характер ее изменения:  

1) увеличилась    

2) уменьшилась  

3) не изменилась  

Решение:

Время полета зависит только от высоты:  , и при увеличении скорости не изменится.

Дальность полета уменьшиться в 2 раза.

Ускорение шарика постоянно и равно g.

Время полета	Дальность полета	Ускорение шарика
3	2	3

Потенциальная энергия — механическая энергия системы тел, которая определяется характером сил взаимодействия между ними и их взаимным расположением.

Потенциальная энергия в поле силы тяжести                     ,где  h отсчитывается от уровня, на котором потенциальная энергия полагается равной нулю.

Потенциальная энергия в поле упругих сил  , если принять потенциальную энергию недеформированной пружины равной нулю. k – коэффициент жесткости пружины, х – величина абсолютной деформации.

Кинетическая энергия равна половине произведения массы тела на квадрат его скорости:

Задача 1.

Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина все время остается растянутой. Как  ведет  себя  потенциальная  энергия  пружины,  кинетическая  энергия  груза,  его  потенциальная  энергия  в  поле  тяжести,  когда  груз  движется  вниз к положению равновесия?    

Для каждой величины определите соответствующий характер изменения:        

1) увеличивается  

2) уменьшается    

3) не изменяется  

 

Запишите в таблицу выбранные цифры для каждой физической величины.        

Цифры в ответе могут повторяться.  

Решение:

Так как пружина всегда растянута, при движении груза вниз, к положению равновесия относительная деформация возрастает, значит потенциальная энергия пружины увеличивается.

Скорость груза при движении к положению равновесия увеличивается, значит кинетическая энергия возрастает.

Высота груза над Землей  уменьшается, значит уменьшается потенциальная энергия груза.

Потенциальная энергия пружины	Кинетическая энергия груза	Потенциальная энергия груза
1	1	2

       

Задача 2.

Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина все время остается растянутой. Как  ведет  себя  потенциальная  энергия  пружины,  кинетическая  энергия  груза,  его  потенциальная  энергия  в  поле  тяжести,  когда  груз  движется  вниз  от положения равновесия?    

Для каждой величины определите соответствующий характер изменения:        

1) увеличивается  

2) уменьшается    

3) не изменяется  

 

Запишите в таблицу выбранные цифры для каждой физической величины.        

Цифры в ответе могут повторяться.  

Решение:

Так как пружина всегда растянута, при движении груза вниз, от положения равновесия относительная деформация возрастает, значит потенциальная энергия пружины увеличивается.

Скорость груза максимальна при прохождении положения равновесия и равна нулю в точках максимального отклонения от положения равновесия. При движении груза от положения равновесия скорость и кинетическая энергия уменьшаются.

Высота груза над Землей  уменьшается, значит уменьшается потенциальная энергия груза.

Потенциальная энергия пружины	Кинетическая энергия груза	Потенциальная энергия груза
1	2	2

       

Задача 3.

Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина все время остается растянутой. Как  ведет  себя  потенциальная  энергия  пружины,  кинетическая  энергия  груза,  его  потенциальная  энергия  в  поле  тяжести,  когда  груз  движется  вверх от положения равновесия?    

Для каждой величины определите соответствующий характер изменения:        

1) увеличивается  

2) уменьшается    

3) не изменяется  

 

Запишите в таблицу выбранные цифры для каждой физической величины.        

Цифры в ответе могут повторяться.  

Решение:

Так как пружина всегда растянута, при движении груза вверх , к положению равновесия относительная деформация уменьшается, значит потенциальная энергия пружины уменьшается.

Скорость груза максимальна при прохождении положения равновесия и равна нулю в точках максимального отклонения от положения равновесия. При движении груза к положению равновесия скорость и кинетическая энергия увеличиваются.

Высота груза над Землей увеличивается, значит увеличивается потенциальная энергия груза.

Потенциальная энергия пружины	Кинетическая энергия груза	Потенциальная энергия груза
2	1	1

       

Задача 4.

Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина все время остается растянутой.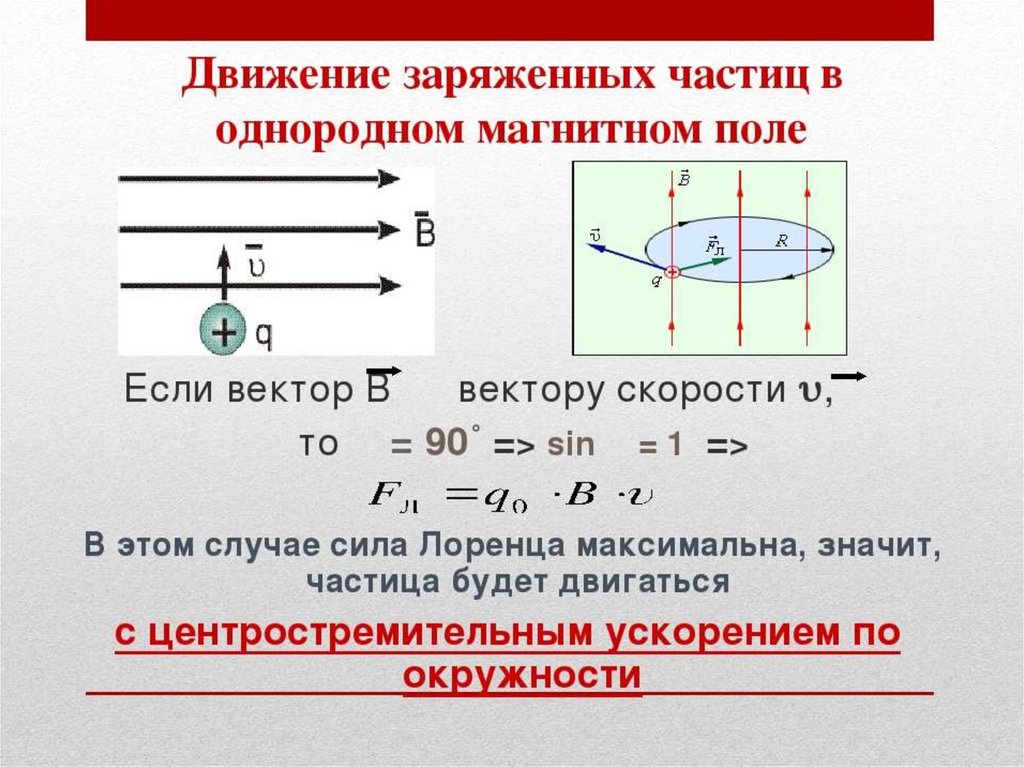 Как  ведет  себя  потенциальная  энергия  пружины,  кинетическая  энергия  груза,  его  потенциальная  энергия  в  поле  тяжести,  когда  груз  движется  вверх  от положения равновесия?    

Для каждой величины определите соответствующий характер изменения:        

1) увеличивается  

2) уменьшается    

3) не изменяется  

 

Запишите в таблицу выбранные цифры для каждой физической величины.        

Цифры в ответе могут повторяться.  

Решение:

Так как пружина всегда растянута, при движении груза вверх , от положения равновесия относительная деформация уменьшается, значит потенциальная энергия пружины уменьшается.

Скорость груза максимальна при прохождении положения равновесия и равна нулю в точках максимального отклонения от положения равновесия. При движении груза от  положения равновесия скорость и кинетическая энергия уменьшаются.

Высота груза над Землей увеличивается, значит увеличивается потенциальная энергия груза.

Потенциальная энергия пружины	Кинетическая энергия груза	Потенциальная энергия груза
2	2	1

       

[PDF] Контрольная работа по теме «Магнитное поле».

Вариант 1. Уровень 1.

Контрольная работа по теме «Магнитное поле». Вариант 1. Уровень 1. №1. Длина активной части проводника 15 см. Угол между направлением тока и индукцией магнитного поля равен 900. С какой силой магнитное поле с индукцией 40мТл действует на проводник, если сила тока в нем 12 А? №2. На протон, движущийся со скоростью 107 м/с в однородном магнитном поле перпендикулярно линиям индукции, действует сила 0,32∙10-12 Н. Какова индукция магнитного поля? №3. Определите индуктивность катушки, которую при силе тока 8,6 А пронизывает магнитный поток 120мВб. №4. Определите по условию задачи №2 радиус окружности, по которой движется протон, период обращения, импульс электрона, его кинетическую энергию, а также ускоряющую разность потенциалов, которую прошел протон, прежде чем попал в магнитное поле. Уровень 2. №1. Участок проводника длиной 10см находится в магнитном поле. Сила электрического тока, протекающего по проводнику, 10 А. При перемещении проводника на 8 см в направлении действия силы Ампера она совершила работу 4мДж.

Чему равна индукция магнитного поля? Проводник расположен перпендикулярно линиям магнитной индукции. №2. По катушке протекает ток, создающий магнитное поле энергией 0,5 Дж. Магнитный поток через катушку 10 мВб. Найти силу тока. №3. Частица массой m, несущая заряд q, движется в однородном магнитном поле с индукцией В по окружности радиуса R со скоростью υ. Что произойдет с радиусом орбиты, периодом обращения и кинетической энергией частицы при увеличении индукции магнитного поля? Физические величины А. радиус орбиты Б.период обращения В. кинетическая энергия А

Их изменение 1. увеличится 2. уменьшится 3. не изменится Б

В

№4. Горизонтальные рельсы находятся на расстоянии 30 см друг от друга. На них лежит стержень массой 100г перпендикулярно рельсам. Вся система находится в вертикальном магнитном поле с индукцией 0,5 Тл. При пропускании по стержню тока 2 А, он движется с ускорением 2 м/с2. Найти коэффициент трения между рельсами и стержнем. №5. Частица массой 10-5 кг и зарядом 10-6 Кл ускоряется однородным электрическим полем напряженностью 10 кВ/м в течение 10 с.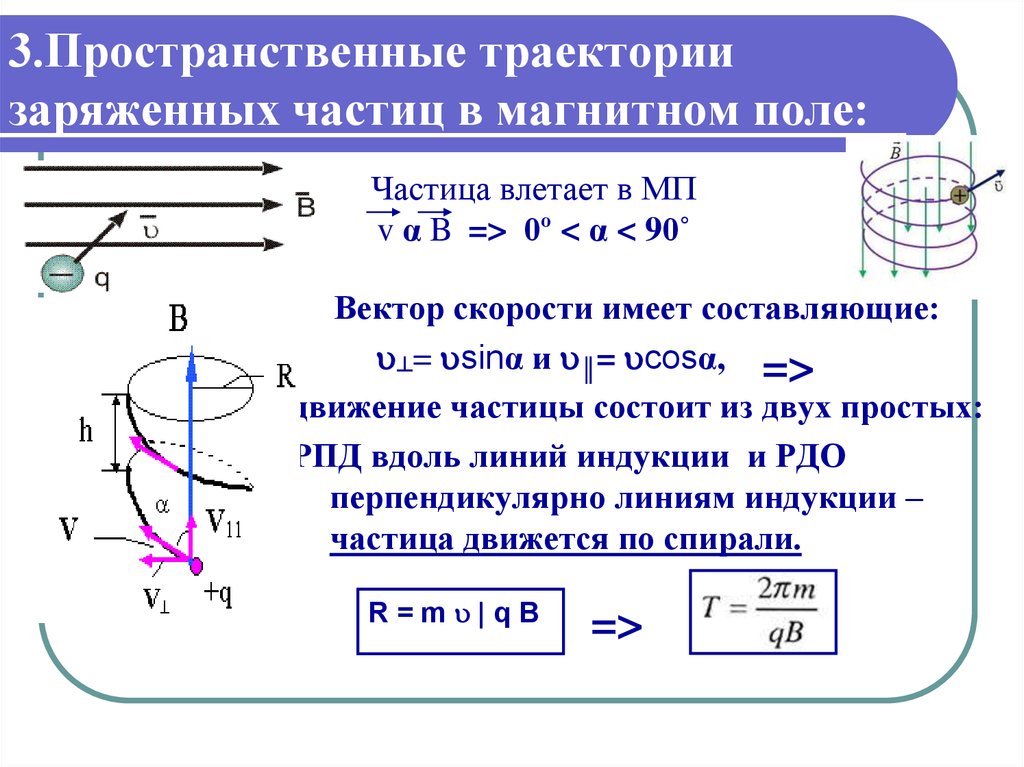

Затем она влетает в однородное магнитное поле индукцией 2,5 Тл, силовые линии которого перпендикулярны скорости частицы. Найти силу, действующую на частицу со стороны магнитного поля. Начальная скорость частицы равна нулю.

Контрольная работа по теме «Магнитное поле». Вариант 2. Уровень 1. №1. Определите силу тока, проходящего по прямолинейному проводнику, перпендикулярному однородному магнитному полю, если на активную часть проводника длиной 20 см действует сила в 50 Н при магнитной индукции 10 Тл. №2. Электрон со скоростью 5 ∙107 м/с влетает в однородное магнитное поле с индукцией 0,8 Тл под углом 300 к линиям индукции. Найти силу, действующую на электрон. №3. В катушке с индуктивностью 0,6 Гн сила тока 20 А. Какова энергия магнитного поля катушки? №4. Определите по условию задачи №2 радиус окружности, по которой движется электрон, период обращения, импульс электрона, его кинетическую энергию, а также ускоряющую разность потенциалов, которую прошел электрон, прежде чем попал в магнитное поле.

Уровень 2. №1. Участок проводника длиной 20 см находится в магнитном поле индукцией 25 мТл. Сила Ампера при перемещении проводника на 8 см в направлении своего действия совершает работу 4 мДж. Проводник расположен перпендикулярно линиям магнитной индукции. Чему равна сила тока, протекающего по проводнику? №2. Плоская прямоугольная катушка из 200 витков со сторонами 10 см и 5 см находится в однородном магнитном поле с индукцией 50 мТл. Какой максимальный вращающий момент может действовать на катушку в этом поле, если сила тока в ней 2 А? №3. Частица массой m, несущая заряд q, движется в однородном магнитном поле с индукцией В по окружности радиуса R со скоростью υ. Что произойдет с радиусом орбиты, импульсом частицы и периодом обращения при увеличении заряда частицы? Физические величины А. радиус орбиты Б. импульс частицы В. период обращения А

Их изменение 1. увеличится 2. уменьшится 3. не изменится Б

В

№4. Прямой проводник длиной 20 см и массой 50 г подвешен на двух легких нитях в однородном магнитном поле, вектор индукции которого направлен горизонтально и перпендикулярно проводнику. Какой силы ток надо пропустить через проводник, чтобы нити разорвались? Индукция поля 50 мТл. Каждая нить разрывается при нагрузке 0,4 Н. №5. Заряженный шарик массой 0,1 мг и зарядом 0,2 мКл влетает в область однородного магнитного поля индукцией 0,5 Тл, имея импульс 6 ∙10-4 кг∙м/с, направленный перпендикулярно линиям магнитной индукции. Какой путь шарик пройдет к тому моменту, когда вектор его скорости повернется на 30 0?

Контрольная работа по теме «Магнитное поле». Вариант 3. Уровень 1. №1. Под каким углом расположен прямолинейный проводник к линиям индукции магнитного поля, если на каждые 10 см длины проводника действует сила 3 Н. Сила тока в проводнике 4 А, индукция магнитного поля 15 Тл. №2. В однородное магнитное поле индукцией 8,5 мТл влетает электрон со скоростью 4,6 ∙106 м/с, направленной перпендикулярно линиям индукции. Рассчитайте силу, действующую на электрон в магнитном поле. №3. Магнитный поток, пронизывающий один виток катушки, равен 15 мВб. Сила тока в катушке 5 А. Сколько витков содержит катушка, если ее индуктивность 0,06 Гн? №4. Определите по условию задачи №2 радиус окружности, по которой движется электрон, период обращения, импульс электрона, его кинетическую энергию, а также ускоряющую разность потенциалов, которую прошел электрон, прежде чем попал в магнитное поле. Уровень 2. №1. Участок проводника находится в магнитном поле, индукция которого 0,04 Тл. Сила электрического тока, протекающего по проводнику, равна 12,5 А. При перемещении проводника на 4 см в направлении действия силы Ампера, поле совершает работу 4 мДж. Проводник расположен перпендикулярно линиям магнитной индукции. Чему равна длина участка проводника? №2. Какую ускоряющую разность потенциалов проходит протон, влетающий в однородное магнитное поле индукцией 2 Тл перпендикулярно его силовым линиям, если он движется по окружности радиусом 50 см? №3. Частица массой m, несущая заряд q, движется в однородном магнитном поле с индукцией В по окружности радиуса R со скоростью υ. Что произойдет с радиусом орбиты, периодом обращения и импульсом частицы при уменьшении индукции магнитного поля? Физические величины А.

радиус орбиты Б.период обращения В. импульс А

Их изменение 1. увеличится 2. уменьшится 3. не изменится Б

В

№4. В вертикальном однородном магнитном поле на двух тонких нитях подвешен горизонтально проводник длиной 20 см и массой 20,4 г. Индукция магнитного поля равна 0,5 Тл. На какой угол от вертикали отклонятся нити, если сила тока в проводнике равна 2 А? №5. Частица зарядом q и массой m влетает в область однородного магнитного поля с индукцией ⃗В. Скорость частицы 𝜗 направлена перпендикулярно силовым линиям поля и границе области. После прохождения области поля частица вылетает под углом α к первоначальному направлению движения. На каком расстоянии d от точки входа в поле вылетит частица из области, «занятой» полем?

Контрольная работа по теме «Магнитное поле». Вариант 4. Уровень 1. №1. Определите длину активной части прямолинейного проводника, помещенного в однородное магнитное поле с индукцией 400 Тл, если на проводник действует сила 100 Н. Проводник расположен под углом 300 к линиям магнитной индукции, сила тока в проводнике 2 А.

№2. С какой скоростью влетел протон в однородное магнитное поле индукцией 10 Тл перпендикулярно силовым линиям поля, если на частицу действует поле с силой 8 ∙10-11Н? №3. Магнитное поле катушки с индуктивностью 95 мГн обладает энергией 0,19 Дж. Чему равна сила тока в катушке? №4. Определите по условию задачи №2 радиус окружности, по которой движется протон, период обращения, импульс электрона, его кинетическую энергию, а также ускоряющую разность потенциалов, которую прошел протон, прежде чем попал в магнитное поле. Уровень 2. №1. Участок проводника длиной 5 см находится в магнитном поле индукцией 50 мТл. Сила электрического тока, протекающего по проводнику, равна 20 А. Проводник расположен перпендикулярно линиям магнитной индукции. Какое перемещение совершает проводник в направлении действия силы Ампера, если работа этой силы 0,004 Дж? №2. Чему равен максимальный вращающий момент сил, действующих на прямоугольную обмотку электродвигателя, содержащую 100 витков провода, размером 4 х 6 см, по которой проходит ток 10 А, в магнитном поле индукцией 1,2 Тл? №3. Частица массой m, несущая заряд q, движется в однородном магнитном поле с индукцией В по окружности радиуса R со скоростью υ. Что произойдет с радиусом орбиты, периодом обращения и кинетической энергией частицы при уменьшении заряда частицы? Физические величины А. радиус орбиты Б.период обращения В. кинетическая энергия А

Их изменение 1. увеличится 2. уменьшится 3. не изменится Б

В

№4. В горизонтальном однородном магнитном поле индукцией 3 Тл перпендикулярно к силовым линиям расположен горизонтальный проводник массой 3 кг. По проводнику протекает электрический ток силой 5 А. Какова длина проводника, если за 0,1 с, двигаясь из состояния покоя, он поднимается вертикально вверх на 2,5 см? №5. В однородном магнитном поле индукцией 2 Тл движется протон. Траектория его движения представляет собой винтовую линию с радиусом 10 см и шагом 60 см. Определить кинетическую энергию протона.

сила Лоренца | Уравнение, свойства и направление

Связанные темы:

магнитное поле

Просмотреть все связанные материалы →

Сила Лоренца , сила, действующая на заряженную частицу q , движущуюся со скоростью v через электрическое поле E и магнитное поле 4 3 Вся электромагнитная сила F on the charged particle is called the Lorentz force (after the Dutch physicist Hendrik A.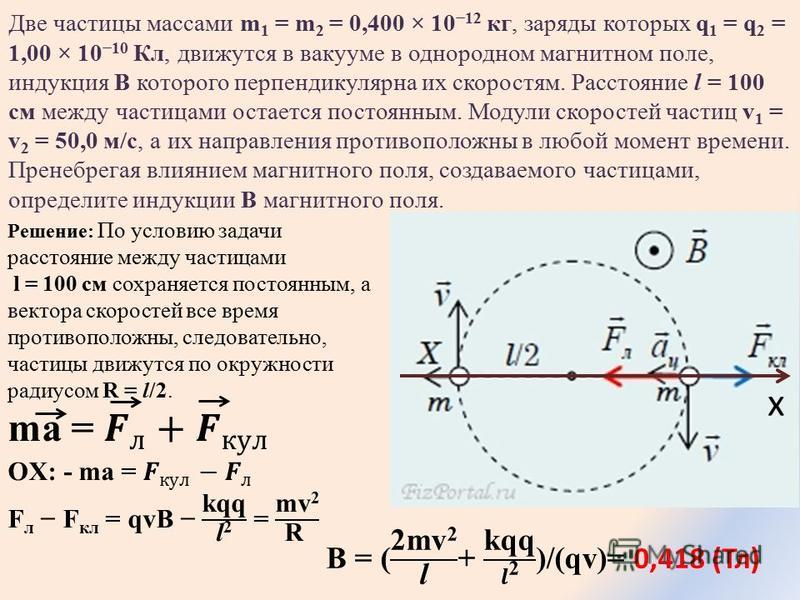 Lorentz) and is given by F =

q E + q v × Б .

В первый член вносит вклад электрическое поле. Второй член представляет собой магнитную силу и имеет направление, перпендикулярное как скорости, так и магнитному полю. Магнитная сила пропорциональна q и величине векторного векторного произведения v × B . В терминах угла ϕ между v и B модуль силы равен q v B sin ϕ. Интересным следствием действия силы Лоренца является движение заряженной частицы в однородном магнитном поле. Если v перпендикулярно B (т. е. угол ϕ между v и B 90°), частица будет двигаться по круговой траектории с радиусом r = м v / q 4 Если угол ϕ меньше 90°, орбита частицы будет представлять собой спираль с осью, параллельной силовым линиям. Если ϕ равно нулю, на частицу не будет действовать магнитная сила, и она будет продолжать двигаться, не отклоняясь, вдоль силовых линий. Ускорители заряженных частиц, такие как циклотроны, используют тот факт, что частицы движутся по круговой орбите, когда v и B расположены под прямым углом. Для каждого оборота тщательно синхронизированное электрическое поле придает частицам дополнительную кинетическую энергию, которая заставляет их двигаться по все более крупным орбитам. Когда частицы приобретают желаемую энергию, их извлекают и используют различными способами, от изучения субатомных частиц до лечения рака.

Магнитная сила, действующая на движущийся заряд, определяет знак носителей заряда в проводнике. Ток, текущий справа налево в проводнике, может быть результатом движения положительных носителей заряда справа налево или отрицательных зарядов, движущихся слева направо, или их комбинации. Когда проводник помещается в B поле перпендикулярно току, магнитная сила на обоих типах носителей заряда имеет одинаковое направление. Эта сила вызывает небольшую разность потенциалов между сторонами проводника. Это явление, известное как эффект Холла (открытое американским физиком Эдвином Х. Холлом), возникает, когда электрическое поле совпадает с направлением магнитной силы. Эффект Холла показывает, что электроны доминируют в проводимости электричества в меди. Однако в цинке преобладает проводимость за счет движения положительных носителей заряда. Электроны в цинке, возбужденные из валентной зоны, оставляют дырки, которые представляют собой вакансии (то есть незаполненные уровни), которые ведут себя как носители положительного заряда. Движение этих отверстий объясняет большую часть проводимости электричества в цинке.

Если провод с током i поместить во внешнее магнитное поле B , как сила, действующая на провод, будет зависеть от ориентации провода? Поскольку ток представляет собой движение зарядов в проводе, сила Лоренца действует на движущиеся заряды. Поскольку эти заряды связаны с проводником, магнитные силы движущихся зарядов передаются на провод. Сила на небольшой длине d l проволоки зависит от ориентации проволоки относительно поля. Величина силы равна I D LB SIN ϕ, где ϕ — угол между B и D L . Сила отсутствует, когда ϕ = 0 или 180°, оба из которых соответствуют току в направлении, параллельном полю. Сила максимальна, когда ток и поле перпендикулярны друг другу. Сила определяется как d F = i d l × Б .

Опять же векторное векторное произведение обозначает направление, перпендикулярное обоим d l и B .

Редакторы Британской энциклопедии Эта статья была недавно отредактирована и дополнена Эриком Грегерсеном.

Частица с зарядом $ — q$ и массой $m$ входит в однородное магнитное поле $\\overrightarrow B$(перпендикулярно бумаге внутрь) в точке P со скоростью ${v_o}$ под углом $\\alpha $ и покидает поле в точке Q со скоростью $v$ под углом $\\beta$, как показано на рисунке.

Тогда\n \n \n \n \n A. $\\alpha = \\beta $B. $v = {v_0}$C. $PQ = \\dfrac{{2m{v_0}\\sin \\alpha }}{{Bq}}$D. Частица остается в поле в течение времени $t = \\dfrac{{2m\\left( {\\Pi

Ответ

Проверено

228,9 тыс.+ просмотров

Подсказка Когда применяется однородное поле, частица всегда описывает симметричный путь. Поскольку скорость частицы перпендикулярна магнитному полю, она будет описывать круговой путь. Из этой информации мы можем рассчитать радиус круга, а также время, необходимое для описания круга.

Используемая формула
$\overrightarrow {{F_m}} = q\left( {\overrightarrow v \times \overrightarrow B } \right)$ Где $\overrightarrow {{F_m}} $ — действующая магнитная сила на частице с зарядом $q$, движущейся со скоростью $\overrightarrow v$ в магнитном поле $\overrightarrow B$. 92}}{r}$, где $r$ — радиус окружности, описываемой частицей, а $m$ — масса частицы.

Полный пошаговый ответ
Магнитное поле может воздействовать на движущийся заряд или проводник с током. Эта сила может быть представлена ​​как
$\overrightarrow {{F_m}} = q\left( {\overrightarrow v \times \overrightarrow B} \right)$
Где $\overrightarrow {{F_m}} $ — сила, действующий на частицу с зарядом $q$, движущуюся со скоростью $\overrightarrow v$ в магнитном поле $\overrightarrow B$.
Вдоль магнитной силы, если существует электрическое поле $\overrightarrow E $, то полная электромагнитная сила на заряде будет равна $\overrightarrow F = q\left[ {\overrightarrow E + \overrightarrow v \times \overrightarrow B } \right]$
Это называется силой Лоренца.
Частица входит в магнитное поле под углом $\alpha $
Известно, что магнитное поле по своей природе однородно. Итак, частица, войдя в магнитное поле, движется по окружности и выходит из поля, образуя угол $\beta $
Поскольку магнитное поле однородно, угол падения и угол выхода должны быть одинаковыми.
Следовательно, $\alpha = \beta $
Опять же, в однородном магнитном поле скорость частицы остается постоянной.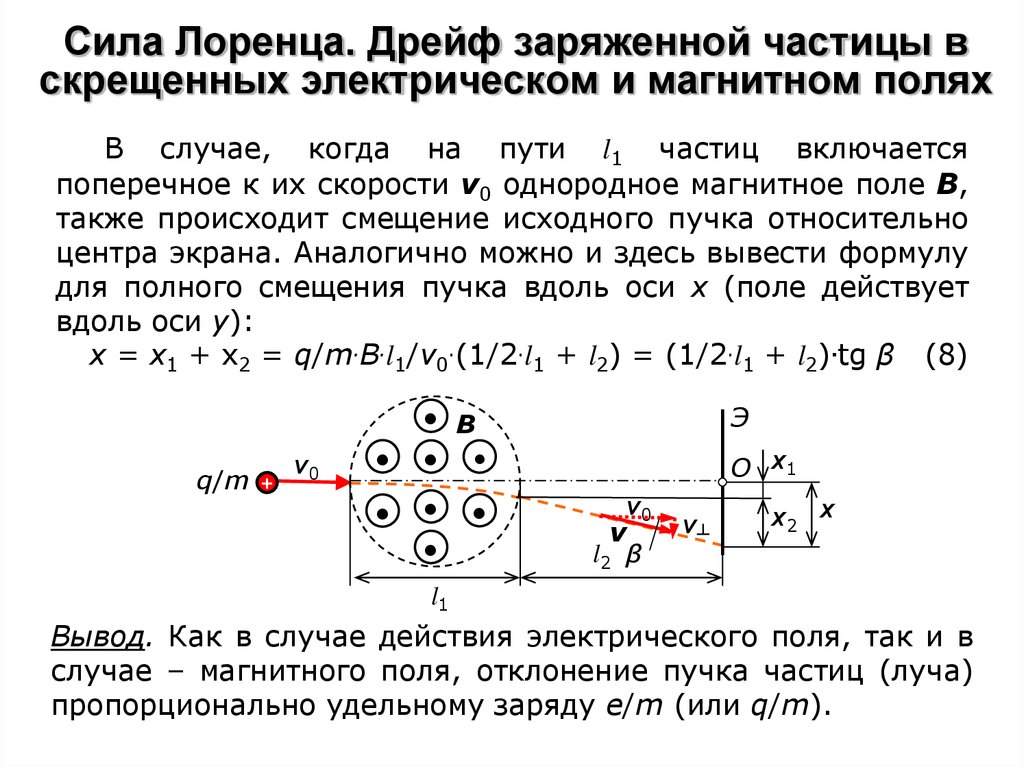 Поэтому скорость частицы перед входом в поле и ее скорость после выхода из поля должны быть одинаковыми.
Таким образом, имеем $v = {v_0}$
 PQ — дуга окружности, описывающая частицу в магнитном поле.
Для этого круга центробежная сила должна быть равна магнитной силе, испытываемой частицей 92}}{r} \\
   \Rightarrow r = \dfrac{{m{v_0}}}{{qB}} \\
\end{gathered} $ ( Так как скорость частицы перпендикулярна направлению магнитного поля.)
Итак, длина дуги PQ определяется выражением $2r\sin \alpha = \dfrac{{2m{v_0}\sin \alpha }}{{qB}}$
Период времени для описания полный круг:
$\begin{gathered}
  T = \dfrac{{2\Pi r}}{{{v_0}}} \\
   \Rightarrow T = \dfrac{{2\Pi m{v_0} }}{{qB{v_0}}} \\
   \Rightarrow T = \dfrac{{2\Pi m}}{{qB}} \\
\end{gathered} $
Где $2\Pi r$ — длина окружности.
Теперь, поскольку частица описывает окружность только под углом $2\alpha $ до того, как покинет поле,
Период времени частицы внутри поля равен $T \times \dfrac{{\left( {2\Pi — 2\alpha } \right)}}{{2\Pi }}$$ = \dfrac{{2\Pi m}}{{qB}} \times \dfrac{{\left( {2\Pi — 2\ alpha } \right)}}{{2\Pi }} = \dfrac{{\left( {2\Pi — 2\alpha } \right)m}}{{qB}}$

Следовательно, все выше варианты верны.

No related posts.