Деление в столбик | интернет проект BeginnerSchool.ru
Деление многозначных или многоразрядных чисел удобно производить письменно в столбик. Давайте разберем, как это делать. Начнем с деления многоразрядного числа на одноразрядное, и постепенно увеличим разрядность делимого.
Итак, поделим 354 на 2. Для начала разместим эти числа как показано на рисунке:
Делимое размещаем слева, делитель справа, а частное будем записывать под делителем.
Теперь начинаем делить делимое на делитель поразрядно слева на право. Находим первое неполное делимое, для этого берем первый слева разряд, в нашем случае 3 и сравниваем с делителем.
3 больше 2, значит 3 и есть неполное делимое. Ставим точку в частном и определяем, сколько ещё разрядов будет в частном – столько же, сколько осталось в делимом после выделения неполного делимого. В нашем случае в частном столько же разрядов, сколько в делимом, то есть старшим разрядом будут сотни:
Для того чтобы 3 разделить на 2 вспоминаем таблицу умножения на 2 и находим число при умножении которого на 2 получим наибольшее произведение, которое меньше 3.
2 × 1 = 2 (2 < 3)
2 × 2 = 4 (4 > 3)
2 меньше 3, а 4 больше, значит, берем первый пример и множитель 1.
Записываем 1 в частное на место первой точки (в разряд сотен), а найденное произведение записываем под делимым:
Теперь находим разность, между первым неполным делимым и произведением найденного разряда частного и делителем:
Далее находим второе неполное делимое, для этого значение следующего разряда делимого опускаем к разности:
Полученное значение сравниваем с делителем. 15 больше 2, значит, мы нашли второе неполное делимое. Для того чтобы найти результат деления 15 на 2 вновь вспоминаем таблицу умножения на 2 и находим наибольшее произведение, которое меньше 15:
2 × 7 = 14 (14 < 15)
2 × 8 = 16 (16 > 15)
Искомый множитель 7, записываем его в частное на место второй точки (в десятки). Находим разность между вторым неполным делимым и произведением найденного разряда частного и делителя:
Находим разность между вторым неполным делимым и произведением найденного разряда частного и делителя:
Продолжаем деление, для чего находим третье неполное делимое. Спускаем следующий разряд делимого:
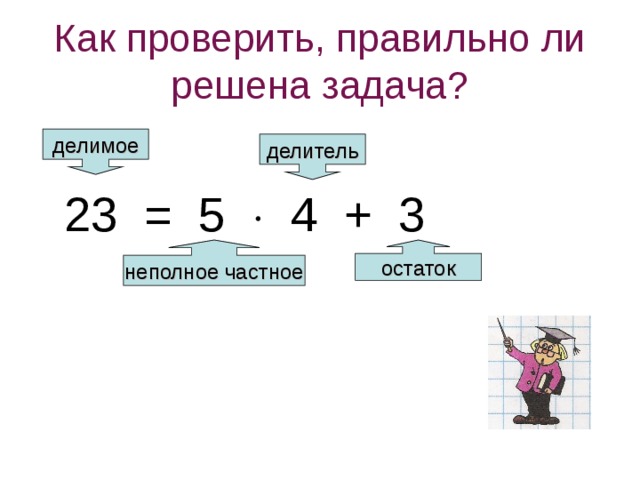
Делим неполное делимое на 2, полученное значение ставим в разряд единиц частного. Проверим правильность деления:
2 × 7 = 14
Результат деления третьего неполного делимого на делитель пишем в частное, находим разность:
Разность мы получили равную нулю, значит деление произведено правильно.
Усложним задачу и приведем другой пример:
1020 ÷ 5
Запишем наш пример в столбик и определим первое неполное частное:
Разряд тысяч делимого составляет 1, сравниваем с делителем:
1 < 5
Добавляем в неполное делимое разряд сотен и сравниваем:
10 > 5 – мы нашли неполное делимое.
Делим 10 на 5, получаем 2, записываем результат в частное. Разность между неполным делимым и результатом умножения делителя и найденного разряда частного.
Разность между неполным делимым и результатом умножения делителя и найденного разряда частного.
10 – 10 = 0
0 мы не пишем, опускаем следующий разряд делимого – разряд десятков:
Сравниваем второе неполное делимое с делителем.
2 < 5
Нам следует добавить в неполное делимое ещё один разряд, для этого в частное, на разряд десятков ставим 0:
20 ÷ 5 = 4
Записываем ответ в разряд единиц частного и проверяем: записываем произведение под второе неполное делимое и вычисляем разность. Получаем 0, значит пример решён правильно.
И ещё 2 правила деления в столбик:
1. Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить, например:
Сколько нулей в младшем разряде делимого мы убираем, столько же нулей убираем в младших разрядах делителя.
2. Если в делимом после деления остались нули, то их следует перенести в частное:
Итак, сформулируем последовательность действий при делении в столбик.
- Размещаем делимое слева, делитель справа. Помним, что делимое мы делим, поразрядно выделяя неполные делимые и деля их последовательно на делитель. Разряды в неполное делимое выделяются слева направо от старших к младшим.
- Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить.
- Определяем первый неполный делитель:
а) выделяем в неполный делитель старший разряд делимого;
б) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (в), если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4;
в) добавляем в неполное делимое следующий разряд и переходим к пункту (б).
- Определяем сколько разрядов будет в частном, и ставим столько точек на месте частного (под делителем) сколько будет в нем разрядов. Одна точка (один разряд) за все первое неполное делимое и остальных точек (разрядов) столько же, сколько осталось разрядов в делимом после выделения неполного делимого.

- Делим неполное делимое на делитель, для этого находим число, при умножении которого на делитель получилось бы число либо равное неполному делимому, либо меньше его.
- Найденное число записываем на место очередного разряда частного (точки), а результат умножения его на делитель записываем под неполным делимым и находим их разность.
- Если найденная разность меньше или равна неполному делимому значит, мы правильно поделили неполное делимое на делитель.
- Если в делимом остались еще разряды, то продолжаем деление, иначе переходим к пункту 10.
- Опускаем к разности следующий разряд делимого и получаем очередное неполное делимое:
а) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (б), если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4;
б) добавляем к неполному делимому следующий разряд делимого, при этом в частное на место следующего разряда (точки) пишем 0;
в) переходим к пункту (а).
10. Если мы выполняли деление без остатка и последняя найденная разность равна 0, то мы правильно выполнили деление.
Мы говорили о делении многоразрядного числа на одноразрядное. В случае, когда разрядность делителя больше, деление выполняется аналогично:
Спасибо, что вы с нами.
Понравилась статья — поделитесь с друзьями:
Оставляйте пожалуйста комментарии в форме ниже
Педагогическая |
| |||||||||||
Тип, вид урока | Урок открытия новых знаний | |||||||||||
Планируемые |
| |||||||||||
Универсальные | Личностные: осознание математических составляющих окружающего мира. Метапредметные: Регулятивные: освоение способов объединения предметов и выделения их из группы по определённым признакам. Познавательные: осмысление понятия «компонентов деления» на предметно-конкретном уровне. Коммуникативные: умение использовать простые речевые средства; включаться в диалог с учителем и сверстниками, в коллективное обсуждение; отвечать на вопросы учителя. | |||||||||||
Формы и методы | Формы: фронтальная, индивидуальная. Методы: словесный, наглядный, практический | |||||||||||
Основное и термины | Делимое, делитель, частное. | |||||||||||
Образовательные ресурсы | Дорофеев Г. Дорофеев Г.В., Миракова Т.В. «Математика. Методические рекомендации. 2 класс. ФГОС»– М. : Просвещение, 2019. Наглядный материал – проектор, экран, цветные карандаши. | |||||||||||
Этап (элемент) | Обучающие и развивающие компоненты, задания и упражнения | Деятельность учителя | Деятельность учащихся | Формы орга- низации взаимодейст- вия на уроке | Текущий | |||||||
осуществляемые действия | формируемые умения | |||||||||||
1 | 2 | 3 | 4 | 5 | 6 | |||||||
I. | Подготовка и эмоциональный настрой к уроку | Приветствует учащихся, проверяет готовность класса и оборудования; эмоционально настраивает на урок -Улыбнемся друг другу и пожелаем удачи. | Приветствуют учителя. Организуют рабочее место, проверяют наличие индивидуальных учебных принадлежностей на столе. Желают друг другу удачи | Личностные: проявляют эмоциональную отзывчивость. Регулятивные: контролируют свои действия | Фронтальная | Наблюдение учителя | ||||||
II. Актуализация знаний | 1.Устный счет «Игра Молчанка» | Разминка для ума. Запишите только ответы в тетради.
Положили ручку, взяли карандаш Я даю образец, эталон, как должно быть: (6) (15) (20) (4) (17) (14) (9) (18) (слайд 1) — Встаньте те, у кого нет ошибок. — Встаньте те, у кого 1 ошибка. МОЛОДЦЫ! | Записывают ответы в тетрадь. Осуществляют самопроверку, сверяют написанное с образцом. | Познавательные: осуществляют анализ объектов; используют наглядный материал для решения учебной задачи Коммуникативные: осознанно и произвольно строят речевые высказывания в устной форме. | Фронтальная | Наблюдение учителя | ||||||
III. Постановка проблемы. Открытие новых знаний. | 1.Постановка проблемной задачи 2. «Открытие» нового знания. 3.Сообщение темы | На экране даны числовые выражения: 6 + 3 8: 2 4 * 5 7 — 2 (слайд 2) — На какие известные группы вы можете разделить эти математические выражения? — Давайте прочитаем эти математические выражения, используя названия компонентов. Проблемная ситуация: -Какое выражение нам не известно? -Можем ли мы прочитать его? — Почему мы не можем прочитать? (не знаем компонентов при делении). ЧЕМУ МЫ ДОЛЖНЫ НАУЧИТЬСЯ НА УРОКЕ? (слайд 3) Ответы детей (узнать, как называются числа при делении). Зачем нужно знать название чисел при делении? (чтобы уметь читать выражения) И так, цели нашего урока: (слайд 4)
Что за тема урока? Как вы думаешь? Попробуйте сформулировать тему урока. (Компоненты действия деления) 8: 2 (на доске) -Назовите первое число в выражении. (8) -Что делают с этим числом? -Прочитайте, как называется число, которое делят (делимое) -Назовите число в выражении, на которое делят. (2) -Прочитайте, как оно называется … делитель Чему равно значение этого выражения? (4) 4 – это часть от деления чисел 8 и 2. (частное) — Давайте все вместе повторим компоненты при делении -Какие же главные слова будут звучать на уроке математики сегодня? (слайд 5) Делимо Делитель Частное
— А теперь, когда вы узнали, как называются числа при делении, попробуйте прочитать пример 8: 2 = 4 математическим языком. (8 разделить на 2, получится 4.) — Прочитайте пример, называя компоненты и результат. (Делимое 8, делитель2, частное 4.) — Прочитайте пример, называя выражение. | Предлагают варианты ответов. Называют тему урока | Познавательные: осознают познавательную задачу Коммуникативные: строят свои высказывания и слушают другого. | Фронтальная | |||||||
4.Физкульт- минутка 5.Первичное закрепление. | Проводит физкультминутку В чистом поле теремок Был ни низок, ни высок. Звери разные там жили, Жили дружно, не тужили. Там и мышка, и лягушка Зайчик с лисонькой –подружкой Серый волк –зубами щелк В дружбе знали они толк. Но набрел на теремок Мишка косолапый. Раздавил он теремок Своей огромной лапой. Звери очень испугались, Поскорее разбежались. А потом собрались снова Чтоб построить терем новый. Ребята, давайте откроем учебник на странице 88 и прочитаем правило. Итак, с правилом мы с вами познакомились, а теперь давайте «завяжем узелки на память», УПРАЖНЕНИЕ 1, страница 88. | Выполняют движения присели, встали руки вытянуты вверх поклон на носочках, присели прыжки показали руками «пасть» изобразить мишку кулачок об кулачок бег на месте сели на стульчики Прочитывают выражения разными способами | Осуществляют профилактику утомления. Познавательные: осознают познавательную задачу. Регулятивные: понимают и сохраняют учебную задачу. Коммуникативные: Высказывают и аргументируют свое мнение. | Наблю-дение учителя Устные ответы | ||||||||
IV. | 1.Первичная проверка понимания 2.Работа по учебнику с.89 упр.3 | — ЗАДАЧА: стр. 89, № 5 — Читаем условие задачи. -О ком говорится в задаче? (о мальчиках) -Читаем вопрос задачи. -Что значит поровну? -Что нам известно? -Каким арифметическим действием мы можем решить эту задачу? -Что вы будете делить? А теперь давайте запишем эту задачу в тетрадь. ЗАДАЧА: стр. 89, №6 — Читаем условие задачи. -О ком говорится в задаче? (о мальчиках) -Читаем вопрос задачи. -Что значит каждый? -Что нам известно? -Каким арифметическим действием мы можем решить эту задачу? -Что вы будете делить? Давайте проверим правильность выполнения задания.(выборочно) Самостоятельная работа по учебнику стр. 89 № 3 Решай только те примеры, в которых делимое больше 10 Сколько примеров ты решил? Сверь с экраном (слайд 7) 18: 2 = 9 14: 2 = 7 16: 2 = 8 Оцени себя. | Читают, отвечают на вопросы учителя. Составляют краткую запись, оформляют решение и отвтр задачи. Читают, отвечают на вопросы учителя. Составляют краткую запись, оформляют решение и отвтр задачи | Регулятивные: принимают и сохраняют учебную цель и задачу. Познавательные: понимают информацию в форме схем и рисунков. Коммуникативные: Вступают в сотрудничество с одноклассниками. Личностные: осознают ответственность за свои действия. Регулятивные: контролируют процесс и результаты деятельности. Познавательные: осуществляют анализ объектов. Коммуникативные: строят рассуждения в форме связи простых суждений об объекте. | Фронтальная работа Индивидуальная работа | Наблюдение учителя Работа в тетради Самопроверка | ||||||
V. | Обобщающая беседа | Анализирует и оценивает успешность -Давайте вспомним тему сегодняшнего урока? -Как называют первое число при делении? Второе число? -Как называется результат деления? -Какое задание было самым трудным? А задачи которые были на уроке , трудные? | Формулируют полные ответы на вопросы. | Коммуникативные: формулируют собственное мнение. Регулятивные: адекватно воспринимают качественную оценку своей работы. Личностные: показывают отношение к предмету. | ||||||||
VI. Рефлексия. | Продолжи предложения: Я узнал… Я запомнил… Я научился… Я удивился… — Оцените свою работу на уроке с помощью сигнального светофора. | Высказывают предположения. Дают оценку своей работы на уроке | ||||||||||
Делимость или неделимость: понятие преемственности от досократиков до Аристотеля | История Continua: философские и математические перспективы
Фильтр поиска панели навигации Oxford AcademicThe History of Continua: Philosophical and Mathematical PerspectivesMetaphysicsBooksJournals Мобильный телефон Введите поисковый запросЗакрыть
Фильтр поиска панели навигации Oxford AcademicThe History of Continua: Philosophical and Mathematical PerspectivesMetaphysicsBooksJournals Введите поисковый запрос
Расширенный поиск
Иконка Цитировать Цитировать
Разрешения
- Делиться
- Твиттер
- Подробнее
Укажите
Сэттлер, Барбара М. , «Делимость или неделимость: понятие непрерывности от досократиков до Аристотеля», в Стюарт Шапиро и Джеффри Хеллман (редакторы), История континуума: философские и математические перспективы (
, «Делимость или неделимость: понятие непрерывности от досократиков до Аристотеля», в Стюарт Шапиро и Джеффри Хеллман (редакторы), История континуума: философские и математические перспективы (
, 2020 ; онлайн-издание, Oxford Academic, 17 декабря 2020 г.), https://doi.org/10.1093/oso/9780198809647.003.0002, по состоянию на 26 февраля 2023 г.
Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Фильтр поиска панели навигации Oxford AcademicThe History of Continua: Philosophical and Mathematical PerspectivesMetaphysicsBooksJournals Мобильный телефон Введите поисковый запрос
Закрыть
Фильтр поиска панели навигации Oxford AcademicThe History of Continua: Philosophical and Mathematical PerspectivesMetaphysicsBooksJournals Введите поисковый запрос
Advanced Search
Abstract
Цель этой главы — показать, что самая ранняя дискуссия о непрерывности в западной мысли — это дискуссия в рамках метафизики и натурфилософии об однородности и делимости. Все стороны в этом споре — главными сторонниками являются Парменид, Зенон и Аристотель — соглашаются, что непрерывные величины ( сунэч ) однородны и не имеют пропусков. Однако они расходятся во мнениях относительно того, какие выводы следует из этого сделать для возможности делимости — подразумевает ли это неделимость, как предполагали Парменид и Зенон, или делимость, как утверждал Аристотель, основываясь на математическом понимании протяженных величин. Более того, хотя современное понимание непрерывности может показаться по существу антиаристотелевским, показано, что Аристотель подготовил многие из важнейших черт современного понимания непрерывности в этих дебатах.
Все стороны в этом споре — главными сторонниками являются Парменид, Зенон и Аристотель — соглашаются, что непрерывные величины ( сунэч ) однородны и не имеют пропусков. Однако они расходятся во мнениях относительно того, какие выводы следует из этого сделать для возможности делимости — подразумевает ли это неделимость, как предполагали Парменид и Зенон, или делимость, как утверждал Аристотель, основываясь на математическом понимании протяженных величин. Более того, хотя современное понимание непрерывности может показаться по существу антиаристотелевским, показано, что Аристотель подготовил многие из важнейших черт современного понимания непрерывности в этих дебатах.
Ключевые слова: делимость, отношение часть-целое, бесконечность, предел, актуальная/потенциальная, парадоксы, однородность
Субъект
Метафизика
В настоящее время у вас нет доступа к этой главе.
Вы вошли как
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Щелкните Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Вход через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. См. ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.
д.
Покупка
Наши книги можно приобрести по подписке или купить в библиотеках и учреждениях.
Информация о покупке
Делимое имущество в Северной Каролине
Раздел имущества во время бракоразводного процесса может стать очень сложным, а иногда и спорным. Существуют различные виды имущества, которое суд должен разделить между супругами, включая совместное имущество, раздельное имущество и делимое имущество. Если вы не знакомы с концепцией делимого имущества в Северной Каролине, читайте дальше, чтобы узнать больше.
Что такое делимое имущество?
Как правило, отдельным имуществом является имущество, которое каждый из супругов вносит в брак. Совместно нажитое имущество – это имущество, которое супруги приобрели совместно во время брака и до даты их развода. Однако стоимость имущества может измениться в течение годичного периода разделения. Или супруг может получить имущество во время раздельного проживания, которое он или она заработали во время брака. Как классифицировать это имущество, если оно не является совместной собственностью? Закон Северной Каролины называет это «делимой собственностью».
Как классифицировать это имущество, если оно не является совместной собственностью? Закон Северной Каролины называет это «делимой собственностью».
Примеры делимого имущества
Делимое имущество включает:
- Сумма увеличения или уменьшения стоимости совместно нажитого имущества после раздельного проживания, но до окончательного раздела имущества (за исключением имущества, которое увеличилось/уменьшилось в цене из-за пост- разделительные действия)
- Имущество, полученное супругами после даты развода, которое было приобретено благодаря усилиям одного из супругов во время брака
- Пассивный доход, такой как проценты или дивиденды от военного имущества, полученные после даты увольнения
- Другие пассивные увеличения и уменьшения стоимости имущества супругов (например, расходы на финансирование или начисленные проценты)
Некоторыми примерами делимого имущества могут быть проценты, начисляемые в период раздельного проживания по совместным кредитам, или премия, которую один из супругов заработал до развода, но получает во время раздельного проживания.
Как делится делимое имущество?
При разводе суд либо разделяет делимое имущество поровну, либо решает, что равное деление не справедливо. Если равное деление несправедливо, то суд принимает справедливое решение с учетом всех обстоятельств. Этот процесс может помочь избежать споров о том, какое имущество принадлежит какому из супругов.
Может ли соглашение о раздельном проживании повлиять на делимое имущество?
Если вы и ваш супруг соглашаетесь подписать соглашение о раздельном проживании, оно может включать положения о разделе вашего делимого имущества. Вы можете решить, что не хотите, чтобы суд занимался разделом имущества. Или у вас могут быть другие идеи о том, как разделить его, чем указано в законах Северной Каролины по умолчанию. Вы и ваш супруг можете заключить соглашение о раздельном проживании с помощью ваших юристов.
Кроме того, вы можете воспользоваться альтернативными методами разрешения споров, такими как посредничество или арбитраж.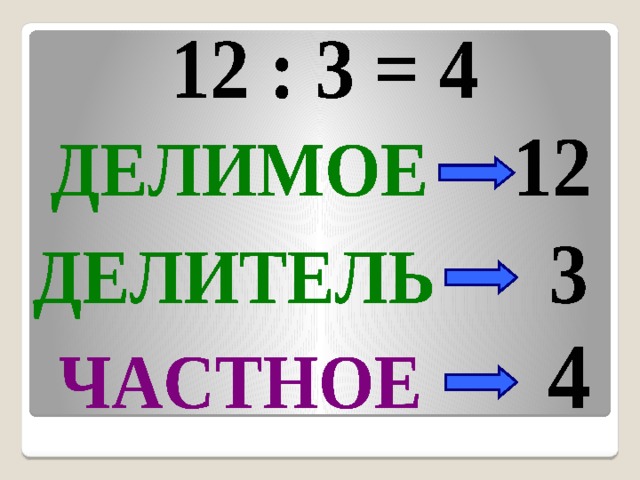


 В., Миракова Т.В. Математика: Учебник: 2 класс 1 часть; – М. : Просвещение, 2017.
В., Миракова Т.В. Математика: Учебник: 2 класс 1 часть; – М. : Просвещение, 2017.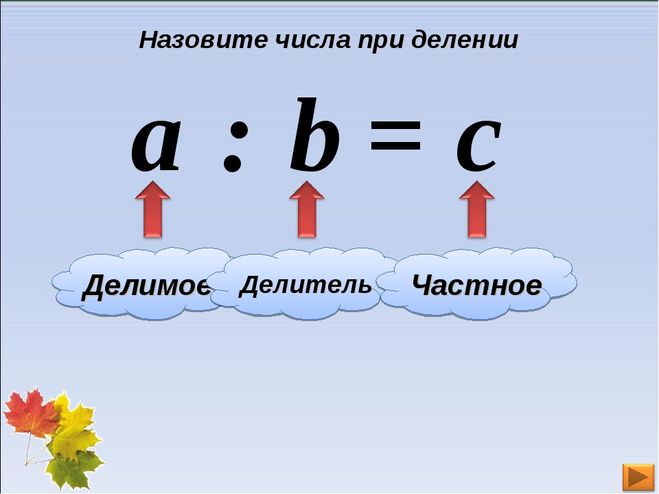 Организационный момент
Организационный момент (6)
(6)

 (Частное чисел 8 и 2 равно4.) Молодцы! Теперь вы умеете читать математические выражения разными способами, называя компоненты деления.
(Частное чисел 8 и 2 равно4.) Молодцы! Теперь вы умеете читать математические выражения разными способами, называя компоненты деления. 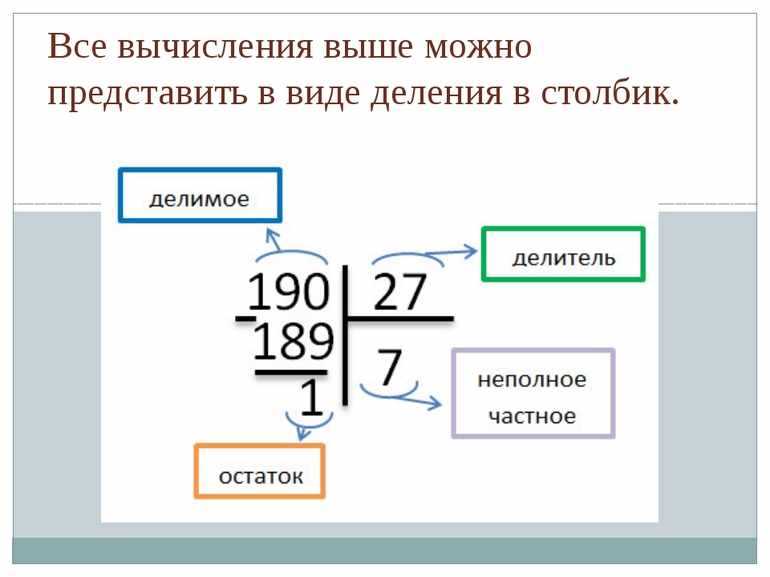
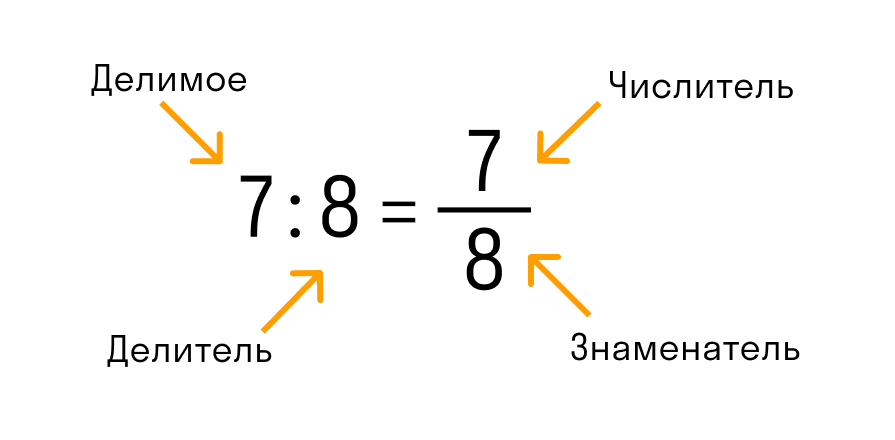 Закрепление знаний
Закрепление знаний Поставь «+», если ты справился верно.
Поставь «+», если ты справился верно.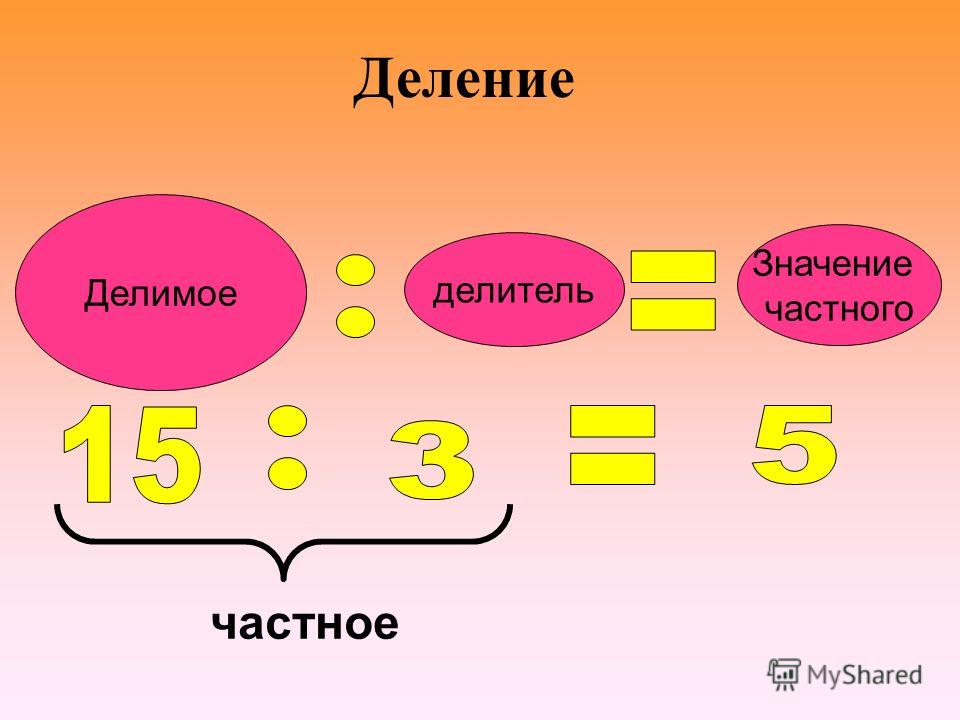 Итог урока.
Итог урока.