Частные производные калькулятор: Частная производная. Онлайн калькулятор с примерами

Производная функции нескольких переменных. Нахождение частных производных функции нескольких переменных. Применение производной к исследованию функций нескольких переменных

ОГБПОУ «НОВГОРОДСКИЙ АГРОТЕХНИЧЕСКИЙ ТЕХНИКУМ»

Инструкционная карта на выполнение

Практического занятия № 5 по дисциплине

«Математика»

Тема: Производная функции нескольких переменных

Наименование работы:. Нахождение частных производных функции нескольких переменных. Применение производной к исследованию функций нескольких переменных

Наименование объектов контроля и оценки	Основные показатели оценки результата
Умения: Решать прикладные задачи в области профессиональной деятельности. Знания: Значение математики в профессиональной деятельн ости и при освоении ППССЗ; Основные математические методы решения прикладных задач в области профессиональной деятельности; Основы интегрального и дифференциального исчисления	Оценка результатов выполнения практических работ

Норма времени: 4 часа;

Условия выполнения: учебный кабинет;

Оснащение рабочего места: инструкционная карта, калькулятор

Правила по технике безопасности: С правилами техники безопасности на рабочем месте ознакомлены;

Литература: Хрипунова М.Б. Высшая математика. Учебник и практикум для спо М.:Юрайт.2018г.-474с

Уровни усвоения: 1 – 4 задания – 2 уровень

Домашнее, самостоятельное задание – 3 уровень

Теоретическая часть.

1.Частные производные первого порядка

Определение. Если существует конечный предел отношения частного приращения по х функции z=f(x;y) в точке М₀(х₀;у₀) к приращению , то этот предел называется частной производной по х функции z=f(x;y) в точке М₀ и обозначается одним из символов:

Аналогично частная производная по у от функции z=f(x;y) определяется как предел отношения частного приращения функции у к приращению при стремлении к нулю. Частная производная по у обозначается одним из символов:

Пример. Вычислить частные производные следующих функций:

2. Частные производные высших порядков.

Определение. Частными производными второго порядка от функции z=f(x;y) называются частные производные от функций Общее число вторых производных от функции двух переменных – четыре, так как каждую производную можно продифференцировать как по х, так и по у.

Пример. Найти вторые частные производные от функции

Сначала находим первые частные производные:

Находим вторые производные:

3. Экстремум функции нескольких переменных.

Теорема. (необходимое условие экстремума). Если функция u=f(M) непрерывна в некоторой области D и во внутренней точке М₀ области D имеет экстремум, то в этой точке все ее частные производные первого порядка или не существуют, или обращаются в нуль.

Точки, в которых частные производные не существуют, или равны нулю, называются критическими точками функции.

Рассмотрим функцию двух переменных. Обозначим значения вторых частных производных в точке

М₀(х₀,у₀) через А, В, С.

Достаточные условия экстремума. Пусть в некоторой области, содержащей точку М₀(х₀,у₀), функция u=f(x,y) непрерывна со своими частными производными до третьего порядка включительно и пусть М₀(х₀,у₀) — критическая точка функции f(x,y), т. е. . Тогда в точке М₀:

1. Функция u=f(x,y) имеет максимум, если АС-В²0, А

2. Функция u=f(x,y) имеет минимум, если АС-В²0, А0;

3. Функция u=f(x,y) не имеет экстремума, если АС-В²

4. Если АС-В²=0, то требуются дополнительные исследования, т.к. в этом случае функция может иметь, а может не иметь экстремума.

Пример. Исследовать на экстремум функцию

Решение:

1. Находим первые частные производные и приравниваем их к нулю.

1. После решения уравнений мы нашли точки, подозреваемые на экстремум:

1. Вычисляем вторые частные производные в точках, подозреваемых на экстремум:

1. Проверяем выполнение достаточных условий экстремума:

В точке , — функция имеет минимум

В точке — функция не имеет экстремума

Практическая часть.

1. Найти частные производные первого порядка:

а) б)

1. Найти частные производные функции в точке

1. Найти частные производные второго порядка для функций. Покажите, что

а) б)

1. Исследовать функции на экстремум.

а) б)

Домашнее задание:

1. Найти частные производные второго порядка функции

1. Исследовать функцию на экстремум:

Самостоятельная работа:

1 вариант.

1. Найти частные производные второго порядка функции

1. Исследовать функцию на экстремум:

2 вариант.

1. Найти частные производные второго порядка функции

1. Исследовать функцию на экстремум:

Критерии оценки:

«5» — Правильно решены 2 задания.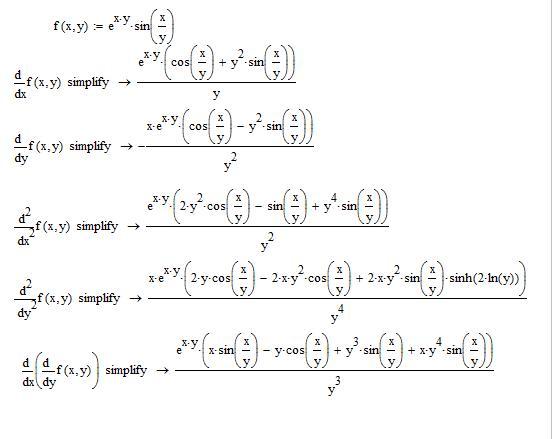

«4» — Правильно решено 1-е задание, второе выполнено не до конца, либо допущена одна вычислительная ошибка.

«3» — Правильно решено 1 задание.

«2» — Одно задание выполнено, но с ошибками; либо не выполнено ничего

Дискретная производная или Коротко о том, как суммировать ряды / Хабр

Бывало когда-нибудь такое, что вы хотите просуммировать какой-то бесконечный ряд, но не можете подобрать частичную сумму ряда? Вы все ещё не пользовались дискретной производной? Тогда мы идём к вам!

Определение

Дискретной производной последовательности назовем такую последовательность , что для любых натуральных выполняется:

Рассмотрим примеры:

Ну, суть вы поняли. Чем-то напоминает производную функции, правда? Мы поняли как вычислять дискретные производные «простейших» последовательностей. Кхм, но что делать с суммой, разностью, произведением и частным последовательностей? У «обычной» производной есть некоторые правила дифференцирования. Давайте-ка придумаем для дискретной!

Сначала рассмотрим сумму. Логично, что сумма последовательностей это тоже какая-то последовательность. Попробуем найти производную по определению:

Феноменально! Мы получили, что производная суммы последовательностей есть сумма производных этих последовательностей!

спасибо, кэп

Попробуем доказать тоже самое с разностью

А мы переходим к произведению!
Аналогично, найдем по определению:

Круто, правда? Рассмотрим частное:

Cool. ..

Но это все производная. Может, есть и дискретная первообразная? Оказывается, есть!

Еще определения

Дискретной первообразной последовательности называют такую последовательность что для любых натуральных выполняется:

С этим понятно. Го придумаем аналог Ньютона-Лейбница!

Да ладно! Вот это

прикол

совпадение! А теперь то же самое покрасивее:

И обобщим на множество натуральных чисел от до :

Кто помнит ту самую формулу для суммы ряда квадратов натуральных чисел от до ? А вот и я не помню. Давайте-ка ее выведем!
Но для начала надо найти первообразную для последовательности :

А теперь, собственно, сама сумма:

Как насчет суммы кубов?

Сначала вычислим

Первообразная для :

Кхм, казалось бы, ничего сложного…

Для продвинутых

Не всегда так просто найти интеграл, правда? Что мы делаем в трудных случаях? Правильно, интегрируем по частям. Быть может, есть аналог? Не буду вас томить, он есть, и сейчас мы его выведем.

Допустим, надо вычислить сумму ряда

Что делать? Вряд ли вы сможете так просто подобрать дискрентную первообразную к последовательности. Давайте смотреть.

Мы уже знаем, что:

Тогда

А теперь один нетривиальный шаг:

Все внутренние слагаемые взаимно уничтожились.

Подставим в полученное до этого равенство:

Финита ля комедия.

Найдем ту самую сумму:

Кому-то может показаться, будто формула стала еще более громоздкой, и мы только усложнили себе работу. Но это не так. Пусть , тогда:

Воу! Мы нашли явную формулу для частичной суммы ряда. Неплохо, правда?
Никто и не спорит, что было достаточно непросто. Но как говорил Александр Суворов: Тяжело в учении — легко в бою.
Так давайте же попробуем применить наши новые знания в боевых действиях!

Прикольная задачка

Предлагаю попрактиковаться с этим на примере задачки с отбора в Tinkoff Generation на курсы по Machine Learning. Вот сама задачка:

Вы устали решать задачки с отборов на курсы Tinkoff Generation и решили устроить перерыв, посмотрев несколько серий нового сериала, о котором все говорят.

Вы начинаете смотреть все серии, начиная с первой. Каждая серия длится один час. После просмотра очередной серии, вы с постоянной вероятностью ppp начинаете смотреть следующую, иначе ваш перерыв заканчивается, и вы возвращаетесь к работе.

Голод, сон и прочие нужды вас не останавливают, а в сериале бесконечное количество серий; в теории, ваш перерыв может длиться бесконечно.

Сколько в среднем будет длиться ваш перерыв?

Строго говоря, здесь нам нужно найти математическое ожидание. Давайте разбираться.

Решение

Вероятность того, что перерыв будет длиться 1 час, равна:

2 часа

n часов:

Тогда математическое ожидание равно:

Знакомо, правда?

Мы уже находили, что

тогда совсем очевиден нужный нам ряд:

И задача сводится к нахождению предела последовательности

где , так как — вероятность события.
Докажем теперь, что

• 
  

• 
  

Теперь легко понять, что

И

Some up

Фух… Это было

easy-peasy

жестко, даже для меня, дорогие читатели. Список достижений за сегодня:

1. Мы поняли, что такое дискретная производная
2. Вывели свойственные ей правила дифференцирования
3. Мы поняли, что такое дискретная первообразная
4. Мы вывели аналог формулы Ньютона-Лейбница
5. Вывели аналог интегрирования по частям
6. Решили сложную задачку с отбора на курс по Machine Learning в Tinkoff Generation

Неплохо для начала, а вы как считаете?

Комментарии приветствуются!

Пошаговый пример обратного распространения — Мэтт Мазур

Предыстория

Обратное распространение — распространенный метод обучения нейронной сети. В Интернете нет недостатка в статьях, пытающихся объяснить, как работает обратное распространение ошибки, но лишь немногие из них содержат примеры с реальными числами. Этот пост — моя попытка объяснить, как это работает, на конкретном примере, с которым люди могут сравнить свои собственные расчеты, чтобы убедиться, что они правильно понимают обратное распространение.

Обратное распространение в Python

Вы можете поиграть с написанным мной скриптом Python, который реализует алгоритм обратного распространения в этом репозитории Github.

Визуализация обратного распространения

Для интерактивной визуализации, показывающей нейронную сеть по мере ее обучения, ознакомьтесь с моей визуализацией нейронной сети.

Дополнительные ресурсы

Если вы считаете этот учебник полезным и хотите продолжить изучение нейронных сетей, машинного обучения и глубокого обучения, я настоятельно рекомендую ознакомиться с новой книгой Адриана Роузброка «Глубокое обучение для компьютерного зрения с помощью Python». Мне книга очень понравилась, скоро будет полноценный обзор.

Обзор

В этом уроке мы будем использовать нейронную сеть с двумя входами, двумя скрытыми нейронами и двумя выходными нейронами. Кроме того, скрытые и выходные нейроны будут иметь смещение.

Вот базовая структура:

Чтобы иметь некоторые числа для работы, вот начальные веса, смещения и входные/выходные данные обучения:

Цель обратного распространения — оптимизировать веса так, что нейронная сеть может научиться правильно отображать произвольные входы в выходы.

В оставшейся части этого руководства мы будем работать с одним обучающим набором: при входных данных 0,05 и 0,10 мы хотим, чтобы нейронная сеть выдавала значения 0,01 и 0,99.

Прямой проход

Для начала давайте посмотрим, что в настоящее время предсказывает нейронная сеть, учитывая приведенные выше веса и смещения и входные данные 0,05 и 0,10. Для этого мы будем передавать эти входные данные по сети.

Мы вычисляем суммарных входных данных для каждого нейрона скрытого слоя, сквош общий чистый ввод с использованием функции активации (здесь мы используем логистическую функцию ), затем повторите процесс с нейронами выходного слоя.

Общий чистый вход также упоминается как чистый вход в некоторых источниках.

Вот как мы вычисляем общий чистый вход для:

Затем мы сжимаем его, используя логистическую функцию, чтобы получить результат:

Выполняя тот же процесс, мы получаем:

Мы повторяем этот процесс для нейронов выходного слоя, используя выходные данные нейронов скрытого слоя в качестве входных данных.

Вот результат для:

Выполняя тот же процесс для мы получаем:

Вычисление общей ошибки

900 квадрат ошибки для каждого нейрона функция теперь мы можем вычислить ошибку ошибки для каждого нейрона04 и просуммируйте их, чтобы получить общую ошибку:

Некоторые источники называют цель как идеальный и вывод как фактический .

Включено, чтобы показатель степени отменялся, когда мы позже будем дифференцировать. Результат в конечном итоге умножается на скорость обучения, поэтому не имеет значения, что мы вводим здесь константу [1].

Например, целевой вывод для равен 0,01, но вывод нейронной сети 0,75136507, поэтому ее ошибка:

Повторяя этот процесс для (помня, что цель равна 0,99), мы получаем:

Общая ошибка нейронной сети представляет собой сумму следующих ошибок:

Обратный проход

Наша цель с обратным распространением — обновить каждый из весов в сети, чтобы они привели к тому, что фактический результат будет ближе к целевому выходу, тем самым минимизируя ошибку для каждого выходного нейрона и сети в целом.

Выходной слой

Учитывать . Мы хотим знать, насколько изменение влияет на общую ошибку, также известную как .

читается как «частная производная по отношению к». Вы также можете сказать «градиент по отношению к».

Применяя цепное правило, мы знаем, что:

Визуально, вот что мы делаем:

Нам нужно вычислить каждую часть в этом уравнении.

Во-первых, насколько изменится общая ошибка по отношению к выходу?

иногда выражается как

Когда мы берем частную производную полной ошибки по , величина становится равной нулю, потому что не влияет на нее, что означает, что мы берем производную константы, которая равна нуль.

Далее, насколько изменится выпуск по отношению к его общему чистому входу?

Частная производная логистической функции представляет собой выпуск, умноженный на 1 минус выпуск:

Наконец, насколько изменится общий чистый ввод по отношению к ?

Складываем все вместе:

Вы часто будете видеть этот расчет в виде дельта-правила:

В качестве альтернативы у нас есть и , который можно записать как , он же (греческая буква дельта), он же узел дельта .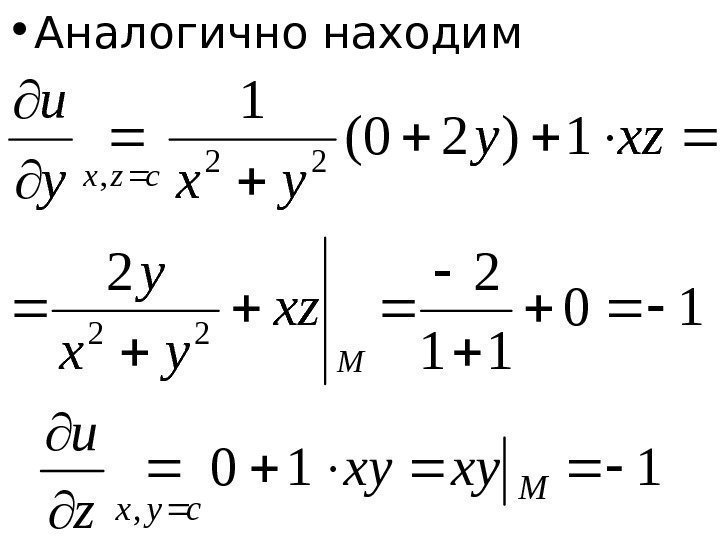 Мы можем использовать это, чтобы переписать приведенный выше расчет:

Следовательно:

Некоторые источники извлекают отрицательный знак, поэтому это будет записано как:

Чтобы уменьшить ошибку, мы затем вычитаем это значение. от текущего веса (необязательно умноженного на некоторую скорость обучения, eta, которую мы установим равной 0,5):

Некоторые источники используют (альфа) для представления скорости обучения, другие используют (эта), а третьи даже используют (эпсилон).

Мы можем повторить этот процесс, чтобы получить новые веса , и : мы используем исходные веса, а не обновленные веса, когда мы продолжаем алгоритм обратного распространения ниже).

Скрытый слой

Далее мы продолжим обратный проход, вычислив новые значения для , , и .

Общая картина, вот что нам нужно выяснить:

Визуально:

выход каждого нейрона скрытого слоя способствует выходу (и, следовательно, ошибке) нескольких выходных нейронов. Мы знаем, что это влияет на оба, и поэтому необходимо учитывать его влияние на оба выходных нейрона:

Начало с:

Мы можем рассчитать с использованием значений, которые мы рассчитали ранее:

и равны:

Подключив их в:

. получаем:

Следовательно:

Теперь, когда у нас есть , нам нужно вычислить и затем для каждого веса:

как мы сделали для выходного нейрона:

Сделать все вместе:

Вы также можете увидеть это написано как:

Мы можем обновить:

Наконец-то мы обновили все наши веса! Когда мы изначально передавали входы 0,05 и 0,1, ошибка в сети была 0,298371109. После этого первого раунда обратного распространения общая ошибка снизилась до 0,29.1027924. Может показаться, что это немного, но после повторения этого процесса, например, 10 000 раз, ошибка падает до 0,0000351085. В этот момент, когда мы упреждаем 0,05 и 0,1, два выходных нейрона генерируют 0,015912196 (против целевого значения 0,01) и 0,984065734 (против целевого значения 0,99).

Если вы дочитали до этого момента и обнаружили какие-либо ошибки в чем-либо из вышеперечисленного или думаете, как сделать это более понятным для будущих читателей, не стесняйтесь, напишите мне. Спасибо!

И пока ты у меня есть…

Помимо занятий наукой о данных, я запускаю Preceden timeline maker, лучшее программное обеспечение для создания хронологий в Интернете. Если вам когда-либо понадобится создать временную шкалу или дорожную карту высокого уровня, чтобы организовать или согласовать свою команду, Preceden — отличный вариант.

Нравится:

Нравится Загрузка…

Калькулятор частных производных — Найдите многомерную производную

Знакомство с калькулятором частных производных

Калькулятор частных производных представляет собой онлайн-инструмент для нахождения производных нескольких переменных. Этот калькулятор уравнения частичного дифференцирования является бесплатным инструментом.

Калькулятор частичного дифференцирования — это инструмент для понимания природы функции, зависящей от более чем одной переменной. Этот калькулятор производных с несколькими переменными позволяет учащимся и другим пользователям быстро выполнять дифференцирование.

На этом веб-сайте мы также предлагаем калькулятор n-й производной для нахождения производной один, два, три и до n-го раз.

Что такое калькулятор частичной дифференциации?

Частные производные в исчислении — это функции, имеющие более одной переменной в составе функции, но мы дифференцируем всю функцию по одной из этих переменных. Этот процесс расчета сбивает с толку студентов, поэтому мы предлагаем этот бесплатный калькулятор. Калькулятор частных производных обеспечивает пошаговое и точное решение любого типа задач, связанных с частным дифференцированием.

Калькулятор частичного дифференцирования очень прост в использовании. Вы можете использовать его прямо на своем устройстве. Калькулятор частных производных — это инструмент для вычисления функции обычной производной переменной с фиксированным значением другой переменной.

Калькулятор многомерной производной — это онлайн-калькулятор, который используется для нахождения производной различных переменных. Калькулятор можно использовать бесплатно, и пользователь может использовать его самостоятельно и решить столько задач, сколько сможет.

Формула, используемая калькулятором частных производных с шагами

Парциальная производная любой функции f(x,y) зависит от двух разных переменных «x» и «y» одновременно. Но для вычисления частичного дифференцирования функции мы дифференцируем всю функцию по одной из этих переменных.

Ниже приведена формула, используемая в калькуляторе для получения частной производной функции f(x,y) относительно «x»:

$$ \frac{∂f}{∂x} = \frac{∂f}{∂u}\frac{∂u}{∂x} \;+\; \frac{∂f}{∂v}\frac{∂v}{∂x} $$

Аналогично, частная производная функции по «у»:

$$ \frac{∂f}{∂y} = \frac{∂f}{∂u}\frac{∂u}{∂y} \;+\; \frac{∂f}{∂v}\frac{∂v}{∂y} $$

Давайте посмотрим, как вычислить частную производную на примере:

Пример: Интегрируем следующую функцию относительно «x»

$$ u(x,y) \;=\; \инт ху дх \;+\; е(у) $$

где

f(y)= любая дифференцируемая функция y 92}{2} \;+\; 3 года $$

Таким же образом наш калькулятор вычисляет частные производные функции с подробным решением.

Как работает калькулятор с частными производными?

Пользовательский интерфейс калькулятора частных производных очень прост в использовании и понимании. Следуя простым данным шагам, можно получить решение своих проблем. Этот калькулятор обычно выполняет следующие шаги для вычисления частной производной данной функции:

1. Прежде всего, введите функцию в необходимое поле ввода.
2. Выберите переменную, относительно которой вы хотите провести различие.
3. Теперь нажмите кнопку «РАССЧИТАТЬ», чтобы получить частную производную.
4. Наконец, на экране отобразится производная функции, имеющей более одной переменной. Он содержит не только частную производную, но и возможные промежуточные шаги, графики и тригонометрическую форму заданной функции.

Как найти калькулятор уравнения в частных производных?

Найти онлайн-калькулятор многомерных производных — это не то же самое, что забраться на Эверест. Следующие методы помогут вам найти калькулятор частных производных с шагами:

Метод 1: Введите в поиск ключевые слова, такие как « калькулятор частных производных », « калькулятор частных производных » или «вычислить частную производную». панель Google, Bing, Yandex или любой поисковой системы, которую вы предпочитаете использовать. Надеюсь, мы будем доступны на верхних результатах вашей поисковой системы.

Способ 2: Найдите калькулятор частной производной по нашей прямой ссылке, например, https://derivative-calculators.com/partial-derivative-calculator.

Также вы можете посетить лучший калькулятор производных и найти любой из удивительных инструментов, связанных с поиском производной функции.

Преимущества калькулятора частных производных в точке

Пошаговый калькулятор уравнений в частных производных имеет следующие преимущества:

• Калькулятор частных производных первого порядка дает точные и достоверные результаты.

  No related posts.