Чем алгебра отличается от математики
Чем отличается алгебра от математики?
МАТЕМАТИКА — научная дисциплина о пространственных формах и количественных отношениях действительного мира. АЛГЕБРА — раздел математики, изучающий свойства переменных числовых величин и общих методов решения задач при помощи уравнений.
То есть, с точки зрения лингвистики (науки о языке) , МАТЕМАТИКА — это ГИПЕРОНИМ — слово с более широким значением, выражающее общее, родовое понятие, название класса (множества) предметов (свойств, признаков) , а АЛГЕБРА -это ГИПОНИМ, так называют слово с более узким значением, называющее предмет (свойство, признак) как элемент класса (множества).
Дорогой Артемий, как говорилось выше — алгебра это часть такой обширной дисциплины как математика.
Я просто вижу, что Вы многим поставили малое число голосов? За что? Они же правы. Или Вы путаете математику и арифметику?
Кстати спискок дисциплин, который включает в себя математика (сперто из википедии) :
Математический анализ
Дифференциальные уравнения
Математическая физика
Геометрия и топология
Теория вероятностей и математическая статистика
Математическая логика, алгебра и теория чисел
Вычислительная математика
Дискретная математика и математическая кибернетика
А то что изучается в школе на алгебре — это элементарная алгебра.
Ибо их тоже огромное количество. Различных алгебр всмысле.
Чем алгебра отличается от арифметики
Обе науки являются разными сторонами одной медали. Арифметика досконально владеет цифрами, что дает возможность использовать ее в быту для любых расчетов. Азы арифметики закладываются в раннем детстве родителями, когда они учат малышей счету. В школе ребенок овладевает элементарной арифметикой и с помощью четырех основных действий, хорошо известных всем, может решить задачу разной степени сложности. Алгебра – изучает объективные свойства идеализированных объектов, используя числа и буквы. Это вторая математическая ступень по степени сложности.
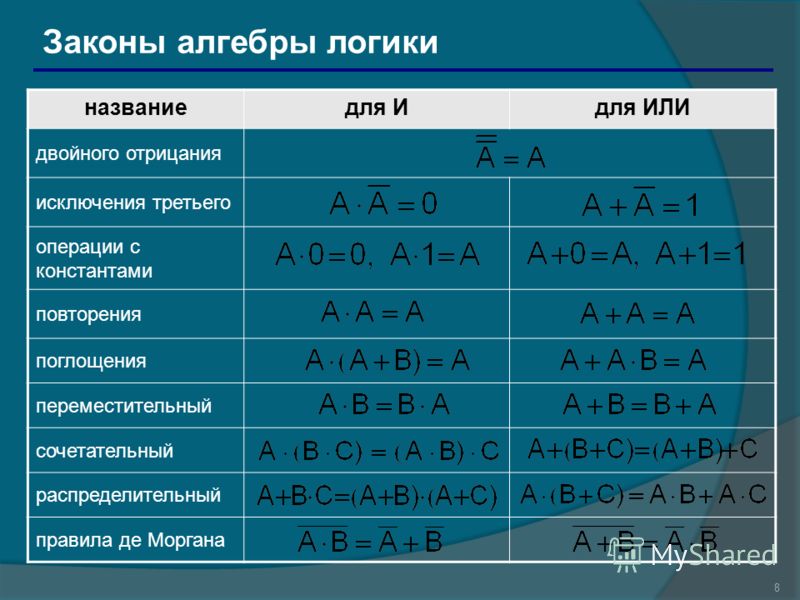
В чем разница
Арифметика переводится с греческого как «число», что полностью раскрывает ее сущность. Она изучает числа, анализирует действия с ними. Высшая арифметика, которая использует действительные, иррациональные числа, известна как теория чисел.
Алгебра – арабский термин, заимствованный в медицине. Он переводится как «соединение нарушенных частей». Эта наука занимается не просто числами, а самыми разными множествами (не обязательно числовые, но и буквенные). Она решает уравнения, системы уравнений, изучает симметрию, константы, логические операции (булева алгебра).
Эта наука занимается не просто числами, а самыми разными множествами (не обязательно числовые, но и буквенные). Она решает уравнения, системы уравнений, изучает симметрию, константы, логические операции (булева алгебра).
Иными словами – алгебра – родная сестра арифметики, имеющая дело с более сложными объектами. Правила решения задач у них общие. Найти решение онлайн дифференциальных уравнений сегодня можно на любом сервисе, популярном у школьников и их родителей, студентов и абитуриентов.
1+3 =3+1. Это чисто арифметическое числовое равенство, показывающее определенную регулярность.
а+b = b+а. Это алгебраическое уравнение, которое подходит для целого ряда ситуаций на основе определенных закономерностей. Алгебра – ряд условий, справедливых для любых чисел.
Основные сравнительные характеристики
Основные различия между родственными науками заключаются в следующем:
1. Арифметика – важнейшая часть математики, апеллирующая цифрами, складывая, умножая, вычитая и деля их. Алгебра – иная математическая ветвь, которая решает поставленные задачи, используя не только числа, но и буквы (неизвестные величины), опираясь на общие правила вычислений.
Алгебра – иная математическая ветвь, которая решает поставленные задачи, используя не только числа, но и буквы (неизвестные величины), опираясь на общие правила вычислений.
2. Арифметика – первая ступень, математика начальных классов школы. Алгебра – вторая, связанная с образованием в средних классах школы.
3. Арифметика в качестве методики использует действия с известными числами. Алгебра – это действия с абстрактными величинами, имеющими общее значение.
4. Арифметика в качестве инструмент решения пользуется четырьмя основными математическими действиями: сложением, вычитанием, умножением, делением. Алгебра – это действия с числами и буквами (множества, переменные) на основе общих правил математики.
5. Способ решения арифметики – поиск ответа по условиям задачи с итогом в виде небольших чисел. Алгебра – использование стандартных алгоритмов элементарной алгебры (алгебраические формулы).
Арифметика и алгебра – две ступени самой точной науки математики, действующие в одном направлении.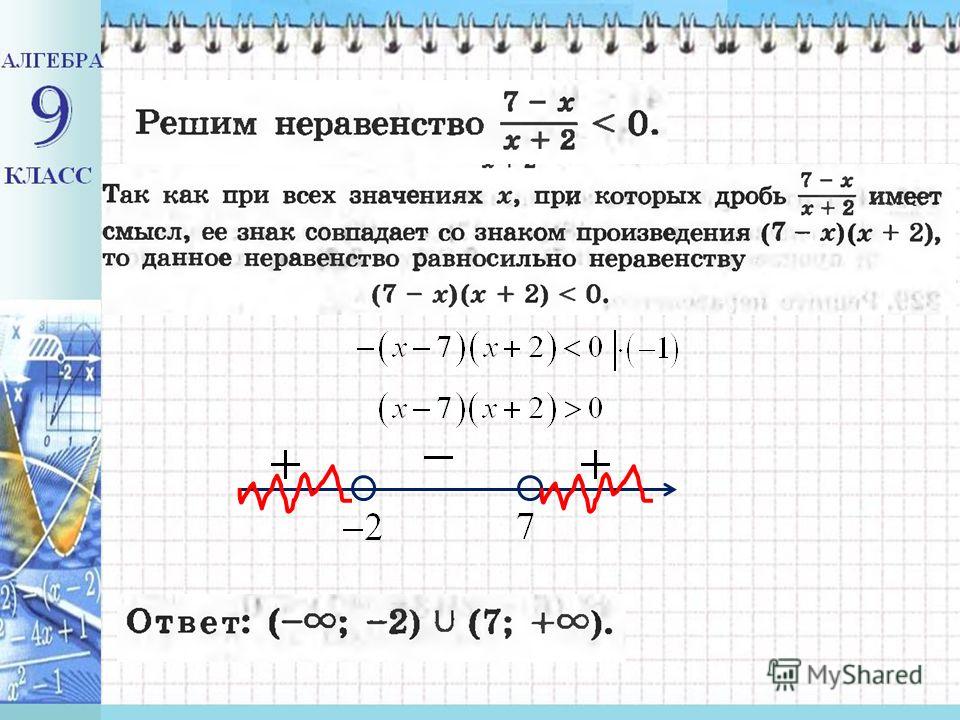
Наш искусственный интеллект решает сложные математические задания за секунды.
Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!
Математика и алгебра отличие
Математика — это основа алгебры и геометрии. Математика представляет собой простые функции: вычитание, сложение, умножение и деление простых чисел. А вот алгебра, это уже более углубленное изучение чисел и функций: алгоритмы, сложные уравления, логарифмы, производные и т.д.
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
40%
- Презентация по математике на тему «Решение задач на нахождение двух чисел» (5 класс) по их сумме и разности
- Презентация по информатике на тему «Сетевые черви и защита от них» (11 класс)
- Входная контрольная работа по алгебре 11 класс (Никольский)
У автора в друзьях: 1
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Математика: арифметика, алгебра, геометрия
Математика – один из основных школьных предметов; наука о структурах, порядке и отношениях. Математика относится к точным наукам. Проект Infoogle.ru предлагает Вам статьи по математике: формулы, примеры, правила по математике – своеобразный урок математики для интернет пользователей.
Чтобы узнать нужную формулу, искомое правило, требуемые примеры, воспользуйтесь поиском на сайте.
Математика – это очень важная наука для любого человека. Она нужна с раннего детства. Мы считаем сдачу от покупки мороженного, количество человек в футбольной команде, сколько времени осталось до интересного мультфильма, количество опыта, необходимого для получения нового уровня в какой-нибудь онлайн-игрушке. Математика нужна и в старшем возрасте, чтобы рассчитать кредит или ипотеку, определить количество свободных денег с зарплаты после оплаты всех коммунальных платежей, рассчитать доход со своего сайта при различных параметрах и показателях.
Математика пригодится каждому!
Арифметика, алгебра и геометрия.
Если в начальных классах основой математики является арифметика, то в средних классах математика разделяется на два других больших раздела: алгебру и геометрию.
Арифметика – точная наука, большой раздел математики, изучающий числа, их отношения и свойства. На портале Infoogle.ru Вы сможете найти по арифметике всё, что Вам интересно.
На портале Infoogle.ru Вы сможете найти по арифметике всё, что Вам интересно.
Алгебра – точная наука, большой раздел математики, характеризующийся как обобщающий и расширяющий арифметику. На портале Infoogle.ru Вы можете найти правила и формулы по алгебре, примеры и методы их решения.
Геометрия – точная наука, большой раздел математики, изучающий пространственные структуры, отношения и их обобщения. На портале Infoogle.ru Вы можете найти теоремы и аксиомы геометрии.
Самые популярные материалы
Множества
Задача про волка, козу и капусту.
Что такое синус?
Линейные уравнения
Решите задачу «4 4 4 4 4 = 15, 40, 80, 160, нужно расставить знаки».
Последние публикации
Меры длины и массы на Руси — какими они были, и как рассчитывались?
17.
 06.2021
Категория: Образование и наука Подкатегория: Математика
Популярность
06.2021
Категория: Образование и наука Подкатегория: Математика
ПопулярностьВ настоящее время во всем мире принято использовать унифицированную систему мер и весов. Это очень удобно — но необходимо помнить, что существовала она не всегда…
Тождество — суть математического понятия и отличия от равенства
19.08.2019 Категория: Образование и наука Подкатегория: Математика Популярность
Тождество – математическая тема, которая кажется очень простой, но на деле нередко вызывает затруднения. В данной статье разберёмся, что такое тождество.

Теорема Пифагора – формулировка и доказательство
07.02.2019 Категория: Образование и наука Подкатегория: Математика Популярность
Для треугольника с прямым углом будут равны: квадрат гипотенузы и сложенные вместе квадраты катетов. Теорема Пифагора: формулировка и доказательство.
Сумма углов треугольника — чему она равна?
07.02.2019 Категория: Образование и наука Подкатегория: Математика Популярность
Сумма углов треугольника — важная, но достаточно простая тема 7 класса, которая состоит из теоремы, короткого доказательства и нескольких логичных следствий.

Признаки равенства треугольников
07.02.2019 Категория: Образование и наука Подкатегория: Математика Популярность
Треугольники и признаки равенства между ними — тема, которую проходят на уроках геометрии в 7 классе.
Как найти площадь и периметр прямоугольника?
07.02.2019 Категория: Образование и наука Подкатегория: Математика Популярность
Прямоугольник — одна из простейших геометрических фигур.
Поэтому нахождение периметра и площади очень редко становится проблемой, но тем не менее…
Катет и гипотенуза – что это такое?
07.02.2019 Категория: Образование и наука Подкатегория: Математика Популярность
Треугольник с прямым углом — фигура, в которой две стороны называются катетами, а третья гипотенузой…
Площадь трапеции — по какой формуле ее найти?
07.02.2019 Категория: Образование и наука Подкатегория: Математика Популярность
Трапеция — интересная геометрическая фигура, которая остается достаточно простой, но все-таки является сложнее прямоугольника или треугольника.
 Как найти площадь трапеции?
Как найти площадь трапеции?Линейные уравнения — что это такое, и как их решать?
16.10.2018 Категория: Образование и наука Подкатегория: Математика Популярность
Линейные уравнения — одна из самых простых тем в математике, которую проходят в 7 классе. Давайте разберёмся, что это такое, и как их решать.
-
Одночлен — что это за понятие в алгебре, и какими бывают одночлены?
15.10.2018 Категория: Образование и наука Подкатегория: Математика Популярность
Базовым алгебраическим понятием считаются одночлены и состоящие из них числовые выражения и уравнения.
 Что такое одночлены, и какими они бывают?Базовым алгебраическим понятием считаются одночлены и состоящие из них числовые выражения и уравнения. Что такое одночлены, и какими они бывают?
Что такое одночлены, и какими они бывают?Базовым алгебраическим понятием считаются одночлены и состоящие из них числовые выражения и уравнения. Что такое одночлены, и какими они бывают?
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Математика от 12 августа 1997 – Учительская газета
Точность и гуманизация растут по спирали
Существенных изменений содержания математического образования в этом учебном году не предвидится. Перемены лишь готовятся. Главный специалист по математике Управления общего среднего образования Министерства образования Г.КУЗНЕЦОВА сообщила нам, что “министерство предложило Институту общего среднего образования РАО к концу этого года рассмотреть проект нового содержания математического образования. Программа будет переработана, может быть, сместятся акценты, произойдет перераспределение по классам, появятся новые содержательные линии”.
Эти планы касаются будущего. Но ученые пытаются помочь школьным учителям математики уже сегодня, разрабатывая новые подходы к преподаванию и новые учебники. В первую очередь это касается обеспечения среднего звена – 5-9-е классы. Почему необходимы такие перемены, замена традиционных, привычных пособий и программ?
КАКОЙ ДОЛЖНА БЫТЬ МАТЕМАТИКА В ШКОЛЕ?
Заведующий отделом математического образования Института общего среднего образования РАО, профессор Г. ДОРОФЕЕВ считает, что за последние 10 лет изменилась парадигма преподавания предмета: “Математика служит потребностям ученика, а не наоборот, не потому ее изучают, что математика существует две тысячи лет. Мы перешли от концепции “вся математика для всех” сначала к “математике для всех”, а сейчас – к “математике для каждого”, когда человек может выбрать из предмета то, что ему интересно. Из трех главных функций образования: обучающей, развивающей и воспитательной мы провозгласили приоритет развивающей функции. То есть общество получит свои научно-технические кадры не в меньшем обьеме, чем получало, но остальные не будут по окончании школы ненавидеть математику”. Профессор имеет прежде всего в виду стандарты образования, которые разрабатываются в том числе и для математических дисциплин: “Мы даем массовому ученику развить интеллект, мышление – математическое, логическое, общее – и одновременно даем базу, достаточную для тех, кто уйдет в углубленное изучение, станет профессионалом в будущем”.
ДОРОФЕЕВ считает, что за последние 10 лет изменилась парадигма преподавания предмета: “Математика служит потребностям ученика, а не наоборот, не потому ее изучают, что математика существует две тысячи лет. Мы перешли от концепции “вся математика для всех” сначала к “математике для всех”, а сейчас – к “математике для каждого”, когда человек может выбрать из предмета то, что ему интересно. Из трех главных функций образования: обучающей, развивающей и воспитательной мы провозгласили приоритет развивающей функции. То есть общество получит свои научно-технические кадры не в меньшем обьеме, чем получало, но остальные не будут по окончании школы ненавидеть математику”. Профессор имеет прежде всего в виду стандарты образования, которые разрабатываются в том числе и для математических дисциплин: “Мы даем массовому ученику развить интеллект, мышление – математическое, логическое, общее – и одновременно даем базу, достаточную для тех, кто уйдет в углубленное изучение, станет профессионалом в будущем”. Такой подход спасает школы от полного забвения математики в классах для гуманитариев или просто “слабых” учеников. Это, увы, уже не редкость. С другой стороны, новый взгляд на эту школьную дисциплину не означает ее упрощения. Наоборот, нужно понять важность предмета для личностного роста ребенка. “Математика является одним из самых важных средств интеллектуального развития человека, которыми располагает человечество. Математика является также важнейшим средством оценивания уровня интеллектуального развития человека. Геометрия, впрочем, как и алгебра, является носителем собственного метода познания мира. Овладение этим методом – важнейшая цель образования”. Это мнение другого ученого, ведущего научного сотрудника Института общего среднего образования РАО России И.ШАРЫГИНА. Дорофеева и Шарыгина можно назвать идеологами математического образования в Институте общего среднего образования РАО. Они же – авторы известных школьных учебников нового поколения. В этом учебном году школы получат “свежий” учебник И.
Такой подход спасает школы от полного забвения математики в классах для гуманитариев или просто “слабых” учеников. Это, увы, уже не редкость. С другой стороны, новый взгляд на эту школьную дисциплину не означает ее упрощения. Наоборот, нужно понять важность предмета для личностного роста ребенка. “Математика является одним из самых важных средств интеллектуального развития человека, которыми располагает человечество. Математика является также важнейшим средством оценивания уровня интеллектуального развития человека. Геометрия, впрочем, как и алгебра, является носителем собственного метода познания мира. Овладение этим методом – важнейшая цель образования”. Это мнение другого ученого, ведущего научного сотрудника Института общего среднего образования РАО России И.ШАРЫГИНА. Дорофеева и Шарыгина можно назвать идеологами математического образования в Институте общего среднего образования РАО. Они же – авторы известных школьных учебников нового поколения. В этом учебном году школы получат “свежий” учебник И. Шарыгина “Геометрия 7-9”, заявленный в федеральном комплекте 1997 года, и “Алгебру” Г.Дорофеева и др. для 7 кл. – пока пробным изданием. “Алгебра” скорее всего войдет в федеральный комплект-98.
Шарыгина “Геометрия 7-9”, заявленный в федеральном комплекте 1997 года, и “Алгебру” Г.Дорофеева и др. для 7 кл. – пока пробным изданием. “Алгебра” скорее всего войдет в федеральный комплект-98.
ГЕОМЕТРИЯ
В последние годы в школах появилось несколько новых учебников по геометрии. Учителя могут выбирать: или “обкатанная” “Геометрия” А.В.Погорелова, или новый учебник авторского коллектива под руководством Л.Атанасяна, есть книга А.Александрова и А.Вернера. И вот – принципиально новое слово. Комплект учебников для 7-9-х классов, выпущенный в издательстве “Дрофа” в этом году.
Шарыгин И.Ф. Геометрия. 7-9 кл.
Шарыгин И.Ф. и др. Геометрия. 7 кл. Рабочая тетрадь.
Шарыгин И.Ф. и др. Геометрия. 8 кл. Рабочая тетрадь.
Шарыгин И.Ф. и др. Геометрия. 9 кл. Рабочая тетрадь.
Концепция школьной геометрии И.Шарыгина – не что-то принципиально новое. Многие учителя увидят, что учебник соответствует их представлениям, как нужно преподавать геометрию. Другие обрадуются или, наоборот, огорчатся, что новая “Геометрия” не похожа на погореловскую. То, что учебник Погорелова грешит логическими ошибками, неудобоваримыми определениями и другими недостатками, известно всем. И.Шарыгин: “Вот вам пример. Читаем: “Для каждого треугольника найдется треугольник в заданном расположении относительно данной полупрямой”. Это не по-русски сказано. Что здесь утверждается? Что для каждого треугольника можно построить треугольник, ему равный, где угодно. Но сказано так, что перестало быть понятно. Такое изложение заставляет людей зазубривать. Пустые сочетания слов выдаются за умозаключения. Я считаю безнравственным заставлять ребенка доказывать очевидные вещи. Доказательство надо мотивировать. В итоге совершается методическое преступление, потому что уже в начале седьмого класса, когда начинается геометрия, такой учебник отбивает интерес к предмету. Пока есть интерес – его надо использовать. А тут в течение года человек не получает никакой новой информации. Он учит свойства параллелепипеда или шара. Но ничего нового для себя не выносит, разве что само слово “параллелепипед”, но это проблема языковая, а не геометрическая.
То, что учебник Погорелова грешит логическими ошибками, неудобоваримыми определениями и другими недостатками, известно всем. И.Шарыгин: “Вот вам пример. Читаем: “Для каждого треугольника найдется треугольник в заданном расположении относительно данной полупрямой”. Это не по-русски сказано. Что здесь утверждается? Что для каждого треугольника можно построить треугольник, ему равный, где угодно. Но сказано так, что перестало быть понятно. Такое изложение заставляет людей зазубривать. Пустые сочетания слов выдаются за умозаключения. Я считаю безнравственным заставлять ребенка доказывать очевидные вещи. Доказательство надо мотивировать. В итоге совершается методическое преступление, потому что уже в начале седьмого класса, когда начинается геометрия, такой учебник отбивает интерес к предмету. Пока есть интерес – его надо использовать. А тут в течение года человек не получает никакой новой информации. Он учит свойства параллелепипеда или шара. Но ничего нового для себя не выносит, разве что само слово “параллелепипед”, но это проблема языковая, а не геометрическая. Или шар – ребенок уже знает его свойства с детства, в футбол-то мальчишки не кирпичами играют”.
Или шар – ребенок уже знает его свойства с детства, в футбол-то мальчишки не кирпичами играют”.
Чем же заменить этот вредный, с точки зрения оппонентов, подход? Микрозадачи трех классов в рамках курса И.Шарыгина можно выразить в трех словах: заинтересовать, научить, повторить. Особенности этого учебника преподаватели смогут увидеть, познакомившись с книгой. Скоро выйдет методика для 7-го класса, написанная, кстати, методистом по учебнику А.Погорелова – А.Минченко. Пока несколько слов об основных принципах нового учебника. Слово автору:
“Принцип историзма. Я называю свой курс ретро-модернистским. Это совершенно новый курс, но вместе с тем весь модернизм – это восстановление старого и поиски возможностей в самой геометрии, которые были упущены. Я отказываюсь даже от некоторых современных формальных научных подходов, например от аксиоматического подхода. Очень опасно аксиоматизировать свойства, известные нам на основании нашего опыта, знаний, интуиции.
Элементы фузионизма, то есть смешения разных направлений. Есть пространство и плоскость. Изучая теорию, удобнее идти в такой последовательности: точка, прямая, плоскость, пространство. Но ребенок приходит в школу с хорошим пространственным мышлением, и эта способность в нем подавляется. Мы приходим к стереометрии в старшем звене, когда уже поздно. Я против полного фузионизма, то есть смешения в одном курсе планиметрии и стереометрии. Предлагаю такой выход. Начинаем с пространства. Потом работаем в плоскости, но пространство остается интерьером, в котором происходит действие. Я использую обьекты пространства для изучения формул планиметрии, чтобы человек поддерживал в напряжении свое пространственное мышление.
Есть пространство и плоскость. Изучая теорию, удобнее идти в такой последовательности: точка, прямая, плоскость, пространство. Но ребенок приходит в школу с хорошим пространственным мышлением, и эта способность в нем подавляется. Мы приходим к стереометрии в старшем звене, когда уже поздно. Я против полного фузионизма, то есть смешения в одном курсе планиметрии и стереометрии. Предлагаю такой выход. Начинаем с пространства. Потом работаем в плоскости, но пространство остается интерьером, в котором происходит действие. Я использую обьекты пространства для изучения формул планиметрии, чтобы человек поддерживал в напряжении свое пространственное мышление.
Две основные фигуры геометрии – треугольник и окружность. Не нужно заниматься мелочами, надо выделить главные вещи и их изучить досконально, они за собой остальные потащат. Треугольник – клетка геометрии. Окружность – душа геометрии, большим недостатком Погорелова является еще и то, что у него исчезла линия окружности. Треугольник и окружность как бы ограничивают учебное пространство. Между ними расположены всевозможные многоугольники, исчерпывая тем самым все изучаемые в школе фигуры.
Между ними расположены всевозможные многоугольники, исчерпывая тем самым все изучаемые в школе фигуры.
Система задач. Она должна быть полноценным компонентом курса геометрии. Сегодня произошел отрыв: курс геометрии отдельно – задачи отдельно. За века существования геометрии накопился запас красивых задач. Без знакомства с этими задачами геометрическое знание не может быть полным. Ведь задача – это не только умения, это еще и элемент знаний. Полноценный геометрический курс – это обьединение теории и соответствующей системы задач.
Предлагаемый мною курс геометрии – наглядно-эмпирический. Я против формул. Я хочу, чтобы на страничке была картинка, а не сложные формулы. Горжусь, что привлек к работе художника Вадима Иванюка, он сделал блестящие иллюстрации”.
АЛГЕБРА
Чего ждут от учебника математики учителя? Преподаватель 35-й кировской школы М.ПРОКАШЕВА: “В 5-7-х классах мы используем обычные программы, но стараемся делать упор на арифметику. Стараемся не переходить на решение задач с помощью уравнений. Работаем по учебникам Г.Дорофеева, ждем в новом учебном году очередной – для 7-го класса”. По нашей информации, к сентябрю издательство “Дрофа” выпустит этот учебник в свет, но пока как пробный. Вам решать, войдет ли он в федеральный комплект 1997-1998 года. На следующий год ожидается появление пробного издания учебника для 8-го и, возможно, 9-го класса. А в будущем создатели этой серии надеются обеспечить книгами и 10-11-е общеобразовательные классы. Г.Дорофеев: “У нас очень много умных людей занимаются изучением математики, физико-математическим профилем, а меня и мою лабораторию привлекает массовый ученик. Эта работа приоритетна для нас”.
Работаем по учебникам Г.Дорофеева, ждем в новом учебном году очередной – для 7-го класса”. По нашей информации, к сентябрю издательство “Дрофа” выпустит этот учебник в свет, но пока как пробный. Вам решать, войдет ли он в федеральный комплект 1997-1998 года. На следующий год ожидается появление пробного издания учебника для 8-го и, возможно, 9-го класса. А в будущем создатели этой серии надеются обеспечить книгами и 10-11-е общеобразовательные классы. Г.Дорофеев: “У нас очень много умных людей занимаются изучением математики, физико-математическим профилем, а меня и мою лабораторию привлекает массовый ученик. Эта работа приоритетна для нас”.
Теперь давайте посмотрим, насколько заложенные в учебник идеи совпадают с требованиями учителей, о которых сказала кировский педагог? И что еще характерно для учебного комплекта, созданного этим авторским коллективом, для конкретного нового учебника “Алгебра-7”? Предоставляем слово авторам.
С.СУВОРОВА, ведущий научный сотрудник отдела математического образования ИОСО РАО:
“Мы, – пожалуй, единственный авторский коллектив, который честно говорит, что существующий курс для большинства детей, где-то для 70%, недоступен. Математика не соответствует возрастным возможностям детей в силу излишней теоретизации, абстракции. Предмет чрезмерно алгебраизирован: уже с 1-го класса дети решают задачи с помощью уравнений. Это не безобидно. Несоответствие возрастным возможностям не позволяет развиваться. Нужно чуть-чуть “стоять на цыпочках”, тогда происходит интеллектуальный рост. То, что мы сделали в 5-6-м классе, – это курс арифметико-геометрический. Сейчас в школе практически не осталось арифметики в классическом смысле слова. Мы восстановили в правах арифметику, учим детей считать. Арифметика в традиционном курсе заканчивается в 6-м классе, у нас арифметика продолжается и в седьмом. Натуральными числами, наверное, они могут заниматься с 1-го по 11-й классы. Мы немножко отодвинули алгебру и насытили 5-6-й класс геометрией. Плюс – появилась линия анализа данных – вероятностно-статистический материал, комбинаторные задачи, работа с таблицами, диаграммами”.
Математика не соответствует возрастным возможностям детей в силу излишней теоретизации, абстракции. Предмет чрезмерно алгебраизирован: уже с 1-го класса дети решают задачи с помощью уравнений. Это не безобидно. Несоответствие возрастным возможностям не позволяет развиваться. Нужно чуть-чуть “стоять на цыпочках”, тогда происходит интеллектуальный рост. То, что мы сделали в 5-6-м классе, – это курс арифметико-геометрический. Сейчас в школе практически не осталось арифметики в классическом смысле слова. Мы восстановили в правах арифметику, учим детей считать. Арифметика в традиционном курсе заканчивается в 6-м классе, у нас арифметика продолжается и в седьмом. Натуральными числами, наверное, они могут заниматься с 1-го по 11-й классы. Мы немножко отодвинули алгебру и насытили 5-6-й класс геометрией. Плюс – появилась линия анализа данных – вероятностно-статистический материал, комбинаторные задачи, работа с таблицами, диаграммами”.
Г.до╡офеев:
“Мы сознательно снижаем уровень вычислительных навыков. Мы учим складывать дроби, мы их не выбрасываем, для нас главное не то, что ребенок умеет складывать дроби, а способы, которые он применяет, как он думает над примером. Умение складывать дроби – это приятное последствие. Процесс обучения математической деятельности имеет приоритетное значение по сравнению с конкретными достижениями. Например, вряд ли кто-нибудь после школы будет решать квадратные уравнения. Но процесс обучения квадратным уравнениям богат интеллектуальными возможностями – людям приходится думать, формулы запоминать. Он просто полезен для интеллектуального развития”.
Мы учим складывать дроби, мы их не выбрасываем, для нас главное не то, что ребенок умеет складывать дроби, а способы, которые он применяет, как он думает над примером. Умение складывать дроби – это приятное последствие. Процесс обучения математической деятельности имеет приоритетное значение по сравнению с конкретными достижениями. Например, вряд ли кто-нибудь после школы будет решать квадратные уравнения. Но процесс обучения квадратным уравнениям богат интеллектуальными возможностями – людям приходится думать, формулы запоминать. Он просто полезен для интеллектуального развития”.
с.суво╡ова:
“Наше математическое образование уже во многом строится на основе стандарта, хотя он еще не принят. Идея уровневой дифференциации – основная педагогическая идея, которая заложена в этих учебниках. По каждой теме у нас есть рубрика – “Задания для самопроверки”. Это и есть обязательные результаты, они явно выделены, это тот уровень, ниже которого опускаться нельзя, это сухой остаток. Нельзя получить “три”, если ты этого не умеешь делать. Но содержание учебника гораздо богаче. Каждый учитель, работая по комплекту, может использовать его для преподавания в “слабом” классе (расчет на 5 часов), в “сильном” классе (6 или даже 7 часов). Он строит обучение в зависимости от своих возможностей и от возможностей класса. Внешне учебник имеет два уровня, но на самом деле их больше. Все упражнения разбиты на группы А и Б. А – попроще, Б – посложнее. Кроме того, в дидактических материалах для 5-6-х классов есть дополнительные работы. Для 7-го класса эти материалы включены в учебник, располагаются по разделам. Это вопросы, расширяющие представления о предмете для тех, кто интересуется, из разряда необязательных. И получается, что четко выделен только минимальный, а вот выше – у каждого класса и у каждого ученика получается свой уровень. Диапазон сложности – это такая особенность, которой не было раньше. Но при этом мы считаем, что трудные задачи надо решать со всеми. Кто-то решит сам, другой просто послушает и сможет повторить на доске решение, третий решит аналогичную.
Но содержание учебника гораздо богаче. Каждый учитель, работая по комплекту, может использовать его для преподавания в “слабом” классе (расчет на 5 часов), в “сильном” классе (6 или даже 7 часов). Он строит обучение в зависимости от своих возможностей и от возможностей класса. Внешне учебник имеет два уровня, но на самом деле их больше. Все упражнения разбиты на группы А и Б. А – попроще, Б – посложнее. Кроме того, в дидактических материалах для 5-6-х классов есть дополнительные работы. Для 7-го класса эти материалы включены в учебник, располагаются по разделам. Это вопросы, расширяющие представления о предмете для тех, кто интересуется, из разряда необязательных. И получается, что четко выделен только минимальный, а вот выше – у каждого класса и у каждого ученика получается свой уровень. Диапазон сложности – это такая особенность, которой не было раньше. Но при этом мы считаем, что трудные задачи надо решать со всеми. Кто-то решит сам, другой просто послушает и сможет повторить на доске решение, третий решит аналогичную. Каждый возьмет свое”.
Каждый возьмет свое”.
г. до╡офеев:
“Мы хотим напомнить, что математика – не мертвая наука. Математическое мышление – часть общечеловеческого мышления. Отсюда – человеческий язык изложения материала в книге и гуманитарный, исторический фон учебника”.
с. суво╡ова:
“Наши дидактические принципы. Во-первых, мы стараемся излагать теорию на уровне, доступном детям. Мы отказались от массы исключений, оговорок, потому что мы хотим сказать о них тогда, когда это становится нужным. Теория стала проще. Многое показываем, что называется, на пальцах. Дифференциация, усложнение идет не за счет теории, а за счет задач. У нас масса сложных задач, но их решают не “сильные” дети, потому что учитель, который преподает по нашей программе, говорит детям – решайте, пробуйте, эспериментируйте, не бойтесь, что вам поставят “два”. Задачу можно не решить, ее важно решать. Поскольку мы надеемся, что в старшем звене ребята будут изучать разные курсы математики, то есть смогут в старших классах “добрать”, мы кое-что отодвигаем дальше, и у нас более медленное продвижение по курсу. У нас меньше специальных умений, но более широкий круг вопросов. Мы строим курс по спирали. Ко всем принципиальным вещам мы возвращаемся на более высоком уровне. Например, проценты проходят четыре раза. Иногда мы строим так: первый “проход” на интуитивном уровне – это игра, второй – появляются некоторые термины, третий – вводятся правила, как вербальное обобщение, выражение того, что уже интуитивно понятно. Не от правила к примеру, а правило ложится на опыт. Детям должно быть интересно. Ведь в 5-6-м классе рано говорить о профильной дифференциации, а потому надо втягивать, заманивать, чтобы можно было себя испытать, чтобы получилось. И – возник новый интерес. Интересно то, что получается”.
У нас меньше специальных умений, но более широкий круг вопросов. Мы строим курс по спирали. Ко всем принципиальным вещам мы возвращаемся на более высоком уровне. Например, проценты проходят четыре раза. Иногда мы строим так: первый “проход” на интуитивном уровне – это игра, второй – появляются некоторые термины, третий – вводятся правила, как вербальное обобщение, выражение того, что уже интуитивно понятно. Не от правила к примеру, а правило ложится на опыт. Детям должно быть интересно. Ведь в 5-6-м классе рано говорить о профильной дифференциации, а потому надо втягивать, заманивать, чтобы можно было себя испытать, чтобы получилось. И – возник новый интерес. Интересно то, что получается”.
ЗАГЛЯНЕМ В ФЕДЕРАЛЬНЫЙ КОМПЛЕКТ-98
В этом учебном году в издательстве “Мнемозина” выходит учебник профессора А.Г.Мартковича “Алгебра” для 7-го и 8-го классов, пока не вошедший в федеральный комплект. Учебник написан под авторскую концепцию, которая отличается от типовой программы Министерства образования. Может быть, он займет полноправное место в федеральном комплекте будущего года. Более вероятные претенденты занять место в этом списке под рубрикой “новое”:
Может быть, он займет полноправное место в федеральном комплекте будущего года. Более вероятные претенденты занять место в этом списке под рубрикой “новое”:
Дорофеев Г.В. и др. Математика. Арифметика, алгебра, анализ данных. 7 кл. Изд-во “Дрофа”.
Дорофеев Г.В. и др. Математика. Дидактические материалы. 7 кл. Изд-во “Дрофа”.
Кузнецова Л.В. и др. Сборник задач для проведения школьного экзамена по алгебре и началам анализа за курс средней школы (по трехчасовой программе). Изд-во “Дрофа”.
Чем отличается математика от прикладной математики
Математика – это фундаментальная наука, которая занимается изучением разных структур, их отношений и порядков. Математика, как наука, появилась очень давно, наверное, с возникновением человечества. Уже в раннем палеолите люди были знакомы с основами счета. У людей всегда была необходимость что-то подсчитать или пересчитать. Известно, что для счета люди пользовались и пальцами, и камнями, и палками и различными метками. Историю развития математики отсчитывают именно с того момента, как люди научились считать.
Историю развития математики отсчитывают именно с того момента, как люди научились считать.
Для того чтобы понять, чем отличается прикладная математика от математики, нужно рассмотреть основные понятия, которыми оперирует одна и вторая наука.
Математика
Если посмотреть определение математики в различных словарях и энциклопедиях, то можно заметить, что единого точного определения математики не существует. Однако мы все интуитивно понимаем, что такое математика. Наилучшее определение было дано, наверное, Бурбаки.
Бурбаки – это псевдоним группы математиков, которые написали серию книг по математике. По определению Бурбаки, математика изучает отношения между какими-то объектами. Каждый объект описывается с точки зрения его количественных характеристик. Сущностью математики является описание некоторого набора абстрактных структур.
Из этого определения становится понятно, чем занимается теоретическая математика. Она должна описать отношения различных структур данных.
Математика делится на элементарную и высшую части. Элементарную математику изучают в школе.
Она включает в себя такие разделы, как:
- Арифметика.
- Начала алгебры.
- Геометрия.
Высшая математика состоит из:
- Математического анализа.
- Алгебры.
- Аналитической геометрии.
- Дифференциальных уравнений.
- Теории вероятности.
- Математической статистики.
- Теории чисел.
- Функционального анализа.
В теоретической математике разработан математический аппарат, основу которого составляют обозначения, аксиомы, утверждения. А на базе уже этого аппарата развивается дальнейшая теория, доказываются теоремы и выводятся определенные правила.
Например, в математическом анализе используются такие понятия, как бесконечно малая величина, дифференциал, функция. Алгебра оперирует понятиями множество, группа, кольцо и т.д. Дифференциальные уравнения работают с производной и интегралом. Таким образом, видно, что теоретическая математика разрабатывает некий понятийный аппарат. Английский математик Годфри Харди говорил, что чистая математика не приносит никакой практической пользы.
Таким образом, видно, что теоретическая математика разрабатывает некий понятийный аппарат. Английский математик Годфри Харди говорил, что чистая математика не приносит никакой практической пользы.
Прикладная математика
Прикладная математика является частью математики. Если говорить обычным языком, прикладная математика – это математика, которая используется на практике. Прикладная математика изучает и разрабатывает способы применения теоретической математики в других дисциплинах. Если вернуться к словам математика Харди, то в отличие от чистой математики, прикладная математика приносит практическую пользу.
Разделы прикладной математики
- Численные методы.
- Математическая физика.
- Программирование.
- Оптимизация вычислений.
- Теория игр.
- Криптография.
- Теория оптимального управления.
- Биоматематика.
- Биоинформатика и др.
Предметом исследования прикладной математики является применение теоретических математических методов чистой математики в других науках. Например, строятся экономические модели и с помощью методов теории оптимального управления вырабатываются наилучшие управленческие решения.
Например, строятся экономические модели и с помощью методов теории оптимального управления вырабатываются наилучшие управленческие решения.
В физике или химии для проведения каких-либо экспериментов или опытов, не всегда представляется возможным провести испытания на реальном объекте. Поэтому строится его модель. Модель – это уменьшенная или увеличенная копия реального объекта, которая имеет точно такие же свойства.
Модели бывают математическими. Модель может быть создана и на компьютере с помощью графических редакторов. Моделирование разных физических или химических процессов заканчивается решением с использованием численных методов.
Криптография – это наука, которая занимается шифрованием. В шифровании используются различные математические методы и алгоритмы.
Таким образом, из вышеприведенного понятно, что и чистая математика, и прикладная математика использует одни и те же методы. Но чистая математика использует эти методы для дальнейшего развития теории, а прикладная математика использует математические методы и теорию чистой математики для того, чтобы можно было решать реальные задачи в физике, химии, биологии, статистике, экономике и в других науках.
НаукаКомментировать
Обзор учебника по алгебре 7 класс Мерзляк А.Г.
- Text Link
Об учебнике
В седьмом классе привычная математика разделяется на алгебру и геометрию. Школьники начинают глубже изучать математические законы, и главным помощником в этом становится учебник. Сейчас в Федеральном перечне Министерства просвещения РФ более десятка пособий, соответствующих ФГОС нового поколения. Они отличаются друг от друга содержанием, последовательностью тем, подачей материала и набором задач и упражнений.
Для разработки программы по математике «Экстерната и домашней школы Фоксфорда» выбрали один из самых распространённых учебников — «Алгебру» А.Г. Мерзляка, В.Б. Полонского и М.С. Якира.
Мерзляка, В.Б. Полонского и М.С. Якира.
Почему выбрали этот учебник
У учебника Мерзляка и соавторов много преимуществ.
✅Разноуровневое обучение. Есть задания попроще, есть посложнее. Освоить программу можно вне зависимости от исходного уровня ребёнка.
✅Практические задачи. Ребята учатся сразу же применять знания: прочитали параграф и выполняют к нему задания.
✅Логичное и подробное изложение тем. Материала в параграфе, как правило, достаточно, чтобы разобраться в теме. Новая информация вытекает из предыдущей — если что-то подзабыли, легко вернуться назад и повторить.
✅Понятные объяснения, которые приятно читать. Авторы написали учебник простым языком — так, чтобы не перегрузить школьников, но дать всю необходимую для седьмого класса информацию.
✅Примеры и иллюстрации.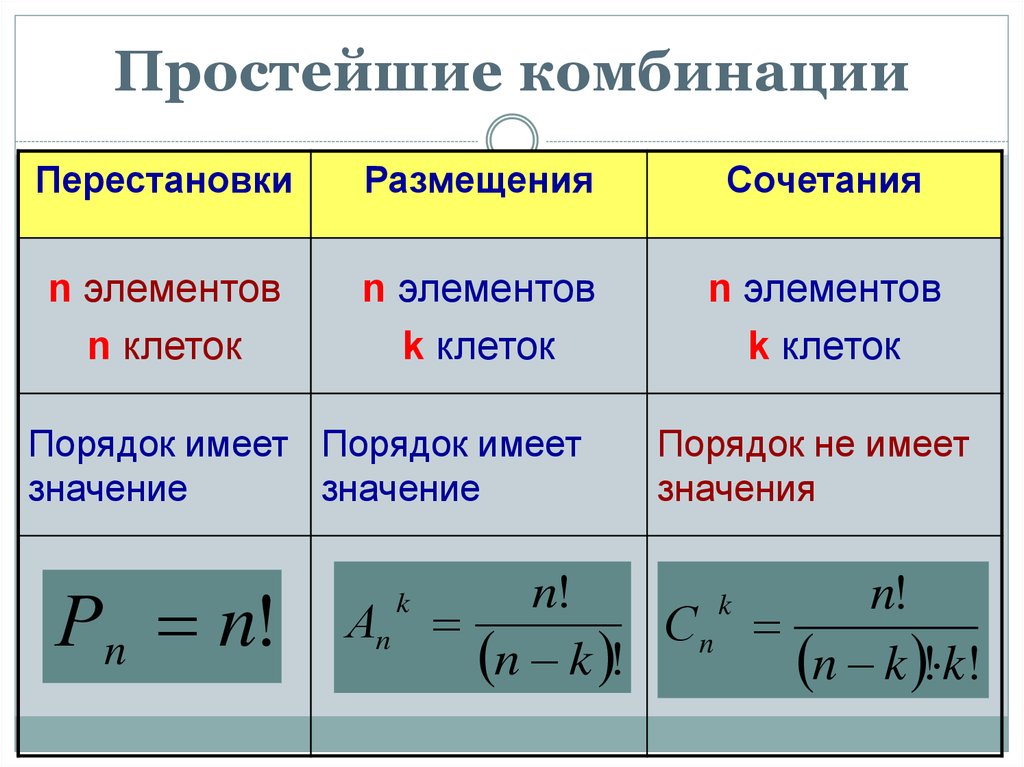 Объяснения и разбор тем сопровождается примерами из жизни, схемами, диаграммами.
Объяснения и разбор тем сопровождается примерами из жизни, схемами, диаграммами.
✅Дополнительные факты и справочные материалы. Если хочется глубже разобраться в теме — без информации не оставят.
✅Нравится взрослым и детям. В интернет-магазинах и на форумах — положительные отзывы.
Обзор тем
В учебнике Мерзляка последовательно разбираются эти и другие темы:
✅ «Линейное уравнение с одной переменной»: понятие линейного уравнения с одной переменной, решение уравнений и текстовых задач.
✅ «Целые выражения»: тождества, степень с натуральным показателем, одночлены, многочлены и действия с ними.
✅ «Функции»: способы задания функции, график функции, свойства и график линейной функции.
✅ «Системы линейных уравнений с двумя переменными»: уравнения с двумя переменными, линейное уравнение с двумя переменными и его график, методы решения систем линейных уравнений.
Это базовый набор, который школьники должны освоить в седьмом классе. Учебник Мерзляка помогает изучить весь нужный материал и потренироваться на интересных задачах, которые затем встретятся на контрольных и экзаменах.
<<Форма демодоступа>>
Как учат алгебру в «Экстернате и домашней школе Фоксфорда»
Программа седьмого класса построена по традиционному принципу последовательного изложения материала с включением разноуровневых заданий и интересных фактов из истории математики. Она повторяет последовательность тем учебника Мерзляка.
<<Перелинковка>>
Алгебраические задачи развивают все виды мышления: абстрактное, логическое и алгоритмическое. Изучая этот раздел математики, школьники учатся планировать и критически оценивать свою деятельность, анализировать и систематизировать информацию, принимать самостоятельные решения, отстаивать свои убеждения и взгляды.
Наш преподаватель математики Анна Эккерман даёт школьникам рекомендации, как не бояться курса и с успехом его освоить.
Будьте внимательны на занятиях. Это половина успеха — усваивать материал сразу из первоисточника. Не стесняйтесь задавать вопросы. Быть в диалоге с преподавателем — круто. Погружаясь в контекст, вы поймёте и запомните гораздо больше.
Изучение математического языка должно быть последовательным и понятным для школьника — и на это направлена программа домашней онлайн-школы «Фоксфорда» по алгебре.
Углубите ваши знания!
В домашней онлайн-школе «Фоксфорда» вы можете выбрать индивидуальный образовательный маршрут и уже с 5 класса начать двигаться к профессии мечты! Оставьте ваши контакты для получения подробной бесплатной консультации об обучении в нашей школе.
Принимаю условия соглашения и политики конфиденциальности
Записали!
Скоро с вами свяжется консультант, расскажет об обучении в нашей онлайн-школе.
Проверьте вашу электронную почту — там письмо о том, что стоит сделать перед консультацией.
Упс 🙁 Что-то пошло не так. Попробуйте позвонить нам по телефону +7 (800) 500-17-81 либо написать на почту [email protected].
«Математика прокачивает мозги» — интервью с преподавателем Анной Эккерман
Анна Эккерман может на пальцах объяснить любую сложную тему. В интервью она даёт советы, как бороться с психологическим страхом математики, в чём заключаются трудности ОГЭ и ЕГЭ и почему не всегда нужно слушать окружающих.
Читать
Арифметика, геометрия и алгебра – Различия
Математика означает «знание, изучение, обучение». Он включает изучение таких тем, как арифметика, алгебра, геометрия и математический анализ. У него нет общепринятого определения.
Несколько цивилизаций в Китае, Индии, Египте, Центральной Америке и Месопотамии внесли одинаковый вклад в развитие математики. Система счета была впервые разработана шумерами. Математики разработали арифметику, которая включает в себя основные операции, такие как сложение, вычитание, умножение, дроби и квадратные корни.
По мере развития цивилизации математики начали работать с геометрией, которая имеет дело с площадями и объемами для измерения углов. Геометрия используется везде, от строительства дома до моды и дизайна интерьера. Кроме того, геометрия — это раздел математики, изучающий пространственные отношения между несколькими объектами, форму отдельных объектов и свойства окружающего нас пространства. Геометрия считается одной из старейших ветвей математики, хотя этот термин происходит от греческого языка, поскольку гео означает землю, а материал означает измерение, то есть измерение земли.
Однако после определенного момента люди начали понимать, что геометрия не должна ограничиваться изучением твердых трехмерных объектов или плоских и плоских поверхностей, а может быть использована или представлена с помощью самых абстрактных образов и мысли. Кроме того, основные разделы геометрии состоят из аналитической геометрии, евклидовой геометрии, проективной геометрии, неевклидовой геометрии, топологии и дифференциальной геометрии. Тем не менее, студентам не нужно углубляться во все эти понятия.
Тем не менее, студентам не нужно углубляться во все эти понятия.
Теперь давайте немного поговорим об алгебре. Это тот раздел математики, где учащиеся обычно используют символы, буквы алфавита для решения поставленных задач. Теперь, говоря о его истории, его можно разделить на три части. Первый этап — письменный этап, когда использовались только слова, второй этап включал сокращённый или синкопированный этап, когда в уравнениях появлялись символы. Третий этап — современный или символический этап. Более того, алгебра была изобретена в девятом веке персидским математиком Мухаммедом ибн Мусой аль-Хорезми. Он также разработал быстрые методы умножения и деления чисел, известные как алгоритмы. Изучение алгебры означало, что математики решали линейные уравнения и системы, а также решения квадратичных уравнений.
Арифметика. Числа и операции
Арифметика — один из первых предметов, которые вы изучаете в младших классах. Он имеет дело с числами и основными операциями над ними. Это основа для изучения других разделов математики.
Это основа для изучения других разделов математики.
Арифметика произошла от греческого слова arithmos, который представляет собой раздел математики, состоящий из изучения подсчета чисел и свойств традиционных операций с ними, таких как сложение (+), вычитание (-), умножение (x), и деление (). Арифметика является элементарной частью теории чисел.
В дополнение к основным операциям этот предмет также включает более сложные операции, такие как проценты, квадратные корни, возведение в степень, логарифмические функции, тригонометрические функции и многие другие.
Четыре основные операции сложения, вычитания, умножения и деления обычно называют четырьмя арифметическими операциями.
Четыре основных свойства операций:
Переместительное свойство
Ассоциативное свойство
Распределительное свойство
Аддитивный идентификатор
Правило BODMAS или PEMDAS используется для порядка операций, включая +, −,× и ÷. Порядок действий:
Порядок действий:
B:- Скобки
O: -Порядок
D: -Разделение
M:- Умножение
A: -Сложение
S: -Вычитание
Геометрия 190-3 Формы является изучение форм. Он широко подразделяется на два типа: плоскостная геометрия и объемная геометрия. Планиметрия имеет дело с двумерными фигурами, такими как квадраты, круги, прямоугольники, треугольники и многие другие. Принимая во внимание, что геометрия твердого тела занимается изучением трехмерных форм, таких как куб, прямоугольный параллелепипед, цилиндр, конус, сфера и многие другие.
Изучение этой формы необходимо для нахождения длины, ширины, площади, объема, периметра и многих других терминов.
В математике нам снова и снова нужны определенные термины для решения задач. Становится трудно повторно писать полные термины, поэтому обнаруживаются сокращения для этих терминов, и это называется символом.
(Изображение будет загружено в ближайшее время)
Алгебра
Алгебра — это один из разделов математики, изучающий переменные и числа. Сочетание констант и переменных, соединенных знаками основных операций сложения, вычитания, умножения и деления, называется алгебраическим выражением. Различные части алгебраического выражения, разделенные знаками + или -, называются членами выражения. Алгебраическое выражение определяется как сумма, разность, произведение или частное констант и переменных.
Рассмотрим,
12x + 50
Здесь это выражение называется алгебраическим выражением, где значения x варьируются, поэтому это переменная, а 50 — константа. 12x и 50 — это термины, разделенные знаком +. Вместо переменных мы можем написать что угодно a, b, c….z.
Алгебра состоит из различных методов решения пары линейных уравнений:
1. Метод исключения
2. Метод подстановки
Метод подстановки
3. Метод перекрестного умножения
Давайте поймем разницу между арифметикой и алгеброй.
Difference Between Arithmetic and Algebra
Arithmetic | Algebra |
Arithmetic, being the most basic of all branches of mathematics, deals with the basic counting of numbers and by используя такие операции, как сложение, умножение, деление и вычитание над ними. | Алгебраика — это раздел математики, который имеет дело с переменными и числами для решения задач. Он использует обобщенные правила для решения проблем. |
В целом, связанный с математикой начальной школы | , как правило, связанные с математикой старших классов |
Вычисления с удельными номерами | . |
Четыре действия (сложение, вычитание, умножение и деление) | В алгебре для решения задач используются числа и переменные. Он основан на применении обобщенных правил решения задач |
На основе информации, содержащейся в задаче (запоминающие результаты для малых значений чисел) | На основе стандартных ходов элементарной алгебры |
Связанный номер | Связанные переменные |
Различия между арифметикой и алгеброй сделают понятия арифметики и алгебры более понятными.
Давайте понимаем разницу между алгеброй и геометрией
Алгебра | Геометрия |
Algebra Algebra | |
Algebra Algebra Argebra Argebra. | Геометрия — это раздел математики, изучающий точки, линии, объекты и формы различных размеров, поверхности и твердые тела. |
Основное внимание в алгебре уделяется арифметике, уравнениям и пониманию взаимосвязей между переменными или отношениями. | Геометрия фокусируется на понимании геометрических фигур и использовании их формул. Большинство формул объясняют, как найти пропущенные числа, градусы и радианы. |
Алгебра не использует углы или градусы. | Измерения состоят из определения градусов или радиан углов, площадей, периметров и точек. |
Алгебра связана с уравнениями и формулами | Геометрия связана с объектами и формами. |
Различия между алгеброй и геометрией сделают понятия алгебры и геометрии более понятными.
Интересные факты:
Алгебру придумали вавилоняне в 1900 году до нашей эры.
Использование знаков сложения (+) и вычитания (-) оказывается полезным при выполнении алгебраических уравнений. До этого люди использовали письменные слова для выражения функций сложения и вычитания, что отнимало много времени.
Арифметика всегда рядом с вами. Просто взгляните на лоток для льда и вытащите из него два кубика льда, сколько всего осталось? Чтобы найти ответ на него, нужно вычесть общее количество слотов для кубиков льда на 2.
История математики уходит в далекое прошлое, но большинство математических символов не были изобретены до 16 века, так как до этого уравнения записывались словами.

Нет сомнений в том, что греки были увлечены, но они использовали геометрию в создании произведений искусства, таких как здания и многое другое, что дает учащимся еще одну причину любить этот предмет.
Два наиболее важных инструмента геометрии, которые считаются мощными, поскольку они помогают в продвижении и построении предмета, — линейка и циркуль.
В чем разница между арифметикой и алгеброй?
Арифметика — это математическая операция, связанная с системами счисления и их операциями. Он традиционно применялся для получения определенного единственного значения. Термин произошел от греческого слова «арифмос», что означает числа. Традиционные операции, связанные с арифметикой, включают сложение, вычитание, умножение и деление. Эти операции осуществляются в сфере трейдинга, маркетинга и монетизации на протяжении столетий.
Арифметика — это элементарная ветвь математики, специально занимающаяся изучением чисел и свойств традиционных операций, таких как сложение, вычитание, умножение и деление.
Помимо традиционных операций сложения, вычитания, умножения и деления арифметические операции также включают расширенные вычисления процентов, логарифмов, возведения в степень, квадратных корней и т. д. Статья посвящена изучению и объяснению этих основных типов арифметических операций.
История арифметики
- Индийский математик XVII века Брахмагупта — «отец арифметики».
- Карл Фридрих Гаусс в 1801 году сформулировал Основополагающий принцип теории чисел.
Ниже рассматриваются четыре основных арифметических операции: сложение, вычитание, умножение и деление:
Сложение (+)
Простым определением сложения будет то, что это операция по объединению двух или более значений или чисел в одно значение. Процесс сложения n значений называется суммированием.
Процесс сложения n значений называется суммированием.
0 считается элементом идентичности сложения, поскольку добавление 0 к любому значению дает тот же результат. Например, если мы добавим 0 к 5, результат будет таким же, как и 5.
0 + 5 = 5
И обратный элемент включает добавление противоположного значения. Результатом добавления инверсных элементов будет элемент идентичности, равный 0. Например, если мы добавим 3 с его противоположным значением -3, то результатом будет
3 + (-3) = 0
Вычитание (-)
Вычитание — это арифметическая операция, которая вычисляет разницу между двумя значениями (т. е. уменьшаемое минус вычитаемое). В случае, когда уменьшаемое больше вычитаемого, разница положительна. Это обратное сложение.
4 – 1 = 3
При этом, если вычитаемое больше уменьшаемого, разница между ними будет отрицательной.
1 – 4 = -3
Умножение (× )
Две величины, участвующие в операции умножения, известны как множимое и множитель.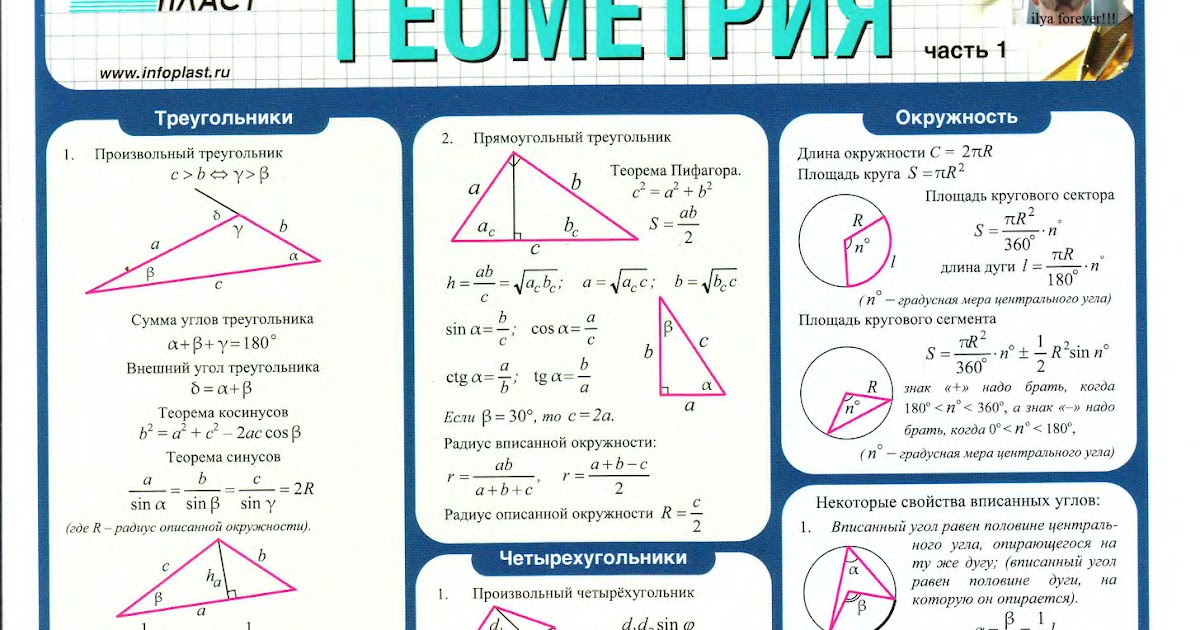 Он объединяет два значения, которые являются множителем и множителем, чтобы получить один продукт.
Он объединяет два значения, которые являются множителем и множителем, чтобы получить один продукт.
Произведение двух значений, предположительно a и b, выражается в форме a.b или a × b.
2 × 3 = 6
Деление (÷)
Деление — это операция, которая вычисляет частное двух чисел. Это обратное умножение. Два значения, участвующие в нем, известны как дивиденды по делителю, и если частное больше 1, если делимое больше делителя, результатом будет положительное число.
6/3 = 2
Алгебра
Алгебра обычно связана со средним школьным образованием. Мы не используем его в наших повседневных вычислениях как арифметика чаще. Но алгебраическое приложение можно увидеть повсюду. Представьте себе измерение высоты здания, если мы знаем расстояние, на котором оно находится от любого другого объекта поблизости любой высоты. Высота здания легко определяется с помощью алгебраического выражения.
Алгебра – это раздел элементарной математики, изучающий отношения переменных и констант.
Алгебраические выражения состоят из переменных, констант и основных знаков сложения, вычитания, умножения и деления. Каждое выражение, соединенное этими знаками, называется терминами выражения.
История алгебры
- Происхождение алгебры было прослежено вавилонянами в 1900 г. до н.э.
- Персидского математика Аль-Хорезми называют «отцом алгебры».
Типы алгебраических выражений
Одночлен
Алгебраические выражения, имеющие только один член, известны как мономы. Например: 5x,10xy и т. д.
Биномиальное
Алгебраические выражения, содержащие два маловероятных члена, называются биномами. Например: 5xy + 3, 2x + y и т. д.
Многочлен
Алгебраические выражения, содержащие более двух членов, называются полиномами. Например: ab+bc+ca и т. д.
Difference between Arithmetic and Algebra
S No.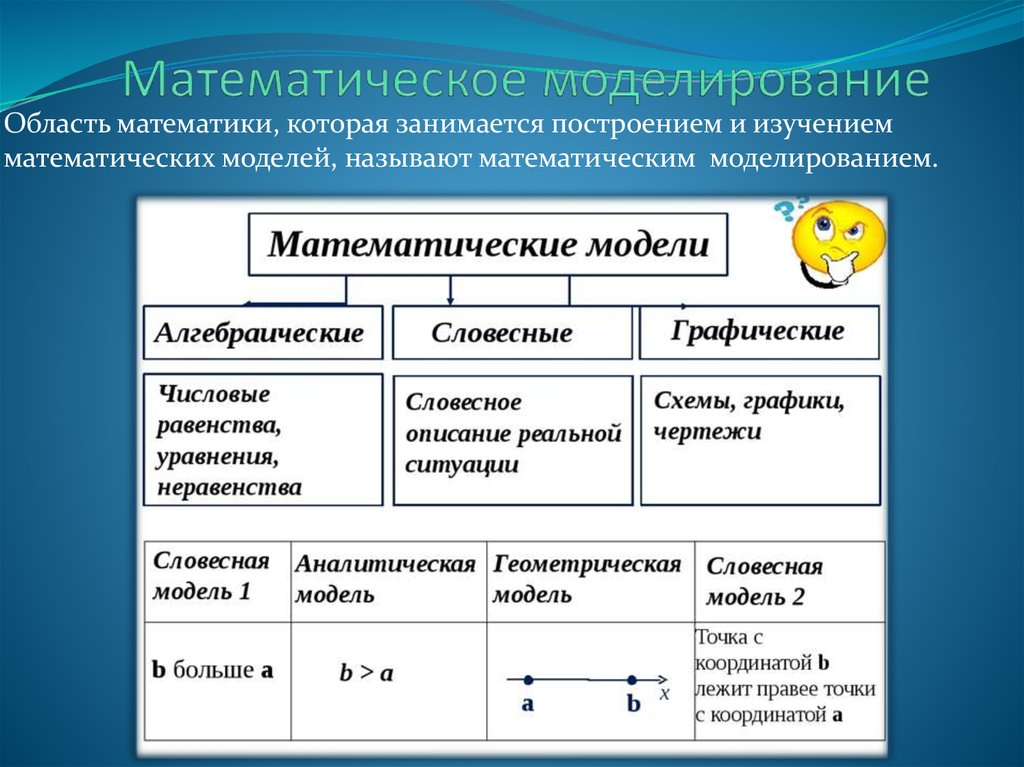 | Arithmetic | Algebra |
|---|---|---|
| 1 | It is the branch of mathematics that deals with numbers, their writing systems, и их свойства. | Это раздел математики, изучающий переменные и константы. |
| 2 | Операции выполняются с помощью предоставленной информации. | Операции выполняются с помощью стандартных формул и выражений. |
| 3 | Обычно применим в реальной жизни и связан с начальным образованием. | Его прямое применение не часто наблюдается в повседневной жизни и связано со средним школьным образованием. |
| 4 | Он имеет четыре основных метода работы (сложение, вычитание, умножение и деление). | Для решения задач используются числа, переменные и общие правила или формулы. |
| 5 | Это связано с числами и системами счисления. | Это связано с уравнениями и формулами. |
Примеры задач
Вопрос 1: Кто известен как отец алгебры?
Ответ:
Персидский математик Хорезми известен как отец алгебры.
Вопрос 2: Каково применение арифметики в реальной жизни?
Ответ:
Арифметика используется для целей вычислений,
- Анализ данных
- Основные расчеты
- Monetization
- Sales, Trade
- SACUTICATION
- , торговля
- . разделы математики?
Ответ:
Основные разделы математики:
- Алгебра
- Геометрия
- Тригонометрия
- Исчисление
- Арифметика
Вопрос 4: Какие бывают типы алгебраических уравнений?
Answer:
The types of algebraic equations are listed below:
- Polynomial equation
- Quadratic equation
- Cubic equation
- Rational equation
- Trigonometric equation
Algebra vs calculus | Линейная алгебра против исчисления и многое другое
ВведениеАлгебра и исчисление относятся к разным разделам математики и тесно связаны друг с другом.
Применяя основные алгебраические формулы и уравнения, мы можем найти решение многих наших повседневных проблем.
Исчисление в основном применяется в профессиональных областях из-за его способности находить решения для многих типов структур.
АлгебраАлгебраические формулы и понятия используются при решении почти всех математических задач. Алгебра незаменима при решении задач арифметики, тригонометрии, исчисления и т. д., кроме использования ее при решении задач других отраслей науки и техники.
Алгебра включает в себя абстрактную алгебру, линейную алгебру, универсальную алгебру, элементарную алгебру, алгебраическую геометрию, алгебраическую теорию чисел, алгебраические системы и т. д. Это изучение изменения функций и их производных с использованием предельного процесса.
Это математическая отрасль, которая использует небольшие приращения или убывания с особым упором на скорость роста, чтобы найти решения широкого круга проблем в науке и технике.
Исчисление далее делится на
дифференциальное исчисление и интегральное исчисление.
Читайте также:
- Для чего используется исчисление?
- Исчисление каламбуров
Загружаемый PDF-файлЕсли вы когда-нибудь захотите прочитать его столько раз, сколько захотите, вот загружаемый PDF-файл, чтобы узнать больше.
Алгебра против исчисленияАлгебра и исчисление тесно связаны, поскольку при выполнении вычислений приходится постоянно использовать алгебру. Знакомство с алгеброй позволяет чувствовать себя комфортно в исчислении. Алгебра позволит вам лучше понять темы исчисления и наоборот. Но мы также можем провести анализ алгебры и исчисления 9.0003
В следующем пронумерованном списке описывается общая тема «алгебра против исчисления» и разница в применении между алгеброй и исчислением.
- Алгебра сосредоточена на решении уравнений, тогда как исчисление в основном сосредоточено на скорости изменения функций.
Двумя основными операциями исчисления являются дифференцирование (нахождение скорости изменения функции) и интегрирование (нахождение площади под кривой функции).
- Эти две важные операции связаны между собой основной теоремой исчисления.
- Алгебра, как и большинство математических дисциплин, является важным инструментом в исчислении, и хорошее понимание алгебры и пределов имеет основополагающее значение для понимания исчисления
- исчисление имеет дело с операциями над функциями и их производными, тогда как алгебра имеет дело с операциями над переменными и числами.
- Алгебра помогает найти наклон линии, а исчисление — наклон кривой.
- Алгебра помогает найти направление движения по прямой линии, тогда как исчисление делает то же самое по любой кривой.
- Алгебра используется для нахождения длины отрезка прямой, а исчисление используется для нахождения длины части кривой.
В заключение, несмотря на то, что есть много моментов для алгебры и исчисления, алгебра и исчисление, как и все в математике, имеют синергию и используются вместе при решении задач.
Линейная алгебра против исчисленияЛинейная алгебра — это изучение свойств векторных пространств и матриц. Исчисление и линейная алгебра лежат в основе практически всей высшей математики и ее приложений в естественных, социальных и управленческих науках.
Таким образом, эти темы составляют основу основных требований по математике как для студентов, изучающих математику, так и для студентов, изучающих естественные и инженерные науки.
Следующие пункты описывают широкую тему «линейная алгебра против исчисления» и разницу в применении между линейной алгеброй и исчислением.
- Чистая механика линейной алгебры очень проста, она намного проще, чем что-либо существенное в исчислении. Сложность заключается в том, что линейная алгебра в основном связана с пониманием терминов и определений и определением типа вычислений и анализа, необходимых для получения требуемого результата.
- Линейная алгебра проще элементарного исчисления.
Как только теоремы линейной алгебры будут хорошо поняты, можно будет ответить на большинство сложных вопросов.
- Это не относится к исчислению, и вычислительные вопросы в исчислении могут быть очень неловкими даже при глубоком строгом понимании материалов.
- À активно вовлеченный мозговой штурм в классе исчисления применения производных может быть значительно сложнее, чем в классе алгебры курса линейной алгебры, посвященного вычислениям.
- Хотя основы линейной алгебры легче понять, правила исчисления могут сбивать с толку при их применении.
- Расчет можно использовать для прогнозирования роста растений, нагрузок на движущиеся части, точек напряжений на мостах, высотных зданиях и других конструкциях.
Производные могут привести вас от скорости к ускорению, но чтобы визуализировать их практическое применение, вам нужно изучить физику, информатику и т. д.Понятия линейной алгебры чрезвычайно полезны в физике, экономике, социальных и естественных науках и технике.
Линейная алгебра против многомерного исчисления —Линейная алгебра называется линейной, потому что она изучает прямые линии. Это математика для решения систем, моделируемых несколькими линейными функциями.
Многие системы в природе можно описать несколькими линейными уравнениями. Будучи легко решаемой, каждая область современной науки содержит модели, в которых уравнения аппроксимируются линейными уравнениями.
В многомерном исчислении мы изучаем функции двух или более независимых переменных, например. z = f (x, y), p = f (x, y, z) и т. д. Многомерное исчисление расширяет ваши знания об исчислении с одной переменной и применимо к трехмерному миру.
Другими словами, мы будем изучать функции двух переменных, которые описываются в трехмерной системе координат.
В заключение, хотя линейная алгебра и исчисление с несколькими переменными демонстрируют разные уровни сложности, нельзя исключать их взаимозависимость и вклад в науку и технику.
Линейная алгебра сложнее исчисления?Как следует из названия, линейная алгебра — это изучение прямых линий с использованием линейных уравнений. Исчисление — это понимание плавно изменяющихся вещей, включая производные, интегралы, векторы, матрицы, параметрические кривые и т. д.
Итак, линейная алгебра сложнее исчисления?
Далее упоминается уровень сложности вопроса: линейная алгебра сложнее исчисления.
- Линейная алгебра требует меньше умственной работы, чем исчисление. Линейная алгебра проще элементарного исчисления. В исчислении вы можете обойтись без понимания интуиции, стоящей за теоремами, и просто запоминая алгоритмы, что не будет хорошо работать в случае линейной алгебры.
- Поняв теоремы линейной алгебры, можно решить все вопросы. Это не относится к исчислению, и вычислительные вопросы могут быть очень сложными даже при хорошем знании теории.
- Вы не будете каждый день изучать новые технологии в линейной алгебре, как в исчислении.
Метод Ньютона, объем цилиндра, правило частных, определение предела и многое другое, что трудно запомнить, являются частью курса математического анализа.
- Вычисление 3 или исчисление с несколькими переменными – самый сложный курс математики. Математический анализ — самый сложный математический предмет, и лишь небольшой процент учащихся достигает его в средней школе или где-либо еще.
- Линейная алгебра является частью абстрактной алгебры в векторном пространстве. Однако с матрицами он более конкретен, следовательно, менее абстрактен и легче для понимания.
- И линейная алгебра, и исчисление включают определение длины, площади и объема. Что касается определения длины, линейная алгебра имеет дело с прямыми линиями, включающими линейные уравнения, тогда как исчисление может вычислять длину кривых линий, включающих нелинейные уравнения с показателями, которые труднее взломать, чем линейные.
Линейная алгебра имеет дело с площадями идеальных окружностей и объемами тел правильной формы, а линейная алгебра имеет дело с площадями идеальных окружностей и объемами тел правильной формы, в то время как исчисление используется для нахождения замкнутых областей с изогнутыми краями и объемов тел неправильной формы.
В то время как в первом используются простые квадратные уравнения, во втором используются уравнения с более высокими показателями, которые, безусловно, сложнее, чем простые квадратные уравнения.
После ответа «линейная алгебра сложнее исчисления», сложность предмета зависит от способностей человека к предмету. Следовательно, тема, трудная для кого-то, может быть легкой для другого. Конечно, будут разные мнения. Поэтому трудно сделать вывод: «Сложнее ли линейная алгебра исчисления?» определенно.
РезюмеСпор о том, что сложнее — алгебра или исчисление, — классический. Это будет продолжаться вечно. Тем не менее, давайте суммируем здесь их общие сходства и различия.
1. Алгебра и математический анализ хотя и относятся к разным разделам математики, но неразрывно связаны друг с другом. Рассматривая алгебру и исчисление, применяя основные алгебраические формулы и уравнения, мы можем найти решения многих наших повседневных проблем.
Исчисление в основном применяется в профессиональных областях из-за его способности находить решения для многих типов структур
2. Знакомство с алгеброй позволяет чувствовать себя комфортно в исчислении. Алгебра позволит вам лучше понять темы исчисления и наоборот. Фактически, хорошее понимание алгебры помогает лучше освоить исчисление.
Следовательно, это нужно иметь в виду после изучения алгебры и исчисления.
3. Что касается линейной алгебры и исчисления, давайте рассмотрим контекст на примере. И линейная алгебра, и исчисление включают определение длины, площади и объема.
Что касается определения длины, линейная алгебра имеет дело с прямыми линиями, используя линейные уравнения, тогда как исчисление может вычислять длину кривых линий, используя нелинейные уравнения с показателями. Какой путь человек выберет для достижения своего ответа, зависит от его математического мышления.
4. Что касается ответа на вопрос «Линейная алгебра сложнее исчисления?»
Многомерное исчисление считается самым сложным курсом математики.
Математический анализ — самый сложный математический предмет, и лишь небольшой процент учащихся достигает его в средней школе или где-либо еще.
5. Однако, как и во всех других дисциплинах, более трудный выбор в конечном счете зависит от интересов и способностей человека, занимающегося им.
Автор Арти Агарвал
О CuemathCuemath, удобная для учащихся математическая платформа, проводит регулярные интерактивные онлайн-занятия для академиков и развития навыков, а их приложение Mental Math для iOS и Android универсальное решение для детей, чтобы развить несколько навыков. Ознакомьтесь со структурой оплаты Cuemath и подпишитесь на бесплатную пробную версию.
Часто задаваемые вопросы об алгебре и исчислении Алгебра — это то же самое, что исчисление?Нет. Хотя они тесно связаны, они оба принадлежат к разным разделам математики. В то время как исчисление имеет дело с операциями над функциями и их производными, алгебра включает операции с числами и переменными.
Можно ли научиться математике, не изучая алгебру?Ответ снова — нет. Исчисление основано на наших знаниях алгебры и на шаг впереди алгебры. Будет почти невозможно выучить или понять исчисление, если у человека нет прочной основы в алгебре.
Почему алгебра считается сложной?
Алгебра отличается от большинства других разделов математики тем, что включает в себя логическое осмысление чисел. Большинство людей склонны думать о числах в терминах арифметического, а не алгебраического смысла. Поэтому им трудно. Как только вы научитесь мыслить в алгебраическом смысле, вам будет очень легко.
В чем разница между алгеброй и исчислением?Алгебра фокусируется на решении уравнений, тогда как исчисление в основном сосредоточено на скорости изменения функций. Двумя основными операциями исчисления являются дифференцирование (нахождение скорости изменения функции) и интегрирование (нахождение площади под кривой функции).
- Эти две важные операции связаны между собой основной теоремой исчисления.
- Алгебра, как и большинство математических дисциплин, является важным инструментом в исчислении, и хорошее понимание алгебры и пределов имеет основополагающее значение для понимания исчисления
- исчисление имеет дело с операциями над функциями и их производными, тогда как алгебра имеет дело с операциями над переменными и числами.
- Алгебра помогает найти наклон линии, а исчисление — наклон кривой.
- Алгебра помогает найти направление движения по прямой линии, тогда как исчисление делает то же самое по любой кривой.
- Алгебра используется для нахождения длины отрезка прямой, а исчисление используется для нахождения длины части кривой.
Разница между алгеброй и исчислением [обновлено в 2022 г.]
Последнее обновление: 21 сентября 2022 г. / Автор Piyush Yadav / Факт проверен / 5 минут
Математика занимает свое место в нашей повседневной жизни.
Это помогает систематически решать наши проблемы.
Математика имеет различные разделы, а именно алгебру, исчисление, тригонометрию, геометрию и т. д. У каждого раздела есть своя важность и разные области применения.
Алгебра против исчисленияОсновное различие между алгеброй и исчислением заключается в том, что алгебра — это раздел математики, который занимается нахождением значений неизвестной переменной путем решения линейных, кубических или квадратных уравнений, которые называются алгебраическими уравнениями, тогда как Исчисление — это раздел математики, изучающий скорость изменения функций.
Алгебра — это раздел математики, который служит основой современной арифметики и современной математики. Алгебра находит значения переменных.
Математический анализ — сложная для понимания отрасль, которая используется на продвинутых уровнях обучения. Исчисление изучает скорость изменения событий.
Таблица сравнения алгебры и исчисления (в табличной форме)
Параметр сравнения Алгебра Исчисление Основная идея Алгебра занимается нахождением значений неизвестных переменных. Исчисление занимается нахождением скорости изменения функций. Время происхождения Возникло в древности, развитие восходит к средневековому периоду. Возникла в 17 веке. Сфера деятельности Работает в пределах известной области и получает результат в ней. Не иметь какой-либо определенной области, при решении проблемы можно узнать что-то новое, и результаты могут быть или не быть в области. Основные операции Решение уравнений. Дифференциация и интеграция. Использование Используется в математике повседневной жизни, такой как определение расстояния, смещения, наклона линии и т. д. Используется в сложных областях и углубленных исследованиях.
Что такое алгебра?
Раздел математики, использующий буквы и символы для представления чисел, работающих по заранее определенным правилам.
Эти символы или буквы называются переменными.
Таким образом, можно сказать, что алгебра — это отношение между различными переменными, определенными операторами, известными как алгебраические уравнения.
Другими словами, алгебра — это обобщенная арифметика, в которой переменные представляют все возможные числа на месте. Алгебра помогает в формировании коррелированных уравнений и последующем их решении для получения значений переменных.
Корни алгебры были заложены вавилонянами, которые также ответственны за развитие продвинутой арифметики. Они разработали формулы для решения задач с использованием линейных или квадратных уравнений.
Во времена Платона греки разработали другую тактику для решения таких проблем, которую они назвали геометрической алгеброй. Греческий математик Диофант позже стал известен как «отец алгебры».
Первое полное решение алгебраических уравнений с нулевыми и отрицательными значениями было дано индийским математиком Брахмагуптой в его книге Brahmasphitasiddhanta.
В 16 веке работы Франсуа Виета оказались важным шагом на пути развития современной алгебры. В середине 16 века другим событием, ознаменовавшим дальнейшее развитие А., стало решение кубических и квадратных уравнений.
Алгебру можно условно разделить на две категории: элементарная алгебра, которая в основном состоит из базовой части алгебры, необходимой для любого математического исследования, и абстрактная или современная алгебра, состоящая из продвинутой алгебры,
в основном изучается профессиональными математиками или академиками.
Алгебра используется во всех областях повседневной жизни. Он занимает важное место в статистике, технике, экономике, компьютерном программировании и т. д.
Что такое исчисление?
Исчисление — это раздел математики, изучающий изменение функций, связанных друг с другом. Другими словами, исчисление — это изучение скорости изменения функций.
В 17 веке Исаак Ньютон и Готфрид Вильгельм Лейбниц независимо друг от друга разработали современное исчисление.
До изобретения исчисления можно было только рассчитать значения переменных, но нельзя было вывести их коэффициенты.
Изобретение исчисления стало первым достижением современной математики. Ньютон разработал формулы для расчета скоростей, разложение функций в ряды по ряду Тейлора.
Есть две ветви исчисления, а именно — дифференциальное исчисление, которое использует производные для определения скорости изменения наклонов или кривых, и интегральное исчисление, которое находит величину, для которой скорость изменения уже известна.
Исчисление имеет огромное значение в физических науках, актуарных науках, информатике, статистике, демографии и т. д.
Основные различия между алгеброй и исчислением
- неизвестные переменные. Это отношения между различными переменными. С другой стороны, исчисление — это раздел математики, который помогает найти скорость изменения сущностей или функций по отношению друг к другу.
- Алгебра — это отрасль, зародившаяся в древние времена и получившая развитие в средние века, тогда как исчисление было изобретено Исааком Ньютоном в 17 веке.
- Алгебра называется Старой математикой, а Математика известна как Современная математика.
- У алгебры есть определенная область работы; он работает внутри него и получает результаты в том же, в то время как исчисление не имеет области работы, после решения проблемы можно получить неожиданные результаты.
- Основная операция алгебры состоит в решении алгебраических уравнений, в то время как исчисление занимается дифференцированием и интегрированием.
- Алгебра известна как повседневная математика, поскольку она помогает решать задачи, связанные с повседневной жизнью, в то время как исчисление используется в передовых областях, таких как статистика, актуарные науки, информатика и т. д.
Заключение это разные разделы математики, они взаимосвязаны. Алгебра имеет дело с переменными, а исчисление — со скоростями, даже если они взаимосвязаны. Оба иногда используются синхронно друг с другом для решения определенных проблем.
Алгебра и исчисление имеют преимущества в соответствующих областях. На уровне начальной школы алгебру легко понять, но нет исчисления.
Ссылки
- https://dl.acm.org/doi/abs/10.1145/49346.49347
- https://arxiv.org/pdf/cond-mat/0304545
Искать «Спроси любую разницу» в Google. Оцените этот пост!
[Всего: 0]
Один запрос?
Я приложил столько усилий, чтобы написать этот пост в блоге, чтобы он был вам полезен. Это будет очень полезно для меня, если вы подумаете о том, чтобы поделиться им в социальных сетях или со своими друзьями/семьей. SHARING IS ♥️
Содержание
сообщите об этом объявлении
Сравнение алгебры и исчисления | Actforlibraries.org
В чем разница между алгеброй и исчислением?
Алгебра и исчисление — две совершенно разные области математики; сказать, что они не связаны, вероятно, не совсем правильно, поскольку большинство разделов математики так или иначе взаимосвязаны, но это не означает, что они очень тесно связаны.
АЛГЕБРА:
Учащихся знакомят с алгеброй довольно рано – обычно в средней школе. На начальных этапах изучения алгебры вводится понятие символа. Например, алгебраические символы используются для представления определенных величин, которые могут изменяться или не изменяться. Скажем, студент должен вырезать прямоугольник из манильского картона, учитывая, что длина прямоугольника должна быть в 3 раза больше его ширины. В такой ситуации алгебра учит нас, что мы должны принять х за ширину прямоугольника, и в этом случае длина прямоугольника будет 3 х, и, следовательно, площадь прямоугольника должна быть (длина), умноженная на (ширину), что переводится как (3x )(x) или 3×2 , читается как «три х в квадрате». А если, кроме того, требуется, чтобы рассматриваемый прямоугольник имел площадь, равную некоторому постоянному числу, то, если число не указано, алгебра говорит, что мы могли бы записать площадь прямоугольника как 3 x 2 = a , где a — символ, представляющий константу. Конечно, если нам известно, что площадь прямоугольника равна 50 см2, то наша формула для площади принимает вид 3×2 = 50,9.
0003
Теперь математическое утверждение 3×2 = 50 — это то, что известно как алгебраическое уравнение, а точнее, это квадратное уравнение, которое можно решить, чтобы найти значения неизвестного x, на этом рисунке представляющие ширину прямоугольника в см.
Вообще говоря, алгебра — это раздел математики, изучающий различные алгебраические выражения и функции, классифицируя их и манипулируя ими, а также обнаруживая их атрибуты. На самом деле, термин «функция» сам по себе является важным математическим понятием, в которое мы не будем углубляться, за исключением того, что скажем, что это способ показать взаимосвязь между переменными, величинами, значения которых изменяются и которые обычно представляются символами х, у, г и т. д.
Алгебру можно изучать с самого начального уровня до продвинутого, бакалавриата и даже магистратуры. Если вы немного занимались алгеброй в младших и старших классах средней школы, вы могли быть хорошо знакомы с такими терминами, как «линейная функция» или «линейное выражение», «квадратичные/кубические выражения», «квадратные уравнения» и т.
д., а также с различными методами разложения на множители. упомянутые «квадратичные/кубические выражения». Вы могли бы также изучить построение графиков некоторых выражений/функций с учетом их алгебраических уравнений. А на продвинутых курсах в колледже и магистратуре можно было углубленно изучать такие алгебраические понятия, как линейные системы — системы линейных уравнений, включающие множество неизвестных, и изучать различные методы «манипулирования» этими системами. Конечно, это всего лишь одна из множества тем в алгебре. Есть много других разделов алгебры, например. Булева алгебра, алгебраические структуры, поля и кольца, и это лишь некоторые из них.
ИСЧИСЛЕНИЕ:
Можно с уверенностью сказать, что не все старшеклассники, изучающие математические курсы, изучали исчисление, раздел математики, который одновременно стимулирует интеллектуально и концептуально сложно. Из-за предполагаемой трудности и сложности не все старшеклассники предпочитают изучать эту область математики.
Фундаментальной концепцией исчисления является идея «скорости изменения», величины, которая измеряет, как две или более переменных изменяются по отношению к другим. Говоря математическим языком, для вычисления скорости изменения, скажем, двух переменных x, y (представленных двумя алгебраическими символами, x и y) вводится новое математическое понятие, обозначаемое dy/dx, известное как производная от y по отношению к х. И процесс нахождения этой производной является одной из важнейших задач в изучении исчисления.
Конечно, необходимо уметь находить производные математических функций, таких как y = x3 – x2; из приемов дифференцирования (приемов нахождения производных) получается выражение dy/dx = 3×2 – 2x. Без сомнения, это алгебраические выражения, и для вывода общих правил дифференцирования использование общих алгебраических выражений неизбежно. Здесь алгебра встречается с исчислением, но методы исчисления сильно отличаются от методов алгебры. Но исчисление — это гораздо больше, чем просто нахождение производных алгебраических функций — в картину также входят другие функции, такие как тригонометрические функции.
Применение исчисления встречается во многих областях: инженерии, экономике и других социальных науках, физических и биологических науках, где вопрос с заданными параметрами (например, температура, давление, влажность; население, затраты на производство, спрос и предложение и т. д.) анализируются параметры, представленные алгебраическими символами, и вопрос становится вопросом математики, в частности исчисления. В зависимости от поставленного вопроса инженер, экономист или ученый должен будет составить некоторые математические уравнения (например, дифференциальные уравнения), и при определенных начальных условиях относительно значений параметров вопрос может быть решен путем решения дифференциальное уравнение с использованием техники нахождения «противопроизводных» или «интегрирования».
ЗАКЛЮЧЕНИЕ: РАЗНИЦА МЕЖДУ АЛГЕБОЙ И ВЫЧИСЛЕНИЕМ
Я выделил больше места для обсуждения алгебры, чем исчисления, потому что большинство читателей будут более знакомы с (элементарной) алгеброй, чем с исчислением.
У большинства студентов были бы некоторые элементарные знания алгебры — алгебраические дроби; умножение и деление алгебраических выражений; факторизация и т. д. Некоторые простые повседневные вопросы требуют простых знаний о том, как применить алгебру к этим вопросам — вышеупомянутый вопрос о прямоугольнике является одной из иллюстраций. Вы должны быть в состоянии найти множество относительно простых повседневных ситуаций, в которых можно с пользой применить знания, полученные на курсе алгебры в средней школе.
Большинство людей согласится с тем, что в отличие от алгебры исчисление, возможно, является более «продвинутой» областью математики в том смысле, что вам не нужно знать исчисление, чтобы решать простые повседневные вопросы, которые могут возникнуть. Было бы неверным утверждать, что только в более сложных сценариях, возникающих в области инженерии, наук, в игру вступают методы исчисления, дифференцирующие различные функции и объединяющие их.
Другими словами, алгебра, по крайней мере на элементарном уровне, является изучением символического представления переменных и неизменных величин и различных операций с ними.
Исчисление, с другой стороны, не имеет «элементарной» стадии; даже на начальном уровне необходимо усвоить относительно более сложную концепцию скорости изменения переменных. И алгебру, и исчисление можно изучать на очень продвинутом уровне, но, возможно, исчисление немного сложнее понять даже на начальном уровне.
Какая разница в математике? Определение, символ, примеры, факты
Введение
Давайте посмотрим на две фигуры:
Их цвет также отличается. Один больше, другой меньше. Это означает, что их размер также отличается. Различие означает способ, которым два или более объектов или людей не похожи друг на друга.
Но разница в математике означает другое. Давайте узнаем, что означает разница в математике.
Определение разницы в математике
Разница в математике является результатом одной из важных математических операций, которая получается путем вычитания двух чисел. Он говорит нам, насколько одно число отличается от другого. Цель поиска разницы в математике состоит в том, чтобы сказать, сколько чисел лежит между двумя заданными числами.
Разница в математическом символе минус (-).
Уменьшаемое — первое число в предложении вычитания. Вычитаемое — это второе число в предложении вычитания, и результат, который мы получаем, — это разница между двумя числами.
Нахождение разницы между числами с помощью числовой строки
Числовая строка очень удобна для нахождения разницы меньших чисел. Находя разницу между числами на числовой прямой, мы движемся к левой стороне числовой строки. Мы начинаем с уменьшаемого и двигаемся влево к числу по направлению к вычитаемому.
Пример: Найдите разницу между 4 и -6 на числовой прямой.
Разница =10
Нахождение разницы между двумя числами
Чтобы найти разницу между натуральными числами и целыми числами, необходимо выполнить следующие шаги:
- Первый шаг – расположить значения вертикально в порядке их разрядности. Также убедитесь, что большее число должно быть вверху, а меньшее — внизу.
- Начните вычитать числа, начиная с разряда единиц.
Без заимствования
Например, нам нужно найти разницу между 2342 и 6758.
В этом случае мы видели, что каждая цифра вычитаемого меньше соответствующей цифры уменьшаемого. Получаем
С заимствованием
В этом случае некоторые цифры в вычитаемом при определенном разряде больше, чем соответствующее значение уменьшаемого.
Предположим, нам нужно найти разницу между 3456 и 1287.
- Вычесть 7 из 6. Мы не можем вычесть большее число из меньшего, поэтому мы заимствуем 1 из цифры, стоящей на десятом месте в уменьшаемом. В данном случае это число равно 5. Таким образом, мы заимствуем 1 из 5, и 5 на разряде десятков в уменьшаемом конце становится 4. Но число на месте единиц в уменьшаемом конце после заимствования 1 становится 16. Теперь мы можем вычесть 7 из 16 и мы получаем 9на месте как ответ.
- Мы переходим к вычитанию разряда десятков. Помните, что цифра в разряде десятков теперь равна 4, а не 5.
Итак, нам нужно вычесть 8 из 4, что опять-таки невозможно. Таким образом, мы снова повторяем шаги, которые мы делали для вычитания цифр в разряде единиц. Мы заимствуем 1 из цифры в разряде сотен и даем 4 в разряде десятков. Таким образом, 4 в разряде сотен уменьшаемого становится 3, а 4 в разряде десятков уменьшаемого становится 14. Теперь мы можем вычесть 8 из 14, и мы получим 6 как ответ в разряде десятков.
- Теперь посмотрим на значения сотен. Здесь у нас есть 2 в качестве вычитаемого и 3 в качестве уменьшаемого, которое можно легко вычесть. Таким образом, мы получаем 1 в качестве ответа в разряде сотен.
- Наконец, мы проверяем значения на разряде тысяч. У нас есть 1 в качестве вычитаемого и 3 в качестве уменьшаемого. Следовательно, мы получаем 2 в качестве ответа на разряде тысяч.
Следовательно, 3456 – 1287 = 2169
Нахождение разницы между двумя десятичными числами
Чтобы найти разницу между двумя десятичными числами, необходимо выполнить следующие шаги:
- Преобразовать разные десятичные числа в одинаковые десятичные числа.
- Разместите десятичные числа так, чтобы разряд десятков был меньше десятков, единиц меньше единиц, десятичная точка меньше десятичной точки, десятая цифра меньше десятой, сотая цифра меньше сотой и так далее.
- Вычтите так же, как и для целого числа. Занять, если необходимо.
- Поместите запятую в разнице точно под запятой в десятичных числах.
Например: Нам нужно найти разницу между 28,06 и 7,984.
Сначала мы преобразуем оба десятичных числа в одинаковые десятичные числа, добавив один ноль в 28.06.
28.06 можно записать как 28.060.
Следующий шаг — вычесть их как целые числа и поставить десятичную точку.
Нахождение разницы между двумя дробями
Чтобы найти разницу между двумя дробями, мы должны использовать следующие шаги:
- Проверка, похожи ли дроби на дроби или нет. Если они подобны дробям, переходим к шагу 4, иначе — переходим к шагу 2.
- Когда дроби разные, находим НОК знаменателей.
- Преобразование каждой дроби в эквивалентную дробь, знаменатель которой равен НОК, полученному на предыдущем шаге.
- После того, как дроби станут похожими на дроби, вычитаем их так же, как мы делаем для подобных дробей, т. е. вычитаем их числители.
- Приведение дроби к простейшей форме, если требуется.
Например: Рецепт требует 2/7 чайной ложки соли и 1/3 чайной ложки паприки. Насколько больше паприки добавлено по сравнению с солью?
Доля соли, необходимая в рецепте = $\frac{2}{7}$
Доля соли красного перца, необходимая в рецепте = $\frac{1}{3}$
LCM(7, 3) = 21
$\frac{2\times3}{7\times3}=\frac{6}{21}$ и $\frac{1\times7}{3\times7}=\frac{7}{21} $
Разница = $\frac{7}{21}-\frac{6}{21}=\frac{1}{21}$
Решенные примеры
1. Найдите разницу между -2 и 5 на числовой прямой.
Решение :
Разница = 7
2.
В саду 2052 муравья. Улетело 1156 муравьев. Сколько муравьев осталось сейчас?
Решение : Количество муравьёв в саду = 2052
Количество муравьёв, которые улетели = 1156
Количество муравьёв, оставшихся сейчас = 2052 – 1156
3. Питер купил сироп за $\$$40,00 , коробку с печеньем за $\$$19,50 и флакон с маслом для волос за $\$$30 . Она дала $\$$100 продавцу, сколько денег продавец вернул в качестве остатка?
Решение : Сумма, которую Питер потратил = $\$$40,00 + $\$$19,50 + $\$$30 = $\$$89,50
Сумма, которую Питер дал продавцу = $\$$100
Сумма, владелец магазина вернет баланс = $\$$100 – $\$$89.50
Сумма, которую продавец вернет в балансе = $\$$10,50
Практические задачи
$\frac{3}{16}$
$\frac{1}{4}$
$\frac {1}{2}$
$\frac{5}{16}$
Правильный ответ: $\frac{3}{16}$
$\frac{1\times4}{4\times4}= \фракция{4}{16}; \frac{4}{16}-\frac{1}{16}=\frac{3}{16}$188
$-208$
$-188$
208
Правильный ответ: : $-188$
$-198-(-10)=-198+10=-188$$\frac{5}{6}$
$\frac{1}{3}$
$\frac{1}{2}$
$\frac{1}{6}$
Правильно ответ: $\frac{1}{6}$
Часть земли, которую он дал =$\frac{1}{3}+\frac{1}{2}=\frac{5}{6}$
Осталось land =$1-\frac{5}{6}=\frac{6}{6}-\frac{5}{6}=\frac{1}{6}$Часто задаваемые вопросы
Как разница в математике, используемой в нашей повседневной жизни?
Разница используется для определения расстояния, понимания обратного счета, внесения сдачи в супермаркете и некоторых игр, среди прочего.

 06.2021
Категория: Образование и наука Подкатегория: Математика
Популярность
06.2021
Категория: Образование и наука Подкатегория: Математика
Популярность


 Как найти площадь трапеции?
Как найти площадь трапеции? Что такое одночлены, и какими они бывают?Базовым алгебраическим понятием считаются одночлены и состоящие из них числовые выражения и уравнения. Что такое одночлены, и какими они бывают?
Что такое одночлены, и какими они бывают?Базовым алгебраическим понятием считаются одночлены и состоящие из них числовые выражения и уравнения. Что такое одночлены, и какими они бывают? 🙂 Тут математика с физикой, безусловно, едины
🙂 Тут математика с физикой, безусловно, едины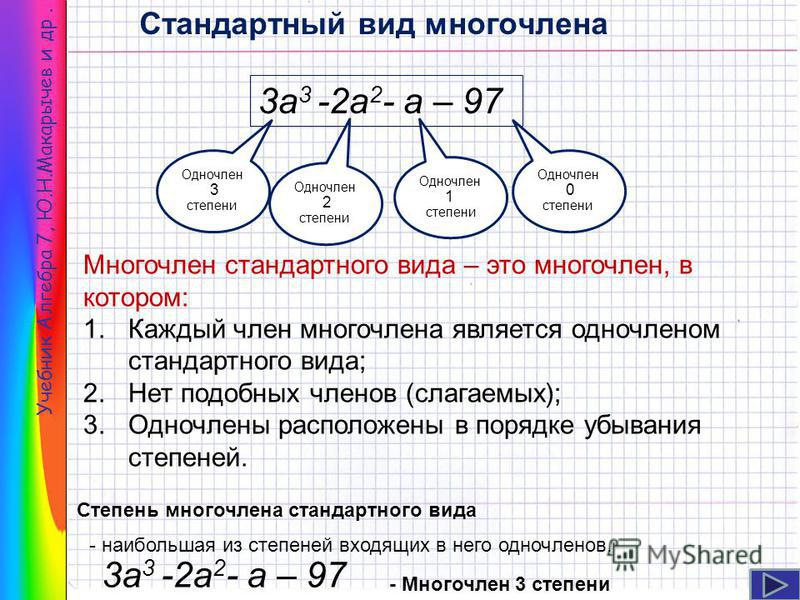 Какое-то время он терпит все расхождения:), потом отправляется искать новую, более сложную модель.:) И никаких обид!:) А теперь представим, что математику объединят с физикой? Откуда физику модели брать — и, главное, как с ними работать?:)
Какое-то время он терпит все расхождения:), потом отправляется искать новую, более сложную модель.:) И никаких обид!:) А теперь представим, что математику объединят с физикой? Откуда физику модели брать — и, главное, как с ними работать?:) П. Хавин) выдвигал почти такое же суждение, что и Арнольд: это только кажется, что математики занимаются искусством и изобретательством и , а на самом деле они совершают открытия
П. Хавин) выдвигал почти такое же суждение, что и Арнольд: это только кажется, что математики занимаются искусством и изобретательством и , а на самом деле они совершают открытия
 Всем нам и болеть, и умирать…
Всем нам и болеть, и умирать…
 🙂 У адронного коллайдера тоже практических применений негусто.:)
🙂 У адронного коллайдера тоже практических применений негусто.:) А нафига?:) На шутку не похоже, симпатий от коллег это ему вряд ли добавит.
А нафига?:) На шутку не похоже, симпатий от коллег это ему вряд ли добавит.
 «Проверил бы теорему Ферма экспериментально» — это как?
«Проверил бы теорему Ферма экспериментально» — это как?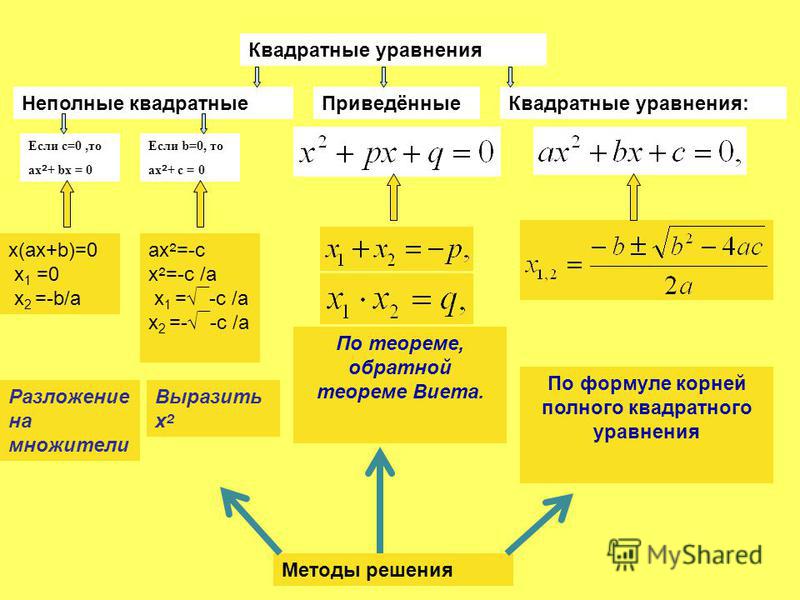
 например, была в какой-то момент выдвинута теория, что атомы — это узлы. реальность этого не подтвердила,
например, была в какой-то момент выдвинута теория, что атомы — это узлы. реальность этого не подтвердила, так лучше ?
так лучше ? е. использовать интегралы по пространству кривизн и проч., как это делалось до того, как математика с физикой разделились, т.е. до середины 20 века
е. использовать интегралы по пространству кривизн и проч., как это делалось до того, как математика с физикой разделились, т.е. до середины 20 века Читал.:)
Читал.:)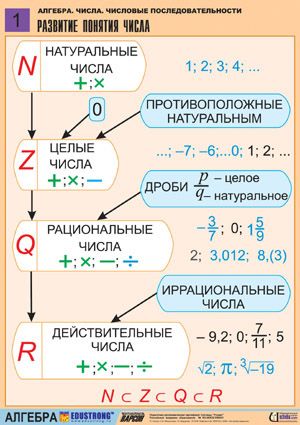 0103
0103 , действовать как числа или величины в уравнениях и формулах.
, действовать как числа или величины в уравнениях и формулах.

 Применяя основные алгебраические формулы и уравнения, мы можем найти решение многих наших повседневных проблем.
Применяя основные алгебраические формулы и уравнения, мы можем найти решение многих наших повседневных проблем.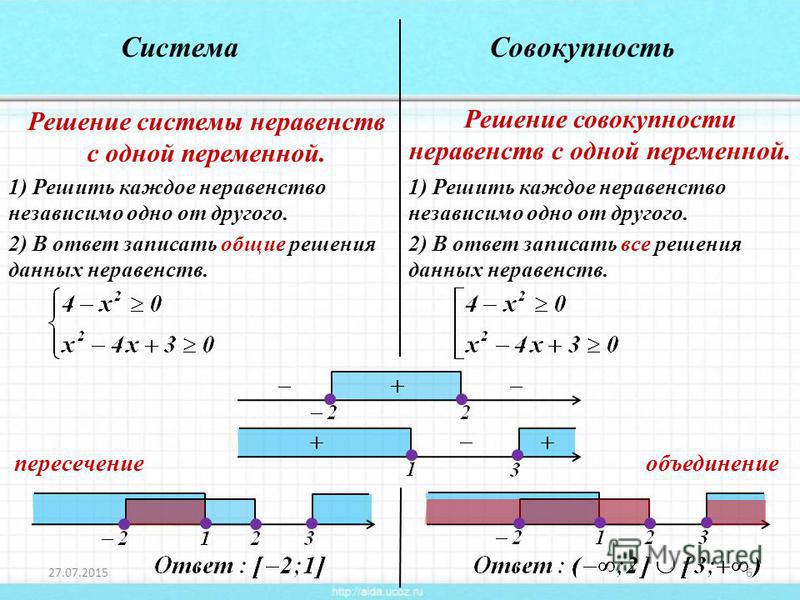 Исчисление далее делится на
Исчисление далее делится на Двумя основными операциями исчисления являются дифференцирование (нахождение скорости изменения функции) и интегрирование (нахождение площади под кривой функции).
Двумя основными операциями исчисления являются дифференцирование (нахождение скорости изменения функции) и интегрирование (нахождение площади под кривой функции).
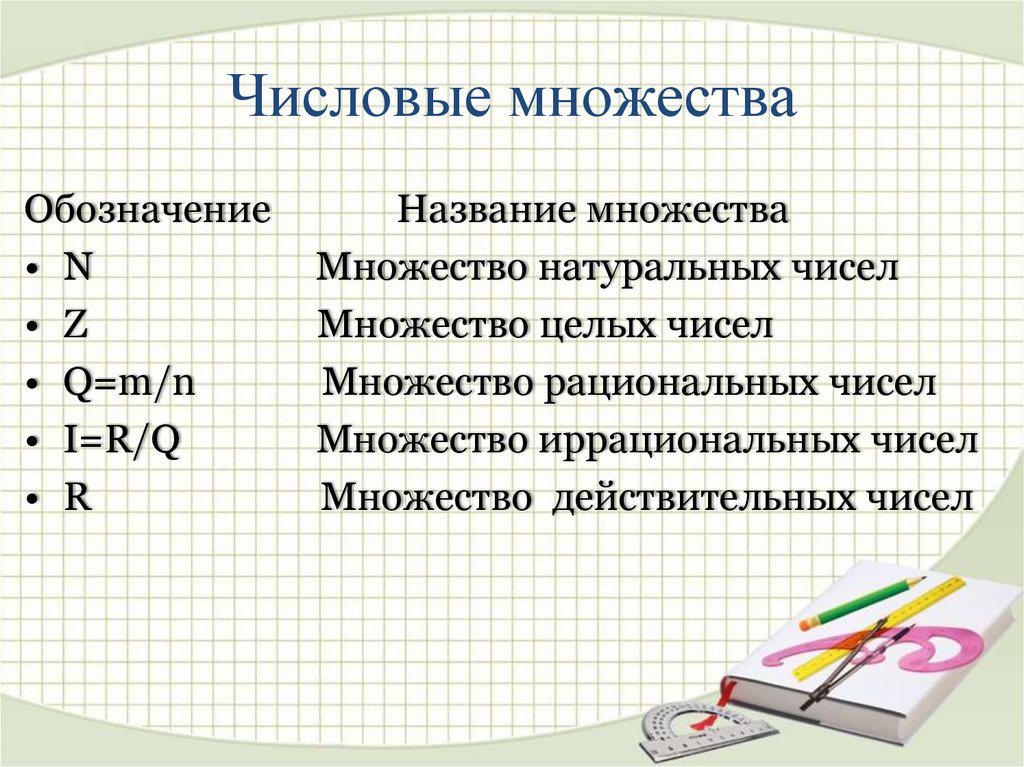 Как только теоремы линейной алгебры будут хорошо поняты, можно будет ответить на большинство сложных вопросов.
Как только теоремы линейной алгебры будут хорошо поняты, можно будет ответить на большинство сложных вопросов.

 Метод Ньютона, объем цилиндра, правило частных, определение предела и многое другое, что трудно запомнить, являются частью курса математического анализа.
Метод Ньютона, объем цилиндра, правило частных, определение предела и многое другое, что трудно запомнить, являются частью курса математического анализа.
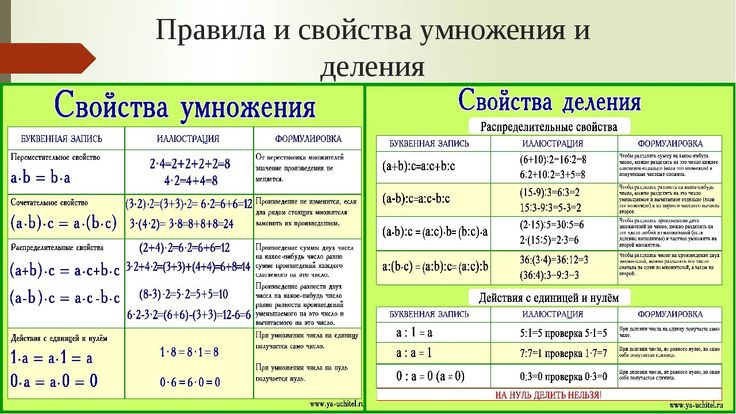
 Математический анализ — самый сложный математический предмет, и лишь небольшой процент учащихся достигает его в средней школе или где-либо еще.
Математический анализ — самый сложный математический предмет, и лишь небольшой процент учащихся достигает его в средней школе или где-либо еще.
 Это помогает систематически решать наши проблемы.
Это помогает систематически решать наши проблемы.
 Эти символы или буквы называются переменными.
Эти символы или буквы называются переменными.
 До изобретения исчисления можно было только рассчитать значения переменных, но нельзя было вывести их коэффициенты.
До изобретения исчисления можно было только рассчитать значения переменных, но нельзя было вывести их коэффициенты.

 0003
0003 д., а также с различными методами разложения на множители. упомянутые «квадратичные/кубические выражения». Вы могли бы также изучить построение графиков некоторых выражений/функций с учетом их алгебраических уравнений. А на продвинутых курсах в колледже и магистратуре можно было углубленно изучать такие алгебраические понятия, как линейные системы — системы линейных уравнений, включающие множество неизвестных, и изучать различные методы «манипулирования» этими системами. Конечно, это всего лишь одна из множества тем в алгебре. Есть много других разделов алгебры, например. Булева алгебра, алгебраические структуры, поля и кольца, и это лишь некоторые из них.
д., а также с различными методами разложения на множители. упомянутые «квадратичные/кубические выражения». Вы могли бы также изучить построение графиков некоторых выражений/функций с учетом их алгебраических уравнений. А на продвинутых курсах в колледже и магистратуре можно было углубленно изучать такие алгебраические понятия, как линейные системы — системы линейных уравнений, включающие множество неизвестных, и изучать различные методы «манипулирования» этими системами. Конечно, это всего лишь одна из множества тем в алгебре. Есть много других разделов алгебры, например. Булева алгебра, алгебраические структуры, поля и кольца, и это лишь некоторые из них.

 У большинства студентов были бы некоторые элементарные знания алгебры — алгебраические дроби; умножение и деление алгебраических выражений; факторизация и т. д. Некоторые простые повседневные вопросы требуют простых знаний о том, как применить алгебру к этим вопросам — вышеупомянутый вопрос о прямоугольнике является одной из иллюстраций. Вы должны быть в состоянии найти множество относительно простых повседневных ситуаций, в которых можно с пользой применить знания, полученные на курсе алгебры в средней школе.
У большинства студентов были бы некоторые элементарные знания алгебры — алгебраические дроби; умножение и деление алгебраических выражений; факторизация и т. д. Некоторые простые повседневные вопросы требуют простых знаний о том, как применить алгебру к этим вопросам — вышеупомянутый вопрос о прямоугольнике является одной из иллюстраций. Вы должны быть в состоянии найти множество относительно простых повседневных ситуаций, в которых можно с пользой применить знания, полученные на курсе алгебры в средней школе. Исчисление, с другой стороны, не имеет «элементарной» стадии; даже на начальном уровне необходимо усвоить относительно более сложную концепцию скорости изменения переменных. И алгебру, и исчисление можно изучать на очень продвинутом уровне, но, возможно, исчисление немного сложнее понять даже на начальном уровне.
Исчисление, с другой стороны, не имеет «элементарной» стадии; даже на начальном уровне необходимо усвоить относительно более сложную концепцию скорости изменения переменных. И алгебру, и исчисление можно изучать на очень продвинутом уровне, но, возможно, исчисление немного сложнее понять даже на начальном уровне. Разница в математическом символе минус (-).
Разница в математическом символе минус (-).
 Итак, нам нужно вычесть 8 из 4, что опять-таки невозможно. Таким образом, мы снова повторяем шаги, которые мы делали для вычитания цифр в разряде единиц. Мы заимствуем 1 из цифры в разряде сотен и даем 4 в разряде десятков. Таким образом, 4 в разряде сотен уменьшаемого становится 3, а 4 в разряде десятков уменьшаемого становится 14. Теперь мы можем вычесть 8 из 14, и мы получим 6 как ответ в разряде десятков.
Итак, нам нужно вычесть 8 из 4, что опять-таки невозможно. Таким образом, мы снова повторяем шаги, которые мы делали для вычитания цифр в разряде единиц. Мы заимствуем 1 из цифры в разряде сотен и даем 4 в разряде десятков. Таким образом, 4 в разряде сотен уменьшаемого становится 3, а 4 в разряде десятков уменьшаемого становится 14. Теперь мы можем вычесть 8 из 14, и мы получим 6 как ответ в разряде десятков.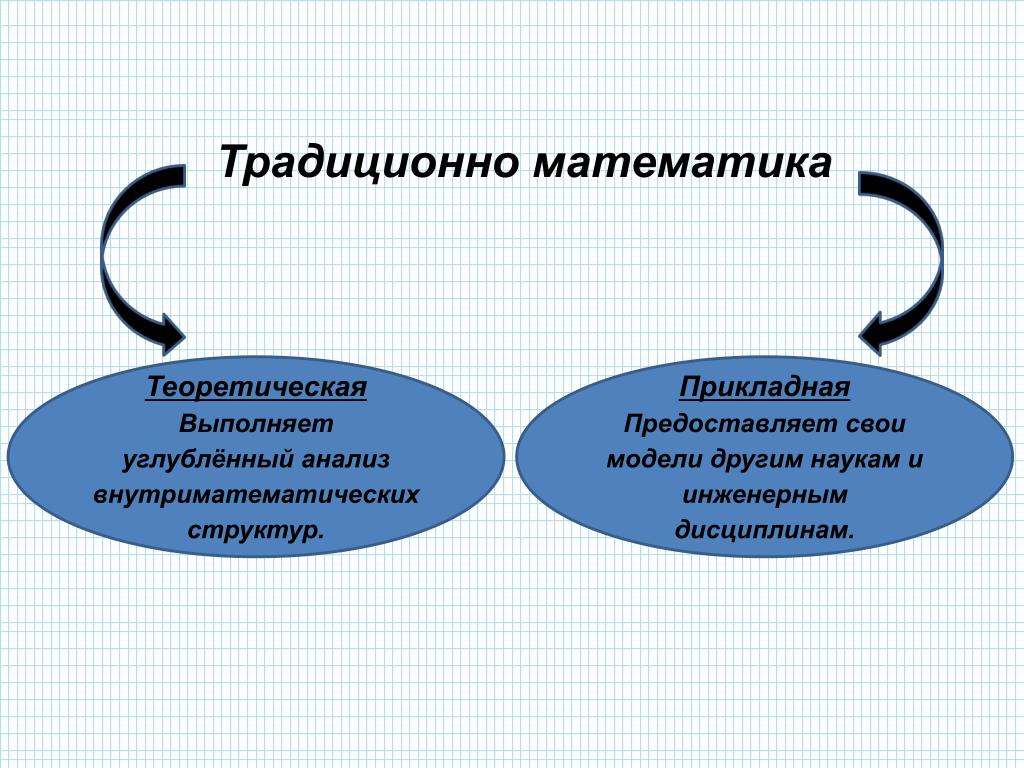

 В саду 2052 муравья. Улетело 1156 муравьев. Сколько муравьев осталось сейчас?
В саду 2052 муравья. Улетело 1156 муравьев. Сколько муравьев осталось сейчас? 