Чему равен cos 90: Чему равен косинус 90° градусов

alexxlab / / Разное
2

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8Найти точное значениеcos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15Найти точное значениеcsc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21
Найти точное значение		cos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значение sin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73		Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град.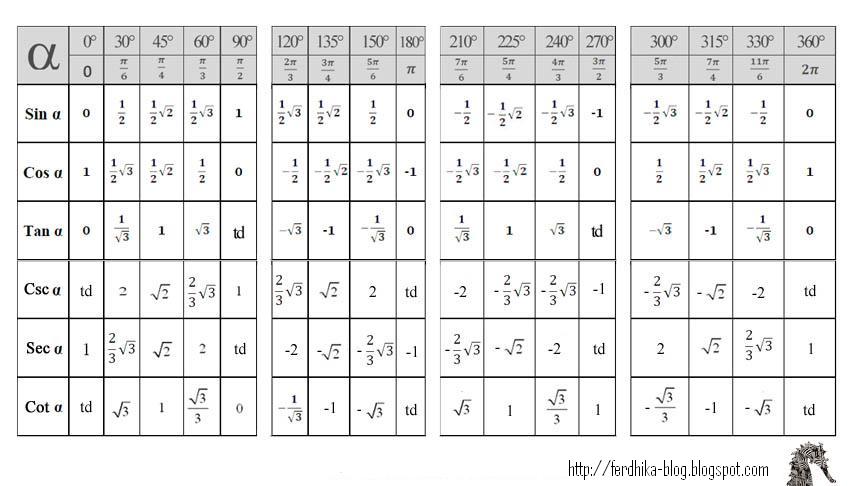
)
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )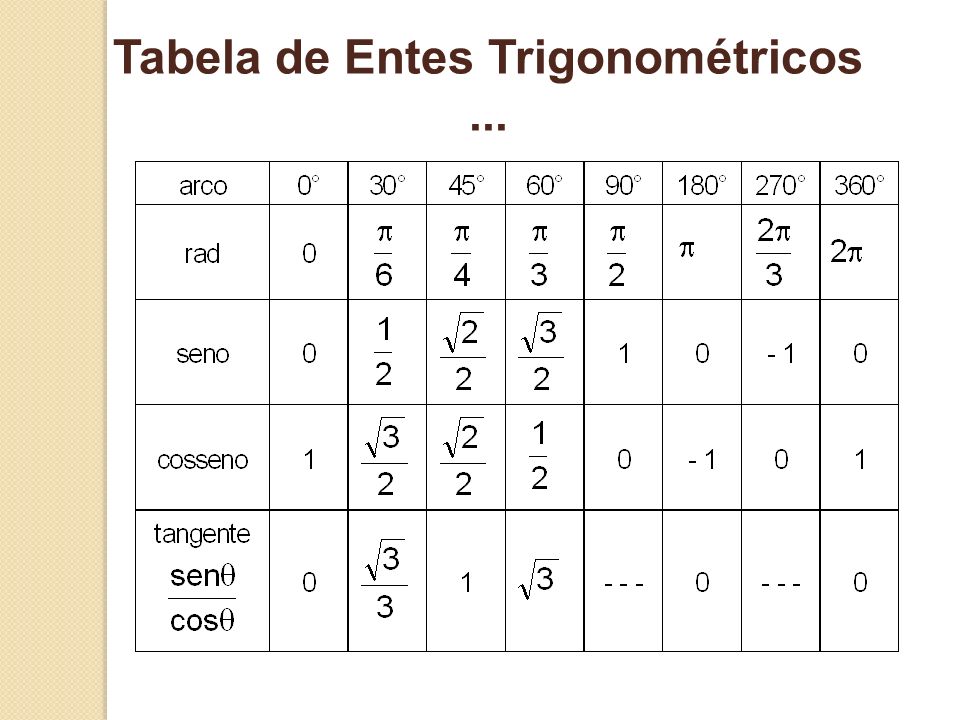
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Cos 90 градусов — Найти значение Cos 90 градусов

LearnPracticeDownload

Значение cos 90 градусов равно 0 . Cos 90 градусов в радианах записывается как cos (90° × π/180°), т. е. cos (π/2) или cos (1,570796…). В этой статье мы обсудим методы нахождения значения cos 90 градусов на примерах.

  • Кос 90°: 0
  • Cos (-90 градусов): 0
  • Cos 90° в радианах: cos (π/2) или cos (1,57079)63 . . .)

Каково значение Cos 90 градусов?

Значение cos 90 градусов равно 0. Cos 90 градусов также можно выразить с помощью эквивалента данного угла (90 градусов) в радианах (1,57079 . . .)

Мы знаем, используя преобразование градусов в радианы, θ в радианы = θ в градусах × (pi/180°)
⇒ 90 градусов = 90° × (π/180°) рад = π/2 или 1,5707. . .
∴ cos 90° = cos(1,5707) = 0

Объяснение:

Для cos 90 градусов, угол 90° лежит на положительной оси Y. Таким образом, значение cos 90° = 0
Поскольку функция косинуса является периодической функцией, мы можем представить cos 90° как cos 90 градусов = cos(90° + n × 360°), n ∈ Z.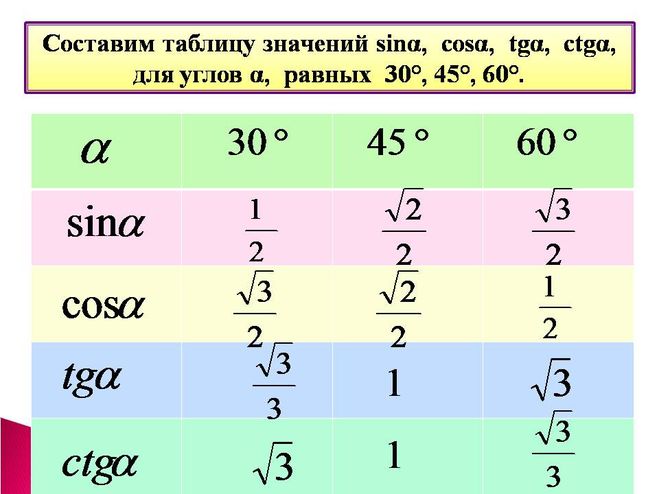
⇒ cos 90° = cos 450° = cos 810° и так далее.
Примечание: Поскольку косинус является четной функцией, значение cos(-90°) = cos(90°) = 0.

Методы определения значения Cos 90 градусов задан как 0. Мы можем найти значение cos 90 градусов по:

  • Используя тригонометрические функции
  • Использование единичного круга

Cos 90° в терминах тригонометрических функций

Используя формулы тригонометрии, мы можем представить cos 90 градусов как:

  • ± √(1-sin²(90°))
  • ± 1/√(1 + tan²(90°))
  • ± кроватка 90°/√(1 + кроватка²(90°))
  • ±√(косек²(90°) — 1)/косек 90°
  • 1/сек 90°

Примечание. Поскольку 90° лежит на положительной оси Y, конечное значение cos 90° будет 0.

Мы можем использовать тригонометрические тождества для представления cos 90° как

  • -cos(180° — 90°) = -cos 90°
  • -cos(180° + 90°) = -cos 270°
  • sin(90° + 90°) = sin 180°
  • sin(90° — 90°) = sin 0°

Cos 90 градусов с помощью единичной окружности

Чтобы найти значение cos 90 градусов с помощью единичной окружности:

  • Поверните ‘r’ против часовой стрелки, чтобы образовать угол 90° с положительной осью x.
  • Cos 90 градусов равен x-координате (0) точки пересечения (0, 1) единичной окружности и r.

Отсюда значение cos 90° = x = 0

☛ Также проверьте:

  • cos 2 градуса
  • потому что 53 градуса
  • соз 15 градусов
  • потому что 38 градусов
  • потому что 226 градусов
  • потому что 1170 градусов

Примеры использования Cos 90 градусов

  1. Пример 1: Упростить: 5 (cos 90°/sin 90°)

    Решение:

    Мы знаем cos 90° = 0 и sin 90° = 1
    ⇒ 5 cos 90°/sin 90° = 5 (0)
    = 0

  2. Пример 2. Найдите значение 2 cos(90°)/3 cos(0°).

    Решение:

    Используя тригонометрические тождества, мы знаем, что cos(90°) = 0 и cos 0° = 1.
    ⇒ Значение 2 cos(90°)/3 cos(0°) = 0

  3. Пример 3: Используя значение cos 90°, решите: (1-sin²(90°)).

    Решение:

    Мы знаем, (1-sin²(90°)) = (cos²(90°)) = 0
    ⇒ (1-sin²(90°)) = 0

перейти к слайдуперейти к слайдуперейти к слайду

 

Готовы увидеть мир глазами математика?

Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.

Запишитесь на бесплатный пробный урок

Часто задаваемые вопросы о Cos 90 Degrees

Что такое Cos 90 Degrees?

Cos 90 градусов — значение тригонометрической функции косинуса для угла, равного 90 градусам. Значение cos 90° равно 0.

Как найти Cos 90° с точки зрения других тригонометрических функций?

Используя формулу тригонометрии, значение cos 90° может быть выражено через другие тригонометрические функции следующим образом:

  • ± √(1-sin²(90°))
  • ± 1/√(1 + tan²(90°))
  • ± кроватка 90°/√(1 + кроватка²(90°))
  • ± √(косек²(90°) — 1)/косек 90°
  • 1/сек 90°

☛ Также проверьте: тригонометрическую таблицу

Каково значение Cos 90° в пересчете на Cosec 90°?

Поскольку функция косинуса может быть представлена ​​с помощью функции косеканса, мы можем записать cos 90° как [√(cosec²(90°) — 1)/cosec 90°].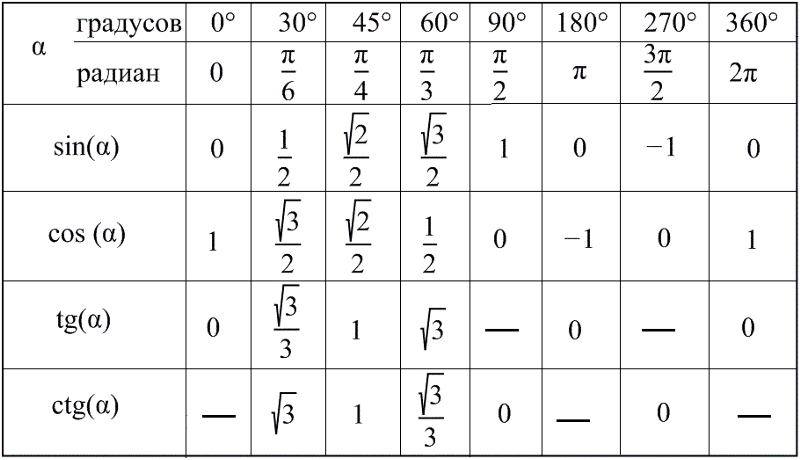 Значение cosec 90° равно 1.

Каково значение Cos 90 градусов с точки зрения греха 90°?

Используя тригонометрические тождества, мы можем записать cos 90° через sin 90° как, cos(90°) = √(1 — sin²(90°)). Здесь значение sin 90° равно 1.

Как найти значение Cos 90 градусов?

Значение cos 90 градусов можно рассчитать, построив угол 90° с осью x и затем найдя координаты соответствующей точки (0, 1) на единичной окружности. Значение cos 90° равно координате x (0). ∴ cos 90° = 0.

 

Скачать БЕСПЛАТНО учебные материалы

Тригонометрия

Рабочие листы по математике и
визуальные учебные программы

Cos 90 Value

Тригонометрия — один из самых важных математических инструментов, используемых в повседневной работе. Тригонометрия используется для измерения углов и сторон треугольника, которые неизвестны. Однако это справедливо только для прямоугольных треугольников. Он использует отношения и обратные величины, чтобы найти измерения неизвестных значений. Тремя основными составляющими тригонометрии являются Sin, косинус и тангенс, на основе которых производятся все расчеты и измерения. Косинус или косинус — одно из тех важных тригонометрических соотношений, которое на самом деле является отношением длин смежных сторон и гипотенуз. Чтобы узнать об этих важных тригонометрических функциях, мы начнем со значения Cos 9.0-я степень, относящиеся к ней законы, обратные величины, а также относящиеся к ней производные с помощью единичного круга. Значение косинуса 90 градусов было получено равным 0.

 

Значение косинуса 90

Чтобы определить функцию косинуса острого угла, мы рассмотрим прямоугольный треугольник с интересующим углом и сторонами треугольника. . Три стороны треугольника определяются как:

 

(изображение будет загружено в ближайшее время)

 

Противоположная сторона прямоугольного треугольника — это сторона, противоположная интересующему углу.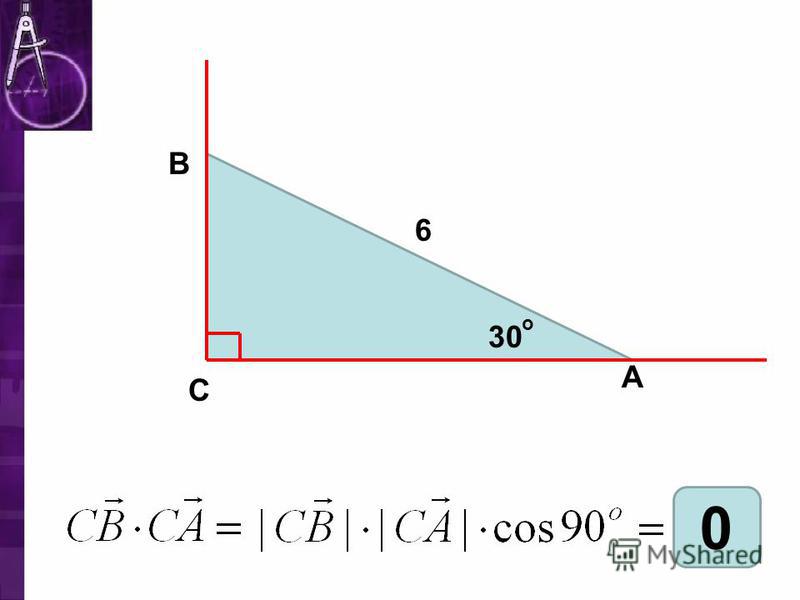

 

Самая длинная сторона прямоугольного треугольника, то есть гипотенуза, является противоположной стороной прямого угла в треугольнике.

 

Оставшаяся сторона треугольника, т. е. смежная сторона, образующаяся между углом интереса и прямым углом.

 

Функция косинуса угла определяется как отношение длины прилежащей стороны прямоугольного треугольника к гипотенузе.

 

\[Cos Ө = \frac{\text{Смежная сторона}}{\text{сторона гипотенузы}} \]

 

Получение Cos 90 градусов с использованием единичной окружности

Теперь мы вычислим значение cos 90°, используя единичную окружность с радиусом 1 единицу и центром окружности, расположенным в начале координат осей «x» и «y». Возьмем точку P (a,b) в любом месте окружности, образующей угол AOP=x радиан. Отсюда следует, что длина дуги AP эквивалентна x. При этом мы определим следующее значение,

 

(Изображение будет загружено в ближайшее время)

 

Cos x= a и Sin x =b.

Используя единичную окружность, мы теперь рассмотрим прямоугольный треугольник OMP.

по питагорской теореме, мы получаем

OM2 + MP2 = OP2

или

A2 + B2 = 1

Таким образом, каждая точка на единичном круге определяется как

A2 + B2 = 1

или

2020220. Cos2 x + Sin2 x = 1

Примечание. Один полный оборот образует угол 2 π радиан в центре окружности и от единичной окружности. Он определяется как:

\[\угол AOB = \frac{\pi}{2}\]

 

\[\угол AOC = \pi\] и  \[\угол AOD = 3\frac{\pi}{2} \]

 

Все углы треугольника являются целыми кратными π/2, и это обычно называется квадрантным углом. Координаты точек A, B, C и D задаются как (1, 0), (0, 1), (-1,0) и (0,-1) соответственно. Мы получим значение Cos 90 через угол квадранта.

 

Следовательно, значение Cos 90° равно 0

  9{2} — 2ab Cos (c) \]

При этом будет легко запомнить 0°, 30°, 45°, 60° и 90°, так как все эти значения присутствуют в первом квадранте.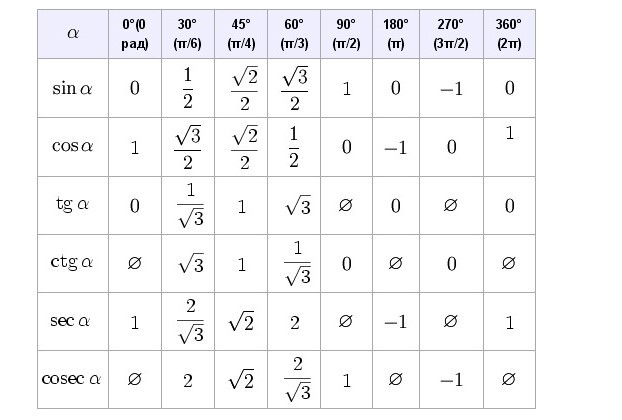 Каждая функция синуса и косинуса в первом квадранте принимает вид  \[\sqrt{\frac{n}{2}}\] или \[\sqrt{\frac{n}{4}}\].

 

Мы можем легко найти значение функции косинуса, если мы знаем значения функции синуса.

 

Sin 0°   = \[\sqrt{\frac{0}{4}}\].

Sin 30° = \[\sqrt{\frac{1}{4}}\].

Sin 45° = \[\sqrt{\frac{2}{4}}\].

Sin 60° = \[\sqrt{\frac{3}{4}}\].

Sin 90° = \[\sqrt{\frac{4}{4}}\].

Теперь через значение синуса мы можем легко найти значение косинуса, потому что

Cos 0° = Sin 90° = 1

Cos 30° = Sin 60° =   \[\sqrt{\frac{3}{4} }\] =  \[\frac{\sqrt{3}}{2}\]

Cos 45° = Sin 45 ° =  \[\sqrt{\frac{2}{4}}\] = \[\ frac{1}{\sqrt{2}}\]

Cos 60° = Sin 30°  = \[\sqrt{\frac{1}{4}}\] = \[\frac{1}{2} \] 9{2}) \]

=\[4 (\frac{1}{4} + \frac{1}{4}) — 3(\frac{1}{2} -1) \]

= \[ (4 \times \frac{2}{4}) — (3 \times \frac{-1}{2}) \]

= \[ (4 \times \frac{1}{2}) — ( \frac{-3}{2}) \]

=\[ (\frac{4}{2}) + ( \frac{3}{2}) \]

=\[ \frac{ 4+3}{2} \]

=\[ \frac{7}{2} \]

 

b. Если Cos Ө или Sin Ө =\[\sqrt{2}\]Cos Ө, покажите, что Cos Ө –Sin Ө =\[\sqrt{2}\] Sin Ө.

Решение: Cos Ө или Sin Ө =\[\sqrt{2}\] Cos Ө

9{2}\] — 1) Cos Ө = (2 — 1) Cos Ө = Cos Ө

= \[\sqrt{2}\] Sin Ө = Cos Ө –Sin Ө

Следовательно, доказано

 

Интересные факты

В тригонометрии закон косинусов также известен как формула косинуса, правило косинуса или теорема аль-Каши.

 

Положение корабля можно определить с помощью тригонометрии и морского хронометра.

 

Гиппарх, составивший первую тригонометрическую таблицу, также известен как «отец тригонометрии».

 

Время викторины

  1. Для любого острого угла косинус будет равен

a. –Cos (180°- Ө)

б. Cos (180° — Ө)

c.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *