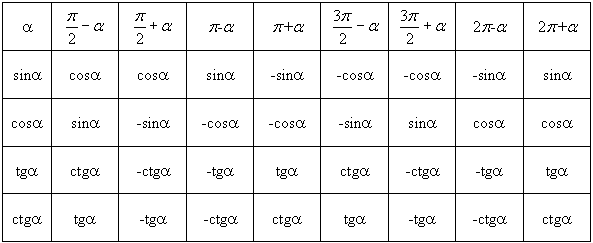Чему равен sin альфа: Синус, косинус и тангенс угла — урок. Геометрия, 9 класс.

Задача 15. В треугольнике  Найдите высоту

Решение: + показать

Задача 16. В равностороннем треугольнике высота равна  Найдите стороны этого треугольника.

Решение: + показать

Задача 17. В треугольнике   угол равен  Найдите высоту .

Решение: + показать

Задача 18. В треугольнике  высота равна Найдите угол Ответ дайте в градусах.

Решение: + показать

Задача 19. В треугольнике угол равен   Найдите угол Ответ дайте в градусах.

Решение: + показать

Задача 20. Один угол равнобедренного треугольника на  больше другого. Найдите меньший угол. Ответ дайте в градусах.

Решение: + показать

Задача 21.  Угол при вершине, противолежащей основанию равнобедренного треугольника, равен  Боковая сторона треугольника равна Найдите длину основания этого треугольника.

Решение: + показать

Задача 22. В треугольнике  Внешний угол при вершине равен  Найдите угол Ответ дайте в градусах.

Решение: + показать

Вы можете пройти тест по теме «Равнобедренный треугольник. Вычисление  углов  и длин».

Автор: egeMax | комментариев 12

Решение Ященко ОГЭ 2023 Вариант №36 (36 вариантов) Математика

Решение заданий варианта №36 из сборника ОГЭ 2023 по математике И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.

ЧАСТЬ 1

Задание 1-5.
    Маша летом отдыхает у дедушки и бабушки в посёлке Дачном. Маша с дедушкой собираются съездить на машине на железнодорожную станцию Путятино. Из Дачного в Путятино можно проехать по прямой грунтовой дороге. Есть более длинный путь по шоссе – через деревню Ковылкино до деревни Лесной, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Путятино. {3}}.

Задание 9.
Решите уравнение (х – 6)(–5х – 9) = 0.
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

Задание 10.
В группе туристов 20 человек. С помощью жребия они выбирают трёх человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист К., входящий в состав группы, пойдёт в магазин?

Задание 11.
Установите соответствие между формулами, которыми заданы функции, и графиками этих функций.

ФОРМУЛЫ

   А)  у = –х² + 6х – 10
   Б)  у = –х² – 6х – 10
   В)  у = х² – 6х + 10

ГРАФИКИ

В таблице под каждой буквой укажите соответствующий номер.

Задание 12.
Теорему синусов можно записать в виде \frac{a}{sin\alpha}=\frac{b}{sin\beta}, где а и b – две стороны треугольника, а α и β – углы треугольника, лежащие против этих сторон соответственно. Пользуясь этой формулой, найдите величину sinα, если а = 21, b = 5, sin β = \frac{1}{6}. 

Задание 13.
Укажите решение неравенства

x² – 25 > 0.

1) (–∞; –5) ∪ (5; +∞)
2) (–5;5)
3) нет решений
4) (–∞; +∞)

Задание 14.
К концу 2011 года в городе проживало 102 300 человек. Каждый год число жителей города возрастало на одну и ту же величину. В конце 2018 года в городе проживало 114 340 человек. Какова была численность населения этого города к концу 2016 года?

Задание 15.
Точки М и N являются серединами сторон АВ и ВС треугольника АВС, сторона АВ равна 57, сторона ВС равна 74, сторона АС равна 48. Найдите МN.

Задание 16.
Угол А трапеции АВСD с основаниями АD и ВС, вписанной в окружность, равен 83°. Найдите угол В этой трапеции. Ответ дайте в градусах.

Задание 17.
В ромбе АВСD угол АВС равен 58°. Найдите угол АСD. Ответ дайте в градусах.

Задание 18.
На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.

Задание 19.
Какие из следующих утверждений верны?

1) Сумма углов равнобедренного треугольника равна 180 градусам.
2) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
3) В прямоугольном треугольнике квадрат гипотенузы равен разности квадратов катетов.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

ЧАСТЬ 2

Задание 20.
Найдите значение выражения 31a – 4b + 55, если \frac{a–4b+7}{4a–b+7}=8.

Задание 21.
Семь одинаковых рубашек дешевле куртки на 9 %. {2}+4)(x+1)}{–1–x} и определите, при каких значениях k прямая у = kх имеет с графиком ровно одну общую точку.

Задание 23.
Биссектриса угла А параллелограмма АВСD пересекает сторону ВС в точке К. Найдите периметр параллелограмма, если ВК = 8, СК = 13.

Задание 24.
Окружности с центрами в точках P и Q пересекаются в точках K и L, причём точки P и Q лежат по одну сторону от прямой KL. Докажите, что PQ⊥KL.

Задание 25.
В треугольнике АВС биссектриса ВЕ и медиана АD перпендикулярны и имеют одинаковую длину, равную 12. Найдите стороны треугольника АВС.

Источник варианта: Сборник ОГЭ 2023 по математике. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 0 / 5. Количество оценок: 0

Оценок пока нет. Поставь оценку первым.

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

• Запись опубликована:17.12.2022
• Рубрика записи+ Типовые экзаменационные варианты ОГЭ
• Автор записи:Andrei Maniakin

Мэтуэй | Популярные задачи

1	Найти точное значение	грех(30)
2	Найти точное значение	грех(45)
3	Найти точное значение	грех(30 градусов)
4	Найти точное значение	грех(60 градусов)
5	Найти точное значение	загар (30 градусов)
6	Найти точное значение	угловой синус(-1)
7	Найти точное значение	грех(пи/6)
8	Найти точное значение	cos(pi/4)
9	Найти точное значение	грех(45 градусов)
10	Найти точное значение	грех(пи/3)
11	Найти точное значение	арктан(-1)
12	Найти точное значение	cos(45 градусов)
13	Найти точное значение	cos(30 градусов)
14	Найти точное значение	желтовато-коричневый(60)
15	Найти точное значение	csc(45 градусов)
16	Найти точное значение	загар (60 градусов)
17	Найти точное значение	сек(30 градусов)
18	Найти точное значение	cos(60 градусов)
19	Найти точное значение	cos(150)
20	Найти точное значение	грех(60)
21	Найти точное значение	cos(pi/2)
22	Найти точное значение	загар (45 градусов)
23	Найти точное значение	arctan(- квадратный корень из 3)
24	Найти точное значение	csc(60 градусов)
25	Найти точное значение	сек(45 градусов)
26	Найти точное значение	csc(30 градусов)
27	Найти точное значение	грех(0)
28	Найти точное значение	грех(120)
29	Найти точное значение	соз(90)
30	Преобразовать из радианов в градусы	пи/3
31	Найти точное значение	желтовато-коричневый(30)
32
35	Преобразовать из радианов в градусы	пи/6
36	Найти точное значение	детская кроватка(30 градусов)
37	Найти точное значение	арккос(-1)
38	Найти точное значение	арктан(0)
39	Найти точное значение	детская кроватка(60 градусов)
40	Преобразование градусов в радианы	30
41	Преобразовать из радианов в градусы	(2 шт. )/3
42	Найти точное значение	sin((5pi)/3)
43	Найти точное значение	sin((3pi)/4)
44	Найти точное значение	тан(пи/2)
45	Найти точное значение	грех(300)
46	Найти точное значение	соз(30)
47	Найти точное значение	соз(60)
48	Найти точное значение	соз(0)
49	Найти точное значение	соз(135)
50	Найти точное значение	cos((5pi)/3)
51	Найти точное значение	cos(210)
52	Найти точное значение	сек(60 градусов)
53	Найти точное значение	грех(300 градусов)
54	Преобразование градусов в радианы	135
55	Преобразование градусов в радианы	150
56	Преобразовать из радианов в градусы	(5 дюймов)/6
57	Преобразовать из радианов в градусы	(5 дюймов)/3
58	Преобразование градусов в радианы	89 градусов
59	Преобразование градусов в радианы	60
60	Найти точное значение	грех(135 градусов)
61	Найти точное значение	грех(150)
62	Найти точное значение	грех(240 градусов)
63	Найти точное значение	детская кроватка(45 градусов)
64	Преобразовать из радианов в градусы	(5 дюймов)/4
65	Найти точное значение	грех(225)
66	Найти точное значение	грех(240)
67	Найти точное значение	cos(150 градусов)
68	Найти точное значение	желтовато-коричневый(45)
69	Оценить	грех(30 градусов)
70	Найти точное значение	сек(0)
71	Найти точное значение	cos((5pi)/6)
72	Найти точное значение	КСК(30)
73	Найти точное значение	arcsin(( квадратный корень из 2)/2)
74	Найти точное значение	загар((5pi)/3)
75	Найти точное значение	желтовато-коричневый(0)
76	Оценить	грех(60 градусов)
77	Найти точное значение	arctan(-( квадратный корень из 3)/3)
78	Преобразовать из радианов в градусы	(3 пи)/4
79	Найти точное значение	sin((7pi)/4)
80	Найти точное значение	угловой синус(-1/2)
81	Найти точное значение	sin((4pi)/3)
82	Найти точное значение	КСК(45)
83	Упростить	арктан(квадратный корень из 3)
84	Найти точное значение	грех(135)
85	Найти точное значение	грех(105)
86	Найти точное значение	грех(150 градусов)
87	Найти точное значение	sin((2pi)/3)
88	Найти точное значение	загар((2pi)/3)
89	Преобразовать из радианов в градусы	пи/4
90	Найти точное значение	грех(пи/2)
91	Найти точное значение	сек(45)
92	Найти точное значение	cos((5pi)/4)
93	Найти точное значение	cos((7pi)/6)
94	Найти точное значение	угловой синус(0)
95	Найти точное значение	грех(120 градусов)
96	Найти точное значение	желтовато-коричневый ((7pi)/6)
97	Найти точное значение	соз(270)
98	Найти точное значение	sin((7pi)/6)
99	Найти точное значение	arcsin(-( квадратный корень из 2)/2)
100	Преобразование градусов в радианы	88 градусов

Как сделать… R-sin-alpha вопросы

В документах C3 есть очень типичный вопрос, который выглядит примерно так:

«Выразите $3 \sin (x) + 5 \cos (x)$ в виде $R \sin (x + \alpha)$».

(Иногда это другая триггерная функция или в ней может быть знак минус, но тот же принцип работает для любого типа вопроса, подобного этому, который я буду называть вопросом R-sin-alpha ) .

Есть студенты, которые запаникуют, но вам не обязательно быть одним из них. Все, что вам нужно для этого, есть в вашей книге формул, и это полностью механический процесс, когда вы знаете, что делаете.

Весь фокус в том, чтобы начать с $R \sin (x + \alpha)$. Вам дана формула для $\sin(A+B)$, которая представляет собой $\sin(A) \cos (B) + \sin (B) \cos (A)$. ((Очевидно, что если вы делаете другую триггерную функцию, используйте соответствующую формулу. Это не просто R-sin-alpha, это может быть и R-cos-alpha.))

Это означает $R \sin ( x + \alpha) = R ( \sin (x) \cos (\alpha) + \sin (\alpha) \cos (x)) \\= R \sin (x) \cos (\alpha) + R \ грех (\ альфа) \ соз (х) $.

А теперь самое умное. Это выражение должно быть ТОЧНО таким же, как $3 \sin (x) + 5 \cos (x)$ — вам нужно такое же количество $\sin(x)$s и такое же количество $\cos(x)$ с.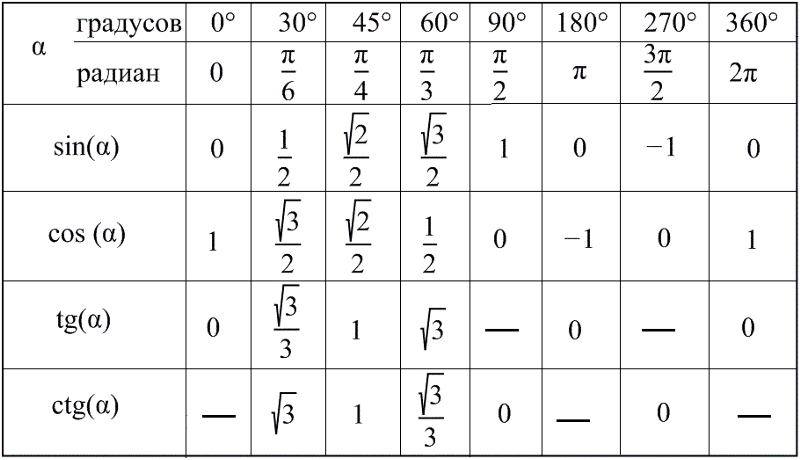 В первом выражении $3 \sin(x)$s, а во втором $R \cos(\alpha)$ $\sin(x)$s, поэтому $3 = R \cos (\alpha)$. Точно так же $5 = R \sin (\alpha)$.

Два уравнения? Два неизвестных? Это выглядит как одновременное уравнение для меня. Это немного сложно, потому что они нелинейны, но пусть вас это не беспокоит: разделите единицу $R \sin(\alpha)$ на единицу $R\cos(\alpha)$ и $R$ отменяется, и у вас остается $\tan(\alpha) = \frac{5}{3}$. Вы можете бросить это в свой калькулятор и получить ответ — вероятно, где-то около 1 радиана, позвольте мне проверить. (1.03, здесь написано.)

Что это? Нет, градусов — ерунда . Не используйте их, если вам явно не сказано об этом. 92 = 34$; вы можете использовать известную триггерную идентичность, чтобы избавиться от $\cos$ и $\sin$, чтобы оставить вам $R = \sqrt{34}$.

В качестве альтернативы, поскольку вы знаете, что такое $\alpha$, вы можете просто работать с одним из уравнений — $3 = R \sin (\alpha)$, поэтому $R = \frac{3}{\sin (\alpha )}$.