Чему равен синус и косинус: Синус, косинус угла треугольника

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )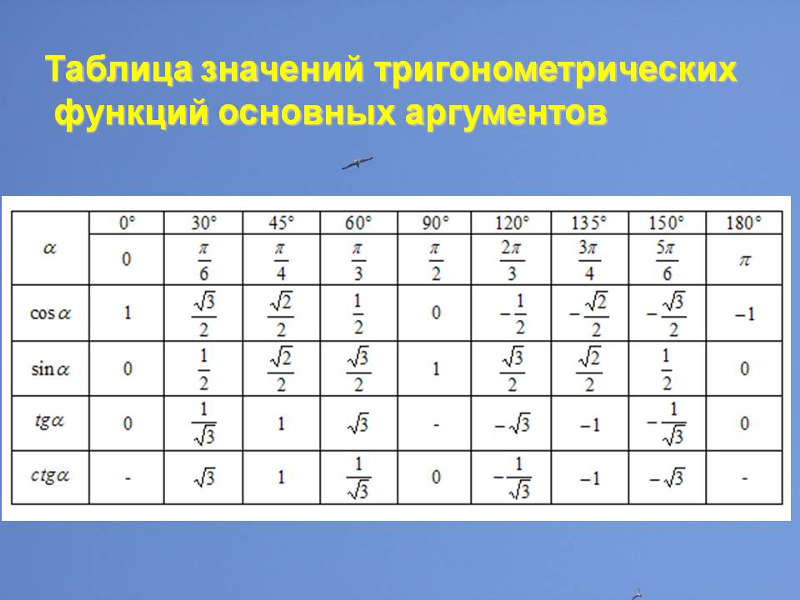
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значение sin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73		Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град.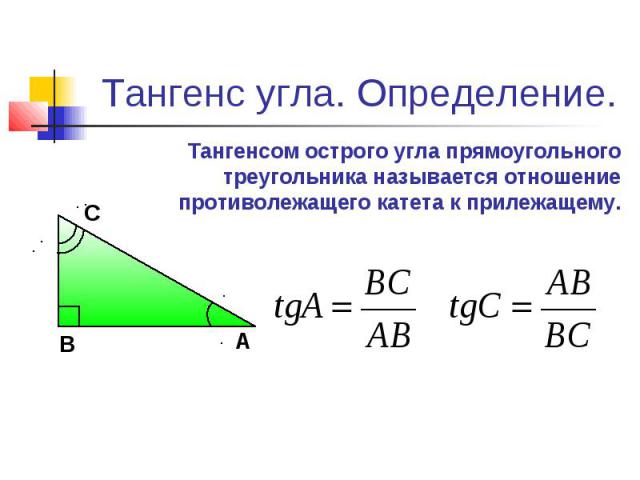
)
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значение
cos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. 3
6Risolvere per ?cos(x)=1/2
7Risolvere per xsin(x)=-1/2
8Преобразовать из градусов в радианы225
9Risolvere per ?cos(x)=( квадратный корень из 2)/2
10Risolvere per xcos(x)=( квадратный корень из 3)/2
11Risolvere per xsin(x)=( квадратный корень из 3)/2
12Графикg(x)=3/4* корень пятой степени из x
13Найти центр и радиусx^2+y^2=9
14Преобразовать из градусов в радианы120 град. 2+n-72)=1/(n+9)

SINE COSINE

void ARM_SIN_COS_F32 (float32_T THETA, Float32_T *PSINVAL, FLOAT32_T *PCOSVAL)
FLOUTY-POINT). Подробнее …
void ARM_SIN_COS_Q31 (Q31_T THETA, Q31_T *PSINVAL, Q31_T *PCOSVAL)
Q31. Подробнее…
 

Вычисляет тригонометрические значения синуса и косинуса, используя комбинацию поиска по таблице и линейной интерполяции. Существуют отдельные функции для Q31 и типов данных с плавающей запятой. Вход для версии с плавающей запятой находится в градусах, в то время как Q31 с фиксированной точкой имеет масштабированный ввод с диапазоном [-1 0,9999], отображающим до [-180 +180] градусов.

Функция с плавающей запятой также допускает значения, выходящие за пределы обычного диапазона. Когда это произойдет, функции потребуется дополнительное время, чтобы настроить входное значение в диапазоне [-180 180].

Результат с точностью до 5 знаков после запятой.

Реализация основана на поиске по таблице с использованием 360 значений вместе с линейной интерполяцией. Используемые шаги:

  1. Вычисление ближайшего целочисленного индекса таблицы.
  2. Вычислить дробную часть (фракцию) входных данных.
  3. Получить значение, соответствующее индексу , из таблицы синусов в y0 , а также значение из index+1 в y1 .
  4. Значение синуса вычисляется как *psinVal = y0 + (fract * (y1 - y0)) .
  5. Получить значение, соответствующее индексу , из таблицы косинусов в y0 , а также значение из index+1 в y1 .
  6. Значение косинуса вычисляется как *pcosVal = y0 + (fract * (y1 - y0)) .

пустота arm_sin_cos_f32 ( float32_t тета ,
float32_t * pSinVal ,
float32_t * pCosVal  
)

Параметры
[in] theta входное значение в градусах
[out] pSinVal указывает на обработанный синусоидальный выход.
[out] pCosVal указывает на обработанный выход cos.
[в] Theta Входное значение в градусах
[Out] PSINVAL указывает на обработанную синусную выход
[Out]. 0005 pCosVal указывает на обработанный выход косинуса
Возвращает
нет

void arm_sin_cos_q31 ( q31_t тета ,
q31_t * pSinVal ,
q31_t * pCosVal  
)

Параметры
[in] theta масштабированное входное значение в градусах
[out] pSinVal указывает на обработанный синусоидальный выход.
[выход] pCosVal указывает на обработанный вывод косинуса.
[In] Theta Масштабированное входное значение в градусах
[Out] PSINVAL указывает на обработанную синусную выход
[Out] 9005141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414. выход
Возвращает
нет

Входное значение Q31 находится в диапазоне [-1 0,999999] и отображается в значение градуса в диапазоне [-180 179].

Краткий обзор синуса, косинуса и углов

  • Home /
  • Geometry /
  • Right Triangles and Trigonometry /
  • Topics /
  • Trigonometry /
  • Sine, Cosine, and Angles
  • Trigonometry /
  • Sine, Cosine, and Angles

Topics

  • Введение

  • Темы
  • Altitudes and Side Lengths
  • Geometric Mean
  • The Pythagorean Theorem
  • Special Right Triangles
  • 45-45-90 Triangles
  • 30-60-90 Triangles
  • Trigonometry
  • Trig Ratios
  • Inverse Trig Ratios
  • Синус, косинус и углы
  • Земельные законы
  • Закон синусов
  • Закон косинусов

  • Примеры
  • Упражнения
  • Задачи Math Shack
  • викторины
  • Условия
  • Раздаточный материал
  • Лучшее из Интернета
  • Содержание
  •  НАЗАД
  • СЛЕДУЮЩИЙ

Также важно знать соотношение между синусом и косинусом. Мы не собираемся лезть в их личную жизнь, но это действительно важно. Чтобы выяснить, каковы их отношения, мы можем сделать несколько вычислений.

We already know that sin A = a ⁄ h and cos A = b ⁄ h but what about ∠ B ? Вспоминая Sohcahtoa, мы видим, что SIN B = B ⁄ H и COS B = A A H . Был ли это звук задыхающейся земли? Да это правильно.

sin A = cos B
cos A = sin B

Подождите. Становится лучше. Мы знаем, что в треугольнике 180°, но 90° убирает из уравнения половину этого числа. Это означает, что A + B = 90°. Используя это соотношение, мы можем уточнить наше соотношение синус-косинус.

sin A = cos(90° – A )
cos A = sin(90° – A )

Это означает, что синус и косинус равны дополняют триггерных функций (поскольку углы дополняют друг друга).

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *