Чему равен вертикальный угол: Конспект «Угол. Смежные и вертикальные углы»

Содержание

Конспект «Угол. Смежные и вертикальные углы»

«Угол. Смежные и вертикальные углы»

Ключевые слова конспекта: углы, биссектриса, виды углов, измерение углов, смежные и вертикальные углы, свойства смежных и вертикальных углов, углы при пересечении двух прямых секущей.

Угол — фигура, образованная двумя лучами, которые выходят из одной точки (вершины).
Биссектриса — луч, который выходит из вершины угла и делит его пополам.

Виды углов. Измерение углов

Развернутый угол — угoл, стороны которого лежат на одной прямой.
Прямой угoл — угoл, который равен половине развернутого угла.
Острый угол — угoл меньше прямого угла.
Тупой угoл — угoл больше прямого, но меньше развернутого.

Единицы измерения углов:
Градус — величина (градусная мера) угла, равная части развернутого угла.
Минута — часть градуса.
Секунда — часть минуты.

Смежные и вертикальные углы

Смежные углы — два угла, у которых одна сторона общая,а две другие стороны являются дополняющими лучами.
Вертикальные углы — два угла, стороны одного из которых являются дополняющими лучами сторон другого.

Теорема. Сумма смежных углов равна 180°.

Теорема.

Вертикальные углы равны.

Свойства смежных и вертикальных углов

Углы при пересечении двух прямых секущей

Это конспект по теме «Смежные и вертикальные углы». Выберите дальнейшие действия:

Вертикальные углы — это… Что такое Вертикальные углы?

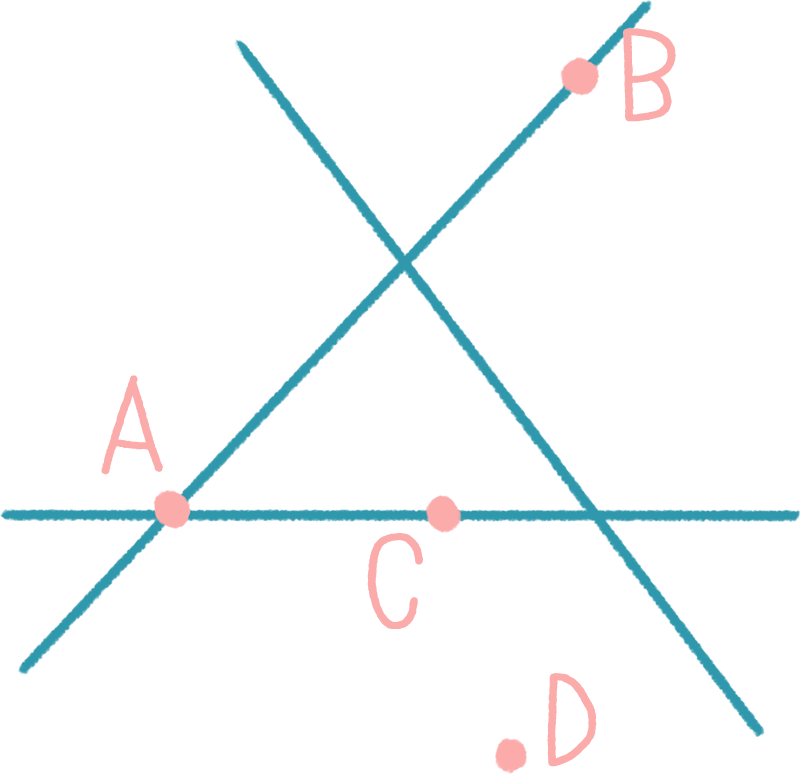
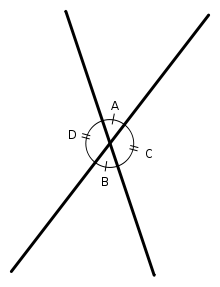Две прямые пересекаются, создавая пару вертикальных углов. Одна пара состоит из углов A и B, другая — из C и D.

В геометрии, два угла называются вертикальными, если они созданы пересечением двух прямых и не являются прилегающими. Такие углы имеют общую вершину. Они имеют одинаковую градусную меру и могут рассматриваться как равные.

Теорема о вертикальных углах

Если две прямые пересекаются в точке, образуются четыре угла. Несмежные углы называются вертикальными или противоположно вертикальными углами. Также, каждая пара прилегающих углов образует прямую, а эти углы называются смежными^[1]. Поскольку каждая пара вертикальных углов является смежными к прилегающим, то градусные меры вертикальных углов — равны.

Алгебраическое решение вертикальных углов

Например, угол A на рисунке — неизвестен. Обозначим A = x. Если два прилегающих угла образуют прямую, то они — смежные. Тогда, градусная мера C = 180 − x. Аналогично, градусная мера D = 180 − x. Углы C и D имеют одинаковую меру, которая равна 180 — x и являются вертикальными. Поскольку, угол B является смежным для обоих углов C и D, для того, чтобы вычислить размер B можно использовать градусную меру любого из них. Используя меру угла

C или угла D, найдём градусную меру угла B = 180 — (180 — x) = 180—180 + x = x. Отсюда, оба угла A и B имеют г

См. также

Литература

↑ Euclid The Elements. — c. 300 BC. Proposition I:13.

Ссылки

Смежные и вертикальные углы. Перпендикулярные прямые [wiki.eduVdom.com]

Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.

Сумма смежных углов равна 180°
Рис.1
Теорема 1. Сумма смежных углов равна 180°.
Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .
Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.

Вертикальные углы равны
Рис.2
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).
Теорема 2. Вертикальные углы равны.
Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1 ∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.
Отсюда заключаем, что ∠ АОВ = ∠ COD.
Следствие 1. Угол, смежный с прямым углом, есть прямой угол.

Рис.3
Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.

Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.

АН — перпендикуляр к прямой
Рис.4
Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.

Чертежный угольник
Рис.5
Справедлива следующая теорема.
Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).
Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».
Пример 1. Один из смежных углов равен 44°. Чему равен другой?
Решение. Обозначим градусную меру другого угла через x, тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.
Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?
Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.
∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.
Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.
Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.
Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.
Решение.
Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° — 50° = 130°.
Вертикальные углы | Треугольники
Какие углы вертикальные? Каким свойством обладают вертикальные углы?
Рассмотрим определение вертикальных углов и их свойство, а также применим свойство вертикальных углов для решения задач.
Определение.
Вертикальные углы — это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.
При пересечении двух прямых образуется две пары вертикальных углов:
∠1 и ∠2 — вертикальные углы

∠3 и ∠4 — вертикальные углы

Свойство вертикальных углов.

Вертикальные углы равны.

∠AOC =∠BOD

∠AOD =∠BOC

Таким образом, при пересечении двух прямых образуется две пары равных межу собой углов.
Задачи.
1) Сумма вертикальных углов равна 140º. Найти эти углы.
Решение:
Так как вертикальные углы равны, а в условии сказано, что их сумма равна 140º, то каждый из них равен по 140:2=70º.
Ответ: 70º, 70º.
2) Сумма двух углов, образованных при пересечении двух прямых, равна 100º. Найти эти углы.
Решение:
При пересечении двух прямых образуются углы двух видов — вертикальные и смежные.
Так как сумма смежных углов равна 180º, а по условию, сумма углов равна 100º, то эти углы — вертикальные.
А так как вертикальные углы равны, то каждый из них равен по 100:2=50º.
Ответ: 50º, 50º.
Вертикальные углы во многих задачах — важный элемент при доказательстве равенства треугольников и подобия треугольников.

Вертикальные углы и их свойства
Вертикальные углы и их свойства.

Вертикальные углы – это два угла с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого

Вертикальные углы (понятие и определение)
Свойства вертикальных углов
Вертикальные углы, прямой угол, развернутый угол, смежные углы, тупой угол

Вертикальные углы (понятие и определение):
Вертикальные углы – это два угла с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.
Две пары вертикальных углов образуют полный угол, т.е. угол, градусная мера которого равна 360°.
Рис. 1. Вертикальные углы
∠ α, ∠ β; ∠γ, ∠δ – смежные углы,
∠ α, ∠γ; ∠ β ∠δ – вертикальные углы
Вертикальные углы равны друг другу.
∠ α = ∠γ; ∠ β = ∠δ

Свойства вертикальных углов:
1. При пересечении двух прямых образуются две пары вертикальных углов.
Рис. 2. Вертикальные углы
∠ α, ∠ β; ∠γ, ∠δ – смежные углы,
∠ α, ∠γ; ∠ β ∠δ – вертикальные углы
2. Синусы, косинусы и тангенсы вертикальных углов равны.
sin α = sin γ, sin β = sin δ
cos α = cos γ, cos β = cos δ
tg α = tg γ, tg β = tg δ

Вертикальные углы
Квадрат
Овал
Остроугольный треугольник
Полукруг
Прямой угол
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Ромб
Смежные углы
Трапеция
Тупой угол
Шестиугольник

Примечание: © Фото https://www.pexels.com, https://pixabay.com

карта сайта

Коэффициент востребованности 1 612
Урок 6. смежные и вертикальные углы. аксиомы и теоремы — Геометрия — 7 класс
Геометрия
7 класс
Урок № 6
Смежные и вертикальные углы. Аксиомы и теоремы
Перечень вопросов, рассматриваемых в теме:
Понятие смежных и вертикальных углов
Свойства смежных и вертикальных углов
Отличие аксиомы от теоремы
Тезаурус
Два угла, у которых одна сторона общая, а две другие являются продолжениями друг друга, называются смежными.
Свойства смежных углов:
Сумма смежных углов равна 180⁰.
Если два угла равны, то и смежные с ними углы равны.
Угол, смежный с прямым углом, есть прямой угол.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Свойство вертикальных углов: вертикальные углы равны.
Аксиома– положение, принимаемое без доказательств.
Основная литература:
Атанасян Л. С. Геометрия: 7 – 9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
Погорелов А. В. Геометрия: 7 – 9 класс. // Погорелов А. В. – М.: Просвещение, 2017. – 224 с.
Теоретический материал для самостоятельного изучения
Давайте построим развёрнутый угол АОС и проведём в нём луч ОВ. В результате у нас получилось два угла ∠АОВ – острый угол и ∠ВОС– тупой угол. Стороны АО и ОС – продолжают друг друга, ВО– общая сторона. Углы АОВ и ВОС – это смежные углы. На основании этого сформулируем определение смежных углов.
Два угла, у которых одна сторона общая, а две другие являются продолжениями друг друга, называются смежными.
Обратите, внимание, что смежные углы АОВ и ВОС лежат на развёрнутом угле АОС. Отсюда можно сделать вывод: сумма смежных углов равна 180^о.
Свойство смежных углов: сумма смежных углов равна 180^о.
Давайте докажем это свойство.
Доказательство. Пусть углы ∠АОВ и ∠ВОС – смежные, луч ОВ – проходит между сторонами развёрнутого угла ∠АОС. Поэтому, сумма углов ∠АОВ и ∠ВОС равна ∠АОС, а этот угол развёрнутый, он равен 180^о. Свойство доказано.
Укажем ещё одно свойство смежных углов.
Если два угла равны, то и смежные с ними углы равны.
Сейчас давайте вспомним определение прямого угла: угол, равный 90⁰, называется прямым углом. Опираясь на свойство суммы смежных углов, можно сделать вывод: угол, смежный с прямым углом, есть прямой угол.
Теперь построим две пересекающиеся прямые, АС и BD. Посмотрите, при пересечении прямых у нас получилось четыре угла: ∠АОВ, ∠АОD, ∠CОD, ∠BОC. Из них попарно являются смежными углы: ∠АОВ и ∠АОD, ∠АОD и ∠CОD, ∠CОD и ∠BОC, ∠АОВ и ∠BОC.
Углы, которые не являются смежными:
∠АОВ и ∠CОD; ∠АОD и ∠BОC. Пары этих углов называются вертикальными углами.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Свойство вертикальных углов: вертикальные углы равны. Убедимся в справедливости этого свойства, докажем его.
Доказательство. Посмотрим на чертёж: пары углов 1 и 2, 2 и 3, 3 и 4, 4 и 1– смежные углы. Угол 2 одновременно является смежным с углом 1 и с углом 3. По свойству смежных углов
∠1+ ∠2= 180⁰ и ∠3+ ∠2= 180⁰. Получаем, что ∠1+ ∠2= ∠3+ ∠2, значит, ∠1= ∠3. Углы ∠1 и ∠3 – вертикальные. Мы доказали справедливость этого свойства.
Свойства смежных и вертикальных углов, которые мы сегодня рассмотрели– в геометрии называются теоремами. Правильность утверждения о свойстве той или иной геометрической фигуры устанавливается путём рассуждения. Это рассуждение называется доказательством. А само утверждение, которое доказывается, называется теоремой.
На предыдущих уроках вы познакомились с понятием аксиомы.
В чём же различие между аксиомой и теоремой? Ответ на этот вопрос таков: аксиома – положение, принимаемое без доказательств.
Разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.
Используя чертёж, найдите угол ∠ВОК.
Ответ: ∠ВОК=____⁰
Решение. Воспользуемся свойством смежных углов: сумма смежных углов равна 180⁰. По условию задачи ∠АОК= 11⁰, то ∠ВОК+ ∠АОК= 180⁰
∠ВОК+ 11⁰= 180⁰
∠ВОК= 180⁰– 11⁰= 169⁰.
Ответ: ∠ВОК= 169⁰
№2. Тип задания: единичный / множественный выбор.
Используя чертёж, найдите угол ∠AOD.
Варианты ответов:
112⁰
64⁰
116⁰
68⁰
Решение. На чертеже указано, что углы ∠СОЕ= ∠DOE. Значит, ∠COD= ∠СОЕ+ ∠DOE= 32⁰+ 32⁰= 64⁰. ∠AOD смежный с углом ∠COD, по свойству смежных углов: ∠AOD= 180⁰–∠COD= 180⁰– 64⁰=116⁰.
Ответ: 116⁰
№3. Тип задания: выделение цветом.
Используя чертёж, найдите градусную меру угла ∠BMD, если ∠AMD= 125⁰, ∠BMC= 115⁰.
∠BМD=____⁰.
Выделите верный ответ из списка:
60⁰; 30⁰; 75⁰; 90⁰
Решение. По чертежу можно увидеть, что ∠BМD является частью ∠AMD и ∠BMC. Рассмотрим ∠DMC и ∠AMD. Эти углы – смежные, т.е. их сумма равна 180⁰. Значит, зная градусную меру ∠AMD, мы сможем найти градусную меру ∠DMC= 180⁰–∠AMD= 180⁰-–125⁰= 55⁰. Теперь рассмотрим ∠BMC= ∠BMD+ ∠DMC. Мы знаем градусные меры ∠BMC и ∠DMC, значит, мы сможем найти градусную меру ∠BMD.
∠BMD= ∠BMC–∠DMC= 115⁰– 55⁰= 60⁰.
Верный ответ: 60⁰
Онлайн урок смежные и вертикальные углы.
Давай повторим определения, которые ты уже знаешь и которые мы будем использовать на нашем уроке.

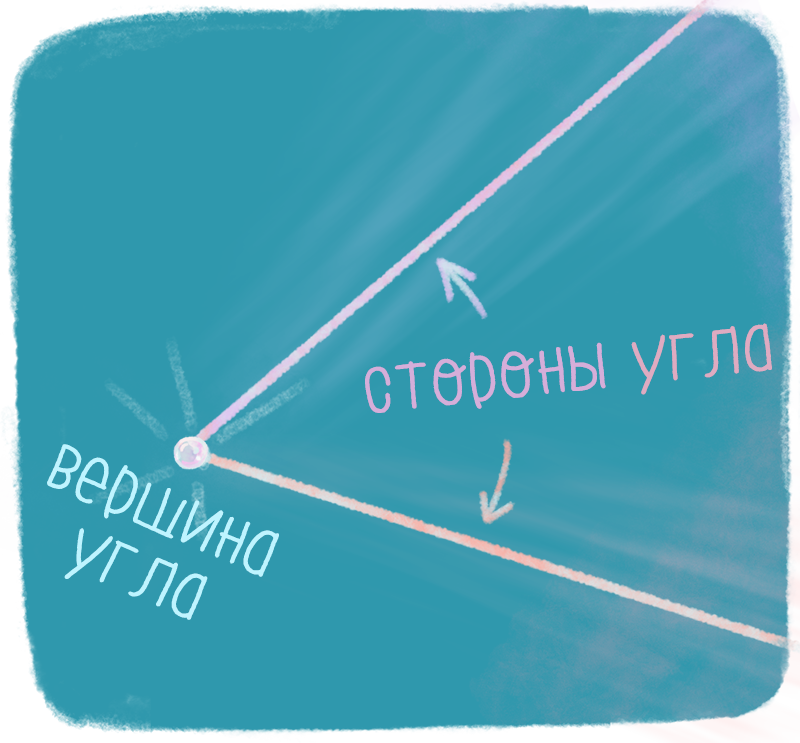
Углом называют фигуру, которая состоит из точки – вершины угла и двух различных полупрямых, исходящих из этой точки, – сторон угла.

Угол называется развернутым, если стороны угла являются дополнительными полупрямыми.

Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.

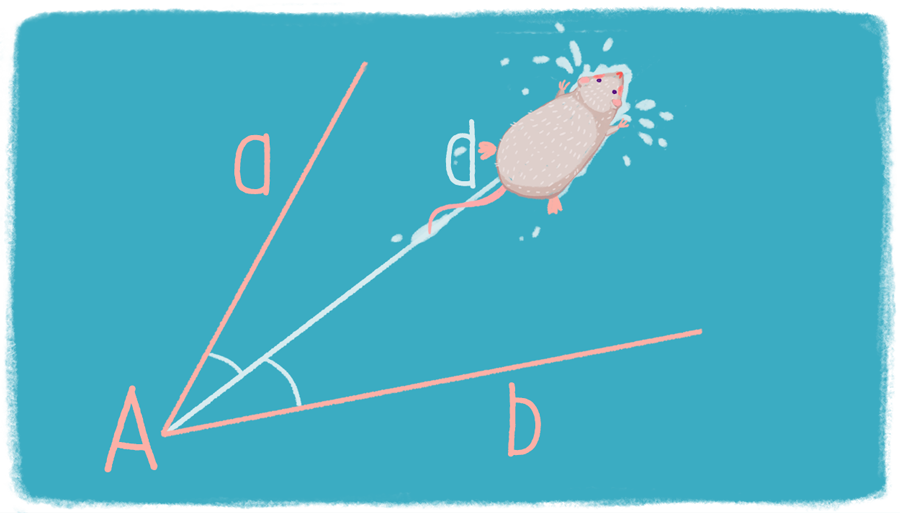
Биссектриссой угла называют луч, который исходит из его вершины, проходит между его сторонами и делит угол пополам.

Теперь выбери соответствия между картинками и определениями, которые мы только что повторили.

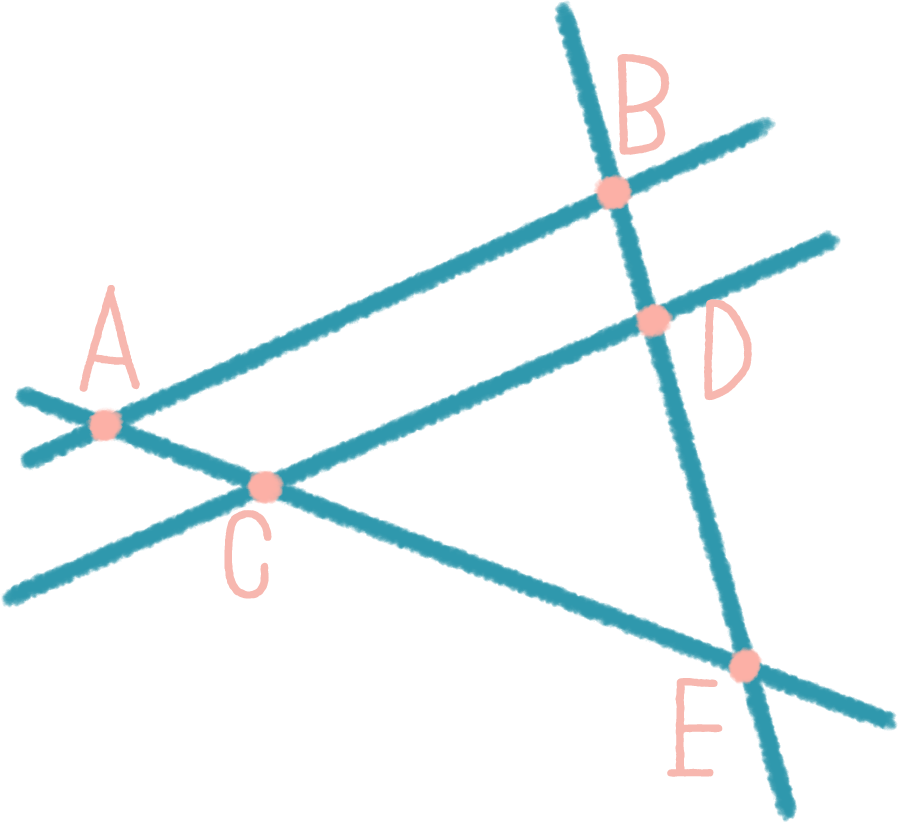
BE = BA + AECD = AB + EAD = AC + CDAE = AC + CE

∠ABD, ∠BCA, ∠BAD∠ABB, ∠BCA, ∠BAD∠ABD, ∠BA, ∠ABAD∠ABD, ∠BCB, ∠BAD

∠АЕВ тупой∠BDE развернутый∠СDA полный∠ADE острый

Прежде чем мы начнем основную часть урока, перечислю для тебя определения, с которыми мы познакомимся сегодня:

1. Смежные углы.
2. Теорема о сумме смежных углов.
3. Вертикальные углы.
4. Теорема о вертикальных углах.
Прилегающие углы и вертикальные углы
Классы
Класс 1-3
Класс 4-5
Класс 6-10
Класс 11-12
КОНКУРСНЫЙ ЭКЗАМЕН
BNAT 000 NC
000 NC Книги
Книги NCERT для класса 5
Книги NCERT для класса 6
Книги NCERT для класса 7
Книги NCERT для класса 8
Книги NCERT для класса 9
Книги NCERT для класса 10
Книги NCERT для класса 11
Книги NCERT для класса 12
NCERT Exemplar
NCERT Exemplar Class 8
NCERT Exemplar Class 9
NCERT Exemplar Class 10
NCERT Exemplar Class 11
9000 9000
NCERT Exemplar Class
Решения RS Aggarwal, класс 12
Решения RS Aggarwal, класс 11
Решения RS Aggarwal, класс 10
90 003 Решения RS Aggarwal класса 9
Решения RS Aggarwal класса 8
Решения RS Aggarwal класса 7
Решения RS Aggarwal класса 6
Решения RD Sharma
RD Sharma Class 6 Решения
Решения RD Sharma
Решения RD Sharma класса 8
Решения RD Sharma класса 9
Решения RD Sharma класса 10
Решения RD Sharma класса 11
Решения RD Sharma класса 12
PHYSICS
Механика
Оптика
Термодинамика Электромагнетизм
ХИМИЯ
Органическая химия
Неорганическая химия
Периодическая таблица
MATHS
Теорема Пифагора
0004
000300030004
Простые числа
Взаимосвязи и функции
Последовательности и серии
Таблицы умножения
Детерминанты и матрицы
Прибыль и убыток
Полиномиальные уравнения
Деление фракций
000
000
000
000
000
000 Microology
000
000 Microology
000 BIOG3000
FORMULAS
Математические формулы
Алгебраические формулы
Тригонометрические формулы
Геометрические формулы
КАЛЬКУЛЯТОРЫ
Математические калькуляторы
0003000 PBS4000
000300030002 Примеры калькуляторов химии
Класс 6
Образцы бумаги CBSE для класса 7
Образцы бумаги CBSE для класса 8
Образцы бумаги CBSE для класса 9
Образцы бумаги CBSE для класса 10
Образцы бумаги CBSE для класса 11
Образцы бумаги CBSE чел. для класса 12
CBSE — вопросник за предыдущий год
CBSE — вопросник за предыдущий год, класс 10
CBSE — за предыдущий год — вопросник, класс 12
HC Verma Solutions
HC Verma Solutions Class 11 Physics
Решения HC Verma, класс 12, физика
Решения Лакмира Сингха
Решения Лакмира Сингха, класс 9
Решения Лакмира Сингха, класс 10
Решения Лакмира Сингха, класс 8
Заметки CBSE
, класс
CBSE Notes
Примечания CBSE класса 7
Примечания CBSE класса 8
Примечания CBSE класса 9
Примечания CBSE класса 10
Примечания CBSE класса 11
Примечания CBSE класса 12
Примечания к редакции CBSE
Примечания к редакции
CBSE
Примечания к редакции класса 10 CBSE
Примечания к редакции класса 11 CBSE 9000 4
Примечания к редакции класса 12 CBSE
Дополнительные вопросы CBSE
Дополнительные вопросы по математике класса 8 CBSE
Дополнительные вопросы по науке 8 класса CBSE
Дополнительные вопросы по математике класса 9 CBSE
Дополнительные вопросы по науке класса 9 CBSE
Дополнительные вопросы по математике для класса 10
Дополнительные вопросы по науке, класс 10 по CBSE
CBSE, класс
, класс 3
, класс 4
, класс 5
, класс 6
, класс 7
, класс 8
, класс 9 Класс 10
Класс 11
Класс 12
Учебные решения
Решения NCERT
Решения NCERT для класса 11
Решения NCERT для класса 11 по физике
Решения NCERT для класса 11 Химия
Решения для биологии класса 11
Решения NCERT для математики класса 11
9 0003 NCERT Solutions Class 11 Accountancy
NCERT Solutions Class 11 Business Studies
NCERT Solutions Class 11 Economics
NCERT Solutions Class 11 Statistics
NCERT Solutions Class 11 Commerce
NCERT Solutions For Class 12
NCERT Solutions For Класс 12 по физике
Решения NCERT для химии класса 12
Решения NCERT для класса 12 по биологии
Решения NCERT для класса 12 по математике
Решения NCERT Класс 12 Бухгалтерия
Решения NCERT, класс 12, бизнес-исследования
Решения NCERT, класс 12 Экономика
NCERT Solutions Class 12 Accountancy Part 1
NCERT Solutions Class 12 Accountancy Part 2
NCERT Solutions Class 12 Micro-Economics
NCERT Solutions Class 12 Commerce
NCERT Solutions Class 12 Macro-Economics
NCERT Solutions For Класс 4
Решения NCERT для математики класса 4
Решения NCERT для класса 4 EVS
Решения NCERT для класса 5
Решения NCERT для математики класса 5
Решения NCERT для класса 5 EVS
Решения NCERT для класса 6
Решения NCERT для математики класса 6
Решения NCERT для науки класса 6
Решения NCERT для социальных наук класса 6
Решения NCERT для класса 6 Английский
Решения NCERT для класса 7
Решения NCERT для класса 7 Математика
Решения NCERT для класса 7 Наука
Решения NCERT для класса 7 по социальным наукам
Решения NCERT для класса 7 Английский
Решения NCERT для класса 8
Решения NCERT для класса 8 Математика
Решения NCERT для класса 8 Science
Решения NCERT для социальных наук 8 класса
Решение NCERT ns для класса 8 Английский
Решения NCERT для класса 9
Решения NCERT для социальных наук класса 9
Решения NCERT для математики класса 9
Решения NCERT для математики класса 9 Глава 1
Решения NCERT для Математика класса 9 Глава 2
Решения NCERT для математики класса 9 Глава 3
Решения NCERT для математики класса 9 Глава 4
Решения NCERT
для математики класса 9 Глава 5
Решения NCERT для математики класса 9 Глава 6
Решения NCERT для Математика класса 9 Глава 7
Решения NCERT для математики класса 9 Глава 8
Решения NCERT
для математики класса 9 Глава 9
Решения NCERT
для математики класса 9 Глава 10
Решения NCERT для математики класса 9 Глава 11
Решения NCERT для Математика класса 9 Глава 12
Решения NCERT для математики класса 9 Глава 13
Решения
NCERT для математики класса 9 Глава 14
Решения NCERT для математики класса 9 Глава 15
Решения NCERT для науки класса 9
Решения NCERT для науки класса 9 Глава 1
Решения NCERT для науки класса 9 Глава 2
Решения NCERT для класса 9 Наука Глава 3
Решения NCERT для Науки Класса 9 Глава 4
Решения NCERT для Науки Класса 9 Глава 5
Решения NCERT для Науки Класса 9 Глава 6
Решения NCERT для Науки Класса 9 Глава 7
Решения NCERT для Класса 9 Наука Глава 8
Решения NCERT для Науки Класса 9 Глава 9
Решения NCERT для Науки Класса 9 Глава 10
Решения NCERT для Науки Класса 9 Глава 12
Решения NCERT для Науки Класса 9 Глава 11
Решения NCERT для Класса 9 Наука Глава 13
Решения NCERT для класса 9 Наука Глава 14
Решения NCERT для класса 9 по науке Глава 15
Решения NCERT для класса 10
Решения NCERT для класса 10 по социальным наукам
Решения NCERT для математики класса 10
Решения NCERT для математики класса 10 Глава 1
Решения NCERT для математики класса 10 Глава 2
Решения NCERT для математики класса 10 Глава 3
Решения NCERT для математики класса 10 Глава 4
Решения NCERT для математики класса 10 Глава 5
Решения NCERT для математики класса 10 Глава 6
Решения NCERT для математики класса 10 Глава 7
Решения NCERT для математики класса 10 Глава 8
Решения NCERT для математики класса 10 Глава 9
Решения NCERT
для математики класса 10 Глава 10
Решения
NCERT для математики класса 10 Глава 11
Решения NCERT для математики класса 10 Глава 12
Решения NCERT для математики класса 10 Глава 13
NCERT Sol Решения NCERT для математики класса 10 Глава 14
Решения NCERT для математики класса 10 Глава 15
Решения NCERT для науки класса 10
Решения NCERT для науки класса 10 Глава 1
Решения NCERT для науки класса 10 Глава 2
Решения NCERT для науки 10 класса, глава 3
Решения NCERT для науки 10 класса, глава 4
Решения NCERT для науки класса 10 Глава 5
Решения NCERT для науки класса 10 Глава 6
Решения NCERT для науки класса 10 Глава 7
Решения NCERT для науки 10 класса, глава 8
Решения NCERT для науки класса 10 Глава 9
Решения NCERT для науки класса 10 Глава 10
Решения NCERT для науки класса 10 Глава 11
Решения NCERT для науки класса 10 Глава 12
Решения NCERT для науки 10 класса Глава 13
Решения NCERT для науки 10 класса Глава 14
Решения NCERT для науки 10 класса Глава 15
Решения NCERT для науки 10 класса Глава 16
Учебный план NCERT
NCERT
Commerce
Class 11 Commerce Syllabus
ancy Account
Учебный план по бизнесу, класс 11
Учебный план по экономике, класс 11
Учебный план по коммерции, класс 12
Учебный план по бухгалтерии, класс 12
Учебный план по бизнесу, класс 12
Учебный план по экономике, класс 12 9000 9000
Образцы документов по коммерции класса 11
Образцы документов по коммерции класса 12
TS Grewal Solutions
TS Grewal Solutions Class 12 Accountancy
TS Grewal Solutions Class 11 Accountancy
Отчет о движении денежных средств
Что такое Entry eurship
Защита прав потребителей
Что такое основной актив
Что такое баланс
Формат баланса
Что такое акции
Разница между продажей и маркетингом
ICSE
Документы ICSE
Вопросы ICSE
ML Aggarwal Solutions
ML Aggarwal Solutions Class 10 Maths
ML Aggarwal Solutions Class 9 Maths
ML Aggarwal Solutions Class 8 Maths
ML Aggarwal Solutions Class 7 Maths
ML 6 Maths
ML Aggarwal Solutions Class 6 Maths
ML Aggarwal Solutions Class
Selina Solutions
Selina Solutions для класса 8
Selina Solutions для Class 10
Selina Solutions для Class 9
Frank Solutions
Frank Solutions для математики класса 10
Frank Solutions для математики класса 9
Класс ICSE 9000 2
ICSE Class 6
ICSE Class 7
ICSE Class 8
ICSE Class 9
ICSE Class 10
ISC Class 11
ISC Class 12
IAS
Exam
IAS
Civil
Сервисный экзамен
Программа UPSC
Бесплатная подготовка к IAS
Текущие события
Список статей IAS
Пробный тест IAS 2019
Пробный тест IAS 2019 1
Пробный тест IAS 2019 2

Экзамен KPSC KAS
Экзамен UPPSC PCS
Экзамен MPSC
Экзамен RPSC RAS 
TNPSC Group 1
APPSC Group 1
Экзамен BPSC
WBPS3000 Экзамен 9000 MPC 9000 9000 MPC4000 Jam
Вопросник UPSC 2019
Ключ ответов UPSC 2019
Коучинг IAS
IA S Coaching Бангалор
IAS Coaching Дели
IAS Coaching Ченнаи
IAS Coaching Хайдарабад
IAS Coaching Мумбаи
JEE
BYJU’SEE
9000 JEE 9000 Основной документ JEE 9000 JEE 9000
Вопросник JEE
Биномиальная теорема
Статьи JEE
Квадратичное уравнение
NEET
Программа BYJU NEET
NEET 2020
NEET Приемлемость 9000 Критерии 9000 NEET4 9000 Пример 9000 NEET 9000 9000 NEET
Поддержка
Разрешение жалоб
Служба поддержки клиентов
Центр поддержки
Государственные советы
GSEB
GSEB Syllabus
GSEB4
GSEB3 Образец статьи
004
MSBSHSE
MSBSHSE Syllabus
MSBSHSE Учебники
Образцы статей MSBSHSE
Вопросники MSBSHSE
AP Board
APSCERT
APS4
Syll
AP
Syll 9000SC4
Syll
AP 9000S4 9000 Syll
Syll
MP Board
MP Board Syllabus
MP Board Образцы документов
Учебники MP Board
Assam Board
Assam Board Syllabus
Assam Board Учебники 9000 9000 Board4
Assam Board Учебники 9000 Board4 BSEB
Bihar Board Syllabus
Bihar Board Учебники
Bihar Board Question Papers
Bihar Board Model Papers
BSE Odisha
Odisha Board Syllabus
Odisha Board Syllabus
Программа PSEB
Учебники PSEB
Вопросы PSEB
RBSE
Rajasthan Board Syllabus
RBSE Учебники
RBSE Question Papers
HPBOSE
HPBOSE
000 Syllab HPBOSE000 HPBOSE
JKBOSE
Программа JKBOSE
Образцы документов JKBOSE
Шаблон экзамена JKBOSE
TN Board
TN Board Syllabus
TN Board 9000 Papers 9000 TN Board 9000 Papers 9000 TN Board 9000 Papers 9000 TN Board 9000 Papers 9000 Paper 9000 Paper
JAC
Учебник JAC
Учебники JAC
Вопросники JAC
Telangana Board
Telangana Board Syllabus
Telangana Board Учебники
Papers
Telangana Board Учебники
KSEEB Syllabus
Типовые вопросы KSEEB
KBPE
KBPE Syllabus
Учебники KBPE
KBPE Вопросы
9000 UPMSP Board 9000 UPMSP Board2
Совет по Западной Бенгалии
Учебный план Совета по Западной Бенгалии
Учебники по Совету по Западной Бенгалии
Вопросы для Совета по Западной Бенгалии
UBSE
TBSE
Гоа Совет
000
NBSE000
Mega Board
Manipur Board
Haryana Board
Государственные экзамены
Банковские экзамены
Экзамены SBI
Экзамены IBPS
Экзамены RBI
IBPS
03
Экзамены SSC
9SC2
SSC GD
SSC CPO 900 04
SSC CHSL
SSC CGL
Экзамены RRB
RRB JE
RRB NTPC
RRB ALP
O Экзамены на страхование
LIC4
LIC4 9000 ADF UPSC CAPF
Список статей государственных экзаменов
Обучение детей
Класс 1
Класс 2
Класс 3
Академические вопросы
Вопросы по физике
Вопросы по химии
Вопросы по химии
Вопросы
Вопросы по науке
Вопросы для общего доступа
Онлайн-обучение
Домашнее обучение
Полные формы
CAT
BYJU’S CAT Program
CAT3 9000 Предварительный курс CAT3
Экзамен 9000 9000 CAT3 Экзамен Шаблон экзамена CAT 2020
Обзор приложения Byju по CAT
КУПИТЬ КУРС
.
вертикальных углов | Определение, теорема и примеры (видео)
В этом уроке используются два слова, которые часто неправильно понимают: вертикальный и дополнительный . Слово «вертикальный» обычно означает «вверх и вниз», но с вертикальными углами оно означает «относящийся к вершине» или углу. Дополнительный в математике означает «прибавление к 90 °», но это также прилагательное, обычно используемое для обозначения «объединение таким образом, чтобы что-то усилить», как два человека с дополнительными навыками — например, один готовит, а другой печет.
Держите в уме математическое значение этих двух слов, и вы четко определите вертикальные углы и дополнительные углы.
Содержание
Определение вертикальных углов
Теорема о вертикальных углах
Пример дополнительных углов
Что такое вертикальные углы?
Определение вертикальных углов
Когда две прямые пересекаются в геометрии, они образуют четыре угла. Углы прицела — углы, противоположные друг другу.Любые две пересекающиеся линии образуют две пары вертикальных углов, например:

При беглом взгляде на рисунок возникает несколько назойливых вопросов:
Вертикальные углы совпадают?
Смежны ли вертикальные углы?
Вертикальные углы являются дополнительными?
Вертикальные углы дополняют друг друга?
Давайте займемся этим по очереди. Возьмите два прямых предмета, например бамбуковые шпажки или карандаши. Перебросьте их так, чтобы они пересеклись и образовали две пары углов.Теперь посмотрите на углы, которые они образуют.
Если вы изучите любую пару противоположных углов в предметах, которые вы выбросили, вы увидите, что они имеют общую точку в своих вершинах, своих углах. Это делает их вертикальными углами. Вы также заметите, что, большие или маленькие, они кажутся зеркальными отражениями друг друга. Они есть; они имеют одинаковый угол, отраженный поперек вершины.
Теорема о вертикальных углах
Вертикальные углы Теорема утверждает, что вертикальные углы, углы, которые противоположны друг другу и образованы двумя пересекающимися прямыми линиями, совпадают.Вертикальные углы всегда совпадают, поэтому, когда кто-то задает следующий вопрос, вы уже знаете ответ.

Соответствуют ли вертикальные углы?
Да, согласно теореме о вертикальном угле, независимо от того, как вы бросаете шпажки или карандаши, чтобы они пересекались, или как пересекаются две пересекающиеся линии, вертикальные углы всегда будут конгруэнтны или равны друг другу. Это закреплено в математике в теореме о вертикальных углах.

Смежны ли вертикальные углы?
Вертикальные углы по определению не могут быть рядом с (рядом друг с другом).Другая пара вертикальных углов прерывается, поскольку противоположных углов являются вертикальными. Смежные углы принимают один угол из одной пары вертикальных углов и другой угол из другой пары вертикальных углов.
Вертикальные углы являются дополнительными?
Дополнительные углы добавляют к 180 °, и только одна конфигурация пересекающихся линий дает дополнительные, вертикальные углы; когда пересекающиеся линии перпендикулярны.

Это становится очевидным, когда вы понимаете противоположные, совпадающие вертикальные углы, называя их обязательным решением этого простого алгебраического уравнения:
2a = 180 °
а = 90 °
У вас есть шанс 1 к 90 случайным образом получить дополнительные вертикальные углы в результате случайного выброса двух отрезков прямой так, чтобы они пересекались.
В то время как вертикальные углы не всегда являются дополнительными, смежные углы всегда являются дополнительными . Возьмите любые два смежных угла из четырех углов, образованных двумя пересекающимися линиями. Эти два смежных угла всегда будут составлять 180 °. Мы можем убедиться в этом, если начнем с верхнего левого угла и обойдем цифру по часовой стрелке:

EMI является дополнением к IMU и ∠EMP
IMU является дополнением к PMU и EMI
∠UMP является дополнением к IMU и EMP
∠EMP является дополнением к EMI и ∠UMP
Вертикальные углы дополняют друг друга?
Если вертикальные углы не всегда являются дополнительными, составляют ли они по крайней мере дополнительных углов , то есть прибавляя к 90 °?

Опять же, мы можем использовать алгебру для подтверждения того, что очевидно на чертежах для вертикальных углов a:
2a = 90 °
а = 45 °
Только когда вертикальные углы a составляют 45 °, они могут быть дополнительными. Острый вертикальный и
.
Теорема о вертикальных углах
Теорема о вертикальных углах касается углов, противоположных друг другу. Мы объясняем концепцию, приводим доказательства и показываем, как использовать ее для решения проблем.
Эти вертикальные углы образуются, когда две линии пересекаются друг с другом, как вы можете видеть на следующем рисунке.

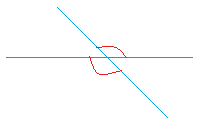
Теорема: Вертикальные углы конгруэнтны.
«Конгруэнт» — довольно необычное слово. Проще говоря, это означает, что вертикальные углы равны.Например, посмотрите на два угла, выделенные красным выше. У них такая же мера.
Если один из них измеряет 140 градусов, например, верхний, нижний также равен 140 градусам.
Доказательство теоремы о вертикальных углах
Доказательство простое. Доказательство начнем с того, что вы уже знаете о прямых линиях и углах.
Мы будем использовать постулат сложения углов и свойство замещения равенства, чтобы прийти к заключению.
Постулат сложения углов гласит, что если два соседних угла образуют прямой угол, то сумма этих двух углов составит 180 градусов.
Свойство замещения утверждает, что если x = y, то y может заменить x в любом выражении. Или x может заменить y в любом выражении.
Используйте этот рисунок для доказательства.

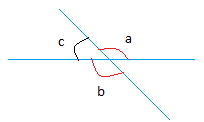
Дано: ∠ a и ∠ b — вертикальные углы
Докажите, что m ∠ a = m ∠b
Обратите внимание, что m ∠ a означает меру угла a
Согласно постулату сложения углов
m ∠ a + m ∠ c = 180 градусов
m ∠ b + m ∠ c = 180 градусов
Путем подстановки m ∠ a + m ∠ c может заменить 180 градусов в уравнении внизу.
Получаем:
m ∠ b + m ∠ c = m ∠ a + m ∠ c
Вычтем m ∠ c из обеих частей уравнения
m ∠ b + m ∠ c — m ∠ c = m ∠ a + m ∠ c — m ∠ c
m ∠ b = m ∠ a
Использование теоремы о вертикальных углах для решения задачи

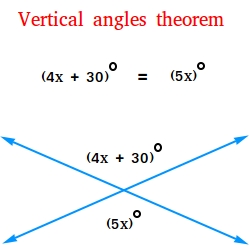
Используйте теорему о вертикальных углах, чтобы найти меры двух вертикальных углов.
Поскольку вертикальные углы равны или равны, 5x = 4x + 30
5x = 4x + 30
Вычтем 4x из каждой части уравнения
5x — 4x = 4x — 4x + 30
x = 30
Используйте 4x + 30, чтобы найти меры вертикальных углов
4 раза 30 + 30 = 120 + 30 = 150
Два вертикальных угла составляют 150 градусов.
Новые уроки математики
Ваша электронная почта в безопасности. Мы будем использовать его только для информирования вас о новых уроках математики.
,
% PDF-1.4 % 470 0 объект > endobj Xref 470 349 0000000016 00000 н. 0000008680 00000 н. 0000008765 00000 н. 0000009003 00000 н. 0000010824 00000 п. 0000010871 00000 п. 0000010918 00000 п. 0000010965 00000 п. 0000011012 00000 п. 0000011058 00000 п. 0000011106 00000 п. 0000011153 00000 п. 0000011200 00000 п. 0000011247 00000 п. 0000011293 00000 п. 0000011340 00000 п. 0000011387 00000 п. 0000011434 00000 п. 0000011487 00000 п. 0000011533 00000 п. 0000011611 00000 п. 0000011687 00000 п. 0000011764 00000 п. 0000012066 00000 п. 0000012402 00000 п. 0000012728 00000 п. 0000013118 00000 п. 0000013508 00000 п. 0000013898 00000 п. 0000014323 00000 п. 0000014371 00000 п. 0000014419 00000 п. 0000014465 00000 п. 0000014511 00000 п. 0000014558 00000 п. 0000014605 00000 п. 0000014652 00000 п. 0000014698 00000 п. 0000040827 00000 н. 0000041139 00000 п. 0000041436 00000 п. 0000042089 00000 п. 0000042664 00000 п. 0000042982 00000 п. 0000043154 00000 п. 0000043799 00000 н. 0000044050 00000 п. 0000044574 00000 п. 0000044674 00000 п. 0000045109 00000 п. 0000045447 00000 п. 0000045522 00000 п. 0000045580 00000 п. 0000045640 00000 п. 0000067487 00000 п. 0000093425 00000 п. 0000094208 00000 п. 0000094314 00000 п. 0000094925 00000 п. 0000095035 00000 п. 0000095072 00000 п. 0000120845 00000 н. 0000146881 00000 н. 0000147402 00000 н. 0000173493 00000 н. 0000174114 00000 н. 0000174320 00000 н. 0000174490 00000 н. 0000174786 00000 н. 0000174845 00000 н. 0000175219 00000 н. 0000175874 00000 н. 0000177057 00000 н. 0000177404 00000 н. 0000177779 00000 н. 0000177830 00000 н. 0000178095 00000 н. 0000204175 00000 н. 0000204954 00000 н. 0000205126 00000 н. 0000205388 00000 н. 0000205649 00000 н. 0000230277 00000 н. 0000232969 00000 н. 0000233021 00000 н. 0000238969 00000 н. 0000244824 00000 н. 0000245007 00000 н. 0000245059 00000 н. 0000246014 00000 н. 0000247970 00000 п. 0000258236 00000 п. 0000259673 00000 н. 0000263520 00000 н. 0000269426 00000 н. 0000272159 00000 н. 0000276111 00000 н. 0000278576 00000 н. 0000281416 00000 н. 0000282144 00000 н. 0000282916 00000 н. 0000282987 00000 н. 0000283073 00000 н. 0000283177 00000 н. 0000283316 00000 н. 0000283393 00000 н. 0000283464 00000 н. 0000283577 00000 н. 0000283666 00000 н. 0000283755 00000 н. 0000283915 00000 н. 0000284517 00000 н. 0000284691 00000 н. 0000284801 00000 п. 0000284999 00000 н. 0000285243 00000 н. 0000285359 00000 п. 0000285436 00000 н. 0000287402 00000 н. 0000287684 00000 н. 0000287801 00000 н. 0000289013 00000 н. 0000289265 00000 н. 0000289625 00000 н. 0000290342 00000 н. 0000290448 00000 н. 0000290578 00000 н. 0000335400 00000 н. 0000335439 00000 н. 0000376835 00000 н. 0000376874 00000 н. 0000418716 00000 н. 0000418755 00000 н. 0000418825 00000 н. 0000418914 00000 н. 0000419063 00000 н. 0000419136 00000 п. 0000419209 00000 н. 0000419318 00000 н. 0000419467 00000 н. 0000419540 00000 н. 0000419613 00000 п. 0000419722 00000 н. 0000419872 00000 н. 0000419945 00000 н. 0000420018 00000 н. 0000420127 00000 н. 0000420275 00000 н. 0000420348 00000 н. 0000420421 00000 н. 0000420530 00000 н. 0000420680 00000 н. 0000420753 00000 н. 0000420826 00000 н. 0000420935 00000 н. 0000421085 00000 н. 0000421158 00000 н. 0000421231 00000 н. 0000421340 00000 н. 0000421488 00000 н. 0000421561 00000 н. 0000421634 00000 н. 0000421743 00000 н. 0000421893 00000 н. 0000421966 00000 н. 0000422039 00000 н. 0000422148 00000 п. 0000422298 00000 п. 0000422370 00000 н. 0000422443 00000 н. 0000422552 00000 н. 0000422701 00000 п. 0000422774 00000 п. 0000422847 00000 н. 0000422956 00000 н. 0000423105 00000 п. 0000423178 00000 п. 0000423249 00000 н. 0000423358 00000 п. 0000423507 00000 н. 0000423580 00000 н. 0000423653 00000 п. 0000423762 00000 н. 0000423912 00000 н. 0000423985 00000 п. 0000424057 00000 н. 0000424166 00000 н. 0000424316 00000 п. 0000424389 00000 п. 0000424461 00000 п. 0000424570 00000 н. 0000424719 00000 н. 0000424792 00000 н. 0000424865 00000 н. 0000424974 00000 п. 0000425124 00000 н. 0000425197 00000 н. 0000425270 00000 н. 0000425379 00000 н. 0000425527 00000 н. 0000425599 00000 н. 0000425672 00000 н. 0000425781 00000 н. 0000425931 00000 н. 0000426004 00000 п. 0000426077 00000 н. 0000426186 00000 п. 0000426334 00000 н. 0000426407 00000 н. 0000426480 00000 н. 0000426589 00000 н. 0000426739 00000 н. 0000426812 00000 н. 0000426885 00000 н. 0000426994 00000 н. 0000427144 00000 н. 0000427217 00000 н. 0000427290 00000 н. 0000427399 00000 н. 0000427548 00000 н. 0000427621 00000 н. 0000427694 00000 н. 0000427803 00000 н. 0000427951 00000 н. 0000428024 00000 н. 0000428097 00000 п. 0000428206 00000 н. 0000428356 00000 п. 0000428429 00000 п. 0000428502 00000 н. 0000428611 00000 п. 0000428760 00000 н. 0000428833 00000 н. 0000428906 00000 н. 0000429015 00000 н. 0000429165 00000 н. 0000429238 00000 п. 0000429311 00000 п. 0000429420 00000 н. 0000429569 00000 н. 0000429642 00000 н. 0000429715 00000 н. 0000429824 00000 н. 0000429973 00000 н. 0000430046 00000 н. 0000430119 00000 п. 0000430228 00000 п. 0000430378 00000 п. 0000430451 00000 п. 0000430524 00000 н. 0000430633 00000 п. 0000430782 00000 н. 0000430855 00000 н. 0000430928 00000 н. 0000431037 00000 н. 0000431187 00000 н. 0000431260 00000 н. 0000431333 00000 н. 0000431442 00000 н. 0000431592 00000 н. 0000431665 00000 н. 0000431738 00000 н. 0000431847 00000 н. 0000431997 00000 н. 0000432070 00000 н. 0000432143 00000 н. 0000432252 00000 н. 0000432402 00000 н. 0000432474 00000 н. 0000432546 00000 н. 0000432655 00000 н. 0000432805 00000 н. 0000432877 00000 н. 0000432948 00000 н. 0000433057 00000 н. 0000433206 00000 н. 0000433268 00000 н. 0000433339 00000 н. 0000433448 00000 н. 0000433598 00000 н. 0000433669 00000 н. 0000433740 00000 н. 0000433811 00000 н. 0000433940 00000 н. 0000434094 00000 н. 0000434581 00000 п. 0000434730 00000 н. 0000435354 00000 п. 0000435504 00000 н. 0000435575 00000 н. 0000435645 00000 н. 0000435754 00000 п. 0000435908 00000 н. 0000435970 00000 п. 0000436079 00000 п. 0000436230 00000 н. 0000436303 00000 п. 0000436376 00000 п. 0000436485 00000 н. 0000436635 00000 н. 0000437087 00000 н. 0000437193 00000 п. 0000437266 00000 н. 0000437339 00000 н. 0000437448 00000 н. 0000437597 00000 п. 0000437670 00000 н. 0000437743 00000 н. 0000437852 00000 н. 0000438002 00000 н. 0000438073 00000 н. 0000438146 00000 п. 0000438255 00000 н. 0000438404 00000 п. 0000438477 00000 п. 0000438550 00000 н. 0000438659 00000 н. 0000438809 00000 н. 0000441502 00000 н. 0000441714 00000 н. 0000441917 00000 н. 0000442215 00000 н. 0000442477 00000 н. 0000442732 00000 н. 0000443105 00000 н. 0000444877 00000 н. 0000449820 00000 н. 0000449987 00000 н. 0000450730 00000 н. 0000450975 00000 н. 0000454801 00000 п. 0000455049 00000 н. 0000455306 00000 п. 0000456702 00000 н. 0000456884 00000 н. 0000457267 00000 н. 0000457438 00000 п. 0000458023 00000 н. 0000459387 00000 н. 0000459869 00000 н. 0000461440 00000 н. 0000462919 00000 н. 0000463128 00000 н. 0000465278 00000 н. 0000465623 00000 п. 0000465835 00000 н. 0000466091 00000 н. 0000466346 00000 н. 0000007276 00000 н. прицеп ] / Назад 3187644 >> startxref 0 %% EOF 818 0 объект > поток ч UPSG ޴ =! грамм Q (Z ~ b% H-TQ, FqE- ~ R `QPBX * # * Т ڢ uXtzwwmr6 WA
.
No related posts.