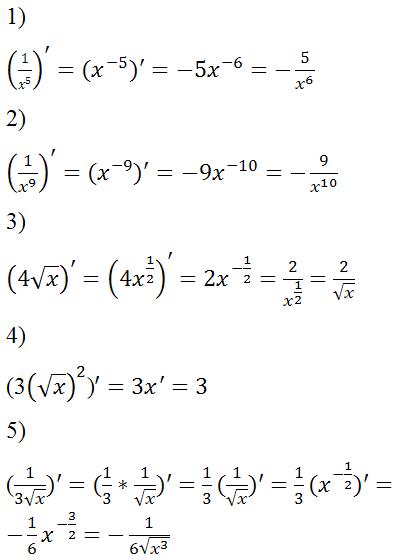чему равна, формула, примеры решения задач
Понятие производной, чему равна Х* корня из Х
Определение
Производной функции \(y=f(x)\) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует).
Говоря проще, производная есть скорость изменения функции в конкретной точке. Скорость оценивается с помощью вычисления отношения изменения функции \(\triangle y\) к изменению аргумента \(\triangle x\). Данное отношение рассматривается в пределе, где \(\triangle x\rightarrow0.\)
Обычно производную обозначают как f'(x).
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Перед тем, как приступать к изучению частного случая производной x\times\sqrt x, рассмотрим, чему равна производная из \(\sqrt x\).
\(g'(x)=3\)
Комбинируем найденные произведения по правилу дифференцирования сложных функций.
Таким образом:
\(y’=\frac1{2\times\sqrt g}\times3=\frac1{2\sqrt{(3x+2)}}\times3=\frac3{2\times\sqrt{(3x+2)}}\)
Ответ: \(y’=\frac3{2\times\sqrt{(3x+2)}}.\)
С помощью упрощенного правила дифференцирования корня
Определение
Производная квадратного корня, под которым стоит переменная или фукнция, будет равна производной подкоренного выражения, поделенной на удвоенный первоначальный квадратный корень
или
\(f'(x)=\frac{u’}{2\times\sqrt u},\) если \(f(x)=\sqrt u\).
Рассмотрим на примере производной функции \(\sqrt{5x+2}.\)
В ней подкоренным выражением будет \((5x+2)\), а его производной — \(5\).
Вспомним определение производной корня. Получим:
\(f(x)=\sqrt{5x+2}\)
\(f'(x)=\frac5{2\times\sqrt{5x+2}}\)
По правилу дифференцирования квадратных корней нужно было делить числитель на удвоенное произведение первоначального корня, что мы и сделали для получения ответа.
Примеры решения задач по теме «Производная корня»
Задача 1
Найти производную функции \(y(x)=2\sqrt x.\)
Решение
\(y'(x)=(2\sqrt{x)}’\)
Применим уже изученные правила. Получим:
\(y'(x)=2\times(\sqrt{x)’}=2\times\frac1{2\times\sqrt x}=\frac1{\sqrt x}\)
Ответ: \(y'(x)=\frac1{\sqrt x}.\)
Задача 2
Найти производную функции \(y(x)=\sqrt{2x}.\)
Решение
\(y'(x)=(\sqrt{2x})’\)
Применим уже изученные правила. Получим:
\(y'(x)=(\sqrt{2x})’=\frac1{2\times\sqrt{2\times x}}\times(2x)’\)
\(y'(x)=\frac1{2\times\sqrt{2\times x}}\times2\times\;(x)’=\frac1{\sqrt{2x}}\times1=\frac1{\sqrt{2x}}\)
Ответ: \(y'(x)=\frac1{\sqrt{2x}}.\)
Задача 3
Попробуем решить производную частного случая \(x\times\sqrt x\).
Найти производную от \(x\times\sqrt x.\)
Решение
Применим уже изученные правила и получим:
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Производная x — Формула, Доказательство, Примеры
LearnPracticeDownload
Производная x равна 1.
Она относится к результату, полученному путем дифференцирования x с использованием различных методов. Дифференцирование — это процесс, который используется для нахождения скорости изменения функции. Есть два основных метода, используемых при нахождении производной x. Это первый принцип и правило степени дифференциации.
В этой статье мы увидим, как найти производную x, используя различные методы оценки производных. Мы также будем решать различные примеры, основанные на производной функций, используя производную от x для лучшего понимания концепции.
| 1. | Что такое производная x? |
| 2. | Производная от x Формула |
| 3. | Производная x по первому принципу |
| 4. | Дифференциация x по правилу степени |
| 5. | Часто задаваемые вопросы о производной x |
Что такое производная x?
Дифференцирование x — это процесс вычисления производной x.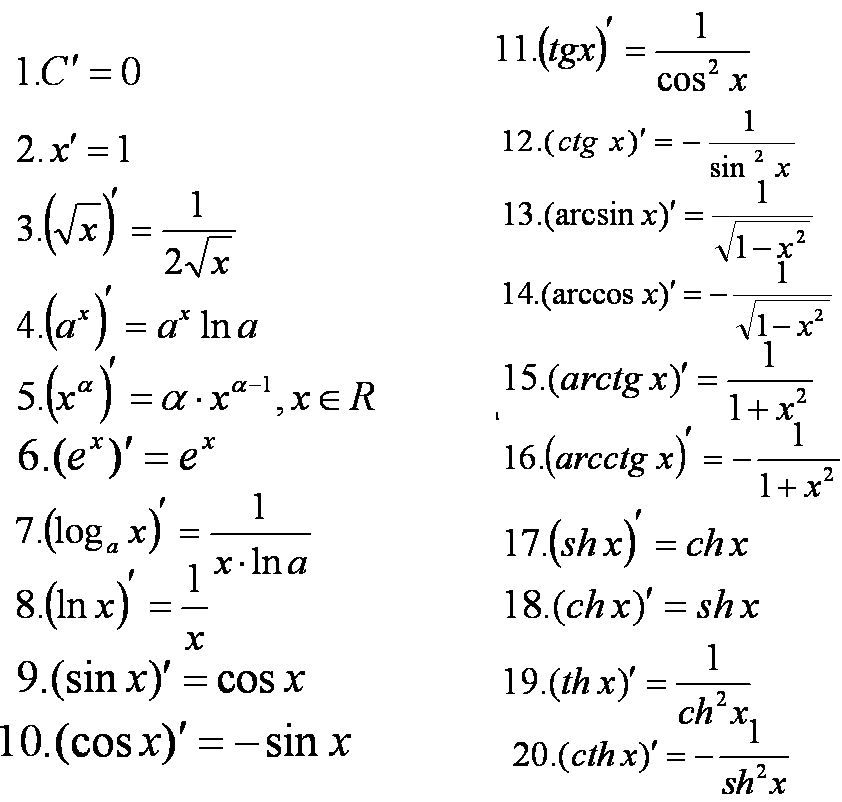
Дифференцирование используется для обозначения очень небольшого изменения данной функции по отношению к одной из ее переменных. Обозначение дифференцирования функции f(x) дается как f'(x) = d[f(x)]/dx. Здесь f(x) обозначает функцию, а dx показывает переменную, по которой функция будет дифференцирована. Дифференцирование x можно представить как dx/dx, равное 1. Мы знаем, что производная линейной функции f(x) = ax + b равна a, где a, b — действительные числа. При f(x) = x имеем a = 1 и b = 0. Используя эти факты, мы получаем производную от x, равную 1.
Производная от x Формула
Формула для производной x представлена как dx/dx (OR) (x)’ = 1. Эта формула может быть вычислена с использованием различных методов дифференцирования, включая первый принцип производных и степенное правило дифференцирования. На изображении ниже показана формула дифференцирования x. Интуитивно понятно, что производная функции в точке представляет собой наклон касательной к графику этой функции в этой конкретной точке.
Поскольку f(x) = x представляет собой прямую линию, производная от x будет равна 1 во всех точках.
Производная x по первому принципу
Первый принцип также известен как определение производной. Согласно первому принципу производную функции можно определить, вычислив предельную формулу f'(x) = lim
dx/dx = f'(x) = lim h→0 [x + h — x]/h
= lim h→0 h/h
= lim h→0 1
= 1
Таким образом, производная от x равна 1.
Дифференциация x по правилу мощности
Степенное правило дифференцирования — самый простой способ вычисления производных функций вида x n , где n не равно -1. Правило степени задается следующим образом: dx n / dx = nx н-1 .
Поскольку показатель степени x равен 1, таким образом, чтобы найти производную x, n = 1 необходимо заменить в вышеупомянутой формуле.
дх 1
/ дх = 1 . х 1 -1= 1 . х 0
= 1 . 1
= 1
Таким образом, используя правило степени, значение производной x также равно 1.
Статьи по теме:
- Калькулятор производных
- Расчетный калькулятор
- Производная от ln x
- Дифференцируемые функции
Важные замечания о производной x
- Производная x будет равна 1. Для нахождения производной x можно использовать как степенное правило, так и первый принцип.
- Используя n = 1 в степени, заданной выражением dx n /dx = nx n-1 , можно определить производную x.
- Поскольку f(x) = x представляет прямую линию, следовательно, производная будет равна 1 во всех точках.
Примеры производной от x
Пример 1: Чему равна производная x, возведенная в 4 ?
Решение: Производную от x, возведенную в 4, можно вычислить с помощью степенного правила.
dx n /dx = nx n-1
Здесь n = 4
dx 4 /dx = 4x 4 -1 = 4x 3
Ответ: д(х 4 )/дх = 4х 3
Пример 2: Найдите производную x, возведенную в 2, используя первый принцип.
Решение: В соответствии с первым принципом формула для вычисления производной имеет вид + h) = (x + h) 2
f'(x) = lim h→0 [(x + h) 2 — x 2 ]/h
Используя алгебраическое тождество ( а + б) 2 = а 2 + 2ab + b 2
f'(x) = lim h→0 [x 2 + h 2 + 2xh — х 2 ]/ч
f'(x) = lim h→0 [h 2 + 2xh]/h
f'(x) = lim h→0 h [h + 2x]/h
f'( x) = 2x (при применении предела)
Ответ: Производная от x, возведенная в 2, равна 2x.
Пример 3: Найдите производную x sin x
Решение: Правило произведения дифференцирования используется для нахождения производной x sin x.
Задается как d[f(x) g(x)]/dx = f'(x)g(x) + f(x)g'(x)
d(xsinx)/dx = 1 ( sin x) + x (cos x) (производная sin x равна cos x)
Ответ: d(x sin x)/dx = sin x + x cos x
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных элементов.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по производной x
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о производной x
Что такое производная x в исчислении?
Производная от x в исчислении относится к значению, полученному после дифференцирования x.
Степенное правило и первый принцип используются для вычисления производной x, равной 1.
Как вычислить производную x с помощью степенного правила?
Степенное правило дифференцирования задается как dx n /dx = nx n-1 = nx n-1 . Подставив n = 1 в эту формулу, можно получить производную x как 1. Мы также можем оценить дифференцирование x, используя первый принцип производных.
Какая формула дифференцирования x?
Формула для дифференцирования x: dx/dx (OR) (x)’ = 1. Она также может быть представлена как f'(x) = 1, где f(x) = x.
Какая производная от x + 1?
х + 1 также может быть записано как х 1 + х 0 . Применяя степенное правило к первому и второму членам, производная x + 1 может быть вычислена как 1.
Как найти производную n
th x? n производная от x может быть определена последовательным дифференцированием. Первая производная от x равна 1.