Чему равно число пи в градусах: Чему равно число Пи в градусах? Правильный ответ.

Градусы и радианы – Круги и Пи – Mathigon

До сих пор в геометрии мы всегда измеряли углы в градусах . Полный оборот на °, половина оборота °, а четверть круга составляет ° и так далее.

Число 360 очень удобно, потому что оно делится на множество других чисел: 2, 3, 4, 5, 6, 8, 9, 10, 12, 15 и так далее. Это означает, что многие части одного оборота также являются целыми числами. Но вы когда-нибудь задумывались, откуда берется число 360?

Так получилось, что 360 градусов — это одно из древнейших понятий в математике, которым мы до сих пор пользуемся. Оно было разработано в древнем Вавилоне более 5000 лет назад!

В то время одним из наиболее важных применений математики была астрономия. Солнце определяет четыре сезона, о которых важно знать фермерам для выращивания урожая. Точно так же луна определяет приливы, что было важно для рыболовов. Люди также изучали звезды, чтобы предсказывать будущее или общаться с богами.

Вавилонская табличка для расчета 2

Астрономы заметили, что созвездия, видимые в определенное время ночью, чуть-чуть смещались изо дня в день — до тех пор, пока примерно через 360 дней они не возвращались назад к своей исходной точке. И это могло стать причиной того, что круг разделили на 360 градусов.

Midnight on day ${day}

Конечно, на самом деле в одном году 365 дней (ну, точнее, 365.242199), но вавилонские математики работали с простыми солнечными часами, и это приближение было вполне адекватным.

Это также хорошо работало с их существующей системой 60-тиричной системой счисления (так как 6×60=360 ). Эта система является причиной того, что у нас по-прежнему есть 60 секунд в минуте и 60 минут в часе — даже если большинство других единиц измеряется по 10-тиричной системе (например, 10 лет за десятилетие или 100 лет за столетие).

Для многих из нас измерение углов в градусах довольно привычно: видео на 360°, скейтбордисты могут сделать поворот на 540°, а кто-то может изменить свое решение на 180°.

Но с математической точки зрения выбор 360 совершенно произвольный. Если бы мы жили на Марсе, у круга могло бы быть 670°, а в году на Юпитере вообще 10 475 дней.

540 McFlip, поворот на 540°

Радиан

Вместо того, чтобы делить круг на некоторое количество сегментов (например, 360 градусов), математики часто предпочитают измерять углы, используя единичную окружность (окружность с радиусом 1).

имеет длину ,

, соответствует расстояние ,

Для , расстояние по окружности ,

И так далее: этот способ измерения углов называется радианами .

Каждый угол в градусах имеет эквивалентный размер в радианах. Преобразование одного в другое очень простое, оно похоже на конвертацию между другими единицами измерения, например, метрами и километрами или градусами Цельсия и Фаренгейта:

360° = 2_π радиан_

⇒ 1° = радиан

⇒ 1 радиан = °

Вы можете записать значение в радианах либо как обыкновенную дробь с π , либо как десятичную дробь. Можете ли вы заполнить эту таблицу эквивалентных угловых размеров в градусах и радианах?

градусы	0	60		180
радианы	0		2		32π

Пройденное расстояние

Вы можете думать о радианах как о «пройденном расстоянии» по окружности единичного круга. Это особенно полезно при работе с объектами, которые движутся по круговой траектории.

Например, Международная космическая станция делает один оборот вокруг Земли каждые 1,5 часа. Это означает, что его скорость вращения радианы в час.

При движении по единичной окружности скорость вращения равна фактической скорости, потому что длина окружности такая же, как один полный оборот в радианах (оба 2π).

Радиус орбиты МКС составляет 6800  км, что означает, что фактическая скорость МКС должна быть = 28483 км в час.

${round(p*1.5,1)}h

Видите, что в этом примере радианы являются гораздо более удобной единицей измерения, чем градусы? Как только мы узнаем скорость вращения, нам просто нужно умножить на радиус, чтобы получить фактическую скорость.

Вот еще один пример: у вашей машины есть колеса с радиусом 0,25  м. Если вы едете со скоростью 20 м / с, колеса вашего автомобиля вращаются со скоростью радианы в секунду (или 802π=13 оборотов в секунду).

Тригонометрия

Для большинства простых геометрических задач градусы и радианы полностью взаимозаменяемы — вы можете выбрать, что из них вам нравится больше, или вам может подсказать вопрос, в каких единицах дать ответ. Однако, как только вы изучите более сложную тригонометрию или исчисление , вы увидите, что радианы намного удобнее, чем градусы.

Большинство калькуляторов имеют специальную кнопку для переключения между градусами и радианами. Тригонометрические функции, такие как sin , cos и tg, берутся от заданных углов, а их обратные функции arcsin , arccos и arctg берутся от чисел и дают угол в результате.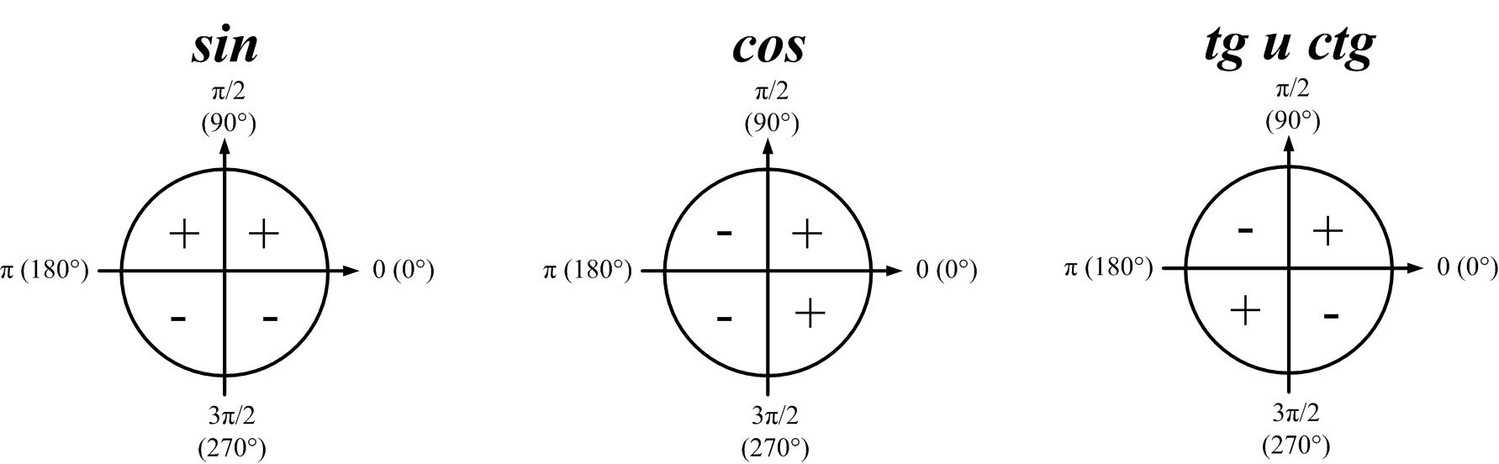 Текущая настройка калькулятора определяет, какие единицы измерения используются для этих углов.

Попробуйте использовать этот калькулятор, чтобы рассчитать

sin (30°) = cos (1°) = Sin (30 рад) = cos (1 рад) =

7

8

9

sin

4

5

6

cos

1

2

3

tan

.

C

mode

Использование радианов имеет одно особенно интересное преимущество при использовании функции синуса. Если θ очень маленький угол (менее 20° или 0,3 рад), то sinθ≈θ , Например,

sin ( ${x} ) ≈${sin(x)} …

Это называется приближением малых углов , и оно может значительно упростить некоторые уравнения, содержащие тригонометрические функции. Вы узнаете намного больше об этом в будущем.

Чему равно число «Пи», или как ругаются математики? Чему равно число ПИ? История открытия, тайны и загадки

Tatiana Durimanova

Я создала на Facebook страницу b назвала ее «Язык как философия жизни». Вообще-то мне хотелось назвать ее «Записки из сумасшедшего дома», ибо что иное, как не сумасшедший дом представляет собой наша современная жизнь? Нет, я не собираюсь говорить о том, что все куда-то бегут, что-то не успевают сделать, чего-то вечно не хватает: времени, денег, и т.д. Что нас захлестнула волна непонимания того, что происходит вокруг, куда катится мир…
Крутимся, как белки в колесе. Ощущаем, что бежим по замкнутому кругу. Теряем круг друзей, попадаем в порочный круг… Знакомо? А утро-день-вечер-ночь, и снова по кругу. Весна-лето-осень-зима, и опять по кругу.
Кстати, кто может точно сказать в какое конкретно время утро сменят ночь, зима, весну? Можно ли вообще проводить четкую разделительную грань между курицей и яйцом, и разделимы ли они? Может лучше признать, что яйцо – это потенциальная курица, курица – это потенциальное яйцо, и они не разделимы. Где кончаюсь я и начинаются мои проблемы, проблемы моих детей, друзей и пр., становящихся моими, просто потому, что мы живем в одной квартире, доме, городе, мире? Разве Господь-Бог сказал нам, что ноль часов нужно определять по Гринвичу, что меня нужно назвать Татьяной, а стул стулом? Где кончается мир реальный (вещественный), и начинается мир, выдуманный нами?

Земля вращается вокруг оси и по орбите (кругу, эллипсу – какая разница?). Галактики вращаются. Ученые открыли торсионные поля, доказали, что … «согласно теории относительности Альберта Эйнштейна, мир устроен не совсем так [как нас учили и учат в школе]), в нём наблюдается искривление пространства, так что две прямые, которые на данном участке пространства параллельны, на каком-то отрезке своей протяжённости, могут пересекаться. Недавно предположение Эйнштейна об искривлении пространства было подтверждено экспериментально» (Александр Бабицкий).
А мы все движемся из пункта А в пункт В, полагая, что они находятся на прямой линии.
И чего это меня, лингвиста, занесло в физику, спросите вы? Да потому что все вокруг нас, и в нас самих и есть физика. Язык есть физика. Разве звук не относится к области физики? А теперь скажите мне, что такое гласный звук? Я вам предлагаю «милое» для 21 века определение звуков: «Звуки мы произносим и слышим, а буквы пишем и видим. При произнесении гласного звука воздух не встречает преград: [а], [о], [у], [и], [ы], [э]. При произнесении согласного звука воздух встречает преграду: губы, зубы, язык. Согласный звук произносится с голосом и шумом или только с шумом.»
В принципе, все верно. Вы можете просто мычать «гласным звуком», не размыкая губ. Мычите на здоровье. А вот если, вы губы разомкнули, то у вас получаются знакомые нам всем звуке, «а», «э», которые различаются лишь степенью округленности, растягивания или вытягивания в трубочку губ. Согласны? Это как арбуз, который можно нарезать ломтиками, кубиками, фигурками, но он ведь не перестает оставаться арбузом!!! И в какой момент звук «а» превращается в «о»? Разве есть четкая граница? Конечно, на качество гласного звука может повлиять положение языка (задние звуки), опускание челюсти, опять же с соответствующим положением языка, но это все тот же арбуз, нарезанный фигурками.
Согласный звук есть барьер на пути гласного звука. Чем можно создать такой барьер? Читайте выше: губами, зубами, языком. Другими словами, инструментарий речи довольно ограничен, но какое обилие языков!!! (А как вам нравятся 7 нот и такое обилие музыки?)
Теперь давайте задумаемся, у кошки этот инструментарий есть, и у собаки, и у дельфина, да и вообще рыб, и т. 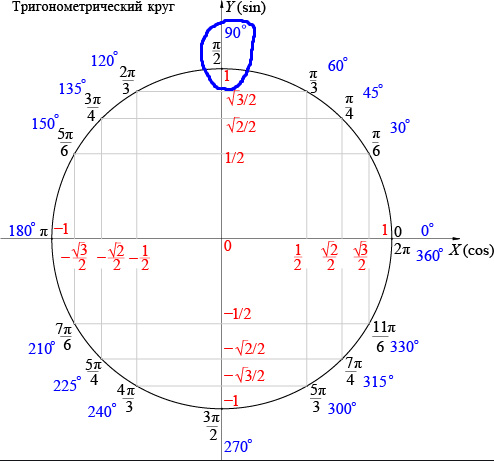д.…
«Ну и заехала», — скажете вы. Да, заехала! А разве не было времени, когда Землю считали блином? А разве электричество не существует просто потому, что мы его не видим и не слышим? Если доказано, что вакуума нет, значит есть все, но это все может быть различимо, опять же, в зависимости от инструментария, который мы используем для рассмотрения и изучения объекта. По мере его совершенствования, мы узнаем все больше нового, чего раньше даже и помыслить не могли.
Язык есть формализация мысли. А где формализуется мысль? Что мы знаем о нашем мире, о самих себе? Мы ищем иные миры, не зная собственного! В этом-то и заключается проблема!
Что мы знаем о языке, кроме того, что он формализуется в звуках. Пожалуйста, формализуйте – куммммарама. Что это? Ничего, потому что гласный звук может «нести на себе» лишь определенное количество согласных звуков, также как я, при моем весе в 50 кг не смогу поднять груз в 150 кг. Физика, понимаете ли!
Теперь обратимся к кривизне пространства и кругу, с которых мы начали. Допустим, мы усомнились в том, что язык развивается не по спирали (в плане контекста), а прямолинейно, и я сообщаю вам, что «в нашем большом городе есть главная улица пересекающая весь город на которой растет много деревьев ходит много людей…». Дурость, скажите вы, где здесь знаки препинания? Где запятые и точки?
Но что есть знаки препинания? Они и есть знаки разделения между подлежащим-сказуемым дополнением (с относящимися к ним определениями) одного предложения и начала другого. Причастие есть ни что иное, как умножение: которая проходит = проходящая, в то время как разворачивание «проходящая» на «которая проходит» – это уже деление. А это уже математика! Ничего удивительного. Мир неделим. Это целостность. Язык тоже – целостность. Нам просто пора взглянуть на все по-новому. Проснуться и оглядеться. Учить детей не правилам, наподобие «Существует отдельная группа слов — предикативы (или категория состояния). Это слова, обозначающие нединамическое состояние и выступающие в функции главного члена (сказуемого, предиката) односоставного безличного предложения. Учёные до сих пор не определились относительно статуса слов категории состояния. Так вот слово НАДО наряду с другими словами (жаль, охота, недосуг, пора и др.) входит в эту группу слов.»
Вы поняли, о чем это? Я нет! Для кого это написано? Наверное, для учеников. Бедные ученики! Если даже ученые до сих пор чего-то там не поняли, то как это должны понимать дети? Интересно, учителя, хотя бы, выучили наизусть такое определение?
Вот для этого я и создала свой канал на YouTube, чтобы просто (человеческим языком) рассказать о главном – о языке.
Если по прочтению, вам все это (написанное, кстати наспех), покажется бредом, не спешите сообщать мне о том, что я ненормальная. Я ведь и назвала это записками и сумасшедшего дома. Если вам это кажется ненормальным, значит вы живете в доме – напротив. Я его определять не собираюсь. Живем в стране победившей демократии и … ценностей. Каждый имеет право на свое мнение.

Изучение числа Пи начинается в начальных классах, когда школьники изучают круг, окружность и встречается значение Пи. Так как значение Пи — это константа означающая отношение длины самой окружности к длине диаметра данной окружности. К примеру если мы возьмем окружность диаметр которой будет равен одному, тогда ее длина равняется числу Пи . Данное значение Пи — бесконечно в математическом продолжении, но так же есть общепринятое обозначение. Взялось оно от упрощенного написания значения Пи, выглядит оно как 3,14.

Историческое рождение числа Пи

Корни свои число Пи предположительно получило в Древнем Египте. Так как древнеегипетские ученые вычисляли с помощью диаметра D площадь у круга, которое принимало значение D — D/92. Что соответствовало 16/92, либо 256/81, а значит число Пи равно 3,160.
Индия в шестом веке до нашей эры, тоже коснулась числа Пи, в религии Джайнизма, были найдены записи в которых говорилось о том что число Пи равно 10 в квадратном корне, а значит 3,162.

Учение Архимеда об измерении круга в третьем веке до нашей эры привели его к следующим выводам:

Уже позже свои выводы он обосновывал последовательностью вычислений на примерах правильно вписанных либо описанных многоугольных форм с удвоением числа сторон данных фигур. В точных расчетах Архимед заключил соотношение диаметра и окружности в числах между 3*10/71 и 3*1/7, следовательно значение Пи равно 3,1419… Так как мы уже говорили о бесконечной форме данного значения, выглядит оно как 3,1415927… И это еще не предел, потому что математик Каши в пятнадцатом веке рассчитал значение Пи уже как шестнадцати-значную величину.

Математик Англии Джонсон У. в 1706 году, начал использовать обозначение числа Пи символом? (с греческого есть первая буква в слове окружности).

Загадочное значение.

Значение Пи иррациональное, его не удается выражать в форме дроби, потому как в дроби применяются целые значения. Корнем в уравнении оно быть не может из-за чего оно так же получается трансцендентным, находится с помощью рассмотрения любых процессов, уточняясь за счет большого количества рассматриваемых шагов данного процесса. Было очень много попыток рассчитать наибольшее количество знаков в числе Пи, которые привели к десяткам триллионов цифр данного значения от запятой.

Интересный факт: У значения Пи как это ни странно есть свой праздник. Называется он международный день числа Пи. Отмечают его 14 марта. Дата появилась благодаря самому значению Пи 3,14 (мм.гг) и физику Шоу Ларри который и начал первым отмечать этот праздник уже в 1987 году.

Заметка: Юридическая помощь в получении справки об отсутствии (наличии) судимости для всех граждан РФ. Перейдите по ссылке госуслуги справка об отсутствии судимости (http://справкаосудимости.рф/) законно, быстро и без очередей!

Если сравнить окружности отличных друг от друга размеров, то можно заметить следующее: размеры разных окружностей пропорциональны. А это значит, что при увеличении диаметра окружности в некоторое количество раз, увеличивается и длина этой окружности в такое же количество раз. Математически это записать можно так:

C 1		C 2
	=
d 1		d 2	(1)

где C1 и С2 – длины двух разных окружностей, а d1 и d2 – их диаметры.
Это соотношение работает при наличии коэффициента пропорциональности – уже знакомой нам константы π . Из отношения (1) можно сделать вывод: длина окружности C равна произведению диаметра этой окружности на независящий от окружности коэффициент пропорциональности π :

C = π d.

Также эту формулу можно записать в ином виде, выразив диаметр d через радиус R данной окружности:

С = 2π R.

Как раз эта формула и является проводником в мир окружностей для семиклассников.

Еще с древности люди пытались установить значение этой константы. Так, например, жители Месопотамии вычисляли площадь круга по формуле:

Откуда π = 3.

В древнем Египте значение для π было точнее. В 2000-1700 годах до нашей эры писец, именуемый Ахмесом, составил папирус, в котором мы находим рецепты разрешения различных практических задач. Так, например, для нахождения площади круга он использует формулу:

			8			2
S	=	(		d	)
			9

Из каких соображений он получил эту формулу? – Неизвестно. Вероятно, на основе своих наблюдений, впрочем, как это делали и другие древние философы.

По стопам Архимеда

Какое из двух числе больше 22/7 или 3.14 ?
— Они равны.
— Почему?
— Каждое из них равно π .
А. А. Власов. Из Экзаменационного билета.

Некоторы полагают, что дробь 22/7 и чисо π тождественно равны. Но это является заблуждением. Помимо вышеприведенного неверного ответа на экзамене (см. эпиграф) к этой группе можно также добавить одну весьма занимательную головоломку. Задание гласит: «переложите одну спичку так, чтобы равенство стало верным».

Решение будет таковым: нужно образовать «крышу» для двух вертикальных спичек слева, используя одну из вертикальных спичек в знаменателе справа. Получится визуальное изображение буквы π .

Многие знают, что приближение π = 22/7 определил древнегреческий математик Архимед. В честь этого часто такое приближение называют «Архимедовым» числом. Архимеду удалось не только установить приближенное значение для π, но также найти точность этого приближения, а именно – найти узкий числовой промежуток, которому принадлежит значение π . В одной из своих работ Архимед доказывает цепь неравенств, которая на современный лад выглядела бы так:

	10		6336					14688				1
3						π					3
	71			1					1			7
			2017					4673
				4					2

можно записать проще: 3,140 909

Как видим из неравенств, Архимед нашел довольно-таки точное значение с точностью до 0,002.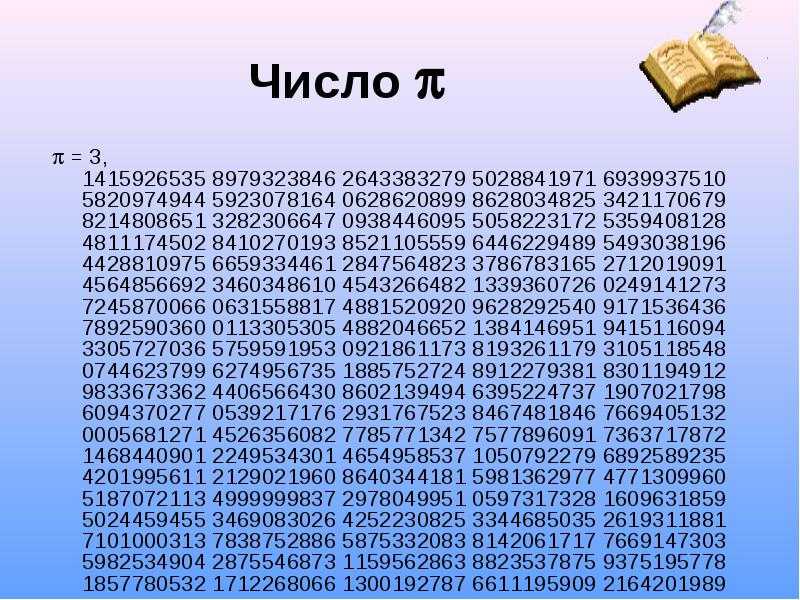 Самое удивительно то, что он нашел два первых знака после запятой: 3,14… Именно такое значение чаще всего мы используем в несложных расчетах.

Практическое применение

Едут двое в поезде:
− Вот смотри, рельсы прямые, колеса круглые.
Откуда же стук?
− Как откуда? Колеса-то круглые, а площадь
круга пи эр квадрат, вот квадрат-то и стучит!

Как правило, знакомятся с этим удивительным числом в 6-7 классе, но более основательно им занимаются к концу 8-го класса. В этой части статьи мы приведем основные и самые важные формулы, которые пригодятся вам в решении геометрических задач, только для начала условимся принимать π за 3,14 для удобства подсчета.

Пожалуй, самая известная формула среди школьников, в которой используется π , это – формула длины и площади окружности. Первая – формула площади круга – записывается так:

	π D 2
S=π R 2 =
	4

где S – площадь окружности, R – ее радиус, D – диаметр окружности.

Длина окружности, или, как ее иногда называют, периметр окружности, вычисляют по формуле:

С = 2 π R = π d,

где C – длина окружности, R – радиус, d – диаметр окружности.

Понятно, что диаметр d равен двум радиусам R.

Из формулы длины окружности можно легко найти радиус окружности:

где D – диаметр, С – длина окружности, R – радиус окружности.

Это базовые формулы, знать которые должен каждый ученик. Также иногда приходится вычислять площадь не всей окружности, а только ее части – сектора. Поэтому представляем вам её – формулу для вычисления площади сектора окружности. Выглядит она так:

			α
S	=	π R 2
			360 ˚

где S – площадь сектора, R – радиус окружности, α – центральный угол в градусах.

Такое загадочное 3,14

И правда, оно загадочно. Потому что в честь этих магических цифр устраивают праздники, снимают фильмы, проводят общественные акции, пишут стихи и многое другое.

Например, в 1998 году вышел фильм американского режиссера Даррена Аронофски под названием «Пи». Фильм получил множество наград.

Каждый год 14 марта в 1:59:26 люди, интересующиеся математикой, празднуют «День числа Пи». К празднику люди подготавливают круглый торт, усаживаются за круглый стол и обсуждают число Пи, решают задачи и головоломки, связанные с Пи.

Вниманием это удивительное число не обошли и поэты, неизвестный написал:
Надо только постараться и запомнить всё как есть – три, четырнадцать, пятнадцать, девяносто два и шесть.

Давайте развлечемся!

Вашему вниманию предлагаются интересные ребусы с числом Пи. Разгадайте слова, какие зашифрованы ниже.

1. π р

2. π L

3. π k

Ответы: 1.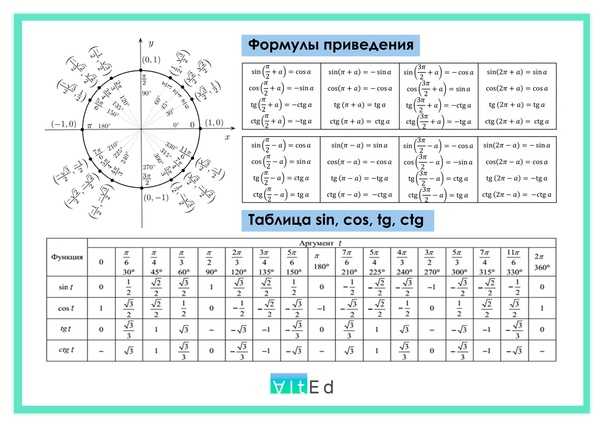 Пир; 2. Надпил; 3. Писк.

), а общепринятым оно стало после работ Эйлера . Это обозначение происходит от начальной буквы греческих слов περιφέρεια — окружность, периферия и περίμετρος — периметр.

Оценки

• 510 знаков после запятой: π ≈ 3,141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 820 974 944 592 307 816 406 286 208 998 628 034 825 342 117 067 982 148 086 513 282 306 647 093 844 609 550 582 231 725 359 408 128 481 117 450 284 102 701 938 521 105 559 644 622 948 954 930 381 964 428 810 975 665 933 446 128 475 648 233 786 783 165 271 201 909 145 648 566 923 460 348 610 454 326 648 213 393 607 260 249 141 273 724 587 006 606 315 588 174 881 520 920 962 829 254 091 715 364 367 892 590 360 011 330 530 548 820 466 521 384 146 951 941 511 609 433 057 270 365 759 591 953 092 186 117 381 932 611 793 105 118 548 074 462 379 962 749 567 351 885 752 724 891 227 938 183 011 949 129 833 673 362…

Свойства

Соотношения

Известно много формул с числом π :

• Формула Валлиса:

• Тождество Эйлера :

• Т. н. «интеграл Пуассона » или «интеграл Гаусса »

Трансцендентность и иррациональность

Нерешенные проблемы

• Неизвестно, являются ли числа π и e алгебраически независимыми.
• Неизвестно, являются ли числа π + e , π − e , πe , π / e , π e , π π , e e трансцендентными.
• До сих пор ничего не известно о нормальности числа π ; неизвестно даже, какие из цифр 0-9 встречаются в десятичном представлении числа π бесконечное количество раз.

История вычисления

и Чудновского

Мнемонические правила

Чтобы нам не ошибаться, Надо правильно прочесть: Три, четырнадцать, пятнадцать, Девяносто два и шесть. Надо только постараться И запомнить всё как есть: Три, четырнадцать, пятнадцать, Девяносто два и шесть. Три, четырнадцать, пятнадцать, Девять, два, шесть, пять, три, пять. Чтоб наукой заниматься, Это каждый должен знать. Можно просто постараться И почаще повторять: «Три, четырнадцать, пятнадцать, Девять, двадцать шесть и пять. »

2. Подсчитайте количество букв в каждом слове в нижеприведенных фразах (без учета знаков препинания ) и запишите эти цифры подряд — не забывая про десятичную запятую после первой цифры «3», разумеется. Получится приближенное число Пи.

Это я знаю и помню прекрасно: Пи многие знаки мне лишни, напрасны.

Кто и шутя, и скоро пожелаетъ Пи узнать число — ужъ знаетъ!

Вот и Миша и Анюта прибежали Пи узнать число они желали.

(Вторая мнемоническая запись верна (с округлением последнего разряда) только при использовании дореформенной орфографии : при подсчете количества букв в словах необходимо учитывать твердые знаки!)

Еще один вариант этой мнемонической записи:

Это я знаю и помню прекрасно:
Пи многие знаки мне лишни, напрасны.
Доверимся знаньям громадным
Тех, пи кто сосчитал, цифр армаду.

Раз у Коли и Арины Распороли мы перины. Белый пух летал, кружился, Куражился, замирал, Ублажился, Нам же дал Головную боль старух. Ух, опасен пуха дух!

Если соблюдать стихотворный размер, можно довольно быстро запомнить:

Три, четырнадцать, пятнадцать, девять два, шесть пять, три пять
Восемь девять, семь и девять, три два, три восемь, сорок шесть
Два шесть четыре, три три восемь, три два семь девять, пять ноль два
Восемь восемь и четыре, девятнадцать, семь, один

Забавные факты

Примечания

Смотреть что такое «Число пи» в других словарях:

Сущ., с., употр. очень часто Морфология: (нет) чего? числа, чему? числу, (вижу) что? число, чем? числом, о чём? о числе; мн. что? числа, (нет) чего? чисел, чему? числам, (вижу) что? числа, чем? числами, о чём? о числах математика 1. Числом… … Толковый словарь Дмитриева

ЧИСЛО, числа, мн. числа, чисел, числам, ср. 1. Понятие, служащее выражением количества, то, при помощи чего производится счет предметов и явлений (мат.). Целое число. Дробное число. Именованное число. Простое число. (см. простой1 в 1 знач.).… … Толковый словарь Ушакова

Абстрактное, лишенное особенного содержания обозначение какоголибо члена некоторого ряда, в котором этому члену предшествует или следует за ним какой нибудь др. определенный член; абстрактный индивидуальный признак, отличающий одно множество от… … Философская энциклопедия

Число, приближенно равное 2,718, которое часто встречается в математике и естественных науках. Например, при распаде радиоактивного вещества по истечении времени t от исходного количества вещества остается доля, равная e kt, где k число,… … Энциклопедия Кольера

А; мн. числа, сел, слам; ср. 1. Единица счёта, выражающая то или иное количество. Дробное, целое, простое ч. Чётное, нечётное ч. Считать круглыми числами (приблизительно, считая целыми единицами или десятками). Натуральное ч. (целое положительное … Энциклопедический словарь

Ср. количество, счетом, на вопрос: сколько? и самый знак, выражающий количество, цифра. Без числа; нет числа, без счету, многое множество. Поставь приборы, по числу гостей. Числа римские, арабские или церковные. Целое число, ·противоп. дробь.… … Толковый словарь Даля

ЧИСЛО, а, мн. числа, сел, слам, ср. 1. Основное понятие математики величина, при помощи к рой производится счёт. Целое ч. Дробное ч. Действительное ч. Комплексное ч. Натуральное ч. (целое положительное число). Простое ч. (натуральное число, не… … Толковый словарь Ожегова

ЧИСЛО «Е» (ЕХР), иррациональное число, служащее основанием натуральных ЛОГАРИФМОВ. Это действительное десятичное число, бесконечная дробь, равная 2,7182818284590…., является пределом выражения (1/) при п, стремящемся к бесконечности. По сути,… … Научно-технический энциклопедический словарь

Количество, наличность, состав, численность, контингент, сумма, цифра; день.. Ср. . См. день, количество. небольшое число, несть числа, расти числом… Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские… … Словарь синонимов

Уже много веков и даже, как ни странно, тысячелетий люди понимают важность и ценность для науки математической постоянной, равной отношению длины окружности к ее же диаметру. число Пи, до сих пор неизвестно, но к нему имели отношение самые лучшие математики на протяжении всей нашей истории. Большинство из них хотели выразить его рациональным числом.

1. Исследователи и истинные поклонники числа Пи организовали клуб, для вступления в который требуется знать наизусть достаточно большое количество его знаков.

2. С 1988 года празднуется «День числа Пи», который приходится на 14 марта. Готовят салаты, торты, печенья, пирожные с его изображением.

3. Число Пи уже переложили на музыку, при этом оно весьма неплохо звучит. Ему даже воздвигли памятник в американском Сиэтле перед зданием городского Музея искусств.

В то далекое время число Пи старались вычислить при помощи геометрии. То, что это число постоянно для самых разных окружностей, знали еще геометры в Древнем Египте, Вавилоне, Индии и Древней Греции, утверждавшие в своих работах, что оно всего лишь немного больше трех.

В одной из священных книг джайнизма (древняя индийская религия, которая возникла в VI в.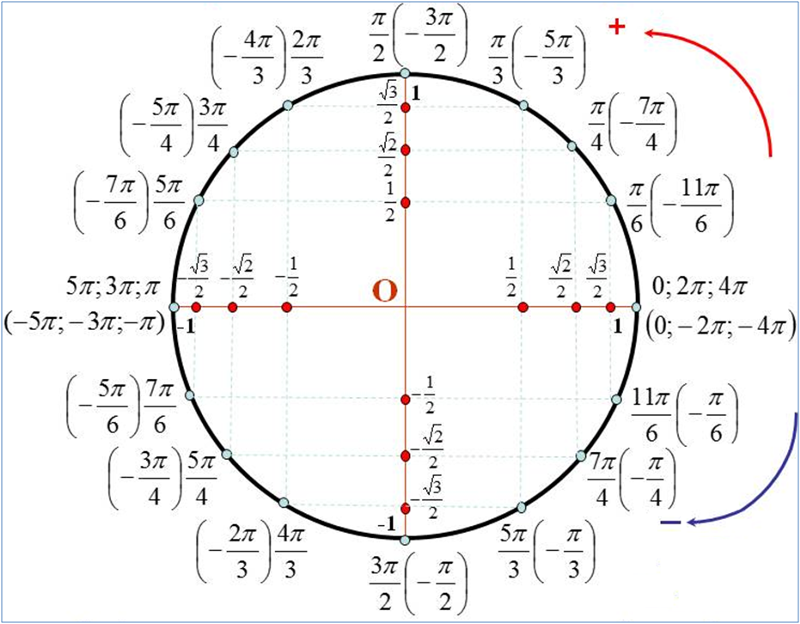 до н. э.) упоминается, что тогда число Пи считалось равным корню квадратному из десяти, что в итоге дает 3,162… .

Древнегреческие математики проводили измерение окружности методом построения отрезка, а вот для того, чтобы измерить круг, им приходилось строить равновеликий квадрат, то есть фигуру, равную ему по площади.

Когда еще не знали десятичных дробей, великий Архимед нашел значение числа Пи с точностью 99,9%. Он открыл способ, который стал основой многих последующих вычислений, вписывал в окружность и описывал вокруг нее правильные многоугольники. В результате Архимед рассчитал значение числа Пи как отношение 22 / 7 ≈ 3,142857142857143.

В Китае, математик и придворный астроном, Цзу Чунчжи в V веке до н. э. обозначил более точное значение числа Пи, рассчитав его до семи цифр после запятой и определил его значение между числами 3, 1415926 и 3,1415927. Более 900 лет понадобилось ученым, чтобы продолжить дальше этот цифровой ряд.

Средние века

Известный индийский ученый Мадхава, который жил на рубеже XIV — XV веков, ставший основателем Керальской школы астрономии и математики, впервые в истории стал работать над разложением тригонометрических функций в ряды.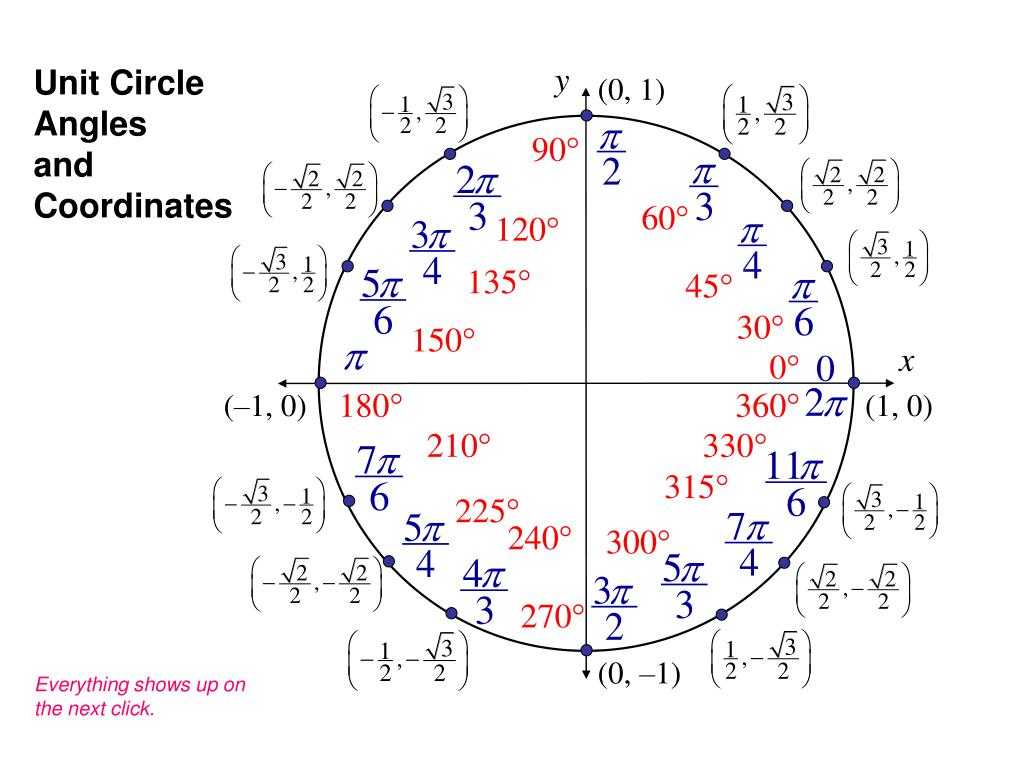 Правда, сохранились всего лишь два его труда, а на другие известны лишь ссылки и цитаты его учеников. В научном трактате «Махаджьянаяна», который приписывают Мадхаве, указано, что число Пи равно 3,14159265359. А в трактате «Садратнамала» приведено число с еще большим количеством точных знаков после запятой: 3,14159265358979324. В указанных числах последние цифры не соответствуют правильному значению.

В XV веке самаркандский математик и астроном Ал-Каши вычислил число Пи с шестнадцатью знаками после запятой. Его результат считался наиболее точным в течение последующих 250 лет.

У. Джонсон, математик из Англии, одним из первых смог обозначить отношение длины окружности к ее диаметру буквой π. Пи — это первая буква греческого слова «περιφέρεια» — окружность. Но этому обозначению удалось стать общепринятым лишь после того, как им воспользовался в 1736 году более известный ученый Л. Эйлер.

Заключение

Современные ученые продолжают работать над дальнейшими вычислениями значений числа Пи.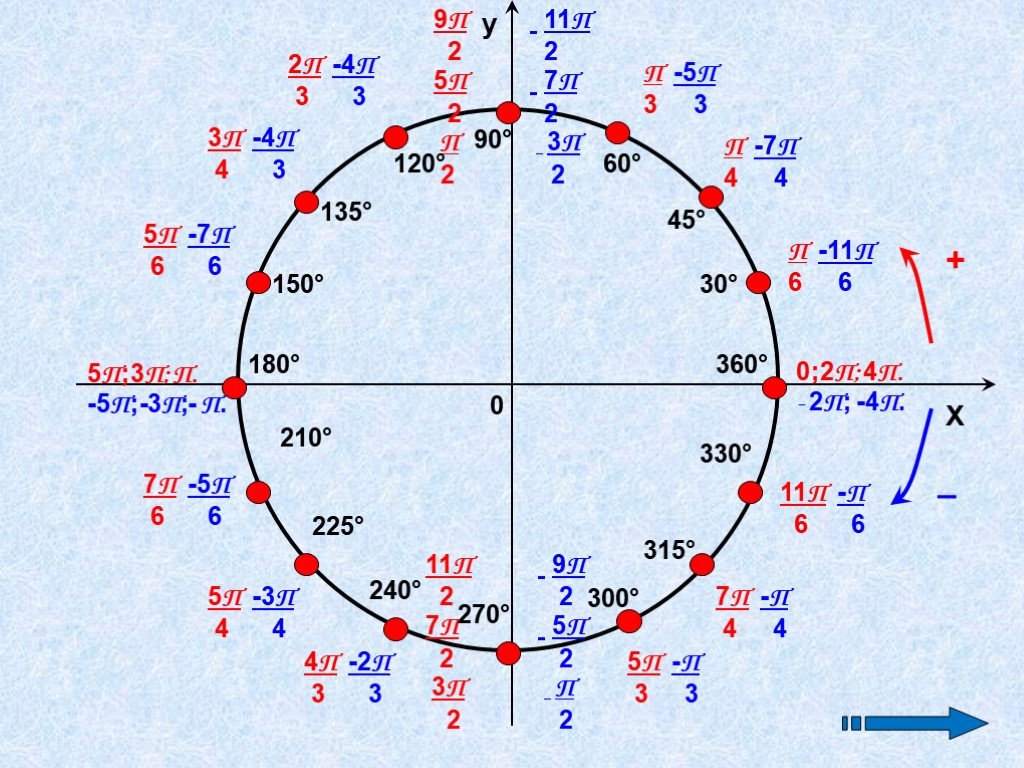 Для этого уже используют суперкомпьютеры. В 2011 г. ученый из Сигэру Кондо, сотрудничая с американским студентом Александром Йи, произвели правильный расчет последовательности из 10 триллионов цифр. Но до сих пор так и неясно, кто открыл число Пи, кто впервые задумался над этой проблемой и произвел первые расчеты этого, по-настоящему мистического числа.

Изменить 20 градусов на радианы в пи

Исчисление

Джессика Г.

спросил 25.08.15

Помогите пожалуйста

Подписаться І 4

Подробнее

Отчет

3 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Джеральд С. ответил 25.08.15

Репетитор

4,8 (60)

Терпение + Навыки сдачи тестов + Структура = Успех

См.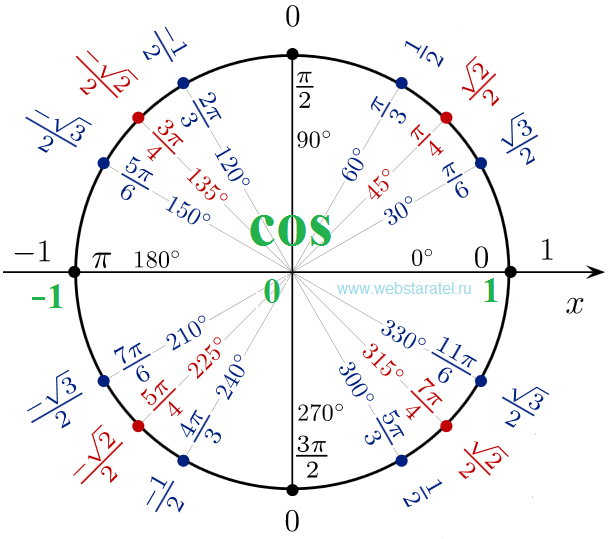 таких репетиторов

Смотрите таких репетиторов

Если 2pi равняется 360 градусам, что также равно 1 полному кругу, то 20 градусов будут 1/18 полного круга. Таким образом, если один полный круг равен 2pi, то 20 градусов будут просто 1/18 от 2pi, что равно (1/9)пи или (пи/9). Версия TLDR:

 

1. Градусы в радианы = градусы x (pi / 360 градусов)

2. Радианы в градусы = радианы x (360 градусов / pi)

 

Я чувствую, что понимание математики важнее, чем грубая сила запоминания уравнения. Это упрощает математику.

 

 

 

Голосовать за 0 голос против

Еще

Отчет

Джордан К. ответил 25.08.15

Репетитор

4.9 (79)

Национальный сертифицированный учитель математики (с 6 по 12 классы)

См. таких репетиторов

Смотрите таких репетиторов

Привет Джессика,

 

Один градус = пи / 180 радиан.

 

Таким образом, 20 градусов = 20 х пи / 180 = пи / 9 радиан.

 

Спасибо за вопрос и рады быть полезными.

 

Благослови Господь, Иордания.

Голосовать за 0 голос против

Подробнее

Отчет

Шрадха С. ответил 25.08.15

Репетитор

4 (1)

Опытный учитель математики со степенью магистра математики

См. таких репетиторов

Смотрите таких репетиторов

180 градусов = ∏

1 градус = ∏/180

20 градусов = (∏/180)*20

= 20 ∏/180

= ∏/

Голосовать за 0 голос против

Подробнее

Отчет

Все еще ищете помощи? Получите правильный ответ, быстро.

Задайте вопрос бесплатно

Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.

ИЛИ

Найдите онлайн-репетитора сейчас

Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.

Купить модуль камеры Raspberry Pi 3 — Raspberry Pi

Классическая компактная камера для Raspberry Pi с 12-мегапиксельным сенсором и автофокусом

Доступна по цене от 25 долларов США с выбором стандартных и широкоугольных объективов, с инфракрасным фильтром или без него

Технические характеристикиКупить сейчас

Качество (натюрморта) жизни

Модуль камеры 3 поставляется с улучшенным 12-мегапиксельным датчиком IMX708 Quad Bayer и имеет режим расширенного динамического диапазона, что делает его самым качественным модулем камеры, который мы когда-либо создавали.

Сосредоточьтесь на хорошем

Модуль камеры 3 в стандартной комплектации оснащен сверхбыстрой автоматической фокусировкой. Богатая библиотека программных команд означает, что вы можете полностью контролировать то, на чем вы сосредоточены и как вы это делаете.

Посмотрите с другой точки зрения

Нужно более широкое поле зрения, чем стандартные 75 градусов? Модуль камеры 3 Wide имеет сверхширокий угол обзора 120 градусов, что означает, что ваш Raspberry Pi может видеть больше мира.

Взгляните на вещи по-другому

Как стандартная, так и широкоугольная камеры поставляются с опцией отсутствия ИК-фильтра, что превращает модуль камеры 3 в камеру ночного видения при использовании с инфракрасным освещением.

Не только для фотографий

Модуль камеры 3 может записывать видео в формате Full HD со скоростью 50 кадров в секунду, причем более высокая частота кадров доступна при более низком разрешении. Благодаря режиму HDR и автофокусу он не только обеспечивает отличное качество фотографий, но также является фантастическим инструментом для записи видео и потоковой передачи. Посмотрите наше видео, полностью снятое на модуль камеры 3, чтобы увидеть его в действии.

Для разработчиков

Модуль камеры 3 использует систему камер с открытым исходным кодом Raspberry Pi на базе libcamera. Этот богатый набор библиотек дает разработчикам точный контроль над обработкой изображений и лучший доступ к внутренним компонентам Camera Module 3.

Узнайте больше о libcamera

Для начинающих

Последняя версия Raspberry Pi OS поставляется с предустановленной бета-версией Picamera2, библиотеки Python, разработанной здесь, в Raspberry Pi в Кембридже. Как для начинающих, так и для продвинутых пользователей, Picamera2 идеально подходит для всего, от домашних проектов до приложений машинного обучения.

Узнайте больше о Picamera2

Документация

Разработчики и пользователи могут найти всю необходимую информацию о модуле камеры 3 в нашей обширной и подробной документации.

Документация модуля камеры 3

Снимок модуля камеры 3

Спецификация

Многослойная 12-мегапиксельная CMOS-матрица Sony IMX708 с задней подсветкой

Высокое отношение сигнал/шум (SNR)

2 Встроенный динамический

2 Встроенный Коррекция дефектных пикселей (DPC)

Фазовый автофокус (PDAF) для быстрой автофокусировки

Функция QBC Re-mosaic

Режим HDR (выход до 3 мегапикселей)

Последовательный вывод данных CSI-2

2-проводная последовательная связь (поддерживает быстрый режим I2C и быстрый режим плюс)

2-проводное последовательное управление механизмом фокусировки

Разрешение: 11,9 мегапикселя

Размер сенсора: диагональ сенсора 7,4 мм

Размер пикселя: 1,4 мкм × 1,4 мкм угол обзора: 75 градусов (модуль камеры 3, модуль камеры 3 NoIR), 120 градусов (модуль камеры 3 широкоугольный, модуль камеры 3 широкоугольный NoIR)

Общие видеорежимы: 1080p50, 720p100, 480p120 : Встроен в стандартные варианты; отсутствует в вариантах NoIR

Размеры: 25 × 24 × 11,5 мм (высота 12,4 мм для вариантов Wide)

Длина ленточного кабеля: 200 мм

Кабельный разъем: 15 × 1 мм FPC

Документы

Совместимость кабелей для всех моделей Raspberry Pi

кабель камеры Raspberry Pi Zero для подключения к модулю камеры Raspberry Pi; стандартный кабель, поставляемый с камерой, не совместим с меньшим разъемом камеры Raspberry Pi Zero.