Отношение площадей подобных треугольников / Подобные треугольники / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Подобные треугольники
- Отношение площадей подобных треугольников
Теорема
| Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. |
Доказательство
Дано: АВСА1В1С1, — коэффициент подобия, и — площади АВС и А1В1С1.
Доказать: .
Доказательство:
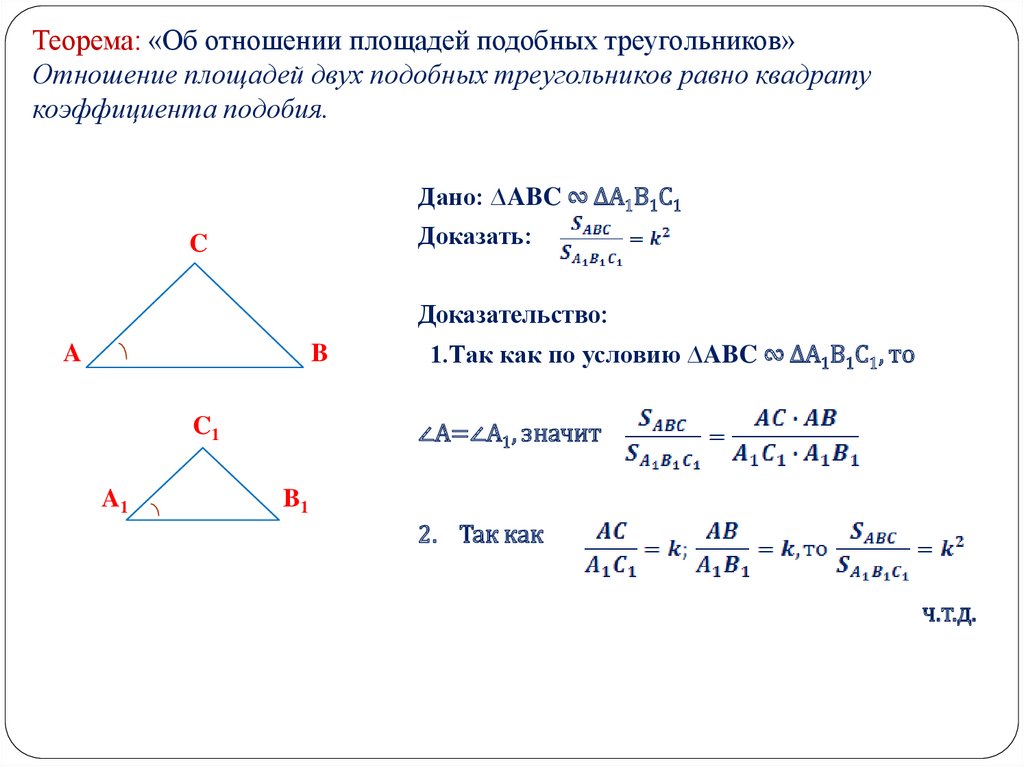
1. АВСА1В1С1, следовательно, А =А1, значит, (т. к. площади треугольников, имеющих по равному углу, относятся как
к. площади треугольников, имеющих по равному углу, относятся как
Теорема доказана.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Пропорциональные отрезки
Определение подобных треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Средняя линия треугольника
Пропорциональные отрезки в прямоугольном треугольнике
Практические приложения подобия треугольников
О подобии произвольных фигур
Синус, косинус и тангенс острого угла прямоугольного треугольника
Значение синуса, косинуса и тангенса для углов 30, 45 и 60
Подобные треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 543, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 544, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 545, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 546, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 622, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 627, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1077, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1143, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1209*, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1308, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Отношение ⭐ площадей подобных треугольников: теорема и доказательство
Понятие подобия треугольников
ОпределениеДва треугольника называются подобными, если их углы попарно равны, а стороны, лежащие напротив соответственных углов пропорциональны.
AB/KL=BC/LM=AC/KM=k, ∠A=∠K, ∠B=∠L, ∠C=∠M ⇒ΔABC~ΔKLM.
Отношение длин подобных треугольников называют коэффициентом подобия (k).
Также пропорциональные стороны подобных треугольников могут быть названы сходственными сторонами.
В подобных треугольниках, кроме сторон, подобны и другие величины: биссектрисы, медианы, высоты и т.д.
Теорема об отношении площадей подобных треугольников
ТеоремаФормулировка теоремы: отношение площадей подобных треугольников равно квадрату коэффициента подобия.
В геометрии существует три признака подобия треугольников:
1. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
3. Если три стороны одного треугольника пропорциональны двум сторонам другого треугольника, то такие треугольники подобны.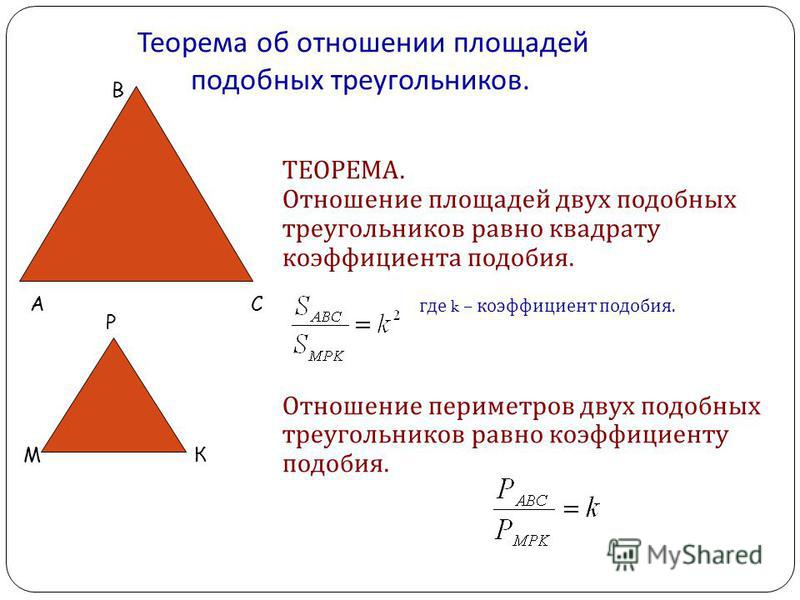
Свойства подобных треугольников:
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
- Отношение периметров подобных треугольников равно коэффициенту подобия.
- Отношение длин соответствующих элементов подобных элементов равно коэффициенту подобия.
Доказательство теоремы
Докажем теорему об отношении площадей подобных треугольников.
Теорема: отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Доказательство: изобразим подобные треугольники ΔABC~ΔKLM.
Из подобия треугольников по определению следует: AB/KL=BC/LM=AC/KM=k.
Воспользуемся следующей теоремой: если у двух треугольников равны углы (∠A=∠K), то их площади относятся, как произведение сторон, заключающих данные углы. Запишем в виде формулы:
Что и требовалось доказать.
Примеры решения задач
Пример 1Площади подобных треугольников ΔABC и ΔA1B1C1 равны соответственно 200 см² и 50 см². Сторона A1B1=5 см.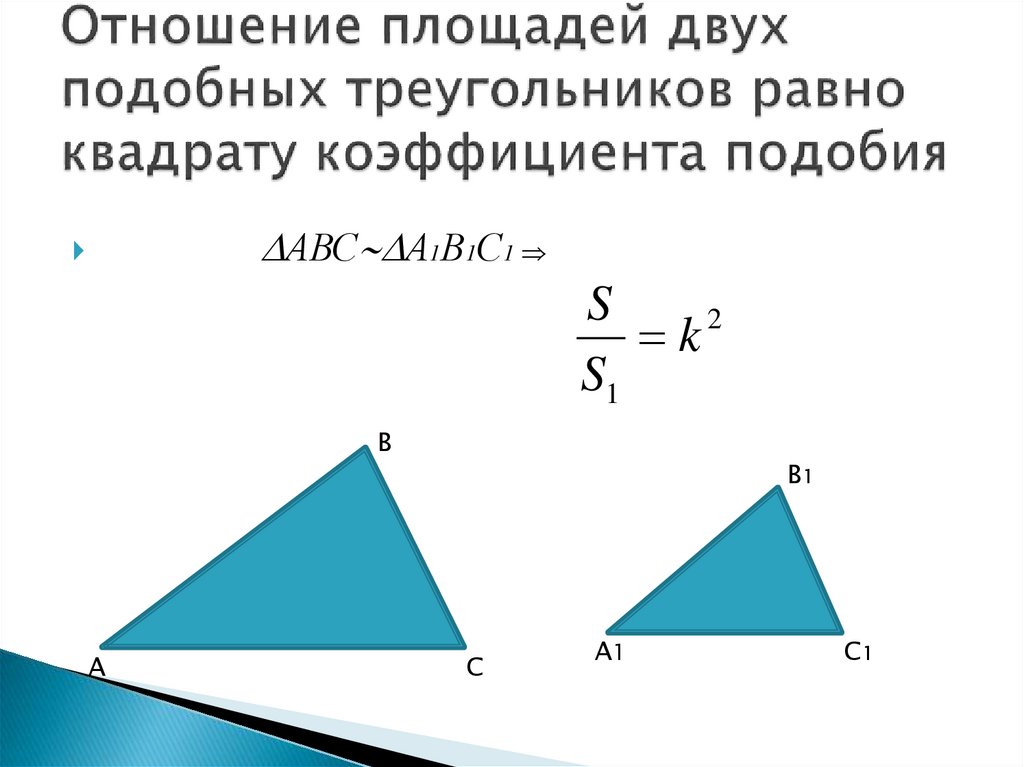 Найдите сходственную ей сторону AB треугольника ABC.
Найдите сходственную ей сторону AB треугольника ABC.
Решение:
По теореме об отношении площадей подобных треугольников: Sabc/Sa1b1c1=k² ⇒ 200/50=k² ⇒ k=2.
AB/A1B1=2, AB=A1B1*2, AB=5*2=10 см.
Ответ: 10 см.
Пример 2ΔABC и ΔA1B1C1 — подобны. Сходственные стороны AC и A1C1 соответственно равны 13 см и 0,1 м.
Найдите отношение периметров ΔABC и ΔA1B1C1.
Решение:
A1C1=0,1 м=10 см
AC/A1C1=13/10=1,3 ⇒ Pabc/Pa1b1c1=1,3
Ответ: 1,3
Задача для самостоятельной работы
Пример 3Треугольники ΔABC~ΔKLM подобны. Площадь ΔABC равна 500 см², площадь ΔKLM равна 125 см². Сторона AC равна 18 см, найти сходственную ей сторону KM.
Проверьте, насколько верный или неверный ваш ответ.
Ответ: 9 см.
Советуем составить краткий конспект для подготовки к уроку.
Отношение площадей двух подобных треугольников равно квадрату отношения их соответствующих сторон.
Последняя обновленная дата: 01 -й января 2023
•
Общее представление: 250,2K
•
Просмотр сегодня: 25,00K
Ответ
Проверено
250,2K+ Просмот рассчитает площадь двух подобных треугольников, а затем разделит их.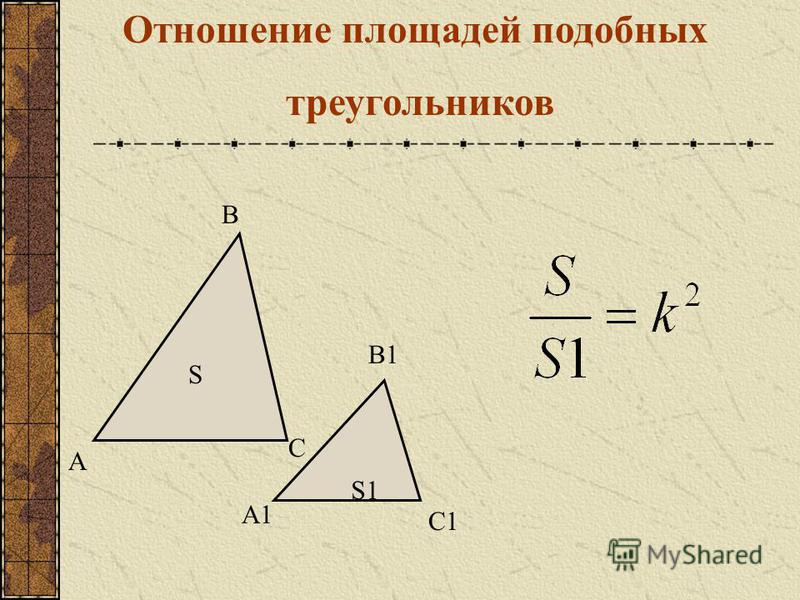 Затем по подобию двух треугольников находят отношения соответствующих сторон.
Затем по подобию двух треугольников находят отношения соответствующих сторон.
Полное пошаговое решение:
Предположим, что есть два треугольника: \[\Delta {\text{PQR}}\] и \[\Delta {\text{ABC}}\].
Мы будем использовать формулу, чтобы найти площадь треугольника, \[{\text{Площадь = }}\dfrac{1}{2} \times {\text{Base}} \times {\text{Высота}} \].
Теперь найдем площади треугольников \[\Delta {\text{ABC}}\] и \[\Delta {\text{PQR}}\] по приведенной выше диаграмме.
\[{\text{Площадь}}\Delta {\text{PQR}} = \dfrac{1}{2} \times {\text{QR}} \times {\text{PS ….. .}}\влево( 1 \вправо)\]
\[{\text{Площадь}}\Delta {\text{ABC}} = \dfrac{1}{2} \times {\text{BC}} \times {\text{AD ….. .}}\left( 2 \right)\]
Разделив \[\left( 1 \right)\] на \[\left( 2 \right)\], получим
\[
\dfrac{{{\ text{Площадь }}\Delta {\text{PQR}}}}{{{\text{Площадь }}\Delta {\text{ABC}}}} = \dfrac{{\dfrac{1}{2 } \times {\text{QR}} \times {\text{PS}}}}{{\dfrac{1}{2} \times {\text{BC}} \times {\text{AD}}} } \\
= \dfrac{{{\text{QR}} \times {\text{PS}}}}{{{\text{BC}} \times {\text{AD}}}}{\text { .
\]
Поскольку мы знаем, что \[\angle {\text{ABC}}\] и \[\angle {\text{PQR}}\] являются углами подобных треугольников, поэтому \[\angle {\text{ ABC}} = \angle {\text{PQR}}\] и оба прямоугольных треугольника \[\angle {\text{ADB}}\] и \[\angle {\text{PSQ}}\] равны.
Следовательно, \[\Delta {\text{PQS}} \sim \Delta {\text{ABD}}\].
\[ \Rightarrow \dfrac{{{\text{PS}}}}{{{\text{AD}}}} = \dfrac{{{\text{PQ}}}}{{{\text{AB }}}}{\text{ ……}}\left( 4 \right)\]
Подставляя это значение в уравнение \[\left( 3 \right)\], получаем
\[\dfrac{{{\text{Площадь}}\Delta {\text{PQR}}}}{{{\text{Площадь}}\Delta {\text{ABC}}}} = \dfrac {{{\text{QR}}}}{{{\text{BC}}}} \times \dfrac{{{\text{PQ}}}}{{{\text{AB}}}}{\ text{ ……}}\left( 5 \right)\]
Так как мы знаем, что треугольники \[\Delta {\text{PQR}}\] и \[\Delta {\text{ABC} }\] подобны,
\[\dfrac{{{\text{PQ}}}}{{{\text{AB}}}} = \dfrac{{{\text{QR}}}}{{{ \text{BC}}}} = \dfrac{{{\text{PR}}}}{{{\text{AC}}}}\]
Использование этого значения в уравнении \[\left( 5 \right) \], получаем 92} \\
\]
Таким образом, отношение площадей двух подобных треугольников равно квадрату отношения их соответствующих сторон.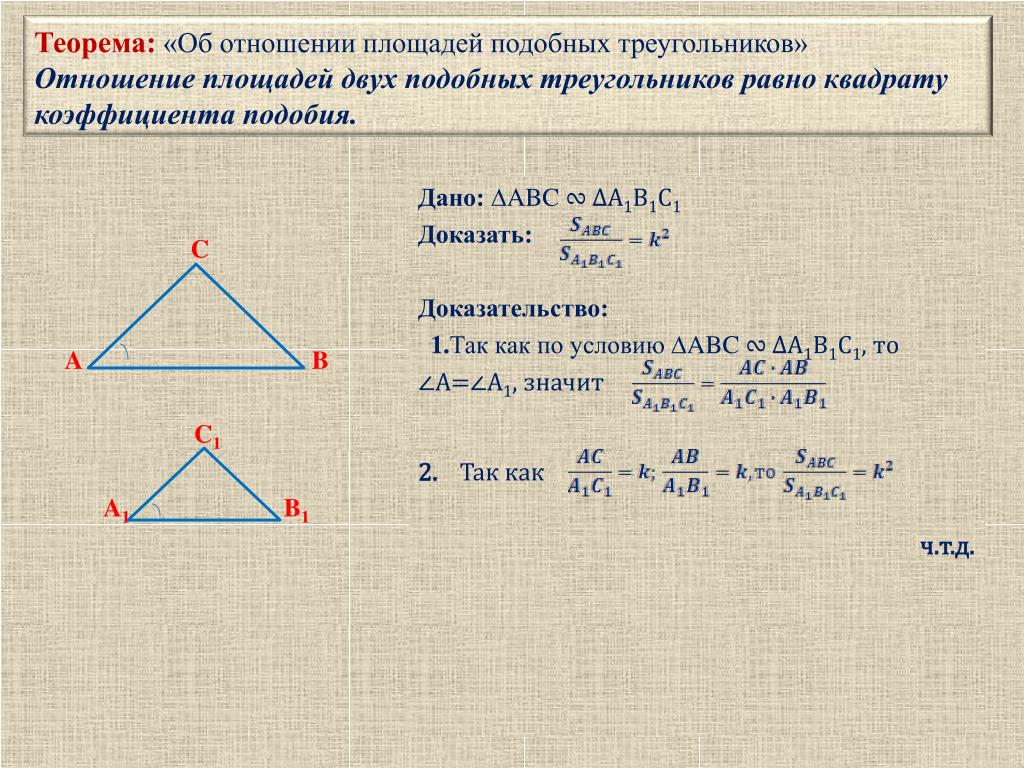
Значит, доказано.
Примечание:
В этом вопросе учащиеся должны правильно написать стороны треугольников. Поскольку общая площадь любого треугольника равна \[{\text{Area = }}\dfrac{1}{2} \times {\text{Base}} \times {\text{Height}}\], нам нужно построить перпендикулярные треугольники для высоты. Студенты должны знать, что когда два треугольника подобны, то отношение их соответствующих сторон совпадает с отношением их соответствующих высот и сторон. Измерение их соответствующих углов также одинаково.
Недавно обновленные страницы
Если пружина имеет период T и разрезана на n равных 11 класс физики CBSE
Планета движется вокруг Солнца по почти круговой орбите 11 класс физики CBSE
В любом треугольнике AB2 BC4 CA3 и D является средней точкой математики класса 11 JEE_Main
В Delta ABC 2asin dfracAB+C2 равно IIT Математика класса 11 JEE_Main
0002 Если в треугольнике rmABC сторона a sqrt 3 + 1rmcm и угол класса 11 по математике JEE_Main
Если пружина имеет период T и разрезана на n равный класс 11 по физике CBSE
Планета движется вокруг Солнца по почти круговой орбите класс 11 по физике CBSE
В любом треугольнике AB2 BC4 CA3 и D является средней точкой класса 11 по математике JEE_Main
C 60circ затем 11 класс математики JEE_Main
Если в треугольнике rmABC сторона равна sqrt 3 + 1rmcm и классу угла 11 по математике JEE_Main
Трендовые сомнения стороны и соответствующие углы конгруэнтны исследованию сравнения площадей.
Если мы возьмем любой треугольник и построим отрезки, пересекающие его середины, то из теоремы о середине отрезка для треугольников мы узнаем, что каждый из этих отрезков равен половине длины третьей стороны и параллелен ей. Отсюда можно сделать вывод, что треугольник разбит на 4 конгруэнтных треугольника, каждый из которых подобен исходному треугольнику. Таким образом, отношение сторон равно 2, а отношение площадей равно 4.
Разделение каждой стороны треугольника или квадрата на трети и построение сегментов, параллельных сторонам, даст аналогичные фигуры со сторонами, равными одной трети длины оригинала. В каждом случае по 9образовались подобные фигуры. Значит, отношение сторон равно 3, отношение площадей равно 9.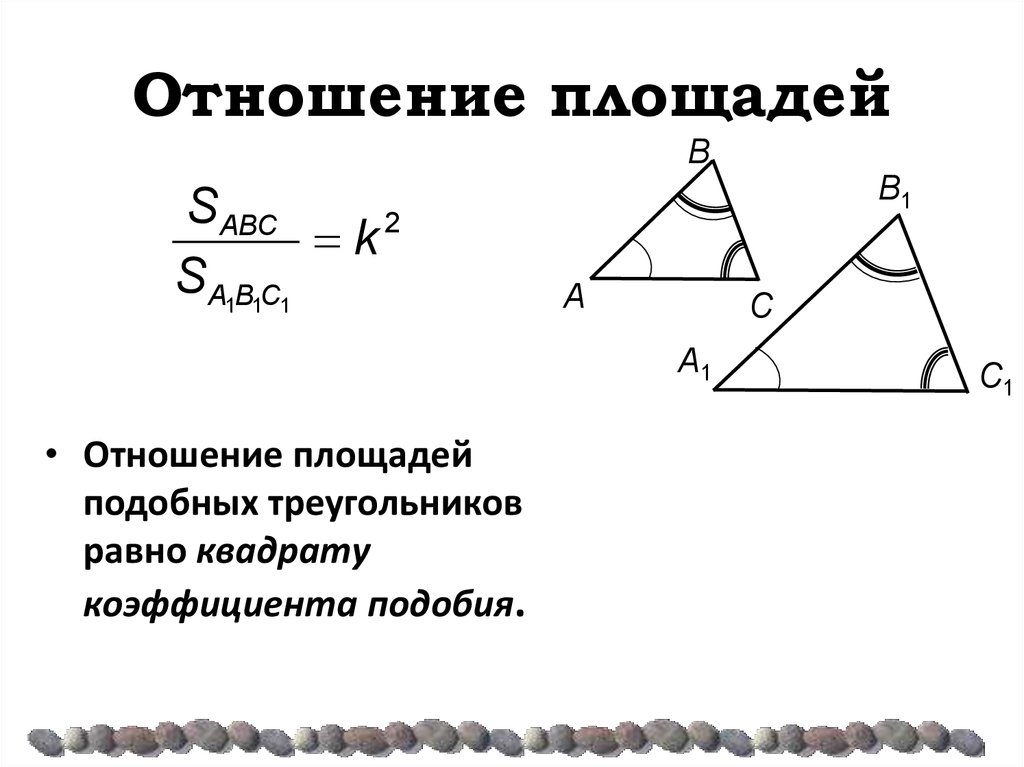
Ясно, что эту стратегию можно распространить на деление стороны на n частей. Мы проведем доказательство в два этапа. В первом случае установлено, что отношение площадей подобных треугольников равно квадрату отношения соответствующих сторон. Затем мы распространим теорему на любой многоугольник, разделив многоугольник на треугольные области. Сначала пара лемм.
Лемма 4.1. Если два треугольника подобны с отношением r, то их соответствующие высоты находятся в том же отношении.
Доказательство: Даны подобные треугольники ABC и A’B’C’. Постройте соответствующие высоты CD и C’D’. Теперь треугольник ADC подобен треугольнику A’D’C’ по условию подобия AA.
Лемма 4.2 . Подобные выпуклые многоугольники на плоскости можно разбить на множество подобных треугольников, построив диагонали из любой вершины.
Следствие 4.2: Диагонали подобных выпуклых многоугольников на плоскости находятся в одном и том же отношении.
Доказательство: Оставлено в качестве упражнения. . . По сути, используйте условие подобия SAS, чтобы показать, что две стороны подобных многоугольников, стягивающие и соответствующие диагонали, дадут подобные треугольники.
Теорема 4.13 : Отношение площадей подобных треугольников равно квадрату отношения соответствующих сторон.
В треугольниках ABC и A’B’C’ (рисунок в лемме 4.1) пусть S — площадь треугольника ABC, а S’ — площадь треугольника A’B’C. Затем
КЭД
Теорема 4.14: Отношение площадей подобных многоугольников равно квадрату отношения соответствующих сторон.
ПРИМЕЧАНИЕ. Хотя утверждение теоремы здесь и в учебнике не является явным, я думаю, мы предполагаем, что это относится к выпуклым многоугольникам на плоскости. Потребуется дополнительная осторожность, чтобы установить теорему для вогнутых многоугольников на плоскости, для непростых многоугольников на плоскости (т. е. многоугольников, стороны которых могут пересекаться) или для неплоских многоугольников .
Хотя утверждение теоремы здесь и в учебнике не является явным, я думаю, мы предполагаем, что это относится к выпуклым многоугольникам на плоскости. Потребуется дополнительная осторожность, чтобы установить теорему для вогнутых многоугольников на плоскости, для непростых многоугольников на плоскости (т. е. многоугольников, стороны которых могут пересекаться) или для неплоских многоугольников .
Доказательство : Используйте лемму 4.2. Возьмем два подобных многоугольника с площадями S и S’. Так как многоугольники похожи,
Решите это 4.10
Правда ли, что площадь просмотра 35-дюймового телевизионного экрана примерно в два раза превышает площадь просмотра 25-дюймового телевизионного экрана. Обосновать ответ.
Предположим, что два экрана представляют собой одинаковые прямоугольники.
.Из лемм и теорем 4.13 и 4.14 мы знаем, что отношение соответствующих сторон такое же, как отношение диагоналей, и поэтому r = 35/25. Таким образом, отношение площадей равно 1,96, что «приблизительно» равно 2,
Пусть S — площадь треугольника ABC. ЗАМЕТИТЕ, ЧТО ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА CQPM БУДЕТ
Файл GSP для примера 4.4
Пример 4.5 .
Дан треугольник ABC. Постройте прямую, параллельную основанию, которая делит треугольник на две равные части.
Подумай об этом : Если отношение площадей двух подобных треугольников равно 2, каково отношение сторон?
Ссылка на файл GSP со скриптом для этой конструкции: Файл GSP
Строительство :
ОБОБЩЕНИЕ
СМ.
ФАЙЛ GSP для этих конструкций и инструментов сценариев
Расширение: Для любого треугольника ABC проведен отрезок, параллельный основанию. Образуется небольшой треугольник в центре, явно похожий на ABC. Каково отношение площадей этого маленького треугольника к треугольнику ABC.
Решение для файлов GSP от Джеки Рафф.
Подробнее см. Половина площади треугольника от EMAT 6600 . . .
Другое удлинение : Постройте линию, параллельную параллельным основаниям трапеции, чтобы разделить трапецию на две равные части.
У Эллисон Холлман есть решение. . .
См. http://jwilson.coe.uga.edu/emt725/IsosTrapEqAr/IsosTrapEqAr.html
Мне показалось полезным найти алгебраическое выражение для длины отрезка, параллельного основаниям, который делит трапецию на две равные части.

 Из лемм и теорем 4.13 и 4.14 мы знаем, что отношение соответствующих сторон такое же, как отношение диагоналей, и поэтому r = 35/25. Таким образом, отношение площадей равно 1,96, что «приблизительно» равно 2,
Из лемм и теорем 4.13 и 4.14 мы знаем, что отношение соответствующих сторон такое же, как отношение диагоналей, и поэтому r = 35/25. Таким образом, отношение площадей равно 1,96, что «приблизительно» равно 2,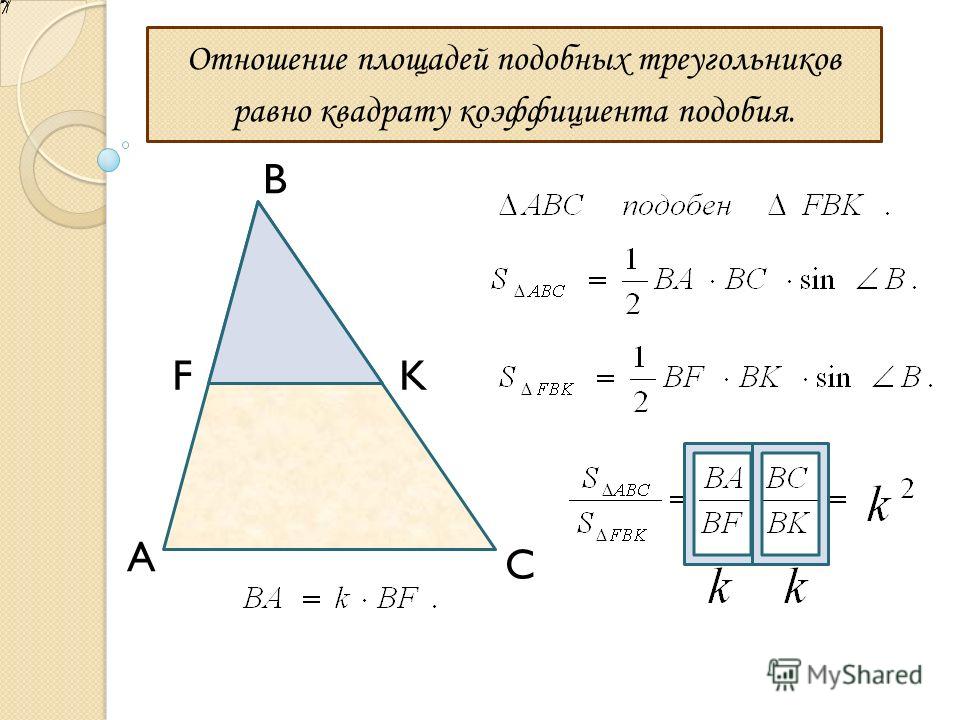 ФАЙЛ GSP для этих конструкций и инструментов сценариев
ФАЙЛ GSP для этих конструкций и инструментов сценариев 