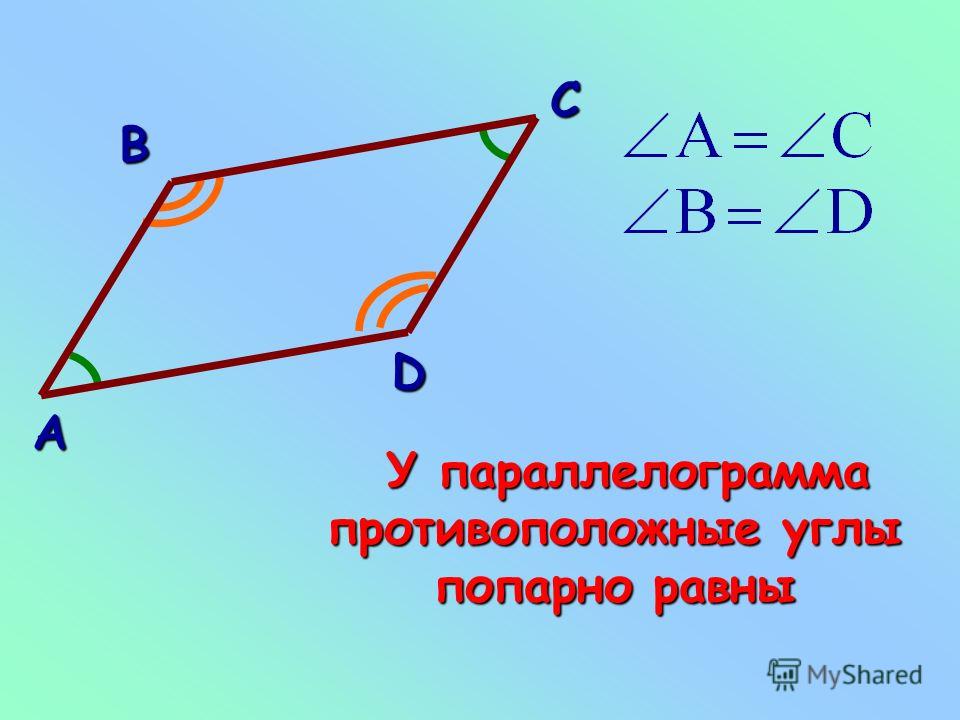
8.1.3. Свойство углов и сторон параллелограмма
Автор Татьяна Андрющенко На чтение 3 мин. Просмотров 16.9k. Опубликовано
Задача 1. Один из углов параллелограмма равен 65°. Найти остальные углы параллелограмма.
Решение.
∠C =∠A = 65° как противоположные углы параллелограмма.
∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма.
∠В = 180° — ∠А = 180° — 65° = 115°.
∠D =∠B = 115° как противолежащие углы параллелограмма.
Ответ: ∠А =∠С = 65°; ∠В =∠D = 115°.
Задача 2. Сумма двух углов параллелограмма равна 220°. Найти углы параллелограмма.
Решение.
Так как у параллелограмма имеется 2 равных острых угла и 2 равных тупых угла, то нам дана сумма двух тупых углов, т.е. ∠В +∠D = 220°. Тогда ∠В =∠D = 220°: 2 = 110°.
∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма, поэтому ∠А = 180° — ∠В = 180° — 110° = 70°.
Тогда ∠C =∠A = 70°.
Ответ: ∠А =∠С = 70°; ∠В =∠D = 110°.
Задача 3. Один из углов параллелограмма в 3 раза больше другого. Найти углы параллелограмма.
Решение.
Пусть ∠А =х. Тогда ∠В = 3х. Зная, что сумма углов параллелограмма, прилежащих к одной его стороне равна 180°, составим уравнение.
х + 3х = 180;
4х = 180;
х = 180 : 4;
х = 45.
Получаем: ∠А =х = 45°, а ∠В = 3х = 3 ∙ 45° = 135°.
Противолежащие углы параллелограмма равны, следовательно,
∠А =∠С = 45°; ∠В =∠D = 135°.
Ответ: ∠А =∠С = 45°; ∠В =∠D = 135°.
Задача 4. Докажите, что если у четырехугольника две стороны параллельны и равны, то этот четырехугольник – параллелограмм.
Доказательство.
Проведем диагональ BD и рассмотрим Δ ADB и Δ CBD.
AD = BC по условию. Сторона BD – общая. ∠1 = ∠2 как внутренние накрест лежащие при параллельных (по условию) прямых AD и BC и секущей BD.
Следовательно, Δ ADB = Δ CBD по двум сторонам и углу между ними (1-й признак равенства треугольников). В равных треугольниках соответственные углы равны, значит, ∠3 =∠4. А эти углы являются внутренними накрест лежащими при прямых AB и CD и секущей BD. Отсюда следует параллельность прямых AB и CD. Таким образом, в данном четырехугольнике ABCD противолежащие стороны попарно параллельны, следовательно, по определению ABCD – параллелограмм, что и требовалось доказать.
Задача 5. Две стороны параллелограмма относятся как 2 : 5, а периметр равен 3,5 м. Найти стороны параллелограмма.
Решение.
Периметр параллелограмма PABCD= 2 ∙ (AB + AD).
Обозначим одну часть через х. тогда AB = 2x, AD = 5x метров. Зная, что периметр параллелограмма равен 3,5 м, составим уравнение:
2 ∙ (2x + 5x) = 3,5;
2 ∙ 7x = 3,5;
14x = 3,5;
x = 3,5 : 14;
x = 0,25.
Одна часть составляет 0,25 м. Тогда AB = 2 ∙ 0,25 = 0,5 м; AD = 5 ∙ 0,25 = 1,25 м.
Проверка.
Периметр параллелограмма PABCD= 2 ∙ (AB + AD) = 2 ∙ (0,25 + 1,25) = 2 ∙ 1,75 = 3,5 (м).
Так как противоположные стороны параллелограмма равны, то CD = AB = 0,25 м; BC = AD = 1,25 м.
Ответ: CD = AB = 0,25 м; BC = AD = 1,25 м.
Углы параллелограмма найти онлайн, формулы и примеры
У параллелограмма 4 угла, это частный случай четырехугольника, у которого противоположные стороны попарно параллельны. Из этого свойства вытекает равенство противоположных сторон, равенство противоположных углов и равенство суммы смежных углов двум прямым. Свойства параллелограмма широко используются в быту и технике.
- Острый угол параллелограмма через боковую сторону и высоту
- Острый угол параллелограмма через высоту, сторону и периметр
- Острый угол параллелограмма через площадь и две стороны
- Острый угол параллелограмма через две стороны и короткую диагональ
- Тупой угол параллелограмма через две стороны и длинную диагональ
Острый угол параллелограмма через боковую сторону и высоту
Если известна боковая сторона и высота, то можно найти острый угол параллелограмма по формуле:
sin α = h / b
где α – острый угол, h – высота, b – боковая сторона.
Высота (h):
ммсмдмм
Сторона (b):
ммсмдмм
Цифр после запятой:
012345678910Результат в: градусыsinрадианы
Пример. Пусть h = 4 см, b = 8 см. sin α = h / b = 8 / 4 = 2. α = 90°.
Острый угол параллелограмма через площадь и две стороны
Если известна площадь и две стороны, то можно найти острый угол параллелограмма по формуле:
sin α= S / ab
где α – острый угол, S — площадь параллелограмма, a и b – его стороны.
Площадь (S):
мм²см²дм²м²
Сторона (a):ммсмдмм
Сторона (b):
ммсмдмм
Цифр после запятой:
012345678910Результат в: градусыsinрадианы
Пример. Пусть S=50 м², a=10 м, b=5 м.
sin α= S / ab = 50 / (10 * 5) = 1. α = 90°.
Угол прямой, смежные стороны не равны, имеем дело с прямоугольником.
Острый угол параллелограмма через высоту, сторону и периметр
Если известна высота, сторона и периметр, то можно найти острый угол параллелограмма по формуле:
sin α = (2h + a) / P
где α – острый угол, h — высота, a — сторона, P — периметр.
Высота (h):
ммсмдмм
Сторона (a):
ммсмдмм
Периметр (P):
ммсмдмм
012345678910Результат в: градусыsinрадианы
Высота опускается на известную и подставляемую в формулу сторону a. Параллелограмм с заданным
периметром приходится строить, если, например, периметр определен длиной веревки, которую требуется
растянуть на местности в форме параллелограмма.
Пример. Пусть h=10 м, a=15 м, P=70 м. sin α=(2h + a) / P= (2 * 10 + 15) / 70 = 0,5. α = 30°.
Острый угол параллелограмма через две стороны и короткую диагональ
Если известны две стороны и короткая диагональ, то можно найти острый угол параллелограмма по формуле:
cos α = (a² + b² — d²) / 2ab
где α – острый угол, a и b – стороны параллелограмма, d – его короткая диагональ.
Сторона (a):
ммсмдмм
Сторона (b):ммсмдмм
Диагональ (d):
ммсмдмм
Цифр после запятой:
012345678910Результат в: градусыcosрадианы
Пример расчета: в данном частном случае 2 прилежащие стороны и короткая диагональ
равны, а именно: a = b = d = 26 мм. cos α=(a² + b² — d²) / 2ab = (26² + 26² — 26²) / (2 * 26 * 26) = 0,5.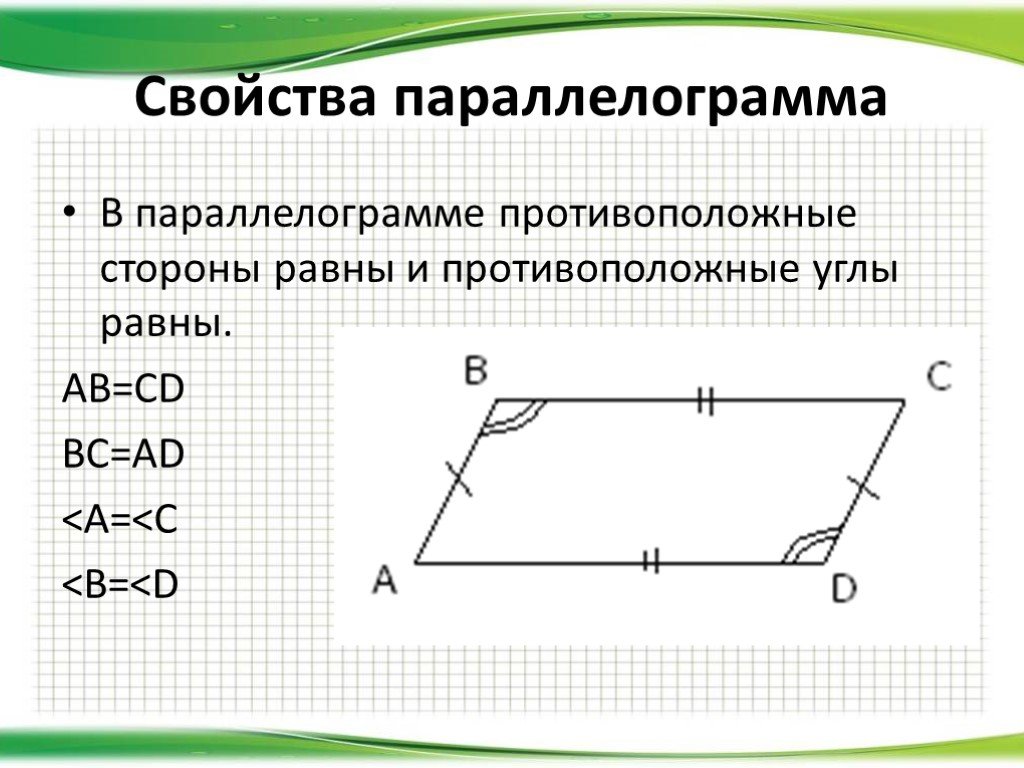
α=60°.
Из равенства прилежащих сторон следует, что это ромб, а результат расчета показывает, что острый угол в ромбе равен 60°. Знаете, что это за ромб с подобными размерами? Это нагрудный академический знак для лиц, окончивших советские высшие учебные заведения, установленный с 1961 года.
Тупой угол параллелограмма через две стороны и длинную диагональ
Если известны две стороны и длинная диагональ, то можно найти тупой угол параллелограмма по формуле:
cos β = (a² + b² — D²) / 2ab
где α – тупой угол, a и b – стороны параллелограмма, D – его длинная диагональ.
Сторона (a):
ммсмдмм
Сторона (b):
ммсмдмм
Диагональ (D):
ммсмдмм
Цифр после запятой:
012345678910Результат в: градусыcosрадианы
Пример расчета: вновь ромб со сторонами a = b = 26 мм и длинной диагональю D=43 мм.
cos β = (a² + b² — D²) / 2ab = (26² + 26² — 43²) / (2 * 26 * 26) = -0,368. α = 112°.
Это опять-таки нагрудный академический знак из предыдущего примера, небольшое отличие полученного
результата от 120° (при остром угле 60° по предыдущему примеру) объясняется округлением исходных
данных до целого числа миллиметров.
Свойства параллелограмма
У любого выпуклого четырехугольника сумма всех внутренних углов равна 360°, исходя из общей формулы суммы внутренних углов выпуклого многоугольника в градусах s = 180 (n — 2), где n – количество сторон. Следовательно, если хотя-бы 1 угол параллелограмма равен прямому (90°), остальные 3 угла также являются прямыми, и параллелограмм вырождается в свой частный вид – прямоугольник.
Если 2 смежные стороны параллелограмма равны, то равны все его 4 стороны, и параллелограмм
вырождается в ромб. И, наконец, если у параллелограмма равны 2 смежные стороны, а угол между ними
прямой, параллелограмм является одновременно и прямоугольником, и ромбом, и вырождается в квадрат.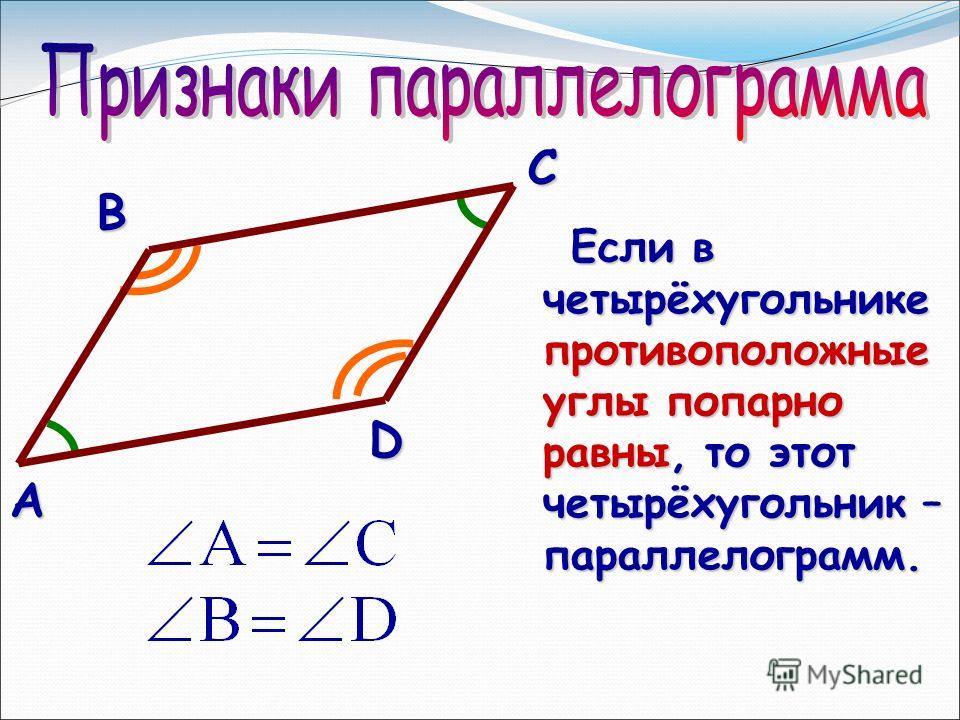
Зачастую возникает необходимость определения неизвестных характеристик параллелограмма через
известные. Выше ряд примеров подобного рода.
Самый наглядный пример параллелограмма – пантограф электропоезда. При подключении опущенного
пантографа к контактной сети железной дороги изменяется конфигурация пантографа при сохранении длин
сторон, в результате изменяется вертикальная диагональ и происходит касание с подачей электрического
тока.
Форму параллелограмма имеет автомобильный реечный домкрат, велосипедная рама (с
диагональю для увеличения жесткости). Ведь параллелограмм — фигура нежесткая, в отличие от
треугольника. Из нежесткости параллелограмма следует, что знания одних длин сторон недостаточно для
вычисления площади фигуры. Так, пантограф электропоезда можно «сложить» до нулевой площади.
Стеклоочиститель лобового стекла автобуса также представляет собой параллелограмм, и именно
нежесткость фигуры позволяет стеклоочистителю «ометать» при движении стекло.
Узнайте о свойствах параллелограммов
Узнайте о свойствах параллелограммов, включая отношения между противоположными сторонами, противоположными углами, смежными углами, диагоналями и углами, образованными диагоналями.
Свойства параллелограмма
Основные свойства параллелограммов
Параллелограмм: Четырехугольник с двумя парами параллельных прямых.
Начнем с основных правил: противоположные стороны параллелограмма всегда имеют одинаковую длину и параллельны.
Внутри параллелограмма противоположные углы всегда равны. Углы, лежащие рядом друг с другом, всегда являются дополнительными (в сумме они составляют 180 градусов).
Диагонали параллелограмма
Диагонали параллелограмма делят друг друга пополам.
При проведении диагоналей образуется множество углов, которые подчиняются тем же правилам, что и углы, образованные двумя параллельными прямыми, пересекаемыми секущей.
Диагональ действует как поперечная и создает чередующиеся внутренние углы с параллельными сторонами.
При проведении обеих диагоналей образуются две пары конгруэнтных вертикальных углов.
При проведении одной диагонали в параллелограмме образуются два конгруэнтных треугольника.
При проведении двух диагоналей в параллелограмме образуются две пары конгруэнтных треугольников.
Специальные параллелограммы
Прямоугольники, ромбы и квадраты являются особыми типами параллелограммов. Следовательно, те же самые правила для углов, сторон и диагоналей справедливы и для квадратов и прямоугольников. Однако эти три формы обладают дополнительными свойствами, которые делают их особенными.
Стенограмма видеоурока
Давайте рассмотрим параллелограммы.
Мы уже нарисовали параллелограмм.
Параллелограмм называется потому, что у него две пары параллельных сторон.
Сторона параллельна стороне .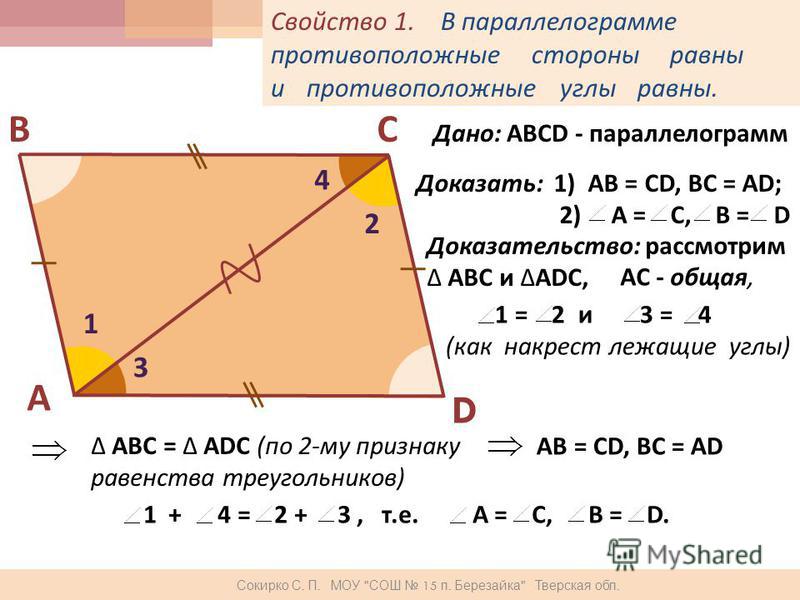
А сторона параллельна стороне.
Помимо того, что эти две пары сторон параллельны, они еще и конгруэнтны.
Углы напротив друг друга равны.
Другой способ спаривания углов — сделать их дополнительными.
Углы, расположенные рядом или рядом друг с другом, составляют в сумме .
Углы напротив друг друга равны. А если они находятся рядом друг с другом, то в сумме они составляют .
Посмотрим, что получится, когда мы начертим диагонали.
Проведем диагональ от туда и от до .
Диагонали на самом деле делят друг друга пополам.
делится пополам.
Аналогично, делится пополам.
Еще кое-что, что происходит, когда мы рисуем эту диагональ, влияет на углы.
Позвольте мне продлить эту диагональную линию и эти линии.
Давайте посмотрим на эти красные линии. Мы увидим, что есть параллельные прямые, и они пересекаются секущей.
И мы знаем, что существует взаимосвязь между углами.
Потому что у нас много параллельных прямых, пересекаемых секущей.
Все это идеальные внутренние углы.
Внутренние углы параллелограмма
Внутренние углы параллелограмма — Открытый справочник по математикеОткрытая математическая ссылка
Главная Контакт О Тематический указатель
Попробуйте это Перетащите оранжевые точки на каждой вершине изменить форму параллелограмма. Обратите внимание на поведение четырех внутренних углов.
В любом многоугольнике внутренние углы обладают определенными свойствами. Видеть Внутренние углы многоугольника. Однако параллелограмм обладает некоторыми дополнительными свойствами.
1. Противоположные углы равны
Когда вы перетаскиваете любую вершину в параллелограмме выше, обратите внимание, что противоположные углы конгруэнтны (равны по мере). Обратите внимание, например, что углы ∠ABD и ∠ACD всегда равны, независимо от того, что вы делаете.2. Смежные углы являются дополнительными
