Четная функция и нечетная функция как определить: Чётные и нечётные функции — урок. Алгебра, 9 класс.

Теория рядов

Теория рядов

Теория рядов. Воробьев Н. Н. 4 изд., перераб. и доп., Наука, Главная редакция физико-математической литературы, М., 1979, — 408 с. В книге излагаются основы теории числовых рядов и функциональных рядов, в том числе степенных рядов и рядов Фурье. Первая часть курса составлена в точном соответствии с разделом «Ряды» программы по высшей математике для инженерно-технических специальностей высших учебных заведений. Ее можно использовать не только как учебное пособие для слушателей курса лекций, но и при самостоятельной работе над предметом. Вторая часть представляет собой цикл очерков, посвященных более глубоким вопросам теории рядов, Оглавление ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ Часть I ГЛАВА 1. ПРОГРЕССИИ § 2. Геометрические прогрессии § 3. Бесконечные прогрессии; их сходимость и расходимость § 4. Элементарные преобразования прогрессий § 5. Функциональные прогрессии: область сходимости; равномерная сходимость § 6. Почленное интегрирование прогрессий § 7. Почленное дифференцирование прогрессий § 8. Прогрессии с комплексными членами ГЛАВА 2. ЧИСЛОВЫЕ РЯДЫ. ОСНОВНЫЕ ПОНЯТИЯ. ОСНОВНЫЕ ТЕОРЕМЫ О СХОДИМОСТИ § 2. Определение числового ряда и его сходимости § 3. Остаток ряда § 4. Принцип сходимости Коши § 5. Критерий Коши сходимости рядов § 6. Необходимый признак сходимости ряда § 7. Желательность систематической теории § 8. Свойства сходящихся рядов, подобные свойствам сумм § 9. Дальнейшие свойства рядов ГЛАВА 3. РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ § 1. Признаки сходимости рядов § 2. Признаки сравнения § 3. Интегральный признак сходимости Маклорена — Коши § 4. Применения интегрального признака сходимости § 5. Сравнительная оценка различных признаков сходимости § 6. Признак сходимости Даламбера § 7. Признак сходимости Коши § 8. Чувствительность признаков сходимости Даламбера и Коши ГЛАВА 4. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ § 2. Абсолютная сходимость и расходимость § 3. Возможность переставлять члены в абсолютно сходящихся рядах § 4. Условно сходящиеся знакопеременные ряды § 5. Умножение абсолютно сходящихся рядов § 6. Признак сходимости Лейбница § 7. Существенность условий признака сходимости Лейбница ГЛАВА 5. ФУНКЦИОНАЛЬНЫЕ РЯДЫ § 2. Область сходимости функционального ряда § 3. Сходимость последовательности функций. Основные определения § 4. Предел последовательности непрерывных функций § 5. Переход к пределу под знаком интеграла § 6. Переход к пределу под знаком производной § 7. Определение равномерной сходимости функционального ряда и признак Вейерштрасса § 8. Непрерывность суммы равномерно сходящегося ряда с непрерывными членами § 9. Почленное интегрирование функциональных рядов § 10. Почленное дифференцирование функциональных рядов ГЛАВА 6. СТЕПЕННЫЕ РЯДЫ. ОБЩИЕ ВОПРОСЫ § 2. Теорема Абеля § 3. Круг сходимости ряда § 4. Вещественный степенной ряд и его интервал сходимости § 5. Равномерная сходимость ряда в круге его сходимости § 6. Вещественные ряды § 7. Комплексные ряды § 8. Разложение функций в степенные ряды § 9. Формула Тейлора § 10. Ряды Тейлора и Маклорена ГЛАВА 7. СТЕПЕННЫЕ РЯДЫ. ПРИМЕРЫ И ПРИЛОЖЕНИЯ § 2. Разложения в ряды Маклорена гиперболических функций ch x и sh x § 3. Разложения в ряды Маклорена тригонометрических функций cos x и sin x § 4. Показательная функция с комплексным значением показателя § 5. Формулы Эйлера § 6. Тригонометрические функции от комплексного значения аргумента § 7. Гиперболические функции от комплексного значения аргумента § 8. Вычисление значений функций при помощи ряда Маклорена § 9. Биномиальный ряд § 10. Приложения биномиального ряда § 11. Разложение в ряд Маклорена логарифмической функции § 12. Приближенное вычисление определенных интегралов при помощи степенных рядов § 13. Приближенное интегрирование дифференциальных уравнений при помощи степенных рядов ГЛАВА 8. ОРТОГОНАЛЬНЫЕ И ОРТОНОРМАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ § 2. Векторы и функции § 3. Нормированные и ортогональные функции § 4. Нормированные и ортогональные системы функций § 5. Нормировка систем функций § 6. Разложение по системам функций ГЛАВА 9. РЯДЫ ФУРЬЕ § 1. Ряды и коэффициенты Фурье § 2. Условия Дирихле и теорема о разложении функции в ряд Фурье § 3. Разложение периодических функций в ряд Фурье § 4. Физическое истолкование разложения функции в тригонометрический ряд Фурье § 5. Разложение функции f(x) = x § 6. Сдвиг сегмента разложения § 7. Изменение длины сегмента разложения § 8. Четные и нечетные функции § 9. Разложение четной функции в ряд Фурье § 10. Разложение нечетной функции в ряд Фурье § 11. Разложение ряд Фурье функций на сегменте от 0 до пи § 12. Комплексная форма записи ряда Фурье § 13. Разложение в комплексный ряд Фурье § 14. Характер сходимости рядов Фурье ГЛАВА 10. УРАВНЕНИЕ СВОБОДНЫХ МАЛЫХ КОЛЕБАНИЙ СТРУНЫ С ЗАКРЕПЛЕННЫМИ КОНЦАМИ § 2. Начальные и граничные условия § 3. Метод разделения переменных § 4. Использование граничных условий. Собственные функции и собственные значения § 5. Использование начальных условий ГЛАВА 11. ИНТЕГРАЛ ФУРЬЕ § 1. Представление функций интегралом Фурье § 2. Простейшие достаточные условия представимости функции интегралом Фурье § 3. Интеграл Фурье для четных функций § 4. Интеграл Фурье для нечетных функций § 5. Комплексная форма интеграла Фурье § 6. Понятие о преобразовании Фурье § 7. Косинус-преобразование Фурье § 8. Синус-преобразование Фурье § 9. Спектральная функция Часть II § 1. Признак сходимости Куммера § 2. Признак сходимости Раабе § 3. Признак сходимости Бертрана § 4. Признак сходимости Гаусса § 5. Сходимость знакопеременных рядов § 6. Признак сходимости Дирихле ГЛАВА 13. ДВОЙНЫЕ РЯДЫ § 1. Определение двойного ряда § 2. Сходимость двойных рядов § 3. Критерии сходимости двойных рядов. Теорема Маркова § 4. Свойства двойных рядов и признаки сходимости § 5. Абсолютная сходимость двойных рядов § 6. Двойные функциональные ряды § 7. Двойные степенные ряды § 8. Разложение функций двух переменных в двойные ряды Тейлора и Маклорена § 9. Ортогональные и ортонормальные системы функций от двух переменных § 10. Двойные ряды Фурье ГЛАВА 14. СУММИРОВАНИЕ СХОДЯЩИХСЯ РЯДОВ § 2. Линейные преобразования рядов § 3. Теорема Абеля и почленное дифференцирование и интегрирование рядов § 4. Последовательности разностей § 5. Преобразование рядов по Эйлеру § 6. Преобразование рядов по Куммеру ГЛАВА 15. СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ § 1. Расходящиеся геометрические прогрессии § 2. Суммирующие функции § 3. Суммирование по Пуассону — Абелю § 4. Линейность и регулярность суммирования по Пуассону — Абелю § 5. Суммируемость рядов по Пуассону — Абелю и их абсолютная сходимость § 6. Теорема Таубера § 7. Суммирование по Чезаро § 8. Соотношение между сходимостью по Чезаро и по Пуассону — Абелю § 9. Суммирование по Эйлеру ГЛАВА 16. СХОДИМОСТЬ РЯДОВ ФУРЬЕ § 2. Исследование двух интегралов § 3. Исследование одного класса интегралов § 4. Доказательство теоремы Дирихле § 5. Теорема Фурье § 6. Коэффициенты Фурье разрывных функций § 7. Скорость сходимости рядов Фурье § 8. Улучшение сходимости рядов Фурье по методу выделения особенностей § 9. О равномерной сходимости рядов Фурье § 10. Неравномерная сходимость последовательностей непрерывных функций § 11. Поведение рядов Фурье функций в точках их разрыва. Явление Гиббса § 12. Экстремальное свойство сумм Фурье § 13. Суммирование рядов Фурье по Чезаро. Теорема Фейера § 14. Равенство Парсеваля § 15. Теорема Вейерштрасса ГЛАВА 17. ПРИМЕНЕНИЕ РЯДОВ ФУРЬЕ В ТЕОРИИ ИЗГИБА БАЛОК § 2. Изгиб балки § 3. Свободно опертая балка § 4. Первая возможность ограничиться двукратным дифференцированием § 5. Случай сосредоточенной нагрузки § 6. Прогиб балки от распределенной нагрузки § 7. Прогиб от сосредоточенного момента § 8. Статически неопределимая балка § 9. Сложный изгиб балки § 10. Балка на упругом основании § 11. Вторая возможность ограничиться двукратным дифференцированием. Потенциальная энергия изгиба балки § 12. Потенциальная энергия изгиба балки в случае нескольких нагрузок § 13. Функции прогиба с ортогональными вторыми производными § 14. Свободно опертая нагруженная балка § 15. Работа продольных сил при сложном изгибе балки § 16. Общий случай изгиба балки § 17. Общий случай изгиба свободно опертой балки § 18. Изгиб симметрично нагруженной балки, жестко заделанной по концам § 19. Функция прогиба симметрично загруженной балки с жестко заделанными концами

это что? Четная и нечетная функция, корни функции.

Что такое функция? Представим себе машину, которая двигается по дороге из одного города в другой. Мы можем в каждый момент времени определить положение машины. То есть у нас есть множество различных моментов времени и множество точек, определяющих положение машины на дороге. При этом положение машины на дороге зависит от того, в какой момент времени мы определяем это положение. То есть одно множестве переменных величин зависит от другого множества, каждая отдельная переменная из одного множества зависит от переменной из другого множества. Зависимость одной переменной от другой называется функциональной зависимостью.

Функция – это что

В этой статье мы рассмотрим что такое функция, дадим определения области определения функции и области ее значений, понятие графика функции.

Содержание

Область определения и область значений функции

– значение функции в точке .

Если область определения функции и область ее значений определены в множестве рациональных чисел, то функцию называют числовой.

Элементы множества еще называют значениями аргумента, а соответствующие им элементы – значениями функции.

Если функция задана формулой и область определения функции не указана, то считают, что область определения состоит из всех значений независимой переменной, при которых эта формула имеет смысл.

Например, область определения функции, заданной формулой , состоит из всех чисел, кроме нуля.

Как найти область определения функции

Для того, чтобы найти область определения функции, мы должны определить – где функция будет существовать, при каких значениях аргумента. Приведем примеры:

Пример 1

Найти область определения функции 

Зададимся вопросом – при каких значениях функция будет существовать? Очевидно, что функция существует, если знаменатель дроби не равен нулю. То есть .

Для определения этого значения решим уравнение:

.

Находим, .

То есть функция не будет существовать при значении . Тогда областью определения функции (где она существует) – будут все значения кроме 5. Через интервалы можно записать так:

.

Пример 2

Найти область определения функции .

Здесь функция определена при любых значениях аргумента. То есть D(f) – все числа.

Пример 3

Определить область определения функции

.

Выражение, стоящее под знаком квадратного корня, должно быть больше или равно нулю. Таким образом, мы можем записать:

Решим данное неравенство и получим: .

Тогда область определения функции будет интервал значений аргумента .

График функции

Графиком функции называется множество всех точек, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции. То есть график функции – это изображение на координатной плоскости множества пар , связанных зависимостью , где .

Способы задания функции

Функция может быть задана аналитически в виде формулы , где переменная – элемент множества значений аргумента, а переменная – соответствующее значение функции.

Например, формула определяет некоторую функцию, где каждому значению переменной , взятому из области определения функции, соответствует единственное значение переменной .

Функция   полностью определяется заданием множества пар ,  где принимает все значения из , а – соответствующие значения функции.

Однако не всякое множество точек координатной плоскости является графиком некоторой функции. Например, если мы рассмотрим следующий график, то увидим, что значению соответствуют три значения , и, следовательно, такое соответствие не является функцией.

График не является графиком функции

Для того, чтобы множество точек координатной плоскости являлось графиком некоторой функции, необходимо и достаточно, чтобы любая прямая, параллельная оси , пересекалась с указанным графиком не более чем в одной точке.

Монотонность функции

Функция называется возрастающей на данном числовом промежутке , если большему значению аргумента соответствует большее значение функции . Это значит, что для любых и из промежутка , таких, что , выполнено неравенство .

Функция называется убывающей на данном числовом промежутке , если большему значению аргумента соответствует меньшее значение функции . Это значит, что для любых и из промежутка , таких, что , выполнено неравенство .

Функция только возрастающая или только убывающая на данном числовом промежутке, называется монотонной на этом промежутке.

О монотонности функции можно судить по ее графику. Например, функция, график которой изображен ниже является монотонно возрастающей на всей числовой оси.

Монотонно возрастающая функция

А вот эта функция является монотонно убывающей.

Монотонно убывающая функция – график функции.

А теперь рассмотрим вот такой график функции – на ней функция убывает на промежутке и возрастает на промежутке .

График функции которая монотонно убывает и монотонно возрастает на определенных интервалах области определения функции.

Пример

Докажите, что функция, заданная формулой , где , возрастающая.

Решение: Пусть , где и . Тогда

.

Поскольку , то и , а, значит, 

. То есть большему значению аргумента соответствует большее значение функции, таким образом, функция возрастающая на промежутке .

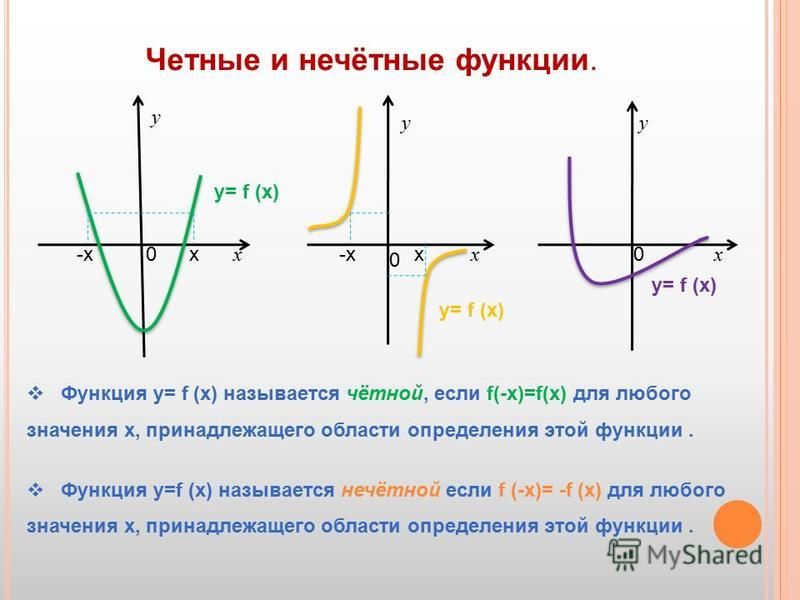
Четные и нечетные функции

Пример 1

Доказать, что функция не является ни четной, ни нечетной.

Доказательство.

Областью определения данной функции является вся числовая прямая, то есть условие 1 выполнено. Проверяем условие 2.

Чтобы доказать, что функция не является четной, нам нужно доказать, что условие 2 для четной функции не выполняется, то есть что .

Пусть , тогда . Проверяем:

, а , таким образом . Функция не является четной.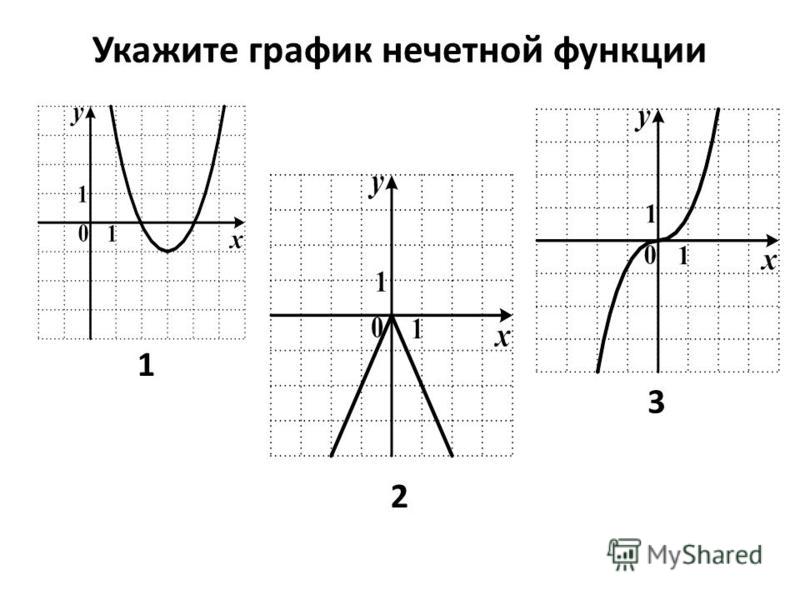 Одновременно, не выполняется и второе условие для нечетной функции, мы получили, что: . То есть функция не является нечетной.

Пример 2

Определите четность или нечетность функции:

Решение: область определения данной функции – вся числовая ось, кроме точки (на ноль делить нельзя).  Найдем .

Получим: . Вынесем минус за скобки:

.

Отсюда выходит, что , то есть выполняется условие для нечетной функции. А, значит, функция – нечетная функция.

Пример 3

Определить четность или нечетность функции:

.

Решение: Первое условие о симметричности области определения функции выполняется, так как область определения функции . Переменим знак аргумента функции и упростим:

.

Получается, что . То есть функция

– четная.

Периодические функции

Если   – период функции, то , где , , также период функции. Следовательно, всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривается наименьший положительный период.

Значения периодической функции через промежуток, равный периоду, повторяются. Это обстоятельство используется при построении графиков.

Промежутки знакопостоянства и корни функции

Числовые промежутки, на которых функция сохраняет свой знак (то есть остается положительной или отрицательной), называются промежутками знакопостоянства функции.

О промежутках знакопостоянства функции можно сделать вывод, посмотрев на график функции. Например, возьмем график функции . Здесь при , при . В первом случае график расположен выше оси , во втором – ниже ее.

График линейной функцииКорни функции

Итак, мы с вами изучили что такое функция, определили когда функция является четной, а когда нечетной, способы задания функции, область определения функции и область ее значений. А также дали понятие периодической функции и корней функции.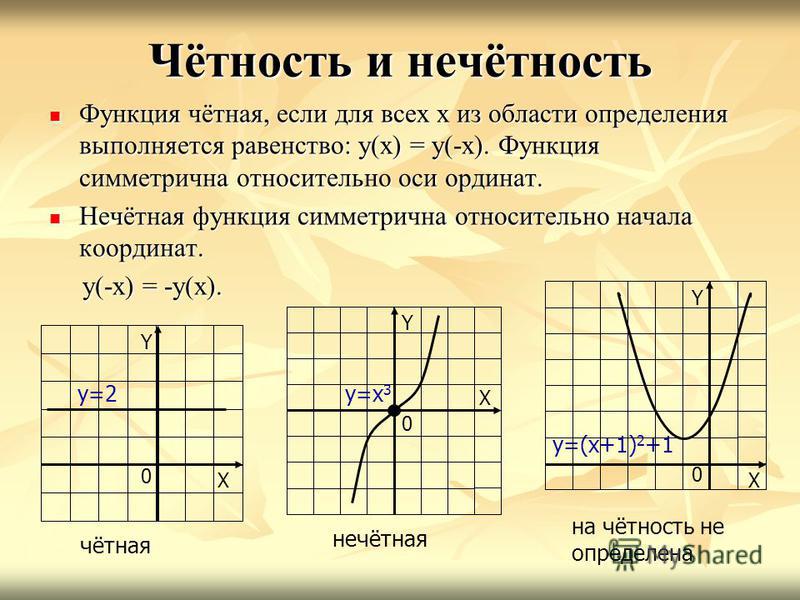 Выяснили, что называется промежутками знакопостоянства функции. Привели примеры.

Читайте еще похожие статьи:

Справка по математике

Справка по математике

Четное и нечетное Функции одной независимой переменной

Критерии:   Если f(x) нечетно, то f( ˗ х) = ˗ f(x) и даже если f(˗ x ) = f(x).

Пример: Определите, выполняется ли следующее функция f(x) четная или нечетная.   ф(х) = х 3 + грех(5х)   Заменить х с ˗ х. Затем f(˗ x) = ( ˗ x) 3 + sin(˗ 5x) = ˗ x 3 ˗ sin( 5x)   В результате f(x) = ˗f(˗x)   Так что эта функция нечетная. (результат)

Пример: Определите, выполняется ли следующее функция f(x) четная или нечетная.   ф(х) = х 4 + cos(5x)   Замените x на ˗ x. f(˗x) = (˗ х) 4 + cos(˗ 5х) = х 4 + cos( 5x)   Так как f(˗x) = f(x) функция ровная. (результат)

Пример: Определите, выполняется ли следующее функция f(x) четная или нечетная.   f(x) = cos (x 3 ) ˗ sin(x 4 ) Заменить х с ˗ х.   f(˗x) = потому что ((˗ х) 3 ) ˗ sin ((˗x) 4 ) = cos (˗x 3 ) ˗ sin (x 4 ) = cos (x 3 ) ˗ грех (х 4 ) = f (х)   Так как f(˗x) = f(x) функция четная. (результат)

Пример: Определите, выполняется ли следующее функция f(x) четная или нечетная.   f(x) = cos (x 3 ) ˗ sin(x 3 ) Заменить x с ˗ х.   Здесь f(˗ x) = потому что ((˗ x) 3 ) ˗ sin( (˗ x) 3 ) = cos (˗ x 3 ) ˗ sin (˗ x 3 ) = cos (x 3 ) + sin (x 3 )   Таким образом: f( ˗ x) ≠ ˗f(x) и f(˗x) ≠ f(x)   Следовательно, f(x) не является ни четным, ни нечетным функция. (результат)

Вернуться к примечаниям по расчетам 1

Copyright © 2019Ричард С. Коддингтон

Все права защищены.

 

√ Функция четности и нечетности

30 ноября 2022 г. от Sigma

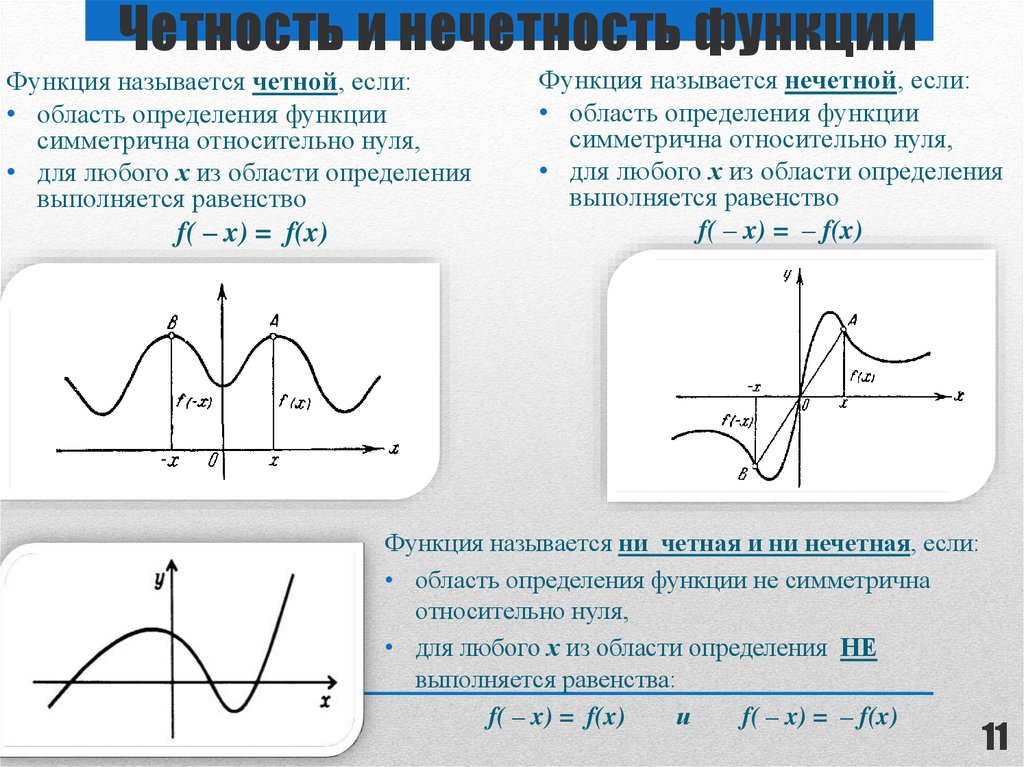
Каждая функция имеет каждый график, но не весь график, симметричный относительно оси x, оси y или других. Если график симметричен, то в конкретном случае делается вывод о том, является ли функция четной или нечетной функцией.

Содержание

Четная функция и график

Четная функция отличается от среднего с четными числами. График четной функции симметричен оси у. Посмотрите на график y = x ² . Это параболический граф.

В математике это можно записать как

f(x) четная функция, если f(-x) = f(x) для любых действительных чисел, x Î D _f .

Нечетная функция и график

Нечетная функция отличается от четной.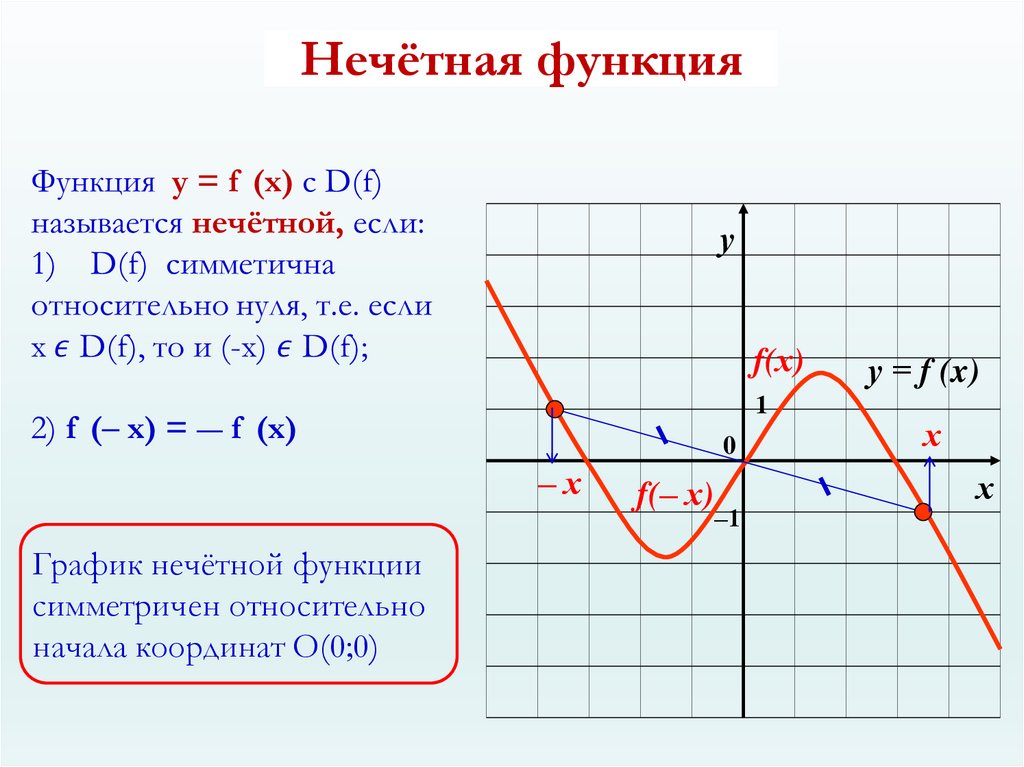 График нечетной функции симметричен точке O(0,0). Посмотрите на график y=x ³ -x.

В математике это может быть записано как

f(x) является нечетной функцией, если f(-x) = -f(x) для любых действительных чисел, x Î D _f .

Характеристики четной и нечетной функции

Существуют некоторые характеристики четной и нечетной функции.

1. Сложение или вычитание между четными функциями, тогда результат также является четной функцией
2. Сложение или вычитание между нечетной функцией, тогда результат также является нечетной функцией
3. Сложение между нечетной и четной функцией, тогда результат не является ни четной, ни нечетной функцией, за исключением того, что одна из них равна нулю.
4. Умножение четной функции, тогда результатом будет четная функция.
5. Умножение нечетной функции на результат четной функции.
6. Умножение между нечетной и четной функциями, тогда результатом является нечетная функция.

Как определить, четная функция или нечетная  

Четность или нечетность функции можно определить, заменив значение x на (-x). Если он выполняет концепцию четной или нечетной функции, то это так. Если x изменить на (-x) и результат равен f(x), то это четная функция. Но если результат равен -f(x), то это нечетная функция.

Ни нечетная, ни четная функция

Несмотря на то, что в теме говорится о четной и нечетной функции, это не означает, что все функции можно отнести к одной из них. Это потому, что есть также много функций, которые не являются ни четными, ни нечетными функциями. Например, если f(x) = x ² — четная функция, а f(x) = x ² — x — 1 — нет. Посмотрите на график.

Примеры

Определите, является ли функция равномерной или нечетной функцией

1. F (x) = x ⁴ -2x ² + 3

Пример

F (x) = (x) = (x) = (x) = (x) = (x) = (x) = (x) = (x) = (x) = (x) = (x) = (x) = (x) = 3

.

No related posts.