Сайт Иванской Светланы Алексеевны — Бином Ньютона
Оглавление:Формула бинома Ньютона
В таблице 1 приведены формулы для натуральных степеней бинома
(x + y)n
в случаях, когда n = 1, 2, 3, 4, 5, 6.
Таблица 1. – Степень суммы
| Название формулы | Формула |
| Квадрат (вторая степень) суммы | (x + y)2 = x2 + 2xy + y2 |
| Куб (третья степень) суммы | (x + y)3 = x3 + 3x2y + 3xy2 + y3 |
| Четвертая степень суммы | (x + y)4 = x4 + 4x3y + 6x |
| Пятая степень суммы | (x + y)5 = x5 + 5x4y + 10x3y2 + 10x2y3 + 5xy4 + y5 |
| Шестая степень суммы | (x + y)6 = x6 + 6x5y + 15x4y2 + 20x3y3 + 15x2y4 + 6xy5 + y6 |
| … | … |
Утверждение. Для любого натурального числа n и любых чисел x и y справедлива формула бинома Ньютона:
Для любого натурального числа n и любых чисел x и y справедлива формула бинома Ньютона:
| (1) |
где
| (2) |
– числа сочетаний из n элементов по k элементов.
В формуле (1) слагаемые
называют членами разложения бинома Ньютона, а числа сочетаний – коэффициентами разложения или биномиальными коэффициентами.
Если в формуле (1) заменить y на – y , то мы получим формулу для n — ой степени разности:
Связь бинома Ньютона с треугольником Паскаля
Напомним, что треугольник Паскаля имеет следующий вид:
| № | Треугольник Паскаля |
| 0 | 1 |
| 1 | 1 1 |
| 2 | 1 2 1 |
| 3 | 1 3 3 1 |
| 4 | 1 4 6 4 1 |
| 5 | 1 5 10 10 5 1 |
| 6 | 1 6 15 20 15 6 1 |
| … | … |
Поскольку числа, составляющие треугольник Паскаля, являются биномиальными коэффициентами, то треугольник Паскаля можно переписать в другом виде:
| № | Треугольник Паскаля |
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| … | … |
Свойства биномиальных коэффициентов
Для биномиальных коэффициентов справедливы равенства:
| 1 | |
| 2 | |
| 3 | |
| 4 |
к доказательству которых мы сейчас и переходим.
Докажем сначала равенство 1.
Это равенство отражает основное свойство треугольника Паскаля, заключающееся в том, что в каждой из строк треугольника Паскаля, начиная со строки с номером 2 , между числами 1 стоят числа, каждое из которых равно сумме двух чисел, стоящих над ним в предыдущей строке.
Для доказательства равенства 1 воспользуемся формулой (2):
что и требовалось.
Для доказательства равенства 2 положим в формуле бинома Ньютона (1) x = 1, y = 1.
Если же в формуле бинома Ньютона (1) взять x = 1, y = –1, то получится равенство 3.
Перейдем к доказательству равенства 4. С этой целью положим в формуле бинома Ньютона (1) y = 1
| (3) |
Воспользовавшись очевидным равенством
перепишем формулу (3) в другом виде
| (4) |
Если теперь перемножить формулы (3) и (4), то мы получим равенство:
| (5) |
Если к левой части формулы (5) применить формулу бинома Ньютона, а затем, раскрыв в правой части скобки и приведя подобные члены, приравнять коэффициенты при xn в левой и в правой частях, то мы получим следующее равенство:
что и требовалось. 2
2
nt.number theory — Сумма четырех четвертых степеней
Этот частный случай задачи оценки числа ${\bf F}_p$-точек на многообразии намного проще, чем оценка Вейля: стандартные оценки по Гауссу суммы хватает. Я надеюсь, что это достаточно элементарно. В конце этого ответа я привожу вывод оценки, которая обобщается на произвольные «диагональные гиперповерхности» и сводит настоящую проблему к простому конечному вычислению (через $p=73$).
С более точной информацией о суммах Гаусса четвертой степени (несколько менее элементарной, но все же известной Гауссу — она в приложении к 92$, где $m=18$ или $-6$ в зависимости от того, что $p$ конгруэнтно $1$ или $5 \bmod 8$. Это показывает, что $p=5$ — единственный случай, когда нет рациональных точек. Формула также согласуется с тем фактом, что диагональная квартика Ферма является поверхностью K3 с максимальным числом Пикара (= ранг Нерона-Севери), поэтому я добавлю тег «k3-surfaces».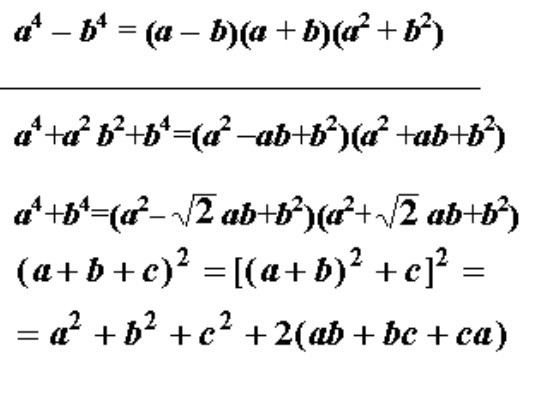
6688 . Это три цифр, а не все четыре. Переместите свой sum() test из вашего для цикла :
для x в цифрах:
а = х**4
list.append(а)
если сумма (список) == я:
печать (сумма (список))
answer.append (сумма (список))
В лучшем случае вы можете отбросить число досрочно, когда сумма уже превышает целевое значение:
digitsum = 0
для d в цифрах:
сумма цифр += d ** 4
если сумма цифр > i:
сломать
еще:
если сумма цифр == i:
ответ. добавить (я)
9n, посчитав его цифры, затем взяв цифр в n-й степени 9 умножить на n-й степени 9 . Если это создает число с большим количеством цифр, продолжайте, пока количество цифр больше не изменится. В том же духе вы можете начать i с max(10, 1 + 2 ** n) , потому что наименьшая сумма, которую вы сможете составить из цифр, будет с использованием одной цифры 2 плюс минимальное количество цифр 1 и 0 , с которыми вы можете справиться, и при любой степени больше 1 степень цифр, отличных от 1 и 0, всегда больше, чем само значение цифры, и вы не можете использовать i = 1 :
определение_границы(n):
"""Для степени n > 1, вернуть нижнюю и верхнюю границы для поиска"""
девять_сил, число_счет = 9 ** n, 1
пока верно:
верхний = число_цифр * девять_степеней
new_count = len (str (верхний))
если new_count == digit_count:
вернуть max(10, 2 ** n), верхний
цифр_счетчик = новый_счетчик
Если вы объедините вышеуказанную функцию с параметром range(*) переменной длины, переходящим в range() , вы можете использовать цикл for :
for i in range(*determine_bounds(4)):
# .

