Re: Ряды : Чулан (М)
| Alena31 |
| ||
23/04/12 |
| ||
| |||
| xmaister |
| |||
03/08/11 |
| |||
|
| ||||
| Alena31 |
| ||
23/04/12 |
| ||
| |||
| |||
30/09/10 |
| ||
|
| |||
| Alena31 |
| ||
23/04/12 |
| ||
| |||
| Toucan |
| |||||
19/03/10 |
| |||||
| ||||||
| Toucan |
| |||
19/03/10 |
| |||
|
| ||||
| Dan B-Yallay |
| |||
11/12/05 |
| |||
| ||||
| Alena31 |
| ||
23/04/12 |
| ||
| |||
| Dan B-Yallay |
| |||
11/12/05 |
| |||
| ||||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| Dan B-Yallay |
| |||
11/12/05 |
| |||
| ||||
| Alena31 |
| ||
23/04/12 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 13 ] |
Модераторы: Модераторы Математики, Супермодераторы
Умножение дробей с разными знаками.
 Умножение и деление отрицательных чисел
Умножение и деление отрицательных чиселВ данном уроке рассматривается умножение и деление рациональных чисел.
Содержание урока
Умножение рациональных чисел
Правила умножения целых чисел справедливы и для рациональных чисел. Иными словами, чтобы умножать рациональные числа, нужно уметь
Также, необходимо знать основные законы умножения, такие как: переместительный закон умножения, сочетательный закон умножения, распределительный закон умножения и умножение на ноль.
Пример 1. Найти значение выражения
Это умножение рациональных чисел с разными знаками. Чтобы перемножить рациональные числа с разными знаками, нужно перемножить их модули и перед полученным ответом поставить минус.
Чтобы хорошо увидеть, что мы имеем дело с числами, у которых разные знаки, заключим каждое рациональное число в скобки вместе со своими знаками
Модуль числа равен , а модуль числа равен . Перемножив полученные модули, как положительные дроби, мы получили ответ , но перед ответом поставили минус, как от нас требовало правило. Чтобы обеспечить перед ответом этот минус, умножение модулей выполнялось в скобках, перед которыми и поставлен минус.
Чтобы обеспечить перед ответом этот минус, умножение модулей выполнялось в скобках, перед которыми и поставлен минус.
Короткое решение выглядит следующим образом:
Пример 2. Найти значение выражения
Пример 3. Найти значение выражения
Это умножение отрицательных рациональных чисел. Чтобы перемножить отрицательные рациональные числа, нужно перемножить их модули и перед полученным ответом поставить плюс
Решение для данного примера можно записать покороче:
Пример 4. Найти значение выражения
Решение для данного примера можно записать покороче:
Пример 5. Найти значение выражения
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Короткое решение будет выглядеть значительно проще:
Пример 6. Найти значение выражения
Переведём смешанное число в неправильную дробь. Остальное перепишем, как есть
Получили умножение рациональных чисел с разными знаками.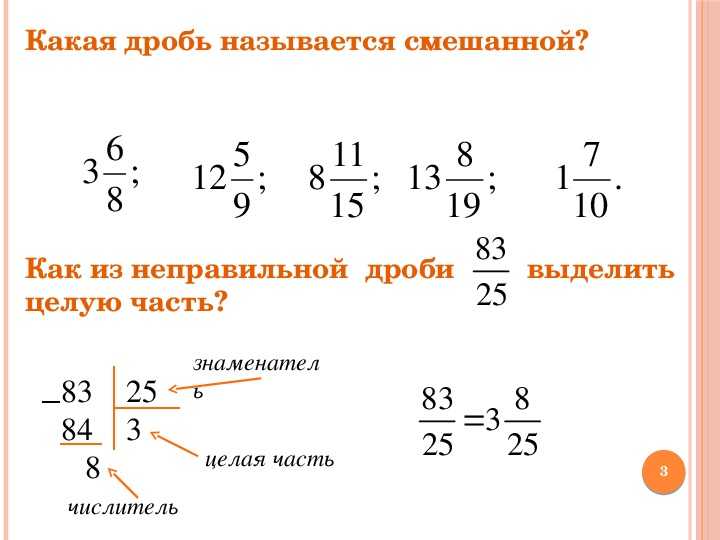 Перемножим модули этих чисел и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение
Перемножим модули этих чисел и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение
Решение для данного примера можно записать покороче
Пример 7. Найти значение выражения
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Сначала в ответе получилась неправильная дробь , но мы выделили в ней целую часть. Обратите внимание, что целая часть была выделена от модуля дроби . Получившееся смешанное число было заключено в скобки, перед которыми поставлен минус. Это сделано для того, чтобы выполнялось требование правила. А правило требовало, чтобы перед полученным ответом стоял минус.
Решение для данного примера можно записать покороче:
Пример 8. Найти значение выражения
Сначала перемножим и и полученное число перемножим с оставшимся числом 5. Запись с модулями пропустим, чтобы не загромождать выражение.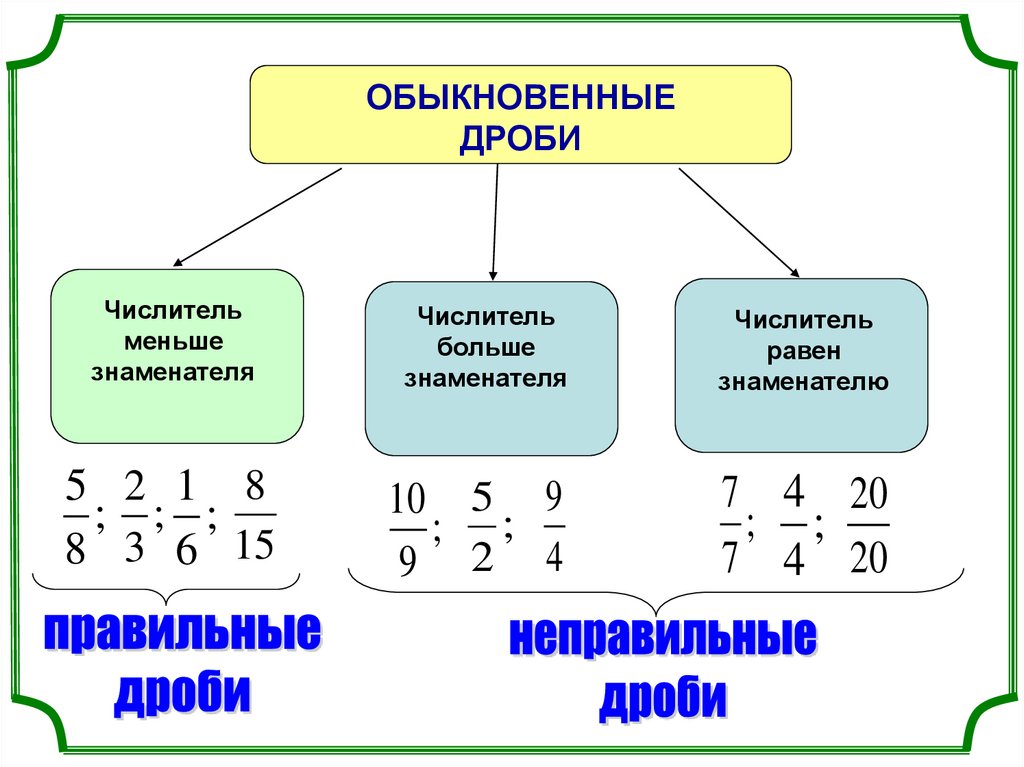
Ответ: значение выражения равно −2.
Пример 9. Найти значение выражения:
Переведём смешанные числа в неправильные дроби:
Получили умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс. Запись с модулями можно пропустить, чтобы не загромождать выражение
Пример 10. Найти значение выражения
Выражение состоит из нескольких сомножителей. Согласно сочетательному закону умножения, если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий. Это позволяет нам вычислить данное выражение в любом порядке.
Не будем изобретать велосипед, а вычислим данное выражение слева направо в порядке следования сомножителей. Запись с модулями пропустим, чтобы не загромождать выражение
Третье действие:
Четвёртое действие:
Ответ: значение выражения равно
Пример 11. Найти значение выражения
Вспоминаем закон умножения на ноль. Этот закон гласит, что произведение равно нулю, если хотя бы один из сомножителей равен нулю.
Этот закон гласит, что произведение равно нулю, если хотя бы один из сомножителей равен нулю.
В нашем примере один из сомножителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения равно нулю:
Пример 12. Найти значение выражения
Произведение равно нулю, если хотя бы один из сомножителей равен нулю.
В нашем примере один из сомножителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения равно нулю:
Пример 13. Найти значение выражения
Можно воспользоваться порядком действий и сначала вычислить выражение в скобках и полученный ответ перемножить с дробью .
Ещё можно воспользоваться распределительным законом умножения — умножить каждое слагаемое суммы на дробь и полученные результаты сложить. Этим способом и воспользуемся.
Согласно порядку действий, если в выражении присутствует сложение и умножение, то в первую очередь нужно выполнять умножение. Поэтому в получившемся новом выражении возьмём в скобки те параметры, которые должны быть перемножены. Так мы хорошо увидим, какие действия выполнить раньше, а какие позже:
Так мы хорошо увидим, какие действия выполнить раньше, а какие позже:
Третье действие:
Ответ: значение выражения равно
Решение для данного примера можно записать значительно короче. Выглядеть оно будет следующим образом:
Видно, что данный пример можно было решить даже в уме. Поэтому следует развивать в себе навык анализа выражения до начала его решения. Вполне вероятно, что его можно решить в уме и сэкономить много времени и нервов. А на контрольных и экзаменах, как известно время очень дорого стоит.
Пример 14. Найти значение выражения −4,2 × 3,2
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось .
Пример 15. Найти значение выражения −0,15 × 4
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Перемножим модули этих чисел и перед полученным ответом поставим минус
Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось суметь .
Пример 16. Найти значение выражения −4,2 × (−7,5)
Это умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс
Деление рациональных чисел
Правила деления целых чисел справедливы и для рациональных чисел. Иными словами, чтобы уметь делить рациональные числа, нужно уметь
В остальном же применяются те же методы деления обыкновенных и десятичных дробей. Чтобы разделить обыкновенную дробь на другую дробь, нужно первую дробь умножить на дробь, обратную второй.
А чтобы разделить десятичную дробь на другую десятичную дробь, нужно в делимом и в делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе, затем выполнить деление, как на обычное число.
Пример 1. Найти значение выражения:
Это деление рациональных чисел с разными знаками. Чтобы вычислить такое выражение, нужно первую дробь умножить на дробь, обратную второй.
Итак, умножим первую дробь на дробь обратную второй.
Получили умножение рациональных чисел с разными знаками. А как вычислять такие выражения мы уже знаем. Для этого нужно перемножить модули этих рациональных чисел и перед полученным ответом поставить минус.
Дорешаем данный пример до конца. Запись с модулями можно пропустить, чтобы не загромождать выражение
Таким образом, значение выражения равно
Подробное решение выглядит следующим образом:
Короткое решение будет выглядеть так:
Пример 2. Найти значение выражения
Это деление рациональных чисел с разными знаками. Чтобы вычислить данное выражение, нужно первую дробь умножить на дробь, обратную второй.
Обратная для второй дроби это дробь . На неё и умножим первую дробь:
Короткое решение будет выглядеть следующим образом:
Пример 3. Найти значение выражения
Найти значение выражения
Это деление отрицательных рациональных чисел. Чтобы вычислить данное выражение, опять же нужно первую дробь умножить на дробь обратную второй.
Обратная для второй дроби это дробь . На неё и умножим первую дробь:
Получили умножение отрицательных рациональных чисел. Как вычисляется подобное выражение мы уже знаем. Нужно перемножить модули рациональных чисел и перед полученным ответом поставить плюс.
Дорешаем этот пример до конца. Запись с модулями можно пропустить, чтобы не загромождать выражение:
Пример 4. Найти значение выражения
Чтобы вычислить данное выражение, нужно первое число −3 умножить на дробь, обратную дроби .
Обратная для дроби это дробь . На неё и умножим первое число −3
Пример 6. Найти значение выражения
Чтобы вычислить данное выражение, нужно первую дробь умножить на число, обратное числу 4.
Обратное для числа 4 это дробь . На неё и умножим первую дробь
Пример 5.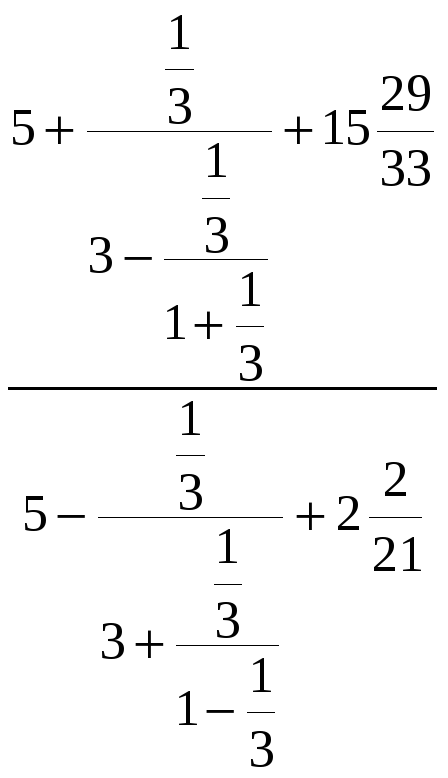 Найти значение выражения
Найти значение выражения
Чтобы вычислить данное выражение, нужно первую дробь умножить на число, обратное числу −3
Обратное для числа −3 это дробь . На неё и умножим первую дробь:
Пример 6. Найти значение выражение −14,4: 1,8
Это деление рациональных чисел с разными знаками. Чтобы вычислить данное выражение, нужно модуль делимого разделить на модуль делителя и перед полученным ответом поставить минус
Обратите внимание, как модуль делимого был разделён на модуль делителя. В данном случае, чтобы сделать это правильно, потребовалось суметь .
Если нет желания возиться с десятичными дробями (а это бывает часто), то эти , затем перевести эти смешанные числа в неправильные дроби, а затем заняться непосредственно делением.
Вычислим предыдущее выражение −14,4: 1,8 этим способом. Переведём десятичные дроби в смешанные числа:
Теперь переведём полученные смешанные числа в неправильные дроби:
Теперь можно заняться непосредственно делением, а именно разделить дробь на дробь . Для этого нужно первую дробь умножить на дробь, обратную второй:
Для этого нужно первую дробь умножить на дробь, обратную второй:
Пример 7. Найти значение выражения
Переведём десятичную дробь −2,06 в неправильную дробь, и умножим эту дробь на дробь, обратную второй:
Многоэтажные дроби
Часто можно встретить выражение, в котором деление дробей записано с помощью дробной черты. Например, выражение может быть записано следующим образом:
В чём же разница между выражениями и ? На самом деле разницы никакой. Эти два выражения несут одно и то же значение и между ними можно поставить знак равенства:
В первом случае знак деления представляет собой двоеточие и выражение записано в одну строку. Во втором случае деление дробей записано с помощью дробной черты. В результате получается дробь, которую в народе договорились называть многоэтажной .
При встрече с такими многоэтажными выражениями, нужно применять те же правила деления обыкновенных дробей. Первую дробь необходимо умножать на дробь, обратную второй.
Использовать в решении подобные дроби крайне неудобно, поэтому можно записать их в понятном виде, используя в качестве знака деления не дробную черту, а двоеточие.
Например, запишем многоэтажную дробь в понятном виде. Для этого сначала нужно разобраться, где первая дробь и где вторая, потому что сделать это правильно удаётся не всегда. В многоэтажных дробях имеется несколько дробных черт, которые могут запутать. Главная дробная черта, которая отделяет первую дробь от второй, обычно бывает длиннее остальных.
После определения главной дробной черты можно без труда понять, где первая дробь и где вторая:
Пример 2.
Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление целого числа −3 на обыкновенную дробь
А если бы мы по ошибке приняли вторую дробную черту за главную (ту, что короче), то получилось бы, что мы делим дробь на целое число 5В этом случае, даже если это выражение вычислить верно, задача будет решена неправильно, поскольку делимым в данном случае является число −3, а делителем — дробь .
Пример 3. Запишем в понятном виде многоэтажную дробь
Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление дроби на целое число 2
А если бы мы по ошибке приняли первую дробную черту за главную (ту, что короче), то получилось бы, что мы делим целое число −5 на дробь В этом случае, даже если это выражение вычислить верно, задача будет решена неправильно, поскольку делимым в данном случае является дробь , а делителем — целое число 2.
Несмотря на то, что многоэтажные дроби неудобны в работе, сталкиваться мы с ними будем очень часто, особенно при изучении высшей математики.
Естественно, на перевод многоэтажной дроби в понятный вид уходит дополнительное время и место. Поэтому можно воспользоваться более быстрым методом. Данный метод удобен и на выходе позволяет получить готовое выражение, в котором первая дробь уже умножена на дробь, обратную второй.
Реализуется этот метод следующим образом:
Если дробь четырехэтажная, например как , то цифру находящуюся на первом этаже поднимают на самый верхний этаж. А цифру, находящуюся на втором этаже поднимают на третий этаж. Полученные цифры нужно соединить значками умножения (×)
А цифру, находящуюся на втором этаже поднимают на третий этаж. Полученные цифры нужно соединить значками умножения (×)
В результате, минуя промежуточную запись мы получаем новое выражение , в котором первая дробь уже умножена на дробь, обратную второй. Удобство да и только!
Чтобы не допускать ошибок при использовании данного метода, можно руководствоваться следующим правилом:
С первого на четвёртый. Со второго на третий.
В правиле речь идет об этажах. Цифру с первого этажа нужно поднимать на четвертый этаж. А цифру со второго этажа нужно поднимать на третий этаж.
Попробуем вычислить многоэтажную дробь пользуясь вышеприведённым правилом.
Итак, цифру находящуюся на первом этаже поднимаем на четвёртый этаж, а цифру находящуюся на втором этаже поднимаем на третий этаж
В результате, минуя промежуточную запись мы получаем новое выражение , в котором первая дробь уже умножена на дробь, обратной второй. Далее можно воспользоваться имеющимися знаниями:
Попробуем вычислить многоэтажную дробь пользуясь новой схемой.
Здесь имеется только первый, второй и четвёртый этажи. Третий этаж отсутствует. Но мы не отходим от основной схемы: цифру с первого этажа поднимаем на четвёртый этаж. А поскольку третий этаж отсутствует, то цифру находящуюся на втором этаже оставляем, как есть
В результате, минуя промежуточную запись мы получили новое выражение , в котором первое число −3 уже умножено на дробь, обратную второй. Далее можно воспользоваться имеющимися знаниями:
Попробуем вычислить многоэтажную дробь , пользуясь новой схемой.
Здесь имеется только второй, третий и четвёртый этажи. Первый этаж отсутствует. Поскольку первый этаж отсутствует, подниматься на четвёртый этаж нечему, но зато мы можем поднять цифру со второго этажа на третий:
В результате, минуя промежуточную запись мы получили новое выражение , в котором первая дробь уже умножена на число, обратное делителю. Далее можно воспользоваться имеющимися знаниями:
Использование переменных
Если выражение сложное и вам кажется, что оно запутает вас в процессе решения задачи, то часть выражения можно занести в переменную и далее работать с этой переменной.
Математики часто так и делают. Сложную задачу разбивают на более лёгкие подзадачи и решают их. Затем собирают решённые подзадачи в одно единое целое. Это творческий процесс и этому учатся годами, упорно тренируясь.
Использование переменных оправдано, при работе с многоэтажными дробями. Например:
Найти значение выражения
Итак, имеется дробное выражение в числителе и в знаменателе котором дробные выражения. Другими словами, перед нами снова многоэтажная дробь, которую мы так не любим.
Выражение, находящееся в числителе можно занести в переменную с любым названием, например:
Но в математике в подобном случае переменным принято давать название из больших латинских букв. Давайте не будем нарушать эту традицию, и обозначим первое выражение через большую латинскую букву A
А выражение, находящееся в знаменателе можно обозначить через большую латинскую букву B
Теперь наше изначальное выражение принимает вид . То есть, мы сделали замену числового выражения на буквенное, предварительно занеся числитель и знаменатель в переменные A и B.
Теперь мы можем отдельно вычислить значения переменной A и значение переменной B. Готовые значения мы вставим в выражение .
Найдём значение переменной A
Найдём значение переменной B
Теперь подставим в главное выражения вместо переменных A и B их значения:
Мы получили многоэтажную дробь в которой можно воспользоваться схемой «с первого на четвёртый, со второго на третий», то есть цифру находящуюся на первом этаже поднять на четвёртый этаж, а цифру находящуюся на втором этаже поднять на третий этаж. Дальнейшее вычисление не составит особого труда:
Таким образом, значение выражения равно −1.
Конечно, мы рассмотрели простейший пример, но нашей целью было узнать, как можно использовать переменные для облегчения себе задачи, чтобы свести к минимуму допущение ошибок.
Отметим также, что решение для данного примера можно записать не применяя переменные. Выглядеть оно будет как
Это решение более быстрое и короткое и в данном случае его целесообразнее так и записать, но если выражение окажется сложным, состоящим из нескольких параметров, скобок, корней и степеней, то желательно вычислять его в несколько этапов, занося часть его выражений в переменные.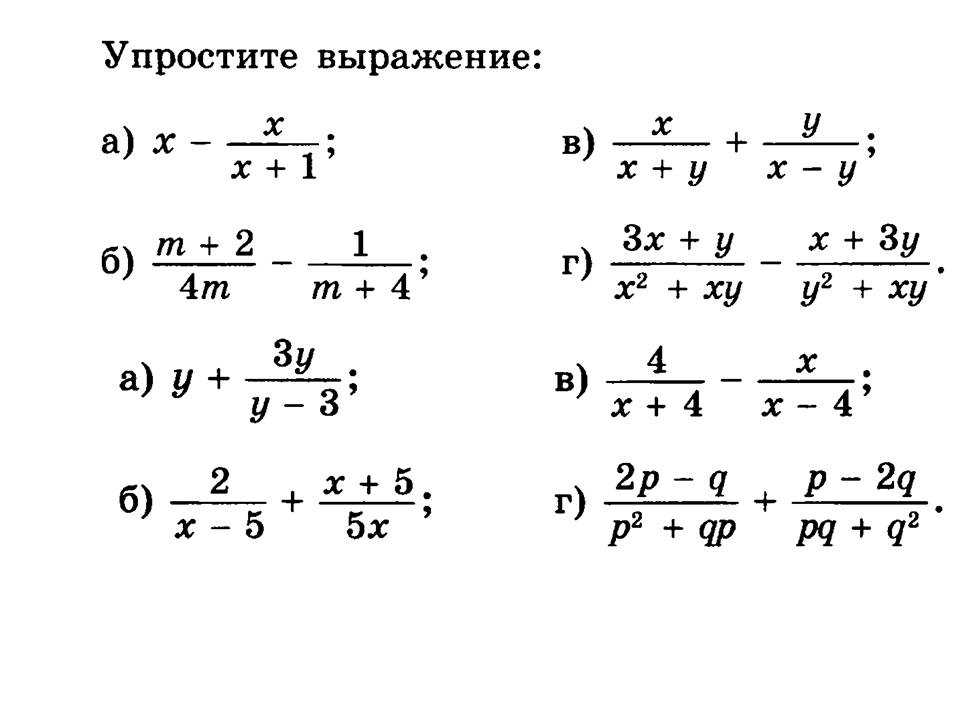
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
В этой статье мы разберемся с умножением чисел с разными знаками . Здесь мы сначала сформулируем правило умножения положительного и отрицательного числа, обоснуем его, а после этого рассмотрим применение данного правила при решении примеров.
Навигация по странице.
Правило умножения чисел с разными знаками
Умножение положительного числа на отрицательное, а также отрицательного на положительное, проводится по следующему правилу умножения чисел с разными знаками : чтобы умножить числа с разными знаками, надо умножить , и перед полученным произведением поставить знак минус.
Запишем данное правило в буквенном виде. Для любого положительного действительного числа a
и действительного отрицательного числа −b
справедливо равенство a·(−b)=−(|a|·|b|) , а также для отрицательного числа −a
и положительного числа b
справедливо равенство (−a)·b=−(|a|·|b|) .
Правило умножения чисел с разными знаками полностью согласуется со свойствами действий с действительными числами . Действительно, на их основе несложно показать, что для действительных и положительных чисел a и b справедлива цепочка равенств вида a·(−b)+a·b=a·((−b)+b)=a·0=0 , которая доказывает, что a·(−b) и a·b – противоположные числа, откуда следует равенство a·(−b)=−(a·b) . А из него следует справедливость рассматриваемого правила умножения.
Следует отметить, что озвученное правило умножения чисел с разными знаками справедливо как для действительных чисел, так и для рациональных чисел и для целых чисел . Это следует из того, что действия с рациональными и целыми числами обладают теми же свойствами, которые использовались при доказательстве выше.
Понятно, что умножение чисел с разными знаками по полученному правилу сводится к умножению положительных чисел.
Осталось лишь рассмотреть примеры применения разобранного правила умножения при умножении чисел с разными знаками.
Примеры умножения чисел с разными знаками
Разберем решения нескольких примеров умножения чисел с разными знаками . Начнем с простого случая, чтобы сосредоточиться на шагах правила, а не на вычислительных сложностях.
Пример.
Выполните умножение отрицательного числа −4 на положительное число 5 .
Решение.
По правилу умножения чисел с разными знаками нам сначала нужно перемножить модули исходных множителей. Модуль −4 равен 4 , а модуль 5 равен 5 , а умножение натуральных чисел 4 и 5 дает 20 . Наконец, осталось поставить знак минус перед полученным числом, имеем −20 . На этом умножение завершено.
Кратко решение можно записать так: (−4)·5=−(4·5)=−20 .
Ответ:
(−4)·5=−20 .
При умножении дробных чисел с разными знаками нужно уметь выполнять умножение обыкновенных дробей , умножение десятичных дробей и их комбинаций с натуральными и смешанными числами.
Пример.
Проведите умножение чисел с разными знаками 0,(2)
и .
Решение.
Выполнив перевод периодической десятичной дроби в обыкновенную дробь , а также выполнив переход от смешанного числа к неправильной дроби , от исходного произведения мы придем к произведению обыкновенных дробей с разными знаками вида . Это произведение по правилу умножения чисел с разными знаками равно . Осталось лишь перемножить обыкновенные дроби в скобках, имеем .
Hate Story IV (2018) — IMDb
Videos1
Trailer 2:42
Watch Hate Story 4 Trailer
Photos64
Top cast
Urvashi Rautela
Gulshan Grover
- Vikram Kurana
Atul Sharma
- Гость отеля Millionaire
Тиа Баджпай
- Бхавна Шривастав
Айвианна Сноу
- Читатель новостей
- Rich Hotel Guest
Manoj Anand
- Millionaire Hotel Guest
Vivan Bhatena
Karan Wahi
- Rajveer
Fiona Thompson
- Wealthy Hotel Guest
- (as Fiona)
Шубханги Латкар
- Мама Таши
Джек Армстронг
- UK News Reporter
Тай Херли
- Bar Diner
Lee Nicholas Harris
- Police officer 401
Ihana Dhillon
- Reshma
Max Dowler
- Police Sgt 492
Mohammad Salman Khan
- Salman
Shivraj Walvekar
- Police Инспектор
- Вишал Пандья
- Сценаристы
- Вишал Пандья (рассказ) (сценарий)
- Самир Арора (сценарий)
- Milap Zaveri (Диалог)
- All Cast & Crew
- Производство, касса и многое другое на Imdbpro
больше похоже на это
Стоимость ненависти 3
Hate Story
Hate Story.
Убийство 3
Великий Гранд -Масти
Baaghi
Девадас
Крриш 3
Judwaa 2
Grand Masti
Krrish
Сюжетная линия
Вы знаете,
.0003
Пользовательские обзоры19
Обзор
Показанный обзор
Великая история
Отличная история, но плохо направленная Just Urvashi Actant была потрясающей
.
- Дата выпуска
- 9 марта 2018 г. (Индия)
- Также известен как
- История ненависти 4
- Лондон, Англия 4 Места съемок
- 018
- Производственная компания
- T-Series
- См.
 Больше кредитов компании по адресу IMDBPRO
Больше кредитов компании по адресу IMDBPRO
. страница
Предложить редактирование или добавить отсутствующий контент
Top Gap
Под каким названием Hate Story IV (2018) был официально выпущен в Канаде на английском языке?
Ответ
Fantastic Four (2005) — IMDb
- Cast & crew
- User reviews
- Trivia
IMDbPro
- 20052005
- PG-13PG-13
- 1h 46m
IMDb RATING
5.7/ 10
332K
Ваше рейтинг
Популярность
Play Trailer1
:
08
2 Видео
99+ Фото чтобы противостоять планам своего врага, доктора Виктора фон Дума. Группа астронавтов получает сверхспособности после воздействия космического излучения и должна использовать их, чтобы противостоять планам своего врага, доктора Виктора фон Дума. Группа астронавтов обретает сверхспособности после космического облучения. радиационное облучение и должны использовать их, чтобы противостоять планам своего врага, доктора Виктора фон Дума.
Группа астронавтов получает сверхспособности после воздействия космического излучения и должна использовать их, чтобы противостоять планам своего врага, доктора Виктора фон Дума. Группа астронавтов обретает сверхспособности после космического облучения. радиационное облучение и должны использовать их, чтобы противостоять планам своего врага, доктора Виктора фон Дума.
IMDb RATING
5.7/10
332K
YOUR RATING
POPULARITY
- Tim Story
- Writers
- Mark Frost
- Michael France
- Stan Lee(Marvel comic book)
- Stars
- Ioan Gruffudd
- Michael Chiklis
- Chris Evans
- Tim Story
- Writers
- Mark Frost
- Michael France
- Stan Lee(Marvel comic book)
- Stars
- Ioan Gruffudd
- Michael Chiklis
- Chris Evans
- 1KUser обзоры
- 124Критические обзоры
- 40Metascore
- Награды
- 4 победы и 13 номинаций
Видео2
Трейлер 1:08
Смотреть Фантастическая четверка
Клип 3:41
Смотреть На какие роли рассматривался Крис Эванс?
Photos338
Top cast
Ioan Gruffudd
- Reed Richards
Michael Chiklis
- Ben Grimm
Chris Evans
- Johnny Storm
Jessica Alba
- Sue Storm
Julian МакМахон
- Victor Von Doom
Hamish Linklater
- Leonard
Kerry Washington
- Alicia Masters
Laurie Holden
- Debbie McIlvane
David Parker
Kevin McNulty
- Jimmy O’ Хулихан
Мария Менунос
- Сексуальная медсестра
Майкл Копса
- Нед Сесил
Эндрю Эйрли
- Compound Doctor
Pascale Hutton
- Nightclub Girlfriend
G. Michael Gray
Michael Gray
- Nightclub Boyfriend
David Richmond-Peck
- Gallery Patron
Penelope Corrin
- Bohemian Girl 1
Аоника Лоран
- Богемская девушка 2
- Тим Стори
- Писатели
- Майкл Франс
- Стэн Ли (комиксы Marvel)
Призрачный гонщик
Люди Икс: Последняя битва
X2: Люди Икс Юнайтед
Халк
Люди Икс
Сорвиголова
Люди Икс Происхождение: Росомаха 90 Фантастика0005
Росомаха
Невероятный Халк
Сюжетная линия
Знаете ли вы
- Цитаты
Джонни Шторм: Проснись, Бен.
 Эй, вставай и свети, большой мальчик. Как ты себя чувствуешь?
Эй, вставай и свети, большой мальчик. Как ты себя чувствуешь?Бен Гримм: Где я?
Джонни Сторм: Снова на Земле. Мы на карантине. Медицинское учреждение Виктора.
Бен Гримм: Рид? Сью?
Джонни Сторм: О, они в порядке. Все остальные в порядке.
Бен Гримм: Что со мной не так?
Джонни Сторм: Клянусь тебе, Бен, они сделали все возможное. Лучшие пластические хирурги мира здесь, Бен. У тебя было лучшее.
[Джонни берет ручное зеркало со столика перед кроватью до того, как Бен успевает дотянуться до него, не желая отдавать его]
Бен Гримм: Дай мне это зеркало.
Джонни Сторм: Не думаю, что это хорошая идея. Они сказали, что шок…
Бен Гримм: Я сказал, дайте мне это проклятое зеркало!
Джонни Сторм: Хорошо, Бен. Просто будь сильным.
[Бен выхватывает у него. Затем медленно поднимает его, чтобы посмотреть и убедиться, что он совершенно нормальный]
Джонни Сторм: К сожалению, врачи ничего не могли сделать, чтобы исправить твое лицо.

- Альтернативные версии
В США/Великобритании модифицированная версия была выпущена на DVD. Например, в версии для Великобритании сцены, диалоги и кадры с эффектами отличаются от гонконгской, французской и немецкой версий. Есть сообщения о том, что затронута и канадская версия. Эти изменения включают в себя:
- Рид и Сью возрождают свой роман в сцене, где пара идет и разговаривает на фоне Статуи Свободы. В гонконгской версии эта сцена отсутствует и заменена на сцену, в которой двое находятся в планетарии, где сцена заканчивается довольно резко, прежде чем пара поцелуется.0018
- Доктор Дум, говорящий «До свидания, Бен», отсутствует в финальной сцене боя в версии для Гонконга, но присутствует в версии для Великобритании. дыхание в выпуске для Гонконга, но этот эффект отсутствует в выпуске для Великобритании
- Реплика доктора Дума, когда он выходит из огня, обрывается в выпуске для Гонконга.
 Слова «Немного тепла?» не появляются, но присутствуют в британском издании
Слова «Немного тепла?» не появляются, но присутствуют в британском издании - Во время финального противостояния в британском издании, когда Существо использует свою ногу, чтобы направить воду на доктора Дума, мистер Фантастик помогает, используя свои силы, чтобы направить воду из пожарного гидранта на доктора Рок. Однако его нет в гонконгской версии, и Существо, похоже, побеждает Дума в одиночку
- Предложение Рида Сью также отличается. В британской версии он наклоняется на одно колено, потягиваясь, сохраняя при этом зрительный контакт со Сью. В гонконгской версии он на самом деле становится на одно колено по-настоящему
- Голос доктора Дума отличается в обеих версиях. В британской версии его голос звучит нормально, в то время как в гонконгской версии его голос становится более жутким и звучит так, будто он говорит из-под маски
Отзывы пользователей1K
Обзор
Избранный обзор
8/
10
Я не испытываю ненависти к этому фильму
Недавно я посмотрел версию «Фантастической четверки» 2005 года в рамках подготовки к перезагрузке, которая сейчас идет в кинотеатрах . Этот фильм и его продолжение «Восстание серебряного серфера» сняты компанией 20th Century Fox. Франшизы «Фантастическая четверка» и «Люди Икс» были сданы в аренду Fox до того, как у Marvel появились собственные киностудии, и, как и другие объекты Marvel, созданные до MCU, этот фильм часто подвергается критике со стороны фанатов комиксов.
Этот фильм и его продолжение «Восстание серебряного серфера» сняты компанией 20th Century Fox. Франшизы «Фантастическая четверка» и «Люди Икс» были сданы в аренду Fox до того, как у Marvel появились собственные киностудии, и, как и другие объекты Marvel, созданные до MCU, этот фильм часто подвергается критике со стороны фанатов комиксов.
Лично я не вижу, что здесь может не понравиться. Действительно, я думаю, что этот фильм отлично показывает историю происхождения FF. Конечно, Существо выглядит немного нелепо в том, что явно является каким-то прорезиненным костюмом, и я думаю, что они наверняка могли бы найти актера, который больше походил бы на Рида Ричардса из комиксов, чем на Иоана Грифита (кстати, это именно то имя). !). Но в целом это…..фантастический….фильм. LOL
Я даю ему 8/10 звезд. Джессика Альба отлично справилась с ролью Сью Сторм, а Джулиан МакМахон — великолепный доктор Дум. Сюжет и актерская игра сделаны хорошо, темп повествования тоже хорош. На мой взгляд, в этом фильме больше нравится, чем не нравится.

 04.2012, 00:42
04.2012, 00:42  04.2012, 01:16
04.2012, 01:16  04.2012, 16:58
04.2012, 16:58 
 04.2012, 22:13
04.2012, 22:13 
 04.2012, 00:33
04.2012, 00:33 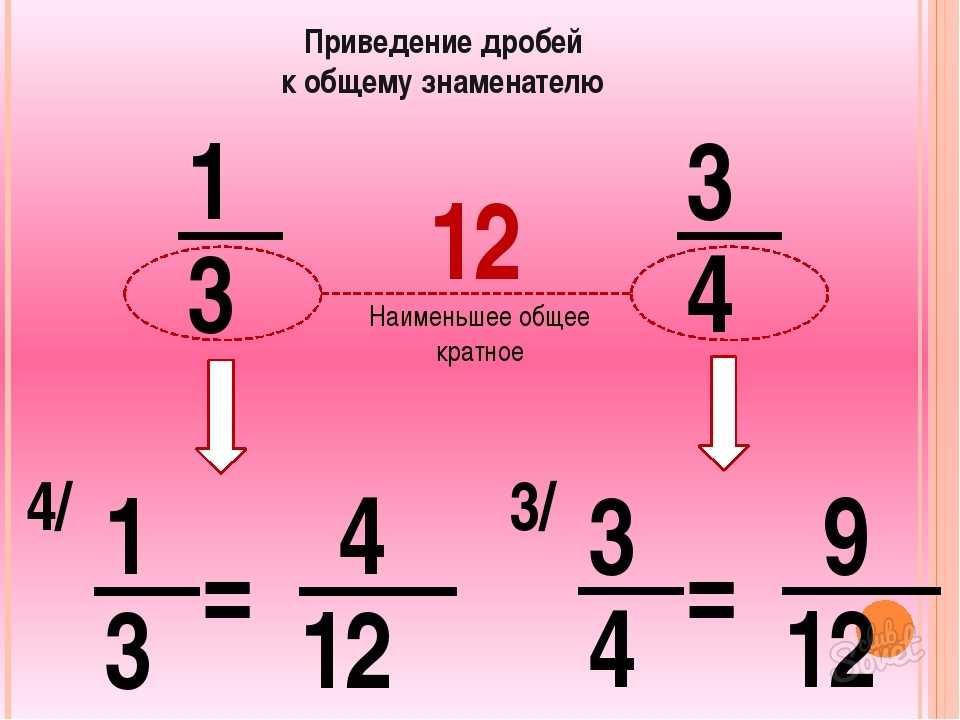 04.2012, 08:05
04.2012, 08:05 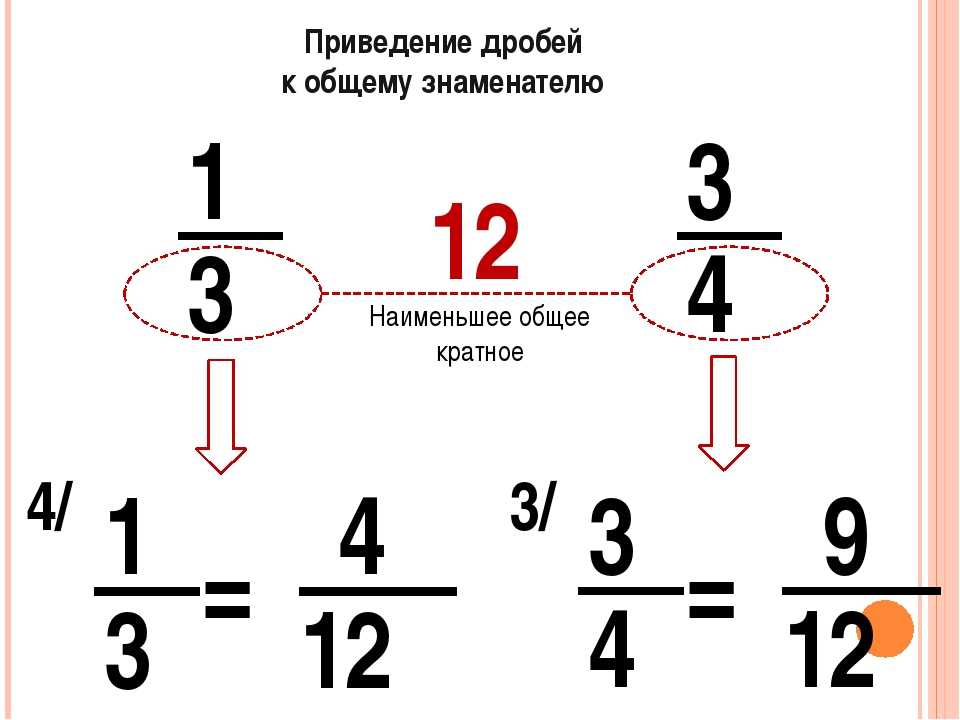 04.2012, 08:49
04.2012, 08:49  04.2012, 19:39
04.2012, 19:39