Число комбинаций: Математическое Бюро. Страница 404

Вывести все сочетания из n по k

Определение числа сочетаний

Пусть имеется $n$ различных объектов. Чтобы найти число сочетаний из $n$ объектов по $k$, будем выбирать комбинации из $m$ объектов все возможными способами, при этом будем обращать внимание на разный состав комбинаций, но не порядок (он тут не важен, в отличие от размещений).

Например, есть три объекта <1,2,3>, составляем сочетания по 2 объекта в каждом. Тогда выборки <1,2>и <2,1>- это одно и то же сочетание (так как комбинации отличаются лишь порядком). А всего различных сочетаний из 3 объектов по 2 будет три: <1,2>, <1,3>, <2,3>.

На картинке наглядно проиллюстрировано получение всех возможных сочетаний из 4 различных объектов по 2 (их будет 6, см. калькулятор сочетаний ниже, который даст формулу расчета).

Общая формула, которая позволяет найти число сочетаний из $n$ объектов по $k$ имеет вид:

Найти сочетания из n по k

Чтобы вычислить число сочетаний $C_n^k$ онлайн, используйте калькулятор ниже.

Видеоролик о сочетаниях

Не все понятно? Посмотрите наш видеообзор для формулы сочетаний: как использовать Excel для нахождения числа сочетаний, как решать типовые задачи и использовать онлайн-калькулятор.

Расчетный файл из видео можно бесплатно скачать

Полезные ссылки

Решебник по ТВ

Решебник с задачами по комбинаторике и теории вероятностей:

Сочетания из N элементов по K в лексикографическом порядке

Постановка задачи. Даны натуральные числа N и K. Рассмотрим множество чисел от 1 до N. Требуется вывести все различные его подмножества мощности K, причём в лексикографическом порядке.

Алгоритм весьма прост. Первым сочетанием, очевидно, будет сочетание (1,2. K). Научимся для текущего сочетания находить лексикографически следующее. Для этого в текущем сочетании найдём самый правый элемент, не достигший ещё своего наибольшего значения; тогда увеличим его на единицу, а всем последующим элементам присвоим наименьшие значения.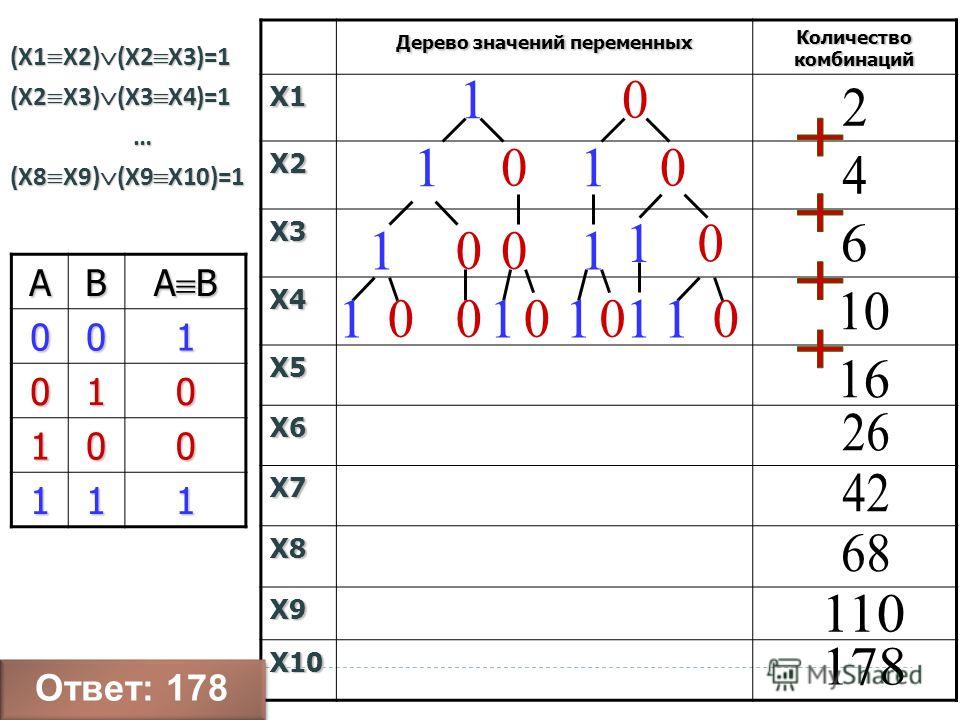

С точки зрения производительности, этот алгоритм линеен (в среднем), если K не близко к N (т.е. если не выполняется, что K = N — o(N)). Для этого достаточно доказать, что сравнения «a[i] k раз, т.е. в (N+1) / (N-K+1) раз больше, чем всего есть сочетаний из N элементов по K.

Сочетания из N элементов по K с изменениями ровно одного элемента

Требуется выписать все сочетания из N элементов по K, но в таком порядке, что любые два соседних сочетания будут отличаться ровно одним элементом.

Интуитивно можно сразу заметить, что эта задача похожа на задачу генерации всех подмножеств данного множества в таком порядке, когда два соседних подмножества отличаются ровно одним элементом. Эта задача непосредственно решается с помощью Кода Грея: если мы каждому подмножеству поставим в соответствие битовую маску, то, генерируя с помощью кодов Грея эти битовые маски, мы и получим ответ.

Может показаться удивительным, но задача генерации сочетаний также непосредственно решается с помощью кода Грея. А именно, сгенерируем коды Грея для чисел от 0 до 2 N -1, и оставим только те коды, которые содержат ровно K единиц. Удивительный факт заключается в том, что в полученной последовательности любые две соседние маски (а также первая и последняя маски) будут отличаться ровно двумя битами, что нам как раз и требуется.

Для доказательства вспомним факт, что последовательность G(N) кодов Грея можно получить следующим образом:

т.е. берём последовательность кодов Грея для N-1, дописываем в начало каждой маски 0, добавляем к ответу; затем снова берём последовательность кодов Грея для N-1, инвертируем её, дописываем в начало каждой маски 1 и добавляем к ответу.

Теперь мы можем произвести доказательство.

Сначала докажем, что первая и последняя маски будут отличаться ровно в двух битах. Для этого достаточно заметить, что первая маска будет иметь вид N-K нулей и K единиц, а последняя маска будет иметь вид: единица, потом N-K-1 нулей, потом K-1 единица. Доказать это легко по индукции по N, пользуясь приведённой выше формулой для последовательности кодов Грея.

Теперь докажем, что любые два соседних кода будут отличаться ровно в двух битах. Для этого снова обратимся к формуле для последовательности кодов Грея. Пусть внутри каждой из половинок (образованных из G(N-1)) утверждение верно, докажем, что оно верно для всей последовательности. Для этого достаточно доказать, что оно верно в месте «склеивания» двух половинок G(N-1), а это легко показать, основываясь на том, что мы знаем первый и последний элементы этих половинок.

Приведём теперь наивную реализацию, работающую за 2 N :

Стоит заметить, что возможна и в некотором смысле более эффективная реализация, которая будет строить всевозможные сочетания на ходу, и тем самым работать за O (C_n k n). С другой стороны, эта реализация представляет собой рекурсивную функцию, и поэтому для небольших n, вероятно, она имеет большую скрытую константу, чем предыдущее решение.

Собственно сама реализация — это непосредственное следование формуле:

Эта формула легко получается из приведённой выше формулы для последовательности Грея — мы просто выбираем подпоследовательность из подходящих нам элементов.

В комбинаторике сочетанием из N различных элементов по M называется набор M элементов, выбранных из множества N элементов. Такие наборы отличаются только вхождением в них M определенных элементов, порядок следования элементов в таком наборе не важен. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, и этим сочетания отличаются от размещений.

Сочетания без повторений

Задача : Найти все возможные сочетания без повторений из множества элементов <1,2,3>по 2.
Существуют следующие сочетания:

1: 1 2
2: 1 3
3: 2 3

Количество возможных сочетаний без повторений из N элементов по M можно определить по формуле (N≥M):

что в M! раз меньше соответствующего количества размещений без повторений (поскольку сочетания без повторений не зависят от порядка следования элементов).

Рассмотрим задачу получения всех сочетаний для чисел 1…N по M.

Реализация на С++

Результат выполнения

Сочетания с повторениями

Сочетаниями с повторениями называются наборы по M элементов, в которых каждый элемент множества N может участвовать несколько раз. При этом на соотношение значений M и N не накладывается никаких ограничений, а общее количество сочетаний с повторениями составляет

Примером такой задачи может служить выбор M открыток из N всеми возможными способами.

Для генерации сочетаний с повторениями воспользуемся решением для генерации размещений с повторениями, рассмотренным в этой статье.

Реализация на С++

Результат работы приведенного выше алгоритма:

Схватка интеллектов

В 1997 году под натиском Deep Blue пал шахматный король Гарри Каспаров. Тот эпохальный шестиматчевый поединок он проиграл со счётом 3,5 на 2,5. После этого стало окончательно понятно, что полное превосходство техники над человеком – лишь вопрос времени. Однако считалось, что в го – одну из сложнейших игр – компьютер выиграет ещё очень не скоро. Кто-то отводил на это целое столетие, но даже в самых оптимистичных прогнозах фигурировали в лучшем случае 2025-2030 годы.

К настоящему моменту компьютер победил человека практически во всех логических настольных играх. Достаточно быстро «сдались»: крестики-нолики, реверси и скрэббл. А вот шашки, шахматы, нарды и, естественно, го продержались куда дольше, ведь победа в них обусловлена не столько умением хорошо считать и перебирать возможные игровые ситуации, сколько такими присущими только человеку свойствами как интуиция, чутьё и жизненный опыт. Только человек, обладая незначительным объёмом информации о противнике и его прошлых играх, а иногда исключительно из вербальных и невербальных символов мог просчитать свои предстоящие ходы и возможные ответы противника, поставить «ловушки» и обманки, разработать победную стратегию.

Вообще надо сказать, что первая победа компьютера в шахматах была зафиксирована в 1956 году. MANIAC I (Mathematical Analyzer, Numerical Integrator and Computer – Математический анализатор, числовой интегратор и компьютер), созданный в 1952 году в Лос-Аламосской национальной лаборатории поставил своему сопернику мат в 23 хода. Правда, играл он тогда с новичком и по упрощённым правилам. Но уже в 1981 году Cray Blitz на закрытом шахматном чемпионате в Миссисипи обыграл всех человеческих соперников, в том числе мастера спорта. С того момента машины стали всё чаще и чаще побеждать титулованных соперников. В 1996 году сильнейший шахматист мира Гарри Каспаров одержал победу над созданной IBM программой Deep Blue. Однако проиграл ей же уже в следующем, 1997 году. Deep Blue была способна отрабатывать 200 миллионов позиций в секунду. В последующих играх наиболее частым результатом становились ничья или победа программы. Так, в 2003 году Каспаров сыграл вничью с двумя программами, а вот Владимир Крамник в 2002-м проиграл усовершенствованному Deep Fritz.

Компьютеры «запоминают» все сыгранные или известные комбинации, поэтому человек способен победить компьютер, но только в совершенно новой, ещё неизвестной ситуации на шахматной доске. Просчитать шахматы до конца компьютер не в состоянии, поскольку число возможных на шахматной доске позиций составляет 10⁴⁶. Для отработки всех этих вариантов даже самым современным компьютерам потребуется несколько миллиардов лет.

А вот в шашках количество комбинаций оценивается куда меньшим числом – 10²⁰. И эта игра уже полностью «решена». Чемпиона мира по шашкам компьютер впервые обыграл ещё в 1994 году, а в 2007-м на суперкомпьютере были просчитаны все возможные ходы. Поэтому модифицированная программа Chinook стала беспроигрышной, так как в любой позиции она знает наилучший ход. Обыграть её человек не способен ни при каких раскладах.

Как ни удивительно, но машина стабильно побеждает человека и в такой игре как камень-ножницы-бумага. Учёные давно выявили оптимальный алгоритм действий, однако какое-то время человеку всё-таки удавалось «обманывать» компьютер и выигрывать. Но теперь искусственный игрок выучивает тактику соперника и при достаточно большом количестве раундов всегда оказывается победителем.

Постепенно разработчики обучили программы и нечёткой логике, позволяющей принимать оптимальные решения в играх с неполной информацией. Считается, что в таких играх есть элемент случайности, везения. Так, например, если победа шахматиста полностью зависит от способностей игрока, то в нардах несколько неудачных выпадений на кубиках может помешать сильному игроку победить. Однако и в нардах победа остаётся за машинами, а не за человеком. Летом 1979 года на Мировом чемпионате по нардам в Монте-Карло программа BKG 9.8 выиграла с разгромным счётом. В этой игре даже при неудачном выбросе кубиков есть оптимальные ходы, позволяющие одержать победу. И компьютеры научились корректировать стратегию в зависимости от таких «случайностей».

Одной из последних «сдалась» машинам игра в покер. В ней помимо случайных вариантов получения собственных карт при раздаче есть элементы неопределённости карт у других игроков и их способности блефовать.

Несмотря на то, что компьютеры блефовать не могут, в 2015 году в научном журнале Science была описана программа, способная победить человека в самой популярной разновидности покера – Техасском холдеме. Перед победой над человеком компьютер сыграл сам с собой 24 триллиона партий. В этих играх программа оценивала ходы – сделанные и потенциально возможные в данной ситуации, исходя из последовавших «денежных» потерь. Бесконечно играя в карты, компьютер вычислил оптимальные стратегии для всех возможных раздач, и теперь победить его невозможно за исключением особо неудачных вариантов карт. Конечно, машина играет без азарта и не имеет цели перехитрить противников. Но она и не совершает ошибок, присущих людям в силу их эмоциональности.

А вот теперь компьютером была одолена и считавшаяся неподвластной искусственному разуму древняя игра го. В октябре 2015 года победу над трёхкратным чемпионом Европы Фанем Хуэем в пяти играх со счётом 5:0 присудили программе AlphaGo, а в марте 2016-го со счётом 4:1 был обыгран лучший игрок последних десяти лет чемпион мира Ли Седоль.

После поражения Фань Хуэй признал, что если бы не знал, что играет с компьютером, то решил бы, что это  человек – немного странный, но сильный и очень техничный игрок. Наблюдая за этими играми, президент Британской ассоциации го Джон Даймонд заключил: «Я был очень впечатлён силой игры AlphaGo, и у меня возникали сложности с определением того, на какой стороне играет компьютер, а на какой – человек, пока я не знал, каким цветом играл Хуэй.  До этой серии игр у меня не было и мысли, что компьютер сможет соперничать с профессионалами, а теперь, похоже, победа машины над топ-игроками является неизбежностью».

Несмотря на проигрыш Фань Хуэя, следующий соперник AlphaGo – Ли Седоль – был уверен, что выиграет у компьютера. Он согласился на матч, даже не посмотрев партии Фань Хуэя. Разрыв в силе между 2 даном и элитным игроком 9 дана столь велик, что партии Фань Хуэя с AlphaGo не позволили бы ему судить о реальной силе программы. Корейский мастер не рассматривал возможности поражения, поэтому даже не оговорил суммы своего гонорара в случае проигрыша, как это делается обычно.

Между тем, призовой фонд матча составлял 1 млн долларов + 20 тысяч долларов за каждую победу (в случае победы AlphaGo деньги шли на благотворительность). В интервью перед матчем Ли Седоль предсказывал, что он легко выиграет со счётом 4-1 или даже 5-0 и последующие 2-3 года Google будут дорабатывать AlphaGo, после чего захотят взять у него реванш; в этом случае играть с обновлённой версией AlphaGo будет действительно интересно.

В стартовой партии Ли Седоль ходил первым по специально разработанному им перед игрой началу. После нескольких начальных ходов партия не имела аналогов в истории, и уже после 186-го хода в безнадёжной позиции Ли Седоль признал своё поражение в первом матче. Чемпион признался, что в игре ни разу не ощущал своего преимущества перед соперником. AlphaGo ходила спокойно и уверенно, а в самые неожиданные моменты делала резкие выпады в сторону противника. В первой половине партии была острая равная борьба, но на 102-м ходу AlphaGo сделала невероятно сильный ход, переломив таким образом весь ход партии.

Впоследствии Ли Седоль проиграл ещё три игры – вторую, третью и пятую. На пресс-конференции, посвящённой единственной выигранной им партии чемпион заявил, что смог найти у программы несколько слабых сторон, приводящих к её неожиданному поведению и итоговому результату. Во-первых, ему показалось, что AlphaGo сложнее играть чёрными камнями, чем белыми. Во-вторых, неожиданные ходы противника буквально ставят программу в тупик и приводят к тому, что возможность хорошего ответного хода с её стороны резко снижается. Однако для победы над компьютером таких выводов оказалось недостаточно.

Наблюдавшие за игрой эксперты не ожидали столь разгромного для человека финала, никто не предполагал, что компьютер способен усовершенствоваться так быстро. Руководитель службы компьютерного зрения и нейросетевых технологий компании «Яндекс» Александр Крайнов сказал после этого матча: «У AlphaGo просто нет слабых мест. Сила его самого слабого хода очень велика. Он не ошибается».

Уникальность программы AlphaGo заключается в том, что в её основе лежат искусственные нейронные сети. Они позволяют программе анализировать абстракции, составлять сложное многоуровневое представление о ситуации и выявлять стратегию, с большой вероятностью приводящую к успеху. Это совершенно новое решение для игровых программ. Именно этим и обусловлен успех AlphaGo. В го количество возможных комбинаций составляет 10

171, и это несоизмеримо больше даже чем у шахмат. Причём для первого хода (361 вариант) и ответа противника (360 вариантов) количество возможных комбинаций на доске уже составляет 129 960. Нужно учитывать и фактор ветвления, увеличивающий возможные комбинации, ведь среднее количество ходов в одной игре составляет примерно 200-250, тогда как в шахматах только 35-40. Поэтому простым перебором возможных ситуаций построить игру машины нельзя. У человека за выбор перспективного хода в большей степени отвечает интуиция или образное восприятие. Далеко не все игроки понимают, почему они ходят именно так, а не иначе: «Просто смотришь на доску и знаешь», – говорят они.

Перед программистами AlphaGo стояла задача не просто научить машину играть по правилам и распознавать ситуацию на доске, но и оценивать перспективность ходов.

Поэтому построена программа была на базе двух нейронных сетей. Нейронные сети по принципу действия схожи с работой нейронов мозга человека, в котором информация никогда не записывается в окончательном варианте – происходит постоянное образование, изменение силы и разрушение нейронных связей. Значит, и компьютерные алгоритмы нужно было научить не просто навсегда фиксировать что-то в памяти, а перестраиваться в процессе обработки информации. Такой алгоритм способен к обучению и именно такие сети позволяют современным программам распознавать образы (лица, буквы, объекты). Они способны действовать самостоятельно, руководствуясь приобретёнными знаниями, а не по заданной человеком схеме.

Первая часть AlphaGo включает 12 слоёв нейронной сети, которые распознают образы, и умеет по текущей картинке определять, как будет выглядеть игровое поле после следующего хода. После обучения программы, которое проходило на 30 миллионах ходов из известных игровых партий, она с вероятностью в 57% стала предсказывать следующий ход живых игроков. Вторая сеть AlphaGo моделирует развитие событий на несколько шагов вперёд и определяет самые выгодные варианты ходов. «Сеть оценок» нужна в первую очередь для того, чтобы резко сократить число возможных ходов на доске и упростить вычисления, а «сеть решений» – для выбора оптимального шага из самых густых ветвей «дерева» возможных решений. Сократив число приемлемых ходов, машина просчитывает наперёд разные комбинации, находя наиболее выигрышные. Но делает это не до конца партии, а лишь на несколько десятков ходов вперёд. Совместная работа этих двух частей напоминает человеческое мышление: на каждом ходу AlphaGo сначала на основании опыта проводит оценку текущей позиции на доске и определяет наиболее вероятные действия противника (по известным аналогиям), а потом на основании проведённого анализа высчитывает плюсы и минусы каждого из них для выбора следующего хода. Таким образом AlphaGo из всех возможных ходов способна выявлять наиболее перспективные. При этом действия AlphaGo не лишены и элемента случайности: программа с определённой вероятностью может выбрать любой из нескольких наиболее выгодных вариантов ходов.

Программа прошла длительную тренировку, вначале изучая игры профессионалов, в том числе онлайн-игры, а также играя сама с собой. Эксперты считают, что именно после игр с самой собой она научилась играть на профессиональном уровне. Алгоритмы обучения отрабатывали в том числе и на консольных играх: через информацию о пикселях на экране и счёт программа постигала логику игры, совершая случайные действия и наблюдая за результатами этих действий. Уже через несколько часов тренировок программа побеждала почти в каждой игре. В этих играх AlphaGo достигла рейтинга в 3,1 тысячи эло, что соответствует уровню гроссмейстера международного уровня в шахматах или профессиональному третьему дану в го. Отработанные программой 30 млн комбинаций позволили ей развить собственное «чувство игры» или интуицию.

Общая стоимость AlphaGo, разумеется, очень высока – она составляет несколько десятков миллионов долларов. На одну программу AlphaGo работает 176 графических карточек Nvidia. Кроме того, нейронная сеть использует 1200 процессоров. Ей требуются сотни часов работы серверов для обучения алгоритма и тысячи человеко-часов работы программистов.

Подпишитесь на eRazvitie.org в Фейсбуке и ВКонтакте, чтобы не пропустить новые материалы.

Сколько комбинаций из 10 цифр. Элементы комбинаторики. Опорный конспект по разделу «комбинаторика»

КОМБИНАТОРИКА

Комбинаторика — раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.

Правила сложения и умножения в комбинаторике

Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В — n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.

Пример 1.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?

Решение

Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.

По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.

Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n 1 способами, второе действие n 2 способами, третье — n 3 способами и так до k-го действия, которое можно выполнить n k способами, то все k действий вместе могут быть выполнены:

способами.

Пример 2.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?

Решение

Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.

После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.

По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.

Сочетания без повторений. Сочетания с повторениями

Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?

Пример 3.

Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?

Решение

Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:

.

Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?

.

Пример 4.

В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Решение

Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

.

Размещения без повторений. Размещения с повторениями

Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?

Пример 5.

В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?

Решение.

В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:

Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.

Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно вы б рать и разместить по m различным местам m из n предметов, с реди которых есть одинаковые?

Пример 6.

У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера- составить каталог. Сколько различных пятизначных номеров может составить мальчик?

Перестановки без повторений . Перестановки с повторениями

Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?

Пример 7.

Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?

Решение

Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.

Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k

Пример 8.

Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?

Решение

Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно

ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»

Все N элементов, и ни один не повторяется, то это задача о количестве перестановок. Решение можно найти простым . На первом месте в ряду может стоять любой из N элементов, следовательно, получается N вариантов. На втором месте — любой, кроме того, который уже был использован для первого места. Следовательно, для каждого из N уже найденных вариантов есть (N — 1) вариантов второго места, и общее количество комбинаций становится N*(N — 1).
Это же можно повторить для остальных элементов ряда. Для самого последнего места остается только один вариант — последний оставшийся элемент. Для предпоследнего — два варианта, и так далее.
Следовательно, для ряда из N неповторяющихся элементов возможных перестановок равно произведению всех целых от 1 до N. Это произведение называется факториалом числа N и обозначается N! (читается «эн факториал»).

В предыдущем случае количество возможных элементов и количество мест ряда совпадали, и их число было равно N. Но возможна ситуация, когда в ряду меньше мест, чем имеется возможных элементов. Иными словами, количество элементов в выборке равно некоторому числу M, причем M Во-первых, может потребоваться сосчитать общее количество возможных способов, которыми можно выстроить в ряд M элементов из N. Такие способы называются размещениями.
Во-вторых, исследователя может интересовать число способов, которыми можно выбрать M элементов из N. При этом порядок расположения элементов уже не важен, но любые два варианта должны различаться между собой хотя бы одним элементом. Такие способы называются сочетаниями.

Чтобы найти количество размещений по M элементов из N, можно прибегнуть к такому же способу рассуждений, как и в случае с перестановками. На первом месте здесь по-прежнему может стоять N элементов, на втором (N — 1), и так далее. Но для последнего места количество возможных вариантов равняется не единице, а (N — M + 1), поскольку, когда размещение будет закончено, останется еще (N — M) неиспользованных элементов.
Таким образом, число размещений по M элементов из N равняется произведению всех целых чисел от (N — M + 1) до N, или, что то же самое, частному N!/(N — M)!.

Очевидно, что количество сочетаний по M элементов из N будет меньше количества размещений. Для каждого возможного сочетания есть M! возможных размещений, зависящих от порядка элементов этого сочетания. Следовательно, чтобы найти это количество, нужно разделить число размещений по M элементов из N на N!. Иными словами, количество сочетаний по M элементов из N равно N!/(M!*(N — M)!).

Друзья! Раз уж есть у меня этот мертвый блокнот, использую-ка я его для того, чтобы задать вам задачку, над которой вчера билось три физика, два экономиста, один политеховский и один гуманитарий. Мы сломали себе весь мозг и у нас постоянно получаются разные результаты. Может быть, среди вас есть программисты и математические гении, к тому же, задачка вообще школьная и очень легкая, у нас просто не выводится формула. Потому что мы бросили занятия точными науками и вместо этого зачем-то пишем книги и рисуем картины. Простите.

Итак, предыстория.

Мне выдали новую банковскую карточку и я, как водится, играючи угадала ее пин-код. Но не подряд. В смысле, допустим, пин-код был 8794, а я назвала 9748. То есть, я триумфально угадала все цифры , которое содержались в данном четырехзначном числе. Ну да, не само число , а просто его составляющие у гадала. Но цифры-то все верные! ПРИМЕЧАНИЕ — я действовала наугад, то есть, мне не надо было расставить уже известные числа в нужном порядке, я просто действовала в духе: вот тут есть неизвестные мне четыре цифры, и я считаю, что среди них могут быть 9, 7, 4 и 8, а порядок их не важен. Мы тут же задались вопросом, сколько у меня вообще было вариантов (наверное, чтобы понять, насколько это круто, что я вот взяла и угадала). То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.

Собственно, суть вопроса. Какова вероятность угадывания (в любом порядке) четырех чисел, содержащихся в четырехзначном числе?

Или нет, переформулируем (я гуманитарий, простите, хотя к математике всегда питала огромную слабость), чтобы было яснее и четче. Сколько не повторяющихся комбинаций цифр содержится в ряду порядковых числительных от 0 до 9999? (пожалуйста, не путайте это с вопросом «сколько комбинаций не повторяющихся цифр»!! ! цифры могут повторяться! в смысле, 2233 и 3322 — это в данном случае одна и та же комбинация!!).

Или еще конкретнее. Мне нужно четыре раза угадать одну цифру из десяти. Но не подряд.

Ну или еще как-нибудь. В общем, нужно узнать, сколько у меня было вариантов числовой комбинации, из которой складывался пин-код карточки. Помогите, люди добрые! Только, пожалуйста, помогая, не начинайте сразу писать, что вариантов этих 9999 (вчера такое всем приходило в голову поначалу), потому что это же глупости — ведь в том ракурсе, который нас волнует, число 1234, число 3421, число 4312 и так далее являются одним и тем же! Ну и да, цифры же могут повторяться, ведь бывает пин-код 1111 или там, например, 0007. Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну?

Пожалуйста, подкрепите свои ответы и рассуждения какими-нибудь точными формулами, потому что мы вчера и так чуть не свихнулись. Заранее всем большое спасибо!

P.S. Один умный человек, программист, художник и изобретатель, только что очень верно подсказал правильное решение проблемы, подарив мне несколько минут прекрасного настроения: «решение задачи такое: у неё обсессивно-комп ульсивное расстройство, лечение такое: замуж и окучивать помидоры. меня бы больше на её месте волновал не вопрос «какова вероятность», а вопрос «схуя ли я обращаю внимание на все эти цифры»? В общем-то, даже нечего добавить:)

Калькулятор ниже предназначен для генерации всех сочетаний из n по m элементов.
Число таких сочетаний, как можно рассчитать с помощью калькулятора Элементы комбинаторики. Перестановки, размещения, сочетания.

Описание алгоритма генерации под калькулятором.

Алгоритм

Комбинации генерируются в лексикографическом порядке. Алгоритм работает с порядковыми индексами элементов множества.
Рассмотрим алгоритм на примере.
Для простоты изложения рассмотрим множество из пяти элементов, индексы в котором начинаются с 1, а именно, 1 2 3 4 5.
Требуется сгенерировать все комбинации размера m = 3.
Сначала инициализуется первая комбинация заданного размера m — индексы в порядке возрастания
1 2 3
Далее проверяется последний элемент, т. е. i = 3. Если его значение меньше n — m + i, то он инкрементируется на 1.
1 2 4
Снова проверяется последний элемент, и опять он инкрементируется.
1 2 5
Теперь значение элемента равно максимально возможному: n — m + i = 5 — 3 + 3 = 5, проверяется предыдущий элемент с i = 2.
Если его значение меньше n — m + i, то он инкрементируется на 1, а для всех следующих за ним элементов значение приравнивается к значению предыдущего элемента плюс 1.
1 (2+1)3 (3+1)4 = 1 3 4
Далее снова идет проверка для i = 3.
1 3 5
Затем — проверка для i = 2.
1 4 5
Потом наступает очередь i = 1.
(1+1)2 (2+1)3 (3+1)4 = 2 3 4
И далее,
2 3 5
2 4 5
3 4 5 — последнее сочетание, так как все его элементы равны n — m + i.

Несмотря на важную роль PIN-кодов в мировой инфраструктуре, до сих пор не проводилось академических исследований о том, как, собственно, люди выбирают PIN-коды.

Исследователи из университета Кембриджа Sören Preibusch и Ross Anderson исправили ситуацию, опубликовав первый в мире количественный анализ сложности угадывания 4-циферного банковского PIN-кода.

Используя данные об утечках паролей из небанковских источников и онлайн анкетирование, учёные выяснили, что к выбору PIN-кодов пользователи относятся гораздо серьёзнее, чем к выбору паролей для веб-сайтов: большинство кодов содержат практически случайный набор цифр. Тем не менее, среди исходных данных присутствуют и простые комбинации, и дни рождения, — то есть, при некотором везении злоумышленник может просто угадать заветный код.

Отправной точкой исследования был набор 4-циферных последовательностей в паролях из базы RockYou (1.7 млн), и базы из 200 тысяч PIN-кодов от программы блокировки экрана iPhone (базу предоставил разработчик приложения Daniel Amitay). В графиках, построенных по этим данным, проступают интересные закономерности — даты, года, повторяющиеся цифры, и даже PIN-коды, заканчивающиеся на 69. На основе этих наблюдений учёные построили линейную регрессионную модель, которая оценивает популярность каждого PIN-кода в зависимости от 25 факторов, — например, является ли код датой в формате ДДММ, является ли он возрастающей последовательностью, и так далее. Этим общим условиям соответствуют 79% и 93% PIN-кодов в каждом из наборов.

Итак, пользователи выбирают 4-циферные коды на основе всего нескольких простых факторов. Если бы так выбирались и банковские PIN-коды, 8-9% из них можно было бы угадать всего за три попытки! Но, конечно, к банковским кодам люди относятся гораздо внимательнее. Ввиду отсутствия сколько-нибудь большого набора настоящих банковских данных, исследователи опросили более 1300 человек, чтобы оценить, насколько реальные PIN-коды отличаются от уже рассмотренных. Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т. д.).

Оказалось, что люди действительно гораздо тщательнее выбирают банковские PIN-коды. Примерно четверть опрошенных используют случайный PIN, сгенерированный банком. Более трети выбирают свой PIN-код, используя старый номер телефона, номер студенческого билета, или другой набор цифр, который выглядит случайным. Согласно полученным результатам, 64% владельцев карт используют псевдослучайный PIN-код, — это гораздо больше, чем 23-27% в предыдущих экспериментах с не-банковскими кодами. Ещё 5% используют цифровой паттерн (например, 4545), а 9% предпочитают паттерн на клавиатуре (например, 2684). В целом, злоумышленник с шестью попытками (три с банкоматом и три с платёжным терминалом) имеет меньше 2% шансов угадать PIN-код чужой карты.

Фактор	Пример	RockYou	iPhone	Опрос
Даты
ДДММ	2311	5.26	1.38	3. 07
ДМГГ	3876	9.26	6.46	5.54
ММДД	1123	10.00	9.35	3.66
ММГГ	0683	0.67	0.20	0.94
ГГГГ	1984	33.39	7.12	4.95
Итого		58.57	24.51	22.76
Клавиатурный паттерн
смежные	6351	1.52	4.99	—
квадрат	1425	0.01	0.58	—
углы	9713	0.19	1.06	—
крест	8246	0.17	0.88	—
диагональная линия	1590	0.10	1.36	—
горизонтальная линия	5987	0.34	1. 42	—
слово	5683	0.70	8.39	—
вертикальная линия	8520	0.06	4.28	—
Итого		3.09	22.97	8.96
Цифровой паттерн
заканчивается на 69	6869	0.35	0.57	—
только цифры 0-3	2000	3.49	2.72	—
только цифры 0-6	5155	4.66	5.96	—
повторяющиеся пары	2525	2.31	4.11	—
одинаковые цифры	6666	0.40	6.67	—
убывающая последовательность	3210	0.13	0.29	—
возрастающая последовательность	4567	3.83	4. 52	—
Итого		15.16	24.85	4.60
Случайный набор цифр		23.17	27.67	63.68

Всё бы хорошо, но, к сожалению, существенная часть опрошенных (23%) выбирает PIN-код в виде даты, — и почти треть из них использует дату своего рождения. Это существенно меняет дело, ведь почти все (99%) респонденты ответили, что хранят в бумажнике с банковскими картами различные удостоверения личности, на которых эта дата напечатана. Если злоумышленник знает день рождения владельца карты, то при грамотном подходе вероятность угадывания PIN-кода взлетает до 9%.

100 самых популярных PIN-кодов

0000, 0101-0103, 0110, 0111, 0123, 0202, 0303, 0404, 0505, 0606, 0707, 0808, 0909, 1010, 1101-1103, 1110-1112, 1123, 1201-1203, 1210-1212, 1234, 1956-2015, 2222, 2229, 2580, 3333, 4444, 5252, 5683, 6666, 7465, 7667.

P.S. На практике, разумеется, злоумышленнику гораздо проще подсмотреть ваш PIN-код, чем угадывать его. Но и от подглядывания можно защититься — даже, казалось бы, в безвыходном положении:

Комбинаторика — это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиально возможное количество различных вариантов развития событий.

Основная формула комбинаторики

Пусть имеется k групп элементов, причем i-я группа состоит из n i элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n 1 *n 2 *n 3 *…*n k .

Пример 1. Поясним это правило на простом примере. Пусть имеется две группы элементов, причем первая группа состоит из n 1 элементов, а вторая — из n 2 элементов. Сколько различных пар элементов можно составить из этих двух групп, таким образом, чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли первый элемент из первой группы и, не меняя его, перебрали все возможные пары, меняя только элементы из второй группы. Таких пар для этого элемента можно составить n 2 . Затем мы берем второй элемент из первой группы и также составляем для него все возможные пары. Таких пар тоже будет n 2 . Так как в первой группе всего n 1 элемент, всего возможных вариантов будет n 1 *n 2 .

Пример 2. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
Решение: n 1 =6 (т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n 2 =7 (т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5, 6), n 3 =4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4, 6).
Итак, N=n 1 *n 2 *n 3 =6*7*4=168.

В том случае, когда все группы состоят из одинакового числа элементов, т. е. n 1 =n 2 =…n k =n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно n k . Такой способ выбора в комбинаторики носит название выборки с возвращением.

Пример 3. Сколько всех четырехзначных чисел можно составить из цифр 1, 5, 6, 7, 8?
Решение. Для каждого разряда четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5 4 =625.

Рассмотрим множество, состоящие из n элементов. Это множество в комбинаторике называется генеральной совокупностью .

Число размещений из n элементов по m

Определение 1. Размещением из n элементов по m в комбинаторике называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.

Пример 4. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.

Число размещений в комбинаторике обозначается A n m и вычисляется по формуле:

Замечание: n!=1*2*3*…*n (читается: «эн факториал»), кроме того полагают, что 0!=1.

Пример 5 . Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные?
Решение: т.к. нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:

Определение 2. Сочетанием из n элементов по m в комбинаторике называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.

Пример 6 . Для множества {1, 2, 3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}.

Число сочетаний из n элементов по m

Число сочетаний обозначается C n m и вычисляется по формуле:

Пример 7. Сколькими способами читатель может выбрать две книжки из шести имеющихся?

Решение: Число способов равно числу сочетаний из шести книжек по две, т.е. равно:

Перестановки из n элементов

Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов.

Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).

Число различных перестановок из n элементов обозначается P n и вычисляется по формуле P n =n!.

Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд?

Решение: эта задача о числе перестановок семи разных книг. Имеется P 7 =7!=1*2*3*4*5*6*7=5040 способов осуществить расстановку книг.

Обсуждение. Мы видим, что число возможных комбинаций можно посчитать по разным правилам (перестановки, сочетания, размещения) причем результат получится различный, т. к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на определения, можно заметить, что результат зависит от нескольких факторов одновременно.

Во-первых, от того, из какого количества элементов мы можем комбинировать их наборы (насколько велика генеральная совокупность элементов).

Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны.

И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере.

Пример 9. На родительском собрании присутствует 20 человек. Сколько существует различных вариантов состава родительского комитета, если в него должны войти 5 человек?
Решение: В этом примере нас не интересует порядок фамилий в списке комитета. Если в результате в его составе окажутся одни и те же люди, то по смыслу для нас это один и тот же вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний из 20 элементов по 5.

Иначе будут обстоять дела, если каждый член комитета изначально отвечает за определенное направление работы. Тогда при одном и том же списочном составе комитета, внутри него возможно 5! вариантов перестановок , которые имеют значение. Количество разных (и по составу, и по сфере ответственности) вариантов определяется в этом случае числом размещений из 20 элементов по 5.

Задачи для самопроверки
1. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
Т.к. число четное на третьем месте может стоять 0, 2, 4, 6, т.е. четыре цифры. На втором месте может стоять любая из семи цифр. На первом месте может стоять любая из семи цифр кроме нуля, т.е. 6 возможностей. Результат =4*7*6=168.
2. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
На первом месте может стоять любая цифра кроме 0, т.е. 9 возможностей. На втором месте может стоять любая цифра, т. е. 10 возможностей. На третьем месте тоже может стоять любая цифра из, т.е. 10 возможностей. Четвертая и пятая цифры определены заранее, они совпадают с первой и второй, следовательно, число таких чисел 9*10*10=900.
3. В классе десять предметов и пять уроков в день. Сколькими способами можно составить расписание на один день?

4. Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек?

n = C 20 4 = (20!)/(4!*(20-4)!)=(16!*17*18*19*20)/((1*2*3*4)*(16!))=(17*18*19*20)/(1*2*3*4)=4845.
5. Сколькими способами можно разложить восемь различных писем по восьми различным конвертам, если в каждый конверт кладется только одно письмо?
В первый конверт можно положить 1 из восьми писем, во второй одно из семи оставшихся, в третий одно из шесть т.д. n = 8! = 1*2*3*4*5*6*7*8 = 40320.
6. Из трех математиков и десяти экономистов надо составить комиссию, состоящую из двух математиков и шести экономистов. Сколькими способами это можно сделать?

Сколько комбинаций в покере ― комбинаторика, количество сочетаний рук в игре

Прибыльная покерная стратегия основывается на математических вычислениях и логических выводах. Опытные игроки анализируют статистику, пишут заметки об оппонентах, отмечают их стили и используют эту информацию для построения точных предположений. Простые математические расчеты помогают понять, сколько комбинаций в покере может быть у того или иного соперника в конкретной ситуации.

Что такое комбинаторика в покере

Раздел математики, называемый комбинаторикой, решает задачи по выбору и расположению элементов множеств. Чтобы применить это определение к покеру, надо заменить термины более простыми словами.

Отсюда и до раздела со спецификой комбинаторики в отдельных игровых дисциплинах рассматриваются примеры для Техасского Холдема.

Главное множество покера — это колода. Она состоит из 52 уникальных карт (элементов), но некоторые из них имеют общие свойства (равные по достоинству или одинаковые по масти). Есть и меньшие множества:

• Рука. Набор, который включает от 2 до 7 карт, используемых игроком для составления комбинации.
• Диапазон. Также называется спектром. Набор карт, которые могут оказаться в руке у соперника. Количество элементов — от 2 до 50.

В покере комбинаторика играет такую же роль, как в других сферах применения. Она отвечает на вопросы о том, какие множества (руки) могут быть у соперника, использующего конкретное количество элементов (карт). Или позволяет предположить, какие готовые комбинации у него могут быть, а какие — нет.

В этом разделе математики есть много сложных конфигураций, но в покере используются только сочетания и перестановки.

Сочетания

Сочетание — набор из k элементов, взятых из множества n без учета порядка и не имеющий повторений. В покере это определение того, сколько вариантов различных комбинаций можно составить из карт.

Вот пример с числами из общей математики для сочетания 3 из 5 элементов множества.

	Элементы
Варианты	1	2	3	4	5
123
124
125
134
135
145
234
235
245
345

Следующий пример приведен для покера. Были взяты сочетания 5 из 7 карт для составления комбинации на вскрытии.

	Карты
Комбинации	А♥	А♣	К♦	К♥	8♦	7♥	4♥
А♥А♣К♦К♥8♦
А♥А♣К♦К♥7♥
А♥А♣К♦К♥4♥
А♥А♣К♦8♦7♥
А♥А♣К♦8♦4♥
А♥А♣К♦7♥4♥
А♥А♣К♥8♦7♥
А♥А♣К♥7♥4♥
А♥А♣К♥8♦4♥
А♥А♣8♦7♥4♥
А♥К♦К♥8♦7♥
А♥К♦8♦7♥4♥
А♥К♦К♥7♥4♥
А♥К♦К♥8♦4♥
А♥К♥8♦7♥4♥
А♣К♦К♥8♦7♥
А♣К♥8♦7♥4♥
А♣К♦8♦7♥4♥
А♣К♦К♥7♥4♥
А♣К♦К♥8♦4♥
К♦К♥8♦7♥4♥

Таким образом, у игрока есть 21 вариант готовой комбинации для вскрытия. По правилам покера, будет использован самый сильный.

Перестановки

Эта конфигурация находит упорядоченные наборы без повторений. Например, сколько вариантов стартовой руки KQ можно составить. В колоде есть по 4 короля и дамы. При подсчете важно учесть, что, например, K♣Q♦ равнозначна Q♦K♣.

Карты	K♣	K♦	K♥	K♠
Q♣	K♣Q♣	K♦Q♣	K♥Q♣	K♠Q♣
Q♦	K♣Q♦	K♦Q♦	K♥Q♦	K♠Q♦
Q♥	K♣Q♥	K♦Q♥	K♥Q♥	K♠Q♥
Q♠	K♣Q♠	K♦Q♠	K♥Q♠	K♠Q♠

Всего получается 16 вариантов. Причем 4 из них одномастные.

Если карты в стартовой руке одного достоинства, количество перестановок сокращается до 6.

Карты	K♣	K♦	K♥	K♠
K♣	╳	K♦K♣	K♥K♣	K♠K♣
K♦	K♣K♦	╳	K♥K♦	K♠K♦
K♥	K♣K♥	K♦K♥	╳	K♠K♥
K♠	K♣K♠	K♦K♠	K♥K♠	╳

Зачем считать покерные комбинации

Математическая работа с множествами и элементами позволяет находить ответы на различные вопросы, связанные со стратегией:

• Сколько вариантов конкретной стартовой руки может быть у соперника.
• Какой процент диапазона получает дро на определенном флопе.
• Какое точное количество стартовых рук у оппонента и как они распределены по категориям (пары, одномастные, коннекторы).
• Сколько вариантов стрит-дро может быть у игрока на флопе A♥T♠7♠.
• Как наличие конкретной карты влияет на эквити оппонента.

Новичку, впервые узнавшему о комбинаторике в покере, может показаться, что это абстрактные вопросы, далекие от практики. О том, как ответы на них влияют на стратегию, рассказывается далее.

Варианты стартовых рук на префлопе в Техасском Холдеме

В Холдеме игроки используют на префлопе 2 карты из 52. Всего есть 1,326 возможных сочетаний. При определении диапазона отталкиваются от количества рук в категориях:

• Пара всегда имеет 6 вариантов составления.
• Двухкарточную руку одной масти можно составить 4 способами. Например, AQs может быть червовой, пиковой, трефовой или бубновой.
• У разномастной непарной стартовой руки 12 вариантов составления.

Подсчеты показывают, что структура диапазона не бывает однородной. Если оппонент делает рейз на префлопе только с AA и AK, вероятность наличия двух тузов равна не 50%, а 20%. Поскольку есть 16 вариантов AK и 4 — AA.

Подсчет рук в диапазоне

Покерист, выстраивающий стратегию по математическим принципам, во время игры «кладет» оппонентов на конкретные диапазоны. Он предполагает, какие карты на руках у соперников. Выводы делаются из истории игры за столом, собранной статистики, заметок об особенностях оппонента.

Умение подсчета возможных комбинаций в покере помогает делать более точные предположения. Например, 10% префлоп-рейза — это 132 стартовые руки.

Если предположить, что игрок использует в примере только лучшие пары и бродвей, получится такая раскладка:

• AA, KK, QQ, JJ, TT, 99 — 36 (по 6 вариантов каждой пары).
• AK, AQ, AJ, KQ, KJ, QJ — 96 (по 16).

Матрица 10% префлоп-рейза

То есть в диапазоне соперника с PFR 10% на префлопе 27. 7% парных и 62.3% непарных рук. Это более глубокое представление, чем обычная запись 99+, AJ+, KJ+, QJ.

Комбинаторика помогает не просто представить, какие карты у соперника. Она дает понять, каких вариантов в диапазоне больше, как он взаимодействует с бордом и высокое ли имеет эквити.

Как работают блокеры

Блокеры — это карты, наличие которых сокращает количество отдельных рук в диапазоне оппонента. Меняется и его структура. Это называется эффектом изъятия.

На префлопе блокеры чаще всего используют при построении спектра 3-бета. Далее представим, что появилась возможность сделать 3-бет против оппонента с 10% PFR из примера выше.

• Например, у Алексея A♣J♠. У соперника не может быть рук с трефовым тузом и пиковым валетом. Следовательно, из предположительного спектра нужно убрать:
• Пары тузов. A♣A♦, A♣A♠, A♣A♥ — 3 из 6.
• Пары валетов. J♠J♣, J♠J♦, J♠J♥ — 3 из 6.
• Бродвей с A♣ или J♠. A♣K♣, A♣K♠, A♣K♦, A♣K♥, A♣Q♣, A♣Q♠, A♣Q♦, A♣Q♦ A♣J♣, A♣J♠, A♣J♦, A♣J♥, A♠J♠, K♣J♠, K♠J♠, K♦J♠, K♥J♠, Q♣J♠, Q♠J♠, Q♦J♠, Q♥J♠ — 21 из 96.

Это меняет структуру диапазона. Теперь он состоит из 105 рук: 28.6% пар и 61.4% бродвея. Разница не кажется большой, но это из-за примера для префлопа. На поздних улицах учет одного-двух блокеров может изменить эквити на 10%+.

Диапазон с учетом блокеров

Тема блокеров широко раскрывается в сложных стратегиях постфлопа со сбалансированными диапазонами. Например, по GTO наличие туза к флешу может стать причиной выбора между чеком и овербетом в блеф на ривере.

Принцип сужения диапазона

Количество рук у покериста на конкретной улице всегда меньше, чем на префлопе. Точный состав зависит от линии розыгрыша. Например, на флопе соперник продолжает ставить с частью карт, а некоторые уводит в чек.

Диапазоны в покере всегда сокращаются от префлопа к вскрытию.

Дерево решений разрастается. Например, на флопе игрок, сделавший открывающий рейз, может продолжить линиями: бет-рейз, бет-колл, бет-фолд, чек-рейз, чек-фолд, чек-колл.

Исключение отдельных карт в некоторых ситуациях позволяет сократить количество возможных рук оппонента к риверу до 3-5.

Примеры подсчета в игре

Комбинаторика практически не используется на первой улице, ее стратегическая важность раскрывается на постфлопе. Однако некоторое влияние все же есть.

Например, эффект изъятия сказывается на диапазонах при 3-бетах и 4-бетах. Если соперник с 3-bet 5% сделал ререйз, его спектр состоит из TT, AQo+ и AJs+. Он содержит 30 карманных пар, 24 разномастных и 12 одномастных тузов. По долям — 45.5%, 36.4% и 18.1%.

Диапазон в 5%

Имея A♥K♣ в раздаче против этого оппонента, необходимо понимать, что фактически состав спектра изменится. В диапазоне не может быть рук с A♥ и K♣:

• По 3 варианта AA и KK.
• 5 — AK разномастные.
• 4 — AQ.
• 2 — AK одномастные.
• 1 — AJs.

Диапазон сократился с 66 до 48 рук. И теперь распределение пары/разные/масть такое: 24 / 16 / 8 или 50% / 33% / 18%. Отличия небольшие, поскольку, как уже было отмечено, комбинаторика важна для принятия решений на постфлопе.

В случае с изолейтами, стилами, защитой блайндов подобные расчеты настолько слабо влияют на эквити, что ими можно пренебречь. Важнее уметь точно определять диапазоны. А работу с удалением из них конкретных карт надо оставить на следующие улицы.

Чтобы показать это, можно продолжить пример из раздела о блокерах. Исходные данные:

• Алексей получает опен-рейз от соперника из ранней позиции и защищает большой блайнд коллом.
• Статистика оппонента говорит, что он выполняет это действие в 10% случаев.
• 10% — 99+, AJs+, KJs+, QJs, AJo+, KJo+, QJo.

Алексей делает колл. Его рука для примера не важна.

Флоп: 6♣5♣J♠. Используя комбинаторику, можно разбить диапазон оппонента на разные категории рук:

• Оверпары. AA, KK, QQ — 18 вариантов.
• Флеш-дро. A♣K♣, A♣Q♣, K♣Q♣ — 3.
• Оверкарты. Любые AK, AQ, KQ, кроме одномастных трефовых — 45.
• Пары валетов. AJ, KJ, QJ — 36.
• Сеты. JJ — 3.

Это позволяет представить структуру диапазона — как часто оппонент получает на таком флопе руки разной силы. В 43% случаев он не попадает в него напрямую. В 51% имеет пару валетов. И лишь в 2.8% — сет.

Следующий пример показывает, как комбинаторика помогает оценить опасность борда. Исходные данные:

1. Михаил делает рейз из ранней позиции с K♣K♦.
2. Соперник на катоффе — колл.
3. Остальные оппоненты — фолд.
4. Флоп: 9♥8♦4♣.

Пара королей — сильная рука на таком борде. Но для построения плана на раздачу надо понять, какие готовые комбинации и дро есть у оппонента.

Теоретически возможны сеты (888, 999, 444), две пары (8989, 9494, 8484), OESD (67, TJ, T7) и гатшоты (57, 56, TQ, QJ, T6, J7). Однако у оппонента не может быть таких рук, как 94, 84, также маловероятны T6, J7. А большая часть диапазона промахивается мимо флопа.

Диапазон соперника

Примерное количество стартовых рук у оппонента на префлопе — 238. Сколько из них попадают в готовую комбинацию или дро:

• Сеты (88, 44) — 6 (2.5%).
• Две пары (98) — 2 (0.8%).
• OESD (TJ, 67, T7) — 20 (8.4%).
• Гатшоты (QJ, QT, 65) — 36 (15.12%).

Следовательно, лишь в 26.82% случаев оппонент будет иметь руку, с которой теоретически готов продолжать. А если убрать хотя бы половину гатшотов, число сократится до 19%.

Следует также обратить внимание на то, что у соперника капнутый диапазон. То есть он не включает руки выше определенного уровня. Например, здесь практически невозможно увидеть AA.

Особенности комбинаторики в разных видах покера

Правила подсчета комбинаций в покере сохраняются независимо от формата или разновидности игры. Однако сложность вычислений увеличивается в соответствии с количеством карманных карт. На практике дальше Холдема расчеты в уме не уходят.

Холдем 6+

В Холдеме с короткой колодой общее количество комбинаций сокращается с 1,326 до 630. Однако правила подсчета стартовых рук сохраняются.

Омаха

Количество комбинаций увеличивается экспоненциально. Если в Холдеме есть 1,326 уникальных стартеров, то в Омахе их 270,725.

Соответственно, отличается и количество вариантов для каждого:

• Разномастная рука без пар (например, A♠K♣T♥9♦) — 24.
• Любые четыре без пар — 256.
• Двумастная без пар — 12.
• Две пары (AA66) — 36.

Это примеры полных стартовых рук. Если отталкиваться от более широких определений, числа уходят в тысячи:

• Любая пара тузов (AAxx) — 9,961.
• Ряд (от 5432 до AKQJ) — 2,560.
• Туз с совпадением по масти — 45,880.
• Двумастная рука — 36,504.

В такой сложной комбинаторике говорить о точных расчетах в уме, как в Холдеме, не приходится. Поэтому игроки используют абстракции. Например, учитывают только карты, связанные с бордом. А подробный анализ проводят в покерных калькуляторах.

Пятикарточная Омаха

Чем больше карт, тем больше вариантов рук и сложнее представление диапазонов. В PLO-5 есть 2,589,960 стартеров. У 5 карт разного достоинства без учета мастей — 1,024, у двух пар — 1,632.

Шестикарточная Омаха

В Омахе с 6 карманными картами применять комбинаторику практически невозможно. Новичкам не следует об этом думать. Сложность расчетов здесь настолько высока, что нет покерного калькулятора, позволяющего задать два диапазона и сравнить эквити.

Частые вопросы

Как быстро посчитать количество вариантов непарной руки?

Перемножить свободные карты. Например, у K♦T♠ на флопе Q♥T♠2♦ их 12: 4 короля * 3 десятки (одна уже вышла). А если на столе лежат KT8, остается 9 вариантов: 3 * 3.

Как посчитать варианты парной стартовой руки?

Изначально их 6. При выходе одной карты количество сокращается до 3.

Почему важно понимать структуру диапазона?

Это помогает решить, на какую часть рук соперника направлено действие (чек или бет) и выбрать эффективный размер ставки.

Можно ли с помощью комбинаторики рассчитать точное эквити?

Теоретически да, но только на ривере, когда понятно, что из колоды не выйдут новые общие карты.

В каком калькуляторе можно проводить вычисления с учетом блокеров?

Лучшая из бесплатных программ для начинающих игроков — Equilab.

Как найти наибольшее или наименьшее количество комбинаций

Все математические ресурсы SAT

16 диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 Следующая →

SAT Math Help » Арифметика » Целые числа » Перестановка / Комбинация » Как найти наибольшее или наименьшее количество комбинаций

У Марка в шкафу 5 брюк и 7 рубашек. Он хочет носить новую комбинацию брюк и рубашки каждый день, не покупая новую одежду, как можно дольше. Сколько недель он может это делать?

Возможные ответы:

Правильный ответ:

5

Объяснение:

Фундаментальный принцип подсчета гласит, что если вы хотите определить количество способов, которыми могут произойти два независимых события, умножьте количество способов, которыми каждое событие может произойти вместе. В этом случае есть 5 * 7 или 35 уникальных комбинаций брюк и рубашек, которые может носить Марк. Если он носит одну комбинацию каждый день, он может продержаться 35 дней или 5 недель, не покупая новую одежду.

Сообщить об ошибке

Двадцать учеников участвуют в школьном конкурсе. Конкурс предлагает первый, второй и третий приз. Сколько различных комбинаций 1-го, 2-х ^-х, -х и 3-х мест может быть?

Возможные ответы:

400

8000

4620

6840

20

Правильный ответ:

6840

Объяснение:

Это задача на перестановку, потому что мы ищем количество групп победителей. Рассмотрите три позиции и количество вариантов для каждой позиции: есть 20 вариантов для 1-го места, 19за 2 место и 18 за 3 место.

20, 19, 18     

Умножьте, чтобы получить 6840.

Сообщить об ошибке

У пекаря есть четыре разных вида глазури, три разных вида посыпки и 8 разных формочек для печенья. Сколько различных комбинаций печенья может создать пекарь, если каждое печенье имеет один тип глазури и один тип посыпки?

 

Возможные ответы:

48

96

15

24

Правильный ответ:

96

Объяснение:

Так как это проблема комбинирования, и мы хотим знать, сколько различных способов могут быть созданы файлы cookie, мы можем решить ее, используя фундаментальный принцип подсчета. 4 x 3 x 8 = 96

Перемножение всех возможных вариантов.

 

 

 

Сообщить об ошибке

Если необходимо изготовить серию номерных знаков, каждая из которых имеет одинаковую схему из трех букв, за которыми следуют три цифры, сколько примерно буквенно-цифровых комбинаций возможно?

Возможные ответы:

180 млн.

11 млн.

1 тысяча

18 млн.

18 тысяча

Правильный ответ:

миллионов

. Объяснение:

Общее количество возможных комбинаций ряда элементов равно произведению общей возможности для каждого из элементов. Таким образом, для букв есть 26 возможностей для каждого из 3-х слотов, а для чисел есть 10 возможностей для каждого из 3-х слотов. Тогда общее количество комбинаций равно: 26 х 26 х 26 х 10 х 10 х 10 = 17 576 000 ≈ 18 миллионов.

Сообщить об ошибке

Если на плоскости 8 точек, и никакие 3 из них не лежат на одной прямой, сколько уникальных линий можно провести между парами этих 8 точек?

Возможные ответы:

30

28

29

27

Правильный ответ:

28

Объяснение:

Формула для количества прямых, определяемых n точками, никакие три из которых не лежат на одной прямой (коллинеарными), равна n(n-1)/2. Чтобы найти количество линий, определяемое 8 точками, мы используем 8 в формуле, чтобы найти 8(8-1)/2=8(7)/2=56/2=28. (Формула получена из двух фактов: того факта, что каждая точка образует прямую с каждой другой точкой, следовательно, n(n-1), и того факта, что это отношение симметрично (т. е. если a образует прямую с b, то b образует линию с a), следовательно, деление на 2.)

 

 

Сообщить об ошибке

8 человек, запертых в комнате, по очереди берутся за руки с каждым человеком только один раз. Сколько захватов рук происходит?

Возможные ответы:

15

21

28

24

Правильный ответ: 4 50

28904 Пояснение:

Первый человек держит 7 рук. Второй держит шестерых в силу уже имеющейся помощи руки первого человека. Так продолжается до тех пор, пока не пройдут все 8 человек. 7+6+5+4+3+2+1=28.

Сообщить об ошибке

В магазине мороженого есть 5 вкусов мороженого: клубничное, ванильное, шоколадное, мятное и банановое. Сколько разных рожков для мороженого с тремя вкусами можно сделать?

Возможные ответы:

10

20

5

60

30

Правильный ответ:

10

Объяснение:

Есть 5x4x3 способов расположить 5 вкусов 3 способами. Однако в этом случае порядок вкусов не имеет значения (например, рожок с клубникой, мятой и бананом такой же, как рожок с мятой, бананом и клубникой). Итак, мы должны разделить 5x4x3 на количество способов, которыми мы можем расположить 3 разных вещи, то есть 3x2x1. Итак, (5x4x3)/(3x2x1) равно 10,  

Можно также использовать формулу комбинации для этой задачи:  _n C _r = n! / (н-р)! р!

Следовательно: ₅ C ₃ = 5! / 3! 2!

= 10

 

(Примечание. Примером задачи подсчета, в которой порядок имеет значение, является ситуация с замком или кодом доступа. Перестановка 3-5-7 для трехзначного замка или кода доступа отличается от 5- 7-3, поэтому оба должны быть учтены.)

Сообщить об ошибке

В гастрономе вы можете выбрать итальянский хлеб, цельнозерновой хлеб или хлеб на закваске. Вы можете выбрать индейку или ростбиф в качестве мяса и проволоне или моцареллу в качестве сыра. Если вам нужно выбрать хлеб, мясо и сыр, сколько возможных комбинаций бутербродов у вас может быть?

Возможные ответы:

12

10

8

7

14

Правильный ответ:

12

Пояснение:

У вас есть 3 возможных вида хлеба, 2 возможных вида мяса и 2 возможных вида сыра. Умножая их, вы получаете 3*2*2, что дает вам 12 возможных комбинаций.

Сообщить об ошибке

Шеннон решила пойти пообедать в соседнее кафе. Она может приготовить бутерброд на пшеничном или белом хлебе. Кафе предлагает выбор сыра чеддер, швейцарский и американский. Из мяса Шеннон может выбрать ветчину, индейку, колбасу, ростбиф или салями. Сколько вариантов сэндвичей с сыром и мясом есть на выбор у Шеннон?

Возможные ответы:

10

30

25

35

20

Правильный ответ:

30

Объяснение:

2 варианта хлеба * 3 варианта сыра * 5 вариантов мяса = 30 вариантов сэндвичей

Сообщить об ошибке

Кафе-мороженое предлагает 36 вкусов мороженого. Вы можете заказать любой вкус в маленьком, среднем или большом размере и выбрать между вафельным рожком и чашкой. Сколько возможных комбинаций вы могли бы заказать?

Возможные ответы:

144

72

172

216

108

Правильный ответ:

216

Пояснение:

36 возможных вкусов * 3 возможных размера * 2 возможных конуса = 216 возможных комбинаций.

Сообщить об ошибке

← Назад 1 2 3 Далее →

Уведомление об авторских правах

Все математические ресурсы SAT

16 Диагностические тесты 660 практических тестов Вопрос дня Карточки Учитесь по концепции

Выбор подмножества независимо от заказа

Мы иногда делаем выборку из набора без оглядки на заказ . Такой выбор называется комбинацией . Если вы, например, играете в карты, то знаете, что в большинстве ситуаций порядок, в котором вы держите карты, не имеет значения.

Пример 1 Найдите все комбинации из 3 букв, взятых из набора из 5 букв {A, B, C, D, E}.

Решение Комбинаций
{A, B, C},         {A, B, D},
{A, B, E},          {A, C, D},
{A, C, E},          {A, D, E} ,
{B, C, D},          {B, C, E},
{B, D, E},          {C, D, E}.
Есть 10 комбинаций из 5 букв, взятых по 3 за раз.

Когда мы находим все комбинации из набора из 5 объектов, взятых по 3 за раз, мы находим все подмножества из 3 элементов. При названии набора порядок элементов не учитывается. Таким образом,
{A, C, B} именует тот же набор, что и {A, B, C}.

Подмножество
Множество A является подмножеством множества B, обозначается, что A является подмножеством и/или совпадает с B, если каждый элемент A является элементом B.

Элементы подмножества не упорядочены. Думая о комбинациях, не думайте о порядке!

Комбинация
Комбинация , содержащая k объектов, представляет собой подмножество, содержащее k объектов.

Мы хотим разработать формулу для вычисления количества комбинаций n объектов, взятых k одновременно, без фактического перечисления комбинаций или подмножеств.

Обозначение комбинаций
Количество комбинаций n объектов, взятых k одновременно, обозначается _n C _k .

Мы называем _n C _k комбинированное обозначение . Мы хотим вывести общую формулу для _n C _k для любого k ≤ n. Во-первых, верно, что _n C _n = 1, потому что множество с n объектами имеет только одно подмножество с n объектами, само множество. Второй, _n C ₁ = n, так как набор из n объектов имеет n подмножеств по 1 элементу в каждом. Наконец, _n C ₀ = 1, потому что множество из n объектов имеет только одно подмножество с 0 элементами, а именно пустое множество ∅. Чтобы рассмотреть другие возможности, давайте вернитесь к примеру 1 и сравните количество комбинаций с количеством перестановок.

Обратите внимание, что каждая комбинация из 3 объектов дает 6, или 3!, перестановок.
3! • ₅ С ₃ = 60 = ₅ P ₃ = 5 • 4 • 3,
поэтому
.
В общем, количество комбинаций n объектов, взятых k за раз, _n C _k , умноженное на количество перестановок этих объектов, k!, должно равняться количеству перестановок n объектов, взятых k в время:
к!. _n C _k = _n P _k
n C _k = _n P _k /k!
_n C _k = (1/k!). _№ Р _к
п С _к =

Комбинаций n объектов, взятых k одновременно
Общее количество комбинаций n объектов, взятых k одновременно, обозначенное как _n C _k , определяется как
(1)          _{n k C} = ,
или
(2)          _n C _k =

Другим видом записи для _n C _k является запись биномиального коэффициента .Причину такой терминологии мы увидим позже.

Обозначение биномиального коэффициента

Вы должны уметь использовать любое обозначение и любую форму формулы.

Пример 2 Оцените , используя формы (1) и (2).

Раствор
а) По форме (1),
.
б) По форме (2),

Обязательно имейте в виду, что это не означает n/k.

Пример 3 Вычислить и .

Решение Мы используем форму (1) для первого выражения и форму (2) для второго. Затем
,
, используя форму (1), и
,
, используя форму (2).

Обратите внимание, что
,
, поэтому использование результата Примера 2 дает нам
.
Это говорит о том, что количество подмножеств из 5 элементов в наборе из 7 объектов такое же, как количество подмножеств из 2 элементов в наборе из 7 объектов. 2 элемента. Чтобы убедиться в этом, рассмотрим множество {A, B, C, D, E, F, G}:

В общем имеем следующее. Этот результат обеспечивает альтернативный способ вычисления комбинаций.

Подмножества размера k и размера
и _n C _k = _n C _n-k
Количество подмножеств размера k множества с n объектами равно количеству подмножеств размер н — к. Количество комбинаций из n предметов, взятых k одновременно, равно количеству комбинаций n предметов, взятых одновременно.

Теперь мы решаем задачи на комбинации.

Пример 4 Мичиганская лотерея. Управляемая штатом Мичиган лотерея WINFALL проводится два раза в неделю с джекпотом не менее 2 миллионов долларов. При цене покупки в 1 доллар игрок может выбрать любые 6 чисел от 1 до 49. Если числа совпадают с номерами, выпавшими в штате, игрок выигрывает. (Источник: Мичиганская лотерея)
а) Сколько существует комбинаций из 6 чисел?
b) Предположим, что на выбор чисел и покупку игрового билета уходит 10 минут. Сколько билетов можно купить за 4 дня?
c) Сколько человек вам пришлось бы нанять на 4 дня, чтобы купить билеты со всеми возможными комбинациями и гарантировать, что вы выиграете?

Решение
а) Порядок здесь не подразумевается. Вы выбираете любые 6 чисел от 1 до 49. Таким образом, количество комбинаций равно

б) Сначала найдем количество минут в 4 днях:
4дня • (24ч/1день). (60мин/1ч) = 5760 мин.
Таким образом, за 4 дня можно было купить 576 билетов.
c) Вам потребуется нанять 13 983 816/576, или около 24 278 человек, чтобы купить билеты со всеми возможными комбинациями и обеспечить выигрыш. (Это предполагает, что лотерейные билеты можно купить 24 часа в сутки.)

Пример 5 Сколько комитетов можно сформировать из группы из 5 губернаторов и 7 сенаторов, если каждый комитет состоит из 3 губернаторов и 4 сенаторов?

Решение 3 губернатора могут быть выбраны ₅ C ₃ способами, а 4 сенатора могут быть выбраны ₇ C ₄ способами. Если мы используем фундаментальный принцип подсчета, то количество возможных комитетов равно

Использование комбинаций для расчета вероятностей

Комбинации в теории вероятностей и других областях математики относятся к последовательности результатов, порядок которых не имеет значения. Например, когда вы заказываете пиццу, не имеет значения, заказываете ли вы ее с ветчиной, грибами и оливками или с оливками, грибами и ветчиной. Вы получите такую ​​же пиццу!

При расчете вероятностей часто требуется подсчитать количество возможных комбинаций.

В этом посте я покажу вам, как рассчитать количество комбинаций с повторениями и без них, и научу вас стандартным обозначениям комбинаций. Я также буду работать с примерами задач, чтобы вы могли увидеть процесс в действии. Вы узнаете, как рассчитать вероятность выигрыша джекпота в лотерее Powerball!

Сравнение комбинаций с перестановками

В теории вероятностей комбинации и перестановки — это разные понятия.

• Комбинации : Порядок исходов не имеет значения.
• Перестановки : Порядок результатов имеет значение.

Давайте используем три буквы, чтобы проиллюстрировать обе концепции: C, J, M.

Предположим, мы используем эти буквы для обозначения людей в команде, таких как Карл, Джек и Мэри. В качестве комбинации членов команды C, J, M эквивалентны M, J, C. В любом случае в команде одни и те же люди. Следовательно, порядок букв не имеет значения, ведь у вас одна и та же команда. Эти три буквы образуют одну комбинацию.

Однако, если вы используете эти буквы для короткого кода доступа, особое значение имеет расположение букв. Если правильный код CJM, то MJC работать не будет. CJM — одна из возможных комбинаций этих трех букв. Используя только эти три буквы, вы можете составить 3 ³ = 27 возможных перестановок.

Если у вас есть хотя бы две перестановки, количество перестановок превышает количество комбинаций. Узнайте больше о различиях между перестановкой и комбинацией.

В этом посте я работаю только с комбинациями. Чтобы узнать о перестановках, прочитайте мой пост об использовании перестановок для расчета вероятностей.

Комбинации с повторением

Когда результаты в комбинации могут повторяться, у вас есть повторение. В нашем примере с пиццей, если вы можете выбрать начинку несколько раз, например, двойную или тройную ветчину, у нас есть комбинации с повторением. Это также известно как комбинации с заменой.

Чтобы рассчитать количество комбинаций с повторениями, используйте следующее уравнение.

Где:

• n = количество вариантов.
• р = размер каждой комбинации.

Восклицательный знак (!) обозначает факториал. В общем, н! равно произведению всех чисел до n. Например, 3! = 3 * 2 * 1 = 6. Исключение 0! = 1, что упрощает уравнения.

Давайте рассмотрим пример количества комбинаций с повторением. Представьте, что у нас есть пиццерия, и у нас есть шесть начинок, из которых клиенты могут выбирать. У нас есть специальное предложение для пиццы с тремя начинками. Сколько потенциальных комбинаций попадает под наше специальное предложение? Поскольку мы разрешаем повторение, клиенты могут получить тройную пиццу с беконом, если они хотят рискнуть посетить больницу!

Чтобы решить эти типы задач, вам нужно определить n и r для уравнения. Количество возможных исходов равно количеству вариантов начинки, то есть шести. Размер каждой комбинации равен трем, потому что это то, что мы допускаем для нашего специального предложения. Итак, n = 6 и r = 3.

Используя стандартные обозначения комбинаций nCr, мы запишем это как ₆ C ₃ .

Ввод этих чисел в уравнение:

₆ C ₃ = 56.

Существует 56 комбинаций из трех начинок, когда у вас есть шесть вариантов начинки и разрешены повторы.

Комбинации без повторения

Когда исходы не могут повторяться, вы работаете с комбинациями без повторения. В этих расчетах в качестве отправной точки используется следующее уравнение для перестановок без повторения.

В перестановках порядок имеет значение. Однако порядок , а не  имеет значение для комбинаций без повторений, которые дают меньшее число, чем перестановки. В следующем уравнении первая часть отражает количество перестановок, где порядок имеет значение. Вторая часть уменьшает это число, потому что порядок не имеет значения для комбинаций. Произведение двух дает окончательное уравнение.

В упрощенной форме:

Где:

• n = количество возможных исходов на старте.
• р = размер каждой комбинации.

Например, представьте себе процесс, который привлекает пять человек в группу из 30. Порядок, в котором процесс привлекает членов команды, не имеет значения. Предположим, в команду входят A, B, C, D, E. Это эквивалентно команде, в которой были выбраны те же люди, но в другом порядке. Кроме того, поскольку процесс может выбрать человека только один раз, повторения нет.

В этом примере n = 30, потому что мы выбираем кандидатов из пула из 30 кандидатов. R = 5, потому что в команде может быть только пять человек. Ввод этих чисел в уравнение:

Используя стандартные обозначения: ₃₀ C ₅ = 142 506.

Существует 142 506 комбинаций команд из пяти человек, когда вы выбираете из пула из 30 человек.

Вы также можете использовать треугольник Паскаля, чтобы найти количество комбинаций без повторений.

Формула для комбинаций без повторений является важной частью биномиального распределения. Чтобы узнать, как это сделать, прочитайте мой пост «Биномиальное распределение».

Использование комбинаций для расчета вероятностей

В предыдущих примерах мы рассчитывали количество комбинаций для различных сценариев. Однако мы не использовали их для расчета вероятностей. В этом контексте вероятность — это количество комбинаций, рассматриваемых как событие, деленное на общее количество комбинаций.

Когда вам дают задачу на вероятности с использованием комбинаций, вам нужно определить несколько вещей, чтобы решить эту задачу.

1. Установите коэффициент для определения вероятности.
2. Определите, требуют ли числитель и знаменатель комбинации, перестановки или смесь? В этом посте мы остановимся на комбинациях.
3. Эти комбинации с повторениями или без?
4. Оба типа комбинаций требуют, чтобы вы определили n и r, чтобы войти в уравнения.

Давайте рассмотрим пример расчета вероятности с использованием комбинаций!

Задача : Какова вероятность выиграть основную игру и джекпот в лотерее Powerball?

Связанный пост : Основы вероятности

Вероятность выигрыша в основной игре в лотерее Powerball

Классическим примером вероятности с использованием комбинаций без повторения является лотерея, в которой машины случайным образом выбирают шары с номерами из пула шаров. Порядок чисел не имеет значения. Вам просто нужно сопоставить числа. Поскольку каждый шар можно вытащить только один раз, он не повторяется.

В этом примере мы рассмотрим лотерею Powerball, которая проводится в 45 штатах США. В базовой игре есть 69 белых шаров в автомате, который случайным образом выбирает пять шаров. Следующее соотношение определяет вероятность выигрыша:

Числитель простой. Есть одна выигрышная комбинация без повторения. Вы можете использовать это уравнение для вычисления ₅ C ₅ , что равно количеству комбинаций, где у вас есть пять номеров в выигрышной комбинации, и есть пять выигрышных номеров, из которых можно выбирать. Но это интуитивно понятно. Есть только одна выигрышная комбинация.

В знаменателе нужно вычислить ₆₉ C ₅ , что равно количеству комбинаций при вытягивании пяти чисел из 69 чисел. Подставим эти числа в уравнение:

₆₉ C ₅ = 11 238 513

Когда вы вытягиваете пять чисел из 69 без повторений, получается 11 238 513 комбинаций.

Используя стандартные обозначения, вероятность выигрыша в основной игре Powerball следующая:

У вас есть шанс 1 из 11 238 513 выиграть основную игру в лотерее Powerball.

Вероятность выиграть джекпот в Powerball

Чтобы выиграть джекпот в Powerball, вам нужно выиграть в основной игре и , угадав один красный номер Powerball. Powerballs — это 26 красных шаров в отдельной машине, которая случайным образом вытягивает один из них. Давайте посчитаем вероятность выигрыша джекпота!

В числителе снова есть одна выигрышная комбинация Powerball. Для знаменателя нам нужно посчитать количество комбинаций для ₂₆ C ₁ = 26. Это неудивительно. Всего 26 комбинаций при выборе одного числа из 26 вариантов! Таким образом, вероятность совпадения Powerball следующая:

Чтобы включить это в расчеты вероятности для базовой игры, нам нужно использовать правило умножения для независимых событий и умножить два отношения.

Используя стандартные обозначения комбинаций, вероятность выиграть джекпот в Powerball следующая:

У вас есть шанс 1 из 292 201 338 выиграть джекпот в лотерее Powerball.

Исправление комбинаций номеров для учащихся с математическими трудностями

• Список журналов
• Рукописи авторов HHS
• PMC34

Перспект Ланг Лит. Авторская рукопись; доступно в PMC 2012 6 ноября. 2011 Весна; 37(2): 11–16.

PMCID: PMC34

NIHMSID: NIHMS367957

PMID: 23139846

Сара Р. Пауэлл, доктор философии, Линн С. Фукс, доктор философии, и Дуглас Фукс, доктор философии.

Информация об авторе Информация об авторских правах и лицензии Отказ от ответственности

Учащиеся с трудностями в математике (MD) часто испытывают трудности с развитием беглости с комбинациями чисел. Проблемы с комбинациями чисел могут привести к трудностям с вычислениями, геометрией, алгеброй, решением задач и большинством других тем математики. В этой статье мы обсудим свободное владение комбинациями чисел и его важность для развития математики. Мы также обсудим, почему учащиеся испытывают затруднения при изучении числовых комбинаций. Затем мы описываем четыре исследования, которые мы провели для устранения проблем с числовыми комбинациями. Наконец, мы предлагаем предложения, которые помогут учащимся с MD выучить комбинации чисел.

Прежде чем продолжить, прокомментируем использование термина MD. Мы, как и другие исследователи, определили низкую успеваемость по математике как математических трудностей. В наших исследованиях учащиеся с трудностями в математике показали результаты ниже 26 ^-го -го процентиля в стандартизированном тесте по математике. У некоторых из этих учеников с MD был официальный школьный диагноз неспособность к обучению математике , но многие учащиеся с MD боролись с низкой успеваемостью по математике без официального диагноза.

Комбинации чисел иногда называют основными фактами или математическими фактами. Мы используем термин числовых комбинаций , чтобы показать, что учащиеся могут работать и решать эти задачи; то есть эти проблемы не нужно вспоминать как факт из памяти. Комбинации чисел включают 390 комбинаций сложения, вычитания, умножения и деления, которые являются одними из основных строительных блоков математики (Hudson & Miller, 2006). См. примеры каждого из следующих типов числовых комбинаций. Комбинации дополнительных чисел имеют слагаемые от 0 до 9.и сумма 0–18. Комбинации чисел вычитания имеют уменьшаемое от 0 до 18, вычитаемое и разность от 0 до 9. Комбинации чисел умножения имеют коэффициенты от 0 до 9 и произведения в диапазоне от 0 до 81, тогда как комбинации чисел деления имеют делимые от 0 до 81, делители от 1 до 9 и частные от 0 до 9. Как правило, комбинации дополнительных чисел с большей вероятностью извлекаются из памяти (а не вычисляются) по сравнению с тремя другими типами комбинаций чисел. Поскольку наша работа над комбинациями чисел была сосредоточена исключительно на сложении и вычитании, мы ограничиваем наше обсуждение комбинациями сложения и вычитания в этой статье. 9Таблица 1

---

Сложение сложение + сложение = сумма 3 + 4 = 7 9 + 6 = 15

---

Вычитание вычитание — вычитание = разность 4 — 1 = 3 13 − 8 = 5

---

Умножение множитель x множитель = произведение 3 × 2 = 6 8 × 7 = 56

---

Division dividend ÷ divisor = quotient 9 ÷ 3 = 3 72 ÷ 8 = 9

Open in a separate window

It is important that students know (i. e. , извлекать из памяти) или уметь решать (т. е. быстро вычислять ответ) числовые комбинации, потому что числовые комбинации необходимы для решения большинства других типов математических задач: вычислений, денег, измерений, геометрии, алгебры и решения задач. Если учащиеся не знают или не могут относительно легко вычислить ответ на числовую комбинацию, то решение других математических задач становится более трудным или невозможным (Kroesbergen & Van Luit, 2003). Подумайте, как сложно может быть вычесть монеты (например, 17 пенни минус 9 монет).пенни) или вычислить периметр прямоугольника (например, 8 дюймов плюс 6 дюймов), если учащийся не демонстрирует свободное владение комбинациями чисел. Кроме того, у учащихся со слабыми навыками составления числовых комбинаций может развиться беспокойство по поводу математики (Hudson & Miller, 2006), что может способствовать негативному отношению к математике и избеганию ситуаций, в которых математика необходима (как обсуждается Лори Ханич, в этом выпуске).

Многие учащиеся, у которых проблемы с математикой, демонстрируют недостаток навыков в сочетании чисел (Andersson, 2008; Geary, Hamson, & Hoard, 2000; Hanich, Jordan, Kaplan, & Dick, 2001). Например, учащиеся второго класса с MD правильно ответили на меньшее число комбинаций чисел, чем учащиеся без MD (Hanich et al., 2001). Аналогичная тенденция проявилась у учащихся третьего и четвертого классов, где учащиеся с MD показали значительно более низкие результаты и сделали больше ошибок в тесте на числовые комбинации, чем учащиеся без MD (Andersson, 2008). Эти недостатки в навыках составления числовых комбинаций могут быть связаны с трудностями в хранении и извлечении числовых комбинаций из долговременной памяти или из-за дефицита хранения числовых комбинаций в рабочей памяти (например, Geary, Hoard, Byrd-Craven, & DeSoto, 2004; Jordan & Montani). , 1997), подробно описанный Даниэлем Берчем в этом выпуске. Поскольку прошлые попытки исправления числовых комбинаций были сомнительными (Kroesbergen & Van Luit, 2003), мы провели четыре исследования, чтобы выяснить, как помочь учащимся развить беглость навыков числовых комбинаций.

Чтобы выяснить, как помочь учащимся с MD с комбинациями чисел, мы провели четыре исследования в течение четырех лет, по одному в год. Каждое исследование проводилось с третьеклассниками. Четыре исследования, которые были сосредоточены на усвоении и беглости при сложении и вычитании комбинаций чисел, составили программу исследований, в которой каждое исследование было разработано для решения вопросов, возникших в предыдущих исследованиях. Таким образом, в исследованиях существует линейная прогрессия, поскольку каждый год мы узнаем больше об обучении и изучении числовых комбинаций. См. блок-схему четырех исследований. Эти четыре исследования более подробно описаны у Fuchs, Powell, Seethaler, Fuchs, et al. (2010). Студенты во всех четырех исследованиях испытывали трудности с математикой (т. е. успеваемость ниже 26 9 баллов).0031-й -й процентиль в стандартизированном тесте по математике сложения, вычитания, умножения и деления), хотя их основные источники математических трудностей могли различаться. Студенты во всех четырех исследованиях были идентифицированы как имеющие MD одинаковым образом с помощью одного и того же стандартизированного теста.

Открыть в отдельном окне

Блок-схема изучения числовых комбинаций (NC)

Учебное задание 1: Практика, практика, практика

Первая итерация обучения числовым комбинациям включала три ежедневных занятия: компьютерные тренировки, карточки и обзор (Fuchs et al., 2008). В ходе компьютерных упражнений учащимся предлагались числовые комбинации в течение 7,5 минут. На экране компьютера «мигала» цифровая комбинация (т. е. 5 + 4 = __). Он исчез через секунду или две; затем студент ввел всю комбинацию (т. е. 5 + 4 = 9).) из памяти. Когда учащийся ввел комбинацию цифр, в верхней части экрана заполнилась картинка с числовой строкой. В задачах на сложение первое дополнение было представлено синими прямоугольниками, а второе добавление — желтыми. В задачах на вычитание уменьшаемое поле заполнялось желтым цветом, а вычитаемое обозначалось крестиком над уменьшаемым полем. Если учащийся правильно ответил на комбинацию цифр, он услышал аплодисменты и заработал очко в пользу сокровищ, собранных в сундуке с сокровищами на экране. Если учащийся ответил неправильно, он должен был перепечатать комбинацию до тех пор, пока не будет дан правильный ответ. По истечении 7,5 минут на экране компьютера отображалась оценка учащегося (т. е. количество правильно отгаданных комбинаций). После этой компьютерной тренировки студенты в течение 2 минут отвечали на карточки с комбинациями чисел, представленные преподавателем. По истечении 2 минут преподаватель и ученик подсчитали правильно отвеченные карточки и записали результат на графике. После 3 последовательных сессий правильного ответа на 35 карточек с комбинациями чисел репетитор затем переключился на карточки с числовыми линиями для работы с карточками. Флэш-карты с числовыми линиями представляли собой комбинации, подобные тем, которые предъявлялись во время компьютерных упражнений. Учащимся было предложено назвать комбинацию, представленную числовой прямой. Подобно карточкам с комбинациями чисел, через 2 минуты учащиеся построили график количества карточек с правильными ответами. Каждая сессия завершалась бумажным обзором 15 комбинаций чисел. У учащихся было 2 минуты, чтобы ответить на максимально возможное число комбинаций.

Условия

Мы сравнили эти числовых комбинаций обучения с тремя другими условиями обучения: (a) двузначное вычисление и оценка , (b) двузначное вычисление и оценка с числовыми комбинациями обучение, и (c ) идентификатор слова . При обучении двузначным вычислениям и оценке учащиеся решали двузначные задачи на сложение и вычитание с помощью компьютерной программы, отвечали на двузначные карточки и отвечали на двузначные задачи в бумажном обзоре. Обучение вычислению и оценке двузначных чисел с использованием числовых комбинаций включало в себя компоненты как обучения двузначным вычислениям и оценке, так и обучения числовым комбинациям. Учащиеся, занимающиеся обучением распознаванию слов, участвовали в компьютерных тренировках по чтению слов с листа и чтении отрывков вслух для беглости речи; это было контрольное состояние. Все студенты получали репетиторство в течение 15 недель, 3 занятия в неделю, 15–30 минут каждое занятие. Занятия с репетиторами проводились в течение учебного дня в назначенное классным руководителем время. Студенты обучались индивидуально в местах за пределами класса студента (например, в коридоре, пустом классе, библиотеке или конференц-зале).

Результаты

(См. результаты четырех исследований. Величина эффекта (ES) указывается для значимых результатов). условие (ES = 0,69), условие двузначных и числовых комбинаций (ES = 0,81) или условие идентификации слова (ES = 0,78). Из этого первого исследования мы узнали, что учащиеся, которых обучали только комбинациям чисел, продемонстрировали более сильные улучшения, чем те учащиеся, которые обучались комбинациям чисел в сочетании с обучением вычислению и оценке двузначных чисел. Мы также узнали, что сочетание компьютерных упражнений, флэш-карт и бумажного обзора, по-видимому, улучшило беглость с комбинациями чисел.

Таблица 2

Результаты исследований комбинаций номеров

44337

Исследование	Условия	Результаты 1	Размеры эффекта	.
1	Комбинации Комбинации (NC)	NC> DD	0,69
	170981 0,69
	170981 0,69
170981 0,69
170981 0,69
.0854
Обучение двузначному вычислению и оценке с комбинациями чисел (COMB) Обучение идентификации слов (CONTROL)	NC > CONTROL	0,78
2	Комбинации числа комбинаций (NC)	NC> DD	0,31
	Exped Number Combination
	Двойной рецепт вычислений и оценки (DD)	E-NC-CONC> DD	0,37
	NOTRIOR
3	Обучение комбинациям чисел со стратегиями счета (NC-COUNT)0854	WP-COUNT > CONTROL	0,62
	Без обучения (CONTROL)	NC-COUNT = WP-COUNT
4	Участие в счете с помощью стратегии подсчета (WP-Count)	WP-Count> Control	0,67
	WARD-ANTRPEM
	WARD-ANTBREM.	0,22
Без обучения (КОНТРОЛЬ)	WP > КОНТРОЛЬ	0.43

Открыть в отдельном окне

¹ Значимые результаты по комбинациям чисел.

Исследование 2: Предоставление концептуального обучения

Чтобы определить важность концептуального обучения для исправления числовых комбинаций, второе исследование сравнило обучение числовым комбинациям из Исследования 1 с расширенным обучением числовым комбинациям с обучением концептуальным числовым комбинациям (Powell, Fuchs, Fuchs , Чирино и Флетчер, 2009 г.). Числовые комбинации репетиторство включало только три вида деятельности, которые были аналогичны действиям по числовым комбинациям в исследовании 1: компьютерная тренировка и практика, карточки с числовыми комбинациями и просмотр бумаги. Расширенное обучение включало шесть занятий: концептуальное обучение, карточки с числовыми комбинациями, компьютерная тренировка и практика, карточки с числовыми линиями, обзор семейства комбинаций и обзор бумаги. (Два упражнения с карточками, компьютерная тренировка и просмотр бумаги были аналогичны действиям, описанным выше.) При концептуальной инструкции преподаватели и ученики работали с манипуляторами (т. е. с синими и желтыми блоками), чтобы показать различные комбинации семейство фактов (т.е. 2 + 4 = 6; 4 + 2 = 6; 6 — 2 = 4; 6 — 4 = 2). Затем учащиеся практиковались в создании семейств числовых комбинаций на обзоре семейства комбинаций.

Условия

Мы сравнили результаты учащихся в условиях двух описанных выше комбинаций чисел, называемых здесь комбинаций чисел и расширенных комбинаций чисел, , с учащимися в двух конкурирующих условиях: (a) двойных- вычисление и оценка цифр с обучением и (б) без обучения (т. е. контроль). Обучение двузначным вычислениям и оценке было похоже на обучение, описанное в исследовании 1. Обучение студентов во всех трех условиях обучения длилось 15 недель, 3 занятия в неделю, 15–25 минут на занятие.

Результаты

Учащиеся в обоих условиях числовых комбинаций показали одинаковые результаты друг с другом. Учащиеся, прошедшие обучение числовым комбинациям (без концептуального обучения), значительно превзошли учащихся в двузначных обучающих (ES = 0,31) и контрольных (ES = 0,50) условиях. Точно так же учащиеся, обучавшиеся расширенным числовым комбинациям, продемонстрировали значительно более высокие баллы, чем обучающиеся с двузначными числами (ES = 0,37) и учащиеся контрольной группы (ES = 0,53). Было интересно отметить, что учащиеся в любых условиях числовых комбинаций показали одинаковые результаты, даже несмотря на то, что учащиеся, получившие расширенное обучение по числовым комбинациям, тратили гораздо больше времени на концептуальную основу числовых комбинаций, им приходилось прорабатывать и думать о том, как числовые комбинации связаны с одним числом. еще один. Это открытие предполагает, что учащимся с MD необходимо было изучить план или стратегию решения числовых комбинаций, когда ответ не сразу вспоминается. По этой причине мы ввели стратегии подсчета в исследовании 39.0005

Исследование 3: Стратегии счета

Обучение комбинациям чисел в исследовании 3 включало инструкции о том, как использовать стратегии счета для решения комбинаций сложения и вычитания (Fuchs et al., 2009). (См. Объяснение стратегий счета.) Обучение комбинациям чисел включало пять видов деятельности: 1) карточки с комбинациями чисел, 2) подробные инструкции, 3) карточки для конкретных уроков, 4) компьютерные упражнения и 5) обзор бумаги. Флэш-карты с комбинациями чисел, компьютерная тренировка и просмотр бумаги, используемые в этом состоянии, были такими же, как описано в исследованиях 1 и 2. Подробные инструкции были сосредоточены на обучении и отработке стратегий счета, наряду с инструкциями, ориентированными на группы (не семьи). ) числовых комбинаций (например, комбинации +0 и -0; комбинации +1 и -1). Карточки для конкретных уроков также были ориентированы на группы; студенты отвечали на эти карточки в течение 1 минуты. По мере того как ученики переходили в следующую группу, им разрешалось брать домой карточки для уроков для практики.

Условия

В дополнение к условиям обучения с комбинацией чисел , использованным в этом исследовании, условиями сравнения в исследовании 3 были (а) обучение словесным задачам и (б) отсутствие обучения (т. е. контроль). Репетиторство по словесным задачам заключалось в том, чтобы научить студентов читать, составлять и решать текстовые задачи по типам задач. Учащиеся также изучили стратегии счета, которым обучали на занятиях по составлению числовых комбинаций. Студенты в каждом из двух условий обучения обучались в течение 16 недель, 3 занятия в неделю, 20–30 минут на занятие.

Результаты

По числовым комбинациям учащиеся, участвовавшие в числовых комбинациях, превзошли контрольных учащихся (ES = 0,52). Не было никаких различий между учащимися, получающими числовые комбинации или репетиторством по задачам со словами, учитывая, что обучение по задачам со словами также включало в себя инструкции по решению числовых комбинаций со стратегиями счета. Интересно, что учащиеся, обучающиеся словесным задачам, превзошли учащихся контрольной группы по числовым комбинациям (ES = 0,62). Из этого исследования мы узнали, что подробные инструкции и практика использования стратегий счета для решения числовых комбинаций, по-видимому, являются важным компонентом обучения числовым комбинациям.

Исследование 4: Ежедневная практика со счетными стратегиями

Поскольку все обучаемые учащиеся, независимо от того, были ли в центре внимания занятия по стратегиям счета и комбинациям чисел, значительно улучшили числовые комбинации в исследовании 3, чем учащиеся из контрольной группы, целью исследования 4 было чтобы определить, сколько практики по стратегиям счета необходимо (Fuchs, Powell, Seethaler, Cirino et al., 2010). В исследовании 4 учащиеся в каждом из двух условий активного обучения получали инструкции по решению текстовых задач. Характер словесно-задачного обучения в обоих условиях был идентичен. Единственная разница между этими двумя условиями заключалась в том, что только одно условие включало ежедневную практику на числовых комбинациях, а другое — нет. Например, в обоих случаях учащиеся получали начальный урок-объяснение по стратегиям счета, но только в одном случае учащиеся также ежедневно практиковались в решении числовых комбинаций со стратегиями счета. В частности, в обоих условиях учащиеся участвовали в разминке словесных задач, подробном обучении словесным задачам, карточках сортировки словесных задач и обзоре работы. Эти занятия были сосредоточены на решении текстовых задач, принадлежащих к трем типам текстовых задач: общее, различие и изменение. Студенты в обоих условиях также участвовали в работе с карточками, но характер деятельности с карточками различался в этих двух условиях. Дети в репетиторстве по словесным задачам без условия практики просто читают цифры на флеш-картах. Дети в инструкции по составлению числовых комбинаций с условием ежедневной практики отвечали на карточки с числовыми комбинациями в течение 1 минуты. Если ученик отвечал неправильно, репетитор просил его или ее использовать стратегию подсчета, пока ученик не ответит правильно. По истечении 1 минуты количество правильно отвеченных карточек фиксировалось на графике. Во время тренировки по счету преподаватель попросил ученика решить четыре числовые комбинации, используя стратегии счета. Подводя итог, можно сказать, что, хотя учащиеся, обучавшиеся словесным задачам без ежедневной практики, получали подробные инструкции по использованию стратегий счета для решения числовых комбинаций, они не участвовали в карточках с числовыми комбинациями или в счетной практике на каждом занятии.

Условия и результаты

Обучение в обоих активных условиях длилось 16 недель, 3 занятия в неделю, 20–30 минут каждое занятие. Мы также включили условие отсутствия обучения (т.е. контроль). Что касается числовых комбинаций, учащиеся, которые прошли курс обучения словесным задачам с ежедневными стратегиями счета, превзошли учащихся в контрольных условиях (ES = 0,67) и учащиеся, которые прошли курс обучения словесным задачам без ежедневных стратегий счета (ES = 0,22). ). Тем не менее, учащиеся, которые занимались репетиторством без ежедневной практики, превзошли контрольную группу (ES = 0,43). Из исследования 4 мы узнали, что учащимся требуется ежедневная практика на числовые комбинации, даже если время, затрачиваемое на числовые комбинации, составляет всего несколько минут за занятие.

В исследованиях 1 и 2 мы предоставили третьеклассникам обучение, полностью сосредоточенное на комбинациях чисел. Инструкция включала в себя множество действий, начиная от карточек и заканчивая компьютерными тренировками и четкими концептуальными инструкциями, а также бумажными обзорами. Мы надеялись, что комплекс упражнений с различными комбинациями чисел станет лучшим путем для исправления навыка сочетания чисел. Однако в Занятиях 3 и 4 мы давали краткие, но подробные инструкции по решению числовых комбинаций и узнали, что учащиеся получают пользу от изучения стратегии решения числовых комбинаций. Студенты извлекли пользу из инструкций по стратегиям счета, встроенных в репетиторство по словесным задачам, так же, как и в программах репетиторства, ориентированных исключительно на комбинации чисел. Итак, мы узнали, что обучение комбинациям чисел может проводиться одновременно с обучением решению задач со словами, и учащиеся по-прежнему извлекают выгоду из комбинаций чисел.

Начиная с Задания 3, мы начали предлагать учащимся стратегии счета для решения числовых комбинаций, когда они не могли автоматически вспомнить ответ (т. е. стратегии счета). Мы чувствовали, что студентам нужен надежный и эффективный резервный план. В исследовании 4 мы выделили влияние практики на обучение стратегиям счета, и наши результаты свидетельствуют о важности ежедневной (хотя и краткой) практики для этой группы учащихся. Таким образом, мы заключаем, что предоставление учащимся явных инструкций (т. е. стратегий счета) по решению числовых комбинаций и отработка этих стратегий счета является важным и эффективным компонентом обучения математике для учащихся с MD.

Кроме того, мы отмечаем, что на протяжении всех исследований студенты участвовали в ежедневных упражнениях с карточками и обзоре бумаги, чтобы улучшить беглость числовых комбинаций. Несмотря на то, что мы никогда не изолировали вклад упражнений с карточками или бумажных обзоров, мы считаем, что просмотр комбинаций чисел и требование к учащимся использовать стратегии подсчета для решения неправильных ответов на карточках и графическое отображение результатов на карточках могут быть еще одним важным компонентом обучения комбинациям чисел. В том же духе просмотр комбинаций чисел на бумаге может быть важен для обеспечения перехода к задачам с бумагой и карандашом.

Как уже упоминалось, в каждом из четырех исследований этой исследовательской программы все участники были учениками третьего класса, у которых были проблемы с математикой. Некоторые из этих учащихся также боролись с трудностями при чтении (RD) (т. е. набрали меньше 26 900 31 900 32 процентиля в стандартизированном тесте на чтение) и поэтому были классифицированы как имеющие MD+RD. Другие учащиеся показали результаты выше 40 ^th процентиля по чтению и поэтому были отнесены к категории имеющих только MD. В каждом из четырех исследований мы искали различия в успеваемости между MD + RD и студентами только MD. Некоторые предыдущие исследования показали разницу в успеваемости по комбинациям чисел между учащимися с MD+RD и учащимися только с MD (Hanich et al., 2001), при этом учащиеся только с MD превосходили учащихся с MD+RD, в то время как другие исследования не продемонстрировали различий между учащимися с MD+RD. MD+RD и MD-только для числовых комбинаций (Geary, Hoard, & Hamson, 1999).

К сожалению, во всех наших четырех исследованиях, рассмотренных здесь, кроме одного, количество студентов в каждой подгруппе было слишком мало, чтобы определить, различалась ли реакция на вмешательство в зависимости от того, испытывали ли студенты МД отдельно или в сочетании с РЗ. Тем не менее, некоторые закономерности в данных обеспечивают основу для гипотезы о том, что по сравнению со студентами только с MD, учащимся с MD + RD может потребоваться более интенсивное вмешательство и различные виды вмешательства, которые имеют более систематическую практику с большим упором на язык. Однако необходимы широкомасштабные интервенционные исследования — с достаточно большими выборками студентов с MD с RD и без — для оценки состоятельности этих гипотез.

Основываясь на этой программе исследований по исправлению числовых комбинаций, многие студенты с MD извлекают пользу из подробных инструкций о том, как решать числовые комбинации. Учащимся должны быть предоставлены стратегии решения комбинаций, когда ответ не сразу вспоминается, и должно быть предоставлено много возможностей попрактиковаться в решении числовых комбинаций в различных форматах (например, карточки, устные викторины, бумажные обзоры). Из того, что мы узнали из нашей исследовательской программы, мы считаем, что чем больше у учащихся возможностей увидеть числовые комбинации и работать с ними, тем больше вероятность того, что они улучшат свои навыки числовых комбинаций. Больше возможностей не обязательно означает больше время отработка числовых комбинаций, потому что, как мы узнали в ходе наших исследований, оказывается, что учащиеся получают пользу от хорошо разработанного и реализованного обучения числовым комбинациям, которое длится несколько минут каждое занятие, точно так же, как обучение числовым комбинациям, которое длится 30 минут каждое сессия. Мы считаем, что учащиеся должны быть подробно проинструктированы о решении числовых комбинаций и должны иметь различные возможности для практики числовых комбинаций в течение учебного года.

Это исследование было частично поддержано грантом P01046261 от Национального института детского здоровья и развития человека им. Юнис Шрайвер (NICHD) Хьюстонскому университету с субподрядом с Университетом Вандербильта, а также основным грантом № HD15052 от NICHD Университету Вандербильта. . Заявления не отражают позицию или политику этих агентств, и не следует делать вывод об их официальном одобрении.

• 

Сара Р. Пауэлл, доктор философии, , научный сотрудник отдела специального образования Университета Вандербильта. Ее исследовательские интересы включают математические вмешательства для учащихся с трудностями в математике и понимание учащимися символов равенства 9.0005

• 

Линн С. Фукс, доктор философии, , профессор специального образования и человеческого развития Николаса Хоббса на факультете специального образования Университета Вандербильта. Ее исследовательские интересы сосредоточены на оценивании в классе, вмешательстве в чтение и математику, а также в когнитивных предикторах, связанных с реакцией на вмешательство. Департамент специального образования Университета Вандербильта. Его исследовательские интересы включают вопросы классификации нарушений обучаемости, вмешательство в чтение и когнитивные предикторы развития чтения 9.0005

• Андерссон У. Математические компетенции у детей с различными видами трудностей в обучении. Журнал педагогической психологии. 2008; 100:48–66. [Google Scholar]
• Fuchs LS, Powell SR, Hamlett CL, Fuchs D, Cirino PT, Fletcher JM. Исправление вычислительного дефицита в третьем классе: рандомизированное полевое испытание. Журнал исследований эффективности образования. 2008; 1: 2–32. [Бесплатная статья PMC] [PubMed] [Google Scholar]
• Fuchs LS, Powell SR, Seethaler PM, Cirino PT, Fletcher JM, Fuchs D, Hamlett CL. Влияние обучения стратегическому счету с преднамеренной практикой и без нее на навыки комбинации чисел у учащихся с трудностями в математике. Обучение и индивидуальные различия. 2010;20:89–100. [Бесплатная статья PMC] [PubMed] [Google Scholar]
• Fuchs LS, Powell SR, Seethaler PM, Cirino PT, Fletcher JM, Fuchs D, Zumeta RO. Исправление числовых комбинаций и дефицита словесных задач среди учащихся с математическими трудностями: рандомизированное контрольное испытание. Журнал педагогической психологии. 2009; 101: 561–576. [Бесплатная статья PMC] [PubMed] [Google Scholar]
• Fuchs LS, Powell SR, Seethaler PM, Fuchs D, Hamlett CL, Cirino PT, Fletcher JM. Основа для устранения дефицита комбинаций номеров. Исключительные дети. 2010;76:135–156. [Бесплатная статья PMC] [PubMed] [Google Scholar]
• Geary DC, Hamson CO, Hoard MK. Численное и арифметическое познание: продольное исследование дефицита процессов и понятий у детей с нарушением обучаемости. Журнал экспериментальной детской психологии. 2000; 77: 236–263. [PubMed] [Google Scholar]
• Geary DC, Hoard MK, Byrd-Craven J, DeSoto MC. Выбор стратегии в простом и сложном сложении: вклад рабочей памяти и счетных знаний для детей с математическими отклонениями. Журнал экспериментальной детской психологии. 2004; 88: 121–151. [PubMed] [Академия Google]
• Geary DC, Hoard MK, Hamson CO. Численное и арифметическое познание: закономерности функций и нарушений у детей, подверженных риску математической инвалидности. Журнал экспериментальной детской психологии. 1999; 74: 213–239. [PubMed] [Google Scholar]
• Ханич Л.Б., Джордан Н.К., Каплан Д., Дик Дж. Результаты в различных областях математического познания у детей с трудностями в обучении. Журнал педагогической психологии. 2001; 93: 615–626. [Google Scholar]
• Хадсон П., Миллер С.П. Разработка и внедрение обучения математике для учащихся с различными потребностями в обучении. Бостон: Pearson Education, Inc.; 2006. [Google Академия]
• Джордан Северная Каролина, Монтани TO. Когнитивная арифметика и решение задач: сравнение детей с особыми и общими математическими трудностями. Журнал неспособности к обучению. 1997; 30: 624–634. 684. [PubMed] [Google Scholar]
• Kroesbergen EH, Van Luit JEH. Математические вмешательства для детей с особыми потребностями: метаанализ. Коррекционное и специальное образование. 2003; 24:97–114. [Google Scholar]
• Пауэлл С.Р., Фукс Л.С., Фукс Д., Сирино П.Т., Флетчер Дж.М. Влияние репетиторства по поиску фактов на учащихся третьего класса с математическими трудностями с трудностями чтения и без них. Исследования и практика с ограниченными возможностями обучения. 2009 г.;24:1–11. [Бесплатная статья PMC] [PubMed] [Google Scholar]

Mathwords: Формула комбинации

Mathwords: Формула комбинации

индекс: нажмите на букву индекс: предметные области
	Комбинированная формула Формула для количества возможных комбинации r объектов из набора n объектов. Этот записывается любым из способов, показанных ниже. Все формы читаются вслух « n выбрать r «.   Формула:   Примечание: , где n P r – формула перестановок n объектов принято р за раз. Пример: Сколько разных комитетов по 4 студента можно выбрать из группы из 15 человек? Ответ: Возможны комбинации 4 учеников из набора 15.   Существует 1365 различных комитетов.   См. также Перестановка биномиальная коэффициент, факториал
	эта страница обновлена 19 июля 17 Математические слова: термины и формулы от алгебры I до исчисления написано, проиллюстрировано и создано веб-мастером Брюсом Симмонсом Copyright © 2000 by Bruce Simmons Все права защищены

комбинаций — The Stats Ninja

(и почему ваша комбинация шкафчиков на самом деле является перестановкой)

Добро пожаловать в третью часть моей Шпаргалки по статистике. Обязательно ознакомьтесь с Частью 1 и Частью 2.

Перестановки и комбинации полезны для тех, кто интересуется определением общего количества элементов в наборе или группе. Это особенно полезно для вероятности при вычислении знаменателя и/или числителя.

Разницу между перестановкой и комбинацией легко понять, если обратить пристальное внимание на то, как выбираются предметы/объекты/люди (и игнорировать семантику). В этом посте я дам вам определения, формулы и примеры перестановок и комбинаций. Но сначала я расскажу о Основной принцип счета и факториалы .

Фундаментальный принцип подсчета

Этот принцип, также известный как правило подсчета умножения, гласит, что необходимо перемножить все возможные события, чтобы найти общее количество результатов.

Простой пример начинается с упаковки вещей в отпуск. Допустим, вы упаковали 4 рубашки, 3 пары брюк и 2 пары обуви. Сколько возможных нарядов вы можете сделать? (Предположим, что они все совпадают, или вам 5 лет, и вам все равно. )

Основной принцип подсчета гласит, что теперь у вас есть:

4 * 3 * 2 = 24 возможных наряда

Вот еще один пример. Предположим, вашей компании требуется пятизначный проверочный код, состоящий из трех цифровых и двух буквенных значений ( в таком порядке, как , с учетом регистра). Сколько возможных кодов подтверждения может быть создано?

Иногда полезно увидеть, что происходит:

И визуализировать значения в каждой позиции:

Всего нужно учитывать 10 цифр (0–9) и 26 букв алфавита — 52, если регистр чувствительный. Хитрость заключается в том, чтобы умножить, чтобы найти общее количество возможных результатов:

= 2 704 000 различных кодов подтверждения

А что, если требование изменилось на 3 цифры и 2 буквы (в том же порядке), но без повторений? Нам пришлось бы вычесть количество вариантов для каждой цифры/буквы по мере их использования:

= 1 909 440 различных кодов подтверждения

Требуется немного больше математики, если вы можете расположить эти значения в любом порядке, и я не буду рассказывать об этом в этом посте.

Факториалы

На первый взгляд факториал выглядит как очень возбужденное число. Например, 5! может показаться, что он кричит: «ПЯТЬ!» (Глупая учительская шутка — работает лучше лично.) Восклицательный знак на самом деле является оператором, говорящим нам умножить это число на все целые числа, меньшие этого числа, вплоть до 1.

Перестановки

Перестановки применяют основной принцип подсчета для определения числа способов, которыми вы можете расположить членов группы. Формула перестановки вычисляет количество расположений n объектов взято r за раз:

Например, предположим, что вы и еще 29 человек боретесь за 3 разных приза. Ваши имена указаны в шапке, и призы присуждаются только первому, второму и третьему разыгранным именам (лучший приз — первый). Количество способов, которыми 30 человек могут получить первый, второй и третий призы, называется перестановкой . В перестановке порядок, в котором расположены предметы или люди, «имеет значение». (И если имеет значение , можно сказать, что порядок равен 9.0007 отмеченный или очевидный. )

не судите о моей внешности, я только что пробежал 5 км за 25:36. Победительница, занявшая первое место, не пришла за своим призом, поэтому табличку держала милая дама, чтобы мы не выглядели болванами.

Для примера с призом вы можете вычислить это, используя формулу перестановок:

И это восходит к фундаментальному принципу подсчета, поскольку часть числителя сокращается со знаменателем:

Упрощение выражения до 30*29*28 = 24 360 способов 3 человека могут быть награждены первым, вторым и третьим призом из группы из 30 человек в случайном порядке. Если бы мы просто разыгрывали 3 имени сразу без разницы в призах, это НЕ считалось бы перестановкой.

К счастью, вам не нужно знать формулу для вычисления перестановки. Функция Excel для перестановок: ПЕРЕСТАВКА :

Примечание. Существует еще одна функция Excel для перестановок с повторениями — ПЕРЕСТАНОВКА . В этом примере вы бы использовали это, если бы мы рисовали имена для трех призов и каждый раз имя возвращалось в шляпу, что позволяло одному и тому же человеку выигрывать все 3 раза.

Комбинации

Теперь предположим, что вы и еще 29 человек соревнуетесь за 3 приза одинаковой стоимости. Ваши имена в шапке и рисуются сразу все три имени. Поскольку не используется порядок или расположение, этот тип метода счета называется комбинацией 9.0016 . Формула комбинации также вычисляет n объектов, взятых r за один раз:

обратите внимание, что знаменатель отличается — и, поскольку вы делите на большее число, вы можете видеть, что комбинация даст меньше возможных групп, чем permutation

В новейшей версии нашего примера с призом мы одновременно берем 3 имени из шляпы, и между призами нет никакой разницы. Вот этот расчет:

Раз 27! в числителе и знаменателе сокращаются, в числителе остается 24 360, но все равно делим на 3! (что 3*2 = 6):

Что дает только 4060 возможных комбинаций .

Функция Excel для комбинаций: COMBIN :

Комбинация шкафчиков на самом деле является перестановкой

Теперь рассмотрим комбинации шкафчиков. Предположим, типичная блокировка циферблата (правая, левая, правая), в которой на циферблате 39 цифр, а ваш код имеет 3 цифры. Имеет ли значение порядок? Абсолютно! Если вы попытаетесь открыть замок, используя свой трехзначный код, но в другом порядке, шкафчик не откроется. Итак, сколько возможных кодов у этого шкафчика?

Если бы числа не повторялись, у нас было бы P(39,3) = 54 834 различных кодов (или то, что мы называем «комбинациями»). Но если числа могут повторяться, существует 39*39*39 = 59 319 возможных кодов — чтобы включить повторяющиеся значения, примените функцию ПЕРЕСТАВКА в Excel.

Попробуй!

Основываясь на том, что вы только что узнали, можете ли вы определить разницу между комбинацией и перестановкой? Бонусные баллы, если вы можете рассчитать результат. (Ответы в конце поста.)

1. Совет директоров состоит из 13 человек. Сколькими способами можно выбрать главного исполнительного директора, директора и казначея?
2. Сколькими способами можно выбрать жюри в составе 12 человек из группы в 40 человек?
3. GM из сети ресторанов должен выбрать 8 ресторанов из 14 для рекламной программы. Сколькими способами можно осуществить этот выбор?
4. В Waffle House оладьи можно заказать 18 различными способами. Как можно сделать заказы, выбрав только 3 из 18?
5. Шкафчик может иметь четырехзначный код. Сколько различных кодов у нас может быть, если существует 25 различных чисел и числа не могут повторяться ни в одном заданном коде?

Ответы:

1. Перестановка. P(13,3) = 1716
2. Комбинация. C(40,12) = 5 586 853 480 порядок здесь не важен
3. Комбинация. C(14,8) = 3003
4. Комбинация. C(18,3) = 816
5. Перестановка. P(25,4) = 303 600 (Повторяющиеся числа в коде дадут 390 625 различных кодов.

   No related posts.