Положительная дробь — Большая Энциклопедия Нефти и Газа, статья, страница 2
Cтраница 2
Множество, состоящее из всех дробей ( их теперь будем называть положительными дробями), всех отрицательных дробей и нуля, называется множеством рациональных чисел, а сами эти числа называются рациональными. [16]
Значит, lg 0 0015 — 3 а, где a — некоторая правильная положительная дробь. [17]
Если р — натуральное число, то число — называется положительным рациональным числом, или положительной дробью. [18]
Та ДО Тт — Таким образом, в интервале ( уа, Tm) i есть правильная положительная дробь. [19]
Выполнение ASRA сдвигает 56-битный аккумулятор полностью на один бит вправо, восстанавливая содержимое А1 и формируя положительную дробь с дополнением до двух в АО. Если результат произведения отрицателен, то исключение знакового бита из дробной части осуществляется в три этапа.
Во-первых, необходимо взять абсолютное значение числа. Во-вторых, сдвиг LSLA, следующий за ASRA, должен сформировать дробь со знаком и дополнением до двух. Наконец, отрицательные значения обеих частей, целой и дробной, должны быть обработаны отдельно.
[20]
Числитель первой дроби равен 2 / г2 — — 3 / г 1, а числитель второй дроби 2ла Зп и ясно, что 2па Зл 1 2п2 — — 3 / г. Мы знаем, что из двух положительных дробей с одинаковыми знаменателями та дробь больше, у которой числитель больше. Значит, хп 1 хп и данная последовательность — возрастающая. [21]
Числитель первой дроби равен 2л2 3л 1, а числитель второй дроби 2п2 Зл и ясно, что 2п2 Зл 1 2п2 Зп. Мы знаем, что из двух положительных дробей с одинаковыми знаменателями та дробь больше, у которой числитель больше. Значит, xn i хп и данная последовательность — возрастающая. [22]
Если же bt, — число дробное, то разность Р / — будет правильной дробью.
Число W ( число микросостояний или, как иногда говорят, число комплексий) называют термодинамической вероятностью данного макросостояния. Это, очевидно, целое положительное число в отличие от математической вероятности, представляющей собой правильную положительную дробь с числом благоприятных случаев в числителе и числом всех возможных случаев в знаменателе. [24]
Из формулы ( 3) следует, что любое возрастание ( снижение) автономных расходов ведет к увеличению ( уменьшению) общего дохода и выпуска. Последнее выражение всегда больше единицы, поскольку по своей экономической природе его знаменатель представляет собой положительную дробь. В силу сказанного, величину, равную [ 1Д1 — МРС) ], принято называть мультипликатором национального дохода. [25]
Вероятно, подразумевающаяся в приведенном примере аналогия с интервалом и отрезком покажется многим читателям неубедительной, даже надуманной.
Обозначим его буквой Б и спросим себя, можно ли утверждать, что среди точек интервала найдется такая, в любой окрестности которой имеется бесконечное подмножество точек из Б1 Оказывается, нельзя. А вот на отрезке [ О, 1 ] подобная точка ( она называется точкой сгущения) обязательно найдется. Пусть Б представляет собой совокупность всех положительных дробей с целыми знаменателями, у которых в числителе стоит единица. Однако нуль не принадлежит интервалу ( О, 1), а отрезку [ О, 1 ] принадлежит. Значит, бывает так, что бесконечная последовательность точек интервала не имеет на нем ни одной точки сгущения.
[26]
Это уравнение нами написано в таком виде, который прямо указывает на связь с уравнением Пифагора. Вопрос заключается в том, существуют ли среди пифагоровых чисел такие, из которых меньшие два — полные квадраты. До сих пор подобные тройки нам не встречались; но это, конечно, еще не означает, что их вовсе нет. Числа, входящие в такие тройки, могут быть очень велики.
Страницы: 1 2
Курс математического анализа
Курс математического анализа
ОглавлениеПРЕДИСЛОВИЕГлава 1. ВВЕДЕНИЕ § 1.2. Множество. Интервал, отрезок § 1.3. Функция § 1.4. Понятие непрерывности функции § 1.5. Производная § 1.6. Первообразная. Неопределенный интеграл § 1.7. Понятие определенного интеграла. Площадь криволинейной фигуры Глава 2. ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО § 2.1. Рациональные и иррациональные числа § 2.2. Определение неравенства § 2.3. Основная лемма. Определение арифметических действий § 2.4.  Основные свойства действительных чисел§ 2.5. Изоморфизм различных представлений действительных чисел. Физические величины § 2.6. Неравенства для абсолютных величин § 2.7. Точные верхняя и нижняя грани множества § 2.8. Символика математической логики Глава 3. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ § 3.2. Арифметические действия с пределами § 3.3. Бесконечно малая и бесконечно большая величины § 3.4. Существование предела у монотонной ограниченной последовательности § 3.5. Число е § 3.6. Леммы о вложенных отрезках, существовании точных граней множества и сечения во множестве действительных чисел § 3.7. Теорема Больцано-Вейерштрасса. Верхний и нижний пределы § 3.8. Критерий Коши существования предела § 3.9. Счетное множество. Счетность множества рациональных чисел. Несчетность множества действительных чисел Глава 4. ПРЕДЕЛ ФУНКЦИИ § 4.1. Понятие предела функции § 4.2. Непрерывность функции в точке § 4.  b§ 4.8. Еще о числе е § 4.9. lim sin oo/oo § 4.10. Порядок переменной, эквивалентность (асимптотика) Глава 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ДЛЯ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ § 5.1. Производная § 5.2. Дифференциал функции § 5.3. Производная функции от функции § 5.4. Производная обратной функции § 5.6. Производные и дифференциалы высшего порядка § 5.7. Возрастание и убывание функции на интервале и в точке. Локальный экстремум § 5.8. Теоремы о среднем значении. Критерии возрастания и убывания функции на интервале. Достаточные критерии локальных экстремумов § 5.9. Формула Тейлора § 5.10. Формулы Тейлора для важнейших элементарных функций § 5.11. Ряд Тейлора § 5.12. Выпуклость кривой в точке. Точка перегиба § 5.13. Выпуклость кривой на отрезке § 5.14. Раскрытие неопределенностей § 5.15. Асимптота § 5.16. Схема построения графика функции § 5.17. Кусочно непрерывные и кусочно гладкие функции Глава 6. n-МЕРНОЕ ПРОСТРАНСТВО.  ГЕОМЕТРИЯ КРИВОЙ§ 6.1. n-мерное пространство. Линейное множество § 6.3. Линейное нормированное пространство § 6.4. Вектор-функция в n-мерном евклидовом пространстве § 6.5. Непрерывная кривая. Гладкая кривая § 6.6. Геометрический смысл производной вектор-функции § 6.7. Длина дуги кривой § 6.8. Касательная § 6.9. Основной триэдр кривой § 6.10. Соприкасающаяся плоскость § 6.11. Кривизна и радиус кривизны кривой § 6.12. Эволюта § 6.13. Формулы Френе. Свойства эволюты Глава 7. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ § 7.1. Открытое множество § 7.2. Предел функции § 7.3. Непрерывная функция § 7.4. Частные производные и производная по направлению § 7.5. Дифференцируемая функция. Касательная плоскость § 7.6. Производная сложной функции. Производная по направлению. Градиент § 7.7. Независимость от порядка дифференцирования § 7.  8. Дифференциал функции. Дифференциал высшего порядка§ 7.9. Теорема Больцано-Вейерштрасса § 7.10. Замкнутые и открытые множества § 7.11. Функции на множестве. Свойства непрерывных функций на замкнутом ограниченном множестве § 7.12. Лемма о вложенных прямоугольниках и лемма Бореля § 7.13. Формула Тейлора § 7.14. локальный (абсолютный) экстремум функции § 7.15. Теоремы существования неявной функции § 7.16. Теорема существования решения системы уравнений § 7.17. Отображения § 7.18. Гладкая поверхность § 7.19. Дифференциалы неявных функций. Линеаризация § 7.20. Локальный относительный экстремум § 7.21. Замена переменных в частных производных § 7.22. Система зависимых функций Глава 8. НЕОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ. АЛГЕБРА МНОГОЧЛЕНОВ § 8.1. Введение. Методы замены переменной и интегрирования по частям § 8.2. Комплексные числа § 8.3. Комплексные функции § 8.4. Многочлены § 8.5. Разложение рациональной функции на простейшие дроби  6. Интегрирование рациональных дробей§ 8.7. Интегрирование алгебраических иррациональностей § 8.8. Подстановки Эйлера § 8.9. Биномиальные дифференциалы. Теорема Чебышева § 8.10. Интегрирование тригонометрических выражений § 8.11. Тригонометрические подстановки § 8.12. Несколько важных интегралов, не выражаемых в элементарных функциях Глава 9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ РИМАНА § 9.2. Ограниченность интегрируемой функции § 9.3. Суммы Дарбу § 9.4. Основная теорема § 9.5. Теоремы о существовании интеграла от непрерывной и монотонной функции на [a, b] § 9.6. Аддитивные и однородные свойства интеграла § 9.7. Неравенства и теорема о среднем § 9.8. Интеграл как функция верхнего предела. Теорема Ньютона-Лейбница § 9.9. Вторая теорема о среднем § 9.10. Видоизменение функции § 9.11. Несобственные интегралы § 9.12. Несобственные интегралы от неотрицательных функций § 9.13. Интегрирование по частям § 9.14. Несобственный интеграл и ряд § 9.  15. Несобственные интегралы с особенностями в нескольких точках§ 9.16. Формула Тейлора с остатком в интегральной форме § 9.17. Формулы Валлиса и Стирлинга Глава 10. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛОВ. ПРИБЛИЖЕННЫЕ МЕТОДЫ § 10.1. Площадь в полярных координатах § 10.2. Объем тела вращения § 10.3. Длина дуги гладкой кривой § 10.4. Площадь поверхности тела вращения § 10.5. Интерполяционный многочлен Лагранжа § 10.6. Квадратурные формулы прямоугольников § 10.7. Формула Симпсона Глава 11. РЯДЫ § 11.1. Понятие ряда § 11.2. Действия с рядами § 11.3. Ряды с неотрицательными членами § 11.4. Ряд Лейбница § 11.5. Абсолютно сходящиеся ряды § 11.6. Условно и безусловно сходящиеся ряды с действительными членами § 11.7. Последовательности и ряды функций. Равномерная сходимость § 11.8. Интегрирование и дифференцирование равномерно сходящихся рядов на отрезке § 11.9. Кратные ряды. Перемножение абсолютно сходящихся рядов § 11.  z, cos z, sinz комплексной переменнойГлава 12. КРАТНЫЕ ИНТЕГРАЛЫ § 12.2. Мера Жордана § 12.3. Важные примеры квадрируемых по Жордану множеств § 12.4. Еще один критерий измеримости множества. Полярные координаты § 12.5. Другие случаи измеримости § 12.6. Понятие кратного интеграла § 12.7. Верхняя и нижняя интегральные суммы. Основная теорема § 12.8. Интегрируемость непрерывной функции на замкнутом измеримом множестве. Другие критерии § 12.9. Свойства кратных интегралов § 12.10. Сведение кратного интеграла к интегрированию по отдельным переменным § 12.11. Непрерывность интеграла по параметру § 12.12. Геометрическая интерпретация знака определителя § 12.13. Замена переменных в кратном интеграле. Простейший случай § 12.14. Замена переменных в кратном интеграле § 12.15. Доказательство леммы 1 § 12.14 § 12.16. Полярные координаты в плоскости § 12.17. Полярные и цилиндрические координаты в пространстве § 12.18. Гладкая поверхность § 12.  19. Площадь поверхностиГлава 13. ТЕОРИЯ ПОЛЯ. ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ ПО ПАРАМЕТРУ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ § 13.1. Криволинейный интеграл первого рода § 13.2. Криволинейный интеграл второго рода § 13.3. Поле потенциала § 13.4. Ориентация плоской области § 13.5. Формула Грина. Выражение площади через криволинейный интеграл § 13.6. Интеграл по поверхности первого рода § 13.7. Ориентация поверхностей § 13.8. Интеграл по ориентированной плоской области § 13.9. Поток вектора через ориентированную поверхность § 13.10. Дивергенция. Теорема Гаусса-Остроградского § 13.11. Ротор вектора. Формула Стокса § 13.12. Дифференцирование интеграла по параметру § 13.13. Несобственный интеграл § 13.14. Равномерная сходимость несобственного интеграла § 13.15. Равномерно сходящийся интеграл для неограниченной области Глава 14. ЛИНЕЙНЫЕ НОРМИРОВАННЫЕ ПРОСТРАНСТВА. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ § 14.2. Пространство L'(L) § 14.3. Пространство L2 (L2) § 14.  4. Пространство …§ 14.5. Полнота системы элементов в банаховом пространстве § 14.6. Ортогональная система в пространстве со скалярным произведением § 14.7. Ортогонализация системы § 14.8. Полнота системы функций в … Глава 15. РЯДЫ ФУРЬЕ. ПРИБЛИЖЕНИЕ ФУНКЦИЙ ПОЛИНОМАМИ § 15.2. Сумма Дирихле § 15.3. Формулы для остатка ряда Фурье § 15.4. Теоремы об осцилляции § 15.5. Критерий сходимости рядов Фурье. Полнота тригонометрической системы функций § 15.6. Комплексная форма записи ряда Фурье § 15.7. Дифференцирование и интегрирование рядов Фурье § 15.8. Оценка остатка ряда Фурье § 15.9. Алгебраические многочлены. Многочлены Чебышева § 15.10. Теорема Вейерштрасса § 15.11. Многочлены Лежандра Глава 16. ИНТЕГРАЛ ФУРЬЕ. ОБОБЩЕННЫЕ ФУНКЦИИ § 16.1. Понятие интеграла Фурье § 16.2. Сходимость простого интеграла Фурье к порождающей его функции § 16.3. Преобразование Фурье. Повторный интеграл Фурье. Косинус- и синус-преобразования Фурье § 16.  4. Производная преобразования Фурье§ 16.5. Обобщенные функции в смысле D § 16.6. Пространство S § 16.7. Пространство S обобщенных функций |
Фактически принят как учебное пособие в некоторых втузах с повышенной программой по математике.
Всеобъемлющее руководство по рациональным числам
Число — это арифметическое значение, используемое для обозначения количества элемента в математике. Наша система счисления содержит различные типы чисел. В этой статье мы рассмотрим рациональные числа, один из типов чисел в математике, а также несколько примеров и их свойства.
Перейти к разделу
- Что такое рациональное число?
- Как найти рациональное число?
- Некоторые распространенные примеры
- Типы
- Представляют рациональные числа на числовой прямой.
- Свойства рациональных чисел
- Другие свойства рациональных чисел
- Связь между рациональным и иррациональным числами
- Заключительные мысли
Что такое рациональное число?
Что такое рациональные числа? Рациональное число — это разновидность действительного числа, которое принимает форму m/n, где n — ненулевое число.
В математике буква «Q» обозначает рациональное число.
Как найти рациональное число?
Рациональное число должно удовлетворять трем условиям, перечисленным ниже:
- Оно может быть представлено простой дробью m/n (числитель делится на знаменатель).
- И знаменатель, и числитель должны быть обычными целыми числами.
- Знаменатель(n) должен быть ненулевым целым числом.
Некоторые распространенные примеры
| m | n | m/n | m/n (десятичное число) | Рационально ли это? |
| 3 | 1 | 3/1 | 3 | Yes |
| 1 | 4 | 1/4 | 0.25 | Yes |
| 2 | 7 | 2/ 7 | 0.28 | Yes |
| 6 | 17 | 6/17 | 0.35 | Yes |
| 16 | 0 | 16/0 | – | No |
Типы
Положительное рациональное число
Положительное рациональное число — это число, имеющее одинаковый знак как в числителе, так и в знаменателе.
Например, 5/8 — положительное рациональное число, так как и 5, и 8 положительны. Точно так же 45, 0,5, 7, 0,75 — некоторые другие примеры положительного рационального числа. Здесь 0,5 и 0,75 также можно записать как 1/2 и 3/4 соответственно.
Отрицательное рациональное число
Отрицательное рациональное число — это число, в котором числитель и знаменатель имеют противоположные знаки.
Например, -2/7 — отрицательное рациональное число. Некоторые другие примеры включают -3/8, -0,25, -9, -17/34 и т. д.
Целочисленная форма
Поскольку мы можем записывать целые числа в виде m/n, все целые числа являются рациональными числами.
Например, 9/1, 6/1, 25/1 и т. д.
Десятичная форма
Повторяющиеся десятичные числа, как конечные, так и неконечные, относятся к рациональным числам.
Например, 0,45, -0,98, 1,65 — рациональные числа.
Представление рациональных чисел на числовой прямой.
Давайте начнем с рисования числовой линии, потому что мы будем учиться представлять на ней рациональное число.
На изображении выше точки справа от 0 обозначены знаком плюс и называются положительными числами. С другой стороны, числа слева от 0 обозначаются знаком минус и называются отрицательными числами.
Например, попробуем изобразить числа 3/4 и -3/4 на числовой прямой. Как рациональное число, -3/4 отрицательно. Он отмечен слева от 0. В отличие от этого, 3/4 отмечен справа от 0 (см. Изображение ниже).
3/4 и -3/4 в числовой строкеВсе другие рациональные числа могут быть выражены аналогичным образом.
Как представить рациональное число на числовой прямой?Свойства рациональных чисел
Свойство замыкания
При вычитании, сложении или умножении двух рациональных чисел a и b результатом всегда является рациональное число.
Свойство замыкания не применяется к делению, так как деление на ноль не определено.
Например,
2/3+ 4/5=22/15
6/7- 8/21=10/21
Переместительное свойство
Когда рассматриваются два целых рациональных числа, a и b, умножение и сложение всегда коммутативны.
Коммутативный закон сложения утверждает, что a+b=b+a
Например, 2/3+1/2=1/2+2/3=7/6
Коммутативный закон умножения утверждает, что a* b=b*a
Например, 2/3*1/2=1/2*2/3=1/3
Ассоциативное свойство
Согласно ассоциативному свойству сложения, a+(b+c)= (а+б)+в.
Например, 1/2+(2/3+2)=(1/2+2/3)+2=19/6
Аналогично, согласно ассоциативному свойству умножения, a(bc)=( ab)c
Например, 1/2(2/3*2)=1/2*2/3)2=2/3
Распределительное свойство
Для трех рациональных чисел a,b и c ; а(б+с)=(аб)+(бс).
Пример: 1/2(2/3+2/5) =(1/2*2/3)+(1/2*2/5)
8/5=8/5
Таким образом, LHS =RHS
Свойство идентичности
0 является аддитивной идентичностью, а 1 известна как мультипликативная идентичность.
Это означает, что число остается неизменным после сложения с 0 и умножения на 1 соответственно.
Пример: 1/2+0=1/2 (Аддитивная идентичность)
4/5*1=4/5 (Мультипликативная идентичность)
Обратное свойство
Для рационального числа m/n аддитивной обратной является -m/n, а мультипликативная обратная — n/m.
Например, аддитивное обратное число 1/2 равно -1/2, а мультипликативное обратное число равно 2/1.
Другие свойства рациональных чисел
Свойство 1:
Если m/n — рациональное число, а x — целое, отличное от нуля, то m/n=(m*x)/(n*x).
Рациональное число останется неизменным, если мы умножим и числитель, и знаменатель на одно и то же число.
Например, 1/2=1*6/2*6=6/12
Свойство 2:
Если m/n — рациональное число, а x — общий делитель, то m/n=(m÷x )/(n÷x)
Следовательно, когда числитель и знаменатель рационального числа делятся на общий делитель, рациональное число остается неизменным.
Например, 12/14=12÷2/14÷2=6/7
Свойство 3:
Если мы допустим, что m/n и o/p — два рациональных числа, то m/n=o/p ⇒ m*p=n*o
Например, 1/2=2/3
1*3= 2*2
Свойство 4:
Для каждого рационального числа a выполняются следующие условия.
- x=0
- x<0
- x>0
Например, 2/3 больше 0.
0/3 равно 0.
-1/2 меньше 0
Свойство 5:
Любое из следующих условий выполняется для любых двух целых рациональных чисел a, b.
- a=b
- a>b
- a
Например, 2/3 и 3/4 — два рациональных числа. 3/4 больше, чем 2/3.
Если 3/6 и 7/114 два рациональных числа, то 3/6=7/14
Свойство 6:
Если a > b и b > c верно для трех рациональных чисел, то a>c.
Например, для трех рациональных чисел 7/9, 13/30 и -5/16 7/9 больше 13/30, а 13/30 больше -5/16. Таким образом, 7/9 больше, чем -5/16.
Связь между рациональным и иррациональным числами
Все мы знаем, что числа, не являющиеся логическими, называются иррациональными числами.
Ниже приведено сравнение между рациональным и иррациональным числом:
- Число, которое можно записать в виде дроби, называется рациональным числом. Например, 4/6, 6/7, 4/8 и т. д. Иррациональные числа — это те, которые нельзя представить в виде дробей. Например, квадратный корень из 2, пи и т. д.
- Рациональное число может быть представлено в виде некончающихся десятичных дробей с повторяющимися шаблонами, чего нельзя сказать об иррациональном числе.
- Целые числа, натуральные числа и целые числа входят в набор рациональных чисел. Набор иррациональных чисел отличается от других наборов чисел, поскольку не содержит ни одного из них.
Заключительные мысли
Рациональные числа — важная концепция для понимания в математике.
Эта исчерпывающая статья идеально подойдет для начинающих студентов, поскольку содержит всю необходимую информацию о рациональных числах. Для получения дополнительной информации и рабочих листов по теме посетите Podium School.
Разница между дробью и рациональными числами
Дробь и рациональные числа — два наиболее часто используемых термина в математике. Внешне немного похожие друг на друга, они часто сбивают людей с толку. Хотя концепции этих жизненно важных математических компонентов в некоторых аспектах связаны между собой, между ними есть заметная разница. Здесь мы готовы дать вам четкое представление о рациональных числах и дробях вместе с некоторыми примерами, чтобы у вас не осталось никаких сомнений.
Дробь
Определение: Дробь или дробное число – это число в форме p/q, где p и q – целые числа, а q не равно нулю (0). Оно выражает часть целого или любое количество равных частей. Его также можно определить как отношение двух целых чисел, где верхнее число (числитель) говорит о том, сколько частей у нас есть, а нижнее (знаменатель) показывает количество равных частей, на которые делится целое.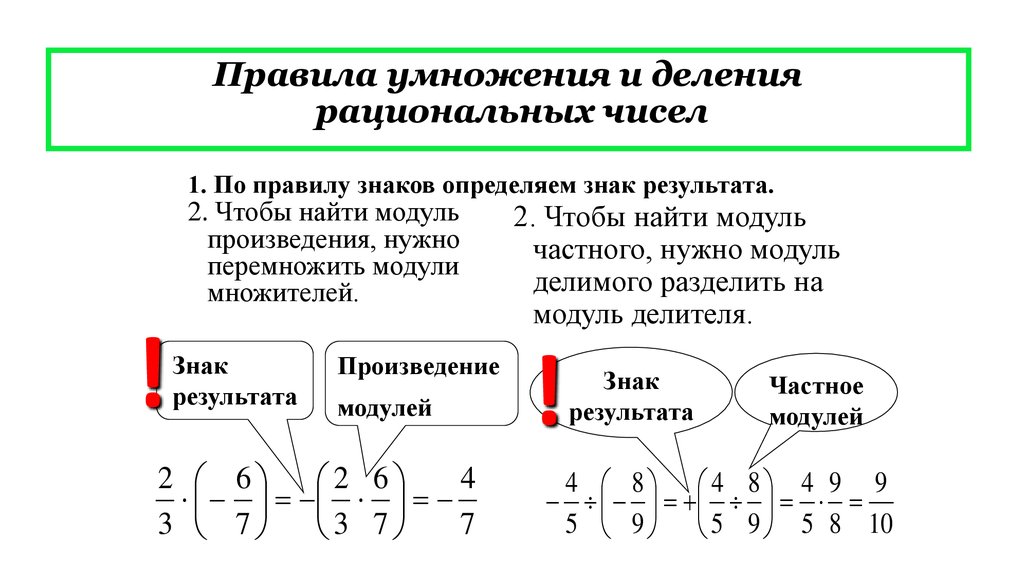
Другими словами, дробь представляет собой выражение деления, в котором делитель и делимое являются целыми числами, а делитель не равен нулю. Например, 3/5, 9/6, 8/4 и т. д. — дробные числа.
Дроби используются нами в повседневной жизни постоянно, и мы даже не осознаем этого. Следовательно, важно узнать о них не только для уроков математики и экзаменов, но и для ежедневных вычислений как жизненного навыка, который будет использоваться на протяжении всей жизни.
Дроби составляют часть нашей мысленной математики в мельчайших деталях вокруг нас. Когда вы ходите по магазинам с семьей, в магазинах действуют праздничные предложения с надписью «Купи сейчас, заплати половину». Помните, что дробь представляет собой часть целого. Точно так же разум видит «половину» скидки от начальной, недисконтированной цены. Когда вы делитесь тортом с друзьями, вы разрезаете торт на равные части или «доли», равные количеству людей в группе.
Возможно, вы этого не чувствуете, но дроби повсюду.
Даже когда кто-то спрашивает у вас время. Часы показывают «без четверти 12». Это означает, что до 12 часов осталось 15 минут. Дроби используются в рецептах, которые говорят вам налить «1/4 бутылки» и «1/2 ложки меда в реальной жизни». Многие соревновательные виды спорта, такие как автоспорт Формулы-1, NASCAR, легкая атлетика и крикет, используют дроби для отслеживания времени реакции, разрывов, например, «одну десятую секунды» между их соперниками, и целей, за которыми нужно преследовать, таких как самое быстрое время круга и самые быстрые пит-стопы.
Даже когда вы идете в супермаркет за продуктами, вы покупаете «полдюжины бананов», что составляет не что иное, как 1/6 дюжины. Когда вам нужно сравнить вещи с точки зрения роста, веса и массы, дроби используются, чтобы сказать такие вещи, как «Раньше я был как минимум вдвое меньше, чем сейчас» и «Как может один из братьев быть на 1/3 роста?» другого?».
Теперь, когда вы знаете, как целые дроби используются в повседневной жизни, вы можете узнать все о них и реальных задачах, связанных с расчетами, связанными с дробями, на Vedantu.
Примеры различных типов дробей
В математике дроби или дробные числа подразделяются на множество типов. Здесь мы проливаем свет почти на все типы фракций, показывая их примеры.
Правильные дроби: числитель всегда меньше знаменателя. Например, 3/8 и 7/9.
Неправильные дроби: числитель всегда больше знаменателя. например, 9/2 и 7/5.
Смешанные дроби: состоят из целого числа и дроби. Например, 3 (3/2) и 5 (2/7).
Равные дроби: Это дроби, числители и знаменатели которых можно разделить на одно и то же число. Например, 2/12 = 3/18 и 5/10 = 10/20.
Подобные дроби: это дробные числа с одинаковыми знаменателями.
например, 2/5; 3/5.В отличие от дробей: это дроби с разными знаменателями. Пример, 2/3; 15/13.
например, 2/5; 3/5.
Рациональные числа
Определение: Рациональные числа — это числа, представленные в форме a/b, где a и b — целые числа, а b не равно нулю (0). Его также можно выразить как отношение целых чисел, т. Е. Можно записать как дробь двух целых чисел с верхним числом в качестве числителя и нижним в качестве ненулевого знаменателя. Поскольку знаменатель может быть равен 1, все целые числа являются рациональными числами. Более того, некоторые числа с плавающей запятой могут быть выражены в виде дробей. Следовательно, они также являются рациональными числами. Например, мы можем записать 1,5 как 3/2, 6/4, 9./6 и более. Соответственно, это рациональное число.
Примеры рациональных чисел
Рациональные числа, как правило, могут встречаться в четырех формах: целые числа, целые числа, натуральные числа и дроби.
Основываясь на этой информации, давайте посмотрим на примеры рациональных чисел.
Поскольку число 8 можно записать как дробь 8/1, это рациональное число.
3/4 — рациональное число, потому что его можно записать в виде дроби
Мы можем записать 1,5 как отношение 3/2. Следовательно, это также рациональное число
O.333… может быть записано как 1/3. Следовательно, это рациональное число
Повторяющиеся десятичные числа, такие как 0,262626…, все конечные десятичные числа и все целые числа также являются рациональными числами.
Разница между дробью и рациональными числами
Надеемся, что после просмотра приведенной выше статистики относительно дробей и рациональных чисел вы теперь сможете различать эти два числа.
Тем не менее, таблица, которая показывает некоторые четкие различия между дробными и рациональными числами, выглядит следующим образом:
Фракционные номера | Рациональные номера |
P и Q — натуральные номера | |
P и Q — натуральные номера | |
P и Q — натуральные номера | |
P и Q — натуральные номера | |
P и Q — натуральные номера | |
. | Не все рациональные числа являются дробями. Только рациональные числа, в которых p и q имеют положительные целые числа, являются дробями |
Пример: 1/2, 25/5, 9/7 | Пример: 8/1, 5/-8, -23/-27, 100/-23 |
3 Примеры 9
Пример 1: В школе Green Valley работают 14 учителей-мужчин и 11 учителей-женщин.
Какую долю от общего числа учителей составляют женщины?
Решение: Согласно вопросу,
Числитель (p) дроби = количество учителей-женщин.
Знаменатель (q) дроби = общее количество учителей в школе.
SO, доля женщин -учителей = количество учителей -женщин/ общее количество учителей
= 11/ (14 + 11)
= 11/ 25.
Пример 2: 2½ — смешанная фракция. Определите, рациональное это число или нет?
Решение: Простая форма 2½ равна 5/2
Где,
Числитель 5 является целым числом
Знаменатель 2 также является целым числом и не равен нулю (0).
Итак, мы можем сказать, что да, 2½ = 3/2 — рациональное число.
Пример 3. Рассмотрим число 12/-32. Теперь давайте посмотрим, является ли это дробью или рациональным числом.
Решение: В числе 12/-32 знаменатель отрицательный, т.