Основные операции в математике | УДОБА
Основные операции в математике
Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).
Операции действия:
сложение (+)
вычитание (-)
умножение (*)
деление (:)
Операции отношения:
равно (=)
больше (>)
меньше (<)
больше или равно (≥)
меньше или равно (≤)
не равно (≠)
Сложение — операция, которая позволяет объединить два слагаемых.
Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.
Вычитание — действие, обратное сложению.
Запись вычитания: 10 — 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.
Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 — 1 = 9.
Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.
Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.
3 * 4 = 3 + 3 + 3 + 3
В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 * 2 = 5 + 5 = 10.
Поэтому и множитель, и множимое называют сомножителями.
Бесплатный вводный урок
Шаг 1 из 2. Данные ученика
Класс
Деление — арифметическое действие обратное умножению.
Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.
В этом случае произведение делителя 6 и частного 5, в качестве проверки, дает делимое 30.
Если в результате операции деления, частное является не целым числом, то его можно представить в виде дроби.
Возведение степень — операция умножения числа на самого себя несколько раз.
Основание степени — число, которое повторяется сомножителем определённое количество раз.
Показатель степени — число, которое указывает, сколько раз берется одинаковый множитель.
4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
2√16 = 4 — корень второй степени называется — квадратным.
При знаке квадратного корня показатель корня принято опускать: √16 = 4.
3√8 = 2 — корень третьей степени называется — кубическим.
Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня попарно представляют обратные друг другу действия. Далее узнаем порядок выполнения арифметических действий.
Порядок вычисления простых выражений
Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:
действия выполняются по порядку слева направо
сначала выполняется умножение и деление, а затем — сложение и вычитание.
Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.
Что первое, умножение или деление? — По порядку слева направо.
Сначала умножение или сложение? — Умножаем, потом складываем.
Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Рассмотрим порядок арифметических действий в примерах.
Пример 1. Выполнить вычисление: 11- 2 + 5.
Как решаем:
В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.
Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.
Ответ: 14.
Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?
Как рассуждаем:
Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.
Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.
Ответ: 7.
Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.
Например, в такой последовательности можно решить пример по действиям:
решение примера
Действия первой и второй ступени
В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.
Действиями первой ступени называют сложение и вычитание, а умножение и деление — действиями второй ступени.
С этими терминами правило определения порядка выполнения действий звучит так:
Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).
порядок действий
Порядок вычислений в выражениях со скобками
Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:
Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.
Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.
Рассмотрим порядок выполнения действий на примерах со скобками.
Пример 1. Вычислить: 10 + (8 — 2 * 3) * (12 — 4) : 2.
Как правильно решить пример:
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.
Начнем с первого 8 — 2 * 3. Что сначала, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание. Получается так:
8 — 2 * 3 = 8 — 6 = 2.
Переходим ко второму выражению в скобках 12 — 4.
Здесь только одно действие – вычитание, выполняем: 12 — 4 = 8.
Подставляем полученные значения в исходное выражение:
10 + (8 — 2 * 3) * (12 — 4) : 2 = 10 + 2 * 8 : 2.
Какое действие в полученном выражении делается первым, умножение или деление? Выполняем слева направо: умножение, деление, затем — вычитание. Получилось:
10 + 2 * 8 : 2 = 10 + 18 : 2 = 10 + 6 = 16.
На этом все действия выполнены.
Что выполняется вперед, деление или умножение?
Что выполняется вперед, деление или умножение?
Рассмотрим примеры.20/4*2. Понятно, что если выполнять сначала деление, потом умножение мы получим правильный результат 20/4 = 5. 5*2 = 10.Если же выполнить сначала умножение, а потом деление то, ответ будет совершенно иным и конечно же неправильным. 4*2 = 8. 20/8 = 2,5. Причина такой ошибки в том, что операции деления умножения и деления выполняются в порядке их расположения, то есть слева направо.Второй пример. 20*5/4. Проверяем правило.
По порядку расположения сначала умножение. Умножаем 20*5=100, 100/4=25. Правильно.Если же выполним сначала деление, а потом умножение, то получим: 5/4 = 1,25. Далее 20/1,25 = 16.Ответ неверный. Вывод: все зависит от порядка расположения этих операций.
Чтобы ответить на данный вопрос необходимо вспомнить последовательность выполнения математических операций. Если в примере есть выражение в скобках, то оно делается в первую очередь. Если выбирать между действиями «сложение», «вычитание», «умножение» и «деление», то в первую очередь делаем «умножение» или «»деление».Если же в примере только деление и умножение, то действия выполняются последовательно слева направо.
Мы должны при присутствии только деления и умножения в примере, и без участия скобок, действовать по порядку. Если сначала действие с делением, а потом с умножением, то делим, результат далее умножаем. Если сначала умножение, потом деление, то умножаем, результат далее делим.
Когда есть действие в скобках, вроде такого (5*2):(2*1), то умножаем что в скобках сначала, а результаты делим, 10(результат первой скобки):2(результат второй скобки). Если знаки вычитания и прибавления есть, все равно, сначала слева направо выполняем деление или умножение, или умножение или деление, что стоит первым среди этих действий. Просто так принято по правилам. Если бы правило было иным, справа налево, то тогда ответы принимались бы те за верные, что даются при подобном порядке. А так у нас априори верные именно слева направо. И для расчетов берутся именно они. Поэтому даже если в решении справа налево и получается целое «вполне нормальное» число, это не признак того, что пример решен верно.
действия выполняются по порядку, слева направо. но если в примере присутствуют еще и сложение и вычитание, то в начале выполняют деление с умножением, потом уже сложение и вычитание. а если присутствуют еще и скобки, то в первую очередь решают то, что в скобках.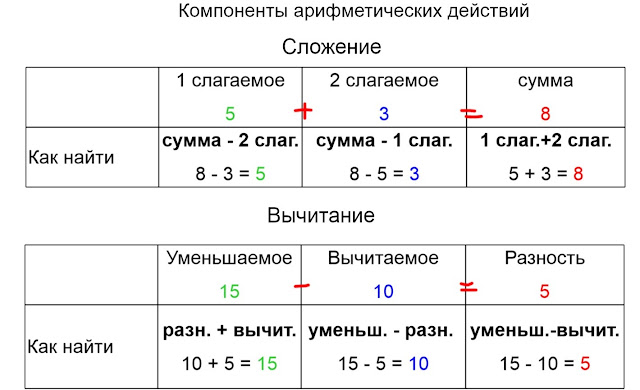
Слева направо если есть сложение и вычитания они делаются в последний очередь
Это часто встречаемый вопрос у ребят и они часто допускают ошибки. Это в заданиях по информатике и математике часто встречается. Деление и умножение равноправны, поэтому они выполняются по порядку. Так в примере 1+250*5/10 сначала 250*5, потом делим на 10 и только потом прибавляем один. Если будет наоборот 15- 250/5*10, то сначала 250/5, потом умножаем на десять по порядку и только потом из 15 вычитаем полученный результат. По приоритету операций у нас 1 возведение в степень, 2 умножение и деление, 3 вычитание и сложение. Если есть скобки, то сначала они.
Очень важно, чтобы правильно решать задачи по математике, знать порядок выполнения вычислений.Рассмотрим пример:20:4*5 (двадцать разделить на четыре и умножить на пять). Решаем такой пример, по порядку выполняя действия (слева направо).Получится вот что: двадцать разделить на четыре — будет пять, теперь пять умножаем на пять, получится двадцать пять.
Share on facebook
Share on twitter
Share on vk
VK
Share on odnoklassniki
OK
Share on tumblr
Tumblr
Share on telegram
Модуль в порядке операций
Автор Анна Щепанек, доктор философии
Отзыв от Rijk de Wet
Последнее обновление: 21 ноября 2022 г.
Содержание:- Что такое модульный оператор?
- Считается ли модуль делением?
- Где модуль в порядке операций?
- Где модуль в PEMDAS?
Задумывались ли вы, как по модулю вписывается в порядок операций ? Вы попали по адресу — в этой статье мы объясним все, что вам нужно знать о PEMDAS и модуле.
Не знаете, что такое PEMDAS? Продолжай читать!
Что такое оператор по модулю?
Оператор по модулю возвращает остаток от деления одного числа на какое-то другое число. Помните, здесь мы имеем дело с целыми числами. В математической записи, если a и n — два целых числа, мы всегда можем найти b и r 9.0032 такое, что
a = b * n + r
, где остаток r удовлетворяет 0 ≤ r < n . Тогда по модулю n = r .
В качестве альтернативы мы можем сказать, что a mod n = r тогда и только тогда, когда n делит a−r без остатка .
Например:
21 mod 5 = 1потому что21 = 4 * 5 + 123 по модулю 10 = 3потому что23 = 2 * 10 + 33 mod 10 = 3потому что3 = 0 * 10 + 3
Считается ли модуль делением?
Модуль связан с делением , но не совсем то же самое .
Посмотрим:
7 / 2 = 3,5
отличается от
7 mod 2 = 1 .
Существует также операция целочисленного деления (часто обозначаемая двойной косой чертой 9).0031//, особенно в программировании):
7//2 = 3 .
Связь между целочисленным делением и делением по модулю может быть выражена следующим соотношением:
7 = 3 * 2 + 1 .
Как видите, целочисленное деление 7 // 2 отвечает на вопрос "Сколько раз 2 вписывается в 7?" и 7 mod 2 отвечает на вопрос "Каков будет остаток при делении 7 на 2?"
Где модуль в порядке операций?
В большинстве языков программирования принято соглашение о том, что оператор по модулю (обозначаемый % , а не по модулю ) занимает то же место в порядке операций, что и умножение и деление . Следовательно, получается ПОСЛЕ операций в скобках, но ДО сложения и вычитания .
Когда есть модуль и умножение или деление, то операции выполняются с слева направо .Например:
2 * 3 % 4преобразуется в2, потому что у нас есть2 * 3 = 6и6 % 4 = 2.3 % 4 * 2преобразуется в6, потому что у нас есть3 % 4 = 3и3 * 2 = 6.
Однако в математике мы иногда отдаем приоритет оператору по модулю перед умножением и сложением. Это потому что 3 mod 4 * 2 подразумевает, что мы выполняем вычисления по модулю 8 , поэтому результатом будет 3 .
Как видите, не всегда очевидно, где находится модуль в порядке операций.
Если вы сомневаетесь при работе с новым языком программирования, просто обратитесь к документации или выполните быструю проверку, попросив компьютер (или калькулятор) оценить несколько примеров. Это может потребовать написания небольшого кода, но ваша проблема будет решена немедленно. В математике , чтобы избежать путаницы, используйте скобки . Столкнувшись с запутанным выражением, проверьте контекст или попросите разъяснений у коллег .
Где модуль в PEMDAS?
PEMDAS — это аббревиатура, обозначающая Скобки, Экспоненты, Умножение/Деление, Сложение/Вычитание . Он кодирует порядок старшинства при выполнении арифметических операций.
🙋 Не стесняйтесь проверить наш калькулятор сложения, калькулятор длинного вычитания, калькулятор длинного деления, калькулятор умножения и калькулятор степени, чтобы помочь вам в этом!
В некоторых странах используется аббревиатура BEDMAS , обозначающая Скобки, Экспоненты, Деление/Умножение, Сложение/Вычитание .
Используются и другие варианты.
Обратите внимание, что в двух приведенных нами версиях порядок умножения и деления кажется обратным. Это не вариант! Помните, что умножение и деление имеют одинаковый приоритет : они занимают одно и то же место, и вы выполняете их слева направо, чтобы получить правильный ответ. То же правило справедливо для сложения и вычитания .
Итак, где в схеме PEMDAS оператор по модулю? Как видите, там не значится . Одна из причин заключается в том, что детей узнают о PEMDAS за несколько лет до того, как детей узнают о модуле. Другая причина в том, что есть различные соглашения о том, где мод должен вписываться в порядок приоритета, и это сильно зависит от контекста. Одно несомненно: большинство языков программирования помещают по модулю на тот же уровень , что и умножение и деление.
Anna Szczepanek, PhD
x Mod Y = R
x (Dividend)
Y (Divisor)
R (остаток)
Проверьте 62 аналогичные арифметические калькуляторы ➗
Абсолютно.
далее
Основной порядок операций (DMAS)
ВведениеПри упрощении математических выражений, состоящих из операций одного типа, мы выполняем одну операцию за раз, как правило, начиная слева направо. Если выражение имеет более одной основной операции, вы не можете выполнять операции в том порядке, в котором они указаны. Некоторые операции должны быть выполнены раньше, чем другие. Это каждая операция имеет свой приоритет. Как правило, порядок, в котором мы последовательно выполняем операции слева направо, таков: деление, умножение, сложение, вычитание. Но когда в выражениях также используются скобки, у нас есть набор правил, определяющих приоритет операций. Давайте узнаем, как определяется это правило.
Давайте разберемся с этим на примере.
Предположим, мы хотим найти значение 2 + 3 x 5
Есть два способа найти значение приведенного выше выражения.
В первом методе будем двигаться слева направо, решая выражение в указанном порядке.
Это означает, что сначала мы найдем сумму 2 и 3. Мы получим, 2 + 3 = 5.
Теперь у нас есть 2 + 3 x 5 = 5 x 5
Теперь мы найдем произведение 5 на 5 чтобы получить ответ как 25. Следовательно, мы имеем
2 + 3 x 5 = 25 ……………………………….. ( 1 )
Теперь найдем значение этого выражения другим способом.
Сначала мы найдем значение 3 x 5 и добавим это произведение к 2. Таким образом, мы получим
3 x 5 = 15 и 15 + 2 = 17
Следовательно, теперь у нас есть
2 + 3 x 5 = 17 ………………………… ( 2 )
Из ( 1 ) и ( 2 ) мы видим, что оба полученных результата не совпадают. Это подтверждает необходимость наличия приоритета операторов, чтобы получить один и тот же ответ на данное алгебраическое выражение. Этот приоритет известен как порядок операций.
Каков основной порядок операций? Порядок работы может быть определен как стандартная процедура, которая указывает, какие вычисления следует начинать в выражении с несколькими арифметическими операциями.
Без последовательного порядка операций можно допустить большие ошибки во время вычислений. Существует ряд правил, определяющих порядок операций в зависимости от задействования операторов, скобок, показателей степени и других математических символов для операций. Это правило известно как DMAS, где
D означает деление (÷)
M означает умножение (x)
A означает сложение (+)
S означает вычитание (–)
Давайте разберемся с правилом более подробно.
Что такое DMAS?MDAS, как определено выше, является основным порядком операций. Другими словами, он определяет порядок, в котором должны выполняться операции над числами, когда возникают ситуации, когда в выражении на две операции больше, чем две. Итак, у нас порядок операций такой –
Рассмотрим пример. Предположим, мы хотим найти значение 3 + 5 x 2.
Здесь у нас есть два оператора, а именно ( x ) и ( + ). Мы знаем, что в математике мы можем выполнять операции между двумя числами только за один раз.
Если у нас есть более 2 чисел, результат первой операции используется для выполнения следующей операции. Итак, в приведенном выше примере необходимо выполнить две операции: (3 + 5) и (5 x 2). Нам нужно решить, с какой из них начать. Здесь вступает в действие правило MDAS.
Из этого правила видно, что умножение предшествует сложению. Поэтому сначала выполним операцию умножения. Полученный таким образом результат будет добавлен к 3. Шаги, связанные с этим процессом, будут –
3 + 5 x 2
= 3 + 10
= 13
Следовательно, 3 + 5 x 2 = 13
Рассмотрим другой пример.
Пример
Упростите следующее выражение, используя порядок операций –
6 + 5 – 4 x 2
Решение
Нам дано выражение 6 + 5 – 4 x 2
Важно отметить, что здесь задействованы три операции. Основываясь на порядке операций, умножение имеет приоритет над сложением и вычитанием, поэтому мы будем умножать первыми.
Затем добавьте, а затем вычтите, так как операция сложения предшествует вычитанию слева направо.
Следовательно, мы имеем
6 + 5 – 4 x 2
= 6 + 5 – 8 (Здесь мы решили 4 x 2, что дало нам результат 8)
= Затем мы сложим 6 и 3, чтобы получить 9. Итак, у нас есть
6 + 5 – 8 = 11 – 8 = 3
Следовательно, 6 + 5 – 4 x 2 = 3
Использование скобок в порядке операцийМы только что узнали о приоритете основных операций сложения, вычитания, умножения и деления. В соответствии с ним порядок, в котором должны выполняться операции, - это сначала деление, затем умножение, после чего сложение и, наконец, вычитание, но иногда в сложных операциях требуется, чтобы набор операций выполнялся до другого. Например, если мы хотим, чтобы сложение выполнялось перед делением или умножением, нам нужно использовать скобки.
Скобки используются для ясности в порядке операций, в котором несколько операций должны выполняться в математическом выражении.
Скобка указывает, что операции внутри нее должны выполняться до операций вне ее. Например, выражение 24 ÷ 3 x 4 обычно решается как –
24 ÷ 3 x 4
= 8 x 4 = 32
Однако, если мы хотим сначала умножить 3 и 4, а затем разделить 24 на получившееся число запишем выражение как
24 ÷ ( 3 x 4 )
Теперь в соответствии с порядком действий сначала разгадаем скобки, чтобы получить,
24 ÷ ( 3 x 4 )
= 24 ÷ 12
= 2
В сложных выражениях иногда необходимо иметь (внутри) в одно и то же время (одно внутри другого может сбивать с толку, потому что чаще всего используются разные типы скобок)
Скобки Имя
( ) Круглые скобки
{ } Скобки или фигурные скобки
[ ] Скобки или квадратные скобки
Здесь важно отметить, что левая часть каждого символа скобки указывает на начало скобки, а правая часть указывает на конец скобки. При написании математических выражений, состоящих более чем из одной скобки, в самой внутренней части используются круглые скобки, за которыми следуют фигурные скобки, и эти две скобки заключаются в квадратные скобки.
Для упрощения выражений, содержащих более одной скобки, мы будем использовать шаги, описанные ниже –
- Посмотреть, содержит ли данное выражение винкулум или нет. Если винкулум присутствует, выполните операции с красным цветом, в противном случае перейдите к следующему шагу. Винкулум — это горизонтальная линия, расположенная над выражением, чтобы показать, что все, что ниже линии, является одной группой, например, $\overline{2\: x\: 3}$.
- Теперь найдите самую внутреннюю скобку и выполните в ней операции.
- Удалите самую внутреннюю скобку, выполнив следующие действия:
- Если скобке предшествует знак плюс, удалите ее, записав ее термины как есть.
- Если скобке предшествует знак минус, измените положительный знак внутри нее на отрицательный и наоборот.
- Если между числом и символом группировки нет знака, то это означает умножение.
- Если перед некоторыми скобками стоит число, то мы умножаем число внутри скобок на число вне скобок.
- Найдите следующую самую внутреннюю скобку и выполните в ней операции. Удалите второй в направлении, используя правила, указанные в предыдущих шагах. Продолжайте этот процесс, пока не будут удалены все скобки.
Давайте разберем приведенные выше шаги на примере.
Пример
Упрощение: 37 – [ 5 + { 28 – ( 19 – 7 ) } ]
Решение
Нам дано выражение, 37 – [ 1 9 – 28 – ( 1 ) } ]
Мы будем использовать порядок операций для решения данного выражения.
Сначала мы удалим самую внутреннюю скобку, чтобы получить
37 – [ 5 + { 28 – 12 } ] …………………… [ Удаление самой внутренней скобки ( ) ]
Далее мы удалим фигурные скобки, чтобы получить
37 — [ 5 + 16 ] …………………………. [ Удаление фигурных скобок ]
Теперь мы удалим квадратные скобки, чтобы получить,
37 – 21 …………………………… [удаление квадратных скобок ]
Наконец, мы найдем разницу между 37 и 21, чтобы получить 16.
Следовательно, упрощение 37 – [ 5 + { 28 – 12 } ] приведет к 16.
Как решать выражения, используя порядок операций?Теперь, когда мы поняли, что мы подразумеваем под порядком операций, давайте узнаем о шагах, связанных с решением математических выражений с использованием порядка операций. Необходимые шаги:
- Всегда начинайте с вычисления всех выражений в круглых скобках
Прежде всего, мы должны искать удаление любых группирующих символов в алгебраическом выражении. Это означает, что в верхней части списка не забывайте всегда упрощать все внутри символов группировки. Примерами символов группировки являются круглые скобки ( ), скобки и фигурные скобки { }. Для вложенных символов группировки проработайте их изнутри и снаружи.
- Упростить все показатели степени, такие как квадратные корни, квадраты, кубы и кубические корни
После удаления скобок мы переходим к следующему шагу решения всех экспоненциальных значений в алгебраическом выражении.
Экспоненциальные выражения, которые могут включать корневые значения, такие как квадратные корни, квадраты, кубы, кубические корни и т. д., сначала вычисляются или оцениваются перед выполнением любой из четырех основных арифметических операций, а именно: сложения, вычитания, умножения и деления.
- Выполните умножение и деление, начиная слева направо
Затем умножьте и/или разделите слева направо перед выполнением сложения и вычитания. Это говорит нам о том, что умножение и деление имеют более высокий уровень важности, чем сложение и вычитание.
- Наконец, аналогично выполните сложение и вычитание, начиная слева направо.
Давайте разберемся на примере.
Пример Найдите значение выражения 4 ( 10 + 15 ÷ 5 × 4 – 2 × 2 )
Решение Нам дано выражение 4 ( 10 + 15 ÷ 5 × 4 – 2 × 2 ). Нам нужно решить ее с помощью MDAS.
Так как данное выражение содержит скобки; мы сначала решим скобки.
Мы получим
4 ( 10 + 15 ÷ 5 × 4 – 2 × 2 )
Теперь в скобках сначала решим раздел деления
4 ( 10 + 15 ÷ 5 x 4 – 2 × 2 )
Далее в самой скобке решим умножение, чтобы получить
4 ( 10 + 3 × 4 – 2 × 2 )
Теперь внутри скобки решим сложение, чтобы получить
4 ( 10 + 12 – 4 )
Далее в скобках мы сложим числа 10 и 12, а затем вычтем из результата 4, чтобы получить
4 ( 22 – 4 )
После того, как скобка решена, возьмите число из снаружи и решить часть «Из» умножением:
= 4 × 18
= 72
Therefore, 4 ( 10 + 15 ÷ 5 × 4 – 2 × 2 )= 72
The steps used can be tabulated as
| Brackets Of | 4 (10 + 15 ÷ 5 × 4 - 2 × 2) |
| Дивизион | 4 (10 + 15 ÷ 5 x 4 - 2 × 2) |
. ( 10 + 3 × 4 – 2 × 2 ) | |
| Addition | 4 ( 10 + 12 – 4 ) |
| Subtraction | 4 ( 22 – 4 ) |
| Answer | = 4 x 18 |
| 72 |
Мы узнали, что в математике порядок операций помогает найти правильное значение выражения. Однако это не ограничивается задачами по математике. Порядок операций имеет значение и в повседневной жизни. Например, вы используете фиксированный порядок действий для приготовления блюда. Точно так же в химических реакциях необходимо соблюдать определенный порядок, чтобы получить желаемые результаты.
Возвращаясь к математике, есть много повседневных дел, в которых используется порядок операций MDAS.
Давайте разберемся на примере.
Пример
Джон покупает 2 рубашки по 8 фунтов каждая. Он также покупает джинсы за 20 фунтов стерлингов, на которые предоставляется скидка в размере 3 фунтов стерлингов. Сколько всего он платит?
Решение
Нам известно, что Джон покупает 2 рубашки по 8 фунтов каждая. Он также покупает джинсы за 20 фунтов стерлингов, на которые предоставляется скидка в размере 3 фунтов стерлингов. Нам нужно узнать, сколько Джон платит за рубашки и джинсы. Чтобы найти это, мы должны сначала разместить все значения в виде выражения. Мы получим,
Цена 2 рубашек + Цена пары джинсов – Скидка = Общая стоимость, уплаченная Джоном
Следовательно,
Общая стоимость, уплаченная Джоном = 2 x 8 + 20- – 3
Здесь мы видим, что есть задействованы три операции. Основываясь на порядке операций, умножение имеет приоритет над сложением и вычитанием, поэтому мы будем умножать первыми.
Затем добавьте, а затем вычтите, так как операция сложения предшествует вычитанию слева направо. Следовательно, мы получаем,
Общая стоимость, уплаченная Джоном = 16 + 20 – 3 = 36 – 3 = 33 £
Следовательно, общая стоимость, уплаченная Джоном за 2 рубашки и пару джинсов, = 33 фунта стерлингов
Теперь мы научились решать выражения, включающие более одного математического оператора. Но что, если в выражении используются скобки. Поступим ли мы так же или внесем некоторые дополнения в правило? Давайте узнаем.
Ключевые факты и сводка- Порядок работы можно определить как стандартную процедуру, которая указывает, какие вычисления следует начинать в выражении с несколькими арифметическими операциями.
- MDAS — это базовый порядок операций, где MDAS, где M означает умножение (x), D означает деление (÷), A означает сложение (+), S означает вычитание (–).
- Скобки используются для ясности в порядке операций, в котором несколько операций должны выполняться в математическом выражении.
