Арифметическая и геометрическая прогрессии – методическая разработка для учителей, Байтурова Аягоз Рыспаевна
|
Цели обучения, которые необходимо достичь на данном уроке: |
учащиеся смогут записывать квадратное уравнение; находить корни неполного квадратного уравнения. |
|||||
|
Цели обучения: |
Все учащиеся будут знать: |
|||||
|
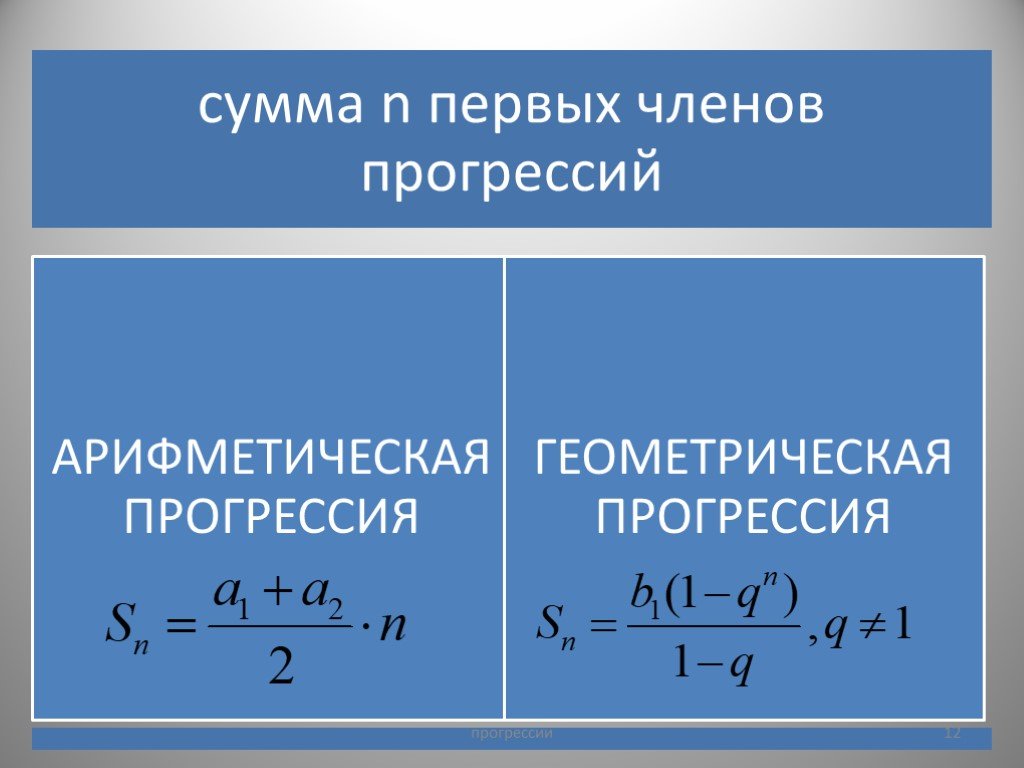
определения арифметической и геометрической прогрессий; формулы n-х членов арифметической и геометрической прогрессий; основное свойство арифметической и геометрической прогрессий; формулы для вычисления значения суммы первых n членов арифметической и геометрической прогрессий. |
||||||
|
|
||||||
|
распознавать арифметическую и геометрическую прогрессии. |
||||||
|
Некоторые учащиеся смогут: |
||||||
|
анализировать и вычислять задачи, опираясь на ранее изученный материал и выявлять связь с пройденными темами; проявить коммуникативную грамотность, организовав работу в группе. |
||||||
|
Ожидаемые результаты: |
возрастание интереса к предмету. Умение применять имеющиеся знания на практике. |
|||||
|
Языковая цель: |
Учащиеся могут: устно и письменно описывать различия между этапами работы, задавать вопросы для перепроверки или пояснения. |
|||||
|
Ключевые слова и фразы: арифметическая и геометрическая прогрессия, формулы n-х членов арифметической и геометрической прогрессий; основное свойство арифметической и геометрической прогрессий; формулы для вычисления значения суммы первых n членов арифметической и геометрической прогрессий. |
||||||
|
Стиль языка, подходящий для диалога/письма в классе. Учащиеся могут использовать новые слова, чтобы показать свое понимание: Таким образом… Мои выводы основаны на… |
||||||
|
|
сотрудничество, уважение, умение работать в коллективе, открытость, творчество и обучение на всем этапе жизненного пути. |
|||||
|
Предыдущее обучение: |
Арифметическая и геометрическая прогрессия. |
|||||
|
План |
||||||
|
Сроки |
Планируемые действия |
Ресурсы |
||||
|
800-803 3 мин |
Организационный момент. Взаимное приветствие. Психологический настрой на урок. Два комплимента друг другу! Лист успеха (Приложение А) |
Лист успеха |
||||
|
Целеполагание. Тема урока. Обобщающий урок. Арифметическая и геометрическая прогрессия. Какова цель урока? |
Слайд 2 |
|||||
|
803-812 9 мин |
ФР — Осуществляет повторение знаний учащихся. Задание №1. Задание №2 Учащиеся применяют формулу бесконечно убывающей геометрической прогрессии в геометрии. Формативное оценивание через наблюдение, уточняющие вопросы. Внесение баллов в лист оценивания. |
Слайд 3, 4, 5
https://bilimland.
|
||||
|
812-817 5 мин |
Работа у доски. Задание №3
Два ученика решают у доски, остальные – в тетрадях. Формативное оценивание через наблюдение, уточняющие вопросы. Внесение баллов в лист оценивания. |
https://bilimland.kz/ru/courses/math-ru/algebra/chislovye-posledovatelnosti/arifmeticheskaya-progressiya/lesson/summa-pervyx-n-chlenov-arifmeticheskoi-progressii
https://bilimland. |
||||
|
817-820 3 мин |
ПР-Задание №4. (Приложение С) Учащиеся устанавливают соответствие между названием и формулами. Самооценивание. Внесение баллов в лист оценивания. |
|
||||
|
820-825 5 мин |
ИР-Задание №5. (Приложение D) Учащиеся выполняют разноуровневый тест. Суммативное оценивание за тест. |
Слайд 3 |
||||
|
825-835 10 мин |
ГР – Задание №3 (Приложение Е) С помощью приема «Задания из конверта» развивает умения и навыки по данной теме. Учащиеся группы получают задания на карточках. Учащимся необходимо решить задачу с применением прогрессией в разных отраслях. Формативное оценивание через наблюдение, уточняющие вопросы. Внесение баллов в лист оценивания. |
карточки | ||||
|
835-840 5 мин |
Домашнее задание. №27,28 стр 115 сборник ВОУД |
|
||||
|
Рефлексия. Желающие высказать свое мнение выступают, придерживаясь данных вопросов.
|
|
|||||
kz/ru/courses/math-ru/algebra/chislovye-posledovatelnosti/geometricheskaya-progressiya/lesson/summa-beskonechno-ubyvayushei-geometricheskoi-progressii
|
Дополнительная информация |
||
| Дифференциация. Как вы планируете поддержать учащихся? Как вы планируете стимулировать способных учащихся? |
Оценивание. Как вы планируете увидеть приобретенные знания учащихся? |
Межпредметные связи соблюдение СанПиН ИКТ компетентность связи с ценностями |
|
Все учащиеся будут следить и принимать участие в деятельности на уроке. Все учащиеся должны знать определения арифметической и геометрической прогрессий; формулы n-х членов арифметической и геометрической прогрессий; основное свойство арифметической и геометрической прогрессий; формулы для вычисления значения суммы первых n членов арифметической и геометрической прогрессий. Большинство учащихся будут распознавать арифметическую и геометрическую прогрессии. Некоторые учащиеся будут анализировать и вычислять задачи, опираясь на ранее изученный материал и, выявив связь с пройденными темами, проявлять коммуникативную грамотность, организуя работу в группе. |
Формативное оценивание учащихся во время урока проводилось с помощью поощрения, наблюдения, комментариев, уточняющих вопросов, методики «Светофор». Суммативное оценивание выставляется после завершения заданий. |
Межпредметная связь: с русским языком путем диалогового обучения; биология, физика, экономика, геометрия через задачи практического характера. |
|
Рефлексия Были ли цели обучения реалистичными? Хорошо ли сработала запланированная дифференциация? Выдерживалось ли время обучения? |
Цели обучения были достигнуты. Одаренные дети проявили коммуникативную грамотность, организовали работу в группе, планировали работу в группе. Учащиеся активно работали на уроке. Время обучения выдержало свой регламент. |
|
Работа в группах позволит организовать деятельность каждого учащегося.
Приложение А.
Лист успеха ФИ _________________________________________
|
Этапы деятельности |
Критерии |
Итого |
|
Обозначение цели урока |
Наблюдал – 0 Составлял – 1 Озвучивал – 1 |
|
|
Фронтальная работа |
Наблюдал – 0 Отвечал устно – 1 Решил у доски – 2 |
|
|
Парная работа |
8 правильных – 2 6-7 правильных – 1 |
|
|
Работа в группе |
Предлагал идею – 1 Решил правильно – 2 Решал с ошибками – 0,5 |
|
|
Рефлексия |
Какие ошибки допустил? Причины. Способы устранения. Какие личностные черты формировались сегодня на уроке? |
|
12 баллов и выше – «5», 10-11 баллов –«4», 8-9 баллов – «3»
|
Индивидуальная работа |
Если все правильно – ставите соответствующую оценку. Если одна ошибка, то снижаете на 1 балл. И т.д. |
Оценка – |
Приложение В
а) Перед вами последовательности чисел:
|
1) 7; 9; 11… |
4) 0,5; 1; 1,5; 2… |
|
2) 1; 4; 9; 16… |
5) – 2; 8; –12; 28… |
|
3) 4; – 4; 4; – 4; 4… |
6) 1; 2; 4; 8; 16… |
Под каким номером записана геометрическая прогрессия? Укажите знаменатель геометрической прогрессии.
Под каким номером записана арифметическая прогрессия? Укажите разность арифметической прогрессии.
б) Из предложенных формул выберите ту, которая является характеристическим свойством арифметической прогрессии (4).
Из предложенных формул выберите ту, которая является характеристическим свойством геометрической прогрессии (8).
в) Известно, что (bn) – геометрическая прогрессия, b3 = 4, b5 =16, q>0. Какой член стоит между ними? Чему равен четвертый член этой прогрессии?
г) Дано: (аn) – арифметическая прогрессия, а3 =4, а5 =16. Найдите а4 .
д) (физика) Имеется радиоактивное вещество массой 256 г, масса которого за сутки уменьшается вдвое. Какова станет масса вещества на вторые сутки? На третьи? На пятые?(Экономика) Срочный вклад, положенный в сберегательный банк, ежегодно увеличивается на 10%. Каким станет вклад через 2 года, если вначале он был равен 10000 тенге?(Биология) Бактерия за 1 секунду делится на три.
Сколько бактерий будет в пробирке через 5 секунд?
Приложение С. Установите соответствие между названием и формулами
Приложение D. Тест
Приложение Е.
Биология: Каждое простейшее одноклеточное животное (инфузория-туфелька) размножается делением на 2 части. Сколько инфузорий было первоначально, если после шестикратного деления их стало 320?
Строительство: За изготовление и установку первого железобетонного кольца колодца заплатили 100 у.е., а за каждое следующее кольцо платили на 20 у.е. больше, чем за предыдущее. Средняя стоимость одного кольца и его установки оказалась равной 220 у.е. Сколько колец было установлено?
В медицине: Больной принимает лекарство по следующей схеме: в первый день он принимает 5 капель, а в каждый следующий день – на 5 капель больше, чем в предыдущий. Приняв 40 капель, он 3 дня пьет по 40 капель лекарства, а потом ежедневно уменьшает прием на 5 капель, доведя его до 5 капель.
Сколько пузырьков лекарства нужно купить больному, если в каждом содержится 20 мл лекарства (что составляет 250 капель)?
В спорте: Альпинисты в первый день восхождения поднялись на высоту 1400 м, а затем каждый следующий день они проходили на 100 м меньше, чем в предыдущий. За сколько дней они покорили высоту в 5000 м?
В строительстве: Бригада маляров красит забор длиной 240 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 60 метров забора. Определите, сколько дней бригада маляров красила весь забор.
Кулинария: Рост дрожжевых клеток происходит делением каждой клетки на две части. Сколько стало клеток после их десятикратного деления, если первоначально было 6 клеток?
геометрическая и арифметическая прогрессии. Предмет исследования
Объектом исследования: геометрическая и арифметическая прогрессии. Предмет исследования
1 2 3 4 5
1 2 3 4 5 ©emirsaba.org 2023 | Басты бет Lessons Curriculum vitae Documents |
06 Kb.
….13
Арифметические и геометрические последовательности
Нужно сначала попрактиковаться с рекурсией и последовательностями? Введение в рекурсию и последовательности
Примечание:
Когда вы говорите об арифметической последовательности ,
слово арифметика (в данном контексте)
произносится как air-ith-ME-tic;
то есть ударение на третьем слоге.
ОПРЕДЕЛЕНИЕ арифметическая последовательность, общая разность
Арифметическая последовательность — это последовательность вида $\,u_n = u_{n-1} + d\,$.
Здесь $\,d\,$ называется общей разностью .
В арифметической последовательности каждый член равен предыдущему члену, плюс (или минус) константа.
Пример
Последовательность
$\,4\,$
$\,7\,$
$\,10\,$
$\,13\,$ $\,\ldots\,$
является арифметической последовательностью.
Общая разница $\,3\,.$
Чтобы перейти от семестра к семестру,
вы продолжаете добавлять $\,3\,.$
Связь между арифметическими последовательностями и линейными функциями
Напомним, что линейных функций график в виде линий и обладают особым свойством: равные изменения на входе дают возрастают до равных изменений выпуска.
Арифметические последовательности имеют то же самое
особое свойство:
равные изменения на входе
(например, переход от термина к термину)
вызвать равные изменения
на выходе (определяется общей разностью).
Таким образом, арифметические последовательности
всегда граф как точек вдоль линии .
График последовательности
$\,4\,$
$\,7\,$
$\,10\,$
$\,13\,$ $\,\ldots\,$
это набор точек
(«точки»), показанные ниже.
Когда ввод $\,1\,$
(для первого члена последовательности),
вывод $\,4\,.$
Когда ввод $\,2\,$
(для второго члена последовательности),
вывод $\,7\,.$
Когда ввод $\,3\,$
(для третьего члена последовательности),
вывод $\,10\,$ и так далее.
Пример (арифметическая последовательность)
Последовательность $\,10\,$ $\,8\,$ $\,6\,$ $\,4\,$ $\,\ldots\,$ является арифметической последовательностью. Общая разница $\,-2\,.$ Чтобы перейти от семестра к семестру, вы продолжаете добавлять $\,-2\,$ (т. е. вычитая $\,2\,$).
График последовательности $\,10\,$ $\,8\,$ $\,6\,$ $\,4\,$ $\,\ldots\,$ показано ниже:
ОПРЕДЕЛЕНИЕ геометрическая последовательность, обыкновенное отношение
Геометрическая последовательность представляет собой последовательность вида
$\,u_n = r\cdot u_{n-1}\,.
$
Здесь $\,r\,$ называется обыкновенное отношение .
В геометрической последовательности каждый член равен предыдущему члену, умножить (или разделить) на константа.
Пример (геометрическая последовательность)
Последовательность
$\,3\,$
$\,6\,$
$\,12\,$
$\,24\,$ $\,\ldots\,$
представляет собой геометрическую последовательность.
Обычное отношение равно $\,2\,.$
Чтобы перейти от семестра к семестру,
вы продолжаете умножать на $\,2\,.
$
Связь между геометрическими последовательностями и экспоненциальные функции
Есть класс функций, называется экспоненциальными функциями , которые обладают особым свойством: равные изменения во входной причине результат, который нужно последовательно умножить по константе.
Геометрические последовательности имеют
это же специальное свойство:
равные изменения на входе
(например, переход от термина к термину)
заставить вывод быть последовательным
умножить на константу
(определяется обыкновенным отношением).
Таким образом, геометрические последовательности
всегда граф как точки на графике
экспоненциальной функции.
График последовательности $\,3\,$ $\,6\,$ $\,12\,$ $\,24\,$ $\,\ldots\,$ показано ниже:
Пример (геометрическая последовательность)
Последовательность
$\,100\,$
$\,50\,$
$\,25\,$
$\,12,5\,$
$\,\ldots\,$
представляет собой геометрическую последовательность.
Общее соотношение равно
$\,\frac{1}{2}\,.
$
Чтобы перейти от семестра к семестру,
вы продолжаете умножать на $\,\frac{1}{2}\,$
(т.е. деление на
$\,2\,$).
График последовательности $\,100\,$, $\,50\,$, $\,25\,$, $\,12.5\,$, $\,\ldots\,$ показано ниже:
Концептуальная практика
Арифметика и геометрия: 5 ключевых отличий, плюсы и минусы, примеры
И арифметика, и геометрия представляют собой последовательности чисел, но имеют разные характеристики. Самая большая разница между арифметическими и геометрическими рядами заключается в типе разницы между последовательными терминами. Последовательные члены арифметической последовательности имеют постоянную разность, в то время как члены геометрической разности находятся в постоянном соотношении.
Werebeasts 🐺 and Lycanthropy in .
..
Please enable JavaScript
Werebeasts 🐺 and Lycanthropy in D&D 5e
Let’s take a closer look at arithmetic vs. geometric here:
| Sequence | И арифметические, и геометрические являются типами последовательностей | ||
| Постоянная разность | Члены арифметики имеют постоянную разность в отличие от геометрической | ||
| Постоянное соотношение | Условия геометрических находятся в постоянном соотношении, в отличие от арифметической | ||
| Вариация | АРИТМЕТИЧЕСКИЕ ТЕРИЧЕСКИ ? Арифметическая прогрессия — это та, в которой каждый последующий член отличается от предыдущего на постоянную разницу. Что такое геометрия? Геометрическая последовательность – это последовательность, в которой каждый последующий член отличается от предыдущего с постоянным коэффициентом. Плюсы и минусы арифметики и геометрииПлюсы и минусы арифметикиПлюсы арифметики
Минусы арифметики
Плюсы и минусы геометрииПлюсы геометрии
Минусы геометрического
Примеры арифметики и геометрической последовательностиПримеры арифметики
Примеры геометрической
Выявление сходства между арифметикой и геометрией для лучшего понимания
5 ключевых различий между арифметикой и геометрией0092 | Арифметическая последовательность — это последовательность, в которой каждый последующий член отличается от предыдущего на постоянную разницу. | Геометрическая последовательность — это последовательность, в которой каждый последующий член отличается от предыдущего с постоянным коэффициентом. |
| Получение следующего члена | Последующие члены получаются сложением и вычитанием. | Последовательные члены получаются путем умножения и деления. | |
| Характер последовательности | Последовательность расходящаяся. | Последовательность может быть расходящейся или сходящейся. | |
| Общая разница и отношение | Последовательные члены показывают общую разницу. | Последовательные члены показывают обычное отношение. | |
| Изменение | Условия показывают линейное изменение. | Условия демонстрируют экспоненциальное изменение. |
Сравнительная таблица
Сравнительное видео
youtube.com/embed/s2IEyZLrAUQ?feature=oembed&enablejsapi=1&origin=https://www.difference101.com» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share» allowfullscreen=»»> Арифметические и геометрические последовательностиЧасто задаваемые вопросы по арифметическим и геометрическим последовательностям
Что такое арифметические и геометрические последовательности?
Арифметическая последовательность — это последовательность, в которой следующее значение получается путем прибавления или вычитания константы к ее предыдущему значению. Чтобы получить геометрическую последовательность, следующее значение в последовательности получается путем деления или умножения константы на предыдущий член.
Чем похожи арифметические и геометрические последовательности?
Как арифметическая, так и геометрическая последовательности имеют постоянную разницу между двумя их последовательными значениями, и эта закономерность не может быть нарушена в последовательности.
В чем разница между арифметической и геометрической прогрессией?
Ряд арифметической прогрессии имеет постоянное значение, которое либо прибавляется, либо вычитается из предыдущего члена. В то время как ряд геометрической прогрессии имеет постоянное значение, которое либо умножается, либо делится на предыдущий член. Арифметическая и геометрическая доходность также различаются в зависимости от этих двух прогрессий.
Из чего состоит арифметическая последовательность?
Определенная последовательность возрастания или убывания образует арифметическую последовательность.
Каковы примеры арифметических последовательностей?
Несколькими примерами арифметической последовательности являются пирамидальные структуры, расположение сидений в многозальном театре или на стадионе или изменения температуры при изменении уровня моря.
В чем разница между геометрией и математикой?
Геометрия — это подмножество или ветвь множества, называемого математикой.
В то время как геометрия имеет дело только с установлением отношений между различными формами, математика имеет дело с установлением отношений между числами.
Что такое общее правило геометрической последовательности?
Общее правило геометрической последовательности состоит в том, чтобы умножить или разделить член на ненулевую константу, чтобы получить следующий член. Последовательность имеет вид a, ar, ar², ar³ и так далее.
В чем разница между арифметическими рядами и геометрическими рядами?
Арифметический ряд имеет постоянную разницу между двумя последовательными членами. В то время как геометрический ряд имеет постоянное отношение между двумя последовательными членами. Среднее арифметическое и среднее геометрическое также различаются в зависимости от различий в этих двух рядах.
Каковы преимущества среднего геометрического?
Ниже приведены некоторые преимущества среднего геометрического:
- Любые колебания выборок не сильно влияют на последовательность.
