Что такое обратно пропорциональные величины: Обратно пропорциональные величины — урок. Математика, 6 класс.

6.1.5. Обратно пропорциональные величины.

Главная » 6 класс. Математика. » 6.1.5. Обратно пропорциональные величины

На чтение 3 мин. Просмотров 7.2k.

I. Обратно пропорциональные величины.

Пусть величина у зависит от величины х. Если при увеличении х в несколько раз величина у уменьшается во столько же раз, то такие величины х и у называются обратно пропорциональными.

Примеры.

1. Скорость и время при одинаковой длине пути. Если от А до В 200 км, то при скорости 50 км/ч понадобится 4 часа, а при скорости 40 км/ч понадобится 5 часов, т.е. если скорость уменьшается, то время увеличивается, а если скорость увеличивается, то время уменьшается. Это изобразится так:

2.  Количество рабочих и время при определенном объеме работ. Если шести рабочим нужно на выполнение определенной работы 4 часа, то трем рабочим на выполнение той же работы потребуется 8 часов, т.е. чем меньше работников, тем больше нужно времени, чтобы выполнить определенную работу.

Смысл: во сколько раз стало меньше рабочих (в 2 раза), во столько же раз больше (в 2 раза) времени потребуется.

 

3) Длина и ширина прямоугольника при постоянной площади прямоугольника. Если площадь участка прямоугольной формы с длиной 8 м, равна 48 м², то его ширина будет равна (48:8=6)м. Если же длину взять больше в 2 раза (16 м), то ширина уменьшится тоже в 2 раза (48:16=3)м.

II. Свойство обратной пропорциональности величин.

Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.

Задача 1. Изготавливая по 42 детали в час, рабочий трудился 8 часов. Сколько времени ему понадобилось бы на эту же работу, если бы он делал в час по 48 деталей?

Решение. Составим схему по условию задачи:

42 детали в час ——— 8 часов.

48 деталей в час ——-  х часов.

Имеем обратно пропорциональную зависимость: во сколько раз больше деталей в час рабочий будет изготавливать, во столько же раз меньше ему потребуется времени на одну и ту же работу. Используя свойство обратной пропорциональности, запишем:

Ответ: рабочий выполнит ту же работу за 7 часов.

Задача 2. Бассейн можно наполнять через одну из двух труб.Через первую трубу, со скоростью 2 литра в 1 секунду, бассейн наполняется за 45 минут.  Какова  скорость наполнения бассейна  через вторую трубу, если весь бассейн наполняется через вторую трубу за 1 час 15 минут.

Решение. 

По условию задачи через первую трубу в бассейн вытекает 2 литра за 1 секунду или 2·60=120 литров за 1 минуту (1 минута=60 секунд), и бассейн наполняется за 45 минут.

Через вторую трубу бассейн наполняется за 1 час 15 минут. Времени требуется больше, значит, скорость наполнения меньше. Имеем обратно пропорциональные величины: скорость наполнения и время наполнения бассейна. Обозначим скорость наполнения бассейна через вторую трубу через х.

120 литров в минуту ——— 45 минут;

х литров в минуту ——— 75 минут.   (1 час 15 минут = 60 минут + 15 минут = 75 минут).

Во сколько раз скорость наполнения меньше, во столько раз больше потребуется времени для заполнения бассейна.

Мы нашли скорость наполнения бассейна через вторую трубу в литрах в минуту. Итак, через вторую трубу бассейн наполняется со скоростью 72 литра в минуту или 72:60=1,2 литров в секунду.

Ответ: через вторую трубу в бассейн вливается 1,2 литра в 1 секунду.  

задачи на обратную пропорциональность обратная пропорциональность обратно пропорциональные величины

( 6 оценок, среднее 3.67 из 5 )

Обратная пропорциональность: обратная пропорциональная зависимость, величины

Обратно-пропорциональные величины

Две взаимосвязанные величины называются обратно-пропорциональными, если для них выполняется такая зависимость: при увеличении (уменьшении) одной величины в несколько раз, вторая величина уменьшается (увеличивается) во столько же раз.

На практике можно встретить много обратно-пропорциональных величин в повседневной жизни – скорость и время на одинаковом расстоянии, длина и ширина прямоугольного земельного участка при неизменной площади и т. д.

Пример. Расстояние между городами Украины составляет 1200 км. В зависимости от скорости транспорта вычисленное время поездки:

Из таблицы мы видим, при увеличении скорости в 2, 3, 4 и т.д. раза, продолжительность поездки уменьшается в 2, 3, 4 и т.д. раза соответственно.

Свойство обратно-пропорциональных величин

Для двух обратно-пропорциональных величин выполняется следующее свойство:

отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений второй величины.

Проверим данное утверждение на предыдущем примере, где указаны обратно пропорциональные величины – скорость и время. Возьмем следующие величины скорости – 10 и 200, соответствующие величине времени – 120 и 6.

Найдем соотношение данных величин: очевидно, что 10 : 200 не равно 120 : 6 (т.е. 10 : 200≠120 : 6). Проверим обратное соотношение: 10 : 200 = 6 : 120, то есть 1 : 20 = 1 : 20

Формула обратной пропорциональности.

Задачи

Для пары обратно пропорциональных величин произведение любого значения одной величины на соответствующее значение второй величины является постоянным числом (т.е. не меняется).

Предположим, значение одной величины – x, значение второй величины – у, тогда, исходя из формулы обратной пропорциональности x ⋅ y = K, где К – постоянное число, произведение величин.

Запишем величину y в качестве неизвестного произведения:

Задача. Бригада из 24 работников монтирует двери в целом здании за 6 дней. За сколько времени установят двери 8 рабочих при условии, что они работают с одинаковой производительностью труда.

Решение:

Количество работников и дней является обратно-пропорциональными величинами, ведь чем больше работников, тем быстрее (за меньшее количество дней) они проделают работу при одинаковой производительности.

Согласно определению обратно-пропорциональных величин их произведение является постоянным числом. Пусть 8 рабочих будут работать х дней, запишем такое равенство:

24 ⋅ 6 = 8 ⋅ х

х = (24 ⋅ 6) / 8 = 3 ⋅ 6 = 18 дней

Ответ: 18 дней

Задача. Бригада из 6 мастеров производят ремонт однокомнатной квартиры под ключ за 21 рабочий день. Сколько мастеров нужно, чтобы сделать ремонт за 18 дней?

Решение:

Это типичная задача на обратно-пропорциональные величины (количество работников и время работы). Пусть х – количество мастеров, делающих ремонт за 18 дней. Произведение обратно пропорциональных величин является постоянным числом, поэтому:

6 ⋅ 21 = х ⋅ 18

Х = 6 ⋅ 21 / 18 = 6 ⋅ 7 ⋅ 3 / 6 ⋅ 3 = 7 мастеров.

Ответ: 7 мастеров

Задача. 2 водяных насоса заполняют бассейн объемом 10 тонн за 3 часа. Сколько времени заполнят бассейн водой 6 насосов.

Решение:

В данной задаче обратно пропорциональны такие величины как количество насосов и время заполнения.

Пусть х – время, за которое 6 насосов заполнят бассейн.

Можем записать произведение обратно пропорциональных величин, которое является постоянным числом:

2 ⋅ 3 = 6 ⋅ х

х = 2 ⋅ 3 / 6 = 1 час.

Ответ: за 1 час.

Задача. Автомобилист проехал расстояние между городами за 3 часа. Если он будет ехать со скоростью 96 км/ч, то он проедет расстояние за 2,5 часа. Какова начальная скорость автомобилиста?

Решение:

Пусть х – начальная скорость автомобиля

х⋅ 3 = 96 ⋅ 2,5

х = 96 ⋅2,5 / 3 = 80 км / час

Ответ: 80 км / час

 

Обратно пропорциональные – определение, формула и примеры

Две величины называются обратно пропорциональными, когда значение одной величины увеличивается по отношению к уменьшению другой или наоборот. Это означает, что эти две величины ведут себя противоположно по своей природе. Например, время, необходимое для выполнения задачи, уменьшается с увеличением числа рабочих, завершающих ее, и будет увеличиваться с уменьшением числа рабочих. Здесь время и количество рабочих обратно пропорциональны друг другу.

Другие термины, которые могут быть использованы здесь для этого типа пропорции: обратная пропорция или обратная вариация или обратная вариация или обратная пропорция. Две переменные говорят, что x и y, которые находятся в обратно пропорциональном отношении, представлены как x ∝ 1/y или x ∝ y ^-1 . Прямо пропорциональные и обратно пропорциональные отношения являются противоположными отношениями по сравнению друг с другом.

1.	Что такое обратно пропорциональная?
2.	Общая формула обратно пропорциональной
3.	Графическое представление обратной пропорциональности
4.	Применение обратно пропорционального
5.	Часто задаваемые вопросы

Что такое обратно пропорциональная функция?

Изучая математику и физику, мы узнаем о величинах, которые зависят друг от друга, и такие величины называются пропорциональными друг другу.

Другими словами, две переменные или величины пропорциональны друг другу, если одна изменяется, то другая также изменяется на фиксированную величину. Это свойство переменных называется пропорциональностью, и для обозначения пропорциональности используется символ «∝». Существует два типа пропорциональности переменных. Их:

• Прямо пропорциональный
• Обратно пропорциональный

Когда две величины связаны друг с другом обратно пропорционально, т. е. когда увеличение одной величины вызывает уменьшение другой и наоборот, то говорят, что они обратно пропорциональны. При этом, если одна переменная уменьшается, другая увеличивается в той же пропорции. Это противоположно прямой пропорциональности. Или говорят, что две величины обратно пропорциональны

, когда одна величина находится в прямой зависимости от обратной величины другой. Например, связь между скоростью и временем. Скорость и время в пути обратно пропорциональны, потому что чем быстрее мы движемся, тем меньше времени требуется, то есть чем больше скорость, тем меньше время.

• По мере увеличения скорости время в пути уменьшается.
• И с уменьшением скорости время в пути увеличивается.

Общая формула обратно пропорциональной

Символ «∝» обозначает пропорциональное соотношение между двумя величинами. Пусть x и y — две величины. Тогда у, обратно пропорциональный х, это то же самое, что у, прямо пропорциональный 1/х. Математически это записывается как y ∝ 1/x.

Общее уравнение обратной вариации: y = k/x, где k — коэффициент пропорциональности. Мы также можем записать это как y × x = k или y × x = константа. Если x и y находятся в обратной вариации и x имеет два значения x

1 и x ₂ , соответствующие y, который также имеет два значения y ₁ и y ₂ соответственно, то по определению обратной вариации имеем x ₁ y ₁ = x ₂ г ₂ = к.

В этом случае получается х ₁ / х ₂ = у ₂ / у ₁ = k.

Графическое представление обратной пропорциональности

Характер графика для обратно пропорционального выглядит следующим образом.

Например, ниже показан график уравнений y = 1/x и y = -1/x, имеющих обратно пропорциональную зависимость.

Применение обратно пропорционального

Понятие обратной пропорциональности широко используется в повседневной жизни, а также при решении многих задач в области науки, статистики и т. д. В физике существует множество формул, выводимых с использованием понятия обратной пропорциональности. Закон Ома, соотношение скорости и времени, длина волны звука и его частота — вот лишь некоторые из них.

Важные замечания по обратно пропорциональной

Для обратно пропорциональности необходимо помнить следующие пункты:

• Если одна величина увеличивается, другая уменьшается.
• х ∝ 1/у или у ∝ 1/х.
• x × y = k, где k называется константой пропорциональности.

Связанные темы по обратно пропорциональным

Проверьте эти интересные статьи, связанные с обратно пропорциональными.

• Формула обратной пропорции
• Константа пропорциональности
• Основная теорема о пропорциональности
• Определение скорости
• Пропорция

Часто задаваемые вопросы по обратно пропорциональным

Что означает обратно пропорциональный?

Обратно пропорциональные переменные или величины, в которых увеличение одной переменной приводит к уменьшению другой, а уменьшение одной переменной приводит к увеличению другой. Это означает, что когда увеличение одной величины приводит к уменьшению другой и наоборот, то говорят, что они обратно пропорциональны. Например, время, необходимое для выполнения работы, обратно пропорционально количеству рабочих.

Как узнать, прямо пропорциональна она или обратно пропорциональна?

Обратно пропорциональную зависимость между двумя величинами можно понимать так, как указано ниже.

• Определите две величины, которые различаются в данной задаче.
• Если x/y постоянны, то они прямо пропорциональны.
• Если x × y постоянно, то обратно пропорционально.

Что такое формула обратно пропорциональной?

Формула обратной зависимости помогает математически представить обратно пропорциональную зависимость. Формула обратной вариации: x × y = k или y = k/x, где x и y — две переменные, а k — константа пропорциональности.

Что является противоположностью обратно пропорциональной?

Прямо пропорциональна обратно пропорциональна. Это означает, что когда увеличение одной величины приводит к увеличению другой и наоборот, то говорят, что они прямо пропорциональны.

Что значит, если две вещи обратно пропорциональны?

Две величины называются обратно пропорциональными, когда значение одной величины увеличивается по отношению к уменьшению другой величины или наоборот. Это означает, что эти две величины ведут себя противоположно по своей природе. Например, связь между скоростью и временем. Скорость и время в пути обратно пропорциональны, потому что чем быстрее мы движемся, то есть больше скорость, тем меньше время.

Что такое Обратно пропорциональный знак?

Для обозначения пропорциональности используется символ «∝». Обратная пропорциональность относится к одной величине, которая прямо пропорциональна обратной величине другой величины. Мы представляем любые две величины в обратной пропорции как x ∝ 1/y или x ∝ y ^-1 .

Какой пример обратно пропорционально?

Обратно пропорциональная зависимость возникает, когда одно значение увеличивается, а другое уменьшается, и наоборот. Например, большее количество рабочих на работе сокращает время, необходимое для выполнения задачи. Таким образом, они обратно пропорциональны.

Обратная пропорция — математика GCSE

Введение

Как использовать обратную пропорцию

Рабочий лист обратной пропорции

Распространенные заблуждения

Практика вопросов обратной пропорции

Вопросы GCSE с обратной пропорцией

Контрольный список обучения

Следующие уроки

Все еще застрял

Математические вмешательства один на один, созданные для успеха KS4

Еженедельные онлайн-уроки повторения GCSE по математике теперь доступны

Узнать больше

Введение

Как использовать обратную пропорцию

Рабочий лист обратной пропорции

Распространенные заблуждения

Практика вопросов обратной пропорции

Вопросы GCSE с обратной пропорцией

Контрольный список обучения

Следующие уроки

Все еще застрял

Здесь мы узнаем об обратной пропорции, в том числе о том, что такое обратная пропорция и как решать проблемы обратной пропорции, включая решение реальных задач. Мы также рассмотрим формулу обратной пропорциональности.

Существуют также рабочие листы с обратной пропорцией, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.

Что такое обратная пропорция?

Обратная пропорция является типом отношения пропорциональности . Если две величины обратно пропорциональны, то при увеличении одной величины другая уменьшается.

Примером обратной пропорции может быть количество часов работы, необходимых для возведения стены. Если одну и ту же стену строит больше людей, время, затрачиваемое на возведение стены, сокращается.

И наоборот, примером прямой пропорциональности может быть то, что площадь круга прямо пропорциональна его радиусу.

Обратная пропорция также известна как косвенная пропорция или обратная вариация .

Обратная пропорция применяется к реальным жизненным задачам, таким как скорость движущегося объекта, определение того, будет ли объект плавать или тонуть в воде, или время, необходимое для выполнения конечной задачи, тогда как прямая пропорция полезна во многих реальных жизненных ситуациях, таких как как обменные курсы, конвертация между единицами измерения и цены на топливо.

Чтобы определить значение переменной, которое обратно пропорционально другому, нам нужно определить взаимосвязь между двумя переменными, а затем использовать это, чтобы найти наше неизвестное значение.

Подобно прямо пропорциональной зависимости, нам необходимо определить константу пропорциональности k.

Пошаговое руководство: Прямая пропорция 

Что такое обратная пропорция?

Формула обратной пропорции

Символ \propto является символом пропорциональности и представляет пропорциональную связь между двумя переменными. Если оно обратно пропорционально x, мы записываем это отношение как y\propto\frac{1}{x}.

Это отношение можно описать с помощью отношения эквивалентности. Когда y обратно пропорционально x , значение x \times y является постоянным значением. Это значение является константой пропорциональности, и мы используем букву k для обозначения этого значения. Используя формулу, мы имеем k=xy.

Преобразовав эту формулу, чтобы сделать y предметом, мы получим формулу обратной пропорции,

y=\frac{k}{x} .

Пошаговое руководство: Формула обратной пропорции 9{3} или даже \sqrt{x}. Каждый из них имеет различное алгебраическое и графическое представление.

Пошаговое руководство: Прямо пропорциональные графики / обратно пропорциональные графики

Как использовать обратную пропорцию формула пропорции.

Определите значение \textbf{k} .

Подставить \textbf{k} и известное значение в формулу обратной пропорции .

Решите уравнение.

Объясните, как использовать обратную пропорцию

Таблица обратной пропорции

Получите бесплатную таблицу обратной пропорции, содержащую более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Икс

Рабочий лист обратной пропорции

Получите бесплатную рабочую таблицу обратной пропорции, содержащую более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Примеры обратной пропорции

Пример 1: заполните таблицу y ∝ ⅟

_x

Учитывая, что y обратно пропорционально x, вычислите недостающее значение y в таблице ниже.

1. Запишите формулу обратной пропорции.

В качестве y\propto\frac{1}{x} мы можем записать формулу y=\frac{k}{x}.

2 Определите значение \textbf{k} .

Подставив известную пару значений (3,20), можно сказать,

\begin{выровнено} 20&=\frac{k}{3}\\\\ 20\times{3}&=k\\\\ k&=60 \end{выровнено}

3 Подставить \textbf{k} и известное значение в формулу обратной пропорции .

Теперь у нас есть уравнение y=\frac{60}{x}. Подставив x=12 в уравнение для вычисления значения y, мы получим

y=\frac{60}{12} .

4 Решите уравнение.

Разделив 60 на 12, мы получим y=5.

Обратите внимание, что по мере увеличения значения x значение y уменьшается.

Пример 2: заполнить таблицу y ∝ ⅟

_x

Пусть y\propto\frac{1}{x}. Вычислите значение x, когда y=20.

Запишите формулу обратной пропорции.

Поскольку y\propto\frac{1}{x}, как указано в вопросе, мы имеем

y=\frac{k}{x} .

Определите значение \textbf{k} .

Поскольку x=5 при y=60, подставляя эти значения в формулу, получаем

\begin{aligned} 60&=\frac{k}{5}\\\\ 60\times{5}& =k\\\\ k&=300 \end{aligned}

Подставляем \textbf{k} и известное значение в формулу обратной пропорции .

Теперь у нас есть y=\frac{300}{x}. Нам нужно определить значение x при y=20, поэтому, подставляя это значение в уравнение, мы получаем 9{2}} .

Решите уравнение.

q=\frac{16}{16}=1

Пример 4: сформулированная задача обратной пропорциональности y ∝ ⅟

_x

2 рабочих красят забор за 9 часов.

Сколько времени потребуется 6 рабочим, чтобы покрасить один и тот же забор?

Запишите формулу обратной пропорции.

По мере увеличения числа рабочих x время y, затрачиваемое на покраску того же забора, будет уменьшаться, и, таким образом, это обратная пропорция формы y\propto\frac{1}{x}.

Это означает, что у нас есть формула y=\frac{k}{x}.

Определите значение \textbf{k} .

Поскольку мы знаем, что x=2 при y=9, подставив эти значения в формулу, получим

\begin{aligned} 9&=\frac{k}{2}\\\\ 9\times{2}&=k\\\\ к&=18 \end{выровнено}

Подставить \textbf{k} и известное значение в формулу обратной пропорции .

Теперь у нас есть уравнение y=\frac{18}{x}. Поскольку мы хотим узнать значение y при x=6, мы подставляем x=6 в уравнение, чтобы получить 9{3}&=3,384444963…\\\\ х&=\sqrt[3]{3.384444963…}\\\\ х&=1,50139795…\\\\ х&=1,501 см\текст{(3dp)} \end{align}

Распространенные заблуждения

• Предположение моделирования

Всякий раз, когда вы решаете текстовые задачи на обратную пропорцию, вы предполагаете, что все имеет одинаковую скорость. Например, если вопрос касается количества работающих людей, мы предполагаем, что все рабочие работают с одинаковой скоростью.

• Константа пропорциональности

Для прямой пропорциональности константа пропорциональности k представляет собой отношение двух переменных, таких как k=y\div{x}. Для обратной пропорции k является произведением двух переменных, например, k=xy.

• График обратно пропорциональной зависимости не пересекает ни одну из осей

График любой обратно пропорциональной зависимости не может пересекать ни одну из осей. Это потому, что если мы используем пример y\propto\frac{1}{x}, если x=0, значение для y не определено, поскольку мы не можем разделить число на 0.

Если y=0, то значение константы пропорциональности должно быть 0 или x=0, но, как мы только что сказали, x ≠ 0, и, таким образом, соотношение между x и y не может существовать для этих двух значений, поскольку k= 0.

• Следите за временем записи, используя правильное десятичное число

Время используется в некоторых текстовых задачах на обратную пропорцию. Если ответ равен 3,1, у вас может возникнуть соблазн записать его как 3 часа 10 минут, но это будет 3 часа 6 минут. (Помните, что в часе 60 минут).

• Графики обратной функции

Стандартный график для y\propto{x} представляет собой прямой график, проходящий через начало координат с градиентом k. Стандартный график для y\propto\frac{1}{x} представляет собой изогнутую линию, не пересекающую ни одну из осей.

Связанные уроки по обратной пропорции

Обратная пропорция являются частью нашей серии уроков, посвященных пересмотру пропорции . Возможно, вам будет полезно начать с урока по основным пропорциям для краткого изложения того, чего ожидать, или использовать пошаговые руководства ниже для получения более подробной информации по отдельным темам. Другие уроки в этой серии включают в себя:

• Доля
• Прямая и косвенная пропорция
• Формула прямой пропорции

Попрактикуйтесь в вопросах обратной пропорции

y=\frac{k}{x} и, следовательно, k=xy.

 

к=2\раз{40}=80

 

у = \ гидроразрыва {80} {х}

 

Когда x=8, \ y=\frac{80}{8}=10 .

106,7 \ (1dp)

13,3 \ (1dp)

m=\frac{k}{n} и, следовательно, k=mn.

 

к=3\раз{40}=120

 

м=\фракция{120}{п}

 

Когда n=8, \ m=\frac{120}{8}=15 .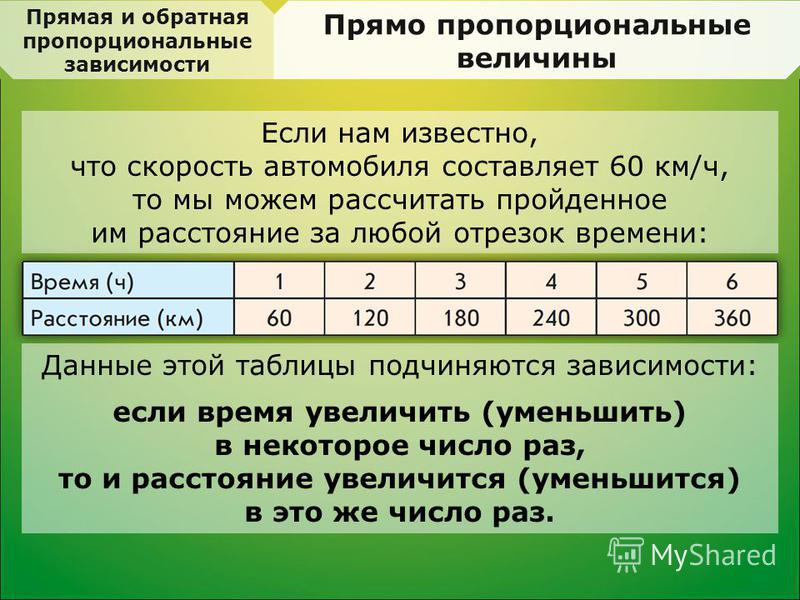

3,9 \ (1dp)

b=\frac{k}{\sqrt{a}} и, следовательно, k=b\sqrt{a}.

 

k = 5 \ раз {\ sqrt {4}} = 5 \ раз {2} = 10

 

b=\frac{10}{\sqrt{a}}

 

Когда a=25, \b=\frac{10}{\sqrt{25}}=\frac{10}{5}=2 .

20 дней

24 дня

12 дней

108 дней

Пусть p представляет количество людей, а d представляет количество дней строительства, тогда

 

d=\frac{k}{p} и, следовательно, k=dp.

 

к=36\раз{20}=720

 

д=\фракция{720}{р}

 

Когда p=60, \d=\frac{720}{60}=12.

60 минут

20 минут

80 минут

10 минут

Пусть s обозначает скорость, а t обозначает затраченное время, тогда

 

s=\frac{k=st.} и поэтому

 

к=8\раз{40}=320

 

с = \ гидроразрыва {320} {т}

 

Когда s=16,

 

\begin{выровнено} 16&=\frac{320}{t}\\\\ 16\times{t}&=320\\\\ т&=320\дел{16}\\\\ т&=20 \end{выровнено}

 

Обратите внимание, что формула скорость-расстояние-время является известным соотношением (скорость = расстояние \дел время). {2}c. 9{2}}

(1)

18

(1)

0,5

(1)

 

2. Шесть рабочих строят за 24 часа противопаводковый барьер.

Стену нужно построить за 8 часов.

Сколько рабочих нужно, чтобы построить такую ​​же аварийную защиту от наводнений за 8 часов?

 

(2 балла)

Показать ответ

6\раз 3

(1)

18 рабочих

(1)

3. Наполнение бассейна из 5 кранов занимает 360 минут.

 

(a) За сколько минут бассейн наполнится тремя кранами?

 

(b) Назовите одно допущение, которое вы сделали, работая над ответом на часть (a).

 

(3 балла)

Показать ответ

(a)

 

к=ху=360 х 5=1800

(1)

1800 \дел 3=600 минут

(1)

 

(b)

3   900

(1)

Контрольный список для обучения

Теперь вы научились:

• решать задачи на обратную пропорцию, включая алгебраические представления

Все еще зависает?

Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning.