Что такое ортоцентр треугольника: Ортоцентр | это… Что такое Ортоцентр?

alexxlab / / Разное

Ортоцентр | это… Что такое Ортоцентр?

ТолкованиеПеревод

Ортоцентр

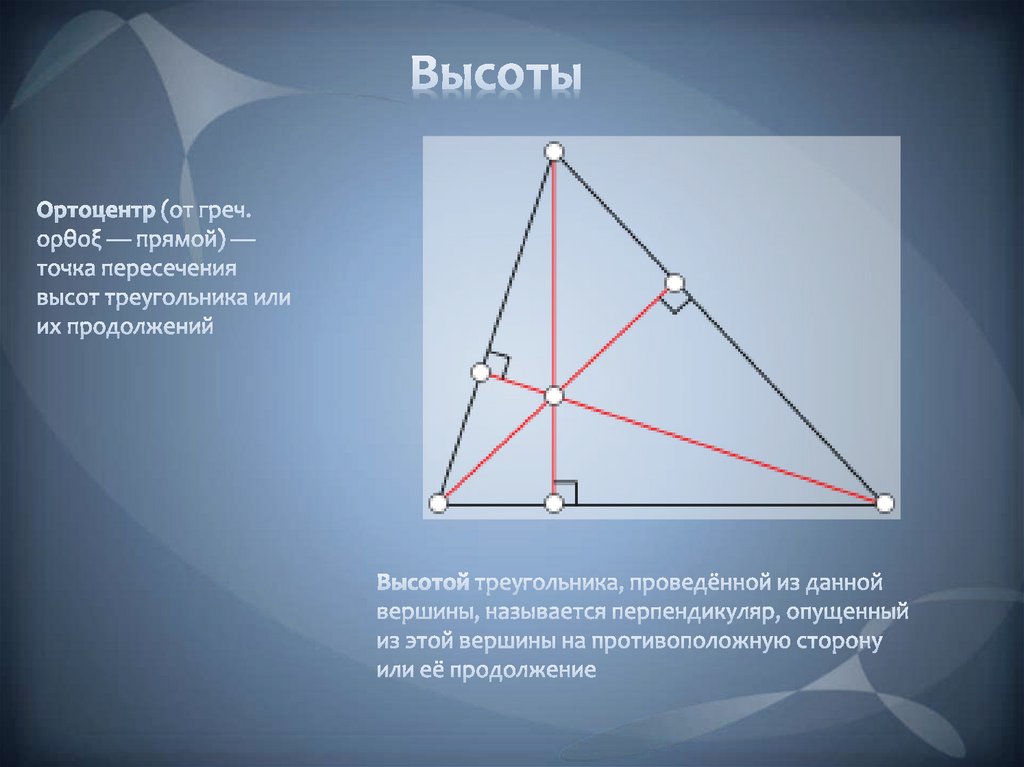
Ортоцентр (от греч. ορθοξ — прямой) — точка пересечения высот треугольника или их продолжений. Традиционно обозначается латинской буквой H. В зависимости от вида треугольника ортоцентр может находиться внутри треугольника (в остроугольных), вне его (в тупоугольных) или совпадать с вершиной (в прямоугольных — совпадает с вершиной при прямом угле).

Содержание

  • 1 Свойства
  • 2 История
  • 3 См. также
  • 4 Литература
  • 5 Ссылки

Свойства

  • Если в четвёрке точек A, B, C, D точка D является точкой пересечения высот треугольника ABC, то и любая из четырёх точек является ортоцентром треугольника, образованного тремя остальными точками.
    Такую четвёрку иногда называют ортоцентрической системой точек.
    • Радиусы окружностей, проходящих через любые три точки ортоцентрической системы, равны.
  • Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).
  • Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.
  • Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника.
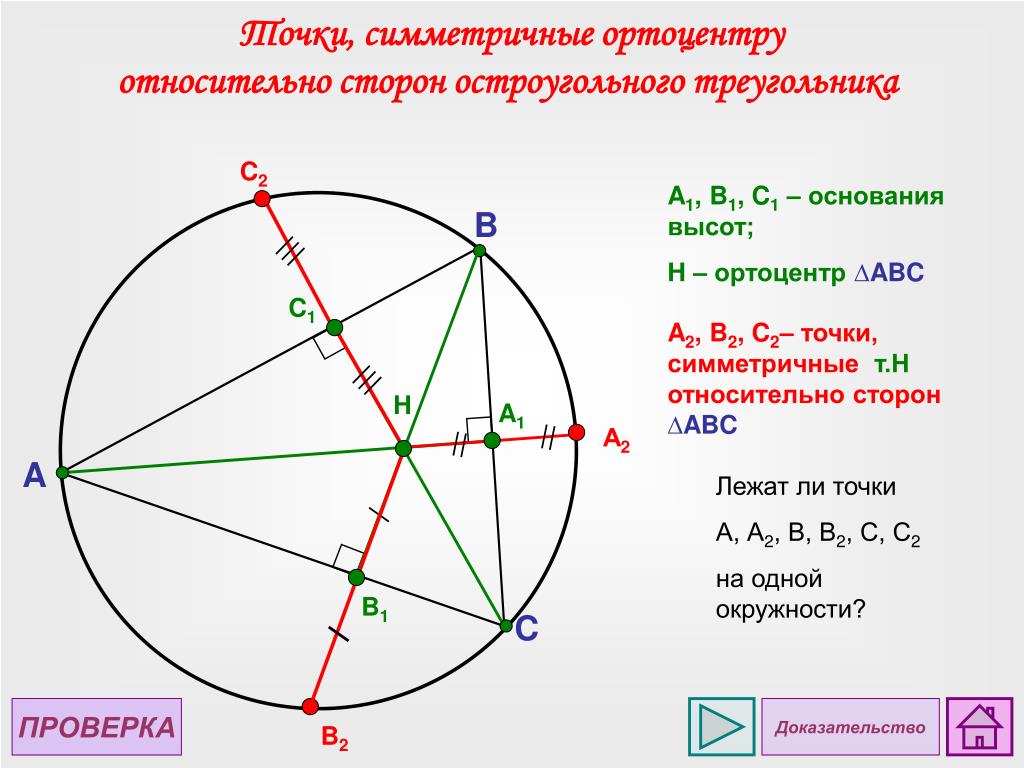
  • Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности.
  • Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
  • Если О — центр описанной окружности ΔABC, то ,
    • , где — радиус описанной окружности; — длины сторон треугольника.
  • Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
  • При изогональном сопряжении ортоцентр переходит в центр описанной окружности.

История

Первое строгое доказательство того, что высоты треугольника пересекаются в одной точке дал Карл Фридрих Гаусс только в XVIII веке[источник не указан 845 дней].

См. также

  • Центроид
  • Инцентр
  • Замечательные точки треугольника

Литература

  • Понарин Я. П. Элементарная геометрия. В 2 тт. — М.: МЦНМО, 2004. — С. 37-39. — ISBN 5-94057-170-0

Ссылки

  • Живой чертёж

Wikimedia Foundation. 2010.

Игры ⚽ Поможем решить контрольную работу

Синонимы:

точка

  • Медиана (значения)
  • Подерный треугольник

Полезное


Ортоцентр треугольника: полезные факты.

Ортоцентр треугольника: полезные факты

В этой статье доказываются некоторые факты, касающиеся точки пересечения высот треугольника (ортоцентра треугольника), которые могут быть весьма полезны при решении задач.

Пусть — точка пересечения высот треугольника ,  — центр описанной окружности.

Тогда:

1) радиусы окружностей, описанных около треугольников , , и равны;

2) расстояние от вершины до точки  вдвое больше расстояния от центра описанной окружности до стороны ;

3) расстояние между серединами отрезков и равно радиусу описанной окружности треугольника ;

4) ;

5)  точки, симметричные точке  относительно прямой  и относительно середины стороны , лежат на описанной окружности треугольника .

Доказательство.

1) Радиусы окружностей, описанных около треугольников , , и равны.

Радиус окружности, описанной около треугольника можно найти по формуле:

   

, где — произвольная сторона треугольника, а — величина противолежащего угла.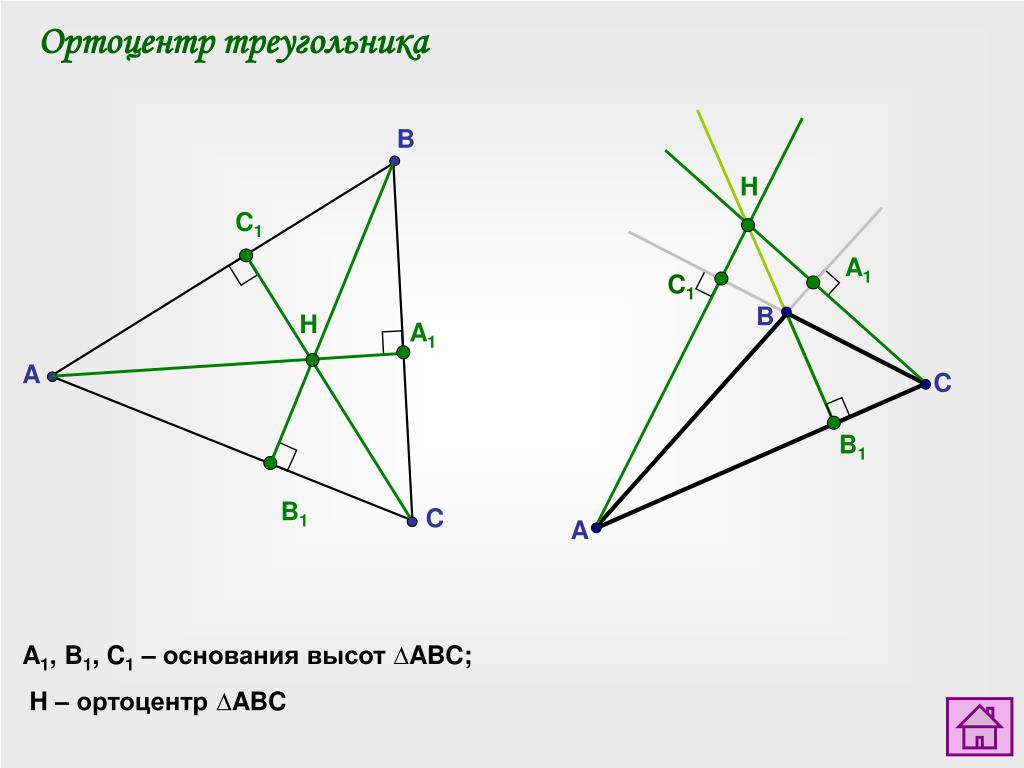

Для треугольника   радиус описанной окружности

Рассмотрим четырехугольник : по свойству вертикальных углов. 

Тогда для треугольника  радиус описанной окружности , то есть равен радиусу описанной окружности треугольника .

 

2) Расстояние от вершины до точки  вдвое больше расстояния от центра описанной окружности до стороны .

Докажем, что , где — центр описанной окружности, а — основание серединного перпендикуляра, опущенного из точки  на сторону . (Вспомним, что центр описанной окружности лежит в точке пересечения серединных перпендикуляров.)

Пусть точка   симметрична точке  относительно отрезка .

Рассмотрим треугольник . 

Из соображений симметрии , следовательно, .

Так как расстояние от точки до точек и равно радиусу окружности, описанной около треугольника , и мы только что доказали, что радиус окружности, описанной около треугольника также равен , следовательно, точка  — центр окружности, описанной около треугольника , и .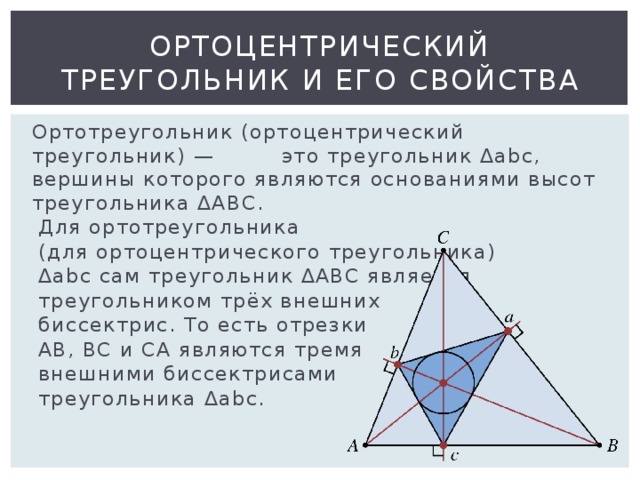  

Проведем окружность с центром в точке , описанную около треугольника :

Мы видим, что при параллельном переносе на вектор  окружность с центром в точке  переходит в окружность c центром в точке , и точка   переходит в точку , следовательно, . Но так как , получили, что .

Что и требовалось доказать.

3) Расстояние между серединами отрезков и равно радиусу описанной окружности треугольника .

Рассмотрим четырехугольник .

 

 

Мы доказали, что . Кроме того, по доказанному выше, . Следовательно, этот четырехугольник  — параллелограмм. Точка — середина отрезка , является также серединой отрезка . Следовательно, отрезок, соединяющий точку  с точкой — серединой отрезка , параллелен отрезкам  и и равен им:

.

Что и требовалось доказать.

4)

Используем доказанные выше факты.

Четырехугольник   — ромб, следовательно, по правилу параллелограмма для сложения векторов получаем :

Далее, четырехугольник   -параллелограмм, следовательно,  .

Утверждение доказано.

5)  Точки, симметричные точке  относительно прямой  и относительно середины стороны , лежат на описанной окружности треугольника .

Пусть точка  симметрична точке  относительно прямой :

 

 

Точка симметрична точке относительно прямой . Следовательно, окружность с центром в точке  симметрична окуржности с центром в точке . Точка лежит на окружности с центром в точке  (см. п. 2), следовательно, симметричная ей относительно прямой точка  симметричной окружности с центром в точке , то есть описанной около треугольника .

Пусть точка  симметрична точке  относительно относительно середины стороны :

Треугольники равны по двум сторонам и углу между ними, следовательно, , и точка  лежит на окружности, описанной около треугольника  .

Утверждение доказано.

И. В. Фельдман, репетитор по математике.

 

 

Brilliant Math & Science Wiki

Содержание
  • Нахождение ортоцентра
  • Доказательство существования
  • Характеристики
  • Ортопедический треугольник
  • Смотрите также
  • использованная литература

Расположение ортоцентра зависит от типа треугольника.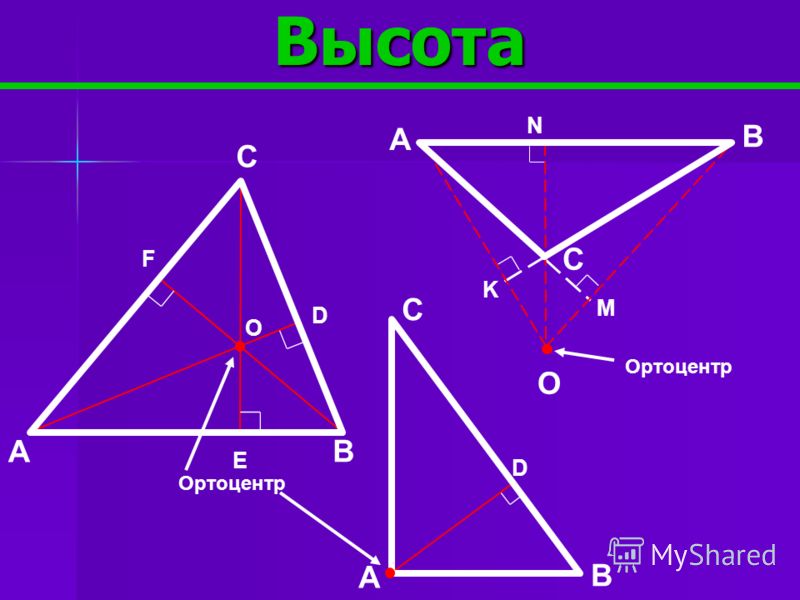 Если треугольник остроугольный, то ортоцентр лежит внутри него. Если треугольник тупоугольный, то ортоцентр лежит вне его. Наконец, если треугольник прямоугольный, ортоцентр будет вершиной под прямым углом.

Поскольку три высоты всегда пересекаются в одной точке (доказательство в следующем разделе), ортоцентр можно найти, определив пересечение любых двух из них. Это особенно полезно при использовании координатной геометрии, поскольку вычисления значительно упрощаются из-за необходимости найти только два уравнения линий (и их пересечение).

Треугольник имеет вершины A=(0,0),B=(14,0)A=(0,0), B=(14,0)A=(0,0),B=(14,0) ) и С=(5,12)С=(5,12)С=(5,12). Каковы координаты ортоцентра?

Легче всего найти высоту от CCC до ABABAB, так как это просто линия x=5x=5x=5. Следующим по простоте поиска является переход от BBB к ACACAC, поскольку ACACAC можно рассчитать как y=125xy=\frac{12}{5}xy=512​x. Прямая, перпендикулярная ACACAC, имеет форму y=−512x+by=-\frac{5}{12}x+by=−125​x+b для некоторого bbb, и поскольку эта линия проходит через (14,0 )(14,0)(14,0), уравнение высоты y=−512x+356y=-\frac{5}{12}x+\frac{35}{6}y=−125​x+ 635​.

Наконец, пересечение этой линии и линии x=5x=5x=5 равно (5,154)\left(5,\frac{15}{4}\right)(5,415​), что, таким образом, является местоположением ортоцентр. □_\квадрат□​

Наиболее естественным доказательством является следствие теоремы Чевы, которая утверждает, что AD, BE, CFAD, BE, CFAD, BE, CF совпадают тогда и только тогда, когда AFFB⋅BDDC⋅CEEA=1,\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA}=1,FBAF​⋅DCBD​⋅EACE​=1, где D,E,FD, E, FD,E,F — футы высот.

Обратите внимание, что △BFC∼△BDA\треугольник BFC \sim \triangle BDA△BFC∼△BDA и, аналогично, △AEB∼△AFC,△CDA∼△CEB\треугольник AEB \sim \треугольник AFC, \треугольник CDA \ сим \треугольник CEB△AEB∼△AFC,△CDA∼△CEB. Следовательно,

BFBD=BCBA,AEAF=ABAC,CDCE=CABC.\frac{BF}{BD} = \frac{BC}{BA}, \frac{AE}{AF} = \frac{AB}{AC}, \frac{CD}{CE} = \frac{CA}{BC}.BDBF​=BABC​,AFAE​=ACAB​,CECD​=BCCA​.

Умножение этих трех уравнений дает нам

BFBD⋅AEAF⋅CDCE=BCBA⋅ABAC⋅CABC=1.\frac{BF}{BD} \cdot \frac{AE}{AF} \cdot \frac{CD}{ CE} = \frac{BC}{BA} \cdot \frac{AB}{AC} \cdot \frac{CA}{BC} = 1.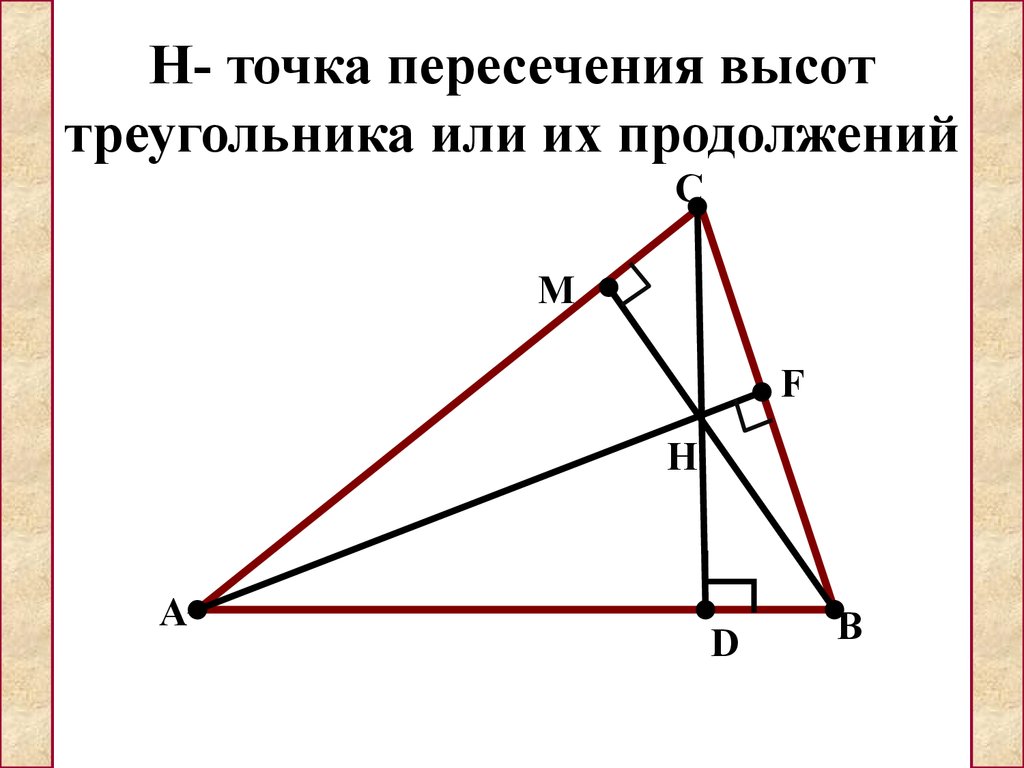

BDBF​⋅AFAE​⋅CECD​=BABC​⋅ACAB​⋅BCCA = 1.

Перестановка левой части дает нам

AFFB⋅BDDC⋅CEEA=1.\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = 1 .FBAF​⋅DCBD​⋅EACE​=1.

Следовательно, три высоты совпадают в одной точке, ортоцентре.

Для удобства при обсуждении общих свойств принято считать, что рассматриваемый исходный треугольник остроугольный. Те же свойства обычно применимы и к тупому случаю, но могут потребовать небольшой переформулировки.

Интересно, что три вершины и ортоцентр образуют ортоцентрическую систему : любая из четырех точек является ортоцентром треугольника, образованного тремя другими.

Невероятно полезное свойство состоит в том, что отражение ортоцентра по любой из трех сторон лежит на описанной окружности треугольника. Существует более наглядный способ интерпретации этого результата: начиная с круглого листа бумаги, нарисуйте треугольник, вписанный в бумагу, и согните бумагу внутрь по трем краям.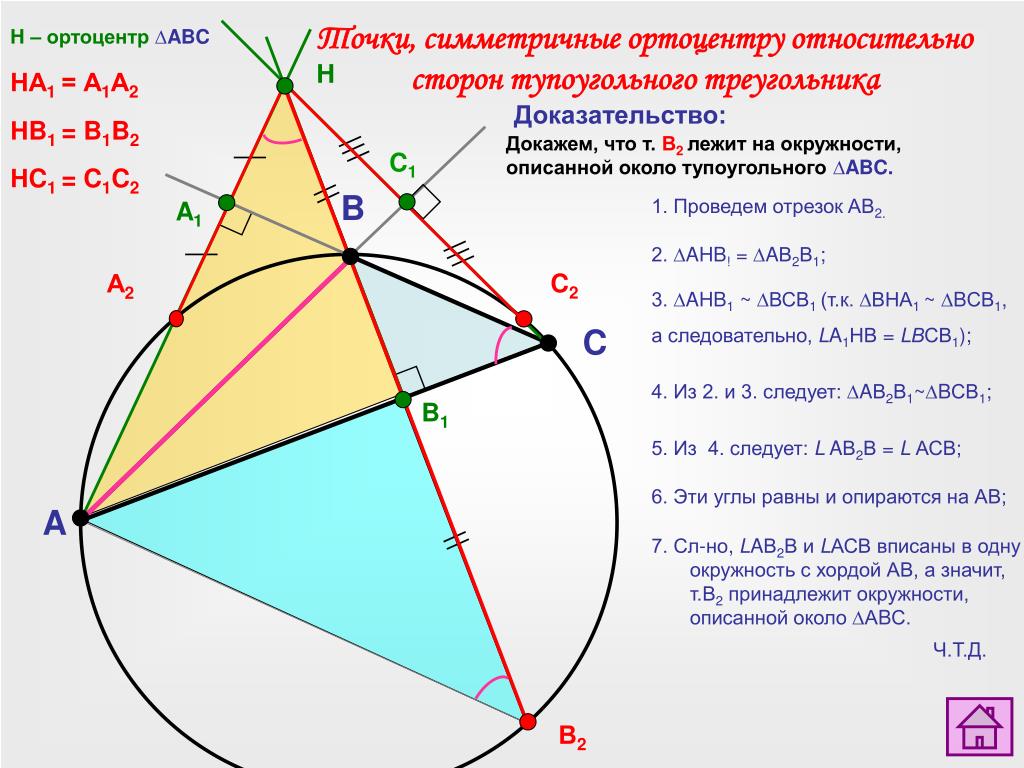

Три дуги встречаются в ортоцентре треугольника.[1]

Этот результат имеет ряд важных следствий. Самый непосредственный состоит в том, что угол, образованный в ортоцентре, является дополнительным к углу в вершине: 9{\ circ} ∠ ABC + ∠ AHC = ∠ BCA + ∠ BHA = ∠ CAB + ∠ CHB = 180 ∘

Другое следует из степени точки: произведение двух длин, на которые ортоцентр делит высоту, постоянно. В частности,

АХ⋅HD=BH⋅HE=CH⋅HFAH \cdot HD = BH \cdot HE = CH \cdot HFAH⋅HD=BH⋅HE=CH⋅HF

Аналогично,

AD⋅DH=BD⋅CDBE⋅EH=AE⋅CECF⋅FH=AF⋅BF.\begin{выровнено} AD \cdot DH &= BD \cdot CD\\ BE \cdot EH &= AE \cdot CE\\ CF \cdot FH &= AF \cdot BF. \end{align}AD⋅DHBE⋅EHCF⋅FH​=BD⋅CD=AE⋅CE=AF⋅BF.​

Применение этого к прямоугольному треугольнику требует отдельного примечания:

Если высота от вершины под прямым углом к ​​гипотенузе делит гипотенузу на две длины ppp и qqq, то длина этой высоты равна pq\sqrt{pq}pq​.

Треугольник ABCABCABC имеет прямой угол при вершине CCC. Точка DDD лежит на гипотенузе ABABAB так, что CDCDCD перпендикулярна ABABAB. Если AD=4AD=4AD=4 и BD=9BD=9BD=9, какова площадь треугольника?

Другое следствие состоит в том, что описанная окружность треугольника, образованная любыми двумя точками треугольника и его ортоцентром, конгруэнтна описанной окружности исходного треугольника. Это связано с тем, что описанную окружность BHCBHCBHC можно рассматривать как локус HHH, когда AAA движется по исходной описанной окружности.

Наконец, этот процесс (замечательно) можно обратить вспять: если любая точка описанной окружности отражается по трем сторонам, получившиеся три точки лежат на одной прямой, а ортоцентр всегда лежит на линии, соединяющей их.

С другой стороны, ортоцентр треугольника глубоко связан с описанной окружностью треугольника: две точки изогонально сопряжены, а это означает, что отражения высот над биссектрисами угла треугольника пересекаются в центр окружности треугольника.

Другое важное свойство состоит в том, что отражение ортоцентра над серединой любой стороны треугольника лежит на описанной окружности и диаметрально противоположно вершине, противоположной соответствующей стороне.

Треугольник, образованный основаниями трех высот, называется ортотреугольником . У него есть несколько замечательных свойств. Например, ортоцентр треугольника также является центром его ортогонального треугольника. Соответственно, высоты исходного треугольника являются биссектрисами ортогонального треугольника.

Стороны прямоугольного треугольника имеют длину acos⁡A,bcos⁡Ba\cos A, b\cos BacosA,bcosB и ccos⁡Cc\cos CccosC, что составляет периметр прямоугольного треугольника acos⁡A+bcos⁡B +ccos⁡Ca\cos A+b\cos B+c\cos CacosA+bcosB+ccosC. Ортотреугольник имеет наименьший периметр среди всех треугольников, которые можно вписать в треугольник ABCABCABC.

Лягушка Кельвин живет в треугольнике ABCABCABC со сторонами 4, 5 и 6. Однажды он стартует в какой-то точке на стороне ABABAB треугольника, прыгает по прямой в какую-то точку на стороне BCBCBC треугольника, прыгает в по прямой линии до некоторой точки на стороне CACACA треугольника и, наконец, прыгает обратно в исходное положение на стороне ABABAB треугольника. Наименьшее расстояние, на которое мог прыгнуть Кельвин, равно mn\frac{m}{n}nm​ для взаимно простых положительных целых чисел mmm и nnn. Что такое м+нм+нм+н?

Окружность, описанная вокруг ортогонального треугольника, содержит середины сторон исходного треугольника, а также точки на полпути от вершин к ортоцентру. Этот круг более известен как девятиконечный круг треугольника.

Ортотреугольник также гомотетичен двум важным треугольникам: треугольнику, образованному касательными к описанной окружности исходного треугольника в вершинах ( касательный треугольник ), и треугольнику, образованному путем увеличения высот до описанной окружности исходный треугольник.

  • Инцентр
  • Циркумцентр
  • Центроид

[1] Ортоцентрические диковинки . Получено 23 января с http://untilnextstop.blogspot.com/2010/10/orthocenter-curiosities.html

Цитировать как: Ортоцентр. Brilliant.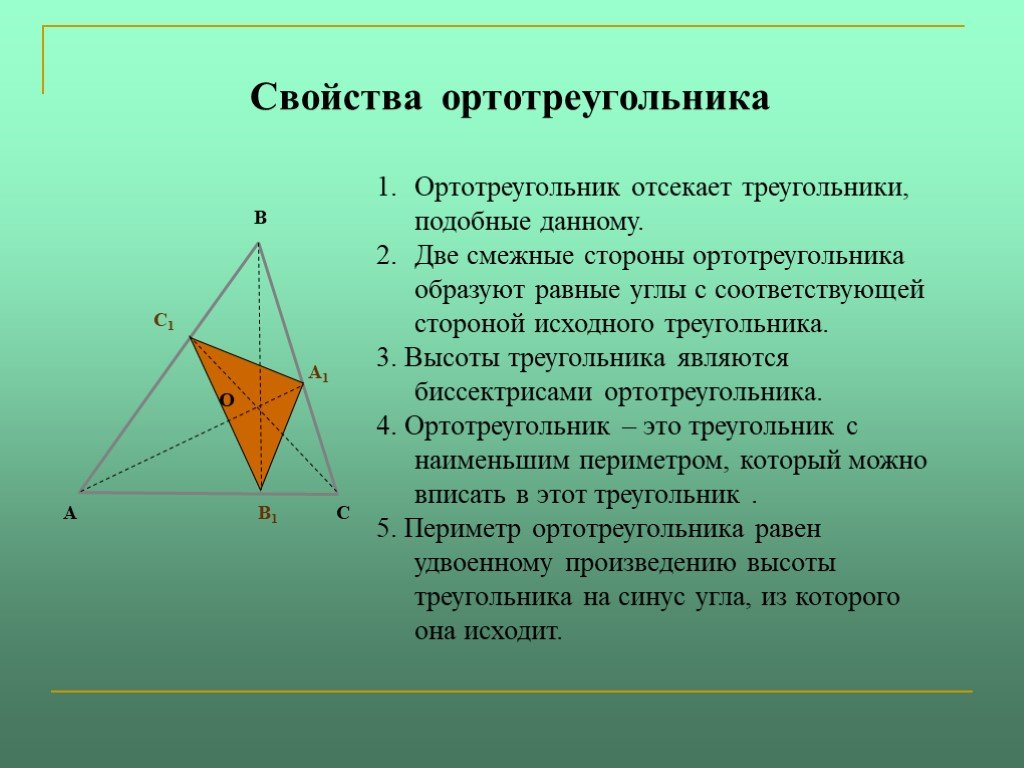 org . Полученное из https://brilliant.org/wiki/triangles-orthocenter/

Ортоцентр треугольника — определение математического слова

Ортоцентр треугольника — определение математического слова — Открытый справочник по математике

Открытый справочник по математике

Дом Контакт О Тематический указатель

Точка, где три высоты из пересекаются треугольники.
Один из треугольников точки совпадения.

Попробуйте это Перетащите оранжевые точки на любую вершину чтобы изменить форму треугольника. Обратите внимание на положение ортоцентра.

Высота треугольника (в том смысле, в каком она используется здесь) — это линия, проходящая через вершина треугольника и перпендикулярна противоположной стороне. Следовательно, возможны три высоты, по одной из каждой вершины. См. определение высоты.

Получается, что все три высоты всегда пересекаются в одной и той же точке — так называемом ортоцентре треугольника.

Ортоцентр не всегда находится внутри треугольника. Если треугольник тупой, он будет снаружи. Чтобы это произошло, линии высот должны быть расширены, чтобы они пересекались. Отрегулируйте рисунок выше и создайте треугольник, где ортоцентр находится вне треугольника. Следите за каждой линией и убедитесь, что три высоты, если их правильно продолжить, действительно пересекаются в ортоцентре.

Сводка центров треугольников

Существует много типов треугольных центров. Ниже приведены четыре самых распространенных.
Инцентр

 Расположен на пересечении ул. биссектрисы угла.

См.

  • Определение центра треугольника
  • Как построить центр треугольника
Циркумцентр
Расположен на пересечении серединных перпендикуляров сторон

См.

  • Определение центра окружности треугольника
  • Как построить центр окружности треугольника
Центроид
Расположен на пересечении медиан