Что такое sgn — значение слова, научные факты — Википедия
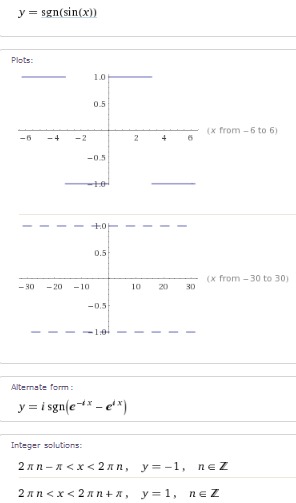
sgn (сигнум, от лат. signum — знак) — кусочно-постоянная функция действительного аргумента. Обозначается sgnx{\displaystyle \operatorname {sgn} x}. Определяется следующим образом:
График функции y = sgn x
- sgnx={ 1,x>0 0,x=0−1,x<0{\displaystyle \operatorname {sgn} x={\begin{cases}\ \ 1,&x>0\\\ \ 0,&x=0\\-1,&x<0\end{cases}}}
Функция не является элементарной.
Часто используется представление
- sgnx=ddx|x|{\displaystyle \operatorname {sgn} x={\frac {d}{dx}}|x|}
При этом производная модуля в нуле, которая, строго говоря, не определена, доопределяется средним арифметическим соответствующих производных слева и справа.
Функция применяется в теории обработки сигналов, в математической статистике и других разделах математики, где требуется компактная запись для индикации знака числа.
Содержание
- 1 История и обозначения
- 2 Свойства функции
- 3 Обобщения функции для комплексного аргумента
- 4 См.
также - 5 Примечания
- 6 Литература
такжеИстория и обозначенияПравить
Функцию sgnx{\displaystyle \operatorname {sgn} x}
ввёл Леопольд Кронекер в 1878 году, сначала он обозначал её иначе: [x]{\displaystyle [x]} . В 1884 году Кронекеру понадобилось в одной статье использовать, наряду с sgn{\displaystyle \operatorname {sgn} } , функцию «целая часть», которая также обозначалась квадратными скобками. Во избежание путаницы Кронекер ввёл обозначение sgn.x{\displaystyle sgn.x} , которое (за вычетом точки перед аргументом) и закрепилось в науке. Иногда функцию обозначают как signx{\displaystyle \operatorname {sign} x} .Свойства функцииПравить
- Область определения: R{\displaystyle \mathbb {R} } .
- Область значений: {−1;0;+1}{\displaystyle \{-1;0;+1\}} .
- Гладкая во всех точках, кроме нуля.
- Функция нечётна.
- Точка x=0{\displaystyle x=0} является точкой разрыва первого рода, так как пределы справа и слева от нуля равны +1{\displaystyle +1} и −1{\displaystyle -1} соответственно. {i\varphi }} , где φ=Argz{\displaystyle \varphi =\operatorname {Arg} z} — аргумент комплексного числа z{\displaystyle z} .
При z≠0{\displaystyle z\neq 0} результатом функции sgnz{\displaystyle \operatorname {sgn} z} является точка единичной окружности, ближайшая к числу z{\displaystyle z} . Смысл данного обобщения заключается в том, чтобы посредством радиус-вектора единичной длины показать направление на комплексной плоскости, отвечающее числу z{\displaystyle z} . Это же направление в полярных координатах задаёт угол φ{\displaystyle \varphi } . Неопределённое направление, отвечающее числу z=0{\displaystyle z=0} , выражается нулевым значением функции.
Например, таким образом функция signum определена в стандартной библиотеке комплексных чисел в языке Haskell
- Другой вариант обобщения функции, обозначаемый как csgn{\displaystyle \operatorname {csgn} } , определяется следующим образом:
- csgn(z)={1,Rez>0−1,Rez<0sgnImzRez=0{\displaystyle \operatorname {csgn} (z)={\begin{cases}1,&\operatorname {Re} z>0\\-1,&\operatorname {Re} z<0\\\operatorname {sgn} \operatorname {Im} z&\operatorname {Re} z=0\end{cases}}}
Данное обобщение используется, например, в приложениях Mathcad и Maple[2].
- Функция Хевисайда
- ↑ Simon Peyton Jones (editor) et al. 13. Complex Numbers // Haskell 98 Language and Libraries : The Revised Report. — 2002.
- ↑ Maple V documentation. May 21, 1998
- Бронштейн И. Н., Семендяев К. А. Справочник по математике. — М.: Наука, 1964. — 608 с.
- Воднев В. Т., Наумович А. Ф., Наумович Н. Ф. Основные математические формулы. Справочник. — Минск: Вышэйшая школа, 1988. — 269 с.
Mathway | Популярные задачи
1 Оценить с использованием заданного значения квадратный корень из 50 2 Оценить с использованием заданного значения квадратный корень из 45 3 Вычислить 5+5 4 Вычислить 7*7 5 Разложить на простые множители 24 6 Преобразовать в смешанную дробь 52/6 7 Преобразовать в смешанную дробь 93/8 8 Преобразовать в смешанную дробь 34/5 9 График y=x+1 10 Оценить с использованием заданного значения квадратный корень из 128 11 Найти площадь поверхности сфера (3) 12 Вычислить 54-6÷2+6 13 График y=-2x 14 Вычислить 8*8 15 Преобразовать в десятичную форму 5/9 16 Оценить с использованием заданного значения квадратный корень из 180 17 График y=2 18 Преобразовать в смешанную дробь 7/8 19 Вычислить 9*9 20 Risolvere per C C=5/9*(F-32) 21 Упростить 1/3+1 1/12 22 График y=x+4 23 График y=-3 24 График x+y=3 25 График x=5 26 Вычислить 6*6 27 Вычислить 2*2 28 Вычислить 4*4 29 Вычислить 1/2+(2/3)÷(3/4)-(4/5*5/6) 30 Вычислить 1/3+13/12 31 Вычислить 5*5 32 Risolvere per d 2d=5v(o)-vr 33 Преобразовать в смешанную дробь 3/7 34 График y=-2 35 Определить наклон y=6 36 Перевести в процентное соотношение 9 37 График y=2x+2 38 График y=2x-4 39 График x=-3 40 Решить, используя свойство квадратного корня x^2+5x+6=0 41 Преобразовать в смешанную дробь 1/6 42 Преобразовать в десятичную форму 9% 43 Risolvere per n 12n-24=14n+28 44 Вычислить 16*4 45 Упростить кубический корень из 125 46 Преобразовать в упрощенную дробь 43% 47 График x=1 48 График y=6 49 График y=-7 50 График y=4x+2 51 Определить наклон y=7 52 График y=3x+4 53 График y=x+5 54 График 3x+2y=6 55 Решить, используя свойство квадратного корня x^2-5x+6=0 56 Решить, используя свойство квадратного корня x^2-6x+5=0 57 Решить, используя свойство квадратного корня x^2-9=0 58 Оценить с использованием заданного значения квадратный корень из 192 59 Оценить с использованием заданного значения квадратный корень из 25/36 60 Разложить на простые множители 14 61 Преобразовать в смешанную дробь 7/10 62 Risolvere per a (-5a)/2=75 63 Упростить x 64 Вычислить 6*4 65 Вычислить 6+6 66 Вычислить -3-5 67 Вычислить -2-2 68 Упростить квадратный корень из 1 69 Упростить квадратный корень из 4 70 Найти обратную величину 1/3 71 Преобразовать в смешанную дробь 11/20 72 Преобразовать в смешанную дробь 7/9 73 Найти НОК 11 , 13 , 5 , 15 , 14 , , , , 74 Решить, используя свойство квадратного корня x^2-3x-10=0 75 Решить, используя свойство квадратного корня x^2+2x-8=0 76 График 3x+4y=12 77 График 3x-2y=6 78 График y=-x-2 79 График y=3x+7 80 Определить, является ли полиномом 2x+2 81 График y=2x-6 82 График y=2x-7 83 График y=2x-2 84 График y=-2x+1 85 График y=-3x+4 86 График y=-3x+2 87 График y=x-4 88 Вычислить (4/3)÷(7/2) 89 График 2x-3y=6 90 График x+2y=4 91 График x=7 92 График x-y=5 93 Решить, используя свойство квадратного корня x^2+3x-10=0 94 Решить, используя свойство квадратного корня x^2-2x-3=0 95 Найти площадь поверхности конус (12)(9) 96 Преобразовать в смешанную дробь 3/10 97 Преобразовать в смешанную дробь 7/20 98 Преобразовать в смешанную дробь 2/8 99 Risolvere per w V=lwh 100 Упростить 6/(5m)+3/(7m^2) Signum-функція
Вікіпедія
Серпень 16, 2021
У математиці, sign функція, signum функція або функція знаку (з латинської signum «знак») — це непарна математична функція, яка «витягує» знак дійсного числа.
У математичних виразах функціяsign часто зустрічається якsgn.Зміст
- 1Означення
- 2Властивості
- 3Комплексний випадок
- 4Узагальнена функція знаку
- 5Див. також
- 6Джерела
Функція знаку y = sgn(x)
Функція знаку дійсного числаx визначається наступним чином:sgn(x)={−1,якщо x<0,0,якщо x=0,1,якщо x>0.{\displaystyle \operatorname {sgn}(x)={\begin{cases}-1,&{\text{якщо }}x<0,\\0,&{\text{якщо }}x=0,\\1,&{\text{якщо }}x>0.\end{cases}}}
Або як:
sgn(x)=ddx|x|,x≠0.{\displaystyle \operatorname {sgn}(x)={\frac {\mathrm {\operatorname {d} } }{\mathrm {\operatorname {d} } x}}\left|x\right|,\quad x\neq 0.}
Будь-яке дійсне число може бути представлене у вигляді добутку його абсолютного значення і його функції знаку:
x=sgn(x)⋅|x|.{\displaystyle x=\operatorname {sgn}(x)\cdot |x|\,.}
Звідси випливає, що приx≠0{\displaystyle \quad x\neq 0}
sgn(x)=x|x|=|x|x.
{n}.}Функціяsgn(x){\displaystyle \operatorname {sgn}(x)} є похідною функціїy=|x|,{\displaystyle y=|x|,} з точністю до невизначеності приx = 0:
d|x|dx=sgn(x) для x≠0.{\displaystyle {\operatorname {d} |x| \over \operatorname {d} x}=\operatorname {sgn}(x){\mbox{ для }}x\neq 0.}
Більш формально, в теорії інтегрування функцій — це слабка похідна, а в теорії опуклих функцій субдиференціалом абсолютного значення приx=0{\displaystyle x=0} є інтервал[−1,1]{\displaystyle [-1,1]}, «заповнення» функції знаку (субдиференціал абсолютного значення не є однозначним приx=0{\displaystyle x=0}).
Функція знаку не є неперервною у точці x = 0
Похідна функціїsgn(x){\displaystyle \operatorname {sgn}(x)} дорівнює 0 для всіхx крім 0. Вона не є диференційовною приx=0{\displaystyle x=0} у звичайному сенсі, але диференційовною в узагальненому сенсі в теорії розподілу, похідною від функціїsgn(x){\displaystyle \operatorname {sgn}(x)} є дельта-функція Дірака, що можна показати за допомогою тотожності
sgn(x)=2H(x)−1,{\displaystyle \operatorname {sgn}(x)=2H(x)-1\,,}
деH(x) — функція Хевісайда,H(0) =12.
{i\arg z}\,,}деarg(z){\displaystyle \arg(z)\,} — аргумент комплексного числа.
Комплексний варіант
З міркувань симетрії та для належного узагальнення функціїsgn(z){\displaystyle \operatorname {sgn}(z)} на множині дійсних чисел, зазвичай дану функцію на комплексній площині визначають і дляz = 0:
sgn(0+0i)=0.{\displaystyle \operatorname {sgn} (0+0i)=0.}
Іншим узагальненням функціїsgn(z){\displaystyle \operatorname {sgn}(z)} для дійсних і комплексних виразів є функціяcsgn, що визначається як
csgn(z)={1,якщо Re(z)>0−1,якщо Re(z)<0sgn(Im(z)),якщо Re(z)=0,{\displaystyle \operatorname {csgn} (z)={\begin{cases}1,&{\text{якщо }}\mathrm {Re} (z)>0\\-1,&{\text{якщо }}\mathrm {Re} (z)<0\\\operatorname {sgn}(\mathrm {Im} (z)),&{\text{якщо }}\mathrm {Re} (z)=0,\end{cases}}}
деRe(z) — дійсна частина числаz, аIm(z) — комплексна частинаz.
{2}}}{z}}.}Для дійсних значеньx можна визначити узагальнену функцію (аналог функції знаку)ε(x), таку, що(ε(x))2 = 1 для всіхx, у тому числі і в точціx = 0 (на відміну від функціїsgn(x){\displaystyle \operatorname {sgn}(x)}, для якої(sgn(0))2 = 0). Ця узагальнена функція дозволяє побудувати алгебру узагальнених функцій, але ціною такого узагальнення є втрата комутативності. Зокрема, узагальнена функція знаку антикомутує з дельта-функцією Дірака
ε(x)δ(x)+δ(x)ε(x)=0;{\displaystyle \varepsilon (x)\delta (x)+\delta (x)\varepsilon (x)=0~;}
крім цього,ε(x) не можливо визначити приx = 0; і спеціальне позначенняε необхідне, щоб відрізнити її від функції знаку (ε(0) не визначено, алеsgn(0) = 0).
- Функція Хевісайда
- Дельта-функція Дірака
- Абсолютне значення
- Від’ємне число
- Сигмоїдна функція
- Прямокутна функція
- Тришляхове порівняння
- Воднев В. Т., Наумович А. Ф., Наумович Н. Ф. Основные математические формулы. Справочник. — Минск: Вышэйшая школа, 1988. — 269 с.
signum, функція, Мова, Спостерігати, Редагувати, змін, цій, версії, очікують, на, перевірку, Стабільну, версію, було, перевірено, жовтня, 2016, математиці, sign, функція, signum, функція, або, функція, знаку, латинської, signum, знак, це, непарна, математична,. Signum funkciya Mova Sposterigati Redaguvati 18 zmin u cij versiyi ochikuyut na perevirku Stabilnu versiyu bulo perevireno 29 zhovtnya 2016 U matematici sign funkciya signum funkciya abo funkciya znaku z latinskoyi signum znak ce neparna matematichna funkciya yaka vityaguye znak dijsnogo chisla U matematichnih virazah funkciya sign chasto zustrichayetsya yak sgn Zmist 1 Oznachennya 2 Vlastivosti 3 Kompleksnij vipadok 4 Uzagalnena funkciya znaku 5 Div takozh 6 DzherelaOznachennya Redaguvati Funkciya znaku y sgn x Funkciya znaku dijsnogo chisla x viznachayetsya nastupnim chinom sgn x 1 yaksho x lt 0 0 yaksho x 0 1 yaksho x gt 0 displaystyle operatorname sgn x begin cases 1 amp text yaksho x lt 0 0 amp text yaksho x 0 1 amp text yaksho x gt 0 end cases Abo yak sgn x d d x x x 0 displaystyle operatorname sgn x frac mathrm operatorname d mathrm operatorname d x left x right quad x neq 0 Vlastivosti RedaguvatiBud yake dijsne chislo mozhe buti predstavlene u viglyadi dobutku jogo absolyutnogo znachennya i jogo funkciyi znaku x sgn x x displaystyle x operatorname sgn x cdot x Zvidsi viplivaye sho prix 0 displaystyle quad x neq 0 sgn x x x x x displaystyle operatorname sgn x x over x x over x Tak samo i dlya bud yakogo dijsnogo chisla x x sgn x x displaystyle x operatorname sgn x cdot x Mi takozh mozhemo perekonatisya sho sgn x n sgn x n displaystyle operatorname sgn x n operatorname sgn x n Funkciya sgn x displaystyle operatorname sgn x ye pohidnoyu funkciyi y x displaystyle y x z tochnistyu do neviznachenosti pri x 0 d x d x sgn x dlya x 0 displaystyle operatorname d x over operatorname d x operatorname sgn x mbox dlya x neq 0 Bilsh formalno v teoriyi integruvannya funkcij ce slabka pohidna a v teoriyi opuklih funkcij subdiferencialom absolyutnogo znachennya pri x 0 displaystyle x 0 ye interval 1 1 displaystyle 1 1 zapovnennya funkciyi znaku subdiferencial absolyutnogo znachennya ne ye odnoznachnim pri x 0 displaystyle x 0 Funkciya znaku ne ye neperervnoyu u tochci x 0 Pohidna funkciyi sgn x displaystyle operatorname sgn x dorivnyuye 0 dlya vsih x krim 0 Vona ne ye diferencijovnoyu pri x 0 displaystyle x 0 u zvichajnomu sensi ale diferencijovnoyu v uzagalnenomu sensi v teoriyi rozpodilu pohidnoyu vid funkciyi sgn x displaystyle operatorname sgn x ye delta funkciya Diraka sho mozhna pokazati za dopomogoyu totozhnosti sgn x 2 H x 1 displaystyle operatorname sgn x 2H x 1 de H x funkciya Hevisajda H 0 1 2 Vikoristovuyuchi cyu totozhnist legko znajti pohidnu d sgn x d x 2 d H x d x 2 d x displaystyle frac operatorname d operatorname sgn x operatorname d x 2 frac operatorname d H x operatorname d x 2 delta x Peretvorennya Fur ye funkciyi sgn x displaystyle operatorname sgn x maye viglyad sgn x e i k x d x p v 2 i k displaystyle int infty infty operatorname sgn x e ikx operatorname d x mathrm p v frac 2 ik de p v golovne znachennya integrala za Koshi Funkciyu sgn x displaystyle operatorname sgn x takozh mozhna viraziti za dopomogoyu duzhki Ajversona sgn x x lt 0 x gt 0 displaystyle operatorname sgn x x lt 0 x gt 0 Funkciyu sgn x displaystyle operatorname sgn x mozhna zapisati z vikoristannyam funkcij pidlogi ta absolyutnogo znachennya sgn x x x 1 x x 1 displaystyle operatorname sgn x Bigg lfloor frac x x 1 Bigg rfloor Bigg lfloor frac x x 1 Bigg rfloor Dlya k 1 neperervne nablizhennya funkciyi znaku maye viglyad sgn x th k x displaystyle operatorname sgn x approx operatorname th kx Inshe nablizhennya maye viglyad sgn x x x 2 e 2 displaystyle operatorname sgn x approx frac x sqrt x 2 varepsilon 2 yake staye gostrishim pri e 0 zauvazhimo sho ce pohidna vid funkciyi x2 e2 Ce gruntuyetsya na tomu fakti sho x x 2 e 2 sgn x displaystyle frac x sqrt x 2 varepsilon 2 operatorname sgn x dlya vsih x 0 yaksho e 0 i daye perevagi dlya prostogo uzagalnennya na bagatovimirni analogi funkciyi znaku napriklad chastinni pohidni funkciyi x2 y2 Kompleksnij vipadok RedaguvatiFunkciyu sgn x displaystyle operatorname sgn x mozhna uzagalniti na kompleksni chisla sgn z z z displaystyle operatorname sgn z frac z z dlya bud yakogo kompleksnogo chisla z krim z 0 Takim chinom znachennya funkciyi sgn z displaystyle operatorname sgn z bude tochkoyu na odinichnomu koli kompleksnoyi ploshini sho najblizhcha do tochki z Todi dlya z 0 sgn z e i arg z displaystyle operatorname sgn z e i arg z de arg z displaystyle arg z argument kompleksnogo chisla Kompleksnij variant Z mirkuvan simetriyi ta dlya nalezhnogo uzagalnennya funkciyi sgn z displaystyle operatorname sgn z na mnozhini dijsnih chisel zazvichaj danu funkciyu na kompleksnij ploshini viznachayut i dlya z 0 sgn 0 0 i 0 displaystyle operatorname sgn 0 0i 0 Inshim uzagalnennyam funkciyi sgn z displaystyle operatorname sgn z dlya dijsnih i kompleksnih viraziv ye funkciya csgn sho viznachayetsya yak csgn z 1 yaksho R e z gt 0 1 yaksho R e z lt 0 sgn I m z yaksho R e z 0 displaystyle operatorname csgn z begin cases 1 amp text yaksho mathrm Re z gt 0 1 amp text yaksho mathrm Re z lt 0 operatorname sgn mathrm Im z amp text yaksho mathrm Re z 0 end cases de Re z dijsna chastina chisla z a Im z kompleksna chastina z Todi dlya z 0 mayemo csgn z z z 2 z 2 z displaystyle operatorname csgn z frac z sqrt z 2 frac sqrt z 2 z Uzagalnena funkciya znaku RedaguvatiDlya dijsnih znachen x mozhna viznachiti uzagalnenu funkciyu analog funkciyi znaku e x taku sho e x 2 1 dlya vsih x u tomu chisli i v tochci x 0 na vidminu vid funkciyi sgn x displaystyle operatorname sgn x dlya yakoyi sgn 0 2 0 Cya uzagalnena funkciya dozvolyaye pobuduvati algebru uzagalnenih funkcij ale cinoyu takogo uzagalnennya ye vtrata komutativnosti Zokrema uzagalnena funkciya znaku antikomutuye z delta funkciyeyu Diraka e x d x d x e x 0 displaystyle varepsilon x delta x delta x varepsilon x 0 krim cogo e x ne mozhlivo viznachiti pri x 0 i specialne poznachennya e neobhidne shob vidrizniti yiyi vid funkciyi znaku e 0 ne viznacheno ale sgn 0 0 Div takozh RedaguvatiFunkciya Hevisajda Delta funkciya Diraka Absolyutne znachennya Vid yemne chislo Sigmoyidna funkciya Pryamokutna funkciya Trishlyahove porivnyannyaDzherela RedaguvatiVodnev V T Naumovich A F Naumovich N F Osnovnye matematicheskie formuly Spravochnik Minsk Vyshejshaya shkola 1988 269 s Otrimano z https uk wikipedia org w index php title Signum funkciya amp oldid 29731193, Вікіпедія, Українська, Україна, книга, книги, бібліотека, стаття,
читати
, завантажити, безкоштовно, безкоштовно завантажити, mp3, відео, mp4, 3gp, jpg, jpeg, gif, png, малюнок, музика, пісня, фільм, книга, гра, ігриМэтуэй | Популярные задачи
1 Оценка с использованием заданного значения квадратный корень из 50 2 Оценка с использованием заданного значения квадратный корень из 45 3 Оценить 5+5 4 Оценить 7*7 5 Найти простую факторизацию 24 6 Преобразование в смешанный номер 52/6 7 Преобразование в смешанный номер 93/8 8 Преобразование в смешанный номер 34/5 9 График у=х+1 10 Оценка с использованием заданного значения квадратный корень из 128 11 Найдите площадь поверхности сфера (3) 12 Оценить 54-6÷2+6 13 График г=-2x 14 Оценить 8*8 15 Преобразование в десятичное число 5/9 16 Оценка с использованием заданного значения квадратный корень из 180 17 График у=2 18 Преобразование в смешанный номер 7/8 19 Оценить 9*9 20 Решите для C С=5/9*(Ф-32) 21 Упростить 1/3+1 1/12 22 График у=х+4 23 График г=-3 24 График х+у=3 25 График х=5 26 Оценить 6*6 27 Оценить 2*2 28 Оценить 4*4 29 Оценить 1/2+(2/3)÷(3/4)-(4/5*5/6) 30 Оценить 1/3+13/12 31 Оценка 5*5 32 Решить для d 2д=5в(о)-вр 33 Преобразование в смешанный номер 3/7 34 График г=-2 35 Найдите склон у=6 36 Преобразование в проценты 9 37 График у=2х+2 38 92+5х+6=041 Преобразование в смешанный номер 1/6 42 Преобразование в десятичное число 9% 43 Найти n 12н-24=14н+28 44 Оценить 16*4 45 Упростить кубический корень из 125 46 Преобразование в упрощенную дробь 43% 47 График х=1 48 График у=6 49 График г=-7 50 График у=4х+2 51 Найдите склон у=7 52 График у=3х+4 53 График у=х+5 54 График 92-9=058 Оценка с использованием заданного значения квадратный корень из 192 59 Оценка с использованием заданного значения квадратный корень из 25/36 60 Найти простую факторизацию 14 61 Преобразование в смешанный номер 7/10 62 Решите для (-5а)/2=75 63 Упростить х 64 Оценить 6*4 65 Оценить 6+6 66 Оценить -3-5 67 Оценить -2-2 68 Упростить квадратный корень из 1 69 Упростить квадратный корень из 4 70 Найди обратное 1/3 71 Преобразование в смешанный номер 20. 11.72 Преобразование в смешанный номер 7/9 73 Найти LCM 11, 13, 5, 15, 14 , , , , 76 График 3x+4y=12 77 График 3x-2y=6 78 График у=-х-2 79 График у=3х+7 80 Определить, является ли многочлен 2x+2 81 График у=2х-6 82 График у=2х-7 83 График у=2х-2 84 у=-2х+1 85 График у=-3х+4 86 График у=-3х+2 87 График у=х-4 88 Оценить (4/3)÷(7/2) 89 График 2x-3y=6 90 График х+2у=4 91 График х=7 92 График х-у=5 93 Решение с использованием свойства квадратного корня 92-2x-3=0 95 Найдите площадь поверхности конус (12)(9) 96 Преобразование в смешанный номер 3/10 97 Преобразование в смешанный номер 7/20 92)Алгебра, линейная алгебра, геометрия, геометрия вектора, тригонометрия, предварительная калькулус и одноразовый расчет
∞
Расширения предела
Правила бесконечности
Правила бесконечно
Расширения предела
Существуют три других типа пределов, которые на самом деле не являются пределами, но по-прежнему являются важными концепциями исчисления.
1. Односторонние пределы: пределы, когда х приближается только с одной стороны а, будь то с положительной или отрицательной стороны а.
2. Пределы на бесконечности: x становится произвольно большим, положительным или отрицательным, из-за того, что L является горизонтальной асимптотой.
3. Бесконечные пределы: L становится произвольно большим, положительно или отрицательно, из-за того, что a является вертикальной асимптотой.Односторонние пределы
Некоторые пределы не существуют по причинам разрыва или наличия скачков на графике функции. Однако мы все же можем определить предел функции на этих разрывах и скачках, если будем рассматривать только непрерывную сторону а, то есть там, где функция все еще определена.
Например, эта функция называется сигнум-функцией, где f(x) = signx.
Если бы мы рассчитали предел, когда x приближается к 0, предел не существовал бы, потому что есть два значения L, которые стремятся к нулю, в зависимости от стороны 0, которые равны 1 и -1.Вместо этого мы можем сказать, что сигнум-функция имеет два односторонних предела, один называется правым пределом, а другой — левым пределом.
Правый предел для f(x) = sgnx определяется следующим образом:
Читается как «предел sgnx при приближении x к 0 справа равен 1».Левый предел для f(x) = sgnx определяется следующим образом:
Читается как «предел sgnx при приближении x к 0 слева равен -1».Определение правых пределов
Функция имеет правый предел, если предел f(x) при приближении x к a справа равен L, при условии, что f(x) определено в интервале (a,b), где b > a, и когда f(x) приближается к L, x уменьшается в сторону a.
Определение левых пределов
Функция имеет левый предел, если предел f(x) при приближении x к a слева равен M, при условии, что f(x) определено в интервале (b,a) , где b < a, и когда f(x) приближается к M, x увеличивается в направлении a.
Пределы на бесконечности
Другой тип предела — это когда функция определена на всей прямой с действительными числами (-∞,∞) или на полубесконечном интервале (a,∞) или (-∞ , а).
Мы описываем поведение функции, когда x становится произвольно большим, положительным или отрицательным.Когда x становится произвольно большим, положительным или отрицательным, константы будут равны нулю.
Положительная бесконечность
Если функция f определена в точке (a,∞) и если функция приближается близко к L при увеличении x до положительной бесконечности, то функция соответствует пределу L, поскольку x соответствует до положительной бесконечности.
Отрицательная бесконечность
Если функция f определена в точке (-∞,a) и если функция приближается близко к M при уменьшении x до отрицательной бесконечности, то функция соответствует пределу M, как x соответствует отрицательной бесконечности.
Горизонтальные асимптоты и пределы на бесконечности
При определении горизонтальных асимптот функции полезно применять пределы. Для этого применяются следующие правила:
Одиночные тригонометрические функции и пределы на бесконечности
Предел любой простой тригонометрической функции при приближении x к положительной или отрицательной бесконечности не будет существовать.
Вот почему обычно применяется теорема сжатия.Оценка пределов бесконечности
1. В выражении разделите все члены на наибольшую степень x от знаменателя. Если высшая степень х находится в радикале, это не означает, что это высшая степень х. Если вы упростите радикал из него, то у вас останется истинная сила этого термина x. Если знаменатель отсутствует, создайте его с его сопряженным.
3. Найдите предел каждого частного члена, помня правила арифметики бесконечности.Следующее выражение используется, чтобы помочь разделить радикалы по наибольшей степени x от знаменателя.
Бесконечные пределы
Когда предел, где x приближается к любой стороне от a, становится произвольно большим, положительным или отрицательным, тогда предел не существует. Однако полезно описать такое поведение a, и поэтому вместо того, чтобы говорить, что предела не существует, поскольку положительная и отрицательная бесконечность не являются действительными числами, мы говорим, что предел приближается либо к положительной бесконечности, либо к отрицательной бесконечности.Определение бесконечных пределов
Если f(x) становится произвольно большим положительно, когда x приближается к значению a, то мы говорим, что f(x) стремится к положительной бесконечности, когда x приближается к a.
Если f(x) становится сколь угодно большой отрицательной величиной, когда x приближается к значению a, то мы говорим, что f(x) стремится к отрицательной бесконечности, когда x приближается к a.
Это определение может также применяться к односторонним пределам и пределам на бесконечности.Вертикальные асимптоты и бесконечные пределы
При определении вертикальных асимптот функции полезно применять пределы. Для этого применяются следующие правила:
Оценка односторонних ограничений
1. Если это обычная функция, упростите ее. Для правого предела подставьте значение, очень близкое к a справа, а для левого предела подставьте очень близкое значение к a слева. Если пределы близки к равным, то это предел функции.
1.1 Если это кусочная функция, включая функции абсолютного значения, используйте их области определения, чтобы определить, какая функция будет оцениваться как правый предел (область x > a), а какая функция будет оцениваться как левый предел (область x < a ). Если пределы равны, то это предел функции.
1.2. Если имеется график, проследите пальцем по графику с правой или левой стороны а, в зависимости от того, какая сторона дана в вопросе, пока ваш палец не приблизится к а. Это правый или левый предел f(x), когда x приближается к a справа или слева.
1. Используйте график зависимости y = g(x) для определения значений следующих пределов, если они существуют.
1.2. Если имеется график, проследите пальцем по графику с правой или левой стороны а, в зависимости от того, какая сторона дана в вопросе, пока ваш палец не приблизится к а. Это правый или левый предел f(x), когда x приближается к a справа или слева.Для a) предел утверждает, что x приближается к левой стороне a, следовательно, предел g(x) при приближении x к 1 слева равен 1.
Для b) предел утверждает, что x приближается правая часть a, поэтому предел g(x) при приближении x к 1 справа равен 1.
Для c) предел утверждает, что x приближается к обеим сторонам a, и поскольку мы уже оценили обе стороны из a) и b), предел g(x) при приближении x к 1 равен 1.
Для d) предел утверждает, что x приближается к левой части a, следовательно, предел g(x) при x приближается к 4 слева 2.
Для e) предел утверждает, что x приближается к правой стороне a, следовательно, предел g(x) при приближении x к 4 справа равен 4.
Для f) предел утверждает, что x приближается к обоим стороны а, и поскольку мы уже оценили обе стороны от а) и б), предел g(x) при приближении х к 4 не существует, потому что есть два разных предельных значения.Если задать вопрос, чтобы оценить следующее количество g(4), ответ будет 4, потому что x = 4 определено в этой точке.
2. Оцените следующий предел:
1. В выражении разделите все члены на наибольшую степень x от знаменателя. Если высшая степень х находится в радикале, это не означает, что это высшая степень х. Вынесите наибольшую степень x как из числителя, так и из знаменателя, если это возможно. Они отменят, оставив замену, чтобы найти предел. Если вы упростите радикал из него, то у вас останется истинная сила этого термина x. Если знаменатель отсутствует, создайте его с его сопряженным.В этом случае наибольшая степень x в знаменателе равна x².
Упрощая:
2. Найдите предел каждого члена частного, помня правила арифметики бесконечности.
Следовательно, предел равен 5.
3. Оцените следующий предел:
1. В выражении разделите все члены на наибольшую степень x из знаменателя. Если высшая степень х находится в радикале, это не означает, что это высшая степень х. Вынесите наибольшую степень x как из числителя, так и из знаменателя, если это возможно. Они отменят, оставив замену, чтобы найти предел. Если вы упростите радикал из него, то у вас останется истинная сила этого термина x. Если знаменатель отсутствует, создайте его с его сопряженным.Чтобы найти наибольший знаменатель, лучше всего разложить два члена.
В этом случае наибольшая степень x в знаменателе равна x².
Упрощая:
2. Найдите предел каждого члена частного, помня правила арифметики бесконечности.
Следовательно, предел равен -3.
4. Оцените следующий предел:
1. В выражении разделите все члены на наибольшую степень x от знаменателя. Если высшая степень х находится в радикале, это не означает, что это высшая степень х. Вынесите наибольшую степень x как из числителя, так и из знаменателя, если это возможно. Они отменят, оставив замену, чтобы найти предел. Если вы упростите радикал из него, то у вас останется истинная сила этого термина x. Если знаменатель отсутствует, создайте его с его сопряженным.В этом случае знаменатель отсутствует, а поскольку радикалов нет, мы не можем составить знаменатель с его сопряженным.
Если мы подставим в выражение отрицательную бесконечность, то получим неопределенный ответ. Это из-за правил бесконечной арифметики.
Вместо этого мы выносим за скобки x² и затем подставляем минус бесконечность.
Следовательно, предел равен -∞.
5. Оцените следующий предел:
1. В выражении разделите все члены на наибольшую степень x от знаменателя. Если высшая степень х находится в радикале, это не означает, что это высшая степень х. Вынесите наибольшую степень x как из числителя, так и из знаменателя, если это возможно. Они отменят, оставив замену, чтобы найти предел. Если вы упростите радикал из него, то у вас останется истинная сила этого термина x. Если знаменатель отсутствует, создайте его с его сопряженным.В этом случае давайте вычтем x из числителя и знаменателя.
Причина, по которой x² стала -x, заключается в том, что x приближается к отрицательной бесконечности.Упрощение:
2. Найдите предел каждого члена частного, помня правила арифметики бесконечности.
Следовательно, предел равен -1.
6. Оцените следующий предел:
1. В выражении разделите все члены на наибольшую степень x от знаменателя. Если высшая степень х находится в радикале, это не означает, что это высшая степень х. Вынесите наибольшую степень x как из числителя, так и из знаменателя, если это возможно. Они отменят, оставив замену, чтобы найти предел. Если вы упростите радикал из него, то у вас останется истинная сила этого термина x. Если знаменатель отсутствует, создайте его с его сопряженным.В этом случае знаменатель отсутствует. Однако, поскольку функция содержит радикал, мы можем создать знаменатель с его сопряженным.
Теперь вынесите x² из корня, а затем факторизуйте знаменатель.
Упрощая:
2. Найдите предел каждого члена частного, помня правила арифметики бесконечности.
Следовательно, предел равен -1.
7. Оцените следующий предел:
1. В выражении разделите все члены на наибольшую степень x от знаменателя. Если высшая степень х находится в радикале, это не означает, что это высшая степень х. Вынесите наибольшую степень x как из числителя, так и из знаменателя, если это возможно. Они отменят, оставив замену, чтобы найти предел. Если вы упростите радикал из него, то у вас останется истинная сила этого термина x. Если знаменатель отсутствует, создайте его с его сопряженным.В этом случае наибольшая степень x в знаменателе равна x². Однако сначала расширим числитель. Это потому, что независимо от того, какие предельные законы вы применяете прямо сейчас к функции, числитель всегда будет равен нулю.
Теперь мы разделим каждое слагаемое на наибольшую степень x в знаменателе, x².
Упрощение:
2. Найдите предел каждого члена частного, помня правила арифметики бесконечности.
Следовательно, предел равен -(√2/4).
8. Оцените следующий предел:
Используя правила тригонометрических функций tanx будет равно бесконечности из-за sinx/cosx = 1/0. Однако мы должны использовать единичный круг, чтобы определить, будет ли tanx положительной бесконечностью или отрицательной бесконечностью.Давайте определим, является ли tanx отрицательным или положительным. Если мы ищем правосторонний предел π/2, то на единичном круге он будет выглядеть так:
Это означает, что любое значение в правой части π/2 находится в квадранте II. Для tanx это будет отрицательная бесконечность, потому что sinx положителен в квадранте II, а cosx отрицателен в квадранте II.
Используя экспоненциальные законы и пределы постоянной Эйлера:
Следовательно, предел равен 0.
9. Используйте пределы, чтобы найти горизонтальную асимптоту и вертикальную асимптоту, если она существует, следующей функции:
Чтобы найти горизонтальную асимптоту, мы берем предел, когда x приближается к положительной бесконечности, и предел, когда x приближается к отрицательной бесконечности. бесконечность функции. Если их пределы равны, то имеется только одна горизонтальная асимптота.Положительная бесконечность:
Отрицательная бесконечность:
Следовательно, эта функция имеет две горизонтальные асимптоты. Один при y = 0 и y = 2,Чтобы найти вертикальную асимптоту, мы берем правый предел, когда x приближается к недопустимому значению, и левый предел, когда x приближается к недопустимому значению функции. Определим недопустимое значение, при котором знаменатель не может быть равен 0.
Значит, x не может равняться ln5, иначе знаменатель будет равен нулю.Правый предел при приближении x к ln5 справа:
Левый предел при приближении x к ln5 слева:
Обратите внимание, что это отрицательная бесконечность из-за приближения x слева.Следовательно, функция имеет одну вертикальную асимптоту при x = ln5.
10. Оцените следующий предел:
Если это кусочная функция, включая функции с абсолютными значениями, используйте их домены, чтобы определить, какая функция будет оцениваться как правильный предел (домен x > a), и какая функция будет оцениваться левым пределом (область x < a). Если пределы равны, то это предел функции.Эта функция является функцией абсолютного значения, поэтому мы должны вычислить эту кусочную функцию, когда x > 0 (правый предел) и x ≤ 0 (левый предел).
Оценка правого предела, когда x > 0:
Оценка правого предела, когда x ≤ 0:
Поскольку правый предел и левый предел не равны, предел при приближении x к 6 функции не существует.
11. Оцените следующий предел. Если оно не существует, определите, стремится ли оно к положительной бесконечности или к отрицательности.
Поскольку этот предел нельзя заменить напрямую из-за невозможности дальнейшего упрощения функции, предел не существует. Вместо этого он стремится к бесконечности. Теперь давайте решим, является ли это положительной бесконечностью или отрицательной бесконечностью.Рассматривая числитель по мере приближения x к -1:
x = -1 = отрицательный числительРассматривая знаменатель по мере приближения x к 0 (-½ и 1):
x² + 2x + 1 = (-½)² + 2(-½) + 1 = ¼ = положительный
x² + 2x + 1 = (1)² + 2(1) + 1 = 4 = положительный
положительный знаменательбесконечность = отрицательный/положительный = отрицательная бесконечность
Следовательно, функция стремится к -∞, когда x приближается к -1.
Определения— Endpoint Security — VIPRE
Загрузить наборы руководств для продуктов VIPRE
Для VIPRE Antivirus+ и VIPRE Advanced Security for HomeИнструкции о том, как вручную загрузить определения клиента, см. здесь.
Для защиты конечных точек VIPREСкачать Версия Дата выпуска Размер файла MD5 CSC43-EN-104896-7. 93014-F.sgnx104896 12.10.2022 11:24 321119488 байт 1Д5674ДФА9АКД82112595ФБ9ФА53К381 CSC43-EN-104872-7.93005-F.sgnx 104872 11. 10.2022 11:23320957925 байт 289BEA407ACD6C164F8A5B2823FDA2F2 CSC43-EN-104846-7.92994-F.sgnx 104846 10.10.2022 11:24 320836484 байт 407EEA6B4DEA32168E6153F4DBAE69Д5 Инструкции по загрузке определений агентов вручную см.
здесь.Загрузка агента VIPRE Версия Дата выпуска Размер файла MD5 CSE43-EN-104896-7.93014-F.sgnx 104896 12.10.2022 11:25 334192768 байт 73BF119F588919878230EFF6B66AA3C9 CSE43-EN-104872-7. 93005-F.sgnx104872 11.10.2022 11:25 334030667 байт 736BEA390F834EA14A85EAAA263A0DEC CSE43-EN-104846-7.92994-F.sgnx 104846 10. 10.2022 11:25333 4 байтE38CA12A7FD0B178EF8818E4B52C83E9 Инструкции по загрузке определений консоли VIPRE вручную см. здесь.
Загрузка консоли VIPRE Версия Дата выпуска Размер файла MD5 vipredefspkg2022-10-12. exe20221012 12.10.2022 16:38 734772304 байт Ф37Д2Э028347Д03Ф9ЭБ46ЭК42103АКК6 vipredefspkg2022-10-11.exe 20221011 11.
{i\varphi }} , где φ=Argz{\displaystyle \varphi =\operatorname {Arg} z} — аргумент комплексного числа z{\displaystyle z} .
При z≠0{\displaystyle z\neq 0} результатом функции sgnz{\displaystyle \operatorname {sgn} z} является точка единичной окружности, ближайшая к числу z{\displaystyle z} . Смысл данного обобщения заключается в том, чтобы посредством радиус-вектора единичной длины показать направление на комплексной плоскости, отвечающее числу z{\displaystyle z} . Это же направление в полярных координатах задаёт угол φ{\displaystyle \varphi } . Неопределённое направление, отвечающее числу z=0{\displaystyle z=0} , выражается нулевым значением функции.
Например, таким образом функция signum определена в стандартной библиотеке комплексных чисел в языке Haskell
У математичних виразах функціяsign часто зустрічається якsgn.
{n}.}
{i\arg z}\,,}
{2}}}{z}}.}
Т., Наумович А. Ф., Наумович Н. Ф. Основные математические формулы. Справочник. — Минск: Вышэйшая школа, 1988. — 269 с.
11.
Если высшая степень х находится в радикале, это не означает, что это высшая степень х. Вынесите наибольшую степень x как из числителя, так и из знаменателя, если это возможно. Они отменят, оставив замену, чтобы найти предел. Если вы упростите радикал из него, то у вас останется истинная сила этого термина x. Если знаменатель отсутствует, создайте его с его сопряженным.
Если знаменатель отсутствует, создайте его с его сопряженным.
Найдите предел каждого члена частного, помня правила арифметики бесконечности.
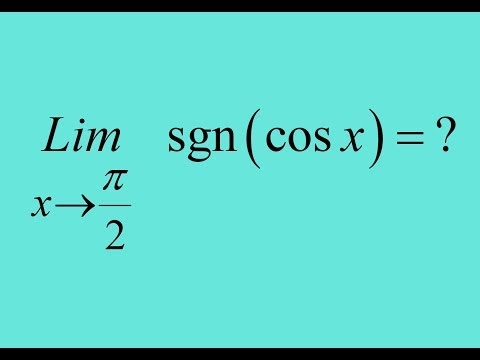
бесконечность функции. Если их пределы равны, то имеется только одна горизонтальная асимптота.
Если пределы равны, то это предел функции.
93014-F.sgnx
10.2022 11:23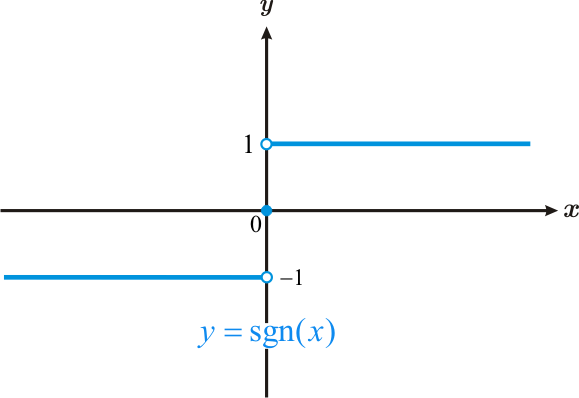
здесь.
93005-F.sgnx
10.2022 11:25
exe