Сказка про Синус и Косинус. : kssernik — LiveJournal
Жил был Синус. Он жил не сам по себе, а вместе с Косинусом, Тангенсом и Котангенсом в Остром Угле Треугольника. Синус считал себя главным в Треугольнике — ведь он был отношением дальнего Противолежащего Катета к Гипотенузе — значит на нём держалась вся конструкция!
Угол этот был всего 30 градусов, и в нём назревало обострение.
«Без меня Треугольник развалится», — думал Синус — «Ну и туда ему дорога! А то Косинус, гад, съел все радианы и выпил градусы!». И вообще Противоположный Угол больше.
«Треугольник должен быть разрушен!» — крикнул Синус и съёжился, ожидая подзатыльник от Косинуса. «От этого Косинуса можно ждать чего угодно. Зачем мне сосед с таким неопределённым значением корень из трёх на два? «, — думал Синус. Сам он равнялся 1/2 одной второй и гордился своей понятностью и значимостью. «Но всё-таки половина меньше целого», — частенько впадал в уныние Синус.
Косинус был крут и тяжёл на руку.
Но неожиданно поддержал Синуса: «Этот Треугольник устарел! Долой Треугольник! Да здравствует Прямая!». Косинусу давно не нравился Тангенс, как отношение Синуса к Косинусу. Другое дело — Котангенс, свой парень. И вообще, Треугольник держится на Косинусе — как на отношении Прилежащего Катета к Гипотенузе. А дальний Катет давно пора укоротить, вмести с Синусом..
Котангенс недоумённо взглянул на Косинус, но тот шепнул Котангенсу: » Нам надо под шумок укоротить Синус. Тогда ты, как отношение Косинуса с Синусу, прирастёшь. Держись меня, не обижу». Котангенс равнялся корню из трёх , ему хватало, но не хотелось обижать Косинус — ведь благодаря ему он достиг такого значения, иррационального числа, носящего гордое название Феодоровской постоянной! Да и если Синус снизить малёхо, он и правда вырастет — чем больше Косинус и меньше Синус, тем больше Котангенс!
Тангенс пока помалкивал. Он равнялся единице, делённой на корень из трёх 1 / , это 0,5773502692. Тангенс не понимал, откуда взялось столько цифр, и почему он меньше Котангенса, у которого их всего четыре: 1, 732.
На всякий случай Тангенс нахмурился, создавая значительный вид.
Синус, не встретив сопротивления, закуражился больше: «Даёшь объединение с Синусом Противоположного Угла! Один Синус — хорошо, а два Синуса — лучше!». И Синус пополз по Гипотенузе. За Синусом ринулся Косинус. Тангенс попытался ухватиь Синус, и даже увеличился до единицы. В то время как Синус с Косинусом сравнялись друг с другом, до корня из двух на два. Отставший Котангенс же уменьшился до единицы.
По пути, в районе 60 градусов, Синус поменялся значением с Косинусом, а Тангенс — с Котангенсом. Достигнув Противоположного угла, Синус воплотил в жизнь свою цель, став полноценной 1 единицей! Как он и рассчитывал, ненавистный Косинус превратился в 0 ноль. Ни с кем больше не надо было делиться. Тангенс исчез, а Котангенс при делении единицы Синуса на ноль Косинуса, стал жалким нолём, как и его друг Косинус.
Но недолго ликовал Синус! Треугольник с двумя прямыми углами невозможен. Поэтому он вытянулся в Прямую Линию, как и провозглашал сдуру Косинус, 90 + 90 = 180.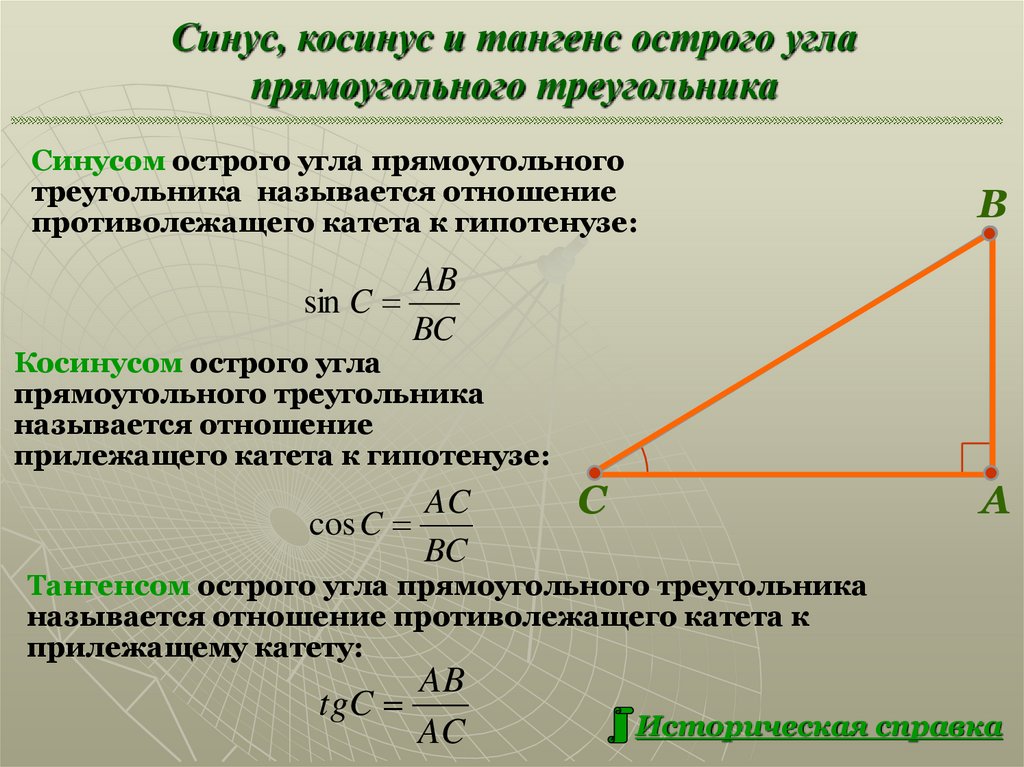
При 180 градусах Косинус возродился в отрицательной величине — 1 минус единица, и вынужден влачить жалкое существование, с тоской вспоминая, как он был корнем из трёх на два. Баламут Синус превратился в ноль 0, вместе с упустившим его Тангенсом. Соблазнившийся Котангенс же исчез бесследно, поскольку на ноль делить нельзя, по законам мироздания.
Диаграммы тангенса и котангенса | Brilliant Math & Science Wiki
Содержание
- Графики тангенса и котангенса
- Связь между тангенсом и котангенсом
- Характеристики
- Примеры
Из определения функций тангенса и котангенса имеем
tan(θ)=sin(θ)cos(θ),cot(θ)=cos(θ)sin(θ). \ tan ( \ theta) = \ frac {\ sin (\ theta)} {\ cos (\ theta)}, \ quad \ cot ( \ theta) = \ frac {\ cos (\ theta)} {\ sin (\ тета)}.
tan(θ)=cos(θ)sin(θ),cot(θ)=sin(θ)cos(θ).
Таким образом, tan(θ)\tan(\theta)tan(θ) не определен для значений θ\thetaθ таких, что cos(θ)=0\cos(\theta) = 0cos(θ)=0 . Теперь рассмотрим график cos(θ)\cos (\theta)cos(θ):
Из этого графика видно, что cos(θ)=0\cos(\theta) = 0cos(θ)=0, когда θ=π2+kπ\theta = \frac{\pi}{2} + k\ piθ=2π+kπ для любого целого числа kkk. Это означает, что касательная функция имеет вертикальные асимптоты при этих значениях θ\thetaθ.
Касательная функция стремится к положительной или отрицательной бесконечности в этих асимптотах? Когда θ\thetaθ приближается к π2\frac{\pi}{2}2π снизу (θ\big(\theta(θ принимает значения меньше, чем π2\frac{\pi}{2}2π, приближаясь к π2),\frac{\pi}{2}\big),2π), sin(θ)\sin (\theta) sin(θ) принимает положительные значения, которые все ближе и ближе к 111, а cos( θ)\cos (\theta)cos(θ) принимает положительные значения, которые все ближе и ближе к 000. Это показывает, что tan(θ)=sin(θ)cos(θ)\tan(\theta) = \frac {\sin(\theta)}{\cos(\theta)}tan(θ)=cos(θ)sin(θ) является положительным и стремится к бесконечности, поэтому tan(θ)\tan(\theta)tan( θ) имеет положительную вертикальную асимптоту при θ→π2\theta \rightarrow \frac{\pi}{2} θ→2π снизу.
График тангенса по всей его области выглядит следующим образом:
Аналогично, cot(θ)\cot(\theta)cot(θ) не определен для значений θ\thetaθ таких, что sin(θ)=0\sin(\theta) = 0sin(θ)=0 . Из графика sin(θ),\sin(\theta),sin(θ) мы видим, что sin(θ)=0\sin(\theta) = 0sin(θ)=0 при θ=0+ kπ\theta = 0 + k\piθ=0+kπ для любого целого kkk, из чего следует, что функция котангенса имеет вертикальные асимптоты при этих значениях θ:\theta:θ:
Заметим, что из определения тангенса и котангенса мы получаем следующее соотношение между функциями тангенса и котангенса: (θ) =1кот(θ).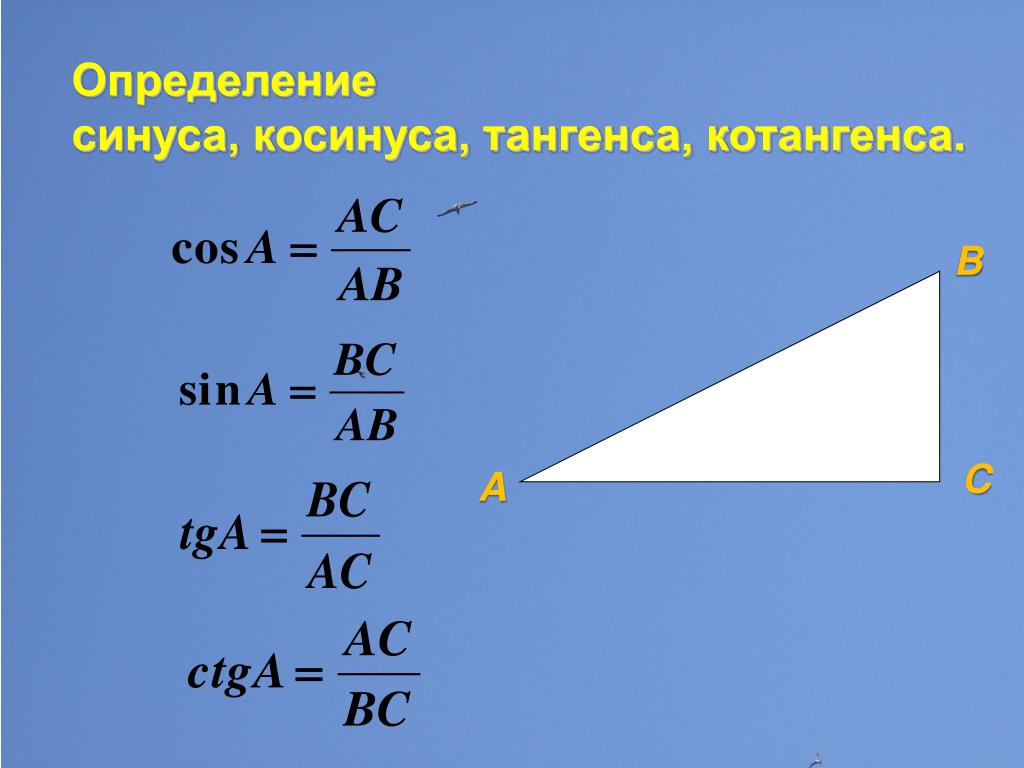
\ tan (\ theta) = \ frac {\ sin (\ theta)} {\ cos (\ theta)} = \ frac {1} {\ \ \ frac {\ cos (\ theta)} {\ sin (\ theta) )}\ \ } = \frac{1}{\cot(\theta)}.tan(θ)=cos(θ)sin(θ)= sin(θ)cos(θ) 1=cot(θ )1.
Действительно, мы можем видеть, что на графиках тангенса и котангенса функция тангенса имеет вертикальные асимптоты, где функция котангенса имеет значение 0, а функция котангенса имеет вертикальные асимптоты, где функция тангенса имеет значение 0.
Графики тангенса и котангенса удовлетворяют следующим свойствам:
- диапазон: (−∞,∞)(-\infty, \infty)(−∞,∞)
- период: π\piπ
- обе нечетные функции.
Из графиков функций тангенса и котангенса мы видим, что период тангенса и котангенса равен π\piπ. В тригонометрических тождествах мы увидим, как доказать периодичность этих функций с помощью тригонометрических тождеств.
Какие значения θ\thetaθ в интервале [0,π][0, \pi][0,π] удовлетворяют tan(θ)=cot(θ)?\tan(\theta) = \cot(\theta )?tan(θ)=cot(θ)? Можем ли мы увидеть это на графиках функций тангенса и котангенса? 92 = 1 (загар (θ)) 2 = 1.
Это выполняется для tanθ=±1\tan\theta = \pm 1tanθ=±1 или θ=π4,3π4\theta = \frac{\pi}{4}, \frac{3\pi}{4 }θ=4π, 43π.
Из графиков тангенса и котангенса также видно, что точками пересечения двух графиков в области [0,π][0,\pi][0,π] являются (π4,1) \big( \ frac{\pi}{4}, 1 \big)(4π,1) и (3π4,−1). □ \big( \frac{3\pi}{4}, -1 \big).\ _\square (43π,−1). □
Это выполняется для tanθ=±1\tan\theta = \pm 1tanθ=±1 или θ=π4,3π4\theta = \frac{\pi}{4}, \frac{3\pi}{4 }θ=4π, 43π.Цитировать как: Графики тангенса и котангенса. Brilliant.org . Извлекаются из https://brilliant.org/wiki/tangent-and-cotangent-graphs/
Тригонометрия — синус, косинус, тангенс
Для угла θ в прямоугольном треугольнике, как показано, стороны обычно называются как следует:
- гипотенуза (сторона, противоположная прямому углу)
- смежный (сторона «рядом» θ )
- напротив (самая дальняя от угла сторона)
We can define the three trigonometrical ratios sine θ , cosine θ , and tangent θ as follows (usually written as sin θ , cos θ , и тангенс θ ):
sin θ = противоположность / гипотенуза
cos θ = смежный / гипотенуза
tan θ = противоположный / смежный
Для облегчения запоминания многие люди используют SOH CAH TOA, то есть:
S в θ = O pposite/6 H YpoteNuse,
C OS θ = A DJACENT/ H YPOTENUSE и
T θ = 6666.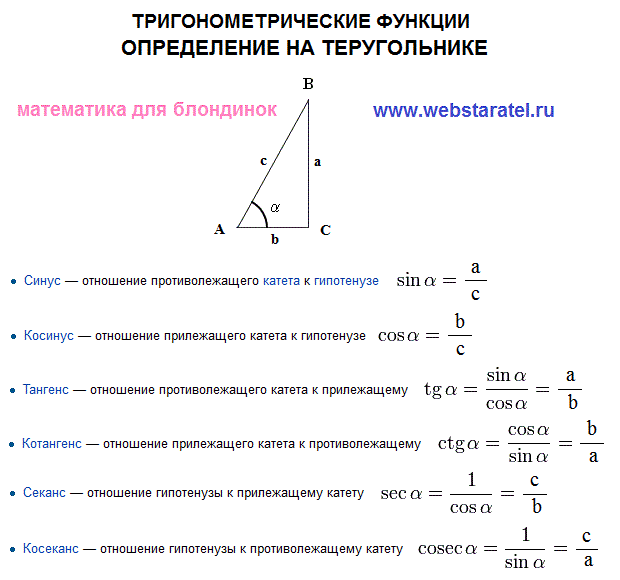
ФУНКЦИИ
Знак тригонометрической функции зависит от квадранта, в котором находится угол.
- Знак зависит от того, положительна или отрицательна противоположная или прилежащая сторона образующегося прямоугольного треугольника.
- Знак функции синуса и косеканса определяется знаком противоположной стороны.
- Знак функции косинуса и секущей определяется знаком прилежащей стороны.
- Знак функции Тангенс и Котангенс определяется знаками противолежащей и прилежащей сторон. Если они разные, то функция тангенса отрицательна. Если они одинаковы, то функция тангенса положительна.
- Гипотенуза всегда положительна.
Знаки в таблице ниже относятся к углам, которые находятся в пределах границы каждого квадранта. Они не относятся к знакам углов на границах. Они особенные, как указано ранее.
Ниже представлена таблица знаков:
| Функция | Квадрант 1 | Квадрант 2 | Квадрант 3 | Квадрант 4 |
| Синус и косеканс | + | + | — | — |
| Косинус и секанс | + | — | — | + |
| Тангенс и котангенс | + | — | + | — |
Компания Homesweet Learning Inc.